Изобретение относится к области геодезических измерений, измерений траектории движения точки, когда необходимо получить угловые направления на точку в местной (топоцентрической) горизонтной системе координат, где одна из плоскостей, например плоскость X0Z, ориентирована по горизонту.
Геодезические приборы, предназначенные для измерений угловых направлений, имеют в своей конструкции элементы, позволяющие установить прибор вертикально, в соответствии с линией отвеса. Точность установки в отвес соответствует классу точности прибора. В практике траекторных измерений, когда применяется оптическая или радиолокационная аппаратура, не всегда имеется возможность выставки прибора в отвес с необходимой точностью, и вертикальная и горизонтальная плоскости поворота прибора не совпадают с вертикальной и горизонтальной плоскостями местной системы координат, в которой предполагается проведение измерений. Результатом такого несовпадения является получение ошибочных углов визирования на точку цели, что приводит к дополнительным ошибкам (которые могут быть значительными) измерения координат цели.
Известен способ определения положения объекта засечкой с двух измерительных пунктов по азимуту, углу места и дальности (патент RU 2684733, опубл. 04.12.2019 г.), способ позиционирования объекта засечкой дальности и угла места с первого измерительного пункта и углу места - со второго (патент RU 2677586, опубл. 17.01.2019 г.), а также способ позиционирования объекта засечкой азимута с первого измерительного пункта и угла места с дальностью второго (патент RU 2667115, опубл. 26.09.2017 г.). Все три способа дают эффективные решения задачи по измерениям координат точки полигона и применяют углы визирования цели (азимут и угол места (угол возвышения)), полученные измерительными приборами первого и второго измерительных пунктов в качестве входных данных для вычислений.
Однако точность определения местоположения объекта в местной горизонтной системе координат полигона существенно зависит от точности горизонтирования координатных систем измерительных пунктов (измерительных приборов).
Вопрос горизонтирования в перечисленных способах не рассматривается, т.е. измерительные приборы считаются установленными в горизонтальной плоскости по определению. Таким образом, предлагаемое изобретение может применяться для повышения точности позиционирования объекта, положение которого в местной горизонтной системе координат определяется согласно способам, изложенным в патентах RU 2684733, RU 2677586, RU 2667115.
Известен способ математического горизонтирования геодезического прибора - тахометра (патент ЕР3410063, «Геодезический прибор с коррекцией наклона инструмента», опубл. 31.05.2018 г.), установленного с перекосом к горизонту. Этот способ реализует коррекцию углов визирования на цель посредством введения угловых поправок, которые вычисляются при помощи тригонометрических формул на основании данных от штатного датчика наклона тахометра и от штатного оптико-электронного дальномера.
Однако данный способ не может быть реализован для измерительного прибора, не оборудованного датчиком наклона и оптико-электронным дальномером.
Предлагаемое изобретение направлено на достижение технического результата, заключающегося в повышении точности угловых измерений в горизонтной системе координат измерительного прибора, предназначенного для измерений углов направления на цель, не только оптического, но и радиотехнического типа, с двумя угломерными шкалами, работающими в перпендикулярных плоскостях.
Одна из особенностей предлагаемого изобретения состоит в том, что горизонтирование измерительного прибора, обычно осуществляемое от линии отвеса, здесь заменено горизонтированием от геодезических координат двух опорных точек, что обеспечивает привязку угломерных измерений к плоскости местного горизонта и меридиану (Северу). Заметим, что горизонтирование от отвеса в горной местности или другой местности с гравитационными аномалиями приводит к значительным ошибкам горизонтирования из-за уклонения отвесной линии.
Применение изобретения дает возможность сведения множества измерительных угломерных приборов в единую горизонтную систему координат простым способом и с высокой точностью, что обеспечивает высокоточные измерения координат.
Точность горизонтирования измерительного прибора предлагаемым способом ограничивается дискретностью угломерных шкал самого прибора и может быть весьма высокой, находясь при этом в соответствии с точностными характеристиками самого измерительного прибора, что позволяет, в принципе, измерить уклонение отвесной линии в точке размещения прибора.
Для получения указанного технического результата в способе коррекции углов визирования на точку, предусматривающем измерение азимутального угла и угла возвышения на цель, в зоне измерений угломерного прибора дополнительно выбирают две опорные точки, хорошо наблюдаемые с точки размещения прибора и позволяющие произвести геодезические привязки и измеряют геодезические координаты первой опорной точки В1, L1, Н1 и второй опорной точки В2, L2, Н2, где Bi - широта, Li - долгота, Hi - высота с соответствующим индексом номера точки i. Затем измеряют углы визирования 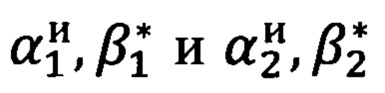 на первую и вторую опорные точки соответственно, при этом измеренные углы относятся к «перекошенной» системе координат угломерного прибора, где αиi - азимутальный угол отсчитываемый от нуля азимутальной шкалы прибора, β*i - угол возвышения отсчитываемый от нуля шкалы углов возвышения прибора, на точку с соответствующим индексом i. Далее определяют углы визирования
на первую и вторую опорные точки соответственно, при этом измеренные углы относятся к «перекошенной» системе координат угломерного прибора, где αиi - азимутальный угол отсчитываемый от нуля азимутальной шкалы прибора, β*i - угол возвышения отсчитываемый от нуля шкалы углов возвышения прибора, на точку с соответствующим индексом i. Далее определяют углы визирования 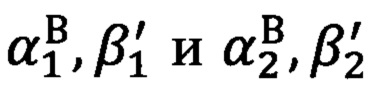 на опорные точки стандартным способом решения обратной геодезической задачи, в процессе которого по известным геодезическим координатам двух точек получают полярные углы визирования из первой точки на вторую, при этом углы визирования относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где
на опорные точки стандартным способом решения обратной геодезической задачи, в процессе которого по известным геодезическим координатам двух точек получают полярные углы визирования из первой точки на вторую, при этом углы визирования относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где 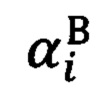 - азимутальный угол на цель и
- азимутальный угол на цель и 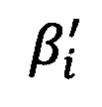 угол возвышения на цель, полученные по обратной геодезической задаче. Определение угла Эйлера β0, выражающего отклонение системы координат измерительного устройства от горизонтали местной горизонтной системы координат, осуществляется путем решения уравнения (1), полученного тригонометрически, методом последовательных приближений
угол возвышения на цель, полученные по обратной геодезической задаче. Определение угла Эйлера β0, выражающего отклонение системы координат измерительного устройства от горизонтали местной горизонтной системы координат, осуществляется путем решения уравнения (1), полученного тригонометрически, методом последовательных приближений
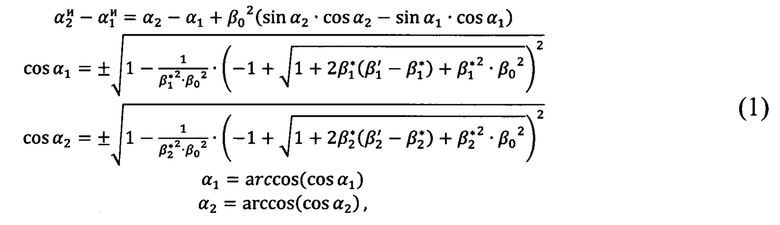
где α1, α2 - переменные величины.
Определение угла Эйлера α0, выражающего угол между направлением на Север и линией узлов, осуществляется по формулам (2а), (2б), (2в), полученным тригонометрически,
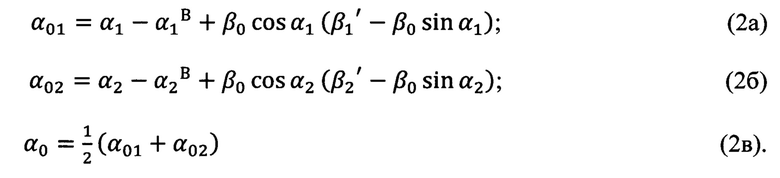
Определение угла Эйлера γ0, выражающего угол между линией узлов и нулевым азимутальным направлением поворотной платформы измерительного прибора, осуществляется по формулам (3а), (3б), (3в), полученным тригонометрически,
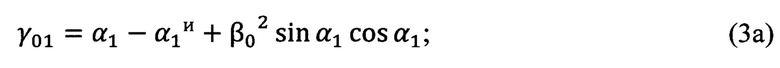
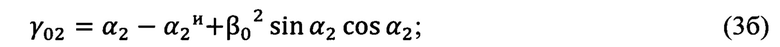

Далее формируется стандартная матрица угловых поправок Р(α0, β0, γ0) (4), выражающая три последовательных поворота на углы (-γ0, -β0, -α0) и преобразующая «перекошенную» систему координат измерительного прибора в топоцентрическую горизонтную систему координат, построенную на найденных углах Эйлера α0, β0, γ0, взятых с противоположными знаками:
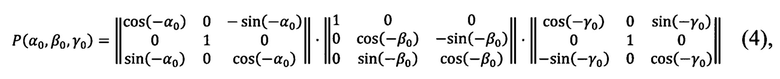
после чего сформированная матрица Р(α0, β0, γ0) применяется для пересчета углов визирования, полученных измерительным прибором в его «перекошенной» координатной системе, в верные азимутальный угол и угол возвышения на цель 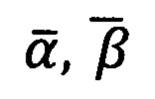 местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г)
местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г)
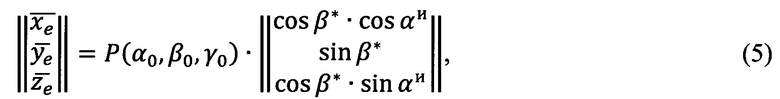



где 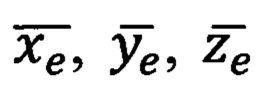 - проекции вектора единичной длины на оси
- проекции вектора единичной длины на оси 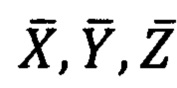 прямоугольной горизонтной системы координат соответственно, а верное значение угла
прямоугольной горизонтной системы координат соответственно, а верное значение угла 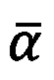 выбирается, исходя из знаков полученных углов
выбирается, исходя из знаков полученных углов 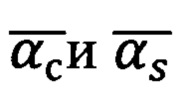 по условию:
по условию:
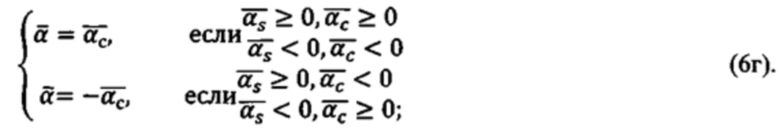
В результате коррекции получаются верные азимутальный угол и угол возвышения на цель 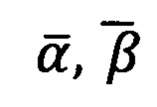 местной горизонтной системы для любой точки на основе измеренных угломерным прибором в «перекошенной» системе координат угла азимута αИ и угла возвышения β* точки цели.
местной горизонтной системы для любой точки на основе измеренных угломерным прибором в «перекошенной» системе координат угла азимута αИ и угла возвышения β* точки цели.
Предлагаемое изобретение иллюстрируется фигурами 1 и 2.
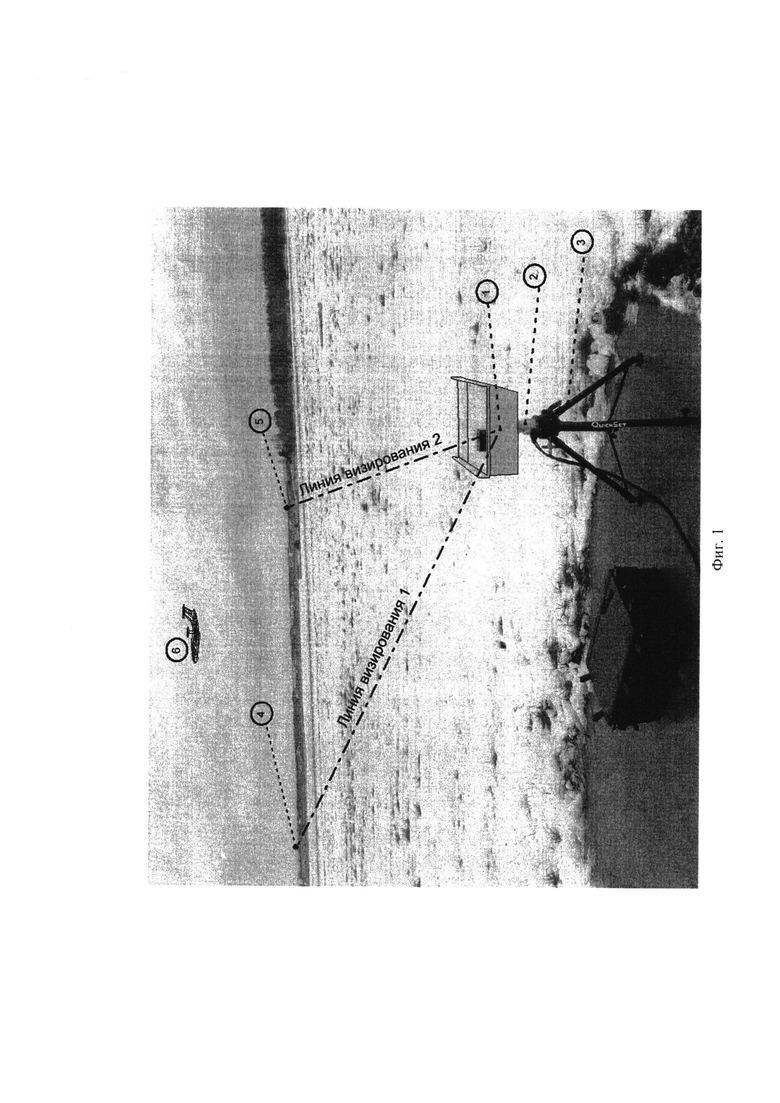
На фиг.1 изображено пояснение к способу коррекции углов визирования, где:
1 - точка размещения геодезического прибора;
2 - поворотная платформа двумя угломерными шкалами;
3 - штатив;
4 - опорная точка 1 с координатами Bl , L1 , H1 ;
5 - опорная точка 2 с координатами B2 , L2 , H2 ;
6 - цель.
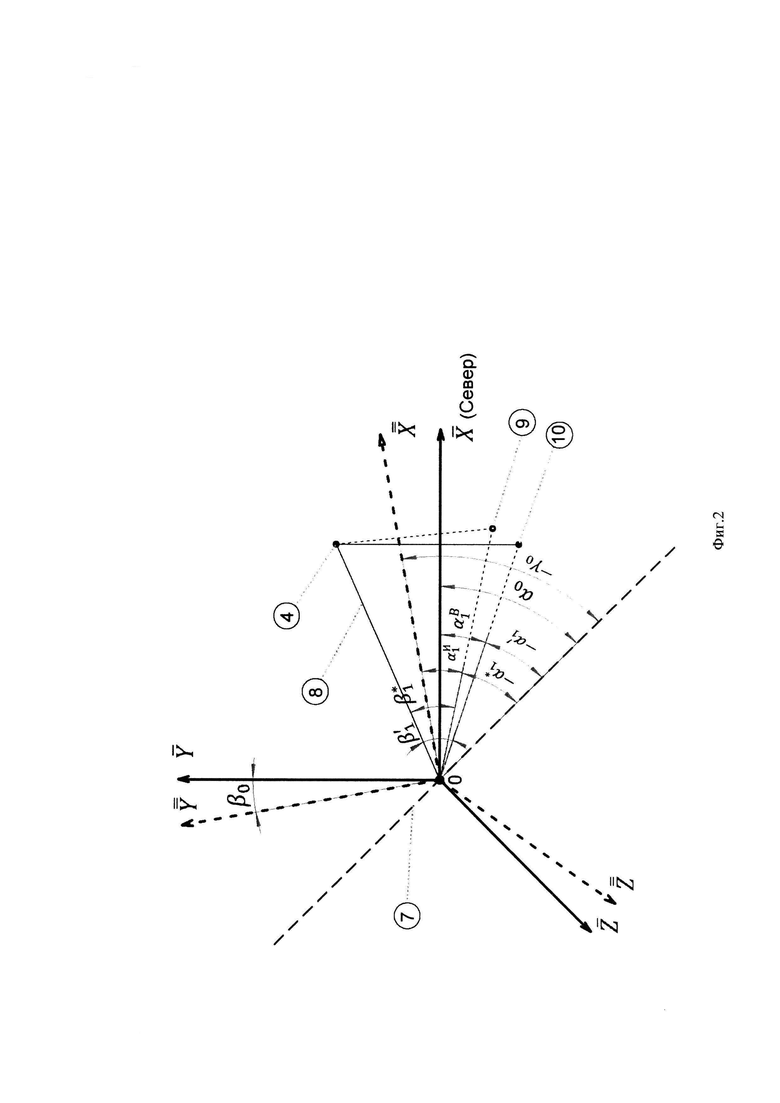
На фиг. 2 представлены углы Эйлера и углы визирования опорной точки 1 (РТ1) в топоцентрической горизонтной системе и системе координат измерительного прибора, где:
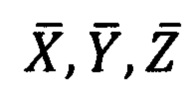 - топоцентрическая горизонтная система координат измерительного пункта (ИП);
- топоцентрическая горизонтная система координат измерительного пункта (ИП);
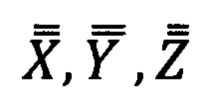 - система координат измерительного инструмента;
- система координат измерительного инструмента;
α0, β0, γ0 - углы Эйлера;
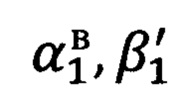 - вычисленные точные углы визирования;
- вычисленные точные углы визирования; 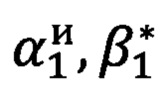 - измеренные углы визирования;
- измеренные углы визирования;
7 - прямая пересечения плоскостей (линия узлов) 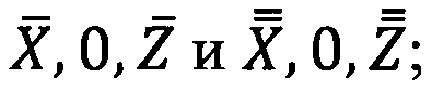 8 - линия визирования;
8 - линия визирования;
9 - точка проекции РТ1 на плоскость горизонта измерительного инструмента 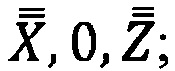
10 - точка проекции РТ1 на плоскость горизонта топоцентрической системы координат Земли 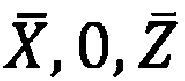 .
.
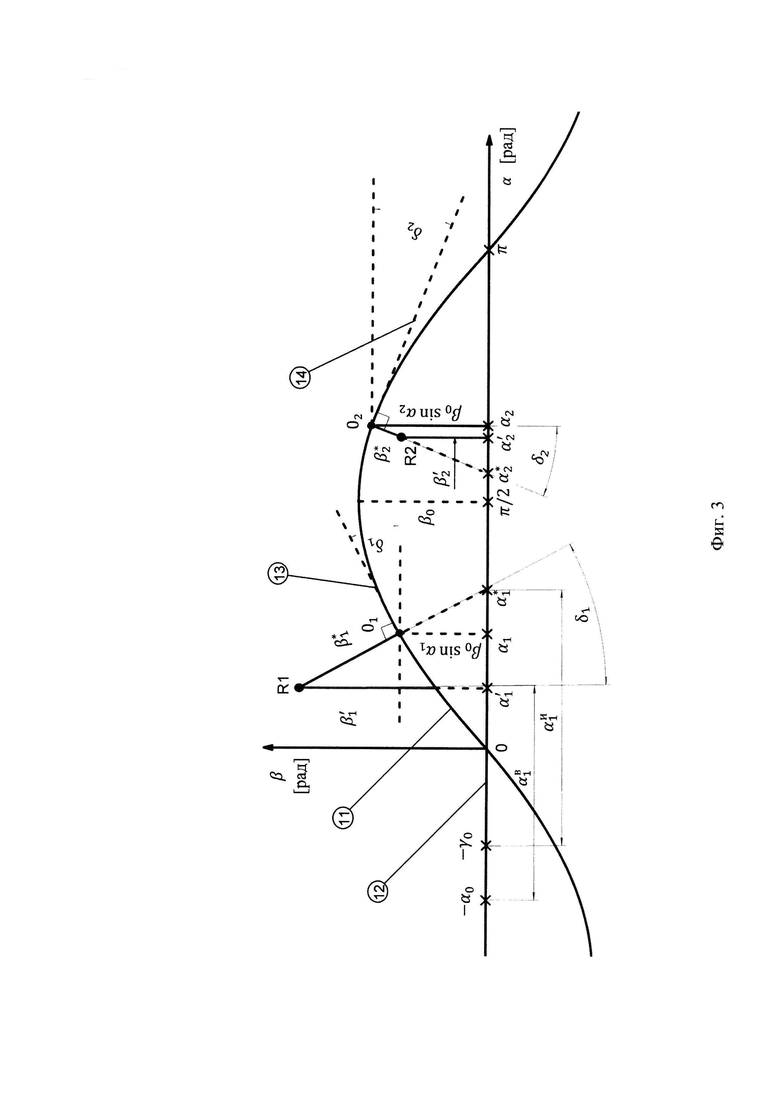
На фиг.3 представлена геометрия задачи наблюдения опорных точек R1 и R2, где:
R1 и R2 - наблюдаемые опорные точки;
11 - горизонт измерительного прибора;
12 - горизонт топоцентрической горизонтной СК;
13 - касательная в т.01;
14 - касательная в т.02;
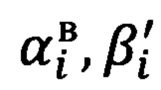 - вычисленные точные углы визирования;
- вычисленные точные углы визирования;
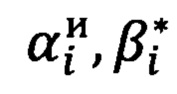 - измеренные углы визирования.
- измеренные углы визирования.
Предлагаемый способ осуществляется следующим образом.
Выполняется определение в зоне измерений прибора двух опорных точек, хорошо наблюдаемых с точки размещения прибора и позволяющих произвести геодезические привязки.Выполняется измерение геодезических координат первой опорной точки B1,L2,H1 и второй опорной точки В2, L2, Н2, где Bi - широта, Li - долгота, Нi - высота с соответствующим индексом.
Выполняется измерение углов визирования 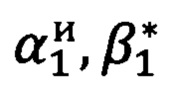 и
и 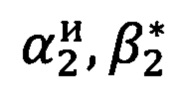 на первую и вторую опорные точки соответственно, которые (углы) относятся к «перекошенной» системе координат измерительного прибора, где αiи - азимутальный угол отсчитываемый от нуля азимутальной шкалы прибора, βi* -угол возвышения отсчитываемый от нуля шкалы углов возвышения прибора, на точку, с соответствующим индексом.
на первую и вторую опорные точки соответственно, которые (углы) относятся к «перекошенной» системе координат измерительного прибора, где αiи - азимутальный угол отсчитываемый от нуля азимутальной шкалы прибора, βi* -угол возвышения отсчитываемый от нуля шкалы углов возвышения прибора, на точку, с соответствующим индексом.
Выполняется определение углов визирования 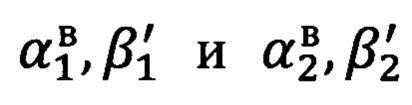 на опорные точки стандартным способом решения обратной геодезической задачи, которые (углы) относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными).
на опорные точки стандартным способом решения обратной геодезической задачи, которые (углы) относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными).
Обратная геодезическая задача решается в три этапа.
Первый этап состоит в переводе геодезических координат опорных точек Bi,Li,Hi в геоцентрическую прямоугольную систему координат. Формулы перевода приведены в книге: Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.7, формулы (3.24)).
 где
где
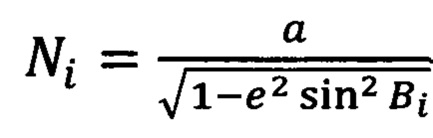 - радиус кривизны первого вертикала, Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.4, формулы (3.11), здесь: а - большая полуось эллипсоида,
- радиус кривизны первого вертикала, Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.4, формулы (3.11), здесь: а - большая полуось эллипсоида, 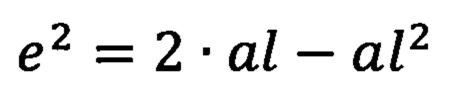 - квадрат первого эксцентриситета,
- квадрат первого эксцентриситета, 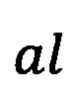 - сжатие эллипсоида (Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.2, формулы (3.1)).
- сжатие эллипсоида (Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.2, формулы (3.1)).
Второй этап заключается в пересчете прямоугольных геоцентрических координат опорных точек Xi, Yi, Zi в прямоугольные декартовы координаты местной (топоцентрической) горизонтной системы координат согласно формулам, приведенным в книге: Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2, формулы (3.1, 3.2, 3.3)).
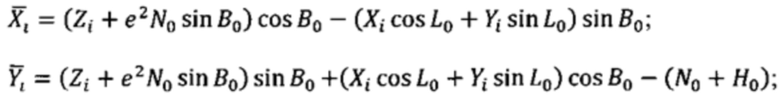
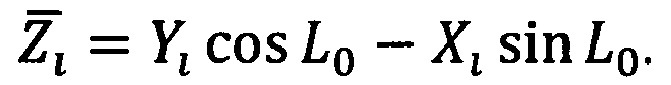
Формулы берутся с той лишь разницей, что в нашем случае ось 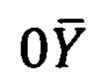 топоцентрической системы координат направлена по нормали вверх, ось
топоцентрической системы координат направлена по нормали вверх, ось 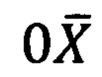 ориентирована на Север, а ось
ориентирована на Север, а ось 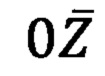 дополняет систему до правой.
дополняет систему до правой.
На третьем этапе из вычисленных в топоцентрической горизонтной системе координат 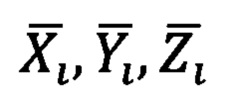 опорных точек находим полярные углы визирования на эти опорные точки по формулам из книги: Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.10, формулы (3.48)). Формулы берутся с учетом того, что в нашем случае ось
опорных точек находим полярные углы визирования на эти опорные точки по формулам из книги: Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.10, формулы (3.48)). Формулы берутся с учетом того, что в нашем случае ось 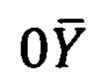 направлена по нормали вверх и система координатных осей образует правую тройку.
направлена по нормали вверх и система координатных осей образует правую тройку.
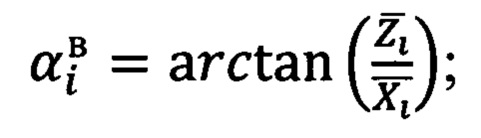
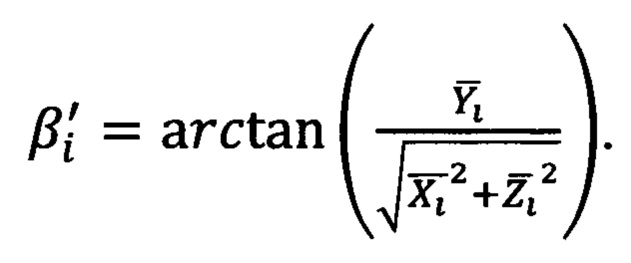
Далее следует сравнение вычисленной разности углов 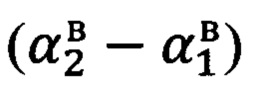 с разностью углов, измеренных прибором
с разностью углов, измеренных прибором 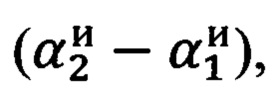 , что приводит к уравнению (1):
, что приводит к уравнению (1):
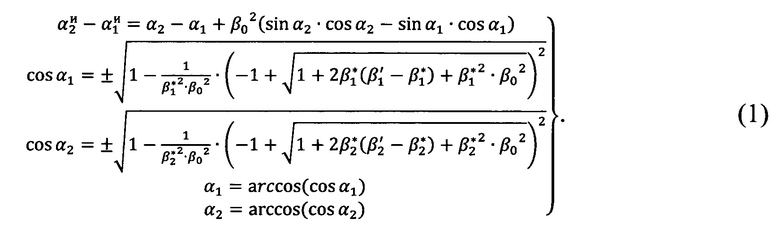
Вывод уравнения (1) основан на рассмотрении Фиг. 3 в предположении, что: «перекошенный» горизонт измерительного прибора задан единственной плоскостью; зависимость углов возвышения от азимутальных углов, задающая «перекошенный» горизонт прибора в плоских декартовых координатах, выражается функцией известного заранее вида β0 sin α (Фиг. 3); вертикальные углы визирования, а также угол β0 «перекоса» горизонта измерительного прибора малы и не превышают 4°-5°.
Из рассмотрения Фиг. 3 и тригонометрических определений следует, что для опорной точки с индексом i можно записать выражение разности вычисленного (по обратной геодезической задаче) угла βi' и измеренного прибором угла βi*:
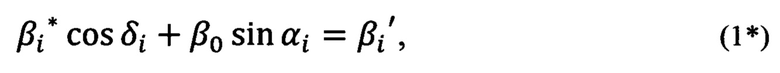
где «αi - азимутальный угол горизонтальной плоскости топоцентрической горизонтной системы координат, отсчитываемый от линии узлов, δi - угол наклона горизонта измерительного прибора в точке 0.
Выражая в формуле (1*) cos δi через tan δi учитывая, что тангенс угла δi в точке 0i есть производная функции β0 sin α в этой точке, принимая во внимание, что β02 cos2 αi << 1 формулу (1*) приводим к виду:

После решения (2*) относительно sin αi отбрасывания одного из решений, которое является физически не обоснованным, приходим к выражению для sin αi
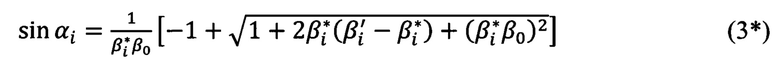
Из рассмотрения Фиг. 3 выводится формула связи углов αi и азимутальных углов αi*:
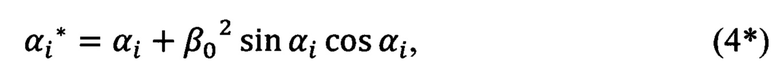
из которой следует формула разности углов для опорных точек с индексами 1 и 2 (см. Фиг. 3):
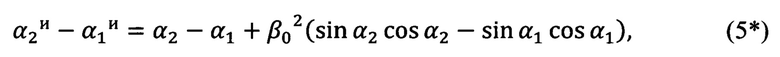
где: 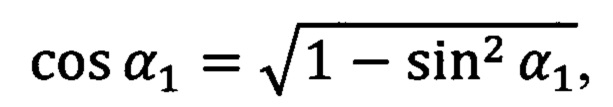
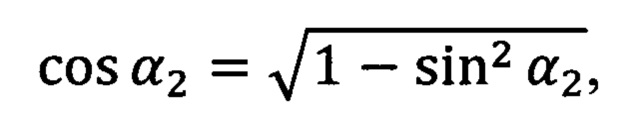
α1 = arcos (cos α1),
α2=arccos(cos α2).
Далее следует решение уравнения (1) методом последовательных приближений и получение в результате решения угла β0 (угла Эйлера, выражающего отклонение системы координат измерительного прибора от горизонтали местной горизонтной системы координат).
Вычисление угла α0 (угла Эйлера, выражающего угол между направлением на Север и линией узлов) выполняется по формулам (2а), (2б), (2в), полученным тригонометрически при рассмотрении фиг. 3:
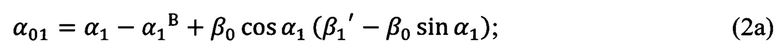
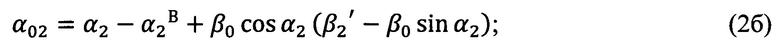

Вычисление угла γ0 (угла Эйлера, выражающего угол между линией узлов и нулевым азимутальным направлением поворотной платформы измерительного прибора) выполняется по формулам (3а), (3б), (3в), полученным тригонометрически при рассмотрении фиг. 3:
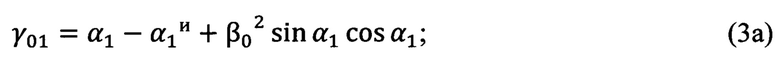
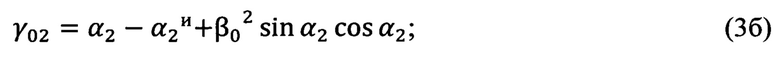

Выполняется формирование стандартной матрицы угловых поправок (4), построенной на найденных углах Эйлера α0, β0, γ0, взятых с противоположными знаками:
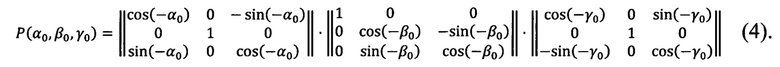
Матрица угловых поправок (4) для прямоугольных систем координат приведена в книге: Н.А. Телеганов, Г.Н. Тетерин. Методы и системы координат в геодезии (Часть 3.2.8, формулы 3.30, 3.31, 3.32, 3.33). Применение формул скорректировано с учетом того, что в нашем случае ось 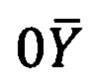 направлена по нормали вверх, ось
направлена по нормали вверх, ось 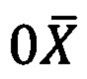 направлена на Север, ось
направлена на Север, ось 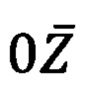 дополняет систему до правой.
дополняет систему до правой.
Матрица (4) применяется далее для пересчета (коррекции) углов визирования, полученных измерительным прибором в его «перекошенной» координатной системе, в углы  местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г):
местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г):
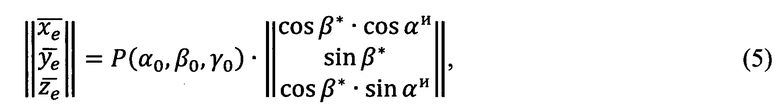
Где 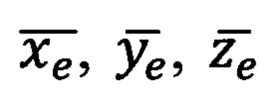 - проекции вектора единичной длины на оси
- проекции вектора единичной длины на оси 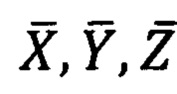 прямоугольной горизонтной системы координат соответственно,
прямоугольной горизонтной системы координат соответственно,



где верное значение угла 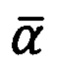 выбирается исходя из знаков полученных углов
выбирается исходя из знаков полученных углов 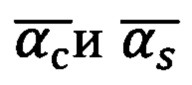 по условию:
по условию:
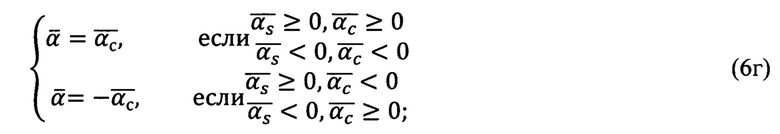
Таким образом «неправильные» угол азимута αи и угол возвышения β* точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат.
Фиг. 1 и 2 иллюстрируют последовательность реализации способа. В зоне измерений геодезического прибора определяются две опорные точки (фиг. 1, метки 4, 5), хорошо наблюдаемые с точки размещения прибора и позволяющие произвести геодезические привязки. Производятся геодезические привязки опорных точек и точки размещения прибора с получением геодезических координат точек В1, L1, Н1; В2, L2, Н2; В0, L0, Н0, где Bi - широта, Li - долгота, Hi - высота с соответствующим индексом. Проводятся измерения углов визирования 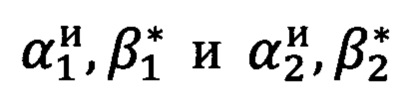 на первую и вторую опорные точки (на фиг. 2 изображена только одна опорная точка, с целью не загромождать рисунок). Решаются обратные геодезические задачи по вычислению углов визирования
на первую и вторую опорные точки (на фиг. 2 изображена только одна опорная точка, с целью не загромождать рисунок). Решаются обратные геодезические задачи по вычислению углов визирования 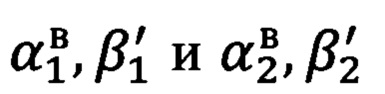 на первую и вторую опорные точки (Фиг. 2). Разности вычисленных
на первую и вторую опорные точки (Фиг. 2). Разности вычисленных 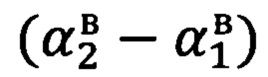 и измеренных
и измеренных 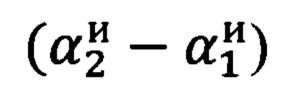 углов сравниваются при помощи уравнения (1), которое решается методом последовательных приближений. Решение уравнения (1) дает угол β0. Значение угла β0 подставляется в формулы (2а), (2б), (2в), и в результате вычислений определяется угол α0. Значение угла β0 подставляется в формулы (3а), (3б), (3в), и в результате вычислений определяется угол γ0. Найденные значения углов α0, β0, γ0, взятые с противоположным знаком, подставляются в матрицу угловых поправок (4). Полученная матрица угловых поправок (4) подставляется в формулу (5), дающую значения проекций единичного вектора оси горизонтной системы координат
углов сравниваются при помощи уравнения (1), которое решается методом последовательных приближений. Решение уравнения (1) дает угол β0. Значение угла β0 подставляется в формулы (2а), (2б), (2в), и в результате вычислений определяется угол α0. Значение угла β0 подставляется в формулы (3а), (3б), (3в), и в результате вычислений определяется угол γ0. Найденные значения углов α0, β0, γ0, взятые с противоположным знаком, подставляются в матрицу угловых поправок (4). Полученная матрица угловых поправок (4) подставляется в формулу (5), дающую значения проекций единичного вектора оси горизонтной системы координат 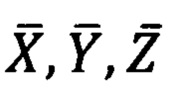 (Фиг. 2).
(Фиг. 2).
Найденные значения проекций единичного вектора подставляются в формулы (6а), (6б), (6в), (6г), которые дают скорректированные значения 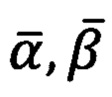 углов визирования на точку цели.
углов визирования на точку цели.
Таким образом, «неправильные» углы визирования точки цели, измеренные прибором в «перекошенной» системе координат прибора, преобразуются (корректируются) в «правильные» углы местной горизонтной системы координат.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ горизонтирования системы координат угломерного прибора по двум опорным точкам | 2024 |
|
RU2832842C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ОПРЕДЕЛЕНИЯ ГЕОДЕЗИЧЕСКИХ ДАННЫХ С ПОМОЩЬЮ УНИВЕРСАЛЬНОГО ТОПОПРИВЯЗЧИКА (УТП) | 2010 |
|
RU2440558C1 |
| Способ совместного определения координат, высот и дирекционных углов направлений | 2022 |
|
RU2798764C1 |
| СПОСОБ СПУТНИКОВОЙ КОРРЕКЦИИ ГИРОСКОПИЧЕСКИХ НАВИГАЦИОННЫХ СИСТЕМ МОРСКИХ ОБЪЕКТОВ | 2008 |
|
RU2428659C2 |
| Способ построения пространственной геодезической сети в виде цепочки треугольников и угломерный прибор для его осуществления | 1986 |
|
SU1613858A1 |
| СПОСОБ ПОСТРОЕНИЯ АСТРОИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2016 |
|
RU2641515C2 |
| СПОСОБ СОГЛАСОВАНИЯ ОСЕЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ С ОСЬЮ НАЗЕМНОГО ТРАНСПОРТНОГО СРЕДСТВА И ИЗМЕРИТЕЛЬНЫЙ КОМПЛЕКС ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2436043C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВЫХ КООРДИНАТ ИЗМЕРИТЕЛЬНОЙ ОСИ АКСЕЛЕРОМЕТРА | 2005 |
|
RU2316009C2 |
| СИСТЕМА ОРИЕНТИРОВАНИЯ МОБИЛЬНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ ПО ИЗВЕСТНОМУ ОРИЕНТИРНОМУ НАПРАВЛЕНИЮ | 2024 |
|
RU2838002C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ И ЦЕЛЕВОЙ ЗНАК ДЛЯ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ | 2000 |
|
RU2202101C2 |
Изобретение относится к области геодезических измерений, измерений траектории движения точки, когда необходимо получить угловые направления на точку в местной (топоцентрической) горизонтной системе координат, где одна из плоскостей ориентирована по горизонту. Способ коррекции углов визирования на точку предусматривает измерение азимутального угла и угла возвышения на цель и заключается в том, что в зоне измерений угломерного прибора дополнительно выбирают две опорные точки, хорошо наблюдаемые с точки размещения прибора и позволяющие произвести геодезические привязки, измеряют геодезические координаты первой и второй опорных точек. Затем измеряют углы визирования на первую и вторую опорные точки, при этом измеренные углы относятся к «перекошенной» системе координат угломерного прибора, определяют углы визирования на опорные точки стандартным способом решения обратной геодезической задачи, в процессе которого по известным геодезическим координатам двух точек получают полярные углы визирования из первой точки на вторую. При этом углы визирования относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными). Определяют углы Эйлера α0, β0, γ0, затем формируют стандартную матрицу угловых поправок, выражающую три последовательных поворота на углы (-γ0, -β0, -α0) и преобразующую «перекошенную» систему координат измерительного прибора в топоцентрическую горизонтную систему координат, построенную на найденных углах Эйлера α0, β0, γ0, взятых с противоположными знаками, пересчитывают углы визирования, полученные измерительным прибором в его «перекошенной» координатной системе. При этом в результате этой коррекции получаются верные азимутальный угол и угол возвышения на цель местной горизонтной системы для любой точки на основе измеренных угломерным прибором в «перекошенной» системе координат угла азимута и угла возвышения точки цели. Технический результат – повышение точности угловых измерений в горизонтной системе координат измерительного прибора, предназначенного для измерений углов направления на цель. 3 ил.
Способ коррекции углов визирования на точку, предусматривающий измерение азимутального угла и угла возвышения на цель, отличающийся тем, что
в зоне измерений угломерного прибора дополнительно выбирают две опорные точки, хорошо наблюдаемые с точки размещения прибора и позволяющие произвести геодезические привязки;
измеряют геодезические координаты первой опорной точки B1, L1, H1 и второй опорной точки B2, L2, H2, где Βi - широта, Li - долгота, Hi - высота с соответствующим индексом номера точки i;
измеряют углы визирования 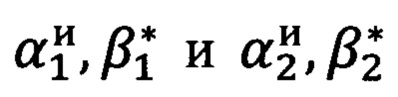 на первую и вторую опорные точки соответственно, при этом измеренные углы относятся к «перекошенной» системе координат угломерного прибора, где αиi - азимутальный угол, отсчитываемый от нуля азимутальной шкалы прибора, β*i - угол возвышения, отсчитываемый от нуля шкалы углов возвышения прибора, на точку с соответствующим индексом i;
на первую и вторую опорные точки соответственно, при этом измеренные углы относятся к «перекошенной» системе координат угломерного прибора, где αиi - азимутальный угол, отсчитываемый от нуля азимутальной шкалы прибора, β*i - угол возвышения, отсчитываемый от нуля шкалы углов возвышения прибора, на точку с соответствующим индексом i;
определяют углы визирования 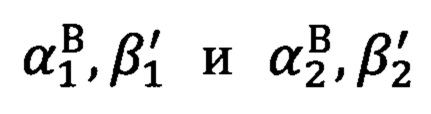 на опорные точки стандартным способом решения обратной геодезической задачи, в процессе которого по известным геодезическим координатам двух точек получают полярные углы визирования из первой точки на вторую, при этом углы визирования относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где
на опорные точки стандартным способом решения обратной геодезической задачи, в процессе которого по известным геодезическим координатам двух точек получают полярные углы визирования из первой точки на вторую, при этом углы визирования относятся уже к местной (топоцентрической) горизонтной системе координат и являются точными (эталонными), где 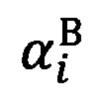 - азимутальный угол на цель и
- азимутальный угол на цель и 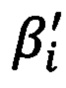 - угол возвышения на цель, полученные по обратной геодезической задаче;
- угол возвышения на цель, полученные по обратной геодезической задаче;
определяют угол Эйлера β0, выражающий отклонение системы координат измерительного устройства от горизонтали местной горизонтной системы координат, путем решения уравнения (1), полученного тригонометрически, методом последовательных приближений
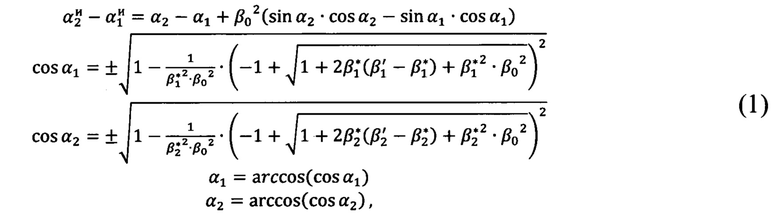
где α1, α2 - переменные величины;
определяют угол Эйлера α0, выражающий угол между направлением на Север и линией узлов, по формулам (2а), (2б), (2в), полученным тригонометрически,
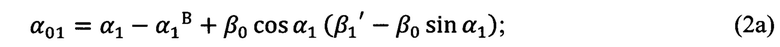
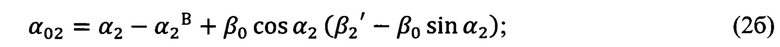

определяют угол Эйлера γ0, выражающий угол между линией узлов и нулевым азимутальным направлением поворотной платформы измерительного прибора, по формулам (3а), (3б), (3в), полученным тригонометрически,
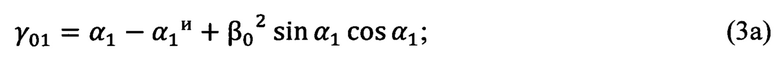
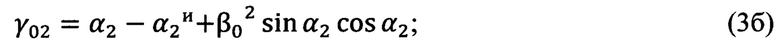

формируют стандартную матрицу угловых поправок Р(α0, β0, γ0) (4), выражающую три последовательных поворота на углы (-γ0, -β0, -α0) и преобразующую «перекошенную» систему координат измерительного прибора в топоцентрическую горизонтную систему координат, построенную на найденных углах Эйлера α0, β0, γ0, взятых с противоположными знаками:
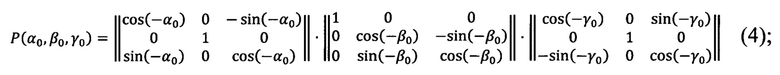
применяют сформированную матрицу Р(α0, β0, γ0) для пересчета углов визирования, полученных измерительным прибором в его «перекошенной» координатной системе, в верные азимутальный угол и угол возвышения на цель 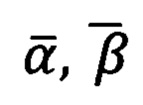 местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г)
местной (топоцентрической) горизонтной системы для любой точки, находящейся в зоне измерений, при помощи формул (5), (6а), (6б), (6в), (6г)
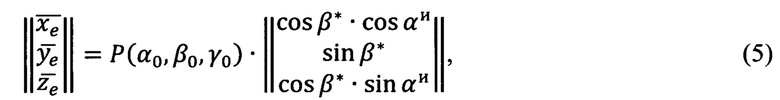



где 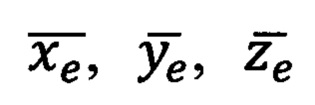 - проекции вектора единичной длины на оси
- проекции вектора единичной длины на оси 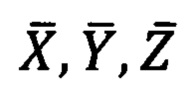 прямоугольной горизонтной системы координат соответственно,
прямоугольной горизонтной системы координат соответственно,
а верное значение угла 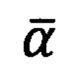 выбирается, исходя из знаков полученных углов
выбирается, исходя из знаков полученных углов 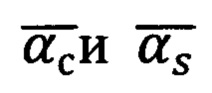 по условию:
по условию:
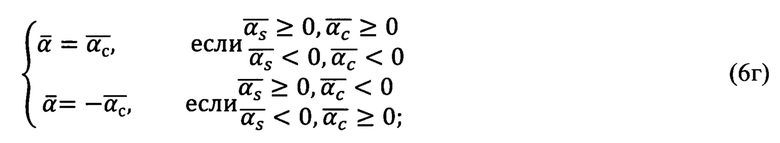
при этом в результате коррекции получаются верные азимутальный угол и угол возвышения на цель 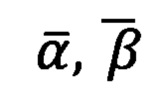 местной горизонтной системы для любой точки на основе измеренных угломерным прибором в «перекошенной» системе координат угла азимута αи и угла возвышения β* точки цели.
местной горизонтной системы для любой точки на основе измеренных угломерным прибором в «перекошенной» системе координат угла азимута αи и угла возвышения β* точки цели.
| СПОСОБ ПОЗИЦИОНИРОВАНИЯ ОБЪЕКТА ЗАСЕЧКОЙ АЗИМУТА С ПЕРВОГО ИЗМЕРИТЕЛЬНОГО ПУНКТА И УГЛА МЕСТА С ДАЛЬНОСТЬЮ - СО ВТОРОГО | 2017 |
|
RU2667115C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ ГЕОДЕЗИЧЕСКИХ ПРИБОРОВ ЗА НЕПРАВИЛЬНОСТЬ ФОРМЫ ЦАПФ И БОКОВОЕ ГНУТИЕ ЗРИТЕЛЬНОЙ ТРУБЫ | 2015 |
|
RU2594950C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ОБЪЕКТА ЗАСЕЧКОЙ С ДВУХ ИЗМЕРИТЕЛЬНЫХ ПУНКТОВ ПО АЗИМУТУ, УГЛУ МЕСТА И ДАЛЬНОСТИ | 2017 |
|
RU2684733C2 |
| СПОСОБ ПОЗИЦИОНИРОВАНИЯ ОБЪЕКТА ЗАСЕЧКОЙ ДАЛЬНОСТИ И УГЛА МЕСТА С ПЕРВОГО ИЗМЕРИТЕЛЬНОГО ПУНКТА И УГЛА МЕСТА - СО ВТОРОГО | 2017 |
|
RU2677586C1 |
| US 6727849 B1, 27.04.2004. | |||
Авторы
Даты
2021-11-02—Публикация
2020-10-09—Подача