I I
Изобретение относится к вычислительной технике и может быть использовано для быстрого умножения десятичных чисел, а также приразработке универсальных быстродействующих устройств умножения двоичных и , десятичных чисел.
Целью изобретения является сокращение количества оборудования.
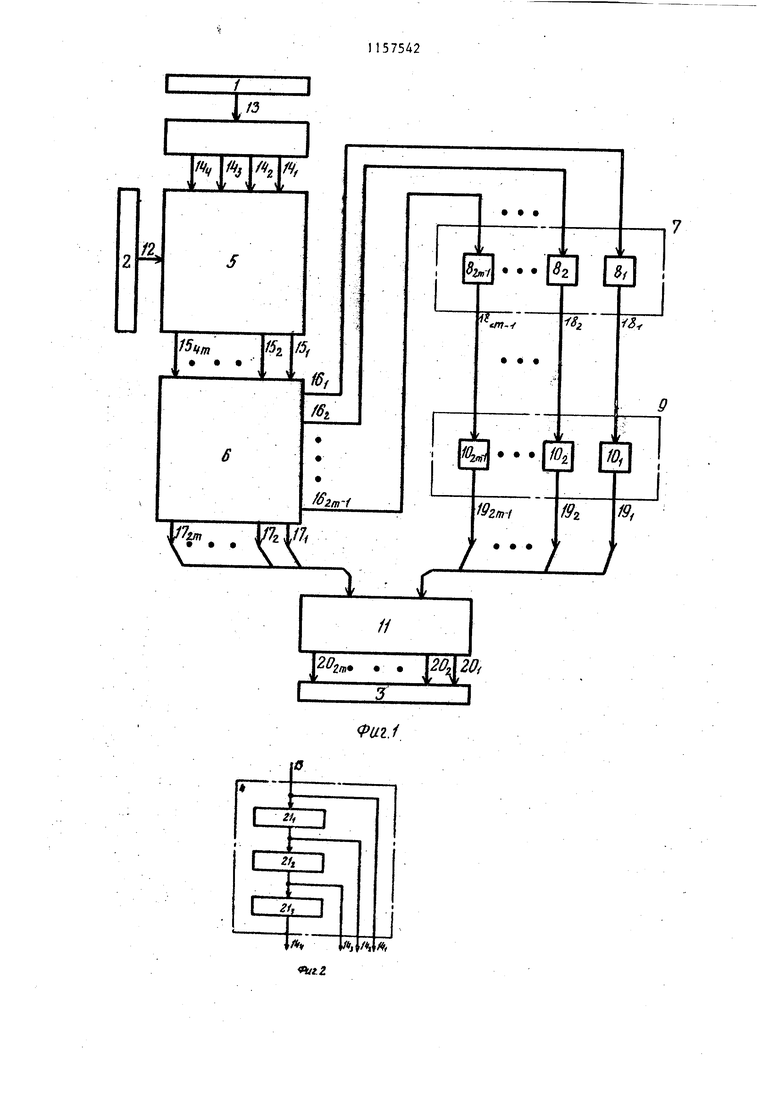
На фиг. 1 изображена структурная схема устройства} на фиг. 2 - функциональная схема блока формирования кратных множимого; на фиг. 3 - функциональная схема блока формирования частичных произведений при m 2; на фиг. 4 - функциональная схема блока суммирования тетрадных переносов при на фиг. 5 - функциональная схема блока коррекции .при на фиг. 6 - функциональная схема блока десятичного суммирова- . ния при m 2,
Устройство содержит регистры 13соответственно множимого, множителя и произведения, блок 4 формирования кратных множимого, блок 5 формирования частичных произведений блок 6 двоичного суммирования, блок 7 суммирования тетрадных переносов, содержащий узлы 8., -8. суммирования тетрадных переносов, блок
9 коррекции, содержащий узлы .i умножения на шесть в десятичном коде, блок II десятичного суммирования . Выходы 12 разрядов регистра 2 множителя подключены к входам первой группы блока 5 формирования частичных произведений, выходы 13 разрядов регистра I подключены к входам блока 4, входы групп с второй по пятую блока 5 соединены соответственно с выходами 14:;-lA;j групп с первой по четвертую блока
4формирования кратньпс множимого, выходы блока 5 формирования частичных произведений подключены к входам блока двоичного суммирования
-выходы . тетрадных переносов которого подключены в соответствии со значениями весов разрядов к входам соответствующих узлов 8 82„ 1 суммирования блока 7 суммирования тетрадных переносов, выходы 17, , тетрадных сумм блока 6 соединены с группой входов блока 11, выходы 18 -18 | узлов , блока 7 суммирования тетрадных переносов подключены к входам соответствующих узлов 10 J02m-i умножения на шесть
75422
в десятичном коде блока 9 коррекции, выходы узлов Ют-Ю. умножения на шесть в де-сятичном коде блока 9 коррекции подключены , к группе входов блока. 11 десятичного суммирования, выходы блока 11 десятичного суммирования соединены с входами регистра Зрезультата.
Блок 4 предназначен для формирования двухкратного, четырехкратного и восьмикратного множимых. Получение этих кратных в двоичной системе счисления не вызывает никакого труда и:все они могут быть образованы простым сдвигом информации соответственно на один, два и три двоичных разряда, в сторону старших разрядов. Что же касается десятичной системы счисления, то при формировании указанных кратных по методу сдвига здесь возникают определенные- трудности, такие как организация десятичных переносов в более .старшие разряды и коррекция результата. На фиг. 2 показан один из возможных вариантов реализации, блока 4 формирования кратных множимого, в основу которого взята операция удвоения. В двоичной систем счисления удвоение может быть вьтолнено с помощью сдвига каждой двоичной цифры в соседний старший разряд. В десятичной системе счисления при использовании кода 8421 может быть применена такая же процедура сдвига, за исключением того, что, если удвоенная цифра равна .или больше десяти, то, как и при сложении двух десятичных цифр, необходимо сформировать десятичный перенос и вьшолнить коррекцию путем добавления 6. Удвоение десятичного числа можно осущест|Вить и несколько другими способами. Блок 4 формирования кратных множимого содержит (фиг. 2) узлы 21 удвоения. На выходе 14 узла 2 удвоения формируется двухкратное множимое, на выходе 14 узла 212 удвоения - четырехкратное множимое и на выходе узла 21з удвоений восьмикратное множимое. Таким образом, в блоке 4 кратные формируются посредством многократного выполнения в узлах 21 .,-21- операций удвоения над исходной информацией. Так, например, восьмикратное множимое формируется в результате последов ател.ьного выполнения трех операций удвое3
ния на первом 2Ц , втором 21 и третьем 21 узлах удвоения.
Блок 5 предназначен для формирования частичных произведений и содержит групп двухвходовых элементов И. На выходах элементов И одной группы образуется одно частичное произведение, а всего в блоке 5 образуется 4 частичных произведений. На фиг. 3 изображена функциональная схема блока 5 при . Первые входы элементов И 22 каждой группы блока 5 подключены к Соответствующему входу его первой группы входов (с выходов 12 регистра 2 поступает в блок 5 через его пер&ую группу входов значение младшей тетрады множителя, а с выходов 122 регистра 2 подается через эту же группу входов значение старшей тетрады ), вторые входы элементов И 22 первой и пятой групп блока 5 подключены к соответствующему входу его второй группы входов, на которую подается значение однократного множимого с выходов 14 блока 4, вторы входы элементов И 22 второй и шестой групп блока 5 подключены к. соответствукщему входу его третьей группы входов, на которую поступает значение двухкратного множимого с выходов 142 блока 4, вторые входы элементов И 22 третьей и седьмой групп блока 5 подключены к соответствующему входу его четвертой группы входов, на которую подается значение четырехкратного множимого с выходов 14, блока 4, вторые входы элементов И 22 четвертой и восьмой групп блока 5 подключены к соответствующему входу его пятой группы входов, на которую поступает значение восьмикратного множимого, с выходов 14 блока 4. На выходах групп элементов И 22 с первой по восьмую соответственно образуется восемь частичных произведений, которые далее поступают на входы блока 6 двоичного суммирования в соответствии со значениями весов их разрядов.
Блок 6 двоичного суммирования предназначен для параллельного,по возможности, суммирования частичных произведений, сформированных в блоке 5 и поступающих на входы блока 6 в соответствии со значениями весов их разрядов. На выходах 17 172ч, блока 6 формируется 2 тетрад
75424
двоичной суммы в однорядном коде, а на выходы 16 |-1б2т,1 из блока 6 поступают тетрадные переносы. Напри мер, на выход 16i подаются только все те переносы, которые образуются в первой наименее 5 лачимой тетраде блока 6 при суммировании в нем частичных произведений и которые должны поступить и поступают в его соседнюю Q более стартую тетраду для правильного формирования двоичной суммы на выхо- дах 17, - Переносы же, которые возникают в первой тетраде блока 6 и в ней же используются на его выход 16 , не должны подаваться. Тетрадные переносы, значения которых поступают на выходы ., блока 6, могут быть как одноразрядными двоичными числами, так и многоразрядными. I Последнее имеет место при использовании в блоке 6 двоичного суммирования многовходовых параллельных счетчиков.
Блок 7 суммирования тетрадных
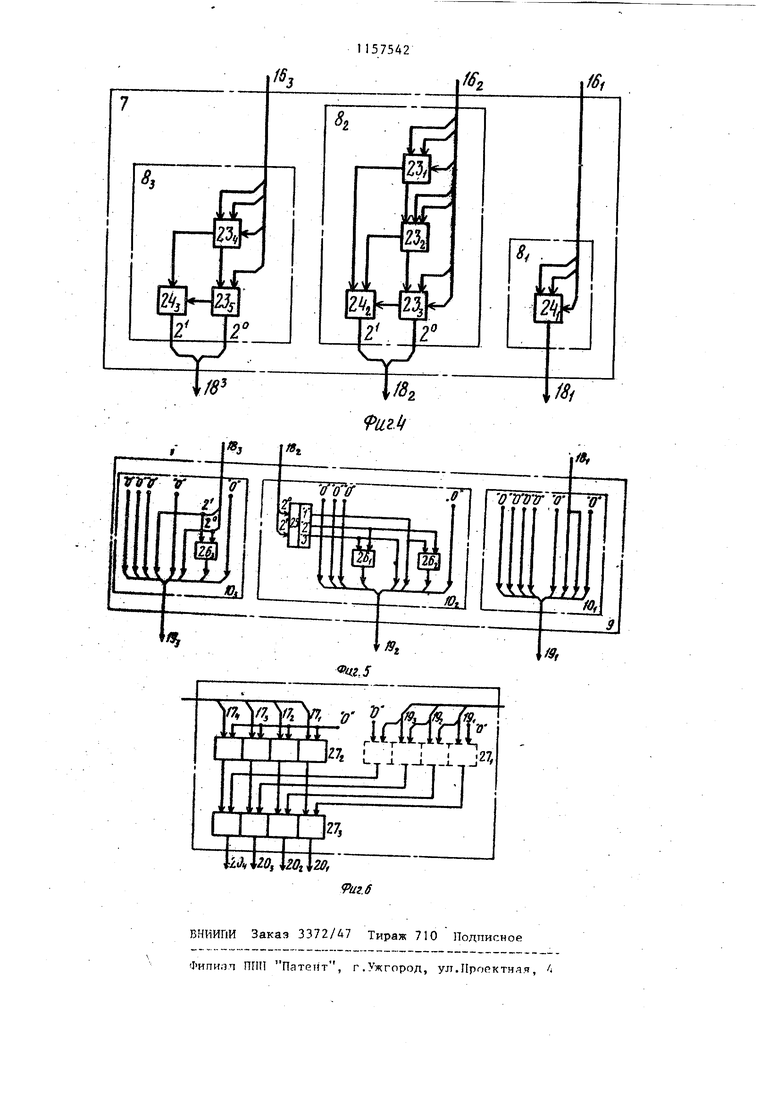
5 переносов (фиг. 1) содержит узлы ) суммирования, каждый из которых осуществляет двоичное суммирование переносов, возникающих только в одной тетраде блока 6. Например, узел 8 производит суммирование только тех (переносов, которые образуются в (гй тетраде блока 6 суммирования и обязательно передаются в его (т+1)-ую или еще в более старшие тетрады. В принципе узлы В -В ыогут осуществлять, если это целесообразно, и десятичное суммирование с формированием на своих выходах I81-182-1 результатов в десятичном коде. Однако в дальнейшем предлагается, что
узлы 8,-8jr.i осуществляют двоичное суммирование и формируют на своих выходах результаты в двоичном коде. На фигТ 4 в качестве примера приведена функциональная схема блока 7 при
и в предположении, что суммирование в блоке 6 осуществляется с помощью одноразрядных двоичных сумматоров с сохранением переносов, образующих древовидную структуру. Анализ
0 этой структуры и возможных значений сомножителей показывает, что на входы первого узла 8 с выходов 16 блока 6 двоичного суммирования не может одновременно поступить больше одного тетрадного переноса, на входы второго узла 8 с выходов (2 блока 6 - не больше трех, на входы третьего узла 8, с выходов 16}
5П
блока 6 - не больше двух тетрадных переносов. Узлы на фиг. 4 построены с использованием одноразря
ных двоичных сумматоров 23i-- 23 и логических элементов ИЛИ 24j, Учитывая невозможность одновременного присутствия некоторых тетрадных переносов на входах узлов 82 и 83 последние могут быть в определенных случаях упрощены. Следует отметить, что все узлы 8 З. блока 7 суммирования тетрадных переносов могут быть построены на основе быстродействующих ПЗУ по соответствунщим таблицам истинности.
Блок 9 предназначен для формирования по значениям сумм тетрадных переносов, полученных на выходах блока 7 коррекции результата, образовавшегося на выходах блока 6 двоичного суммирования. Он содержит (-фиг. 1) узлы . умножения на шесть, формирующие на своих вькодах . произведения в десятичном коде. . Такой принцип формирования коррекции объясняется тем, что при двоичном суммировании в блоке 6 десятичных частичных произведений для получения правильного результата необходимо всякий раз, когда возникает перенос из тетрады,корректировать эту тетраду путем добавления к ней числа 6. С целью же увеличения быстродействия и сокращения количества оборудования это добавление числа 6 в блоке 6 двоичного суммирования не производится. Вместо этого в блоке 7 суммирования тетрадных переносов для каждой весовой позиции блока 6 подсчитывается число тетрадных переносов, по значению которого в блоке 9 формируется правильная коррекция. Если на выходах , блока 7 образуются результаты в двоичном коде, то в узлах .i блока 9 осуществляется двоичное умножение с последующим преобразованием получившихся произведений в десятичный код, если же на выходах ,блока 7 формируются результаты в десятичном коде, то узлы .i блока 9 производят десятичное умножение с получением произведений сразу в десятичном коде. Узлы lOi-lOjn,,-, умножения на шесть могут быть реализованы, в частности, с помощью быстродействующих ПЗУ по соответств
75Д26
ющим таблицам истинности. В этом случае отпадает необходимость преобразования двоичных кодов произведений в десятичные коды, так как
5 все произведения могут быть предварительно записаны в ПЗУ в десятичном коде. В рассматриваемом случае надобность в узле 10 умножения блока 9 фактически отпадает, так
О как на выходах 18., узла 8 не может
образоваться число большее единицы. Узел же 10 умножения должен формировать на своем выходе 192 следующие десятичные результаты: 00 - если
5 на выходах 182 блока 7 присутствует ноль, 06 - если на выходах 18 блока 7 сформирована единица, 12 если на выходах 182 блока 7 присутствует число 2 и 18 - если на
20 выходах 18 блока 7 присутствует число З. Подобньи образом, работает и узел lOj умножения на шесть блока 9 коррекции. На фиг. 5 изображена функциональная схема блока 9 при
tP 2. Второй узел 1 Oj блока 9 содержит двухвходовой дешифратор 25 и элементы ИЛИ 26 и 26j, третий узел lOj блока 9 содержит элемент ИЛИ 26. Б блоке 11 десятичного суммироваQ ния фиксируется окончательный результат умножения в устройстве m -разрядных десятичных чисел. Он сожержит (фиг. 6 ) десятичные сумматоры 27 27} (на фиг. 6 разрядность сумматоров 27-,-27, и подключение их входоввыходов показаны длят 2). В первом сумматоре 27., выполняется быстрое суммирование десятичных результатов, сформированных на выходах 9 -192 блока 9 коррекции. Структура этого сумматора зависит от разрядности умножаемых в устройстве чисел. Так, при первый десятичный сумматор 27 может быть исключен (на фиг. 6 он показан штриховой линией ), так как результаты, сформированные на выходах блока, могут быть просто объединены без подсуммирования. При значениях 3 in:9 этот сумматор двуХвходовой, а при он
50 должен осуществлять суммирование трех десятичных чисел. Надобность в суммировании более трех десятичных чисел в сумматоре во всех практических случаях отсутствует. На
десятичном сумматоре 27 преобразуется сумма, полученная на выходах , блока 6 ДВОИЧНО о суммирования, путем ее потетрадног сложе-, 7 ния с нулями. После этого во всех тетрадах этой суммы будут цифры, не превьшающие значения девяти, так как из тетрад, значения которых .были больше девяти, в сумматоре 272 образуются десятичные переносы и осу ществляется коррекция этих тетрад. Ввиду того,что вдесятичном сумматоре 27 все время вьшолняется суммирование- числа с нулем, то он может быть существенно упрощен. Десятичный сумматор 27j выполняет суммирование результатов десятичных сумматоров 27 и 27j . На выходах десятичного сумматора 27з образуется окончательное произведение. Блок 11 десятичного суммирования может быть вьтолнен и несколько другим способом например на основании десятичных сумматоров с запоминанием переносов и одного сумматора с распространением переносов. Устройство работает следуняцим образом. Одновременно либо последовательно во времени в регистры I и 2 соответственно множимого и множителя загружаются m-разрядные десятичные сомно жители. После загрузки множимого в регистр 1 в блоке 4 формируются кратные множимого, которые с его выходов поступают на соответ ствующие группы входов блока 5, в котором образуется 4 частичных произведений в десятичном коде. С выходов 15;,-15 блока 5 частичные произведения поступают с учетом весов их разрядов на соответствующие входы блока 6, в котором осуществляется быстрое суммирование десятичных частичных произведений как двоичных чисел, и, по возможности, параллельно в блоке 7 формируются суммы тетрадных переносов, по которым в дальнейшем в блоке 9 образуется коррекция. В блоке 11 десятичного суммиро-. вания формируется результат сложения суммы, полученной на выходах блока 6 двоичного суммирова я, с коррекцией блока 9, который далее записывается с выходов . блока 11 в регистр 3 произведения. Предлагаемое устройство для умножения может быть эффективно использовано при разработке универсального устройства умножения двоичных и десятичных чисел. Для этого в блоке 4 кратных необходимо формировать наряду с десятичными и двоич1п 1е кратные множимого, которые могут быть получены простым сдвигом информации соответственно на один, два и три двоичных разряда влево, а также предусмотреть возможность записи результатов в регистр 3 произведения как с выходов 20 -202гр блока 11 десятичного суммирования, так и с выходов 17 -П блока 6 двоичного суммирования. Объем дополнительного оборудования, необходимого для построения на базе данного устройства универсального устройства для умножения двоичных и десятичных чисел, совсем незначителен, а умножение двоичных чисел в нем может быть ос тцествлено так же быстро, как это позволяют известные в настоящее время самые совершенные методы и средства, так как предлагаемый метод умножения десятичных чисел не требует изменения схемной структуры блока 6 двоичного суммирования.
И



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения | 1985 |
|
SU1262481A1 |
| Устройство для умножения | 1982 |
|
SU1229757A1 |
| Множительное устройство | 1982 |
|
SU1116427A1 |
| Устройство для умножения | 1982 |
|
SU1229758A1 |
| Устройство для умножения | 1987 |
|
SU1509875A1 |
| Устройство для умножения | 1988 |
|
SU1670685A1 |
| Устройство для умножения | 1988 |
|
SU1578711A1 |
| Матричное устройство для умножения двоичных и десятичных чисел | 1983 |
|
SU1200282A1 |
| Устройство для умножения | 1985 |
|
SU1262484A1 |
| Множительное устройство | 1982 |
|
SU1053104A1 |

УСТРОЙСТВО ДЛЯ УЙНОЖЕНИЯ, содержащее регистры множимого, множителя и произведения, блок формирования частичных произведений, блок двоичного суммирования, блок десятичного суммирования и блок коррекции, причем выходы разрядов регистра множителя подключены к входам первой группы блока формирования частичных произведений, выходы которого подключены к входам блока двоичного суммирования, выходы блока коррекции подключены к первой группе входов блока десятичного суммирования, выходы которого соединены с входами регистра произведения, отличающееся тем, что, с целью сокращения количества оборудования, устройство содержит блок формирования кратных множимого и блок суммирования тетрадных переносов, блок формирования частичных произведений содержит группы элементов И, блок суммирования тетрадных переносов содержит узлы суммирования тетрадных переносов, коррекции содержит узлы умножения на шесть в десятичном коде, блок: десятичного суммирования содержит три десятичных сумматора, причем Выходы регистра множимого подключены .к входам блока формирования кратных множимого, первые входы элементов И каждой группы блока формирования частичных произведений подключены к соответствующему входу первой группы этого блока, вторые входы элементов И блока формирования частичных произведений
I yj I 4 I
i . I
ИМ
«//2
I Г
гУ
.1.
. -
Ъ
ьг
f8
--. -I
ISi
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Устройство для умножения | 1977 |
|
SU729587A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Устройство для умножения | 1981 |
|
SU1035600A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1985-05-23—Публикация
1982-09-13—Подача