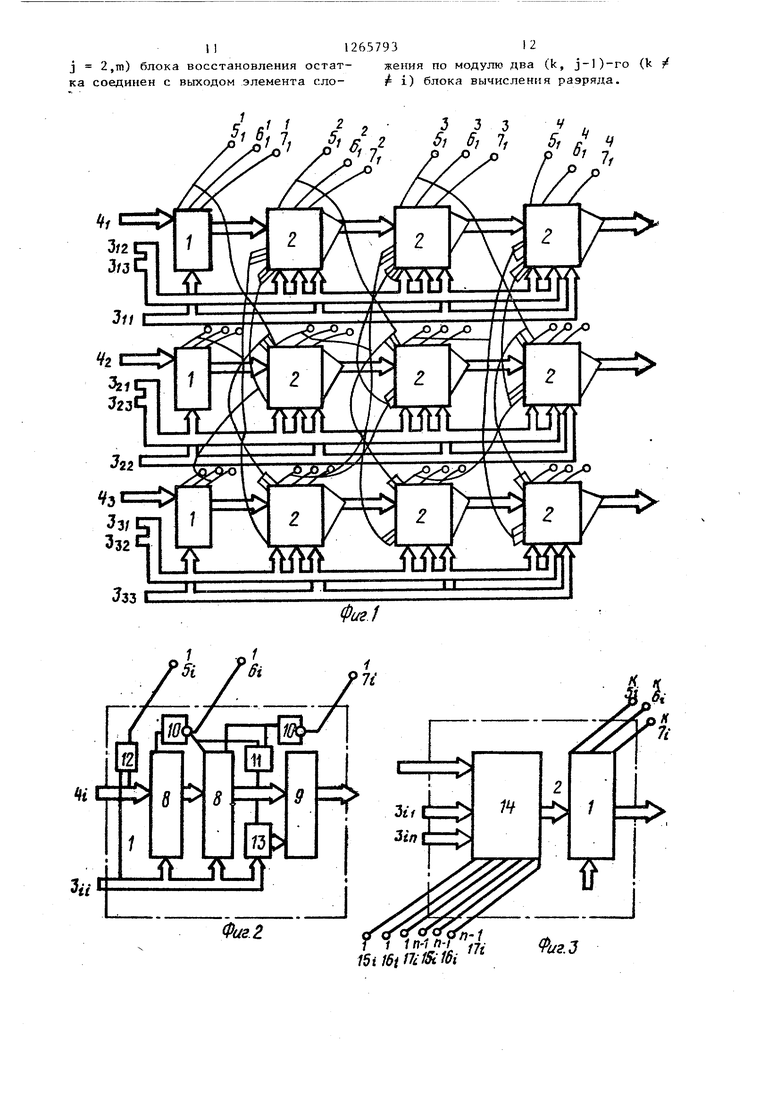
Изобретение относится к вычислительной технике и может быть применено автономно или в качестве спецпроцессора в мультипроцессорных вычислительных системах для оперативно го решения систем алгебраического управления динамическими объектами. Целью изобретения является увеличение быстродействия. На фиг. 1 представлена схема устройства для решения систем линейных алгебраических уравнений для случая когда п Зит 4; на фиг. 2 схема блока вычисления разряда; на фиг. 3 - схема вычислительного блока на фиг. 4 - схема блока восстановления остатка. Устройство для решения систем линейных алгебраических уравнений (фиг. 1) содержит п блоков 1 вычисления разрядов, п- (m-f) вычислитель ных блоков 2, i,j-e входные шины 3,-j, (i I, п, j 1,т), (i,n+l)-e входные шины 41, вькодные шины результата 1-го (1 1 ,М) разряда i-ro неизвестного5-, 6;, 7. Блок вычисления разряда 1 (фиг. 2) содержит два
(1)
f; 3 сумматора-вычитателя 8, сумматор 9, два элемента НЕ 10, элемент И П, элемент сложения по модулю два 12 и группу ключей 13. Вычислительный блок 2 (фиг. 3). содержит блок 1 вычисления разряда, блок 14 восстановления остатка и k-управляющик шин 15., 16;, 17 (k 1,...,п-1). Блок 14 восстановления остатка (фиг. 4) содержит (п -I) сумматоров-вычитателей 18 и (п-1) группу ключей 19. Работу матричной вычислительной структуры для решения систем лииейных алгебраических уравнений порядка п для случая, когда норма матрицы А удовлетворяет условию |lDA(| ь г- ПОЯСНИМ на конкретном примере (где А - матрица коэффициентов; X векторы неизвестных и правых частей; D - диагональная матрица, элементами которой являются диагональные элементы матрицы А). Запишем значения коэффициентов а;,- матриць А и компои fj векторов X и F в разряднент х; J 1 ной форме 3J . t




| название | год | авторы | номер документа |
|---|---|---|---|
| Матричный вычислитель | 1985 |
|
SU1283791A1 |
| Устройство для вычисления элементарных функций | 1985 |
|
SU1298764A1 |
| Матричный вычислитель экспоненты | 1981 |
|
SU1024911A1 |
| Матричный вычислитель логарифмов | 1981 |
|
SU1012251A1 |
| Устройство для решения системлиНЕйНыХ АлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU805336A1 |
| Спектроанализатор | 1985 |
|
SU1302294A1 |
| Устройство для вычисления скалярного произведения двух векторов | 1981 |
|
SU1179369A1 |
| Специализированный процессор | 1983 |
|
SU1144117A1 |
| Устройство для ортогонального преобразования цифровых сигналов по Уолшу-Адамару | 1987 |
|
SU1509930A1 |
| Процессор для цифровой обработки сигналов | 1985 |
|
SU1257662A1 |

Изобретение относится к области вычислительной техники и может быть применено автономно или в качестве спецпроцессора в мультипроцессорных вычислительных системах для оперативного решения систем линейных алгебраических уравнений. Цель изобретения - повышение быстродействия. Устройство содержит п блоков вычисления разрядов, П(т-1) вычислительных блоков. Блок вычисления разряда содержит два сумматора-вьгчитателй, сумматор, два элемента НЕ, элемент И, элемент сложения по модулю два и группу ключей. Вычислительный блок содержит блок вычисления разряда и блок восстановления остатка, содержащий (п-1) сумматоров-воичитателей U) и группу ключей. За счет совмещения во времени вычислительных операций с времеием переходного процесса достигается цель изобретения. 4 ял.
где a;j е 0,l, XjE О, Ij , , 1 , та - разрядность представления информации, а i j 1,2,...,п.
АА1
На основании компонентов разрядных векторов X сформируем следующие векторы бинарных элементов
X.
/ i X - X (х VX, ,Х, . . . ,Х , л .У.
...,х„;: л VX,,хг,...,х„;
... X (х, ,Х2. . .2,,) (3), благодаря которым вектор X исходной - -( -) -2--г -З -э 2 А,Х+ 2А, X + 2 А, X + -( -( -J-2 -Ъ 2 А,,Х+ 2A,jX +2 + . -I -I -2-2 -3 - 2 2А,Х +2 А,Х + .; .1 -1, -3 п 2 А„Х +2 АД +2 А„Х + ...
...А;
(2)
системы уравнений может быть записан как
Г-)с 2 X.
Тогда систему адсгебраических уравнений АХ F в развернутой форме на основании (1)-(3) запишем следующим образом: т гч ,.. + 2 А,Х т т + 2 А,Х . + 2 А,Х -т m + 2 А„Х Сформируем следующие матрицы бинарных элементов V 1 -п V f, -2 а„ X, -( 7 V v -2 а„Х, - f f, -21„Х, -« ч V V -2 .. f,
ч1265793
где |;j - разрядная матрица 3,торов а ,
составленная из разрядных век- 3 имеет вид
Для иллюстрации запишем первую строку уравнений в выражении (4) при m 3 и п 2. Таким образом, в соответствии с (6) каждая строка выражения (4) может быть представлена в виде m разрядных уравнений, по которым организуем вычисление компонентов х следующим образом. Из первых разрядных уравнений выражения (4), записанных в виде f - 2 а X ,( t fj - 2a,j xj j l.n, (7) определим x. При этом считается, что остаток f| в вьфажении (4) может принимать значения соответственно ДО -« -« (1 to СО2 А,Х - Г, f, ; f, -2 (О-г -2 a 2 AjX - f, Определим значения вторых разрядов X., т.е. вектор X (х, ,х,,... ,х„). , , . , - п f; 2 (r-i) . ) К1 .(И А.X - f; - 2 J Ч Алгоритм вычисления каждого компонента xj из выражения (9)(т.е. ре- у шения разрядных уравнений вида fj 9- F -2 а- -f}) осуществляется следующим образом. Знак Х: будет положителен, если f.. и а-.: имеют одинаковые знаки, и отрицательным, когда значендог.
при
которая
(5) /fV/ 2 а Так как матрица А исходной системы уравнений удовлетворяет условию II DA|I 2 то каждый .. , 2 компонент XJ будет не более 2, т.е. I х: ( 2 (фактически для х: можно записать х: е о,±1; i 2J . Далее вы( численные значения ксэмпонентов xj , т.е. вектор X (х, .х,) представляется в вьфажение (4) и на основании вторых разрядных уравнений () |.(«)г - ,ct) I т f ;г . , f, ; |f J 2 I а„/; « . (), -г, j f j ; I fj К2 /. Аналогичным образом, каждый k-й иектор X (х. ,х,..., ) вычисляетгя кяк Ci К/2-/а„/, Г / /Г|а„/ J п ajj имеют разные знаки, что можно записать. . З.н хГ 3 н и а где 3HXj - знак XI принимает значеие О, если хГ О и Г - когда 5- 0; . знак
л
jj принимает значение О, О, а-,550 и I - при .
Таким образом, значение j х. | может 5ыть вычислено в результате реализации одной из строк таблицы, а величина |xj| представляется в виде суммы двух значений |xj| xj + х, благодаря чему при реализации перв |роки |xjj 2, Вектор Х при этом жет быть записан как X (xj +
. к.
«.t
7 v
1 1 I t
+ Хп).
-I- Xt + X
+ X,
X.
k 1 Знх| Зн, ф Зна„ О ФО 0; 3 нх Зн. ф Зна„ ОФО 0.
|а„ 0,5664062 - 2 -0.625 0,2539062 F |а„| 0,6914062 - .8125 0.2851562 F,
Fj 0 F. 0
a,, 0,2539062 - 2 0.625 -0,585938
2
aij 0,2851562 - ,8125 -0. F, -: 0 --, X 0; O - X 0 O - X 0
;
0.0585938 + . 0.625 0.2539062
2 |a,,| 0.1210938 + 2-0,8125 6.2851562
i
. ,
, ° 0.2539062 - f 0,3125 0,0976568 a,. X, 0,2851562 - 0.375 0.0976562 2,UJ 0.0976562 - 2 0.625 0.0585938 2 |а„| 0,0976562 - 2 0,8125 0.1054788 Ff.0 5; 0 -. 0
Ff.O
0
ila,
0.0976562 f, ; 0,0976562
г
0; 0; 0 +
Xi 2 X, 0 -f 0 0.
k 3
- 0.0976562 fr.i ff - 2 a,:l; f 0.0976562 f :
1265793
aj)0. Модуль х определяется в соответствии с таблицей.
Рассмотрим изложенное на конкретном примере.
0,625X1 + 0,3125X2 0,5664062 0,375X1 -ь 0,8125X2 0,6914062 Решение х,,х равно соответственно XI 0,625, Х2 0.5625. Определим, удовлетворяет ли матрица системы уравнений условию
1,4615384.
/О. I
,0
I X,
pC./ p)
-0.1210938 - i 0;
.«
fг
+ x 1 + 0
1 4- 0
+ xi
-f it
fr;
-pW. г
« 0.
0,976562 - 2- 0,625 0,0195312 Г, , 0,0976562 - 2-0,8125 -0,093063
fM I 1 .
|Fri-2 |aJ
0,0195312 - 2 .0,625 0,0585938
F 0; X 0;
iFi;i ..1
-0,0585938 + 2;0,625 0.0195312 0,0093063 - ,8125 0,097656
IFTI %2Ма„|
3 Hx 0;
X, 1 + 0 1 3 Hx 0;
X. 0 + 0 0.
tnr -, 3 -0,0195312 f, ; f - 2 a,jX, 2a, X,
0,0976562 - 2 0,375 0,0507812
- vy,--
if.2-;Taj
0,0195313 - 2--0,625 0,0195313 0,0507812 - 2-0,8125 0 F ;
pf.o,-.: o,
F;; o,5; 1,
f{ 0,0195313;
Решение
X, (1010),625
Xj (1001)0,5625.
Работа устройства происходит следующим образом.
На входные шины 4 ,...,4п подаются соответственно значения компонентов f,,...,f вектора правых частей F решаемой системы уравнений АХ F. На входные шины 3;; (i 1,2,...,п) подаются значения диагональных элементов а;; матрицы А и на входные шины 3;; () подаются значения побочных элементов а; матрицы А. Пбсле этого в схеме протекает переходной процесс, по окончанию которого в каждом (i;-l)-M блоке вычисления разряда 1 моделируется соответственно i-я строка выражения 7, благодаря чему на выходе элемента сложения по модулю два 12 и элементов НЕ 10(1,1)-го блока вычисления разряда 1 и со9тветственно на входной шине первого разряда неизвестного по 5; , 6, , 7,- таблице образуются соответственно значения Знх;; х первого разряда i-ro неизвестного х;. На выходе сумматора 9 (i,) блока вычисления разряда 1 образуется в соответствии с (7) значение f.. .поступающее на второй .информационный вход сумматора-вычитателя 18 блока восстановления остатка 14 (1,2)-го вычислительного блока 2, в
}
г
0;
0;
котором моделируется 1-я строка выражения (8). При этом в блоке восстановления остатка 14 вычисляется значение f; 2 А;X - f, а в блоке выМчисления разряда 1 - соответственно
(,)( 2 2 (2
fj - 2 а..Х: , fj. Благодаря этому на выходе элемента сложения по модулю два 12 и элементов () блока вычисления разряда 1 и на выходных шинах
22
второго разряда 5;, 6j, 7, образуются соответственно знак Знх и , х второго разряда i-ro неизвестного X. А на выходе сумматора 9 на блоке вычисления разряда 1 образуется f., поступающее на второй информационный вход сумматора-вычктателя (1,3)-го блока восстановления остатка 14. Аналогичным образом в каждом i,j-M блоке восстановления остатка 14 модшяируется вы1)ажение (9), т.е. 2 AjX f;I a в соответствующем блоке выI,)
числения разряда 1 выражение Fj - ,--ff сумматора 9 i,j-ro блока
вычисления разряда 1. Образуется значение f j , а на выходных шинах jr-ro разряда 5, , ,j-ro блока, вычисления разряда 1 в соответстрии с таблицей образуются соответственно значения Знх, х|, х j-ro, разряда.i-ro неизвестного X.
Таким образом, за время переходного пррцесса в,схеме на выходных шинах 5| , 6;, 7 i,j блоков вычислеиия разряда 1 образуются i-e компоненты X вектора АХ F неизвестных. X системы уравнений АХ F, которые можно записать как X; 2 (I: .,) I ,.., 1 Формула изобретения Устройство для решения систем линейных алгебраических уравнений, содержащее п (п- порядок системы) блоков вычисления разряда, причем каждый блок вычисления разряда содержит сумматор, отличающееся тем, что, с целью увеличения быстродействия, в него введено п (т-1) блоков вычисления разряда и п.(т -1) блоков восстановления остатка (т разрядность представления информации причем блок вычисления разряда допол нительно содержит два сумматора-вычитателя, элемент И, группу ключей, два элемента НЕ и элемент сложения по модулю два, причем в каждом i,j-M (i 1,п; j 1,m) блоке вычисления разряда информационные выходы первого сумматора-вычитателя j,i-ro блока вычисления разряда соединены с первой группой информационных входов второг сумматора-вычитателя i,j-ro блока вы числения разряда, информационные выходы которого соединены с входами пе вого слагаемого сумматора i,j-ro бло ка вычисления разряда, входы второго слагаемого которого соединены с выхо дами ключей группы i,j-ro блока вычисления разряда, управляющие входы которых подключены к выходу элемента И i,j-ro блока вычисления разряда, выходы знака первого и второго сумматоров-вычитателей i,j-ro ;блока вычисления разряда соединены соответ ственно через первьй и второй элемен ты НЕ 1, блока вычисления разряда соответственно к первому и второ му входам элемента И i,j-ro блока вы числения разряда, 1,д-й блок восстановления остатка (i 1,п; j 2,m) содержит (п-) сумматор-вычитатель и (п-1) группу ключей, причем в каждом i,j-M (i 1,п; j 2,m) блоке восстановления остатка выходы ключей k-й (k 1, п-1) группы i,j-ro блока восстановления остатка соединены с первой группой входов k-ro сумматора вычитателя i,j-ro блока восстановления остатка, информационные выходы которого соединегал с второй группой зходов (k +1)-го сумматора-вычитателя i,j-ro блока восстановления остатка, входы i-x (i l,n) диагональных коэффициентов уравнений устройства соединены с первыми группами входов первого и второго сумматора-вычитателя и информационными входами ключей группы i,j-x (j 1,m) блоков вычисления разряда, i-я (i 1,п) группа входов коэффициентов правых частей уравнений устройства соединена с второй группой входов первого сумматоравычитателя (i,l)-ro блока вычисления разряда, первьй и второй входы элемента сложения по модулю два (i,l)-ro блока вычисления разряда подключены к входам знака соответственно i-й группы входов коэффициентов правых частей уравнений устройства и входам i-x диагональных элементов уравнений устройства ,п выходы сумматора i,j-ro (1 1,п, j 1, га-1) блока вычисления разряда соединены с второй группой входов первого сумматора-вычитателя (i,j+l)-ro блока восстановления остатка, выходы (n-l)-ro сумматора-вычитателя i,j-ro (1 1,п; j 2,m) блока восстановления остатка соединены с второй группой входов первого сумматора-вычитателя i,j-ro блока вычисления разряда, выход знакового разряда (п-1)-го сумматоравычитателя i,j-ro блока восстановления остатка подключен к первому вхоДУ элемента сложения по модулю два i,j-ro блока вычисления разряда, второй вход которого подключен к входу знака 1-го диагонального элемента устройства, входы i 1 (i 1,n, 1 T,n; i 1) элементов устройства соединены с информационными входами ключей 1-й группы i,j-ro (j 2m) блока восстановления остатка, выходы элемента сложения по модулю два, первого и второго элементов НЕ i,j-ro (1 1,п; j l,m) блока вычисления разряда соединены с 1,3-ми выходами соответственно знака и первой и второй компонентами вектора неизвестных системы уравнений устройства, первый и второй управлякяцие входы ключей k-й группы (k 1 ,п) (i,j)-ro (,n; j 2,m) блока восстановления остатка соединены с выходами соответственно первого и второго элементов НЕ (k,j-I)-ro (k i) блока вычисления разряда, управляющий вход k-ro сумматора-вычитателя i,j-ro (1 1,п;
II126579312
j 2,m) блока восстановления остат- жения по модулю два (k, j-l)-ro (k / ка соединен с выходом элемента ело- i) блока вычисления разряда. с с 9 //.

| Устройство для решения системлиНЕйНыХ АлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU805336A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Замок-толкатель | 1979 |
|
SU836396A2 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Пухов Г.Е | |||
| и др | |||
| Разрядно-аналоговые вычислительнью систеьял | |||
| М.: Советское радио, 1978, с | |||
| Гонок для ткацкого станка | 1923 |
|
SU254A1 |
Авторы
Даты
1986-10-23—Публикация
1983-05-24—Подача