1C
00
а to
Изобретение относится к обработке металлов давлением и может быть использовано для исследования основных закономерностей процесса электромеханической обработки зубчатых колес.
Цель изобретения - повышение точности получаемых результатов за счет учета теплоотвода в полюсе зацепления зуба колеса.
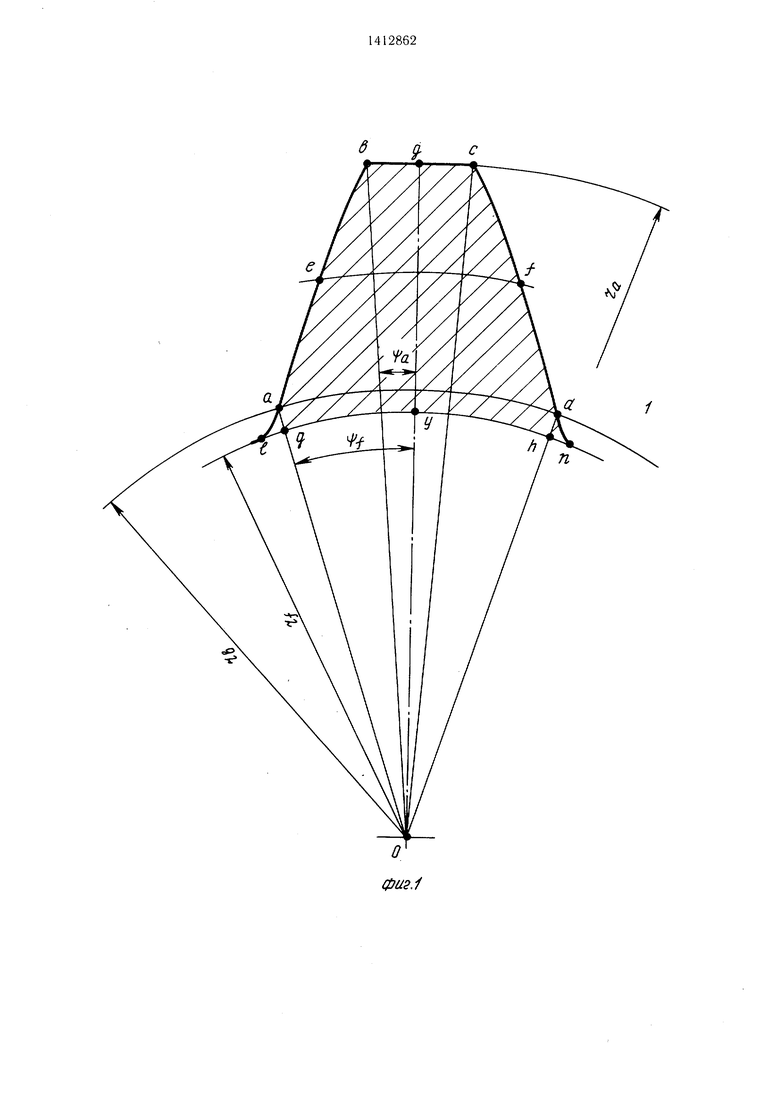
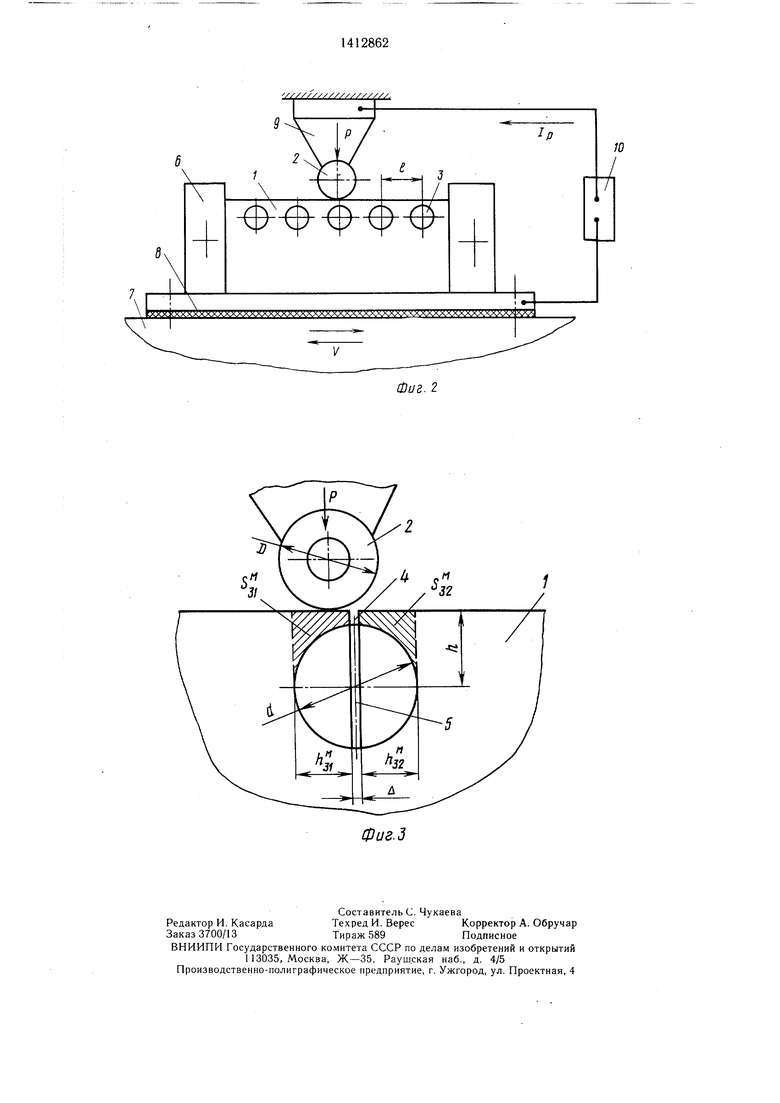
На фиг. 1 представлена схема для расчета площади исследуемого эвольвентного зуба; на фиг. 2 - устройство для осуществления предлагаемого способа; на фиг. 3 - схема, поясняющая способ.
Способ осуществляется следующим образом.
В плоском образце 1, являющемся моделью исследуемого зубчатого колеса, параллельно оси цилиндрического зубчатого инструмента 2 выполняют отверстия 3 диаметром d, располагая их друг от друга на расстоянии f и на глубине h от обрабаты- ваемой поверхности. На части плоского образца между его обрабатываемой поверхностью и отверстием 3 по его оси 4 выполняют сквозной щелевой разрез 5 шириной Л, который по меньшей мере на 2 по- рядка меньше диаметра отверстия 3, т.е. Л « d.
Образец 1 устанавливают в приспособление 6, которое располагают на столе станка 7, изолированном от него диэлектрической прокладкой 8. Инструмент 2 за- креплен в держателе 9. Инструмент 2 вводят в контакт с образцом 1, устанавливая при этом необходимую нагрузку Р. От электрической установки 10 в зону контакта инструмента 2 и образца 1 подводится рабочий ток 1р.
В процессе обработки образец 1 вместе с приспособлением 6 и столом станка 7 совершают возвратно-поступательное движение с заданной скоростью v относительно неподвижного держателя 9. Вращение инст- румента 2 вокруг своей оси осуществляется за счет сил трения. Инструмент проходя над отверстиями, позволяет получить в этом месте такие же тепловые контактные условия, а следовательно, и характер упрочнения, как и у зуба исследуемого зубчатого колеса.
Как видно из фиг. 3 выполнение отверстия в плоском образце 1, являющемся моделью исследуемого зубчатого колеса, позволяет получить два ограниченных объема металла, площади которых в торцовом сечении заштрихованы и обозначены S и , причем З.й (фиг. 3).
Указанные объемы металла являются аналогами зубьев исследуемого зубчатого колеса, так как о ни, как и зубья реального зубчатого колеса, представляют собой полуса- мостоятельные объемы металла и соединяются с основной массой образца через условную пло шадку, показанную на фиг. 3 пунк
тирной линией. С выполнением в плоском образце отверстий в нем образуются как бы два зуба, расположенные друг к другу вер- щинами, расстояние между которыми равно Д (полученные объемы металла - зубья модели). Высота зуба модели, обозначенная через h, очевидно, должна быть равна высоте зуба реального исследуемого зубчатого колеса.
Согласно фиг. 3 диаметр отверстия d равен
d 2Нз + Д,
5
0 5
О
.Q 45
-
5
50
где Из - высота зуба модели, равная высоте зуба исследуемого зубчатого колеса, мм;
/S. - ширина тонкого разреза, соединяющего поверхность отверстия с обрабатываемой поверхностью, мм.
Высота зуба зубчатого колеса обычно вычисляется по формуле Нз 2,25т, где m - модуль зубчатого колеса. Поскольку величина Д много меньше величины 2Нз , т.е. Д « 2Ьз, нею можно пренебречь. В связи с этим зависимость (1) получают в виде
d 4,5m(2)
где m - модуль исследуемого зубчатого колеса, мм.
Величину h, характеризующую расположение отверстия относительно обрабатываемой поверхности, необходимо выбрать такой, чтобы площадь зуба модели в торцовом сечении, т.е. Ssi 5з2 S, была равна площади зуба в торцовом сечении исследуемого зубчатого колеса, т.е. S S, где 5з - площадь зуба исследуемого зубчатого колеса в торцовом сечении. Для этого необходимо найти площади Ss и 5з. Площадь зуба исследуемого зубчатого колеса в торцовом сечении 5з вычисляется по известной зависимости (на фиг. 1 искомая площадь 5з заштрихована, т.е. площадь зуба колеса S ограничена боковыми эволь- вентными поверхностями, окружностью вер- щин и окружностью впадин)
S3 ( - ,) +г|Ч а-г|Уь (3) де Гв, Го, Г; - радиусы окружностей: основной, вершин и впадин соответственно;
«о, а/ - углы профиля на окружностях верщин и впадин, соответственно;
Fa, - углы, стягивающие соответствующие дуги на окружностях вершин и впадин соответственно.
Площадь зуба модели в торцовом сечении находят из фиг. 3. Площадь З з выражается в виде:
25з hd -
d(4)
После преобразований получают
сН
Ьз
М nd 2 16
Приравнивают выражения (3) и (5), т.е. выполняют условие 5з 5з и выражают величину h. После преобразований получают
h J tj() + (6)
Располагают отверстия на таком расстоянии друг от друга, чтобы при обработке участка обрабатываемой поверхности над одним отверстием, аналогичный участок над другим (соседним) отверстием не подвергался термическому влиянию со стороны соседнего отверстия. Предварительные эксперименты показывают, что величину Е можно принимать равной величине Югп, т.е.
F 10m(7)
где ш - модуль исследуемого зубчатого колеса, мм.
Диаметр D цилиндрического инструмента 2 (фиг.З) выбирается из следующих соображений. Для того, чтобы при ЭМО плоского образца достичь таких же тепловых контактных условий как при ЭМО реальных зубчатых колес необходимо, чтобы при прочих равных условиях площадь контакта цилиндрического инструмента и плоского образца была такой же, как в контакте зубьев колес. Как известно, площадь контакта двух тел можно охарактеризовать величиной приведенного радиуса кривизны. Величина приведенного радиуса кривизны в контакте цилиндрической и плоской поверхностей является, как известно, величиной постоянной, независящей от взаи.мно- го положения этих поверхностей и равной величине радиуса цилиндрической поверхности.
Величина приведенного радиуса кривизны в контакте двух эвольвент не является величиной постоянной и зависит от положения контактной точки на эвольвентном профиле, причем наибольшую величину приведенный радиус кривизны имеет в полюсе зацепления. Ввиду того, что приведенный радиус кривизны в полюсе зацепления имеет наибольшую величину по профилю, площадь контакта зубьев в этой точке также будет наибольшей по профилю зуба. Это приводит к тому, что полюс зацепления является той точкой на профиле зуба, которая меньше всего подвергается упрочнению, так как наибольшая площадь контакта зубьев в этой точке обуславливает, при прочих равных условиях, наименьшую по профилю зуба плотность электрического тока в контакте, а следовательно, и наименьшую величину контактных тепловыделений.
Поэтому, обеспечив при ЭМО зубчатых колес требуемое качество упрочнения в полюсе зацепления, можно предположить, что остальная часть эвольвентного профиля бус дет упрочнена не хуже чем в полюсе. В связи с этим контроль качества упрочнения обычно производят в полюсе зацепления. Данное обстоятельство приводит к тому, что в предлагаемом способе моделируется контакт зубьев в полюсе зацепления. При этом обходимо, чтобы площадь контакта, а следовательно, и приведенный радиус кривизны в контакте были одинаковыми при взаимодействии цилиндрического инструмента с плоским образцом и при взаимодействии
J5 двух зубьев в полюсе зацепления.
Приведенный радиус кривизны в полюсе зацепления двух зубьев при одинаковых числах зубьев инструмента и обрабатываемого зубчатого колеса (это допущение принимают для простоты получаемых зависи20 мостей) определяется по известной формуле
|-niz Sin а.
(8)
Поскольку приведенный радиус кривизны в контакте цилиндрической поверхности и плоской равен радиусу цилиндрической поверхности, то радиус цилиндрического инструмента также вычисляется по зависимости (8). Значит, диаметр цилиндрическо- го инструмента в предлагаемом способе определяется по зависимости
D 0,5mz sin ас
(9)
0
5
Пример. При экспериментальной проверке предлагаемого способа моделирования
5 процесса ЭМО зубчатых колес моделируется контакт зубьев в полюсе зацепления инструмента, имеющего параметры m 3 мм; Z 50; Xi 0; ширина зубчатого венца 14 мм, выполненного из стали Р6М5, и обрабатываемого зубчатого колеса, выполненного из стали 45 и имеющего параметры m 3 мм; Zi 50; Х2 О, ширина зубчатого венца 10 мм. В результате моделирования получают модель зубчатого колеса в виде плоского образца,
5 выполненную в соответствии с указанными рекомендациями.
В плоском образце, выполненном из стали 45, на глубине h 10,11 мм (см. формулу (6)) от обрабатываемой поверхности выполняют пять отверстий диамехром d
0 13,5 (см. формулу (2)). Эти отверстия располагаются на расстоянии Е 30 мм (см. формулу (7)) друг от друга. Ширина обрабатываемой поверхности плоского образца равна 10 м.м, аналогично ширине зубчатого венца обрабатываемого колеса. Цилиндрический инструмент, которым производится обработка модели, выполнен из стали Р6М5, имеет диаметр D 25,7 мм (см. формулу (9)) и ширину 14 мм.
Электромеханическая обработка моделей производится на специально оборудованном для этой цели горизонтально-фрезерном станке модели 6М82Г. В качестве источника тока применяется сварочная машина для кон- тактной сварки модели МТП-806У4 мощностью 100 кВт. ЭМО моделей осуществляется при следующем режиме: линейная плотность тока Ь 400 А/мм; усилие в кон- ;такте Р 800 Н; скорость перемещения ;модели относительно инструмента V ; 400 мм/мин; число проходов К 1. Ох- ;лаждение осуществляется проточной водой. Исследование результатов ЭМО моделей: микротвердость поверхностного слоя Н ; 7919 Н/мм (при исходной Н 3550 H/мм), а глубина упрочнения б 0,4 мм.
; Для проверки правильности полученных результатов при ЭМО моделей зубчатых ко- :лес проводят эксперимент на реальных зуб- ;чатых колесах, модели которых исследуются ; предлагаемым способом (параметры зубчатого инструмента и экспериментального зуб- :чатого колеса указаны). ЭМО зубчатых ко- :лес проводится на специально модернизи- рованном резьбонакатном станке модели 5А935. Режим обработки выбран аналогично режиму при обработке моделей, т.е. Ь 400 А/мм; Р 800 Н; V 400 мм/мин (п 1,2 об/мин); К 1 (обработка осуществляется за один оборот обрабатываемого колеса). Охлаждение производится проточной водой.
После ЭМО из обработанного зубчатого колеса вырезается часть зубьев, которые затем подвергаются исследованию. Причем, исследование качественных характеристик упрочненного слоя на боковой поверхности зуба осуществляется в том месте эволь- вентной поверхности, которое при ЭМО находится в полюсе зацепления инструмента и колеса. Результаты исследования следующие: микротвердость упрочненного слоя Ни 8010 Н/мм (при исходной Нд. 3580 Н/мм ), а глубина упрочненного слоя б 0,42 мм.
Таким образом, эксперименты показывают удовлетворительную сходимость результатов ЭМО при обработке моделей и зуб- чатых колес. Предлагаемый способ моделирования процесса ЭМО зубчатых колес позволяет обеспечить при обработке модели такие же условия как и при обработке известных зубчатых колес.
Применение предлагаемого способа поз- воляет приблизить тепловые контактные условия при электромеханической обработке модели к реальным, увеличивая при этом достоверность полученных результатов; сократить затраты на исследование процесса
электромеханической обработки зубчатых колес, так как в этом случае исследование можно проводить на моделях зубчатых колес, которые значительно проще в изготовлении и дещевле самих зубчатых колес.
Формула изобретения
Способ моделирования процесса электромеханической обработки зубчатых колес, при котором осуществляют относительное возвратно-поступательное перемещение модели в виде плоского образца и инструмента в виде цилиндрического зубчатого ролика, установленного с возможностью вращения, причем к последнему прикладывают нагрузку в радиальном направлении, а в место контакта плоского образца и HHctpyMeH- та подают электрический ток, отличающийся тем, что, с целью повыщения точности получаемых результатов за счет учета теплоотвода в полюсе зацепления зуба колеса, в плоском образце параллельно оси цилиндрического зубчатого ролика выполняют отверстия диаметром d на глубине h от обрабатываемой поверхности образца и располагают их друг от друга на расстоянии f, а на части плоского образца между его обрабатываемой поверхностью и отверстием по его оси выполняют сквозной щелевой разрез щириной А, по меньщей мере на два порядка меньшей диаметра отверстия, причем диаметр цилиндрического ролика D, глубину h, диаметр d отверстия, расстояние I и щирину разреза А определяют по зависимостям
D 0,5mzsin o;
nd
2- (tg3aa-tg4) +ri4 a-r|, +
е гв. Га, г/ - радиусы окружностей: основной, вершин и впадин исследуемого зубчатого колеса соответственно;
аа и af - углы профиля на окружностях вершин и впадин соответственно;
Va и Ф - углы, стягивающие соответствующие дуги на окружностях вершин и впадин соответственно:d 4,5m; F 10m; A«d,
m - модуль исследуемого зубчатого колеса;
z - число его зубьев, «о -угол зацепления.
-t i
ООСЮОООСКХХХХЛ-ЛААЛАЛААЛЛХЛЛЛААААА


| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРОЧНЯЮЩЕЙ ОБРАБОТКИ ЗУБЧАТЫХ КОЛЕС С НАНЕСЕНИЕМ ПОКРЫТИЯ | 2001 |
|
RU2213157C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОТИВОЗАДИРНОЙ СТОЙКОСТИ ЗУБЬЕВ ЭВОЛЬВЕНТНОЙ ЦИЛИНДРИЧЕСКОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ | 2007 |
|
RU2334210C1 |
| Дисковый обкатник | 1984 |
|
SU1276408A2 |
| ЗУБЧАТЫЙ ИНСТРУМЕНТ ДЛЯ УПРОЧНЕНИЯ | 2011 |
|
RU2470731C2 |
| СПОСОБ УПРОЧНЕНИЯ ЗУБЧАТЫХ КОЛЕС | 2011 |
|
RU2468881C2 |
| Инструмент для обработки зубчатых колес | 1979 |
|
SU848134A1 |
| СПОСОБ ИГЛОФРЕЗЕРОВАНИЯ СПИРОИДНЫХ ЧЕРВЯКОВ С УПРОЧНЕНИЕМ | 2008 |
|
RU2385798C1 |
| Способ изготовления глобоидно-цилиндрической передачи с нелинейчатым червяком | 2022 |
|
RU2803611C1 |
| ИГЛОФРЕЗЕРНО-УПРОЧНЯЮЩИЙ ИНСТРУМЕНТ ДЛЯ ОБРАБОТКИ СПИРОИДНОГО ЧЕРВЯКА | 2008 |
|
RU2385797C1 |
| СПОСОБ И ИНСТРУМЕНТ ДЛЯ ИЗГОТОВЛЕНИЯ ПЛОСКИХ ЗУБЧАТЫХ КОЛЕС | 2010 |
|
RU2542040C2 |
Изобретение относится к обработке металлов давлением и может быть использовано для исследования процесса электромеханической обработки зубчатых колес. Цель изобретения - повышение точности получаемых результатов. Способ заключается в обкатывании цилиндрического инструмента диаметром D, равным D 0,5mzsinao, по плоскому образцу, в котором на расстоянии h от обрабатываемой поверхности выполняют отверстия диаметром d, равным d 4,5m, располагая их друг от друга на расстоянии , равном Б 10т, а по кратчайшему расстоянию между обрабатываемой поверхностью и поверхностями отверстий выполняют тонкие разрезы, соединяюш,ие эти поверхности и имеюшие ширину А, много меньшую диаметра отверстия. Между плоским образцом и инструментом пропускают ток. По качеству упрочнения в полюсе за- цеп.тения можно судить о качестве упрочнения остальной части эвольвентного профиля зубчатого колеса. 3 ил. с (О

| Шилёнков В | |||
| Ф | |||
| Исследование электромеханического упрочнения зубчатых колес в условиях ремонтного производства | |||
| - Диссертация, шифр ГБЛ DK | |||
| , Ульяновск, 1969, с | |||
| Разборное приспособление для накатки на рельсы сошедших с них колес подвижного состава | 1920 |
|
SU65A1 |
| Насос | 1917 |
|
SU13A1 |
Авторы
Даты
1988-07-30—Публикация
1987-06-08—Подача