ляции, блок 4 вычисления весовых ко- 30 бт следующим образом.
эффициентов, блок 5 определения параметра аппроксимации, первый, второй, третий и четвертый блоки 6 -6 -задержки, первый, второй и третий умножи-. , тели 7, -7э, сумматор 8 и блок 9 35 синхронизации.
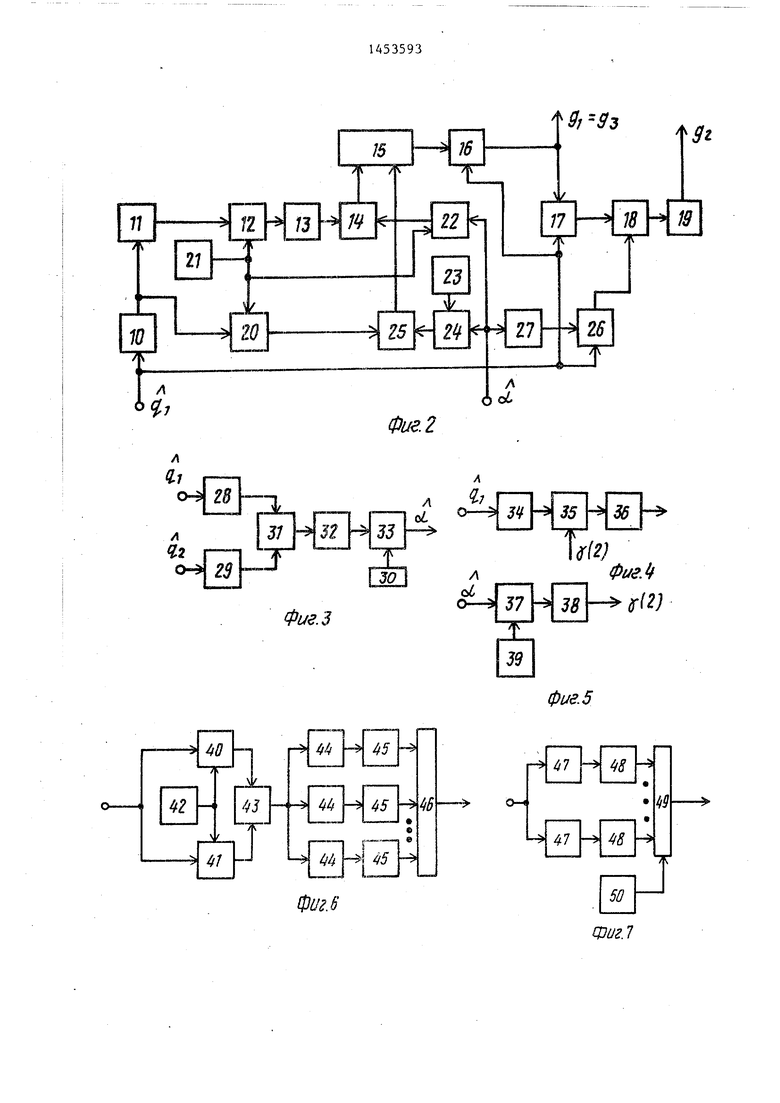
Блок 4 вычисления весовых коэффициентов (фиг.2) содержит первый квадратор 10, второй квадратор 11, первый блок 12 сложения, третий квадратор . Q 13, первый зт ножитель 14, второй блок 15 сложения, блок 16 деления, второй умножитель 17, третий блок 18 сложения, весовой блок 19, четвертый блок 20 сложения, первый регистр 21 д числа, первый блок 22 вычитания, второй регистр 23 числа, второй блок 24 вычитания, третий -умножитель 25, первый функциональный преобразователь 26 и второй функциональный пре- „ образователь 27.
Блок 5 определения параметра ап- проксимации (фиг.З) содержит первый
Б адаптивном цифровом фильтре с прямыми связями, синтезированный в соответствии с адаптивным байесовским подходом по критерию максимального коэффициента улучшения отношения сигнал/помеха, используется для нахождения весового вектора
G (BO (, .--.SN), где N - порядок фильтра, алгоритм вида
Л4(Q. - /W мин
1)0 О,
л г л ) где Q q ,,-.j, i
(1)
i,,N - оценка
lit-j
H-j1 J
корреляционной матрицы помехи;
оценка коэффициента корреляции между i-M и j-M от- счетами; Ч Ачин - минимальное собственное
число матрицы Q.
При условии gp 1, которое исклю чает тривиальное решение, и для случая сильно коррелированных
и второй блоки 28 и 29 вычисления помех уравнение (1) приводится к виг
гарифма, регистр 30 числа, первый блок 31 деления, третий блок 32 вычисления логарифма, второй блок 33 деления.А Л
QG D,
(2)
л Г л т
где О q|, -j| , 1,N - оценк
корреляционной матрицы;
Б адаптивном цифровом фильтре с прямыми связями, синтезированный в соответствии с адаптивным байесовским подходом по критерию максимального коэффициента улучшения отношения сигнал/помеха, используется для нахождения весового вектора
G (BO (, .--.SN), где N - порядок фильтра, алгоритм вида
Л4(Q. - /W мин
1)0 О,
л г л ) где Q q ,,-.j, i
(1)
i,,N - оценка
lit-j
H-j1 J
корреляционной матрицы по
мехи;
оценка коэффициента корреляции между i-M и j-M от- счетами; Ч Ачин - минимальное собственное
число матрицы Q.
При условии gp 1, которое исключает тривиальное решение, и для случая сильно коррелированных
Л
D,
(2)
Г л т
q|, -j| , 1,N - оценк
корреляционной матрицы;
Л
q;
10
31453593
л г 1
D qii.
,N оценка корреляционного вектора;
- оценка коэффициента корреляции за i периодов. Поскольку процесс измерения корре- ляционньпс характеристик сопровождаетг- ся ошибками, то полученные значения
Q и D отличаются от своих истинных . значений Q и D соответственно на матрицу и вектор ошибок 5() . Причем весовой вектор G, определенный из решения уравнения (2), отличается от 15 своего оптимального значения Gg (Г В на величину SG. Относительное по норме возмущение весового вектора
ЛС ||jG(|/|lGll можно определить с помощью соотнощения
UG cond ((&Q + Mi)
cif
(6)
(3)
где V(i) i, 4 2. параметр, зависящий от модели рассматриваемой
5 помехи.
С учетом (6)соотношение(5) гфиводится к виду
8,Uj) п (qf -q,)/(q7- q.)
(7)
где q и q - корни полиномов Рц и S. При этом среди множества корней qf и q,
qf - q,
q ,, a формула (7) переходит в о ноиеиие двух бесконечно малых величин и становится неустойчивой. Ис- , пользуя тот факт, что норма весового вектора является ограниченной
найдутся такие, что .0 и |q7 - q,HO при
20
|JG|kc«(4To следует из общего критерия
где &Q 118(1 II/IIQ II. о.устойчивости импульсной переходной
№ |lSDH/llDll - относительные возму-- «--. пи
щения матрицы и вектора;
COnd Q 111 Make/
/(Имин - ЧИСЛО:обусловленности матрицы; Имакс- максимальное собственное число матрицы;
II II - означает согласованные нормы матрицы 35 и вектора.
Из (3) следует, что в случае сильно коррелированных помех, характеризующихся плохо обусловленной корреляционной матрицей, то есть
у i 7 ri ч tTLit 4.JV-A«« it. .. характеристики любой дискретной системы) , можно показать, что подмножество корней числителя и знаменателя (7), дающих неустойчивость алгоритма, при условии (6) совпадают, а следовательно при конкретном значении 1 ai 6 2 алгоритм (7) приводится к устойчивому виду
q,Ui)V«i; -q,)/ f (),
,дд(1 Q- 00 , вычисленное значение G может сильно отличаться от своего оптимального значения G, что приводит к существенному снижению эффективности подавления помех. Рассмотрим уравнение
QG D,()
где I - размерность подмножества неустойчивых корней. Таким образом на множестве f«i-j
40 можно получить устойчивые значения весового вектора GCelj), j 1 (где Р - число точек аппроксимации). С использованием метода наименьших квадратов вектор аппроксимируется по
всему множеству ci по каждой координате g , для чего ретчается уравнение
X ( ,(9)
из решения которого весовые коэффици- х - х, аппроксимированный енты фильтра g,, k 1 ,N можно выра- gO -« g« f коэффициент; зить как отнопение двух полиноминаль- ,х ) - вектор аппроксимирующих
коэффициентов; А - матрица размерности рк2, j-я строка которой равна (I ) ;
ных функций:
8к Рк(ч,,....
55
Для одномодовых помех корреляционная матрица является теплицевой, а значит ее элементы связаны соотношением
Y - вектор размерности
Р, равный Y 8к( Р, j 1,Р.
cif
(6)
10
15
где V(i) i, 4 2. параметр, зависящий от модели рассматриваемой
5 помехи.
С учетом (6)соотношение(5) гфиводится к виду
8,Uj) п (qf -q,)/(q7- q.)
(7)
где q и q - корни полиномов Рц и S. При этом среди множества корней qf и q,
qf - q,
q ,, a формула (7) переходит в о ноиеиие двух бесконечно малых величин и становится неустойчивой. Ис- , пользуя тот факт, что норма весового вектора является ограниченной
найдутся такие, что .0 и |q7 - q,HO при
20
|JG|kc«(4To следует из общего критерия
устойчивости импульсной переходной
«--. пи
у i 7 ri ч tTLit 4.JV-A«« it. .. характеристики любой дискретной системы) , можно показать, что подмножество корней числителя и знаменателя (7), дающих неустойчивость алгоритма, при условии (6) совпадают, а следовательно при конкретном значении 1 ai 6 2 алгоритм (7) приводится к устойчивому виду
q,Ui)V«i; -q,)/ f (
где I - размерность подмножества неустойчивых корней. Таким образом на множестве f«i-j
можно получить устойчивые значения весового вектора GCelj), j 1 (где Р - число точек аппроксимации). С использованием метода наименьших квадратов вектор аппроксимируется по
всему множеству ci по каждой координате g , для чего ретчается урав55
коэффициентов; - матрица размерности рк2, j-я строка которой равна (I ) ;
- вектор размерности
Р, равный Y 8к( Р, j 1,Р.
g
С использованием описанной проце- дуры синтезируют иерекурсивный цифровой фильтр четвертого порядка, вет- совые коэффициенты которого определяются соотношениями
§4 1. 8г -Zfg.q, + .
g, 8, qr(i п:)(- О
+ .(1 + qf)(2 -A) (10)
A
В качестве параметра c. можно использовать оценку максимального правдоподобия, которая следует из (6) при
J. 1п(1п Hi/In чг)
(, 1Ч..Ч,..-в-ч..
In,,
(И)
Для сравнения можно привести весо вые коэффициенты фильтра, определенные из решения уравнения (2) методом Гаусса:
54 1 8-2 ,5Я1 + qj
83 (1 - 2qi + q4)/q,( -q..(12)
§0
8l
Из анализа (12) следует, что в случае сильно коррелированной помехи () коэффициенты g,, gi и gj будут неустойчивыми,
Фильтрация сигналов производится следующим образом.
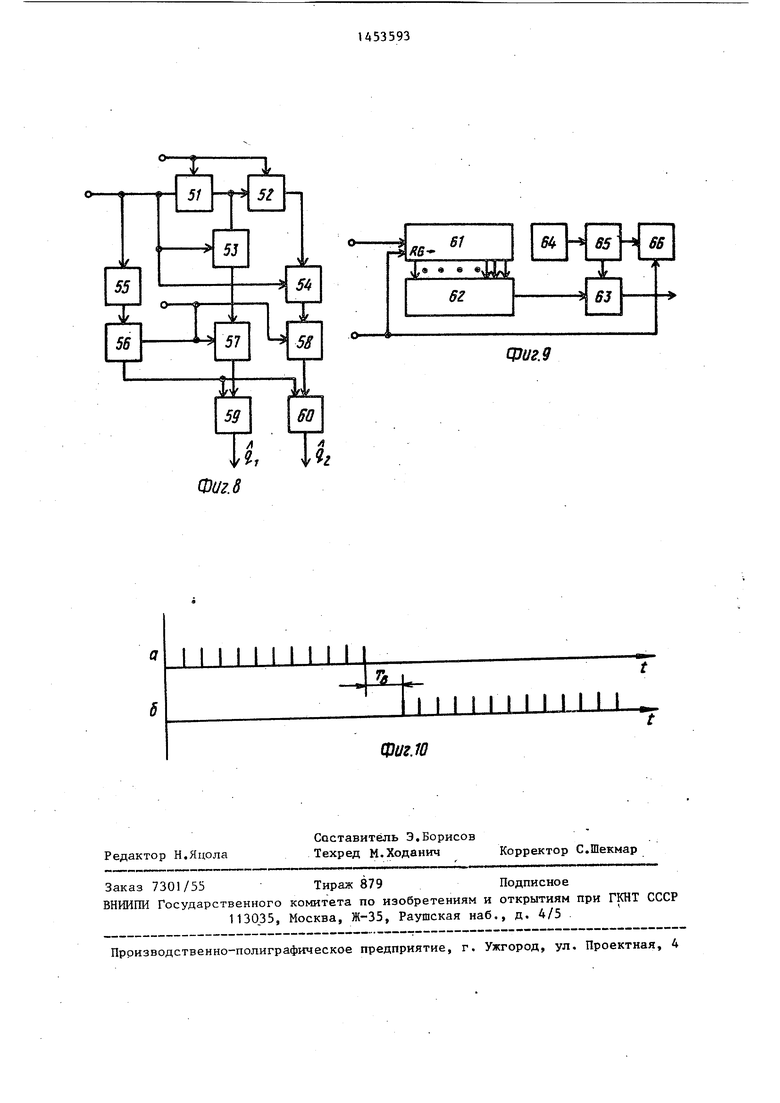
С выхода блока 9 на управляющий вход второго ключа 2 поступают импульсы Т:;, (фиг.Юа), благодаря чему отсчеты входной помехи в параллельной г-разрядной форме поступают в блок 3, который производит оценку коэффициентов корреляции помехи в соответствии с алгоритмом
z:uWu n - i /z:u n, (13)
neln
где - отсчеты выходного сигнала; М - объем выборки оценивания.
+
Для этого задержанные отсчеты сигналов с выходов первого и второго блоков 51 и 52 задержки поступают в первый и второй умножители 53 и 54, в которых умножаются на текущие отг счеты помехи. Полученные таким образом произведения, а также значения квадратов входного процесса U п поступают в накопители 56-58. Импуль сами Т отсчеты тЛ И и подвигаются по регистру 61 сдвига. Одновременно с этим счетчик 66 производит подсчет импульсов Т, а затем
его выходной код сравнивается с цифровым кодом М (хранящимся в регистре 64 числа) в блоке 65 сравнения. В Момент равенства кодов М на выходе блока 65 формируется единичный уровень, поступающий на стробирующий вход блока 63 совпадения. При этом с выхода блока 9 поступает только М
10 импульсов TQ оценки, поэтому накопленные значения сигналов через блоки 63 совпадения подаются в блоки 59 и 60 деления, на выходах которых через tfl (где Т - время деления
15 кодов) устанавливаются цифровые коды оценок q, и qj..
Блок 5 определения параметра апалгорит-для
проксимации в соответствии с
Л
мом (11) вычисляет оценку об , 20 чего значения q и q поступают в блоки 28 и 29 вычисления логарифма. Затем с помощью блока 31 деления формируется величина 1п q,, которая через блок 32 вычисления 25 логарифма подается в блок 33 деления, В этом блоке она нормируется относительно 1п 2, цифровой код которого записан в регистре 30 числа. Для вычисления In X используется стандарт- 30 ное разложение этой функции в ряд Тейлора при х 0:
1
(14)
На выходе блока 43 деления формируется величина (х - 1)/(х + 1), которая затем в соответствии с (14) возводится в нужную степень в блоках 44, а затем через соответствующий весовой блок 45, который осуществляет операцию взвешенного умножения, поступает в блок 46 суммирования, Обычно для достижения удовлетворительной точности применяют не более пяти-шести членов ряда (14).
Блок 4 вычисления весовых коэффи- центов по ;поступившим оценкам q, и oi вычисляет в соответствии с алгоритмом (10) значения g,,82 и g. Для формирования величины q, используются первый и второй функциональные преобразователи 26 и 27. При этом величину у(2) можно представить как
In у(2) Л In 2 -(2) ехр(),
оСЛп
(15)
В соответствии с (15) на выходе умножителя 37 формируется значение оСIn 2, которое затем поступает в блок 38 вычисления экспоненты, пример выполнения которого представлен на фиг.7. Для вьшисления е применяется стандартное разложение этой функции в ряд Тейлора
оэ „п
(16)
n (2) In ,
Полученное таким образом значение j(2) поступает в блок 26, определяюий величину qf , которую можно редставить как
XU exp(z2)
z If (2) In 4,., (17)
В соответствии с (17) на выходе умножителя 35 формируется значение у(2)1п q, , поступающее затем в блок
36 вычисления экспоненты, на выходе
А Х1(г) которого и устанавливается код q ,
Через Tg + 2. ( г Р мя вычисления второго весового коэф-
35
фициента g) на выходах блока 4 формируются значения составляющих весового вектора, которые поступают на вторые входы первого, второго и третьего умножителей 7. Посде этого с второго выхода блока 9 на управляющий вход nepftoro ключа 1 и тактовые входы первого, второго, третьего и четвертого блоков 6,-64 задержки начинают поступать импульсы обра- 40 ботки (фиг.106). В результате этого отсчеты входного сигнала проходят в настроенный адапативный цифровой фильтр, а на выходе сумматора 8 формируется выходной код в виде свертки дЗ входной последовательности и весовой функции. При этом осуществляется устойчивая фильтрация входного сигнала по критерию максимального улучшения отношения сигнал/помеха. JQ
fO
20
25
30
ормула изобретения
Адаптивный цифровой фильтр по вт.св. № 1388896, отличаю- и и с. я тем, что, с цепью повыше- ния точности фильтрации, блок вычисления коэффициентов содержит последовательно соединенные первый квадратор/
вход которого является первым входом блока вычисления весовых коэффициентов, второй квадратор,. первый блок сложения, тр етий квадратор, первый умножитель, второй блок сложения, блок де-- ления, выход которого является первым и третьим выходами блока вычисления весовых коэффициентов, второй умножитель, третий блок сложения и весовой блок, выход которого является
вторым выходом блока вычисления весовых коэффициентов, первый блок вычи- тания, выход которого соединен с вторым входом первого умножителя, последовательно соединенные блок сложения, первый вход которого соединен с выходом первого квадратора, и третий умножитель, выход которого соединен с вторым входом второго блока .сложения, первый регистр числа, выход которого соединен с вторыми выходами первого блока сложения, четвертого блока сложения и первого блока вычитания, последовательно соединенные второй регистр числа и второй блок вычитания, выход которого соединен с вторым входом третьего умножителя, первый функциональный преобразовав тель, первый вход которого соединен
с входом первого квадратора и с вторыми входами блока деления и второго умножителя, а выход соединен с вторым входом третьего блока сложения, а также второй функциональный преобразователь, вход которого объединен с вторыми входами первого и второго блоков вычитания и является вторым входом блока вычисления весовых коэффициентов, а выход соединен с вторым входом первого функционального преоб- разователя.
Фие.2



| название | год | авторы | номер документа |
|---|---|---|---|
| Адаптивный цифровой фильтр | 1986 |
|
SU1388896A1 |
| Адаптивный цифровой фильтр | 1987 |
|
SU1494212A1 |
| Адаптивный цифровой фильтр | 1986 |
|
SU1387173A1 |
| Устройство для цифровой фильтрации | 1981 |
|
SU957416A1 |
| Устройство для цифровой фильтрации | 1983 |
|
SU1113884A2 |
| Устройство для адаптивной обработки сигналов | 1981 |
|
SU1014127A1 |
| ЦИФРОВОЙ КОМПЕНСАТОР ПАССИВНЫХ ПОМЕХ | 1994 |
|
RU2087000C1 |
| АДАПТИВНОЕ УСТРОЙСТВО ЗАЩИТЫ РАДИОЛОКАЦИОННОЙ СТАНЦИИ ОТ ПАССИВНЫХ ПОМЕХ | 1994 |
|
RU2097781C1 |
| Адаптивное устройство анализа | 1986 |
|
SU1386938A1 |
| Цифровое устройство для подав-лЕНия пАССиВНыХ пОМЕХ | 1979 |
|
SU809018A1 |
Изобретение относится к радиотехнике и м.б. использовано для фильтрации сигналов, задаваемых цифровым кодом. Цель изобретения - повышение точности фильтрации. Адаптивный цифровой фильтр содержит ключи I и 2, блок оценки 3 коэффициентов корреляции, блок вычисления 4 весовых коэффициентов, блок определения 5 параметров аппроксимации, четыре блока задержки, три умножителя 7 , сумматор 8, блок синхронизации. Отличием устройства является выполнение блока вычисления 4 весовых коэффициентов. Повышение эффективности подавления коррелированных помех повышается за счет обеспечения устойчивости процедуры вычисления весовых коэффициентов путем аппроксимации корреляционных характеристик входной помехи. 10 ил. (О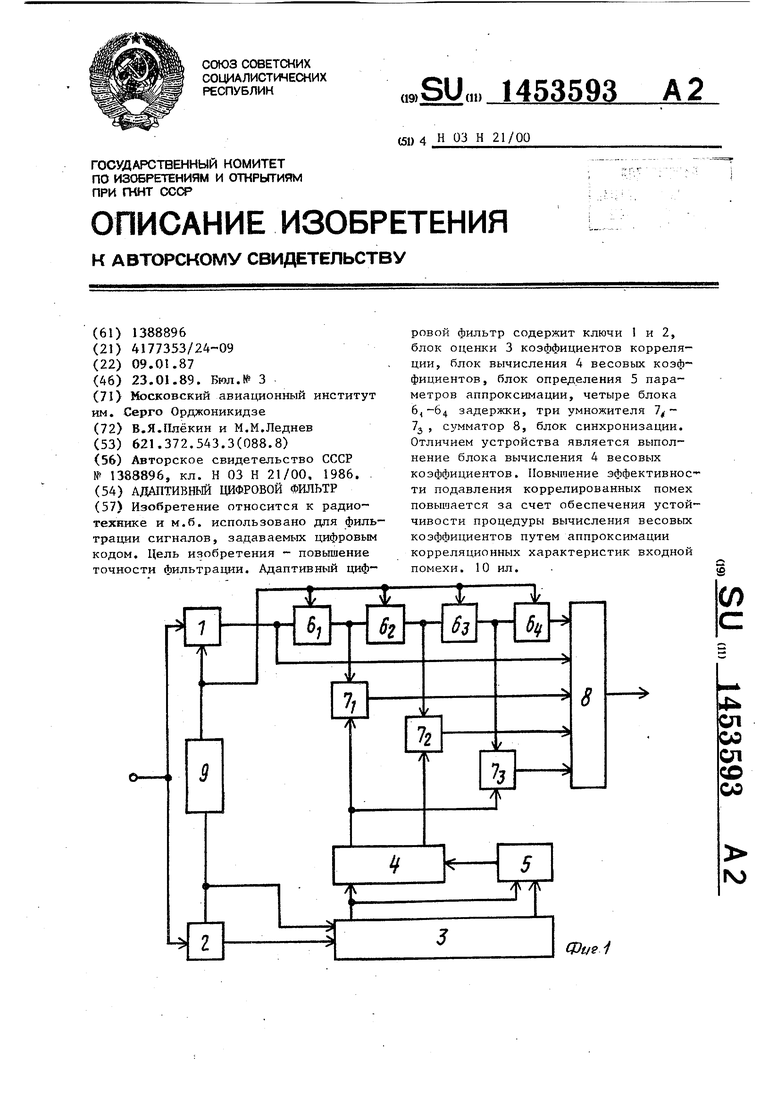
2В
j;
оФие.З
л
г
о-
3
35
36
W)
А оС
Фиг. $-(2)
фие.5
фиг.
Ф(/г.8
JLJJJJJJJ-1Фиг.Ю
| Адаптивный цифровой фильтр | 1986 |
|
SU1388896A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1989-01-23—Публикация
1987-01-09—Подача