77, «
Н
гоон
сл
со
N3
CD
О
Изобретение относится к вычислительной технике и может быть использовано для параллельного суммирования многоразрядных двоичных чисел.
Цель изобретения - расширение области применения за счет суммирования двоичных чисел, представленных в пакетной системе счисления при сохранении возможности суммирования двоичных чисел в традиционной и фи- боначчиевой системах счисления.
На чертеже представлена схема 1-го разряда накапливающего сумматора (для t«2).
i-й разряд сумматора содержит триггер 1, сумматор 2 по модулю два, второй 3, седьмой 4,- первый 5, четвертый 6, пятый 7, шестой 8 и третий 9 элементы И, с первого по четвертый элементы ИЛИ 10-13, элемент 14 задержки, входы 15 и 16 переноса
из (i-3)-ro и (i-l)-ro разрядов сумматора, входы 17 и 18 переноса из (i+2)-ro и (i-l)-ro разрядов сумматора, входы 19 и 20 1-х разрядов первого и второго слагаемых в пакетной системе счисления сумматора, входы 21 и 22 1-х разрядов первого и второго слагаемых в традиционной и фибоQ наччиевой системах счисления сумматора, выход 23 1-го разряда суммы сумматора, выходы 24-26 переноса в (i-H)-ft, 1-2)-й и (1+3)-й разряды сумматора, вход 27 задания традицион5 ной и фибоначчиевой систем счисления сумматора, вход 28 задания пакетной системы счисления сумматора, вход 29 задания фибоначчиевой системы счисления сумматора, вход 30 сброса сум0 матера.
Вес двоичных разрядов Vt (i.) пакетных t-кодов задается следующим реккуррентным соотношением:





| название | год | авторы | номер документа |
|---|---|---|---|
| Накапливающий сумматор | 1985 |
|
SU1278835A1 |
| Накапливающий сумматор | 1980 |
|
SU920706A2 |
| Комбинационный сумматор | 1975 |
|
SU570896A1 |
| Накапливающий сумматор | 1985 |
|
SU1319023A1 |
| Накапливающий сумматор | 1986 |
|
SU1401453A1 |
| Накапливающий сумматор | 1991 |
|
SU1800454A1 |
| Накапливающий сумматор | 1976 |
|
SU577528A1 |
| Накапливающий сумматор избыточного кода | 1988 |
|
SU1603370A1 |
| Последовательный сумматор | 1977 |
|
SU696452A1 |
| Параллельный сумматор кодов фибоначчи | 1978 |
|
SU840891A1 |
Изобретение относится к вычислительной технике и может быть использовано для параллельного суммирования многоразрядных двоичных чисел. Цель изобретения - расширение области применения за счет суммирования двоичных чисел, представленных в пакетной системе счисления, при сохранении возможности суммирования двоичных чисел в традиционной и "фибоначчиевой" системах счисления. Накапливающий сумматор содержит в каждом разряде триггер 1, сумматор 2 по модулю два, элементы И 3-9, элементы ИЛИ 10-13 и элемент 14 задержки с соответствующими связями. Сумматор может быть использован для построения специализированного устройства, работающего в режиме сквозного контроля информации и исправления возникающих ошибок, что позволит этому специализированному устройству длительно функционировать с высоким быстродействием. 1 ил., 5 табл.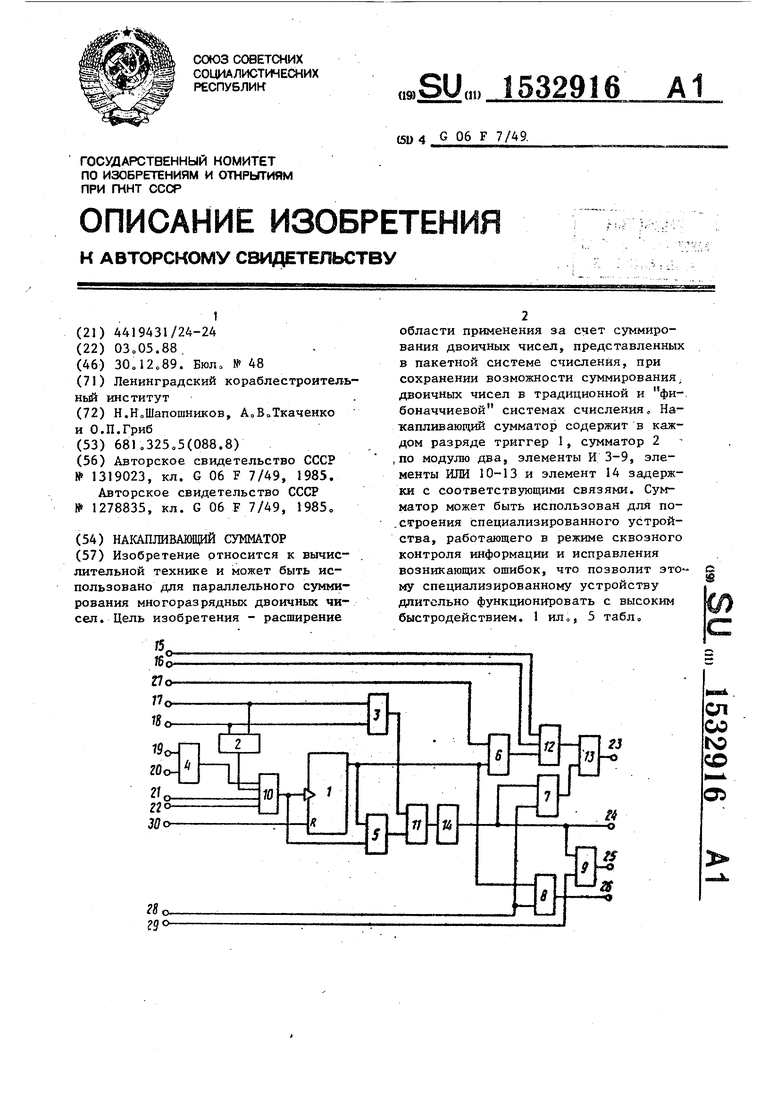
0при i Ј t;
1при t Ј i 2t; Јt(i-t) + jit(irt-)) при 2t i 3t;
&3
EL flt(i-t-k)
при
3t,
где t - натуральное число, задающее номер пакетной t-системы счисления;
i - разрядность кода. Любое натуральное число А в пакет- ном t-коде представляется в следующем виде:
А-1 i... i оо. .0... 11.. «QJj
m t m t
42)
Из (2) для любого натурального числа А в пакетном t-коде видно,что
flt( flttt+l)+...+ flt(i+t-2 + 2t(i+t-l)- #t(i+3t-3); (3)
2 yt(i)+2 #t(i+l)+,. .+2 flt i+t-2)+2 tft(i+t-l ) Ш)+ yt(i+l)+...+
+ yt(i+t-2)+ yt(i+t-l)+ & i+3t-3).(4)
Этот алгоритм вытекает из реккур- рентного соотношения (1) Для пакетного 2-кода () выражения (3) и (4) преобразуются к виду:
yi(i+3); (Ь)
2 ДО+О-ДО) yft(i+O+ 4(i+3).
(6)
0)
при
3t,
для него характерно наличие пакетов из t единиц, а также не менее (2t-2) нулей между пакетами из t единиц.
Сложение слагаемых, в которых пакеты из единиц стоят в различных разрядах, выполняется согласно выражению (3), а при нахождении пакетов из единиц в одних и rex же разрядах - согласно (4).
Накапливающий сумматор позволяет осуществлять сложение по следующему алгоритму:
Сложение любых двух чисел, представленных в пакетном 2-коде, осущег ствляется согласно выражениям (5) и (6). Если при4 сложении слагаемых окажется, что пакеты из единиц, находящиеся в слагаемых, стоят в различных разрядах, то их сложение производится путем переноса единиц из 1-го
515
и (i+l)-ro разрядов первого слагаемого в (1+3)-й разряд суммы, а пакет единиц второго слагаемого переносится также в (1+3)-й разряд суммы, но относительно своей i-й позиции. При сложении i-м считается тот разряд в пакете, у которого наименьшая позиция 1.
Если пакеты из единиц, находящие- ся в слагаемых, стоят в одних и тех же разрядах, то сложение производится по правилу: пакет единиц первого слагаемого переносится из 1-го -и (i-H )-го разрядов в (1+3)-й разряд суммы, а пакет единиц второго слагаемого переходит в сумму без изменения .
При нахождении пакета из единиц в одном кз слагаемых происходит пере- нос единиц из 1-го и (i+1)-го-разрядов этого слагаемого в (1+3)-й разряд суммы.
Сложение чисел, представленных в пакетной системе счисления, осущест- вляется за один такт без образования промежуточных сумм, что является существенным преимуществом этой системы счисления с ранее известными
Сумматор работает следующим об- разом.
При сложении чисел, представленных в традиционной системе счисления, 1м подается лишь на вход 27 „ На входах . 28, 29 присутствует О. При этих условиях сумматор осуществляет алгоритм сложения
ц;(1) V-tt-H).
Следовательно, имеют значение сигнал данного 1-го разряда, сигнал переноса в старший разряд (1+1)-й, сигнал переноса из (i-I)-ro разряда в данный разряд сумматора.
Пример 1 о Сложить числа 12 « 0001100 и 28 0011100.(табл.1).
Процесс сложения разрядов первого и второго слагаемых без учета сигнала переноса состоит в следующем триггер 1 со счетным входом формирует сигнал суммы данного 1-го разряда, поступающий на вход элемента И 6, разрешающего его выдачу. Сигнал переноса в (1+1)-й разряд сумма- тора вырабатывается элементами И 5, ИЛИ 11 и элементом 14 задержки. Сигнал переноса из (i-l)-ro разряда поступает на вход сумматора 2 по моду
5
1
-
0
5
0
5
0
66
лю два, который без изменения выдает его на вход элемента ИЛИ 10, подключенного к счетному входу триггера, и суммирует со значением данного разряда.
При суммировании в традиционной системе счисления сигнал переноса из (i-l)-ro разряда участвует лишь в сложении, не влияя на получение сигнала переноса из данного разряда.
При работе с числами, представленными в фибоначчиевой системе счисления, 1 присутствует на входах 27 и 29. В данном случае сумматор выполняет алгоритм сложения
ч/(1)+ ц/а)цк1-н)+ ).
Следовательно, необходимы сигнал суммы данного разряда, сигналы переноса в (1+1)-й, (1-2)-й разряды, сигналы переноса из (i-l)-ro разряда сумматора и (i+2)-ro разряда.
Рассмотрим особенность сложения чисел в этой системе счисления. Наличие двух сигналов переноса в данный i-й разряд сумматора предполагает необходимость формирования из них сигнала для участия в сложении и сигнала переноса из данного 1-го разряда.
Пример20 Сложить числа 33 - 010101010 и 28 010010100 (табл.2}.
Рассмотрим работу сумматора с учетом изложенного. При наличии лишь одного сигнала переноса в любом разряде на выходе сумматора 2 по модулю два формируется единичный сигнал, который через элемент ИЛИ 10 поступает на счетный .вход триггера 1, где учитывается с поступающим- сигналом в данный разряд сумматора.
При наличии одновременно двух сигналов переноса в любом разряде накапливающего сумматора на выходе сумматора 2 по модулю два формируется нулевой сигнал, который не изменяет состояние триггера, но при этом элементом И 3 формируется единичный сигнал переноса из данного разряда
Сигнал суммы данного разряда с выхода триггера 1 поступает на вход элемента И 6, подключенного к входу 27, 1 на котором разрешает выдачу суммы данного 1-го разряда сумматора„
Сигнал переноса с выхода элемента ИЛИ 11 через элемент 14 задержки поступает в соответствующие разряды сумматора.
При работе сумматора с числами, представленными в пакетной системе Счисления, осуществляется алгоритм, Представленный соотношениями (5) и (6 JB этом случае 1 подается на вход J28, что приводит к работе элементов И 7 и 8, которые разрешают прохожде- kne сигналов переноса в i-й, (i-t-l)-u |и (1+3)-й разряды, а также подключатся входы 15 и 16 переносов из (i- 3)-го и (i-l)-ro разрядов сумматора соответственно.
Наличие О на входах 27 и 29 приводит к тому, что на выходе элементов И 6 и 9 генерируется О Следовательно, сумматор подключен к выходам переносов из (i-3)-ro и (i-1)- го разрядов и выходам переносов в (1+1)-й и (1+3)-й разряды сумматора, а татоке к выходу суммы данного i-ro разряда сумматора Слагаемые подаются на вход сумматора поочередно, по две единицы (так как ) на входы элемента И 4, причем i-м считает - ся тот разряд в пакете из t единиц, у которого наименьшая позиция i.
В силу особенности представления чисел в пакетной системе счисления сигналы переноса в (1+1)-й, (1+3)-й разряды поступают в разряды, заведомо-содержащие О. Это исключает порождение промежуточных сумм и дополнительных переносов, что приводит к повышению быстродействия сумматора
Примерз Сложить числа 0 000000000000 и 7 000011000000 (табл.3)с
При поступлении на вход сумматора слагаемых, в которых пакет из единиц находится только в одном из них, на выходе элемента И 4 формируется единичный сигнал, который черегз элемент ИЛИ 10 поступает на счетный вход триггера 1, переводя его в единичное состояние Единичный сигнал с выхода триггера 1 поступает на вход элемента И 8, который разрешает прохождение сигналов переноса в (1+3)-й разряд сумматора
При мер 4 Сложить числа 5 - 000001100000 и 7 000011000000 (табл. 4).
При поступлении на вход сумматора слагаемых, в которых пакеты из единиц стоят в различных разрядах,
5
0
5
на выходе элемента И 4 после каждого поступления пакета из слагаемых поочередно формируются единичные сигналы, которые через элемент ИЛИ 10 переводят триггер 1 в единичные состояния и формируют переносы в (i + +3)-й разряды сумматора Перенос в i-й и (1+1)-й разряды сумматора не производится, так как 1-е разряды в пакетах слагаемых не совпадают, а перед поступлением на вход каждого 1-го разряда слагаемого на вход 30 сброса подается сигнал, по которому триггеры 1 всех разрядов устанавливаются в нулевое состояние
П р и м е р 5 Сложить числа 7 000011000000 и 7 000011000000 (табл.5).
При поступлении на вход сумматора : слагаемых, в которых пакеты из единиц стоят в одних и тех же разрядах, на выходе элемента И 4 после каждого поступления пакета из слагаемых поочередно формируются два единичных сигнала, которые через элемент ИЛИ
10поступают на счетный вход триггера 1 . Первый единичный сигнал переводит триггер 1 в единичное состоя- ; ние„. Единичный сигнал с выхода триг- гера 1 поступает на элемент И 8, который разрешает перенос в (1+3)-й разряд сумматора Второй единичный сигнал переводит триггер 1 в нулевое состояние, но при этом срабатывает элемент И 5 Единичный сигнал с выхода элемента И 5 через элемент ИЛИ
11поступает на вход элемента 14 задержки, с его выхода - на вход элемента И 7 и через элемент ИЛИ 13 в i-й разряд сумматора, а также одновременно на выход переноса в (1+1)-й разряд.
0
5
0
45 Формула изобретения
Накапливающий сумматор, содержащий в i-м разряде триггер, сумматор по модулю два, с первого по седьмой элементы И, с первого по четвертый элементы ИЛИ и элемент задержки, причем входы 1-х разрядов первого и второго слагаемых в традиционной и фи- боначчиевой системах счисления сумматора (, n - разрядность слагаемых) соединены соответственно с первым и вторым входами первого элемента ИЛИ 1-го разряда сумматора, выход которого соединен со счетным
0
5
входом триггера и с первым входом первого элемента И 1-го рааряда сумматора, вход сброса сумматора соединен с входами установки в О триггеров разрядов сумматора, прямой выход триггера 1-го разряда сумматора соединен с вторым входом первого элемента И 1-го разряда сумматора, выходы первого и второго элементов И 1-го разряда сумматора соединены соответственно с первым и вторым входами второго элемента ИЛИ 1-го разряда сумматора,, выход сумматора по модулю два 1-го разряда сумматора,-. соединен с третьим входом первого элемента ИЛИ 1-го разряда сумматора, выход второго элемента .ИЛИ 1-го раз- ряда сумматора через элемент задержки соединен с первым входом третьего элемента И 1-го разряда сумматора, второй вход которого соединен с входом задания фибоначчиевой системы счисления сумматора, вход задания традиционной и фибоначчиевой систем счисления сумматора соединен с первым входом четвертого элемента И 1-го разряда сумматора, выход которого соединен с первым входом третьего элемента ИЛИ 1-го разряда сумматора, выходы третьего элемента ИЛИ и пятого элемента И 1-го разряда сумматора соединены соответственно с первым и вторым входами четвертого элемента ИЛИ 1-го разряда сумматора, прямой выход триггера 1-го разряда сумматора соединен с первым входом шестого элемента И 1-го разряда сумматора, отличающийся тем, что, с целью расширения области применения за счет суммирования двоичных чисел, представленных в пакетной системе счисления при сохранении воз-
Вес разрядов
±I.
о о о
0
1 1
о 1 1
1
1 о
0
о о
о о
t1
1 1 о
о о
-л
о
0
5
0
5
0
5
0
можности суммирования двоичных чисел в традиционной и фибоначчиевой системах счисления, вход задания пакетной системы счисления сумматора соединен с первым входом пятого элемента И и с вторым входом шестого элемента И 1-го разряда сумматора, выход элемента задержки 1-го разряда сумматора соединен с вторым входом пятого элемента И 1-го разряда сумматора, прямой выход триггера i-го разряда сумматора соединен с вторым входим четвертого элемента И 1-го разряда сумматора, входы 1-х разрядов с первого по t-e слагаемых (t - параметр пакетной системы) в пакетной системе счисления сумматора соединены с соответствующими входами седьмого элемента И 1-го разряда сумматора, выход которого соединен с четвертым входом первого элемента ИЛИ i-го разряда сумматора, выход четвертого элемента ИЛИ 1-го разряда сумматора является выходом 1-го разряда суммы сумматора, выход элемента задержки - 1-го разряда сумматора соединен с первыми входами сумматора по модулю два и второго элемента И (i+)-ro разряда сумматора, выход третьего элемента И 1-го разряда сумматора соединен с вторыми входами сумматора по модулю два и второго элемента И (i-2)-ro разряда сумматора, с второго по t-й входы третьего элемента ИЛИ 1-го разряда сумматора соединены соответственно с выходами элементов задержки с (i-l)-ro no (i-t+l)-ft разрядов сумматора, (t+l)-u вход третьего элемента ИЛИ k-ro разряда сумматора соединен с выходом шестого, элемента И (i-3t-3)-ro разряда сумма то ра„
Таблица 1
Примечание
ОПервое слагаемое
ОВторое слагаемое
ОПромежуточные суммы
О
О О
Сумма
11
1532916
12 Таблица 2
13
i+3
i+1
О О
О
О
о
i+1 1
1
I J
I
1
1532916
14 Таблица5
00 00
00
Сигналы переноса 000 Первое слагаемое 000 Второе слагаемое
Сигналы переноса 000 Сумма
| Накапливающий сумматор | 1985 |
|
SU1319023A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Накапливающий сумматор | 1985 |
|
SU1278835A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-12-30—Публикация
1988-05-03—Подача