(54) ПОСЛЕДОВАТЕЛЬНЫЙ СУММАТОР



| название | год | авторы | номер документа |
|---|---|---|---|
| Последовательный сумматор | 1987 |
|
SU1411734A1 |
| Последовательный сумматор | 1989 |
|
SU1709298A2 |
| Последовательный сумматор кодов с иррациональными основаниями | 1983 |
|
SU1170449A1 |
| Последовательный сумматор | 1988 |
|
SU1571573A1 |
| НАКАПЛИВАЮЩИЙ СУММАТОР | 1993 |
|
RU2043650C1 |
| Устройство для умножения | 1980 |
|
SU960805A1 |
| Сумматор последовательного действия | 1989 |
|
SU1689945A2 |
| Устройство для сложения в избыточной двоичной системе счисления | 1986 |
|
SU1381487A1 |
| Устройство для умножения в избыточной системе счисления | 1984 |
|
SU1229755A1 |
| Конвейерный сумматор | 1989 |
|
SU1714588A1 |

t
Изобретение относится к области вычислительной техники и предназначено для суммирования многоразрядных двоичных последовательных кодов.
Иавествь последовательные сумматоры многоразрядных двоичных кодов, содержашве регвстры.одноразрядный сумматор и элемент задерзкки l.
Из известных последовательных сумматоров наиболее близким по технической сущности к предложенному является последовательный сумматор, содержащий одноразрядный сумматор и элемент задержки, выход которого соединен с одним из входов одноразрядного сумматора, а два других входа одноразрядного сумматора являются входами слагаемых последовательного сумматора 2.
Однако в известных последовательных сумматорах невозможно суммировать многоразрядные последовательные 1-коды Фибоначчи и золотые 1.оды.
Цель изобретения - расширение функциональных возможностей заключающее-.
ся в вьшолненни дополнительных операций сложения чисел в 1-«оде Фибоначчи и в золотом 1-коде.
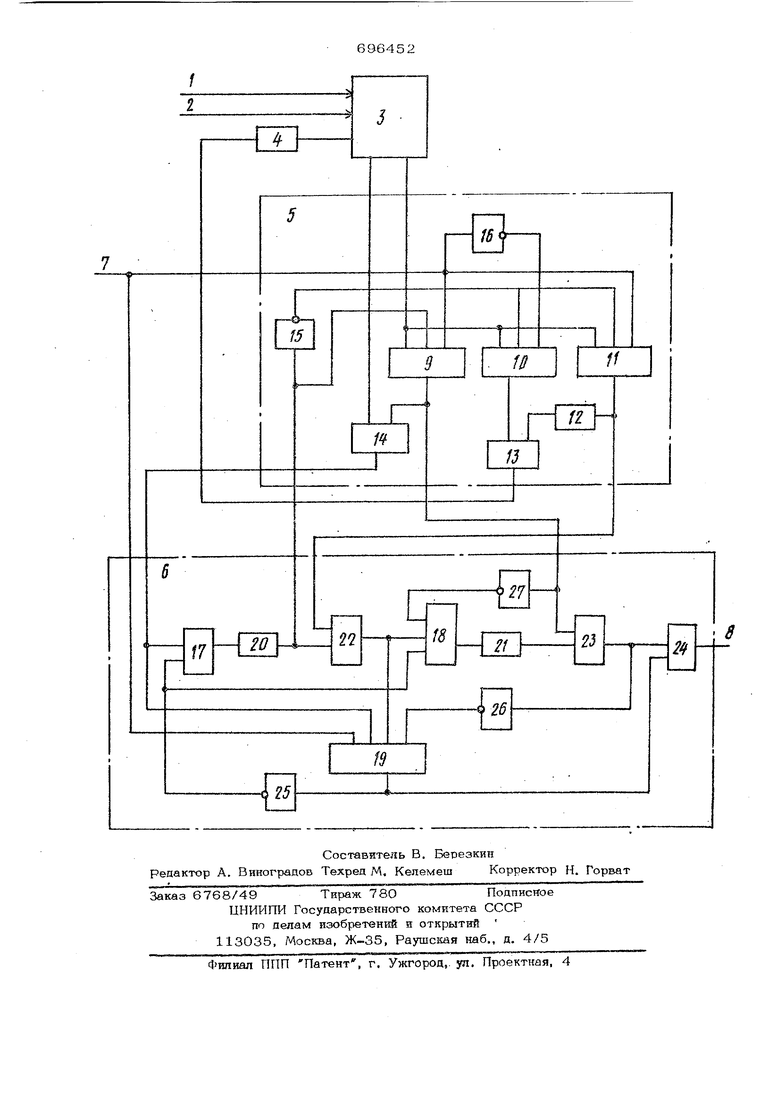
Цель достигается тем, что в последовательный сумматор, содержащий одноразрядный сумматор и элемент задержки, введены блок инвертирования н блок формирования дополнительных сигналов суммы и переноса, первый вход которого соединен с вьосЬдом суммы одноразрядного сумматора, выход переноса которого соединен со вторым входом блока формирования дополнительных сигналов суммы и переноса, третий вход бпока формирования дополнительных сигналов суммы и переноса соединен с первым выходом блока инвертирования, второй выход которого является выходом суммы последовательного сумматора. Первый, второй и третий выходы блока формирования дополнительных сигналов суммы и переноса соединены соответствевпю с первьш, вторым и третьим входами блока инвертирования. Четвертый выход блока формирования дополнительных сигналов суммы и переноса соединен со входом элемента задержки. Четвертый вход блока формирования дополнительных сигналов суммы в переноса соединен с четвертым входом блока инвертирования н является управляющим входом последовательного сумматора. Поставленная цель достигается также тем, что блок формирования дополнительяых сигналов суммы и переноса содержит три элемента И, два элемента ИЛИ, два элемента НЕ и элемент задержки. вход блока является первым входом первого элементаИЛИ. Первый вход первого элемента И соединен с первыми входами второго и третьего элементов И и является вторым входом блока.Второй вход первого элемента И соединен соЪхЗДом первого элемента НЕ и является третьим входом блока. Третий вход первого элемента И соединен со входом второго элемента НЕ и оо вторым входом третьего элйлента И и является четвертым входом . Выход первого элемента НЕ соединен со втордм входом второго элемента И и третьим входом третьего элемента И. Выход второго элемента НЕ соединен с третьим входом второго элемента И, выход которого соединен с первым входом второго элемента ИЛИ. Выход первого элемента ИЛИ является первым выходом блока. Выход третьего элемента И соединен со входом элемента аадвриакк и является вторым выходом блока. Выход первого элемента И соединен со вторым входе первого элемента ИЛИ в является третьим вь1ходом блока;, выход элемента задержки соединен со вторым входом элемента ИЛИ, выход Является чет- верть1м выходом блока. Кроме того, поставленнаа цепь достигается тем, что блок инвертирований содержит три элемента И, три элемента ИЛИ, три элемента НЕ и два элемента задерж кн. Первый вход первого логического элемент И соединен с первым одбм второго элемёнта.И и является первым входом 6nq- ка инвертирования, вторым входом которого является первый вход первого элемента ИЛИ. Первый вход второго элемента ИЛИ соединен со входом первого элемента НЕ и является третьим входом бцока инвертирования, четвертый вход которо го является вторым входом второго элемента И. Выход первого элемента И соединен со входом первого элемента задерж ки, выход которого соединен со вторым входом первого элемента ИЛИ и являет- ся первым выходом блока инвертирования. Выход первого элемента ИЛИ соединен с третьим : входом второго элемента И и первым входом третьего элемента И, второй вход которого соединен с выходом первого элемента НЕ. Выход третьего элемента И соединен со входом второго элемента задержки, вьхход которого соединен со вторым входом второго элемента ЦЛИ. Выход второго элемента ИЛИ соедиден со входом второхх) элемента НЕ и первым входом третьего элемента ИЛИ, выход которого является вторым выходом блока инвертирования. Выход второго элемента НЕ соединен с четвертым входом второго элемента И, выход которого соединен со ВХ9ДОМ третьего элемента НЕ и вторым входом третьего элемента ИЛИ. Выход третьего элемента НЕсоединен со вторым входом первого элемента И и третьим входом третьего элемента И. В Фибоначчиевой 1-ч;ист8ме счисления любое натуральное число N представляется в виде многочлена )(h-.Л....(o),,Гl) (О1ФИ 1 о J 1при , Vi-H i(i-2), 12) О; 1. В золотой 1-система счисления чис- . la представляется следующим образом + . где oi, основание системы счисления,являющееся действительным корнем уравнения, X - Х- - О. Так как для cji. выполняется равенство .. аналогичное равенству (2), То все, что будет сказано о фибоначчиевой -1-системе счисления будет справедливо и для. золотой 1-системы счисления. Представление 11) называется минимальной формой представления при наличии не менее одного нуля после каждой единицы. Сложение двух одноименньгх разрядов в двоичной Фибоначчиевой системе, счисления вьщолняется согласно следующим правилам О + О О; О-+ 1 Ij 1 + О 1; 1 + 1 1 О О 1, что вытекает из рекуррентного соотношения (2) Ч (i)(i) (iHЧ((1-2) 4((-i-2)569 . Если в 1-Х разрядах минимальных форм представления слагаемых имеются единицы, то из свойства минимальной фор МЬ1 следует, что суммы ( i +1) - и (п )т-Х разрядов будут нулевые и, следовательно, единица переноса из -i -fo в ( i +1.) разряд может быть помешена в ( 1+1 )-й разряд суммы, а перенос из 1-го в ( i-2) разряд надо запомнить. Сложение двух многоразрядных чисел начинается со старших разрядов и выполня ется поразрядно последовательно во времени. Сложение со старших разрядов начи нается в силу того, что перенос из 1-го разряда в ( i-2)-fl может вызвать перенос из ( i-2) разряда в ( i -4)-й и т.д., т.е. распространение переносов идет в сторону младших разрядов. Перенос из i-го разряда в I I+l) разряд носит локальный характер, что вытекает из свойства минимальной формы представления кодов слагаемых. Процесс суммирования распадается на ряд операций. Каждая -{-я операция заключается в сложении двух разрядов слагаемых и переноса из { i- 2 го старшего разряда с учетом значения суммы, полученной при выполнении преды- дущей операции. При сложении двух чисел А 1ОО1ОиВ 1ОО1О в первом так те складываются пятые разряды, при этом сумма этих разрядов равняется нулю. Пе ренос вперед помещается в шестой разряд результата, а перенос назад запоминается на два такта. На в тором такте складываются четвертые разряды, образу ющие сумму и перенос, равные нулю. В третьем такте складываются третьи разрады вместе с переносом, запомненным после сложения пятых разрядов. При этом сумма равняется единице, а перенос не возникает. Сложение цифр второго разряда в четвертом так.те порождает перенос и нулевую сумму. При этом перенос впе ред должен быть помещен в третий раз- ряд результата, в который уже помещена единица, полученная на предыдущем, третьем такте, т.е. возникает необходимость совместной обработки цифр результата, полученных при суммировании на предыдушем и данном тактах. Результат суммирования в подобном случае может быть представлен в виде f Ci4l)(i)(i)-4(iV27-«-4(i), что вытекает из рекуррентного соотношения (2. Следовательно, в четвертом такте образуется единичная сумма в четвер2том и во втором разрядах результата, а в третьем - нулевая сумма. В пятом также сумма будет равна нулю, TaKHNi образом, сумма А + В 101010. На чертеже изображена функциональная схема последовательного сумматора. Сумматор содержит входы слагаемых 1 и 2 последовательного сумматора, одноразрядный сумматор 3, элемент задерж- ки 4, блок формирования дополнительных сигналов суммы и переноса 5, блок инвертирования 6, в котором происходит запоминание сигналов суммь и переноса с целью замены двух рядом стоящих единиц в коде результата одной единицей согласно выражения (2) путем инвертирования этих разрядов, управляюший вход 7 последовательного сумматора и выход суммы 8 последовательного сумматора. Блок формирования дополнительных сигналов суммы и переноса. 5, содержит элемент И 9,на выходе которого формируется сигнал переноса в { i + 2)-й разряд, элемент И 10,элемент И 11, который совместно с элементом задержки 12 и элементом ИЛИ 13 формирует сигнал переноса в И - 2)-и разряд, элемент ИЛИ 14, на выходе которрго формируется скгквл суммы 1 -го разряда, элементы НЕ 15 И 16. Блок инвертирования 6 содержит элементы И 1719, элементы задержки 20 и 21, элементы ИЛИ 22-24, элементы НЕ 25, 26,27. Элементы задержки 20 и 21 осуществляют задержку сигналов поступающих на их вход на один такт работы последовательного сумматора. Элемент И 19 в элементы НЕ 25 и 26 выполняют функцию инвертирования, запрещая прохождение сигналов через элементы И 17 и 18 и посылая единичньхй сигнал на вход элемента ИЛИ 24. Для выполнения операции сложения чисел в 1-коде Фибоначчи необходимо подать единичный сигнал на управляющий вход 7 последовательного сумматора. При в блоке 5 будет разрешено прохождение сигналов по цепям, формирующим дополнительно сигналы суммы и переноса. Одновременно с этим будет разрешено инвертирование в блоке 6. При сложении двух чисел, представленных в 1-коде Фиббоначчи, А 10010100 и Б 101001ОО коды чисел А и В поступают на входы 1 и 2 последовательного сумматора, начиная со старшего разряда, На первом такте одноразрядным сумматором 3 формируется нулевой сигнал суммы и единичный сигнал переноса, кото-
76964528
рый пройдя через цепочку элементов И 11,го сумматора 3. При этом формируется
22 и ИЛИ 18 поступит на вход элементаединичный сигнал суммы, который посту- .
задержки 21. Кроме того, единичный сиг-п т через элементы ИЛИ 14 и И 17 на
нал переноса поступит на вход элементавход элемента задержки 20. Окончательзадержки 12. Сложение цифр седьмых раз- sный результат сложения будет получен черздов на втором такте работы приводитрез время, равное двум тактам работы,
к формированию нулевых сигналов суммьгнеобходимое для того, чтобы единичный
и переноса. Но на этом такте единичныйсигнал со входа элемента задержки 20 сигнал в выходах элемента задержки 21 через элементы ИЛИ 23 и 24 поступит на выход суммы 8 последовательного сум- матора. На третьем такте при сложении цифр шестого разряда с переносом, возникшим на первом такте и прошедшим через элементы задержки 12 и 4, формируется единичный сигнал переноса в ti+l)-4i разряд ив ( разряд, так же как это делалось на первом такте, Ва четвертом такте единичный сигнал суммы поступает на вход элемента задержки 20, пройдя эяементы ИЛИ 14 и И 17. Единичный сигнал с выхода элемента задержки 21 поступает на выход суммь 8 через элементы ИЛИ 23 и 24, На пятом такте единины-й сигнал переноса, сформированный на третьем такте, пройдя через элементы задержки 12 и 4, приводит к образованию единичного Сигнала суммы. Этот сигнал через элемент ИЛИ 14 поступит на первый вход элемента И 19, на вто- рой вход которого поступает единичный управляющий сигнал, на третий - единич- ный сигнал с выхода элемента задержки - 20, прошедший через элемент ИЛИ 22, на четвертый - единичный сигаал с выхода элемента НЕ 26. Единичный сигнал с выхода элемента И 19 поступает через элемент ИЛИ 24 на выход суммы 8, а через элемент НЕ 25 - на входы элементов И 17 и 18 в запрещает прохождение единичных сигналов на входы элементов задержки 20 и 21. На шестом такте одпоразрядный сумматорг 3 формирует нулевой сигнал суммы и единичный сигнал переноса, который, йройдя цепочку элемен тов, И 11, ИЛИ 22 и И 18, -поступает на вход элемента задержки 21, а единичный сигнал с выхода элемента И 11 поступает на вход элемента задержки. На седьмом такте единичный сигнал с выхода элемента задержки 12 через элемент ИЛИ 13 поступает на вход элемента задержки 4, Единичнь1й силаал с выхода элемента задержки 21 через элементы ИЛИ 23 и 24 поступает на выход суммы 8 последо. вательного сумматора. На восьмом такте единичньгй сигнал с вьгхода элемента задержки 4 поступает на вход одноразрядно- прошел на выход суммы 8 последовательнего сумматора. Окончательный результат сложения будет следукиций А + В О 1 О 1 1 О 1 О О 1. Для.сложения чисел в двоичной системе счисления необходи- мо подать нулевой сигнал на управляющий вход 7 последовательного сумматора, При этом запрещается инвертирование в блоке 16 и запретцается формирование дополните льны: сигналов суммы и переноса в блоке 5. Сигнал переноса с выходка одноразрядного сумматора 3 на его вход будет поступать ерез цепочку элементов И 10, ИЛИ 13 и элемент задержки 14. Конечный результат также будет сформирован с задержкой на два такта. Введение новых блоков и связей позволяет расширить фзгнкцио альные возможности послвдова1-ельного сумматора и выполнять суммирование чисел, представленных в фнбоначчневой и золотой системах счисления, обладающих высокой ошибкорбнаруживаюшей способностью. В данном последовательном сумматоре контроль пра- вшгьности выполнения сложения может осуществляться путем проверки р езультата сложения, в три подряд идущих разряда не могут иметь единичные значения. Формула изобретения 1. Последовательный сумматор, содержаний одноразрядный сумматор и элемент задержки, выход которого соединен с од- ним из входов одноразрядного сумматора, два других входа-одаоразрядного сумматора являются входами слагаемых последовательного сумматора, отличаю ц и И с я тем, что, с целью рйсширения функциональных возможностей заключаюшегося в вьшолнении дополнительных операций сложения чисел в 1-чкоде Фибоначчи и в золотом 1-«оде, введены блок инвертврования и блок формирования дополнительных сигналов суммы и переноса, первый вход которого соединен с выходом суммы одноразрядного сумматора, выход переноса которого соединен со вторым
Авторы
Даты
1979-11-05—Публикация
1977-08-17—Подача