Ё



| название | год | авторы | номер документа |
|---|---|---|---|
| СТЕНД ДЛЯ ИЗМЕРЕНИЯ СТАТО - ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ФИЗИЧЕСКИХ ОБЪЕКТОВ | 2013 |
|
RU2562445C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ПОДВИЖНОГО ОБЪЕКТА | 2014 |
|
RU2555496C1 |
| СТЕНД ДЛЯ ИЗМЕРЕНИЯ МАССЫ, КООРДИНАТ ЦЕНТРА МАСС И ТЕНЗОРА ИНЕРЦИИ ИЗДЕЛИЯ | 2010 |
|
RU2434213C1 |
| СТЕНД ДЛЯ ИЗМЕРЕНИЯ МАССЫ, КООРДИНАТ ЦЕНТРА МАСС И МОМЕНТОВ ИНЕРЦИИ ИЗДЕЛИЯ | 2012 |
|
RU2506551C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И СКОРОСТЕЙ ОБЪЕКТОВ СКАНИРУЮЩЕЙ МНОГОПОЗИЦИОННОЙ РАДИОСИСТЕМОЙ | 2020 |
|
RU2729459C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ПРОСТРАНСТВЕННОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2589495C1 |
| СПОСОБ ПОЛУЧЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ ПЕРИОДИЧЕСКОГО МАГНИТНОГО ПОЛЯ | 2000 |
|
RU2179323C1 |
| СПОСОБ ИЗМЕРЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ ПЕРИОДИЧЕСКОГО МАГНИТНОГО ПОЛЯ | 2011 |
|
RU2463620C1 |
| Стенд для измерения массы, координат центра масс и моментов инерции изделий | 2024 |
|
RU2830397C1 |
| СПОСОБ ФОРМИРОВАНИЯ ПРОВАЛОВ В НАПРАВЛЕНИЯХ ИСТОЧНИКОВ ПОМЕХ В ДИАГРАММАХ НАПРАВЛЕННОСТИ ПЛОСКИХ ФАЗИРОВАННЫХ АНТЕННЫХ РЕШЕТОК С НЕПРЯМОУГОЛЬНОЙ ГРАНИЦЕЙ РАСКРЫВА | 2013 |
|
RU2559763C2 |

Изобретение относится к весоизмерительной технике и позволяет определить вес отдельных частей неразделимых объектов, например биологических объектов. Объект исследования помещают на трехко- ординатную динамометрическую платформу и- закрепляют, предварительно известными средствами измеряют суммарный вес объекта. Затем производят измерение проекций мгновенных значений вектора силы тяжести геометрического центра масс объекта на оси прямоугольной системы координат с центром в центре платформы. Определение веса отдельных сечений столбцов и элементов объекта производят математическими вычислениями. Для реализации способа требуются трехко- ординатная динамометрическая платформа и компьютер. 4 табл.,3 ил,
Изобретение относится к технологии неразрушающего контроля объектов неживой и живой природы и, в частности, может быть использовано в системах неразрушаю- щего контроля.
Известен способ измерения распределения массы, состоящий в том, что измеряемое тело вращают в заданной плоскости вокруг произвольно фиксированной относительно этого тела точки до получения экстремальной частоты колебаний относительно одной из осей.Затем измеряют расстояния между выбранной точкой и двумя осями, расположенными с ней в одной плоскости. Искомые величины определяют из системы уравнений, связывающей периоды вращения, момент инерции и массы отдельных частей,
Недостатком известного способа является недостаточная точность оценки распределения массы, обусловленная тем, что по измерениям можно определить только
вес отдельных столбцов объекта (т.е. распределение в плоскости).
Кроме того, процесс проведения измерений очень сложен (тело нужно вращать и подбирать экстремальные частоты) и зачастую в практике неразрушающего контроля неприменим, например, для хрупких, сыпучих, биологических объектов и т.п.
Цель изобретения - повышение точности определения веса отдельных частей неразделимых объектов.
Для .достижения поставленной цели предварительно определяют геометриче- ский центр масс объекта, помещают его на трехкоординатную динамометрическую платформу. Далее измеряют мгновенные значения проекций Рх, Ру, Рг вектора силы тяжести геометрического центра масс объекта на оси прямоугольной системы координат с центром в центре платформы. Определяют проекции момента силы тяжости геометрического центра масс объекта на
VJ
О СО Ю 00 00
оси выбранной системы координат. Причем успешно разделяют объект рядом плоскостей, параллельных двум плоскостям системы координат. Далее определяют оценки веса сечений объекта по каждой оси координат, Вычисляют оценки веса отдельных стпбцоп объекта, полученных условным раз; елением парами взаимно перпендикулярных плоскостей. Затем вычисляют вес отдельных частей объекта.
Проекции момента силы тяжести геометрического центра пасс объекта на оси выбранной системы координат определяют по формулам
Mox,Yjpz - zjpy. J T;FX;
MoyrZiPx- XiPZl 1-ijTy; Mozk-ХьРу - YkPx. ,
0)
где величины DX, ny, nz находят как отношение геометрических размеров объекта по осям выбранной системы координат lx, ly, Iz к выбранным дискретам разрешения Д)х, AJy, A Iz.
Оценки оеса отдельных сечений объекта по каждой оси находят посредством минимизации функционала
ЗД
(X T VrMp) 5
при ограничениях
m , 0 ;
,пр-1; (4)
пр
с
2) ,
|
(5)
где т - вес v-ro семенил объекта по координате Р;
, ny, nz;
mjF - общий вес объекта, измеренный заранее;
ПхП (V
Мр X Мох , Л Моу| , 2/ Mozk - СУМ- 11 1 k 1
марный момент сил тяжести; обусловленных действием масс n сечениях вдоль данной оси (X, Y, Z) относительно центра О выбранной системы координат.
Оценки оеса отдельных столбцов, полученных условным разделением объекта сечениями по осям X и Y в плоскости
а (X О Y) находят путем решения системы линейных уравнений:
(6)
,По nx - Пу ;
fjfj fj fj fj /V t tJ
в bn bia ,..bij...binx -b2i ...bij ...bnynj; C7)
6ir«ie6«. N. Of. ,1
m imn mi2 ...mij ...minx ...mij... mnynx J .
«c
где mij - оценка веса столбца объекта, образованного пересечением 1-го, (Ы)-го, j-ro, (J-1)-ro сечений по осям X и Y в плоскости а,
причем элементы вектора свободных членов элементы матрицы А6 рассчитывают по формулам
5
-j
bij mic+ mjc,
1 1-ny.: .(8) , r-0:
pH.vQpi I 1,ny; ,nx; r-M-1:
aJr-Xpij;(9) . p- r.
30
При этом значения элементоо Xpi| строк матрицы вычисляют по формулам
35
(10)
40
Аналогично находят оценки mjk веса столбцов объекта, образованных пересечением J-ro, )-го и k-ro, (k-1}-ro сечений по осям X и Z в плоскости /(XOZ).
Определяют оценки оеса тю| отдель- ных частей (элементов) объекта, образованных пересечением (1-1)-го, 1-го, (. (k-1)-ro, k-ro сечений о плоскостях а л$ путем решения системы линейных уравнений
та
В;
01)
А
ац ... эй ... ain
, n Пх ny пг;
9п1 . . . 3ns . . . Эпп
...bi...bn T:02)
rn rniii...rniinx...minynx---niki|...rrinzriynx
При этом компоненты векторч свободных членов В и элементы матрицы А рэссчи- ТЫРЗЮГ по формулам
1-0; k-lTnl ; 1 Т7гГу; Н,пх:
(13)
Н+1. л
U . Р
+micj;
s°0.
,n; ,nz; ,.;nx;
aps Xpitij;
aps 2,p- s.(14) причем элементы Xpkij строк матрицы А вычисляют по формулам
P °i ,ny; ,n/; ,nx;
,ny;
Xpkij-1: HTn
Xp|Sj 1.
Устройство для реализации предложенного способа включает в себя динамометрическую платформу и компьютер, выполняющий вычисления по формулам ОМ15).
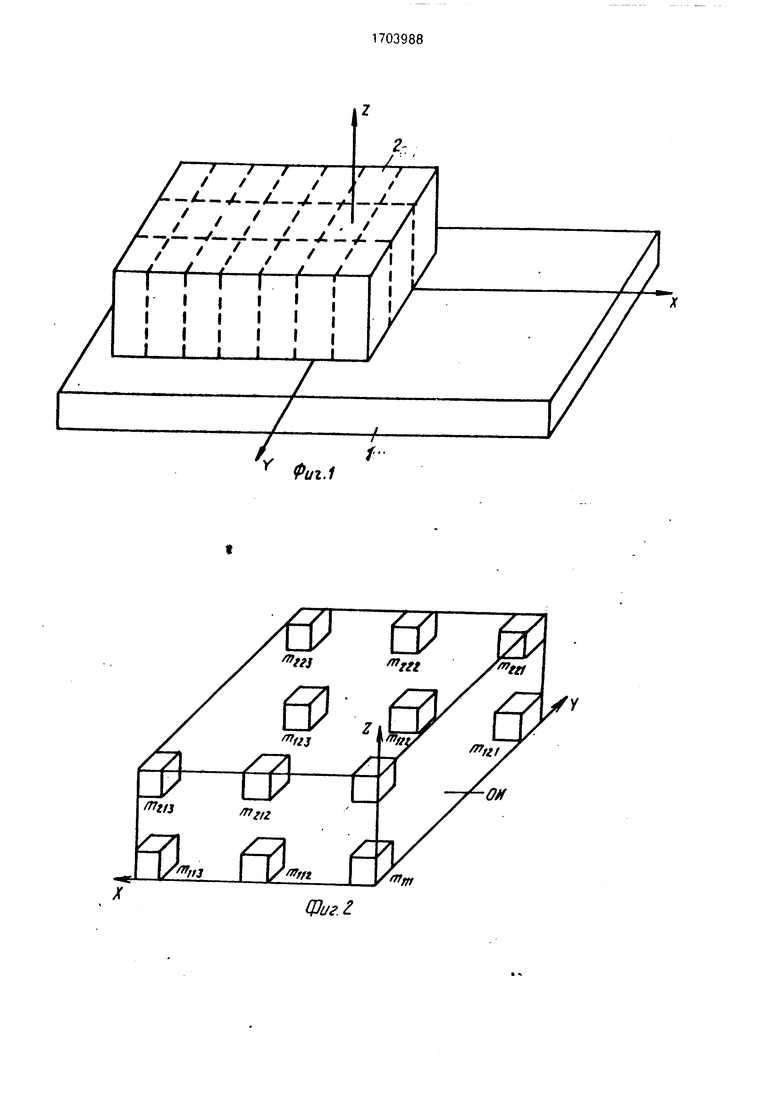
На фиг. 1 показан принцип разбиения объекта на столбцы в плоскости a (XOY); на фиг. 2 - принцип разбиения объекта на элементы сечениями в плоскостях а и р; на Фиг. 3 - портреты матриц А 4размерностью 12х12( ) и А размерностью 12x12 ( ).
На фиг. 1-3 приняты следующие обозначения: 1 - динамометрическая платформа; 2 - объект исследований имеет форму параллелепипеда, однако на практике он может иметь произвольную форму; - коэффициент матрицы А , + - коэффициент матрицы 2; . - коэффициент матрицы-0.
Для пояснения предложенного подхода к определению веса отдельных частей неразделимого объекта рассмотрим в качестве примера его условные сечения в плоскости «по оси ОХ (фиг. 1), считая, что момент силы Мр, вычисленный по формулам (1) по измерениям Рг, Ру, уже известен.
Рассмотрим уравнение моментов сил по оси ОХ, считая, что плечи элементарных J-x сечений отсчитываются от точки 0. а распределение веса в пределах сечения - равномерное:
П уравнении (1C) количество неизвестных Пх,следовательно, количество допустимых решений Пх-1.
Однако, если имеется дополните пая 5 априорная информация ob обьекте исследований, например, в виде ограничений на значения mjc, то может быть получено единственное приближенное решение методами математического программирования. 10 При использовании нелинейного программирования задача сводится к минимизации выпуклого функционала Ф(2).
Ограничения (3) и (5) вытекают из физической сущности задачи, так как вес не мо- 15 жет быть отрицательным и сумма .
Ограничение (4) носит более эмпирический характер и выражает по сути основную идею предложенного способа, состоящую в том, что вес сечений (или других частей) объ- (15) 20 екта можно приближенно определить, если распределение веса есть гладкая функция координат. На практике это означает, что вес j-ro и (|+1)-го сечений могут отличаться лишь на величину, не превышающую W (W- 25 эмпирический коэффициент, выражающий свойство гладкости функции распределения веса объекта, выбран экспериментально . но могут использоваться и
пх 30 другие критерии).
Если уменьшить дискрет Д1х. то практически любой неоднородный объект удовлетворяет условию (4). Однако при этом увеличивается количество дискретов и соот- 35 ветственно возрастают требования к быстродействию используемого компьютера и его программному обеспечению.
Пусть и вес сечений может принимать целые значения при распределении 40 , . . Уравнение (16) имеет вид:
mic-0,5+m2c-1,5+m3c-2.. (17)
45 Будем считать, что измерения осуществляются без ошибок. Тогда , т2 4. Условиям (3) и (5) удовлетворяют следующие допустимые распределения: 50
55
mi
1 О
2
ГП2
2
4 О
тз
1 О
2
mjc 0-0.5) Д1Х Мх
J 1
(16)
Ограничение (4) носит более эмпирический характер и выражает по сути основную идею предложенного способа, состоящую в том, что вес сечений (или других частей) объ- екта можно приближенно определить, если распределение веса есть гладкая функция координат. На практике это означает, что вес j-ro и (|+1)-го сечений могут отличаться лишь на величину, не превышающую W (W- эмпирический коэффициент, выражающий свойство гладкости функции распределения веса объекта, выбран экспериментально . но могут использоваться и
пх другие критерии).
Если уменьшить дискрет Д1х. то практически любой неоднородный объект удовлетворяет условию (4). Однако при этом увеличивается количество дискретов и соот- ветственно возрастают требования к быстродействию используемого компьютера и его программному обеспечению.
Пусть и вес сечений может принимать целые значения при распределении , . . Уравнение (16) имеет вид:
mic-0,5+m2c-1,5+m3c-2.. (17)
Будем считать, что измерения осуществляются без ошибок. Тогда , т2 4. Условиям (3) и (5) удовлетворяют следующие допустимые распределения:
5
mi
1 О
2
ГП2
2
4 О
тз
1 О
2
Однако при этом условию (4) удовлетворяет только распределение 1,2. 1, совпадающее с истинным.
1 Ioii0o;u;o vcTOfi inru.isui к ошибкам измерений методами минимизации Функционала (.} с с р-л пчпмняглм (3). (л) и (5) ягляютс ) мстодм inopainocoii poi уллрмээ- ции.
Однако для неСюльших пх 50 хорошие результаты получаются и при использовании классических методов многомерной оптимизации с ограничениями.
В уравнениях (6) и (11) коэффициенты строк матриц Л определяются способом построении сектора свободных членов, При определении столбцов обьекта р-й элемент вектора свободных членов определяется в виде суммы сечений mjc и пцс (nijc и n,kc о плоскости /3).
Таким образом, столбец ij находится в области пересечения сечений, следовательно, соответствующий р-й коэффициент матрицы /Хранен 2, а коэффициенты при столбцах, составляющих сечения, равны 1, остальные 0.
Днало1пчно строится матрица А, только о этом случае kij-й элемент пересечения образован двумя столбцами в плоскостях а и /.
Размерности матриц А .А соответствуют размерности вектора неиэоестных, но сепии матрицы получаются синмефичными и вырожденными. Поэтому на практике можно получить лишь приближенную оценку решения уравнений (0) и (11).
Хорошие результаты при решении уравнений (С) и (11) дает применение метода квадратных корней с эмпирической регуляризацией решения, при которой параметр регуляризации определяется из выражения П 0.5 vW, где 0 t 0,001,
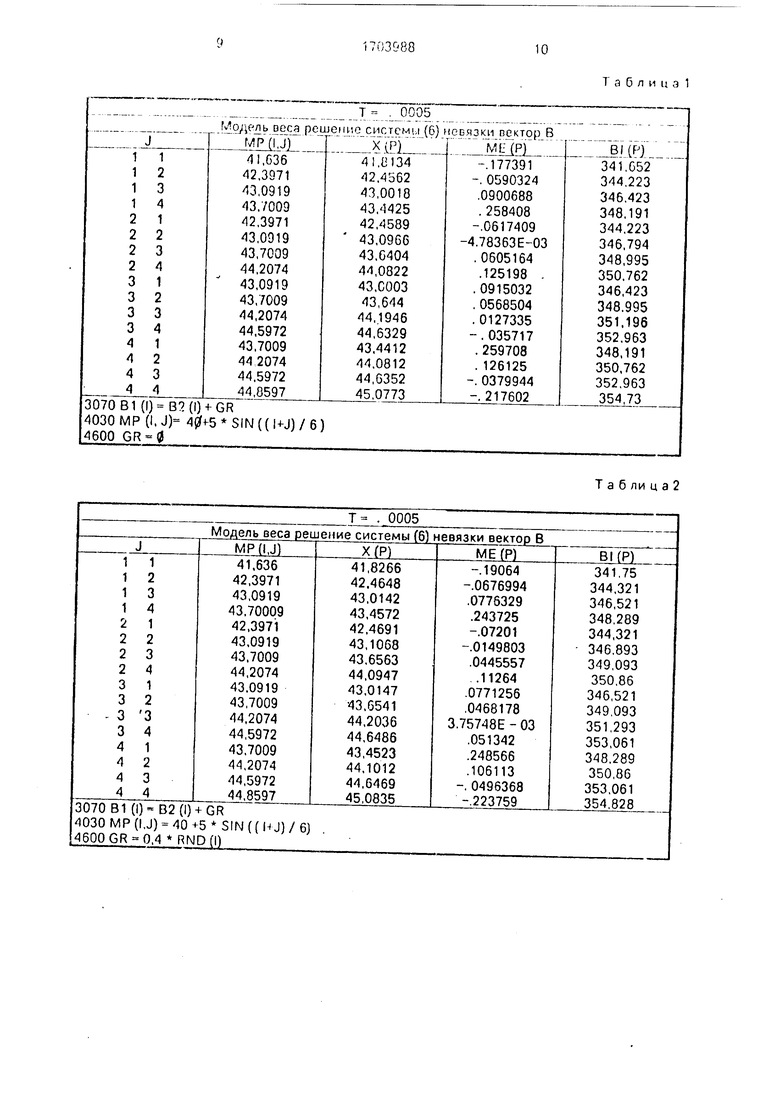
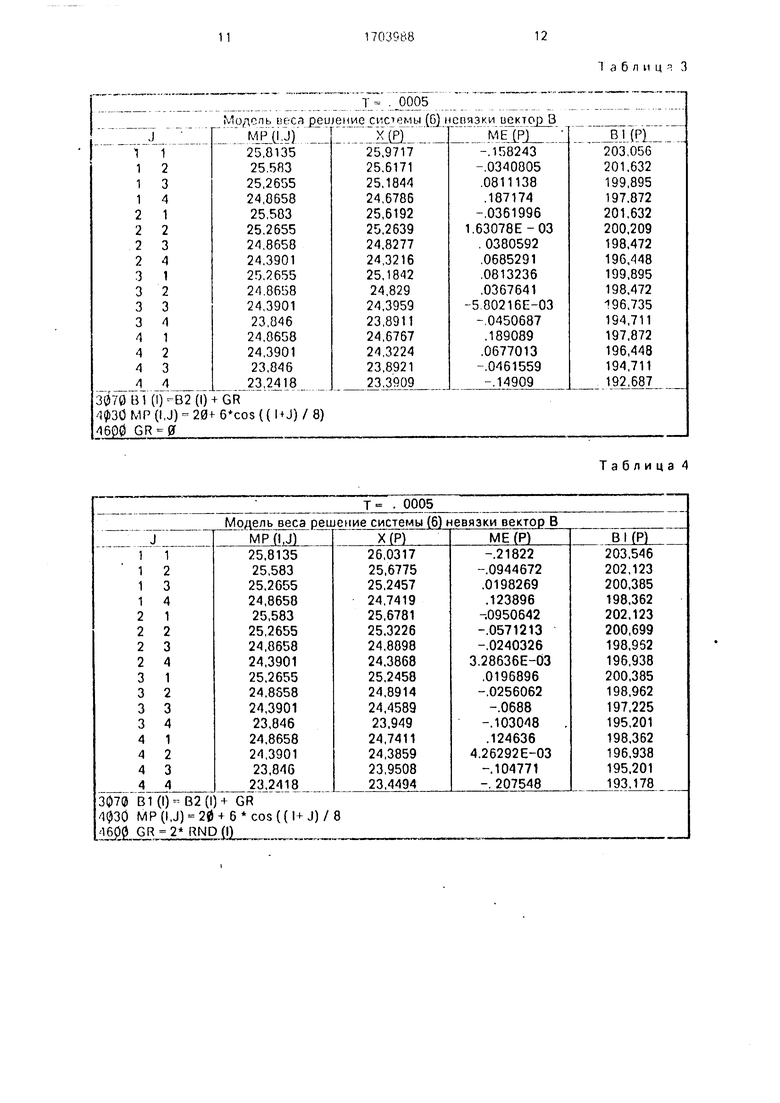
В табл. 1-4 представлены результаты численных экспериментов по определению сеса столбцов объекта в плоскости а для ,0005 и при различной степени зашумле- ния измерений ( вектора ).
Под каждой таблицей приведены фрагменты программы моделирования иабей- сике, поясняющие,, как строилась модель распределения иеса по столбцам и производилось зашумление вектора .
Результаты численного моделирования показывают, что если имеется сколько-ни- Судь гладкая зависимость веса столбцов обьекта от координат, то даже при 10%-ном
згнлумленни правой части /равнение (G) ошибки рс шемия не превосходят 1-2%. что свидетели:. вуот о практической пригодности предлагаемою способа.
5Аналогичные результаты получаются при решении уравнения (11).
Разделение задачи на этапы определения веса столбцов объекта и его отдельных элементов связано с тем, что часто в прак0 тических приложениях достаточно знать лишь распределение веса по столбцам.
Предлагаемый способ имеет обширную область приложений. Например, его можно использовать в устройствах таможенного
5 контроля, когда традиционные методы контроля объектов досмотра, основанные на их просвечивании, нельзя применять. Такая ситуация возникает при досмотре некоторой радиоэлектронной аппаратуры (персо- 0 нальных компьютеров), биологических обьектов.
В настоящее премя также изучается вопрос о применении предлагаемого способа с расширенным набором ограничений в
5 системах гравитационной .компьютерной томографии тела человека,
Формула изобретения Способ определения веса отдельных част ей неразделимого объекта, заключающий0 ся о том, что измеряют суммарный вес обьекта, размещают его на платформе и закрепляют, отличающийся тем, что, с целью повышения точности, определяют геометрический центр масс обьекта,
5 помещают его на трехкоординатную динамометрическую платформу, измеряют мгновенные значения проекций вектора силы тяжести геометрического центра масс объекта на оси прямоугольной системы коорди0 нат с центром в центре платформы, определяют проекции момента силы тяжести геометрического центра масс обьекта на оси выбранной системы координат, условно разделяют объект рядом плоскостей, парал5 лельных двум плоскостям системы координат, определяют оценки веса сечений объекта по каждой оси координат, вычисляют оценки веса отдельных столбцов обьекта, полученных условным разделением
0 объекта парами взаимно перпендикулярных плоскостей, а затем вычисляют вес отдель- ных частей объекта.
Т а б л и ц з 1
Т а б ли ц а 2
Таблиц 3
Таблица 4
/
/
/
Фиг.1
фи г. Z
тт
4х-х. .....
t TT TV
тГ гт Г7Т TT 7t
TV Tt 7T. 7t
}Ј . -X: Ј Ј 3Ј
« X
77 Л TY. T ТГ V
« X X- X t f
Tt T /t TV TC
5f« «)t« X 4- X
. . . . . € . X- X + X
rC TV TT Л TV
rv TV «
7x ПГ
+ -Xt X-
TV
7v
X- . . + . , . . . Я
p i««9r«
7t
TT 7t
/V t 7t T
TV zt T
Редактор О.Голооач
Техред М.Моргентал
Ззклз 55Тираж Подписное
ВНИИПИ Госудгфственного комитета по изобретениям и открытиям при ГКНТ СССР 113035, Москва, Ж-35, Раушская наб.. 4/5
Фиг.З
Корректор Л.Бескид
| Способ измерения распределения массы | 1986 |
|
SU1425459A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1992-01-07—Публикация
1989-10-03—Подача