Изобретение относится к конусным инерционным дробилкам и может быть использовано для рудоподготовительных отделений обогатительных фабрик цветной и черной металлургии.
Известна конусная инерционная дробилка, содержащая станину с наружным конусом и корпусом сферической опоры внутреннего конуса, вал которого соединен с охватывающей его цилиндрической подшипниковой втулкой дебаланса, имеющей сферический подпятник, причем корпус сферической опоры внутреннего конуса выполнен с кольцевой полостью, внутри которой размещен сферический подпятник подшипниковой втулки.
Привод вращения втулки дебаланса в этой дробилке выполнен в виде лепестковой муфты.
При таком исполнении недостатком является ненадежность лепестковой муфты и сложность монтажа и демонтажа дробилки. Кроме того, возникающие в лепестковой муфте при работе дробилки инерционные и упругие силы вызывают неравномерность нагружения подшипника дебаланса, что приводит к снижению надежности дробилки.
Известна конусная инерционная дробилка, отличающаяся от описанной тем, что привод вращения втулки дебаланса выполнен в виде шарового шпинделя.
Такая конструкция дробилки является в настоящее время наиболее широко применяемой и достаточно удобной и надежной. В этой дробилке груз дебаланса обычно располагается посередине подшипниковой втулки. Однако при отклонении внутреннего конуса от вертикальной оси относительно центра сферы его опоры в механизме привода возникают дополнительные инерционные силы от неуравновешенных масс шпинделя и втулки. Эти силы обуславливают неравномерность нагрузки на подшипник втулки дебаланса и, как следствие, снижает его работоспособность и надежность дробилки в целом. Для обеспечения равномерности нагружения подшипника втулки дебаланса необходим критерий расположения центра тяжести груза дебаланса, учитывающий влияние инерционных сил всех элементов привода конуса.
Целью изобретения является повышение надежности дробилки путем равномерного нагружения подшипниковой втулки.
Цель достигается тем, что в конусной инерционной дробилке с приводом в виде шарового шпинделя расстояние от центра тяжести груза дебаланса до центра сферы опоры внутреннего конуса определяется из выражения
Z∂= 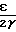 +
+ 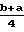 +
+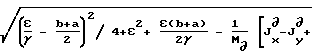 _→
_→
_→ 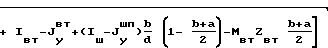 , где ε- эксцентриситет дебаланса;
, где ε- эксцентриситет дебаланса;
γ- угол нутации конуса;
а расстояние от центра сферы опоры конуса до верхней кромки подшипника втулки дебаланса;
b то же, до нижней кромки;
М∂- масса дебаланса;
Jх∂ момент инерции дебаланса относительно горизонтальной оси, проходящей через его центр тяжести;
Jу∂ то же, относительно вертикальной оси;
Iвт момент инерции втулки дебаланса относительно горизонтальной оси, проходящей через центр сферы опоры конуса;
Jувт момент инерции втулки дебаланса относительно ее продольной оси;
Iш момент инерции шпинделя относительно горизонтальной оси, проходящей через точку его опоры;
Iуш момент инерции шпинделя относительно его продольной оси;
Мвт масса втулки дебаланса;
Zвт расстояние от центра сферы опоры конуса до центра тяжести втулки дебаланса.
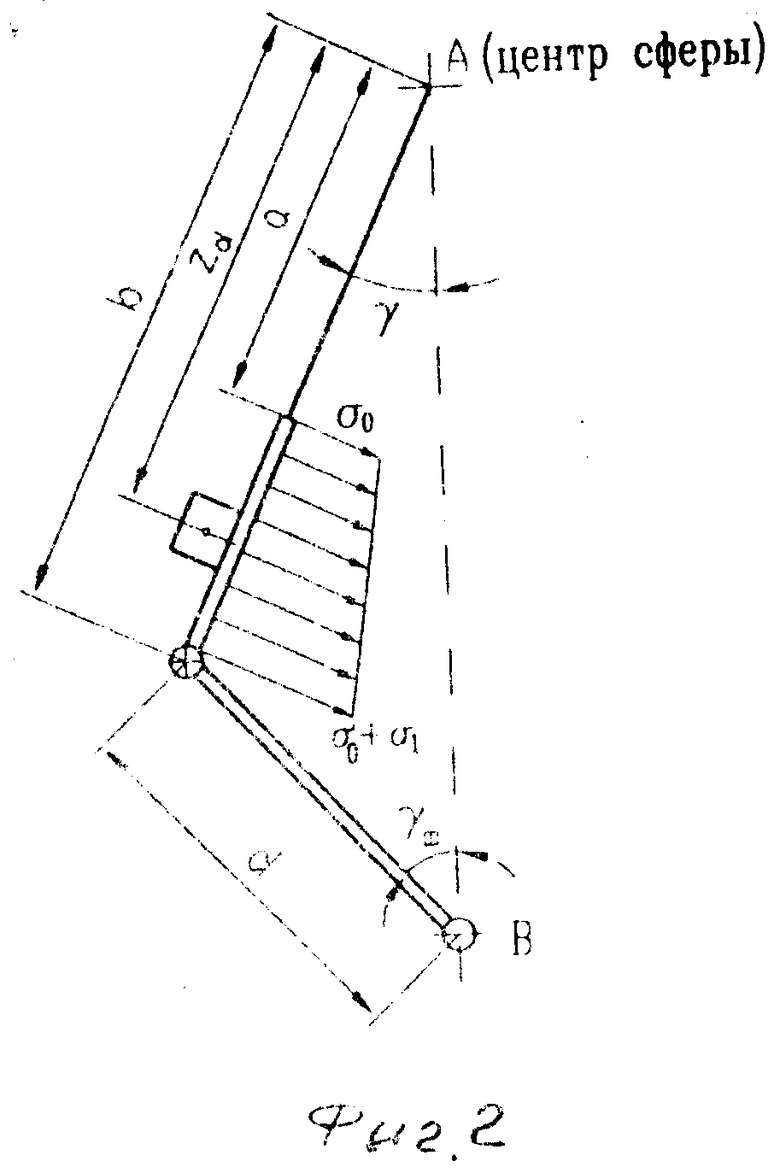
На фиг. 1 показана дробилка, продольный разрез, на фиг.2-3 расчетные схемы.
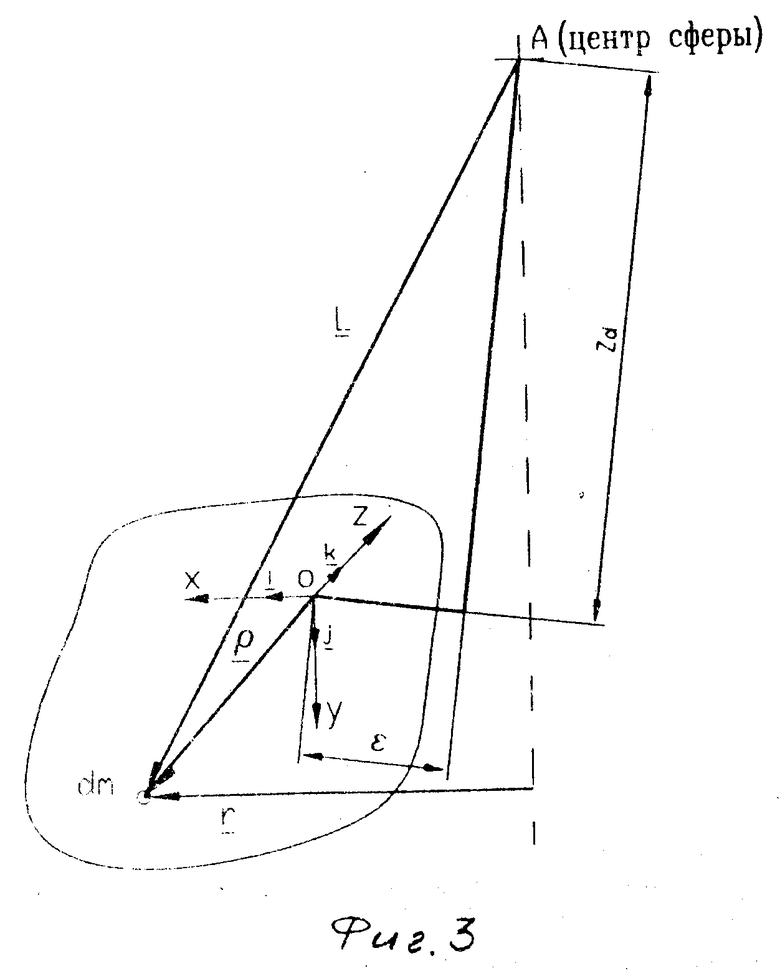
Для вывода приведенной зависимости, соблюдение которой обеспечивает наиболее благоприятные условия работы подшипника втулки дебаланса, составляется уравнение баланса горизонтальных сил, воздействующих на втулку, и уравнение моментов сил относительно центра сферической опоры конуса, используя расчетную схему, приведенную на фиг.2.
Для этого сначала рассмотрим выделенный на фиг.2 элемент массы дебаланса dm. Во вращающейся со скоростью вокруг вертикальной оси системе на него действует сила 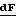
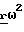 dm, где
dm, где 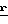 радиус-вектор, лежащий в горизонтальной плоскости. Поскольку дебаланс симметричен относительно плоскости XOY, величина общей силы может быть найдена как
радиус-вектор, лежащий в горизонтальной плоскости. Поскольку дебаланс симметричен относительно плоскости XOY, величина общей силы может быть найдена как
F 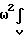 ηxdm здесь ηx- проекция вектора
ηxdm здесь ηx- проекция вектора 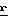 на ось ОХ (интегрирование по объему дебаланса). Положение выделенного элемента массы будем задавать относительно главных центральных осей дебаланса вектором ρ(фиг.2). При этом при отклонении оси конуса на угол γ (малый по абсолютной величине) можно принять
на ось ОХ (интегрирование по объему дебаланса). Положение выделенного элемента массы будем задавать относительно главных центральных осей дебаланса вектором ρ(фиг.2). При этом при отклонении оси конуса на угол γ (малый по абсолютной величине) можно принять
rx= ε+ρx+γ(Z∂+ρy) где ε- эксцентриситет дебаланса;
ρx,ρy- проекции вектора;
Z∂ расстояние, задающее положение центра тяжести дебаланса относительно центра сферы по вертикали.
Таким образом
F 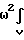 [ε+ρx+γ(Z∂+ρy)]dm ω2M∂(ε+γZ∂); поскольку оси задания ρ центральные
[ε+ρx+γ(Z∂+ρy)]dm ω2M∂(ε+γZ∂); поскольку оси задания ρ центральные
и 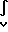 ρxdm
ρxdm 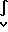 ρydm 0 где М∂- масса дебаланса.
ρydm 0 где М∂- масса дебаланса.
Для того чтобы записать момент центробежных сил, найдем момент силы от выделенного элемента dm относительно центра сферы dM 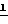 ×
× 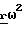 dm где
dm где 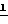 вектор-радиус элемента dm относительно центра сферы (см. фиг.2).
вектор-радиус элемента dm относительно центра сферы (см. фиг.2).
При отклонении на малый угол γвокруг оси OZ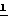
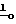 + γx
+ γx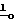 , где
, где 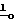 = (ε+ρx)
= (ε+ρx)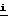 +(Z∂+ρy)
+(Z∂+ρy)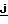 +ρz
+ρz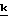
Подставляя, получим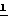 -
-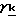 × [(ε+ρx)
× [(ε+ρx)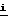 + (Z∂+ρy)
+ (Z∂+ρy)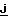 + ρz
+ ρz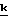 ]+
]+ =
= 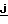 [Z∂+ρy-(ε+ρx)γ]+
[Z∂+ρy-(ε+ρx)γ]+
+ 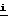 [ε+ρx+(Z∂+ρy)γ]+ρz
[ε+ρx+(Z∂+ρy)γ]+ρz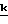
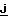 [Z∂+ρy-(ε+ρx)γ]+
[Z∂+ρy-(ε+ρx)γ]+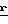
Таким образом j[Z∂+ρy-(ε+ρx)γ]×{i[ε+ρx+(Z∂+ρy)γ]+ρ2
j[Z∂+ρy-(ε+ρx)γ]×{i[ε+ρx+(Z∂+ρy)γ]+ρ2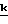 }ω2dm
}ω2dm
Общий момент
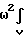 -
-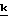 [Z∂+ρy-(ε+ρx)γ]×[ε+ρx+(Z∂+ρy)γ]+
[Z∂+ρy-(ε+ρx)γ]×[ε+ρx+(Z∂+ρy)γ]+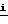 [Z∂+ρy-(ε+ρx)γ] ρz}dm
[Z∂+ρy-(ε+ρx)γ] ρz}dm
Интеграл от последнего слагаемого, включающего сомножитель ρz, равен нулю из-за симметрии дебаланса.
Учитывая, что оси задания ρx и ρyглавные центральные, последняя формула преобразуется к виду
M ω2[M∂(Z∂ε+γZ
Если провести аналогичные выкладки для втулки дебаланса (для которой эксцентриситет ε= 0), получим MBr ω2 γ(Iвт -Jувт), где Iвт момент инерции втулки относительно горизонтальной оси, проходящей через центр сферической опоры, Jувт осевой момент инерционной втулки.
Если записать момент сил инерции для шпинделя (для того чтобы найти силу реакции шпинделя в его верхней обойме, это удобно сделать относительно точки В (фиг.1) получим
Mш= ω2γ(Iш-J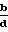
Отсюда горизонтальная реакция шпинделя
Fш= ω2γ(Iш-J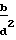
(Соотношение между γш и γ, учтенное в данной формуле, следует из соотнесения размеров b и d) (фиг.1).
Найдем силу и момент относительно центра сферы от распределенной нагрузки в подшипнике дебаланса. Если предположить, что нагрузка изменяется от верхнего края подшипника к нижнему линейно
т. е. σ σo+σ1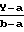 , то горизонтальная сила, передаваемая подшипником на вал конуса
, то горизонтальная сила, передаваемая подшипником на вал конуса
Fn= (b-a)(σо+σ1/2), так как целью предпринятого рассмотрения является получение соотношения параметров, при котором σ1= 0, т.е. нагрузка распределена равномерно, член, содержащий σ1, можно опустить.
То же справедливо и для момента, который в этом случае примет вид
Mп= 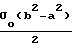 .
.
Запишем уравнение для горизонтальных сил, действующих на втулку, и уравнения для момента относительно центра сферы при условии σ1= 0.
ω2Μ∂(ε+γZ∂)+ω2MвтγZвт+ω2(Iш-J
ω2M∂(Z∂ε+γZ
+ω2γ(J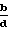
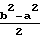 σo
σo
Исключая известное σ0 и разрешая уравнение относительно Z∂, получим
Z∂= 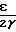 +
+ 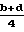 +
+ 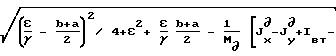 _→
_→
_→ 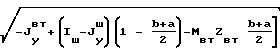
Реальную нагрузку на подшипник всегда можно представить как сумму симметричной и несимметричной частей. Расположение дебаланса груза на расстоянии Z∂ обеспечивает отсутствие кососимметричной части.
При размещении центра тяжести груза дебаланса в соответствии с предлагаемым выражением комплекс инерционных сил, возникающих при работе дробилки, обеспечивает равномерное нагружение подшипника втулки дебаланса по его длине, что приводит к существенному повышению его работоспособности.
Дробилка включает корпус 1 с наружным конусом 2 и сферической опорой 3 внутреннего конуса 4, имеющего вал 5 с размещенной на нем цилиндрической подшипниковой втулкой 6 дебаланса 7, установленной на сферическом подпятнике 8, закрепленном на корпусе сферической опоры 3. Втулка 6 соединена с помощью шарового шпинделя 9 с приводным шкивом 10. Расстояние от центра сферы опоры 3, имеющей радиус R, до центра тяжести дебаланса 7 определяется из приведенного выражения.
Дробилка работает следующим образом.
Вращение от шкива 10 передается через шаровой шпиндель 9 цилиндрической втулке 6 и закрепленному на ней дебалансу 7. Дебаланс своей центробежной силой заставляет внутренний конус 4 совершать гирационное движение, обеспечивающее разрушение материала между конусами 4 и 2.
Расположение дебаланса в соответствии с предлагаемой формулой обеспечивает равномерность нагрузки по длине подшипника втулки дебаланса, что приводит к повышению надежности дробилки за счет исключения возможных перегрузок по краевым участкам подшипника из-за неравномерного его нагружения.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОНУСНАЯ ИНЕРЦИОННАЯ ДРОБИЛКА | 1989 |
|
SU1685000A1 |
| Конусная инерционная дробилка | 1979 |
|
SU814446A1 |
| КОНУСНАЯ ИНЕРЦИОННАЯ ДРОБИЛКА | 1990 |
|
RU2014887C1 |
| Конусная инерционная дробилка | 2001 |
|
RU2225257C2 |
| Конусная инерционная дробилка | 1981 |
|
SU1085624A1 |
| Конусная инерционная дробилка | 1983 |
|
SU1258470A1 |
| Конусная инерционная дробилка | 1986 |
|
SU1609479A1 |
| Инерционная дробилка | 1977 |
|
SU897279A1 |
| Конусная инерционная дробилка | 1977 |
|
SU808130A1 |
| Конусная инерционная дробилка | 1983 |
|
SU1310020A1 |
Изобретение относится к конусным инерционным дробилкам и может быть использовано для рудоподготовительных отделений обогатительных фабрик цветной и черной металлургии. Целью изобретения является повышение надежности путем равномерного нагружения подшипниковой втулки. Конусная инерционная дробилка содержит станину 1 с наружным конусом 2 и корпусом сферической опоры 3 внутреннего конуса 4, вал 5 которого соединен с охватывающей его цилиндрической подшипниковой втулкой 6 дебаланса 7. При этом расстояние от центра тяжести дебаланса 7 до центра сферы опоры внутреннего конуса выполнено в соответствии с зависимостью, учитывающей эксцентриситет дебаланса, угол нутации конуса, взаимное расположение по высоте центра сферы опоры конуса и кромок подшипника втулки дебаланса, а также длину шпинделя и массу втулки дебаланса. Кроме того, зависимостью учитываются моменты инерции основных конструктивных элементов, входящих в состав привода конуса и его опоры. 3 ил.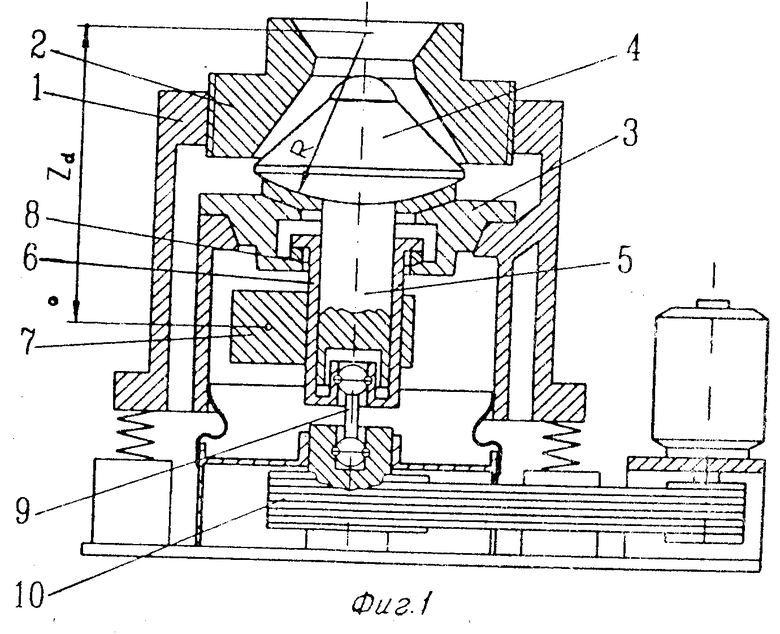
КОНУСНАЯ ИНЕРЦИОННАЯ ДРОБИЛКА, содержащая станину с наружным конусом и корпусом сферической опоры внутреннего конуса, вал которого соединен с охватывающей его подшипниковой втулкой, имеющей сферический подпятник и несущий дебаланс, а также шаровой шпиндель и привод, отличающаяся тем, что, с целью повышения надежности работы путем равномерного нагружения подшипниковой втулки, расстояние от центра тяжести дебаланса до центра сферы опоры внутреннего конуса выполнено в соответствии с зависимостью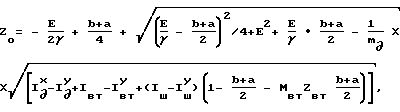
где Z∂ расстояние от центра тяжести дебаланса до центра сферы опоры внутреннего конуса;
ε эксцентриситет дебаланса;
g угол нутации конуса;
d расстояние от центра сферы опоры конуса до верхней кромки подшипника втулки дебаланса;
b расстояние от центра сферы опоры до нижней кромки подшипника втулки дебаланса;
M0 масса дебаланса;
I∂ момент инерции дебаланса относительно горизонтальной оси, проходящей через его центр тяжести;
I
Iвт момент инерции втулки дебаланса относительно горизонтальной оси, проходящей через центр сферы опоры конуса;
I
Iш момент инерции шпинделя относительно горизонтальной оси, проходящей через точку его опоры;
d длина шпинделя;
Mвт масса втулки дебаланса;
Zвт расстояние от центра сферы опоры конуса до центра тяжести втулки дебаланса;
I
| Инерционная дробилка | 1977 |
|
SU897279A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
Авторы
Даты
1995-06-19—Публикация
1990-06-12—Подача