Известны вычислительные машины для минимизации структуры логических схем, содержащие релейные схемы, табло индикации на неоновых лампах и тумблеры ввода данных.
Предлагаемая вычислительная .машина отличается тем, что она содержит релейные устройства набора обобщенных кодов, которые подключены к индикаторам обобщенных кодов и через логическуго схему подсоединены к табло цифрового набора, логическая схема соединена с ключом режима анализ - синтез, с ключами ввода рабочих чисел и с ключами ввода sanpeuieHHbix чисел. Это позволяет решать задачи анализа и синтеза релейных устройств на основе обобщения кодой н онератора С15ер1;ывання.
Логическая схема построения машнтнз определяется формулой
,,„,(1)
где ОК - сумма обобщенных кодов, выраженных в двоичном счислении и характеризующих заданные условия работы; - знак перехода от заданных условий работы к цифровому laбору;
ОЛ,„| - сумма оитима.тьных обобщенных кодов, нри которых выполняются заданные условия работы.
(2)
В общем случае ХОД- 0/(„„.,.
Вычислительная машина анализа и синтеза релейных устройств нозволяет:
а)по последовательности работы элементов дискретного действия построить таблицу включения, одпотактный эквивалент многотактной схемы н графическую свертку;
б)нодсчитать автоматическн весовые состояния элементов в таблице включенпя (однотактном эквиваленте) для определения ее реализуемости;
в)подсчитать автоматически весовые состояния э.тементо ;. в таблице вк/иочення noc.ie введения промежуточных элементов, еслн таблица включения первопачально была нереализуемой;
г)провести минимизацию заданных условий работы х; целью нахождения минимального числа нростых нмплпкаптов. для одпотактных и многотактных релейных устройств: е)провести гшм.шз релейного устройства любой сложности и конфигурации; провести автоматически суммирпваиие V 9; ,0 ж)выдать экономичную документацию. Формула (I), по которой iiocTi)oeiia MaHjHua базируется иа следуюи1,их теоретических разработках: обобщенных кодов; оператора свертывания; графической свертки. Обоби1,енны.м кодом называется нозициоииая комбинация из символов (0,1, -), Обобщенный код оиисыг ает то , что нрису1це двум и более двоичным числам. удо15,1етвориющим некоторвп требованиям. п-Разрядный обобщенный код, в Т разрядах которого стоят тире, связыпаег 2 двоичных //-разрядных чисел. П)и 7 -О oбoбн eпный код превращается в двоичный код. Таким образом, двоичный код есть частный случай обобщенного кода. Для иолучеиия из одного обобщенного кода всех связываемых им чисел необходимо и достаточно нанисать обобщенный код 2 раз, а затем тире заменить всевозможны.ми комбинациями из нулей и единиц. Понятие обобщеиного кода близко к нонятию имнликаит. Однако первое нонятие более иолно отображает суи;иость связей между соседними числами. Соседними называются два двоичных числа, отличаюн.и1еся друг от друга любым одним разрядом. Например, два десятичиых числа О и 1 являются соседними. Получение кодов чисел из обобщенного кода Л осун1,ествляется последовательной заменой тире вначале па О, а затем на 1, Очевидно, число соседних чисел равно числу соседних разрядов, Рационально обобщенный код с любым числом тире Г и с любым их расположением в /1-разрядах изображать единственной точкой на плоскости. Для обеспечения взаимно однозначного соответствия между обоби1еииым кодом и точкой паплоскости достаточио выполнить условия: (I т /) -|- г . 2 const; 1 - У QI/ ; с:- :Q(-);,(Зг) J i где п - разрядность обоби1.енного кода; В этом случае чис.ча а, Ь, с .можно : ассматривать как координаты точки трехмерного нрост1)анства, Ес;1И каждый из п разрядов обобщеиного кода может припимать три значения (0,1, -), то всего существует 3 /г-разрядпых обобщецных кода (в это число входят и 2 двоичных кода), В силу равенства (За) все 5 точки, изобража1ОН1.ие 3 обобщеиных кода в пространстве, располагаются на нлоскости, ограниченной с помощ ю коордииатных плоскостей taK, что образуется ра15носторониий треуго.тьник, наиоминаюии Й букву Д (дельта). По этой причиие диаграмма с 3 точками, обобщеии1.1ми кодамп, названа Л-диагра.ммой. Для практических расчетов достаточио иметь дело с проекцией Д-диаграммы иа оси о и /;, Это означает, что достаточно вычислять суммы а и Ь, поскольку np.i известных а и b одиозиачно оиределяется с. В этом случае А-диаграмма нолучается еиш более комиактной. Не рассматривая с1К)йств Д-диаграммы, укажем, что любой наре координат а и Ь, удов,летворяющих ус.ювию аответствует одиндьчи два (сопряженных) обобщенных кода. Если координата.м а н /; соответствует черная точка на Л-диагра,мме, то эти координаты изображают один обобщенный код. Например, координатам соответствует обобщенный код (1-0); коорд1П1атам Ь () соответствует один обобщенный код (О) и т, д. Если координатам а и b соответствует белая очка, то эта точка описывает два обоб цениых кода. .: -диаграмма наглядно иллюстрирует связи не только между соседними числами, о н между обобщенными кодами. Количество обобщенных кодов е онрееляется но формуле .(4) В фор.му.че (4) О/С содержат коды с одии.м, вумя, тремя и т, д. тире. Подсчет количества обобщеиных кодов, соержащих тире, производится по следуюи1ей ормуле: 3«-2--:/г.2---1-,- :-1.,/г.Оь-1)(« -2) ,.. 1-2-3 6iuee число кодо1} равно
С целью получения ичсгрумента, компактного, чем Д-диаграмма, был исследован зонрое об использовании «свободной обла,, 9/
сти А-диагра мы, т. е. такой, где - iarf
В результате была создана решетка о;)обн1енных кодов.
Решетки обобщенных кодов онределяют связи между числами и обобщенными кодами и позволяют решать задачи анализа и синтеза релейных устройств. Так, нанри1мер, в трехразрядной решетке обобщенных кодов наглядно реализуется метод Квайна-Мак-Класки без всяких нромежуточных выкладок.
В самом деле: д.ля условий F(r). (1,3, 5, 7) по методу Квайна-Мак-Класки задача минимизации решается так:
. . 1 I По решетке обобщенных кодов оиерация но вычис;1е 1ию ОК А проводится в один шаг: но 25
0,1 (00-) 0,2 .--.(О-0)
О, 4-: (-00)
1.3 (0-1) 1,5-: (-01)
2,3 -. (01-)
0,1,4,5.-. 0,4,1,5 (00-) 0,2,4,6 .0,4,2,6 .(0-0) 1,3,5,7. 1,5,3,7-(0-1) 2,3,6,7: 2,6,3,7- (01-) 0,1,2,3 -0,2,1,3:. (00-) 4,5,6,,6,5, (10-)
ОКг - 0,1,2,3,4,5,6,7 0,2,4,6,1,3,5,7 0.1,4.5,2,3,6.7
... (О) . (1 - -) (0) . (1)
--: (- О -) . (- 1 -) ()
Таки.м образов, в решетке обобщенных кодов легко просматриваются всевозможные связи 2. переключательных функций. Обобщенные коды легко согласуются с любой формой записи условий работы.
Например, F(x)abc + ) () 5 /2,3 2,3,5.
Обобщен ые коды жестко связаны с десятичными числами. Решение задачи минимизации заданных условий работы легко осуществляется с помон;ью рещетки обобщенных кодов. Формула (1), ноказываюндая переход от
:о/ к
/,
jSfv: 1
позволяет про11звест11 предварительную iинимизацию заданных условий работы с целью исключения х избыточности.
Например, F(x},.,,.---ac--: с--а- -:(1-1) /(-11)./(01-)-(5,7) /(3.7) ,3)--:- 2.3,5,7.
ЧИСЛ;;л i, 3 находите; o6()6jj 1еп : I Ьк: КОД О--1.
Донолнеинем к обобщенному коду (О---) яиляется код (I - i) чисел 5. 7. Обоб ненны.м кодом двух o6o6iueHi;: ix кодов (О-i) (--1) является код квадрата (- -1). При этпмдпа o6o6uieHf b X кода, связанные второй диагональю квадрат;, ноказь Ба:ст, что тот же результат может быть нолучеи нрп сравнен Н
кодо.;. (-01) и (-П). Такнм образом, решетка обоб11;, кодов учитывает всевозможиые перестановки десятичных чисел и обеснечивает нолучение требуемого результата. , что нроцесс получения обобщ.енных кодов с числом 7 1 но методу КвайиаТ Ьмх-Класки обязательно проходит через ста5дию получения обобнденных кодов с . Решетка обобщенных кодов позволяет получить ответ о связях больнюго количества чисел, минуя промежуточные операции по: чепня обобщенных кодов с 7:, поскольку квадрат
0 с обобнлен; ы: 1 кодом (- -1) верщинами соединен с числами , 3, 5, 7.
Таб.пица 1
2.6: (--lOl
3.7.(-11) 4,5 ..-(10-)
1.6: . (1-0)
5,7. (1-1) б,7 -(11-)
(-01) (-0-)
) (-00) .
()-(0)
) (- -СО) ):-:(- -01).
(- 1J) (1)
(-11 ). ()
) - (-10)
(0-1)-: (О) ) . (0-0) ) (1-0)
(1-1) ЧЬ --
Используя вторую часть формулы (1):
ОЛо;,..
30
(5,7),: (01-)
F{
V (l - l)ab+ac.
Таким образом, запись условий работы возможно проводить в дизъюнктивиой 1шрмаль110.1 форме, от которой легко осуществляется
5 переход к цифровому набору. При таком подходе отпадает необходимость в составлении различного Tiina карт ;1ли таблиц (Карно, Вейча и т. п.), si которых констит С1гты дополнительно кодируются нулями и е.ипшца0ми.
Преимущсст:;а обоб ценных кодов :1появятC5I нри расслютрепии сун ности све;ггь::;а1 ия информации и изображени.я ее в зиде графической свертки.
5
Оператор серт: тапия - это символ L, указывающий на переход от двоичных к 2 сг-ричны.м неременшзш. где сг - нелое по.чожнте.чьii(;p ис.то. На основании табл. 1 пoкaжe : ci-.язи между обобн;.еннымн кодами с/; 3.
Можно показать, что любая таблица двоичных чисел может быть свернута и записана однозначно ей соответствующей формулой вида:
1
F(Xn,Xn-l,- . Al) 2,-(, . . .,,,) ;i -Л
.(,,3,, . . . р„)/гг- . . . -(, . . . ,
(7)
где .v,,,.v...i ,...л| --- база обобщенного кол,:; X - символ логической суммы;
о;., р, ... (1 -2ф-ричные переменные, для которых ф принимает значение 1, L, /«; /,, i,, ... 1 - числа, указывающие количества разрядов для а, р, ...О), соответственно; L - символ оператора свертывания, показывающий, что для перехода от формулы (7) к таблице двоичных чисел необходимо проделать следующие операции:
1)каждое из чисе: а должно быть переведено в двоичный код и записано числом двоичпых разрядов /1 построчно с каждым из чпсел р, которое должно быть записано в двоичном коде числом разрядов /г. При этом числаэк1 ивалепты а располагаются в старших разрядах, а числа-эквиваленты р - в младщих;
2) из строк, полученных в результате предыдущей операции, должна быть дополнена в младщих разрядах двоичным числом-эквивалентом каждого из чисел следующей скобки;
3)операция дополнения строк данного оператора L,. продолжается до тех поп, пока ке будет развернута последняя скоба с числакш OJ, записываемыми через / двоичных разрядов;
4)операции 1-3 повторить для каждого из Р операторов L-(i 1,2,..., Р).
Использование оператора свертывания позволяет проводить анализ многоразрядных релейных структур с числом переменных л 10,
В практических случаях весовые состояния элементов нри онисываются десятичныгчп числами, порядок которых указан в табл. 2.
Из таблицы следует, что при приходится иметь дело с трехзначнЫлМи числами, а при каждое носледующее состояние описывается четырех- и более значными десятичными числами. Такое положение сильно затрудняет перевод условий работы, выраженных в дизъюнктивной форме, в соответствующие цифровые наборы.
аблши 2 Т
71
2048
11 12 13 14 15 16 17 18 19
4096
8192
16384
16
32768
32
65536
64
131072
128
262144
256
524288
512
1018576
90
1024
Суниюсть свертывания условий работы многоразряди й релейной структуры, заданных в дизъюнктивной форме, рассмотрим на примере восьмиразрядного обобщенного кода. Эта функция характеризуется, например, следующими рабочими числами:
) X KiXi K X- X- XoXi ,X,X
.5Х4ХзХ2Х,, (1 - 110 ПО) --- (182,246).
Вычисление цифрового набора - трудое.мкая операция. Рассмотрим свойства обоб1ценного кода при делении его на монады, диады, триады и диады и тетрады. В общем случае желательно делить обобщенные коды на такие ф-ады, которые легко согласовываются с разрядностью решеток обобщенных кодов. Представим /Y-ts-f-..г ( 182,246), где S - знак логической суммы рабочих чисел, при которых структура работает, и виде табл. 3.
Таблица 3
Из табл. 3 видно, что условия работы функции F() ; (182,246) можно выразить через оператор свертывания так:
F(x,-Xi) 1(2,3)2()2(1}2(2)2 или
L(2,3)2(6).5(6)3 или(8)
(ll,15).l(6)4
где i, 2,3,4 - показывает разрядность- чисел в ф-аде.
Из формул (8) видно, что при делении обобLuennoro кода на ф-ады подсчет рабочих чисел резко упрощается. В этом случае нет необходи.юсти производить вычисление чисел 182,246, поскольку переход от чисел, стояпикк
водится элементарно по решеткам обобщенных кодов. Действительно, в формуле (8) оператор свертывания можно представить логическим произведением обобщенных кодов:
f (х. - л-,) - (0/iiv), ()2 (ол:)о (oк:, или
{0/()2(0/()з(0/С)зили
(0/().()(9)
Если вместо OKi подставить числа с указанной разрядностью, то получим те же значения, которые приведены в табл. 3.
Таким образом, оператор свертывания является также средством изображения обобщенных кодогз в более ко.мпактной форме и избавляет от необходимости проводить громоздкие вычисления чисел в десятичном счислении при . Поскольку рещетки обобщенных кодов являются инструментом многоразового использования, изготавливаемым один раз, это является существенным преимуществом способа.
Графическая свертка условий работы представляет собой плоскостное геометрическое изображение оператора свертывания. Она базируется на свойствах обобщенного кода.
Графическая свертка может быть дву.к-, трех-, четырех-, /с-мерной. Поясним супдность сказанного на примере.
Пример. Построить таблицу чисел от О до 63.
Ре имение. Расположим десятичные числа от О до 63 так:
Нетрудно видет:,, что двоич::ь е числа, стоящие перед тире, в каждом обчтбщенном коде представ.т5;101 собой числа от О до 7. Тогда, если разделить оСобщег-пгые коды ка две части, то в одной будут содсрлчаться три тире, а в другой - числа, которы.м:-; будет характеризоваться каждая строка. Г:,образк:,: таблицу чисел так:
О 1 2 3 -4 5 6 7,
о.с.
15 23 31 39 47 55 63
I.S.
2,16.
3 24,
4,32,
5.40,
6.48.
7.56.
Ч1;с.1о м таб.пще может быть получено: из обобщенного кода путем последовательной за.меиы тире вначале на О, а затем на 1; прибавлением к базовому числу, стоя ему в третьей (слевг;) ко.юнке чисел нулевой строки; кодированием числами строк и чгслам;; i:y;:ero строк .
Третий способ и является cyHuiocTbivO представления обобщенных ко;ов десят11чн1)кми числам;-: ьулевой строки.
Действительно, если числа нулевой строки будут представлять собой обобщенш-.п код ОЯ, а числа строк - обобщенный код О/С, то каждое числе: внутри таблицы может быть представлено кодом:
ОК: --- OKi 0X1
Например, число 10 коднруется так:
0 О К . - (П:;-(2):5 (ООП (010): :
-001010.
Числа 4.5.6,7,12,13,14,15 составляют код 0/((О.П,, (4.5,6.7):; (00-) . (1- . -) (00-1).
Следовательно, номера строк показывают, в каких строках повторяются числа нулевой строки.
Таким образсм. таб,1:ща чисел может быть изображена числа:-л11 нулевой строки и числами строк.
В таком виде таблица чисел представляет собой графическуЕО свертку, на поле которой точками могут изображаться коды чнсел. Если в каждой точке таблицы проставить число нулевой строки, то, зная, в каких строках стоят эт числа, легко найти либо полное десятичное число, либо его код. Кроме того, по графической свертке легко определяются соседние числа. Для этого ;1еобходимо апать, как связаны между собой соседние числа от ДО семи. Ответ а этот вопрос дает трехразрядная рещетка обобщенных кодов.
Например, определить являются ли соседними числа 0.1,4,5,8.,16,17,20,21.24,25.28, 29 и если да, то ,1 будет их обобщенный код
Пользуясь таблицей, наносим эти числа на графическую свертку. Методика нанесе:: ;я ч {сел базируется на вычитании из заданных чисел наибольшего числа, стоящего в левой колонке, так числа от О до 7 записываются в нулевой строке, поскольку вычитание нуля не изменяет результата. Бо второй строке :-;-.ii cь:;:lc i те жр чи(:г, что i: :; строке.
аис,1а 7,15,23,31 ; OCiaiJ,:ieiibi ,- ./: ophL::::;;РОБКИ в выборе базового числа ;i определения места расположения члсел в строке. Про;1олжая ту же процедуру, аналогичную второй строке, п.олучаем таблицу:
,) 23 31
Составляем обобщенный код (GI{},,.fO/(). (0-3),(0,1,4,5)3-() (-G-J-.
(О-). Здесь 0/( показывает, в каких строчках Г;овторяегся обобще:-:ный К(;д . Это значит, что Ч1;сла являются соседними и имеют обобщеиньш код (О-).
Махождение кодов С/С и ОД не представляет трудностей, если нользоватвся реинетками обобьценных кодов.
Итак, жесткая о.анозиачиая связв между десятич:илл1и цифрами и обобщеиными кодами положеиа в осиову иосгроения решеток обобщепиых кодоз. Оператор свертывания и его геометричеекое изображение па плоскости - графическая свертка ягляются средствами записи условий работв. Записв условий работы на графической свертке числами нулевой строки легко еогласуется со входом в решетки обобш,еннв1х кодов и 1;озволкет быст()о 1;олучить резулвтат как при анализе, так и ари синтезе.
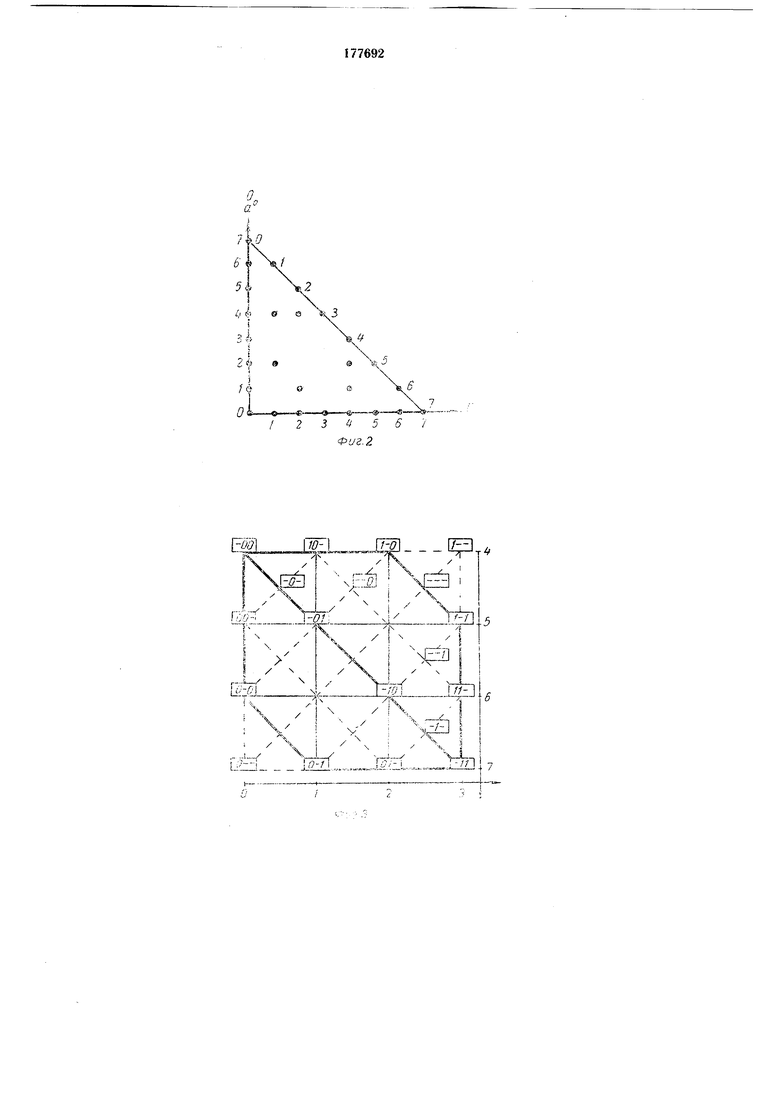
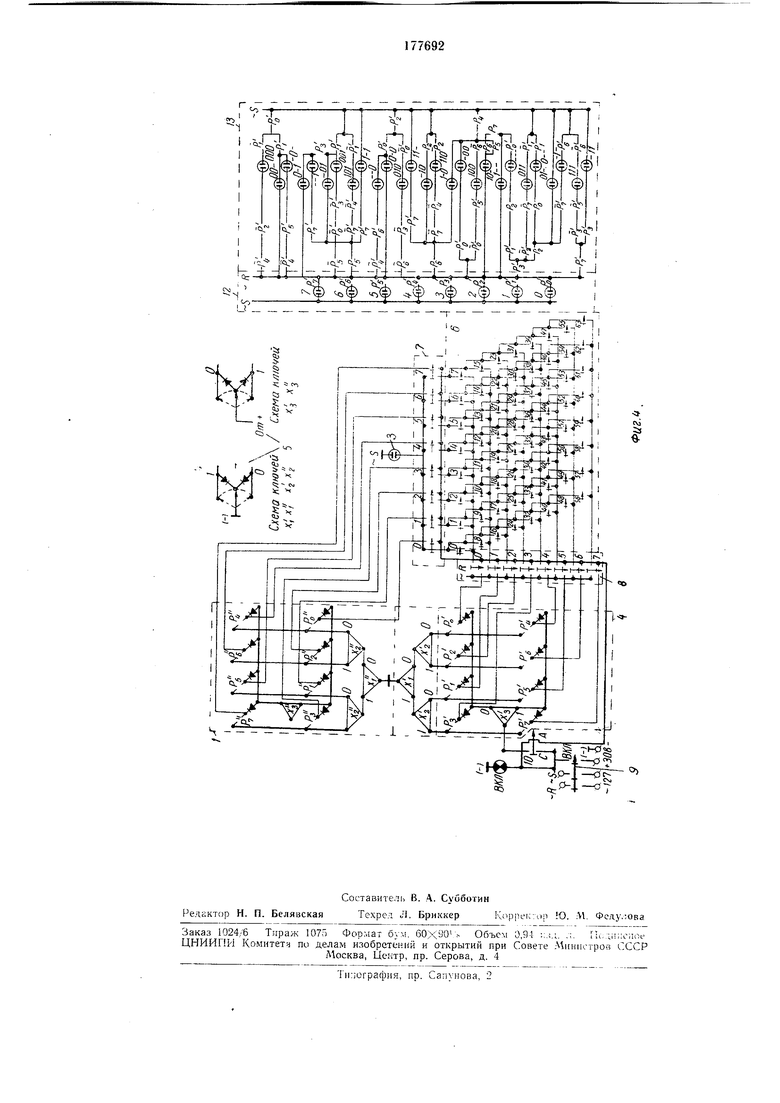
На фиг. 1 иредставлеи общий 1:.ид ввгнислптелвиой машиив ; на фнг. 2 изображена .A-;uiaграмыа; на фиг. 3 -- Т1:ехразрядная рещетка обоби1, кодов; на фиг. 4 - ее иринципиалвиая схема.
Вычислителвная мани-пта состоит из с-недующих осиовнвьх узлов: рещетки-дешифрато а (РД) / обобн,еиных кодов; табло 2 циа)рооого иабора; ламиы 3 запрета; решетки-.чегиифратор;: -: обобщенгалх кодов; ключей 5 ввода обобще1П;ых кодов первой и второй триадвк ключей 6 ввода заире1цеиив1х чисел (О-G3); ключей 7 вг.ода рабочих чисе,1 (ОД ); ключей S ввода рабочих чисел (GK), к.нюча 9- «включено ; ключа /f - «а:1ализ - синтез (А и С соответстве 1но).
При а1;алнзе оператор включает ключ 9 «включено и ключ 13 «анализ, ключами J o6o6iJieHHBix кодо первой и второй триад1з: последователвпо вводит в машину o6o6uienные КОДВ1. Реи;етка-дешифратор рег лизоаа::а на восвми электромагнитнь х реле. а к;;ое .реле сим11о;п-в-ирует одно из BOCBMII чисел трехразрядного обобпдеиного кода.
Следователвно, решетка-деп1ифратор позволяет осугцеетвитв постоянную связв между каждвКЛ обобщеииым кодом и л.ифровыл пабором. Отображением жесткой связи л:е/кду обобще1И1вп 1и лсда: 1и и цифровв1ми иабо)ами :вляетс; : обоб1,цеинв1х кодов.
Сигнализация о введенном обоб1ценно: коде осуп1,еетвляется HeonoBiiLMM лампочка:ли. нитаюнитмнся от сети переменного чере: контактв 1:еле, обмотки которв1х расно;10/кеHBI в рс1петке-деп1И1рраторе. Из 2/ возлюжных кодов, имеюилихся в решетке обобщеннвх кодов, HeoHOSBie лампочк { могут одновременно Бвгсвелггь псе обобн е.п-шш кодв (3 - 20 без кодов { -) или коды И 1;ин)рв, если одии числа об)азуют обоб1не Н1в;е кодв:, а другие -- нет.
Реле peшeтки-дeнJифpaтopa управляют но.леветкой: чисел табло цифрово ю (jpa. расположеинв х но горизонтали (0--7), позиция .У, ч по .гртикали (), нозтп ия 12. Схе.ма нодсвстки обобп.1епиых кодов для решетки-дешифратора (РД) иоказана па принцнпиалв: ОЙ схеме (см фиг. 4) (юзицией 7,3.
1 1ести;:азряд пнй код, разделек:1В Й иа две триадв, вводится каждвш и свою реп;етк 1 или -t- Одновременно реле каждой решеткидещифрато)а :/;:ра:5Ляют иодсветко) ()6o6Hiei:пых ,)доз и иК-рр горизонталвного и вертнкалвного ряда табло цифрового набора. Таким образом, решетка-дешифратор позво.ляет осуп1,ествитв: проверку в};сденного кода nvicM подсветки его к решетке обобп1еннв Х к;,-;и)в: иодсвj:H чисе;1 табло пифровогс набора и
определение па .-иниях нересечення подсвечеппвпх чисе:, ,;есятичивгх чисел, образующих в,веде1:ивп1 обобщен.ивп код. При еи Пезе ключами 7 или 8 табло цифрового .набора оказвь вается воздействие на те же зоселп-, реле решетки-дешифратора. Ключи 5 ввода обобщеиНВ1Х кодов ставятся в иейтралвпое ноложепие, вг;лючается тумблер «си;ггез, чем достигается иеклю/чеиие ключег 5 из ехемвг 1 ;1ючами 7 цифр горизонталвиого ряда включаютея 4iicла нулевой строки так, чтобы на фигуре ре1иетки / 11одевечивался один обобщенный код
ОД , связвшаюший несколвко соседних чисел.
Ключами 8 цифр вертикалвного ряда нключаютея те строки, в которвхдювлоряются числ -, образуюилие ОД. При этом па фигуре реН1етк:-деп1ифратора 4 11олсвеч:- вается одии обоби1епчвп код ОД, связвизающий несколько соседних чисел вертикалвиого ряда.
Резулвтируюн1ий обобщенный ко;; orincbiisaется с ()игур реншток 4 ц 1 и )иде ОД;
--:ОД; )Ki. :aivai ;:роцедура проделвп ается до тех пор, пока пе будут обслужен1л все
рабочие числа за;-1.аьного п, набора.
Определение ОД cyuiecTBcirno об.легчается,
посколвку решетка 4 обобн1енивпх Ko.noii позволяет быстро найти те числа, KOTopijie xai ai-;теризуют меета включения ОД .
Во избежание ошибок i-; определении ОД и ОД 1 маип-1не пpeдyc:vIoтpeпa схема за 1рета.
О;;а г,ключает в свой состав ключи 6 (О-G3), с помонцно ко орв1Х любое чиело от О до оЗ перевотит в состав запреи1,енив1х. :;апрета связвшает ключи горизонталь;юг; и ;;ертнкалвпого рядов, с помощвю которгтх о5ра: уется ОД и ОД. Если в процессе онределе ;ия ОД п ОД в состав рабочих и произво:::Пв:х чисел будет вк, хотя бг.- о;;,по запрОЕцег нос число. тО ю.светится ,та: п1очка «за:) 3. Такое юло/;:с 1-10 сгидететветвует
13
в состав рабочих произвольные числа нулевой строки.
Значит, наряду с произвольными числами в состав вошло одно или несколько запрещенных чисел. оЬмпочка «запрет будет гореть до тех нор. пока не будет устранена ошибка.
При ошибочном определении ОК лампочка «запрет также будет гореть, свидетельствуя о том, что в состав ОК. вошло одно или несколько запрещенных чисел.
Таким образом, схема запрета исключает возможность получения неверного результата при определении ОК и ОК.
14
Предмет и з с 5 р е г е н и я
Вычислительная машина для минимизации структуры логических схем, содержащая релейные схемы, табло индикации на неоновых лампах и тумблеры ввода данных, отличающаяся тем, что, с целью анализа и синтеза релейных устройств на основе обобщенных кодов и оператора свертывания, она содержит
релейные устройства набора обобщенных кодов, которые подключены к индикаторам обобщенных кодов и через логическую схему подсоединены к табло цифрового набора, логическая схема соединена с ключом режима
анализ - синтез, с ключами ввода рабочих чисел и с ключами ввода запрещень:ых чисел.






| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ТЕЛЕГРАФНЫХ СООБЩЕНИЙ С РЕГИСТРАЦИЕЙ ОШИБОК | 1970 |
|
SU263650A1 |
| Устройство для определения минимальных членов при синтезе структур дискретных автоматов | 1977 |
|
SU680174A1 |
| Устройство для сложения п-разрядныхдЕСяТичНыХ чиСЕл | 1979 |
|
SU824203A1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 1969 |
|
SU255993A1 |
| Устройство для суммирования двоично-десятичных кодов | 1977 |
|
SU684542A1 |
| Устройство для умножения | 1981 |
|
SU1035600A1 |
| Устройство для суммирования Фибоначчи-десятичных кодов | 1989 |
|
SU1649535A1 |
| Устройство цифровой фильтрации | 1987 |
|
SU1446627A1 |
| Устройство для задания программы | 1979 |
|
SU849148A1 |
| Устройство для умножения чисел | 1985 |
|
SU1259254A1 |


LU..) .-8).-«) 3
ЧдагЖ ж-sp -p-i- т . I
r-k-loJ-i , r-U-J :i-r
-TfV ,-R4 , rV-fi-i
Даты
1966-01-01—Публикация