Изобретение относится к вычислительной технике и может быть использовано в автоматизированных системах для вычисления собственных значений и собственных векторов положительно определенных симметрических матриц.
Известно устройство для операций над матрицами, содержащее N2 операционных блоков. N-1 элементов задержки и распределитель импульсов (авт.ев СССР № 1443003. кл. G 06 F 15/347 1987).
Однако известное устройство осуществляет только решение систем линейных уравнений и обращение матриц Известное устройство обладает ограниченными функциональными возможностями поскольку не может вычислять собственные значения и собственные векторы положительно определенных симметрических матриц
Наиболее близким по технической сущности к изобретению является устройство для операций над матрицами, содержащее
матрицу из Р х Р вычислителей (где Р - порядок квадратной матрицы) и группы из (Р-1) блоков деления, причем каждый вычислитель матрицы содержит сумматор и блок умножения, выход которого подключен к входу первого слагаемого сумматора того же вычислителя матрицы, вход задания числового компонента К-ro элемента М-й строки матрицы устройства (К- 1. ,, ,,Р) подключен к входу первого сомножителя блока умножения К-го вычислителя М-й строки матрицы, выход сумматора К-ro вычислителя (К Ј Р) М-й строки матрицы подключен к входу второго слагаемого сумматора (К+1)-го вычислителя М-й строки матрицы, выход сумматора Р-ro вычислителя Р-го столбца матрицы является выходом собственного числа устройства и подключен к входу делителя всех блоков деления группы, выход сумматора М-ro вычислителя (М Р) Р-го столбца матрицы подключен к входу делимого М-го блока деления группы, выход
xt ч
vj
СО
которого подключен к входам вторых сомножителей блоков умножения всех вычислителей М-ro столбца матрицы и является выходом М-й компоненты собственного вектора числа устройства, входы вторых слагаемых сумматоров всех вычислителей первого столбца матрицы являются входами задания кода единицы устройства (авт.св. СССР № 1348855, кл. G 06 F 15/347, 1986).
Однако известное устройство обладает ограниченными функциональными возможностями, поскольку вычисляет только доминирующее собственное число и соответствующий ему собственный вектор. Известное устройство не может вычислять все собственные значения и все собственные векторы положительно определенной симметрической матрицы.
Целью изобретения является расширение функциональных возможностей устройства за счет вычисления всех собственных значений и всех собственных векторов положительно определенных симметрических матриц.
Поставленная цель достигается тем, что устройство для операций над матрицами, содержащее матрицу из Р х Р вычислителей (где Р - порядок квадратной матрицы) и первую группу из (Р - 1) блоков деления, причем каждый вычислитель матрицы содержит сумматор-накопитель, сумматор и блок умножения, выход которого подключен к входу первого слагаемого сумматора того же вычислителя матрицы, вход задания числового компонента К-го элемента М-и строки матрицы устройства (К -1. ,Р: М - 1, ..,Р) подключен через сумматор-накопитель к входу первого сомножителя блока умножения К-ro вычислителя М-й строки матрицы, выход сумматора К-ro вычислителя (К Р) М-й строки матрицы подключен к входу второго слагаемого сумматора (К + 1)-го вычислителя М-й строки матрицы, введены (Р - 1}- разрядный регистр сдвига, (Р - 1) групп блоков умножения по (Р - i) блоков умножения в каждой группе(где i - 1 .,Р - 1), (Р - 2) групп блоков деления по (Р - i) блоков деления в каждой группе, первый блок памяти. второй блок памяти, (Р - 1) операционных блоков, (Р - 2) элементов задержки и распределитель импульсов, причем выход сумматора К-ro вычислителя К-го столбца матрицы, кроме выхода сумматора первого вычислителя первого столбца, подключен к входу делителя всех блоков деления (Р - К - 1)-й группы, вход делимого j-ro блока деления (где j 1Р - i) i и группы подключен к
выходу сумматора j-ro вычислителя (Р - i - 1)-го столбца, выход j-ro блока деления i-й
группы подключен к входу первого сомножителя j-ro блока умножения i-й группы, входы вторых сомножителей блоков умножения i-й группы подключены к выходу 1-го
разряда регистра сдвига, тактовый вход которого подключен к выходу распределителя импульсов, выходы которого подключены также к синхровходам операционных блоков, элементов задержки,первого и второго
0 блоков памяти, выходы j-x блоков умножения подключены к входам вторых сомножителей блоков умножения всех вычислителей j-ro столбца матрицы, выход j-ro блока деления i-й группы является выходом j-й компо5 ненты 1-го собственного вектора и подключен к j-му информационному второго блока памяти, первый вход i.T-ю операционного блока подключен к i-му выходу второго блока памяти (i 1, Р-1), пер0 вый выход i.S-ro операционного блока подключен к (Р - i t 1)-му информационному входу второго блока памяти (S - 1, Р - 1), первый вход i.S-ro операционного блока подключен к первому выходу (i 1)(S - 1)-ro
5 операционного блока (i 1ГР - 2, S 2. Р 1), первый вход операционного блока Р -1 .S подключен к выходу (S - 1)-го элемента за держки (S 2, Р - 1), вход которою подключен к второму входу (Р - 1) (S - 1)-го
0 операционного блока, второй вход 1.S-ro операционного блока подключен к второму выходу (i - 1).S-ro операционного блока (i - 2, Р - 1, S 1, Р - 1), значения компонент исходной положительно определенной сим5 метрическои матрицы хранятся в первом блоке памяти, информационные выходы которого подключены к соответствующим входам задания числового компонента вычислителей, Р-й информационный выход
0 первого блока памяти подключен также к дополнительному информационному входу второго блока памяти, i-й информационный выход второго блока памяти (где i 1, ,.,Р - 2) подключен к дополнительному информа5 ционному входу пероого блока памяти, выход сумматора К-го вычислителя К-го столбца матрицы вычислителей, кроме первого вычислителя первого столбца, является выходом значения (Р - К 1)-го собственного
0 числа устройства, (Р + 1)-й выход второго блока памяти является выходом значения Р-ю собственного числа устройства, вычисленные компоненты собственных векторов хранятся во втором блоке памяти.
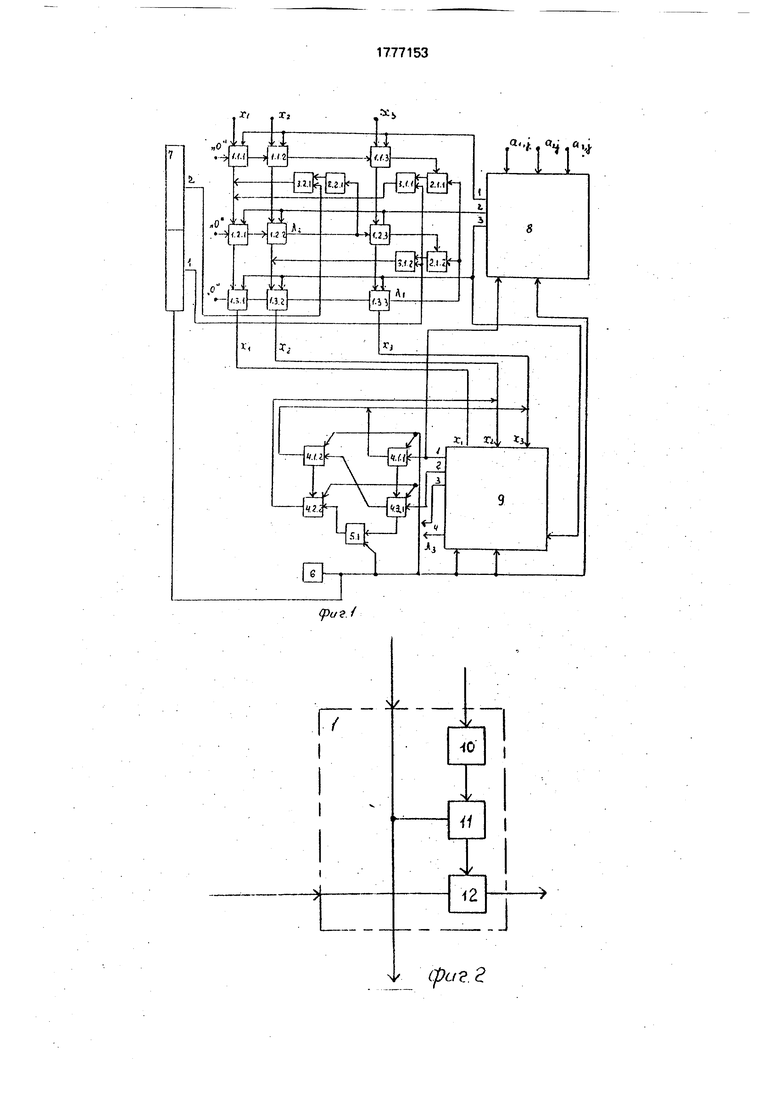
5На фиг 1 представлена функциональная
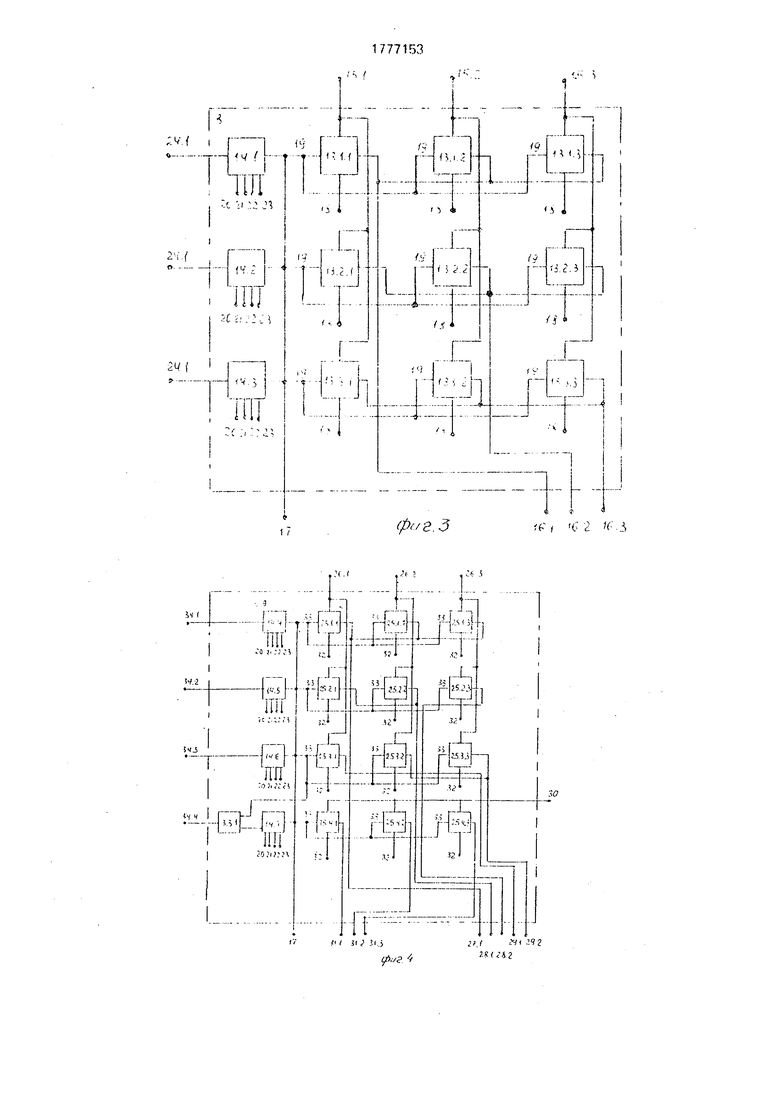
схема предлагаемого устройства для операций над матрицами размерности 3x3; на фиг.2 - функциональная схема вычислителя I: на фиг.З - функциональная схема блока 8 памяти; на фиг 4 функциональная схема
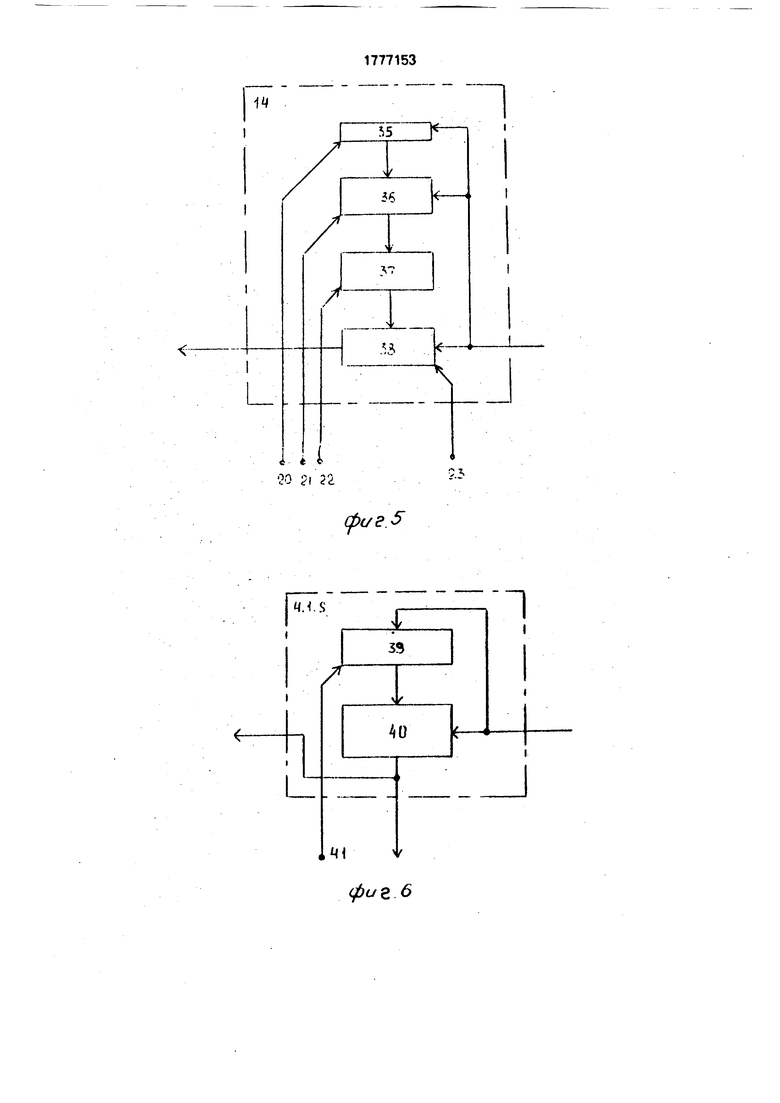
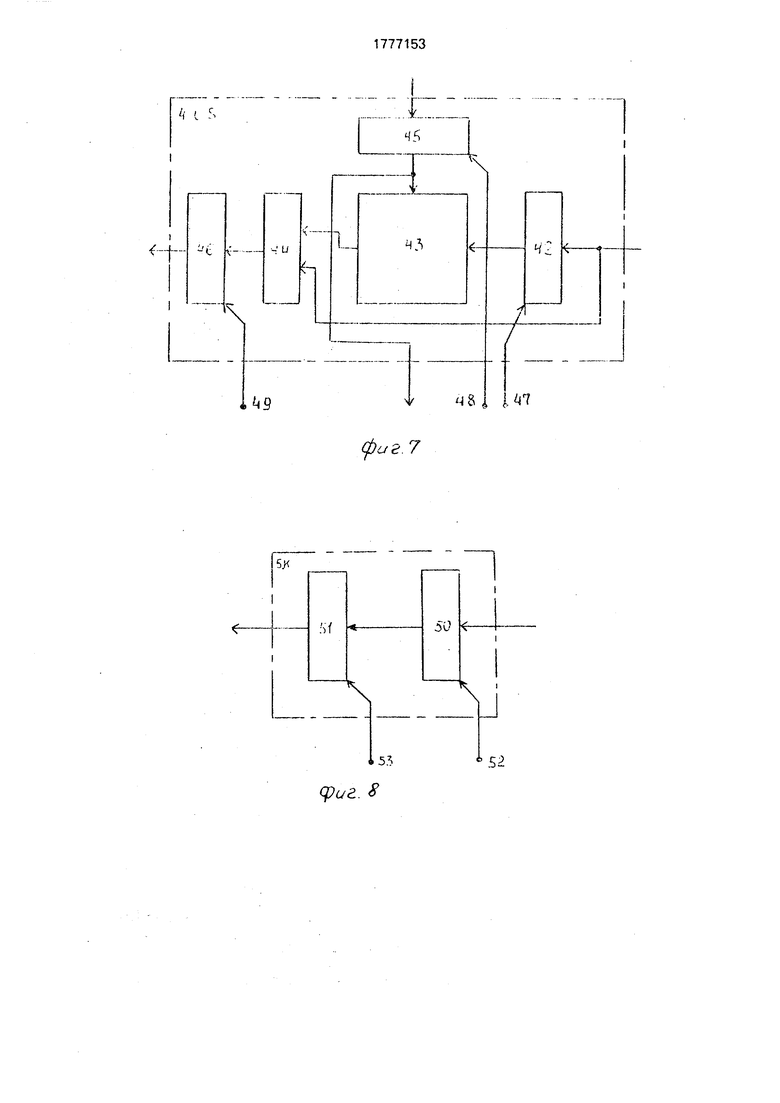
блока 9 памяти; на фиг.5 - функциональная схема блока 14 формирования коэффициентов системы линейных уравнений, на фиг.6 - функциональная схема операционного блока4.1.5(5 1,2); нафиг.7-функционэль- ная схема операционного блока 4.I.S (i 2; S 1,2); на фиг.8 - функциональная схема элемента 5.К (К 1) задержки; на фиг,9 - функциональная схема распределителя 6 импульсов.
Устройство для операций над матрицами содержит вычислители 1, блоки 2 деления, блоки 3 умножения, операционные блоки 4, элемент 5 задержки, распределитель 6 импульсов, регистр 7 сдвига, блок 8 памяти и блок 9 памяти.
Вычислитель 1 содержит сумматор-накопитель 10 блок 11 умножения, сумматор 12, блок 8 памяти содержит элементы 13 памяти, блоки 14 формирования коэффици- ентовсистемы линейных уравнений, информационные входы 15, шины 16 управления записью соответствующих строк, дополнительный информационный вход 17, входы 18 управления считыванием, информацией- ные выходы 19 элементов 13 памяти, синх- ровходы 20 - 23 блока 14 формирования, информационные выходы 24 блока 8 памяти.
Блок 9 памяти содержит элементы 25 памяти, блоки 14 формирования коэффициентов системы линейных уравнений, блок 3.3.1 деления, информационные входы 26. шины 27 - 29 управления записью соответствующих строк, дополнительный информа- ционный вход 30. входы 31 управления записью соответствующих элементов последней строки, входы 32 управления считыванием, информационные выходы 33 элементов 25 памяти, информационные вы- ходы 34 блока 9 памяти.
Блок 14 формирования коэффициентов системы линейных уравнений содержит регистр 35 памяти, блок 36 умножения, управляемый инвертор 37, сумматор-накопитель 38. синхровходы 20 - 23.
Операционный блок 4.1.S содержит входной регистр 39, блок 40 деления, синх- ровход41.
Операционный блок 1.1.S содержит ре- гистр 42 первого сомножителя, умножитель 43, вычитатель 44, регистр 45 второго сомножителя, выходной регистр 46, синхровходы 47 - 49. Элемент 5 задержки содержит регистры 50, б синхровходы 52. 53.
Распределитель 6 импульсов содержит генератор 54 синхроимпульсов, элемент И 55, счетчик 56 тактов, блок 57 памяти микрокоманд, вы -.оды 53 - 123 pacnp-де итепч
Выход 58 подключен к управляющему входу 6 блока 4.1.1; выход 59 - к управляющему входу 47 блока 4.2.1; выход 60 - к входу 6 бпока 4.1.2; выход 61 - к входу 47 блока 4.2.2; выход 62 - к управляющим входам 48 блоков 4.2.1. 4.2.2., к управляющим входам 49 блоков 4 2.1, 4.2.2, к синхровходу 52 и синхровходу 53 блока 5.1 задержки; выход 63 - к тактовому входу регистра 7 сдвига; выход 64 - к управляющей шине 16.1; выход 65 - к управляющей шине 16.2; выход 66- к управляющей шине 16.3; выход 67 - к управляющей шине 27.1; выход 68 - к шине 28,1; выход 69 - к шине 28.2; выход 70
-к шине 29.1; выход 71 - к шине 29.2; выход 72 - к шине 31.1; выход 73 - к шине 31.2; выход 74 - к шине 31.3; выходы 75 - 78 - к управляющим входам блока 14.1; выходы 79
-82 - к управляющим входам блока 14.2; выходы 83 - 86 - к управляющим входам блока 14.3; выходы 87 - 90 - к управляющим входам блока 14.4; выходы 91 - 94 - к управляющим входам блока 14.5; выходы 95 - 98 -куправляющим входам Ьлока 14.6; выходы 99 - 102 - к управляющим входам блока 14.7; выходы 103 - 111 - к управляющим входам 18 считывания элементов 13 памяти, выходы 112 - 123 - к управляющим входам 32 считывания элементов 25 памяти.
Распределитель 6 импульсов реализован на базе ПЗУ согласно известным правилам (авт. св. СССР ish 1443003, кл. G 06 F 15/347, 1987;авт.св. СССР N 1401478, кл. G 06 F 15/347, 1986).
Известно, если действительная матрица A симметрическая и положительно определенная, то
1) корни AI , А2Ал ее характеристического уравнения
ai2...ain
321 322-Я-- Э2п
(1)
Эп1 ап2...Эппдействительны и положительны; 2) собственные векторы
Х1
0)
„(И,
0 1.2п)
ХП
(J)
могут быть взяты действительными и удовлетворяют условиям ортогональности
)(|)х,(к)-0при К
(см. Демидович Б.П.. Марон И.А. Основы вычислительной математики. М.: Наука, 1970. с.437).
Таким образом, положительно определенная симметрическая матрица имеет п собственных значений и п собственных векторов.
Известное устройство для операций над матрицами (авт.св. СССР № 1348855, кл. G 06 F 15/347, 1986) способно вычислять только одно собственное число, являющееся доминирующим, и один собственный вектор, соответствующий этому собственному числу. Это известное устройство не может вычислять компоненты остальных п-1 собственных векторов положительно определенной симметрической матрицы.
Предлагаемое устройство для операций над матрицами имеет более широкие функциональные возможности, так как позволяет вычислять все собственные значения и компоненты всех собственных векторов положительно определенной симметрической матрицы.
Поскольку все вычисления выполняются аналогично для симметрических положи- тельно определенных матриц любой размерности, то для примера может быть рассмотрена работа устройства при вычислении собственных значений и собственных векторов матрицы размерности 3x3.
Устройство для операций над матрицами работает следующим образом.
Пусть исходная действительная симметрическая положительно определенная матрица имеет вид
an ai2.. ain
А -321 322. .Э2п(3)
Эп-1 ап2 ---Эпп
дения 1 в i-м разряде регистра 7 сдвига, поэтому период поступления тактовых импульсов с выхода 63 на тактовый вход регистра 7 сдвига равен времени сходимости
5 итерационного процесса и вычисления оставшейся части компонент собственного вектора.
В течение первого периода работы устройства 1 с выхода первого разряда реги10 стра 7 сдвига поступает на входы вторых сомножителей блоков 3.1.1 и 3.1.2 умножения. На вход второго сомножителя блока 3.2.1 поступает с О с выхода второго разряда регистра 7 сдвига, в результате на вы15 ходе блока 3.2.1 формируется О.
С поступлением последовательности синхроимпульсов с выходов 103 - 111 на управляющие входы 18 считывания элементов 13 памяти значения элементов матрицы
20 А (соотношение 4) последовательно поступают на входы сумматоров-накопителей 10 вычислителей 1 и опоминаются в них.
На входы вторых сомножителей блоков 11 умножения всех столбцов матрицы вы25 числителей 1, кроме последнего, подаются произвольные сигналы хг1 , Х2 . На входах вторых сомножителей блоков 11 умножения вычислителей I последнего столбца присутствует сигнал 1.
30Следовательно, для реализации итерационной процедуры отыскания собственного числа AI матрицы А (соотношение 4) в качестве начального приближения выбирается вектор
.(1)
На выходе сумматора 12 последнего вычислителя 1 последней строки матрицы при этом образуется сигнал
п - 1
&}-Z anjx/u + ann . (5) j 1







| название | год | авторы | номер документа |
|---|---|---|---|
| Генератор функций Попенко-Турко | 1990 |
|
SU1753464A1 |
| ГЕНЕРАТОР СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2016 |
|
RU2615322C1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2021 |
|
RU2773107C1 |
| СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ НА ОСНОВЕ ХАОТИЧЕСКИ ФОРМИРУЕМЫХ АНСАМБЛЕЙ ДИСКРЕТНЫХ МНОГОУРОВНЕВЫХ ОРТОГОНАЛЬНЫХ СИГНАЛОВ | 2010 |
|
RU2428795C1 |
| СИСТЕМА НЕПРЕРЫВНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ АНСАМБЛЯМИ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2022 |
|
RU2801172C1 |
| СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ С ПРИМЕНЕНИЕМ СТОХАСТИЧЕСКИХ ОРТОГОНАЛЬНЫХ КОДОВ | 2021 |
|
RU2780418C1 |
| Устройство для операций над матрицами | 1986 |
|
SU1348855A1 |
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| Матричный вычислитель | 1986 |
|
SU1413644A1 |
| Устройство для решения систем алгебраических уравнений | 1984 |
|
SU1325507A1 |

Изобретение относится к вычислительной технике и можэт быть использовано в автоматизированных системах для вычисления собственных значений и собственных векторов положительно определенных симметрических матриц. Цель изобретения - расширение функциональных возможностей устройства за счет вычисления всех собственных значений и всех собственных векторов положительно определенных симметрических матриц Устройство для операций над матрицами содержит матрицу из Р х Р вычислителей, где Р - порядок квадратной матрицы, первую группу блоков деления, регистр сдвига, (Р-1) групп блоков умножения. (Р-2) групп блоков деления, два блока памяти, (Р-1) операционных блоков. (Р-2) элементов задержки и распределитель импульсов, причем каждый вычислитель матрицы содержит сумматор-накопитель, сумматор и блок умножения 9 ил.
Например, для рассматриваемого случая она имеет следующие элементы: 422
(4)
В исходном состоянии элементы матрицы А (соотношение 2) записаны в элементах 13 памяти блока 8. в регистре 7 сдвига записан код вида 10 ... О (для рассматриваемого случая - 10). причем 1 записана в первом разряде регистра 7 сдвига. Вычисление 1-го собственного значения и соответствующего ему собственною пек гора будет осуществляться п течение оромени нахож
(см.Демидович Б.П., Марон И.А. Основы вычислительной математики. -- М.: Наука. 1970, с. 438, соотношение 3), который является первым приближением собственного числа Ят .
На выходе сумматора 12 последнего вычислителя 1 i-й строки (i - 1п-1) образуется сигнал
х|а1)| 1а.,хЛ0)4ат. (6)
j - 1
(где i - 1, 2п-1). Этот сигнал является i-й
компонентой первого ненормированного
приближения первого собственного еектс- ра матрицы А (соотношение 4):
x(i.D (xjO-i). х2а ). д, ( Нормирование
первого приближения первого вектора осуществляется путем деления всех его компонент на величину последней компоненты
А . Так как в результате нормирования последняя компонента равна 1. то ее деления не производится и 1 поступает на входы вторых сомножителей всех блоков 11 умножения последнего столбца матрицы вычислителей 1. Нормирование остальных компонент осуществляется при помощи блоков 2.1.1 и 2.1.2 путем деления компонент на величину последней компоненты. Сигнал с выхода блока 2.1 1 деления через блок 3.1.1 умножения поступает на входы вторых сомножителей блоков 11 умножения вычислителей 1.2.1 и 1.3.1, т.е. вычислителей 1 первого столбца матрицы. Сигнал с выхода блока 2.1.2 деления через блок 3.1.2 умножения поступает на вход второго сомножителя блока 11 умножения вычислителя 1.3.2, т.е. вычислителя 1 второго столбца матрицы.
Таким образом, в соответствии с соотношением
1
п - 1
(S
-АТ (1.0)
а-,„). (7)
(где , 2.....П-1) (см. Демидович Б.П.. Марон И.А. Основы вычислительной математики. - М.: Наука, 1970, с.439, соотношение 3) после окончания первой итерации на выходах вычислителей 1.3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам первого нормированного приближения первого собственного вектора:
,0-1),
(xi 1-1Wu 1).
x(1-2 (xi(1 2W1 2).1).
Повторение итерационных процессов будет осуществляться до полной сходимости итерационного процесса. В результате на выходах вычислителей 1 3.1, 1.3.2, 1.3.3 присутствуют сигналы, соответствующие компонентам нормированного первого собственного вектора:
х 1-(xf1 , X2 ,1). а на выходе сумматора 12 вычислителя 1.3.3 присутствует сигнал,
Затем итерационный процесс повторяется и после окончания второй итерации на выходах вычислителей 1.3.1,1.3.2,1.3.3 при- сутствуют сигналы, соответствующие компонентам второго нормированного приближения первого собственного вектора:
cooTseTCTByios. ji .n гпостяенно-Му зн чан .:. Ai.
Таким образом, для матрицы А (соотношение 4)система уравнений решается методом итерации в соответствии с соотношением (5) и (7):
х/1) 7Г(4Х1°)Н (1) + 2)
1 г (Г( (1W1)6
10X20) 1L(2X10),)
5
0
5
0
5
0
5
(см.Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970, с.439, соотношение 9). После реализации сходимости итерационного процесса на выходах вычислителей 1.3.1, 1.3.2, 1.3.3 будут получены значения компонент первого соб- ствеиного вектора: хг1 0,8077; Х2 0.7720, - 1, а на выходе сумматора 12 вычислителя 1.3.3 будет получено значение Ai 8,3874.
По окончании времени, необходимого для реализации сходимости итерационного процесса, импульс с выхода 67 поступит на вход27.1 блока 9 памяти и компоненты первого собственного вектора окажутся записанными в элементах 25.1.1. 25.1.2, 25.1.3 памяти, В следующий момент времени на тактовый вход регистра 7 сдвига поступает тактовый импульс с выхода 63, под воздействием которого 1 из первого разряда регистра 7 сдвига сдвигается во второй разряд.
Таким образом 1 с выхода второго разряда регистра 7 сдвига поступает на вход второго сомножителя блока 3.2.1 умножения. На входы вторых сомножителей блоков 3.1.1 и 3.1.2 умножения поступает выхода первого разряда регистра 7 сдвига., в результате на выходах блоков 3.1.1. и 3.1.2 формируются О.
Для определения второго собственного значения и компонент хг , Х2 второго собственного вектора необходимо методом итерации решать систему уравнений
х,(2)4- Ya./2)xj(2)
лг j 1 A2 -rfr-nS1an-i 2,jx/2
(9)
55
(см, Демидович Б.П., Марон И.А. Основы аычислительной математики. - М.:Наука, 1970. с.439. соотношение 7).
Для матрицы А (соотношение 4) вторая система уравнений, решаемая методом итерации, определяется из условия ортогональности векторов х(1 и (соотношение 2). Так как
0.8077xi(2) + 0,7720x2U) + хз(2) О,
хз(2) - -0,8077xi(2) - 0.7720х2(2)(10)
Подставляя это выражение в систему вида
(1) 4х10) + 2х20) + 2хз( Я;хС) 2хО) + (if
Ajx3t))-2x(j) + X2(iT+6x3Ii)
0 1,2.3)(11)
(см. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука. 1970. с.439, соотношение 8), получают
xr -j- (2.3846xi(2) + 0,4560)
(12)
(см. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970, с.440, соотношение 11).
Систему (12) необходимо решать методом итерации, но для этого нужно предварительно сформировать коэффициенты ai/ (соотношение 9). Для этого используются коэффициенты aij, записанные в блоке 8 памяти.
При формировании коэффициента air с выхода 112 на вход 32 считывания элемента 25.1.1 поступает импульс и значение 0,8077 через сумматор 38 блока 14.4 поступает на дополнительный информационный вход 17 блока 8 памяти и после поступления импульса с выхода 79 на вход 20 блока 14.1 записывается в регистре 35 памяти. Затем импульс с выхода 105 поступает на вход 18 считывания элемента 13.1.3 и значение 2 после поступления импульса с выхода 80 на вход 21 блока 14,1 перемножается в блоке 36 умножения со значением 0.8077. После поступления импульсов с выхода 81 на вход 22. с выхода 82 на вход 23 блока 14.1 с его выхода значение - 1.6154 поступает на вход сумматора-накопителя 10 вычислителя 1.1.1, в котором до этого хранилось значение 4. в результате чего в нем станет храниться значение ai г-- - 2,3846.
Аналогичным образом формируются значения ai2(2) - 0,4560: а21(2) - 1,1923, а,) 4,2280, которые будут храниться в сумматорах-накопителях 10 вычислителей 1.1.2, 1.2.1 и 1.2.2 соответственно.
После подачи на входы вторых сомножителей блоков 11 умножения вычислителей 1.1.1 и 1.2.1 произвольного сигнала xv , а на выходы вторых сомножителей блоков 11 умножения вычислителей 1.1.2 и 1.2.2. сигнала 1 начнется реализация итерационного процесса. После достижения сходимости итерационного процесса на выходе делителя 3.2.1 и, соответственно, на выходе вычислителя 1,2.1 будет получено значение хг 0,2170, на выходе вычислителя 1.2.2 будет присутствовать сигнал Х2 1, а на выходе сумматора 12 - значение Я2 4..
Компонента Х2 определяется из соотношения (10), т.е. уравнения с одним неизвестным, с использованием известного устройства для операций над матрицами, способного решать уравнения с одним неизвестным или системы из п уравнений с п
неизвестными по методу Гаусса-Жордана (см. авт.св. СССР № 1443003, кл. G 06 F 15/347, 1987). В его состав входят операционные блоки 4.1.1, 4.1.2,4.1.3. 4.1.4, элемент 5.1 задержки, распределитель 6 импульсов.
В нем выполняется обработка матрицы размерности N х М (N 1,2), которая представляет собой матрицу коэффициентов при неизвестных системы линейных уравнений, к которой справа дописана матрица размерности N х 1 свободных членов.
Таким образом, например, для решения системы из двух линейных уравнений на входы устройства будет поступать матрица В вида
В
bn bi2 bis
D21 Ь 22 Ь23
(13)
где bn, bi2. b2i, 022 - коэффициенты при
неизвестных;
bis, Ьаз - свободные члены. В соответствии в описанием по авт.св. СССР № 1443003, кл.С 06 F 15/347, 1987, элементы матрицы В поступают на входы
операционных блоков 4 построчно со сдвигом на один такт под воздействием синхроимпульсов с выходов распределителя 6 импульсов, т.е. первая строка поступает на первый вход операционного блока 4.1.1, начиная с первого такта, вторая строка поступает на первый вход операционного блока 4.2.1, начиная с второго такта и т.д. На выходах операционных блоков 4.I.J (} - п, I 1п) получается семейство решений системы линейных уравнений.
Таким образом, решения системы из двух уравнений получатся на выходах операционных блоков 4.1.2 и 4.2.2, решение уравнения с одним неизвестным - на выходе операционного блока 4.1.1.
Следовательно при вычислении значения хз будет задействован только операционный блок 4.1.1 Коэффициент при неизвестном и свободный член будут вычислены блоком 14.4 блока 3 памяти.
В соответствии с выражением (10) коэффициент при неизвестном будет сформирован следующим образом. С выхода 90 на вход 23 блока 14.4 и на информационный вход 17 блока 9 памяти поступает 1, в результате чего через сумматор 38 блока 14.4 она поступает на вход операционного блокэ4.1.1.
Затем вычисляется свободный член в соответствии с выражением (10). Синхроимпульс с выхода 112 поступает на вход 32 считывания элемента 25.1.1. памяти, с выхода 87 - на синхровход 20 блока 14.4, и значение х/1 записывается в регистр 35 памяти блока 14.4. Синхроимпульс с выхода 115 поступает на вход 32 считывания элемента 25.2.1 памяти, с выхода 88 - на синхровход 21 блока 14.4. и значение хг перемножается с хг в блоке 36 перемножения блока 14.4. Синхроимпульс с выхода 89 поступает на синхровход 22 блока 14.4, и результат перемножения хг хг инвертируется в управляемом инверторе 37 блока 14.4, после чего значение -хг хг поступает на вход сумматора-накопителя 38 блока 14.4. Синхроимпульс с выхода 113 поступает на вход 32 считывания элемента 25.1.2, с выхода 87 - на синхровход 20 блока 14.4, и значение Х2- записывается в регистр 35 памяти блока 14.4. Синхроимпульс с выхода 116 поступает на вход 32 считывания элемента 25.2.2 памяти, с выхода 88 - на синхровход-21 блока 14.4. и значение Х2 перемножается с Х2 в блоке 36 перемно
жения блока 14.4. Синхроимпульс с выхода 40
89 поступает на синхровход 22 блока 14.4, и результат перемножения Х2 , ха инвертируется в управляемом инверторе 37 блока 14.4, после чего значение -Х2 Х2 поступает на вход сумматора-накопителя 38 блока 14.4. Синхроимпульс с выхода 90 поступает на вход 23 блока 14.4, и значение, находящееся в сумматоре-накопителе 38 блока 14.4/поступает на вход операционного бло- КЭ4.1.1.
Значение хз -0,9473 с выхода операционного блока 4.1.1 поступает на информационный вход 26.3 блока 9 памяти и с поступлением синхроимпульса с выхода 69 на вход 28.2 оказывается записанным в элементе 25.2.3 блока 9 памяти.
Таким образом, в элементах 25.2.1, 25.2.2, 25.2.3 будут записаны компоненты второго собственного вектора матрицы А (соотношение 4).
По окончании времени, необходимого для вычисления компонент второго собственного вектора, с выхода 63 на тактовый вход регистра 7 сдвига поступает тактовый
импульс, в результате чего второй разряд регистра 7 сдвига обнуляется. Так как на вход второго сомножителя блока 3.2.1 умножения поступает О с выхода второго разряда регистра 7, то на выходе, блока 3.2. 1
формируется О.
Вычисление компонент третьего собственного вектора производится следующим образом. На входы вторых сомножителей блоков 11 умножения вычислителей 1.1.1,
памяти значение хз 1 записывается в элемент 25.3.1 памяти.
После этого осуществляется вычисление компонент Х2 и хз с использованием соотношений ортогональности:
0,8077 xi(3) + 0,7720 х2(3) + хз(3) о| 0,2170 х/3) + х2(3) - 0,9473 хзТЗ) 0 ) (14)
(см.Демидович Б.П., Марон И,А. Основы вы- числительной математики. - М.: Наука, 1970, с.441).
Так как значение хг0 1 вычислено и записано в элементе 25.3.1 памяти, то систему уравнений (14) можно представить в виде
0,7720 х2(3) + хз(3) -0,8077 |
х2(3)-0,9473 хз(3) -0,2170 J(15)
Эта система линейных уравнений легко решается методом Гаусса-Жордана. Поскольку коэффициенты при неизвестных и свободные члены записаны в блоке 9 памя5 ти, то уравнение (15) решается следующим образом. При поступлении синхроимпульса с выхода 113 на вход 32 считывания элемента 25.1.2 памяти значение 0,7720 считывается с него, и при поступлении
0 синхроимпульса с выхода 90 на вход 23 блока 14.4 через сумматор 38 блока 14.4 значение 0,7720 поступает на вход операционного блока 4.1,1.
При поступлении синхроимпульса с вы5 хода 116 на вход 32 считывания элемента 25.2.2 памяти значение 1 считывается с него, и при поступлении синхроимпульса с выхода 94 на вход 23 блока 14.5 через сумматор 38 блока 14.5 значение 1 поступает на вход операционного блока 4,2.1.
Аналогичным образом считываются значения 1 из блока 25.1,3 памяти и значение -0,9473 из блока 25.2,3 памяти и поступают на входы операционных блоков
В соответствии с алгоритмом работы операционных блоков 4 на выходах блоков
С поступлением синхроимпульса с выхода 71 на вход 29.2 блока 9 памяти значение -5673 окажется записанным в элементе 25.3.2, а значение -3698 - в элементе 25.3.3 памяти.
Таким образом, в элементах 25.3.1, 25.3.2 и 25.3.3 будут записаны компоненты третьего собственного вектора матрицы А (соотношение 4).
Третье собственное значение матрицы А (соотношение 4) вычисляется с использованием последнего уравнения системы (11) при j 3. Согласно ему
1
хТ3Т
(2x/3W3 4
|-6хз(3)) .(16)
Для вычисления Аз с выходов 109 - 111 последовательно подаются синхроимпульсы на входы 18 считывания элементов 13.3.1, 13.3.2, 13.3.3, в которых записаны соотве Ственно значения 2, 1, 6 матрицы А (соотношение 4). Эти значения с выхода 24.3 последовательно поступают на дополнительный информационный вход 30 блока 9 памяти и с поступлением с выходов 72 - 74 на управляющие входы 31.1, 31.2, 31.3 записи последовательности импульсов записываются в элементах 25.4.1, 25.4.2 и 25.4.3 соответственно.
Затем с выхода 121 на вход 32 считывания элемента 25.4.1 поступает синхроимпульс и значение 2 под воздействием импульса, поступающего с выхода 99 на вход 20 блока 14.7, записывается в регистр 35 памяти блока 14.7 После этого под воздействием синхроимпульса, поступающего с выхода 118 на вход 32 считывания элемента 25.3.1, значениехг - 1 поступает на вход блока 36 умножения, и после поступления синхроимпульса с выхода 100 на вход 21 блока 14.7 результат произведения с выхода блока 36 умножения записывается через управляемый инвертор 37 в сумматор-накопитель 38, Значение произведения не инвертируется, так как на синхровход 22 блока 14.7 синхроимпульс не поступает.
Аналогичным образом вычисляются остальные слагаемые уравнения (16), После этого с выхода 102 на синхровход 23 поступает импульс и значение суммы -0,7861 с выхода сумматора-накопителя 38 блока 14.7 поступает на вход делимого блока 3.3.1 деления. В это же время на вход 32 управления считыванием блока 25.3.3, в котором записано значение -0,3698, с выхода 120 поступает синхроимпульс и с выхода 33 элемента 25.3.3 памяти значение -0.3698 поступает на вход делителя блока 3.3.1 деления, на выходе которого появляется значение Дд 2,1260. На этом процесс вычисления собственных значений и собственных векторов матрицы А (соотношение 4)
заканчивается.
Значение компонент всех собственных векторов хранится в блоке 9 памяти.
Аналогичным образом вычисляются все собственные значения и собственные векторы любой симметрической положительно определенной матрицы размерности 3x3, элементы которой записываются в блок 8 памяти. При увеличении размерности исходных симметрических положительно определенных матриц число элементов предлагаемого устройства для операций над матрицами и обьем памяти блоков 8 и 9. естественно, возрастает. Таким образом, предлагаемое устройство для операций над
матрицами обладает более широкими функциональными возможностями, чем прототип, заключающимся в вычислении всех собственных значений и всех собственных векторов любых положительно определенных симметрических матриц.
Формула изобретения Устройство для операций над матрицами, содержащее матрицу из Р х Р вычислителей (где Р - порядок квадратной матрицы)
и первую группу из Р - 1 блоков деления, причем каждый вычислитель матрицы содержит сумматор-накопитель, сумматор и блок умножения, выход которого подключен к выходу первого слагаемого сумматора,
вход задания числового компонента К-го элемента М-й строки матрицы устройства (К 1Р; М 1Р) подключен к входу сумматора-накопителя, выход которого подключен к входу первого сомножителя блока
умножения (К-го вычислителя М-й строки матрицы, выход сумматора К-го вычислителя (К Р) М-й строки матрицы подключен к входу второго слагаемого сумматора (К + 1)-го вычислителя М-й строки матрицы, о т личающееся тем. что. с целью расширения функциональных возможностей за счет вычисления всех собственных значений и всех собственных векторов положительно определенных симметрических матриц, в него введены (Р - 1)-разрядный регистр сдвига, Р - 1 групп блоков умножения по Р - i блоков в каждой группе (I 1Р
-1), Р - 2 групп блоков деления по Р - i блоков в каждой группе.два блока памяти, (Р - 1)2 операционных блоков, Р - 2 элементов задержки и распределитель импульсов, причем выход сумматора К-го вычислителя К-го столбца матрицы, кроме первого вычислителя первого столбца, подключен к входу де- лителя всех блоков деления (Р - К + 1)-й группы, вход делимого j-ro блока деления (j
1Р - i) i-й группы подключен к выходу
сумматора j-ro вычислителя (Р - i4 1)-го столбца, выход j-ro блока деления i-й группы подключен к входу первого сомножителя j- го блока умножения i-й группы, входы вторых сомножителей блоков умножения 1-й группы подключены к выходу 1-го разряда регистра сдвига, тактовый вход которого подключен к выходу распределителя импульсов, выходы которого подключены к синхровходам операционных блоков, элементов задержки, первого и второго блоков памяти, выходы j-x блоков умножения под- ключены к входам вторых сомножителей блоков умножения всех вычислителей j-ro столбца матрицы, выход j-ro блока деления i-й группы является выходом j-й
компоненты i-ro собственного вектпр;. и подключен к j-му информационному входу второго блока памяти, первый сход i.1-ro операционного блока подключен к i-му ходу второго блока памяти (I - 1, Р - 1), первый выход 1.3-го операционного блока подключен к (Р - i 1)-му информационному входу второго блока памяти (S - 1. Р - 1), первый вход i:S-ro операционного блока подключен к первому выходу (i 1) (S :J}-ro операционного блока (i -- 11, Р - 2: S - 2, Р - 1), первый вход операционного блока (Р - 1, S) подключен к выходу (S - 1)-го элемента задержки (S 2, Р - 1), вход которого подключен к второму входу (Р - 1) (S - 1)-го операционного блока, второй вход i.S-ro операционного блока подключен к второму выходу (i - операционного блока (i - 2, Р -1, S 1, Р- 1), информационные выходы первого блока памяти подключены к соответствующим входам задания числового компонента вычислителей, Р-й информационный выход первого блока памяти подключен к информационному входу второго блока памяти й информационный выход которого (i 1, Р - 2) подключен к информационному входу первого блока памяти, выход сумматора К-го вычислителя К-го столбца матрицы вычислителей, кроме первого вычислителя первого столбца, является выходом значения (Р - К + 1)-го собственного числа устройства, (Р + 1)-й выход второго блока памяти является выходом значения Р-го собственного числа устройства.
, Г/ . Гг
fW
LSium
(риг 5
«U S
фс/г 6
Л
п
-t- c
- u
1
ч
Ь9
45
фиг 8
,5I
T
43
Ј
J
484 H
i/г 7
50
U
S2
рс/е.9

| Аналого-цифровое устройство сбора информации | 1987 |
|
SU1443004A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для операций над матрицами | 1986 |
|
SU1348855A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Пневматический водоподъемный аппарат-двигатель | 1917 |
|
SU1986A1 |
Авторы
Даты
1992-11-23—Публикация
1989-12-26—Подача