Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных машинах и устройствах автоматики.
Известны устройства для возведения чисел в степень--арифметические устройства, в которых результат получается многократным умножением числа самого на себя.
Целью изобретения является уменьшение количества арифметических операций, необходимых для получепия результата.
Предлагаемое устройство отличается тем, что содержит квадратор, умножитель на коэффициент три, умножитель на коэффициент четыре, умножитель на коэффициент шесть, регистр второго блока и регистр результата, причем выход младшего разряда регистра числа соединен с входом младшего разряда регистра результата, выход второго разряда регистра числа - с входом младшего разряда регистра второго блока, выход третьего разряда регистра числа - с входами младших разрядов квадратора и ряда сумматоров второго блока. Выход каждого i-ro из остальных разрядов регистра числа соединен с входом (г - 1)-го разряда квадратора, выход каждого 1-го разряда квадратора (кроме второго) - с входом (г-|-1)-го разряда ряда сумматоров второго блока. Выходы разрядов ряда сумматоров второго блока соединены с входами соответствующих разрядов умножителя на коэффициент три, выход каждого г-го разряда которого соединен с входом (4-1)-го разряда регистра второго блока, выходы разрядов этого регистра - с входами соответствующих разрядов ряда сумматоров третьего блока, выходы разрядов этого ряда сумматоров соединены с соответствующими входами разрядов умножителя на коэффициент четыре, выход каладого f-ro раязряда этого умножителя соединен с входом (/ - 2)-го разряда другого ряда сумматора третьего блока, выход каждого г-го рязряда этого ряда сумматоров соединен с (t + 3)-M разрядом регистра результата, выходы разрядов квадратора соединены с входами соответствующих разрядов умножителя на коэффициент шесть, выходы которых соединены с соответствующими разрядами другого ряда сумматоров третьего блока.
Построение устройства основано на следующих сообрал ениях.
Берется некоторое число, записанное в виде:
.4о + о„-2-г -- + ,..., 4-L а-2Г + о,-г1 + аог°,
где О; - цифры числа,
/ - основание системы счисления. Это можно представить в виде: ( -f -+-,..., + + ) r-f-ao, обозначив часть числа, заключепную в круглые скобки через Л (индекс при букве Л указывает на самую младшую цифру части числа в скобках), получим следующую форму записи числа Ад До Air + UQ. Числа в этой записи возводятся в степень q: А, (Л,г + а,) А . г + а„ -f + q. Af-2a2. г--г + ,...,+ С- . а« + ,..., + q-i. А, .ar-+йоСтепень q у части числа AI здесь сохранилась только в первом члене, все остальные члены разложения содержат более низкие степеничасти числа без младшей цифры AI, но часть числа AI содержит на одну цифру меньще, чем исходное число. Аналогичный прием повторяется к первому члену Af -гч (умножение на г равносильно сдвигу влево на q разрядов и, следовательно, все члены разложения достаточно сдвинуть на q разрядоз влево). Очевидно, что степень q после этого будет содержать также только первый член (А| -ri), но число А2 будет уже без двух младших цифр. Продолжая этот процесс п раз, получим некоторую матрицу, сумма строк которой равна степени q исходного числа, но степени всех частей числа будут не вы, ,. ше, чем (-1), а в степень q будут возводиться только цифры исходного числа, а не его части. Аналогичным образом теперь можно поступить со всеми членами этого разложения и снизить степень каждого из них еще на единицу. Пусть, например, необходимо возвести в квадрат некоторое число, записанное в виде: + ап-2-2«-2 +,...,+ аз + ai2i-f ао.
«4
n-l /г-2
я-1
та „
п-2
л-1
ь
3
«я-2
«2
п-1
Умножение на биноминальный коэффициент 2 в этой матрице выполнено за счет сдвига «а разряд влево.
Нетрудно убедиться, что число слагаемых цифр в этой матрице: -±(п-1 +
где п - разрядность числа, что почти в два раза меньше, чем при обычном способе умножения.
0-1
«2 Яз
а-2.
а.
a-i
другом запоминающем устройстве в двоичной системе счисления, например (для большей наглядности) пятиразрядное в виде:
«42 + аз23 + 0222 + Oi2i + а.
Для этого возведем в куб это число, которое представим в виде
(а423 + аз22 + а221 + а,)2 + .
По известному разложению по биному Ньютона получим (a4a3«2ai)-2 + 3 (0:40:302 1 )-«0-22+ -f 3 (а4«за2Й1) 4- ao но в двоичной системе счисления uf at; умножение на «о не При возведении этого числа в квадрат каждый из квадратов слагаемых а,-2 преобразуют в a i-22. Так как преобразования осуществляются в двоичной системе счисления, то а2 аг, а умножение на 2 равносильно сдвигу влево на 21 разрядов, что соответствует сдвигу на I разрядов слагаемого аг-2. Поскольку цифры исходного числа записываются подряд, то квадраты в силу указанного преобразования оказываются записанными через разряд. После этого прибавляют к квадратам цифр исходного числа удвоенное произведекие кажДой цифры на остальные, т. е. произведение вида 2aj-2-aj2J, нетрудно видет, что 2ai-2iaj-2 Последнее выражение означает, что эти удвоенные произведения получаются сдвигом « «лево на число разрядов, равное Берут самую младшую цифру «о и умножают ее на остальные цифры числа. Очевидно, что при этом получится исходное число, сдвинутое на один разряд влево без младшей цифры. Затем берут следующую цифру и умножают на цифры исходного числа без двух младших цифр, что равносильно сдвинутому исходному числу на два разряда влево без двух младших цифр. Эту операцию продолжают до тех пор, пока не будет умножена предпоследняя цифра на самую старшую. Складывают полученные произведения с квадратами цифр исходного числа и получают следующую матрицу, сумма строк которой равна квадрату исходного числа.
сдвигает выражения («4030201), выражение (a4O3«2ai) сдвигается влево на разряд, так как степень двойки в самом младшем разряде этого ч-исла равна единице и носле возведения в квадрат удвоится, что соответствует сдвигу на один разряд влево. Кроме того, из вышеприведенного примера возведения числа в квадрат известно, что выражение (0.1030201)2 равно сумме строк следующей матрицы:
S со га
«4
л н а S о г
«4
«4
Повторим вышеприведенный прием теперь к выражению (04030201). Поскольку степень двойки при коэффициенте Oi равна единице, то (21)3 23 или самый младший разряд этого числа будет размешен на четвертом месте или через два разряда от OQ.
«4
Оз
До йо
Д4
«1 X До
«2 X «о
взХ «о
a
ai
ai
Д4
Яз X «1
«4 Д4
Дз X ai
a
иг
а-2
«4
Дз
из X 2 Д4
Д:) Д4
Д4
«3
Эта матрица построена для пятиразрядного числа (но таким же способом можно построить матрицу для числа произвольной разрядности). Аналогичным образом строятся матрицы более высоких степеней чисел.
При аппаратурной реализации приведенного способа необходимо учесть общее свойство этих матриц: составляющие части их, например матрицы квадратов частей числа, построены таким образом, что в матрицу квадрата двух старших цифр входит квадрат старшей цифры, в матрицу квадрата трех старших цифр и т. д.
Запишем теперь матрицу квадрата числа для сложения частей исходного числа, начиная €0 старших разрядов:
«3
ai
аг
«4
аз Й4
н S
и о
аз
X S
«4
Перепишем полученный результат с учетом этих соображений и мест цифр в разрядной сетке:
«,)
(«4«3«3
«о
из
«I
Да «1
«4
«2
a.j
Таким образом, матрица для выражения (04030201) не отличается от предыдущей, но смешена на три разряда влево, при этом степень «три оттанется у выражения (040302). Продолжая этот процесс дальше, получим
окончательно следующую матрицу, сумма строк которой равна кубу числа (0403020100):
До
Д1
Д4
д
Д1
Дз Д2 «1 Д2
Дз
Дз
Д2 а„
«4
Дз Дз
Дз Д4
Дг
Д4
«1
«2
«3
Д1
«1 Д4
д.
Дз
До
Очевидно, что для реализации этой матрицы в виде устройства достаточно иметь два регистра: один-исходного числа, а другой- накапливающий сумматор с цепями сдвига влево на два разряда за такт. Вдвигая со стороны старших младших разрядов исходное число по одному разряду в регистр, а содержимое .накапливающего сумматора сдвигая
влево на два разряда за такт и складывая после каждого такта сигнал части числа без цифры, размещенной на месте младшего разряда со сдвигом на разряд влево, и сигнал цифры, размещенной на месте младшего разряда без сдвига с содержанием накапливающего сумматора, в каждом такте будет нолучать квадрат сигнала части числа, вдвинутого в данный момент в регистр исходного числа.
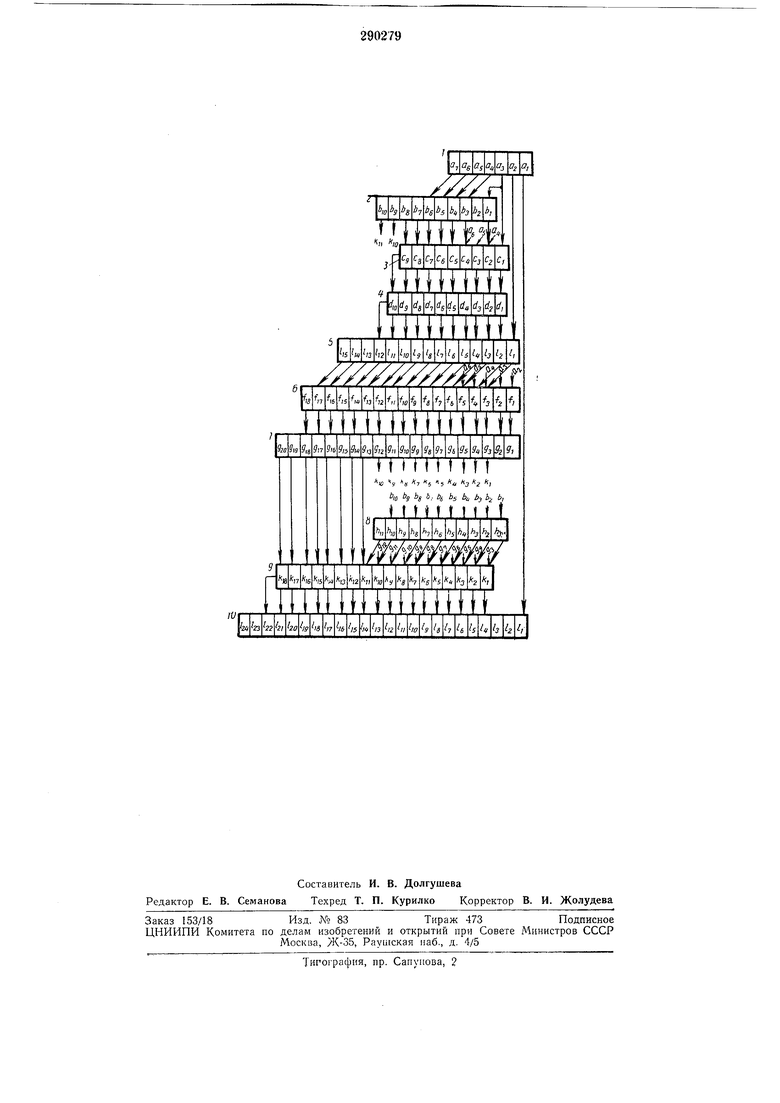
На чертеже изображена схема описываемого устройства. Оно содержит регистр / числа, квадратор (регистр 2 первого блока), первый ряд сумматоров 3 первой группы второго блока, умножитель 4 на коэффициент «три второго блока, регистр 5 второго блока, первый ряд сумматоров 6 первой группы третьего блока, умножитель 7 на коэффициент «четыре третьего блока, умножитель 8 на коэффициент «шесть третьего блока, первый ряд сумматоров 9 второй группы третьего блока и регистр 10 третьего блока (регистр результата) .
Кроме того, на чертеже приведены следующие обозначения: а,-h - разряды соответствующих блоков, причем меньщим цифрам соответствуют младшие разряды.
Стрелки на рисунке показывают направление передачи сигнала между разрядами блоков, цифры с буквами у свободных концов стрелок указывают: цифра на номер разряда, а буква на блок, к которому должен быть подсоединен этот разряд. Регистр / имеет семь разрядов, а регистр 2 - десять, разрядность «сходных чисел - шесть.
Регистры 1, 2, 5 и 10 снабжены цепями сдвига, причем за один такт сдвиг в регистре 1 осуществляется на один разряд влево, в регистре 2 - на два разряда, в регистре 5-на три разряда и в регистре 10 - на четыре разряда.
Вход разряда 6i регистра 2 соединен с выходом разряда а регистра /, а входы разрядов &з, &4. 5 и 6б соединены с выходами разрядов а.|, ог, «6 и «7.
Выходы разрядов Ci, Са, Сз и с ряда сумматоров 3 соединены с выходами разрядов а-,, Ол. «5 и UB регистра /. Вторые входы разрядов Сз и С4 ряда сумматоров 3 соединены с выходами разрядов 64 и Ьз регистра 2 (выход разряда Ьг регистра никуда не подается, так как сигнал выхода этого разряда всегда соответствует нулевому сигналу, для двоичной системы счисления). Выходы разрядов с.-,, Ск, с/, Cs и Сз ряда сумматоров 3 соединены с выходами разрядов Ь, bs, be, b и Ъ, регистра 2, Выходы сумматоров S поразрядно соединены с входами умножителя 4, биноминальный коэффициент этого блока равен трем. Выходы умножителя 4 соединены с входом регистра 5, причем выход младщего разряда умножителя соединен с входом второго разряда регистра 5. Остальные разряды также подсоединены со сдвигом на разряд влево.
первого ряда сумматоров 6 первой группы третьего блока, причем младший разряд ei регистра 5 соедипен с входом разряда fa ряда сумматоров 6. Остальные разряды подсоединены со сдвигом 1на два разряда влево. Входы разрядов /1, f2, fs, 1/4 и /5 соединены с выходами соответственно разрядов а, аз, а., as и ае регистра 1. Выходы ряда сумматоров 6 поразрядно соединены с входами умножителя 7. Поскольку биноминальный коэффициент этого умножителя равен четырем, то, например, в двоичной системе счисления этот блок может быть опущен, а умножение на четыре выполняют, сдвигая входные сигналы влево на два разряда, т. е. соединяя выходы сумматоров 6 с входами первого ряда сумматоров 9 второй группы третьего блока со сдвигом на два разряда влево.
Выходы регистра 2 соединены непосредственно со входами умножителя 8 (биноминальный коэффициент этого умножителя равен шести).
Выходы ряда сумматоров 9 соединены с входами регистра 5, при этом формально необходимо было бы соединить младший разряд К с входом разряда 62, но поскольку в качестве примера рассматривается устройство, работающее в двоичной системе счисления, то в связи с тем, что биноминальные коэффициенты для третьего блока-4 и 6, то первый значащий разряд ряда сумматоров 9 будет совпадать с четвертым разрядом регистра W, таким образом, разряд KI ряда сумматоров 9 соединен с разрядом е регистра W.
Работает устройство следующим образом.
Исходное число последовательно вдвигают в регистр / старшими разрядами вперед. При сдвиге на один разряд влево в регистре 1 одповременно производят сдвиги в регистре 2 на два разряда влево, в регистре 5-на три разряда влево и в регистре 10 - на четыре разряда влево. После каждого сдвига аиализируют состояние разрядов ai, а2 и «з регистра /. Если содержимое разряда аз соответствует сигналу единицы (аз 1), то производят сложение содержимого регистров / и 2; если а9 1, то кода с выхода ряда сумматоров и с содержимым регистра 5 и подают код с выхода умножителя 8 на вход ряда сумматоров 9; если ai I, то подают код с выхода Умножителя 7 на вход ряда сумматоров 9. Если же содержимое какого-либо из этих разрядов равно нулю, то существующие операции в данном цикле запрещают.
Завершается операция после цикла, следующего за тем сдвигом, когда младщий разряд исходного числа займет места разряда az.
Аналогичным образом можио создать устройства более высоких степеней чисел.
Предмет иЗобретения
Устройство для возведения чисел в степень четыре, состоящее из регистра числа и накапливающих сумматоров, отличающееся тем,
что, с целью повышения быстродействия, оно содержит квадратор, умножитель на коэффициент «три, умножитель на коэффициент «четыре, умножитель на коэффициент «шесть, регистр второго блока И регистр результата, причем выход младшего разряда регистра числа соединен с входом младшего разряда регистра результата, выход второго разряда регистра числа соединен с входом младшего разряда регистра второго блока, выход третьего разряда регистра числа соединен с входами младших разрядов квадратора и ряда сумматоров второго блока, выход каждого t-ro ИЗ остальных разрядов регистра числа соединен с входом (t-1)-го разряда квадратора, выход каждого f-ro разряда квадратора (кроме второго) соединен с входом (i + + 1)-го разряда ряда сумматоров второго блока, выходы разрядов ряда сумматоров второго блока соединены с входами сортветствуюших разрядов умножителя ла коэффициент «три, выход каждого /-го разряда которого соединен с входом (г+ 1)-го разряда регистра второго блока, выходы разрядов этого регистра соединены с входами соответствуюших разрядов ряда сумматоров третьего блока, выходы разрядов этого ряда сумматоров соединены с соответствуюшими входами разрядов умножителя на коэффициент четыре, выход каждого 1-го разряда этого умножителя соединен с входом (i - 2)-го разряда другого ряда сумматоров третьего блока, выход каждого ;-го разряда этого ряда сумматоров соединен с (i + 3)-M разрядом реги.стра результата, выходы разрядов квадратора соединены с входами соответствуюших разрядов умножителя на коэффициент «шесть, выходы которых соединены с соответствуюшими разрядами другого ряда сумматоров третьего блока.



| название | год | авторы | номер документа |
|---|---|---|---|
| Преобразователь двоичного кода в р-ичный позиционный код | 1983 |
|
SU1163479A1 |
| Устройство для реализации быстрых преобразований в базисах дискретных ортогональных функций | 1985 |
|
SU1292005A1 |
| Устройство для извлечения корня четвертой степени | 1985 |
|
SU1262487A1 |
| Устройство для возведения в степень | 1983 |
|
SU1087990A1 |
| Устройство для умножения | 1989 |
|
SU1672441A1 |
| Последовательное множительное устройство | 1985 |
|
SU1307455A1 |
| Матричное устройство для решения уравнений в частных производных | 1985 |
|
SU1302276A1 |
| Устройство для возведения в квадрат и извлечения квадратного корня | 1982 |
|
SU1141406A1 |
| Вычислительное устройство | 1988 |
|
SU1532917A1 |
| Устройство для преобразования избыточного двоичного кода в код со смешанным основанием | 1975 |
|
SU618737A1 |



Авторы
Даты
1971-01-01—Публикация