Изобретение относится к области вычислительных дискретных устройств.
Известно арифметическое устройство (АУ), в котором умножение выполняется младшими разрядами вперед со сдвигом множимого влево и сдвигом множителя вправо. Однако в таком методе умножения необходим 2п-разрядный регистр множимого и сумматора.
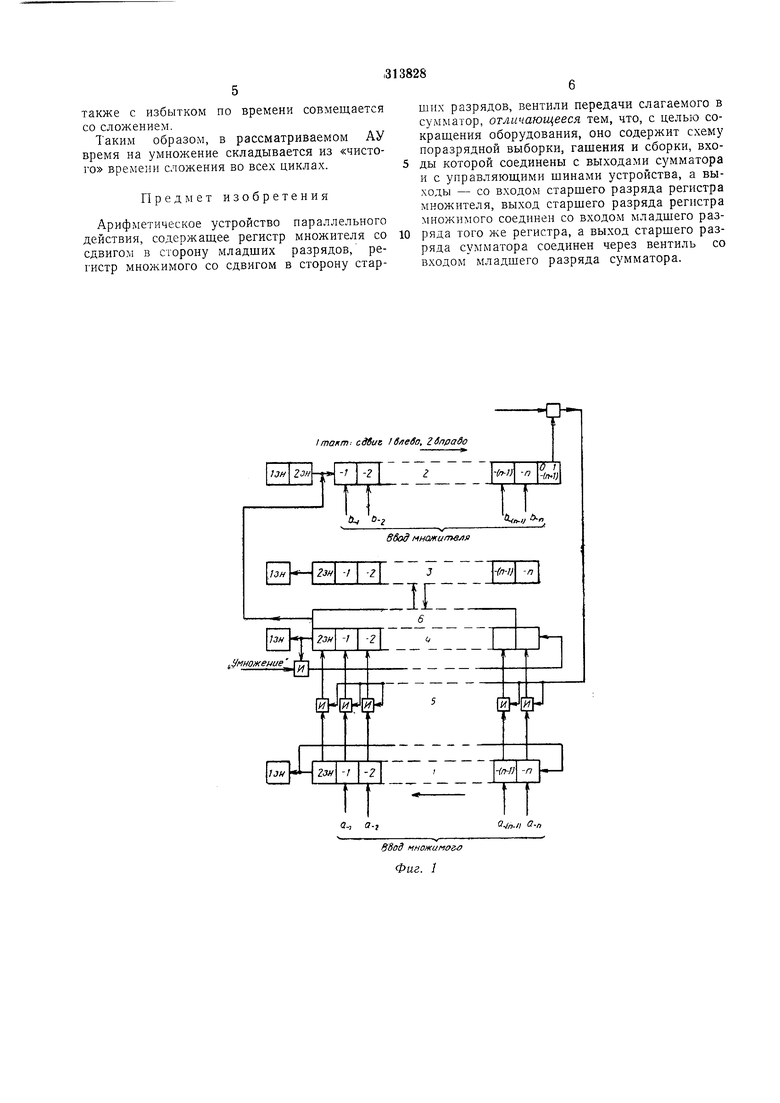
Описываемое устройство отличается от известного тем, что оно содержит схему поразрядной выборки, гашения и сборки, входы которой соединены с выходами сумматора и с управляюш,ими шинами устройства, а выходы - со входом старшего разряда регистра множителя, выход старшего разряда регистра множимого соединен со входом младшего разряда того же регистра, а выход старшего разряда сумматора соединен через вентиль со входом младшего разряда сумматора. Это позволяет сократить оборудование.
Па фиг. 1 - блок-схема арифметического устройства; на фиг. 2 - представлена матрица частичных произведений при выполнении умножения известным способом; на фиг. 3 - то же, при выполнении умножения по описываемому методу.
клапаны для подачи слагаемого в сумматор 5 и схему 6 поразрядной выборки, гашения и сборки. Рассмотрим метод умножения, применяемый в АУ, на примере умножения двух двоичных четырехразрядных чисел Л и В, из которых , а-4-множимое, а В 0, 8-1 б-з 8-4 - множитель. Умножим их «столбиком. Получим матрицу частных
произведений М (см. фиг. 2). В результате деления матрицы на две части (пунктирная линия) и M С границей раздела между -п и -(п+1).и разрядами каждое частичное произведение исходной матрицы
оказывается поделенным на две части, одна из которых относится к М, а другая - к М. Осуществляя последовательное сложение частичных произведений матриц М и М (начиная с верхней точки), получим на каждом
шаге (цикле) соответственно суммы частичных произведений (частичные суммы) Cj и Q., где / - номер сложения.
Если частичная сумма CJ имеет своим старшим разрядом -(п-|-1)-й разряд, то перенос, возникаюш,ий из этого разряда, участвует совместно с членами матрицы М в образовании частичных сумм Cj. После п сложений одновременно в старших
рйзряды произведения в виде С. Готовые младшие разряды произведения образуются последовательно после каждого сложения. Полученный Б данном цикле готовый младший разряд нроизведения в последуюпдих циклах не оказывает влияния на образование частичных сумм Cj и С-, поскольку после своего образования в оставшихся пиклах он суммируется с нулем. Образовавшиеся готовые младшие разряды произведения составляют статическую (неизменную по отношению к последуюш,им циклам) часть частичпой суммы Cl и, следовательно, не влияют на дальнейший процесс вычислений. Если после каждого сложения сразу же после образования выводить из сумматора эти разряды, очиш,ая одновременно разряды сумматора, в которых они находились, то в младших разрядах сумматора получатся частичные суммы Cj. Частичная сумма является динамической частью С, поскольку любой ее разряд в последуюш,ем сложении может измениться (С -это Cf без готовых младших разрядов произведения). Количество разрядов, которое занимает в сумматоре, будет уменьшаться справа на один разряд носле каждого сложения. С другой стороны, количество разрядов, которое занимает С. после каждого сложения, увеличивается справа на один разряд. С учетом возможных переносов для размещения С в сумматоре достаточно иметь такое же количество разрядов, какое занимает участвующее в данном сложении частичное нроизведение матрицы М плюс еше один свободный разряд слева. Обш,ее количество разрядов, которое занимают вместе частичные суммы Cj и C-J, остается неизменным и равным п. Прибавив еиде один разряд, в котором до сиисания находился полученный в данном цикле готовый младший разряд произведения, максимальное количество разрядов сумматора равпо (га-|-1).
Для совмещения вычисления CJ и С-. в (rt-|-l)-разрядном сумматоре, необходимо произвести сдвиг матрицы Л1- влево на (/г-|-1) разряд (см. фиг. 3). Для нереносов, которые при суммировании прежней матрицы Л1 поступали из -()-ro разряда в -п-й разряд, а в новой матрице М должны иоступап из дополнительного разряда в -n-ii разряд сумматора, необходима цепь циклического переноса, которая включается только на время умножения. При последовательном (начиная с верхней строки) суммировании матрицы М , в разрядах сумматора, начиная с -(п-1)-го разряда и кончая дополнительным, на каждом шаге будут получаться готовые младшие разряды произведения. При их выводе после каждого /-го сложения в сумматоре освобождается место для образоваиия последующей частичной суммы Cj.|.j , име 0щей разрядность на едииицу больше, чега С/..
После ti-io сложения в сумматоре образуются готовые старшие разряды произведения в :;иде q.
Для по,;;уч(--ния матрицы М необходимо ис1:ользозать замкнутый (/;-г1)-разрядный регистр / со сдвигом влево (см. фиг. 1), выходы KOiOporo соединены с сумматором через регистр схемы «И, уиравляемый разрядами лпюж;г:-елк. После ввода множимого в регистр ; остается свободным дополнительный (знаковый) разряд. Затем перед каждым сложением I) регистре / ироисходит сдвиг влево на один разряд и умножение в регистре схем ;И его содержимого на разряд множителя.
5 На выходах регистра «И нолучаем в каждом цикле чгстичные произведения в соответствии с матрицей ЛГ.
Рассмотрим возможность реализации цоразрядного вывода готовых младших разрядов
0 произведения из разрядов сумматора (с одновременной очисткой последних) и их сборки для отсылки в требуемое место на хранение. Это достигается с иомощью схемы норазрядпой выборки, гашения и сборки, нред5 ставляюш.ей собой устройство, имеющее п выходоп, па которых последовательпо, в соответствии с номером цикла, образуются сигналы г-ыборки и гашения.
Сигналы выборки и гашения через соответствующие логические элементы в определенные моменты времени носледовательно, начиная с --(П-1)-го и кончая дополнительным, воздействуют на разряды сумматора, осуществляя юразрядную выборку и гашение. Выбранные младшие разряды произведения по адают и сборку, имеющу1о п входов, и с ее выхода ;юступают последовательно на вход регистра множителя.
В качестве дополнительных разрядов сумматора и регистра множимого используются
игорые знаковые разряды этих регистров. Готозые млгдшие разряды поступают из схемы Юразрядной выборки, гашения и сборки на г;;:од (па 1-й разряд) регистра множителя 2
5 и заполняют там разряды, освобождающиеся li процессе умножения. Регистр 2 имеет спраiia одпн дополнительный --(-|-1)-й разряд, оьполокющий роль задержки и обес 1ечГ1ваю|Цкй в первом цикле постуилсиие : 1ладшего
0 разряда лпюжителя на peincip схем «И лишь после сдвига регистров 2 и 1. Если в первом цик. предусмотреть сдвиги только з регистре 1, а в окончательных циклах сдвиг в регистрах / п 2, то дополнительный разряд в регистре 2 не пужен.
В представленной схеме отсутствуют сдвиги в регистре 3 или в сумматоре, если он накапливающего типа. В связи с этим можно совлгестить по времени сдвиг регистров / и ..
со сложением. Сдвиг осуществляется сразу после формирования частичного произведения и поступления его в сумматор.
также с избытком по времени совмещается со сложением.
Таким образом, в рассматриваемом АУ время на умножение складывается из «чистого времени сложения во всех циклах.
Предмет изобретения
Арифметическое устройство параллельного действия, содержащее регистр множителя со сдвигом в сторону младщих разрядов, регистр множимого со сдвигом в сторону старших разрядов, вентили передачи слагаемого в сумматор, отличающееся тем, что, с целью сокращения оборудования, оно содержит схему поразрядной выборки, гащения и сборки, входы которой соединены с выходами сумматора и с управляющими щинами устройства, а выходы - со входом старшего разряда регистра множителя, выход старщего разряда регистра множимого соединен со входом младщего разряда того же регистра, а выход старщего разряда сумматора соединен через вентиль со входом младщего разряда сумматора.

| название | год | авторы | номер документа |
|---|---|---|---|
| ДВОИЧНОЕ АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО | 1968 |
|
SU210491A1 |
| Вычислительное устройство | 1988 |
|
SU1532917A1 |
| Устройство для умножения | 1976 |
|
SU651341A1 |
| Устройство для умножения | 1981 |
|
SU1007101A1 |
| Устройство для умножения чисел | 1990 |
|
SU1714595A1 |
| Устройство для умножения | 1985 |
|
SU1252774A1 |
| Устройство для умножения | 1975 |
|
SU1206773A1 |
| ОДНОТАКТНОЕ ЦИФРОВОЕ АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО | 1972 |
|
SU330450A1 |
| Устройство для умножения | 1988 |
|
SU1615706A1 |
| Устройство для умножения | 1989 |
|
SU1672441A1 |



Iтакт: сдбик Iвлево, 2вправо
УмножениеQ-, а..
о г
-(п-П -r/f.;;
.
0-г
-
вбод мнсикит /1я
лг::
C V/7-// О-п
ввод MHOfKuna&a Фаг. 1
Выборка tomaSbM мл раорядов произведена
м
rq.JIIJ
.,
fuz. J
Даты
1971-01-01—Публикация