Изобретение относится к области вычислительной техники.
В задачах, связанных с распознаванием образов или со слежением за движущимся объектом сложной и меняющейся формы, в конструкторских задачах, требующих перебора различных форм изделия, в устройствах выдачи данных из ЦВМ и т. п. случаях требуется производить геометрические преобразования фигур, изображаемых набором точек с двумя градациями яркости. Обычно такие преобразования, выполняются на ЦВМ, которая вычисляет координаты точек преобразованной фигуры по известным координатам точек исходной фигуры. Однако такой метод требует наличия ЦВМ, специального программирования и занимает много машинного времени, т. к. вычисление координат каждой точки требует нескольких операций (например, для вычисления новых координат точки при аффинном преобразовании фигуры на трехадресной машипе требуется 4 операции сложения и 4 умножения) .
Цель цредлагаемого изобретения заключается в построении автономного и быстродействующего устройства, в котором любое (из заданного множества) геометрическое преобразование фигуры в целом производится одной операцией над кодом всей фигуры (т. е. над всеми точками фигуры одновременно). Эта
цель достигается применением специальной схемы, которая по номеру геометрического преобразования производит преобразование двоичного кода фигуры в целом и образует на выходе двоичный код преобразованной фигуры. Цри этом время преобразования фигуры в целом равно времени одной операции с кодом координаты одной точки этой фигуры на обычной ЦВМ (при постоянной системе элементов), благодаря чему значительно сокращается время решения соответствующих задач. Ограничение состоит в том, что допускаются только аффинные преобразования на плоскости (поворот, сдвиг, смещение и т. п.).
Аппаратурно это выражается в том, что устройство содержит регистр числа, регистр множимого и регистр геометрического кода фигуры, причем выход регистра множимого соединен со входом блока управления, выходы блока управления соединены с одним из управляющих входов регистра геометрического кода фигуры и входом регистра числа,выходы каждого разряда которого соединены с соответствующими управляющими входами регистра
геометрического кода фигуры.
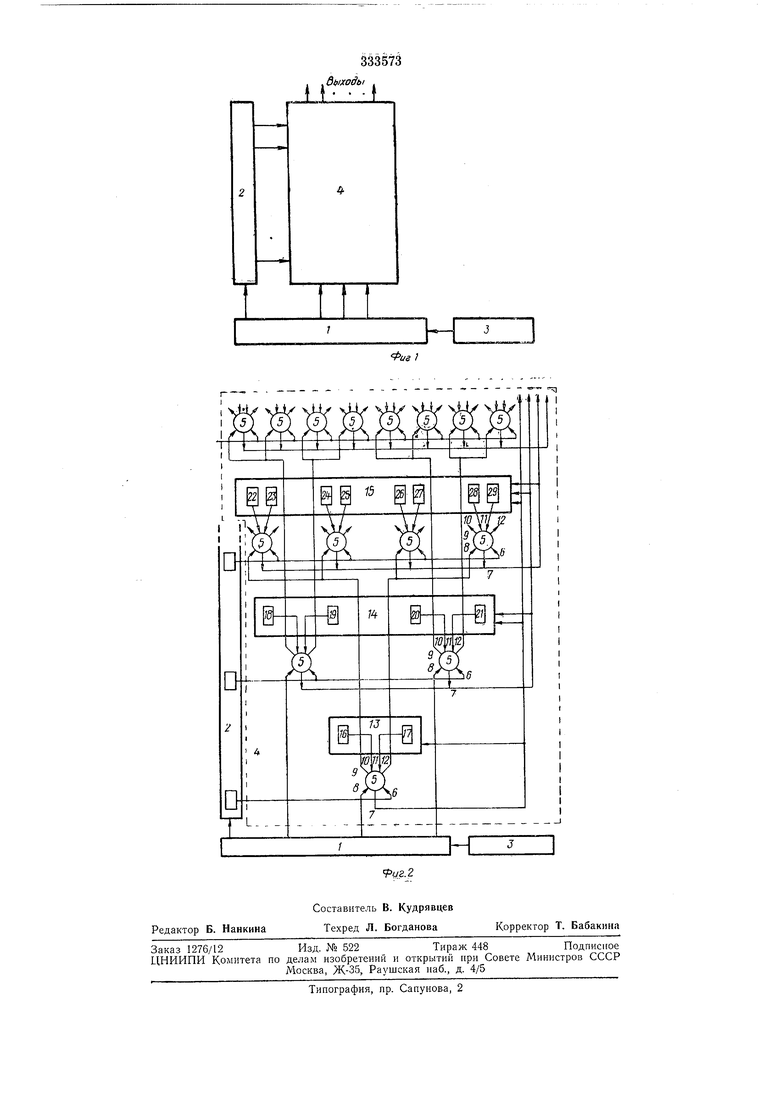
Регистр геометрического кода фи-гуры содержит /С выполненных на триггерах сдвиговых регистров-ярусов, первый из которых имеет два разряда, а каждый последующий - Ки сигналов переноса по количеству пар триггеров каждого регистра, причем одни входы схем выработки сигналов переноса t-ro яруса объединены и подключе1 ы к соответствующим входам, два других входа - к выходам двух соответствующих триггеров данного регистраяруса, четвертые входы каждой пары схем выработки сигналов переноса объединены и подсоединены к соответствующим двум выходам аналогичных схем (f-2)-го яруса, третьи выходы всех схем выработки сигналов переноса каждого яруса объединены вместе и нодключены к сдвиговым входам всех i,, i-r2, ..., к-х регистров-ярусов. На фиг. 1 показана общая блок-схема устройства, фиг. 2 поясняет построение регистра геометрического кода фигуры. На чертежах обозначены: 1 - блок управления; 2 - регистр числа; 3 - регистр множимото; 4 - регистр геометрического кода фигуры; 5 - двухразрядные схемы выработки сигналов переноса; 6-12 - внешние связи схем 5; 13-15 - сдвиговые регистры-ярусы; 16-29 - триггеры сдвиговых регистров-ярусов. Регистр 2 служит для хранения двоичного кода комплексного числа по основанию i Этот код в дальнейшем будем называть базисным. Например, если базисный код-1011, то соответствующее ему . комплексное число S 1 - (/ + 0- 0-1/2) + 1.(/ /2) + + 1. (/1/2 ) 1 - / К2 . Основным узлом устройства является регистр 4 геометрического кода фигуры, состоящий из совокупности регистров 13, 14, 15. Каждьш из этих регистров называется ярусом общего регистра геометрического кода, причем младщий (первый) ярус (регистр 13) содержит 2 разряда, следующий (второй) ярус - 4.разряда, третий - 8 разрядов и т. д. Таким образом, ярус с номером к (/с-ярус) содержит -2 разрядов. В общем случае регистр содержит п ярусов и () разрядов и хранит код геометрической фигуры. . Каждый ярус регистра геометрического ко да содержит 2 схем 5 выработки сигналов переноса и транспонирования. Входы 6 всех схем 5 каждого яруса объединены и соединены с выходом соответствующего триггера регистра 2., Входы 10 и ill этих схем присоединены к выходам двух триггеров данного яруса. Сигналы переносов яа и яр возникают на выходах 9 и 12 соответственно и поступают на объединенные входы 8 переносов двух схем 5, принадлежащих ярусу с номером . Сигнал транспонирования т возникает на выходе 7 схемы 5 И поступает на сдвиговые входы всех ярусов с номерами, не , чем к. Входы 8 переносов трех схем 5 двух младших ярусов подключены к схеме управления. К этой же схеме .присоединены входы регистра 2 и его сигналы управления. Регистр множимого 3 имеет такую же разсвязан с последним через блок управления L Устройство работает следующим образом. В регистр геометрического кода записывается код фигуры, а в регистр базисного кода - код комплексного числа, онределяюш.его вид преобразования. Затем по сигналам из схемы управления производится алгебраическое сложение или умножение геометрического и базисного кодов. Любая из этих операций состоит из циклов сдвига базисного кода, распространения переносов по схемам 5 и транспонирования геометрического кода. Арифметические операции между геометрическим и базисным кодами эквивалентны одпоименной арифметической операции между каждым комплексным числом, изображающим некоторую точку фигуры, и базисным числом. Таким образом, сложение эквивалентно смещению фигуры, умножение - повороту, умножение только мнимых или действительных частей - сдвигу. В общем случае на предлагаемом устройстве можно выполнить любое аффинное преобразование исходной фигуры. Рассмотрим теперь элементарные операции транснонирования и распространения переносов. Транспонирование заключается в перестановке определенных разрядов ярусных регистров, в которые поступил сигнал транспонирования. Это осуществляется на схеме, аналогичной схеме сдвига. Поэтому ярусные регистры 13, 14, 15 ... являются сдвиговыми. Сигнал транспонирования, поступающий из г-яруса в /с-ярус, .производит перестановку разрядов к-яруса, номера которых отличаются на 2, причем перестановке подвергаются лишь разряды, связанные с теми схемами 5, которые .по цепям 8, 9 и 8, 1-2 соединены со схемой 5 t-яруса, выработавшей сиг)ал транспонирования т по цепи 7. Например, если сигнал т БЫработался в схеме 5, соединенной с триггерами 20 и 21 (см. фиг. 2), то перестановке подлежат разряды 20 и 21, 26 и 28, 27 и 29 и т. д. Сигнал переноса яа вырабатывается на выходе 9 схемы 5, а яр - на выходе 12 этой же схемы. Эти сигналы поступают затем в две другие .схемы 5 .старшего яруса. Таким образом, каждая схема 5 вырабатывает сигналы т, яа и лр. Эти сигналы являются функцией сигнала я, пришедщего на вход 8, сигнала б, пришедшего па вход ,6 от триггера регистра 2, и сигналов аир, пришедших на входы 10 и 11 соответственно от триггеров регистра данного яруса. Формулы алгебры логики, связывающие эти величины, имеют следующий вид: (бУя)а; причем сигналы яа и яр вырабатываются с задержкой относительно сигнала т на время t,
Зываемое «обратное с.тожение кодов, которое эквивалентно следующей аперации с числами:
bi -ai-8,
где ш - точка исходной фигуры;
Ы - точка преобразованной фигуры; б - базисное число.
Обратное сложение начинается но сигналам п, поступающим из блока управления / вначале в схему 5 первого яруса, а затем (через время t) в схемы 5 второго яруса.
При обратное сложение эквивалентно инвертированию (умножению на - 1):
Ы - -ai.
Операция выполняется в два этапа:
1) инвертирование и 2) обратное сложение.
Умножение геометрического и базисного кодов состоит в последовательной замене базисным кодом тех разрядов геометрического кода, которые имеют четный номер в данном ярусе п единичное значение.
Умножение выполняется в такой носледосательности:
а)из кода частичного произведения, хра: ящегося в регистре 3, выделяется очередной код ri,K и передается через схему 1 на регистр 4, так, что младший разряд этого кода записывается в триггер 2} регистра фигуры; одновременно в триггеры 16 и 17 этого же регистра записываются «О и «1 соответственно, а в регистре 3 все разряды кода П,к заполняются
б)код П,к в регистре фигуры складывается с базисным кодом Дб, находящимся в регистре 2, но формуле П,к-6;
в)результат -суммирования по пункту б) логически складывается с кодом на регистре 3, причем разряд У7 кода регистра фигуры складывается с разрядом (f-1,к) кода регистра 3.
В начале умножения в регистре 3 записан код множимого.
Процесс умножения начинается с выделения кода Li,K, имеющего максимальный индекс к и минимальный индекс /, и продолжается в сторону уменьшения к и увеличения г. В конце умножения в регистре 3 оказывается произведение кодов множимого п отрицательного базисного числа. Это соответствует преобразованию каждой точки ai псход)1ой фигуры в точку Ы результирующей фигуры по формуле:
ai.
Покомпонентное умножение отличается от обычного умножения, описанного выще, тем, что замене нодвергаются только те разряды ccj.h, у которых к - четное (нечетное). Обозначим (по- г1режнему i - четное):
. , i,k при к-четном, У-- при к - нечетном.
Заметим, что младщему разряду базисного кода соответствует нулевая степень основания ( ), четному разряду базисного кода соответствует нечетная степень основания , а нечетшму разряду - четная степень основания .
Аналогично, четному (нечетному) номеру яруса кода фигуры соответствует нечетная
(четная) степень основания /J/2 в коде числа ai, определяющего точку фигуры. Поэтому замена 5 соответствует операции умножения мнимой части каждой точки ai xi-{-jyi на
отрицательное базисное число bi xi-jdyi; замена разрядов соответствует операции: bi -dxi- jyi.
Таким образом, на предлагаемом устройстве можно выполнить любую (из требуемых для
аффинных преобразований) арифметическую операцию с каждой координатой каждой точки исходной фигуры одновременно. Это резко уменьшает время преобразования на данном устройстве iHo сравнению с ЦВМ.
Пред м е т и з о б р е т е н и я
1. Цифровое устройство для геометрических преобразований изображения, содержащее регистры и блок управления, отличающееся тем, что, с целью сокращения времени преобразования, вхыод регистра множимого соединен со входом блока управления, выходы которого соединены с одним из управляющих входов регистра геометрического кода фигуры и входом регистра числа, вы.ходы каждого разряда которого соединены с другими управляющими входами регистра геометрического кода фигуры.
2. Устройство но п. 1, отличающееся тем, что в нем регистр геометрического кода фигуры содержит к выполненных на триггерах
сдвиговых регистров-ярусов, первый из которых имеет два разряда, а каждый последующий - вдвое больше предыдущего, и схемы выработки сигналов переноса по количеству пар триггеров каждого регистра, причем одни
.входы схем выработки сигналов переноса /-го яруса объединены и подключены к соответствующим входам, два других входа - к выходам двух соответствующих триггеров данного регистра-яруса, четвертые входы каждой пары схемы выработки сигналов переноса объединены и подсоединены к соответствующим двум выходам аналогичных схем (f--2)-го яруса, третьи выходы всех схем выработки сигналов нерепоса каждого яруса объедннены вместе и подключены к сдвиговым входам всех /,/+, i-f2, ..., fc-x регистров-ярусов.
. дтходы . t 1 


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения @ -разрядных двоичных чисел | 1990 |
|
SU1783519A1 |
| Устройство для умножения двоичных чисел | 1989 |
|
SU1784973A1 |
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| СПОСОБ И УСТРОЙСТВО УМНОЖЕНИЯ ДВОИЧНО-ДЕСЯТИЧНЫХ КОДОВ | 2009 |
|
RU2410745C1 |
| СПОСОБ И УСТРОЙСТВО УМНОЖЕНИЯ ДВОИЧНО-ДЕСЯТИЧНЫХ КОДОВ | 2008 |
|
RU2386998C1 |
| Устройство для умножения п-разрядных чисел | 1978 |
|
SU734683A1 |
| Последовательно-параллельное устройство для умножения чисел | 1987 |
|
SU1413625A1 |
| Устройство для транспортирования спектров,начинающихся от нуля | 1984 |
|
SU1205250A1 |
| Множительно-сдвиговое устройство | 1982 |
|
SU1013951A1 |
| Устройство для умножения | 1976 |
|
SU651341A1 |


Даты
1972-01-01—Публикация