1
Изобретение может быть использовано для наведения объектов при ступенчатых управляющих воздействиях, обеспечивая минимальное квадратичное значение ошибки с учетом ограничений значения регулируемой величины.
Известны комбинированные следящие системы, содержащие замкнутый контур регулирования из последовательно соединенных элемента сравнения, усилителя, сумматора, двигателя и объекта регулирования и разомкнутый контур из двух последовательно соединенных дифференцирующих звеньев.
Такие системы обеспечивают минимальное квадратичное значение ощибки при ступенчатых входных воздействиях, не превышающих некоторой величины, при которой возникает режим насыщения тех или иных элементов системы.
Предлагаемая комбинированная следящая система отличается от известной тем, что содержит квадратор, ключевое устройство, первый и второй нелинейные блоки, соединенные выходами с входами сумматора, при этом первые входы нелинейных блоков связаны с входом системы через последовательно соединенные квадратор и ключевое устройство, а вторые входы нелинейных блоков подключены соответственно к выходам дифференцирующих звеньев.
Это позволяет получить минимальную квадратичную интегральную ошибку следящей системы при ограничении квадратичного интегрального значения регулируемой величины и при любых изменениях амплитуды управляющего скачкообразного входного воздействия.
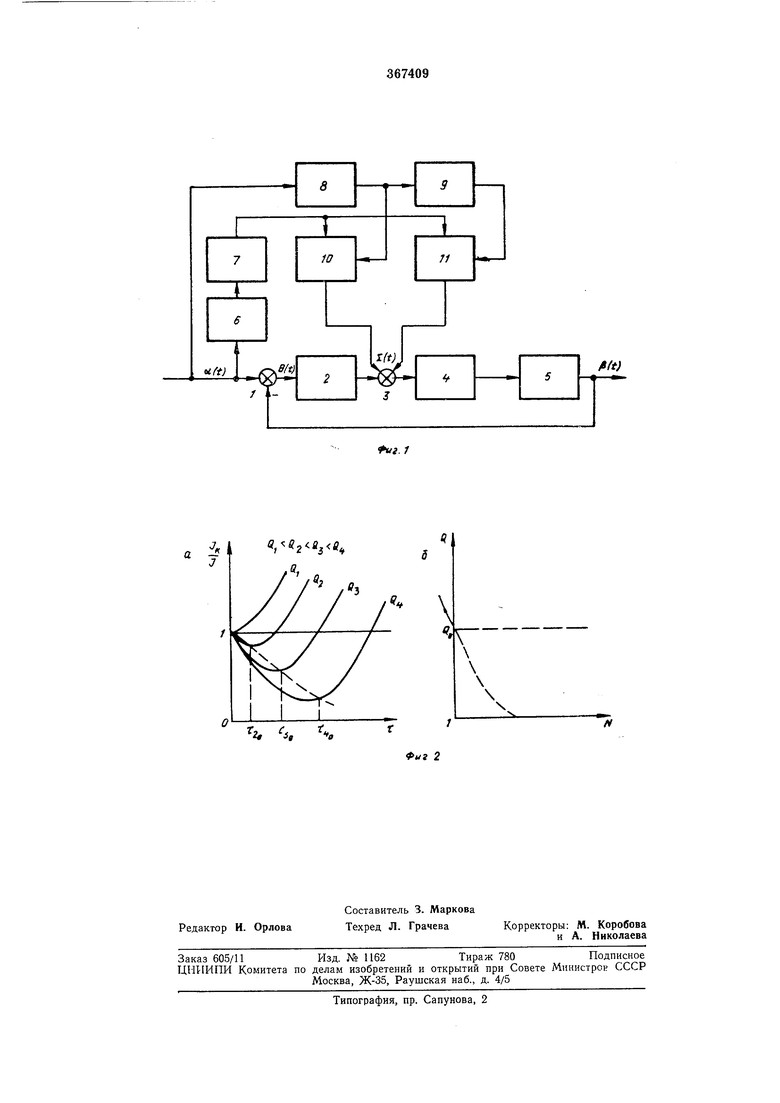
На фиг. 1 изображена структурная схема комбинированной системы, на фиг. 2 - графики изменения квадратичной интегральной ошибки при различных насыщениях.
Комбинированная следящая система содержит элемент 1 сравнения, усилитель 2, сумматор 3, двигатель 4, объект 5 регулирования, ключевое устройство 6, квадратор 7 первое дифференцирующее звено 8, второе дифференцирующее звено 9, первый нелинейный блок 10, второй нелинейный блок //.
Поскольку работа следящей системы, состоящей из замкнутого контура (без разомкнутого контура) общеизвестна, ниже поясняются особенности выбора параметров и работы разомкнутого контура.
Система предназначена для воспроизведения ступенчатого управляющего воздействия с минимальной квадратичной интегральной ошибкой /мин:
/мнн (f)Ydt,
30 о
где8(t) a(t) -p(t) - ошибка системы;
N - амплитуда скачка; а() -управляющее воздействие;
Р(0-регулируемая величина.
При этом на квадратичное интегральное значение ускорения /,з наложено ограничение:
L N (..
или
., где
r(
- ускорение регулируемой величины; Qo - величина ограничения ускорения при a(t) l(t), Q-Qo при .
Как известно, разомкнутый контур регулирования позволяет дополнительно уменьшить ошибку. Параметры связи для линейной системы определяются из решения уравнения:
где ti - параметры связи по управляющему
воздействию (, 2, ...). Для системы с ограничением ускорения регулируемой величины параметры связи /ti, минимизирующие квадратичную интегральную ошибку определяются из уравнения: д( + ) Q д1 .
где р - множитель Лагранжа.
Если /ft - интегральная квадратичная ошибк | комбинированной системы при ограничении Q на величину квадратичного интегрального ускорения, а / - значение интегральной квадратичной ошибки системы без связи (), то график изменения отношения
(fi) при различных величинах ограничения ускорения приведен на фиг. 2, а. Здесь 12,; Тз„; 1 -оптимальные значения параметра ть связи по управляющему воздействию с передаточной функцией
W (, d,,p + d,
полученной с площадью двух дифференцирующих звеньев 4 и 5.
Аналогичен по виду (фиг. 2, а) график изменения - / (тг).
Как видно из фиг. 2, а, оптимальное значение параметра Т а следовательно, параметра Т2, зависит от величины ограничения Q. При увеличении Q оптимальное значение TI (а также Т2) увеличивается и уменьшается в противном случае,
т:2„ 3,С4, ,
В свою очередь величина учитываемого ограничения зависит от амплитуды управляющего воздействия. График этой зависимости показан на фиг. 2,6. При Л ограничение . где QO - заданная величина ограничения ускорения р(0При учитываемая величина ограничения уменьшается:
,
N
ИЛИ
Q, : QN const.
Следовательно, при изменении амплитуды скачка управляющего воздействия величина Q учитываемого ограничения тоже меняется, поэтому необходимо менять настройку параметров TI и Т2 по управляющему во-здействию.
в предлагаемой системе такая подстройка параметров TI и Т2 связи по управляющему воздействию осуществляется с помощью двух нелинейных блоков 10 и 11, изменяющих CBO« коэффициенты усиления в зависимости от величины квадрата амплитуды управляющего воздействия N, поступающей с квадратора 7. Для того, чтобы фиксировать только а1М1Плитуду скач-ка управляющего воздействия во время П1ереходного процесса при любом начальном положении управляющего вала, применяется ключевое устройство 6.
Система работает в широком диапазоне амплитуд управляющего воздействия, обеспечивая минимум квадратичной интегральной
ошибки.
Предмет изобретения
Комбинированная следящая система, содержащая замкнутый контур регулирования
из последовательно соединенных элемента сравнения, усилителя, сумматора, двигателя и объекта регулирования и разомкнутый контур регулирования из последовательно соединенных первого и второго дифференцирующих звеньев, причем вход первого дифференцирующего звена подключен к входу системы, отличающаяся тем, что, с целью повышения точности системы при ступенчатых управляющих воздействиях, она содержит квадратор,
ключевое устройство, первый и второй нелинейные блоки, соединенные выходами с входами сумматора, при этом первые входы нелинейных блоков связаны с входом системы через последовательно соединенные квадратор и ключевое устройство, а вторые входы нелинейных блоков подключены соответственно к выходам дифференцирующих звеньев.
«,
,
Ч
/v

| название | год | авторы | номер документа |
|---|---|---|---|
| КОМБИНИРОВАННЫЙ СЛЕДЯЩИЙ ПРИВОД | 1971 |
|
SU304550A1 |
| Электрогидравлический следящий привод робота | 1990 |
|
SU1740806A1 |
| Следящая система | 1979 |
|
SU881657A1 |
| АВТОКОЛЕБАТЕЛЬНАЯ САМОНАСТРАИВАЮЩАЯСЯ СЛЕДЯЩАЯ СИСТЕМА | 1972 |
|
SU326549A1 |
| Электрогидравлический следящий привод робота | 1989 |
|
SU1723360A1 |
| Следящая система | 1985 |
|
SU1325402A1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ РОТОРА РЕАКТИВНОЙ ГИДРАВЛИЧЕСКОЙ ТУРБИНЫ И ПИД-РЕГУЛЯТОР ЧАСТОТЫ ВРАЩЕНИЯ СИЛЬНОГО ДЕЙСТВИЯ | 2021 |
|
RU2781087C1 |
| Следящая система | 1990 |
|
SU1764030A1 |
| Следящая система | 1975 |
|
SU550617A1 |
| БСЕСОЮЭИАЛ ПДТЕНТЙ.ВTEKH^ECflAn БИ5Л^10Т?КА | 1972 |
|
SU331366A1 |


Авторы
Даты
1973-01-01—Публикация