ОБЛАСТЬ ТЕХНИКИ
Предлагаемый способ регулирования частоты вращения ротора реактивной гидравлической турбины и пропорционально-интегрально дифференцирующий регулятор сильного действия с плоскостью переключения в пространстве переменных состояния системы регулирования относится к области энергетики и предназначен для использования в цифровых и аналоговых системах регулирования частоты вращения (РЧВ) реактивных гидравлических турбин в случае работы приводимых ими генераторов параллельно в составе энергосистемы или изолированно на выделенный район потребителей.
УРОВЕНЬ ТЕХНИКИ
В научной литературе есть сведения о первом применении катаракта (гидравлического контура) для стабилизации регулятора частоты вращения паровой машины, приводящей механизм непрерывного изменения угла наклона телескопа. Изобретателем регулятора является астроном G.Airy (Эри), которому принадлежит идея снижения скорости перемещения заслонки подачи пара к паровой машине механическим соединением ее с поршнем, движущимся одновременно с ней в погруженном в масло цилиндре, полости которого по разные стороны поршня соединены трубопроводом с дросселем [А. И. Павлов, О. А. Титлова. Автоматизация и автоматика как исторический процесс. Опыт по реконструкции начального периода. Интернет ресурс: http://journals.uran.ua/atbp/article/view/35017; Airy G. Supplement to a paper “On the regularion of the clock-work for effecting uniform movements of equatorials”. Memoirs of the Royal Astronomical Society, v.20, 1851; Лекция №1 ТОГУ, интернет ресурс: http://pnu.edu.ru/media/filer_public/2012/12/24/aru.pdf]. Развитием идеи применения катаракта является изодромный гидромеханический регулятор, в котором используется аналогичный предложенному Эри принцип замедления движения поршня изодрома для медленного восстановления статической характеристики регулятора.
Математическое описание движения турбины, как объекта регулирования частоты вращения, было всесторонне исследовано в 60-70 годах ХХ века, [см. например Г. И. Кривченко. Автоматическое регулирование гидротурбин. Энергия. М.-Л., 1964; Б. Е. Сафаров. Расчет режимов регулирования гидроагрегатов на ЦВМ. Энергия. М., 1967; О. И. Башнин и др. Опытные частотные характеристики гидроагрегатов. В кн. Автоматическое управление энергетическими системами и объектами, Наука, Л-е отд., Л., 1968, с.218; В. А. Пивоваров. Проектирование и расчет систем регулирования гидротурбин. Машиностроение, Л., 1973, стр. 184-198; Г. И.Кривченко. Гидравлический удар и рациональные режимы регулирования турбин гидроэлектростанций. Л.- М., 1951. и др.]
На совершенствование структурных решений регуляторов частоты вращения (РЧВ) гидротурбин оказали влияние развитие теории линейных систем автоматического управления и прогресс аппаратных средств реализации законов управления: появление операционных усилителей, микропроцессорных управляющих ЭВМ и совершенных преобразователей малых электрических управляющих сигналов в гидравлические. Решающую роль в этом процессе сыграло массовое применение в 70-х годах ХХ века операционных усилителей, использование которых окончательно позволило разделить регулятор на две части - электронную «голову» и электрогидравлическую силовую часть. А уже в начале 80-х годов стали серийно выпускаться микропроцессорные регуляторы. В настоящее время все выпускаемые регуляторы гидравлических турбин выполнены с применением контроллеров (управляющих вычислительных машин), а количество гидравлических и механических устройств, выполняющих функции управления, ограничивается применением их в последних ступенях аварийных защит при полном отказе электроники, например, при отсутствии питания для нее.
Историю развития структурных схем регуляторов частоты вращения гидравлических турбин можно проследить по международным стандартам:
• IEC 60308:1970, International code for testing of speed governing systems for hydraulic turbines. [1.]
• IEC 60308:2005. Guide to specification of hydraulic turbine governing systems. [2].
• IEC 61362. Edition 2.0 2012-04. Guide to specification of hydraulic turbine governing systems. This publication was withdrawn and replaced by IEC 60308:2005. [3]
• ПНСТ 49-2015 (стандарт России, практически дословный перевод международного документа IEC 61362).[4]
• IEC 60050-351(2013). Международный электротехнический словарь. Часть 351. «Технология управления». [5]
Основные требования к структуре (имеется ввиду закон регулирования) РЧВ в целом изложены в источниках [1,2,3,4]. В частности, на стр. 13-15 [3] приведено описание переходных функций (выходной сигнал элемента системы автоматического управления при подаче на его вход единичного ступенчатого сигнала) двух основных блоков: обязательно входящего в состав регулятора частоты вращения гидротурбины пропорционально-интегрирующего ПИ-блока и дифференцирующего Д-блока, используемого для улучшения качества переходных процессов при реакции регулятора на отклонения частоты вращения агрегата от уставки и на подавления возмущений в нагрузке, признаком которых является отклонения частоты вращения.
ПИ-блок может быть реализован как структурой, образованной находящимся в прямой цепи прохождения управляющего сигнала интегратором с ограниченной скоростью изменения выходного сигнала, охваченного гибкой отрицательной (изодромной) обратной связью, так и более рациональной современной параллельной или параллельно-последовательной структурой, состоящей из двух элементов: пропорционального и интегрирующего, сигналы которых суммируются с требуемыми весами.
Необходимые обозначения
Для переменных состояния объекта управления далее используются следующие обозначения:

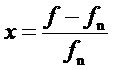 - относительное отклонение частоты вращения
- относительное отклонение частоты вращения 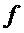 ротора от частоты
ротора от частоты 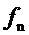 , где
, где  - значение частоты вращения принятого за условную единицу (для России
- значение частоты вращения принятого за условную единицу (для России 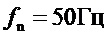 );
);
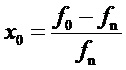 - относительное отклонение уставки частоты вращения
- относительное отклонение уставки частоты вращения 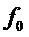 ротора от частоты
ротора от частоты 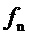 ;
;
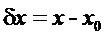 - относительное отклонение частоты вращения от уставки частоты.
- относительное отклонение частоты вращения от уставки частоты.
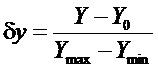 - относительное отклонение положения регулирующего органа от положения, соответствующего установившемуся режиму работы агрегата,
- относительное отклонение положения регулирующего органа от положения, соответствующего установившемуся режиму работы агрегата,
здесь: 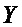 - текущее значение координаты «положения регулирующего органа», отсчитываемое от условного нулевого «положения» -
- текущее значение координаты «положения регулирующего органа», отсчитываемое от условного нулевого «положения» - 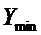 ,
, 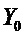 - ожидаемое значение координаты «положение регулирующего органа» в точке равновесия системы,
- ожидаемое значение координаты «положение регулирующего органа» в точке равновесия системы, 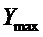 и
и 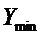 - максимальное и минимальное значения координаты «положение регулирующего органа»;
- максимальное и минимальное значения координаты «положение регулирующего органа»;
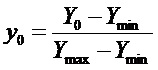 - относительное «положение регулирующего органа» в ожидаемой точке установившегося режима, отсчитываемое от «положения»
- относительное «положение регулирующего органа» в ожидаемой точке установившегося режима, отсчитываемое от «положения» 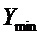 ;
;
величина 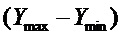 - условная единица для измерения перемещения регулирующего органа:
- условная единица для измерения перемещения регулирующего органа:
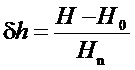 - относительное динамическое отклонение напора от установившегося значения в положении равновесия:
- относительное динамическое отклонение напора от установившегося значения в положении равновесия:
где: 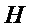 - текущее значение величины напора,
- текущее значение величины напора, 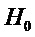 - установившееся значение напора в положении равновесия и расчетное значение напора
- установившееся значение напора в положении равновесия и расчетное значение напора 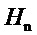 , принятого за условную единицу.
, принятого за условную единицу.
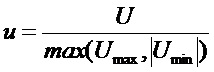 - относительное отклонение управляющего сигнала в структурных схемах регуляторов типа интегратор с отрицательной гибкой обратной связью; здесь:
- относительное отклонение управляющего сигнала в структурных схемах регуляторов типа интегратор с отрицательной гибкой обратной связью; здесь: 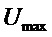 и
и 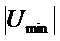 - максимальные по модулю ограничения, наложенные на величину управляющего сигнала.
- максимальные по модулю ограничения, наложенные на величину управляющего сигнала.
Пример структуры ПИ-модуля, главным элементом которого является интегратор с гибкой обратной связью приведен на фиг. 1. Она реализована на операционных усилителях, и серийно выпускалась ЛМЗ начиная с 1981 года [В.А. Марбух. Новая модификация электрогидравлического регулятора гидротурбин ЭГР-2И-1. Энергомашиностроение. 1983 г., №10, стр. 4-7]. Регулятор широко применялся в конце XX столетия. На фиг.1 приведена блок-схема формирователя ПИД-закона регулятора ЭГР-2И-1, на которой обозначены датчик 1 частоты вращения, задатчик 2 уставки частоты вращения, блок 4 выявления ошибки регулирования, блок 5 формирования сигнала пропорционального производной частоты вращения, сумматор 10 сигналов обратной связи от формирователя 13 сигнала гибкой (изодромной) обратной связи и блока 14 задания величины статизма, входным для которых является выход вспомогательного интегратора 12, вход которого через формирующий управляющий сигнал усилитель-ограничитель 11 подключен к выявителю 4 ошибки регулирования, выходом регулятора является подключенный к входу задания положения сервомотора приводу 9 регулирующего органа выход вспомогательного интегратора 12. Блок-схема ПИ-формирователя регулятора ЭГР-2И-1 функционально почти полностью повторяет набор участвующих в формировании закона регулирования элементов гидромеханического регулятора РМ ЛМЗ, структурная схема которого приведена в кн. В. А. Пивоварова рис.70, стр.161.
Передаточная функция изодромного регулятора заимствована с небольшим уточнением из упомянутой статьи Марбуха В.А. [стр.5]:
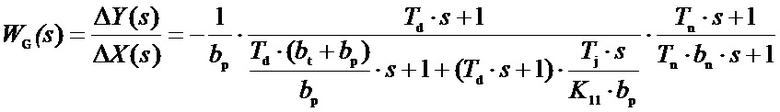 ,
,
где используются обозначения настроечных параметров принятых в нормативных документах МЭК прошлого XX века [1, 2];
Td - постоянная времени изодрома (гибкой обратной связи);
bt - временная неравномерность или временный статизм (интенсивность гибкой обратной связи);
bp - постоянный статизм или статизм;
Tn - постоянная времени ускорения;
bn - коэффициент усиления ускорения.
Идеальный ПИ-закон при изодромной структуре формирователя можно получить если выполнить условия: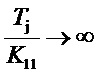 и сформировать сигнал статизма, выполнив его формирователь не простым пропорциональным звеном, а фильтром низкой частоты с передаточной функцией:
и сформировать сигнал статизма, выполнив его формирователь не простым пропорциональным звеном, а фильтром низкой частоты с передаточной функцией:
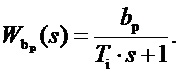
Тогда передаточная функция регулятора примет вид:
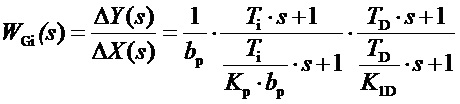 . (1)
. (1)
В приведенной идеальной передаточной функции изодромного ПИД-закона использованы обозначения параметров настройки, рекомендованные IEC 61362.
Специфическим недостатком изодромной структуры является необходимость введения в состав регулятора замкнутого контура с высоким усилением в прямой цепи прохождения сигнала управления и с глубокой обратной связью. Если аппаратура позволяет реализовать интегратор, не имеющий дрейфа нуля, при этом обладающий высокой чувствительностью к входным сигналам, то естественно применение структур, формирующих ПИД-закон регулирования и не имеющих замкнутых контуров. Первые шаги в этом направлении были сделаны при появлении прецизионных операционных усилителей в середине 70-х годов XX-го века. Это, например, выпускавшиеся в 80-х годах XX века регуляторы: SIEMENS (ФРГ), ČKD-VÙAP (Чехословакия), QRVV шведской фирмы ASEA [Tuszyski J. Electrical equipment for turbine governors. - Water Power and Dam Constr., 28, 9, p. 30-33.] и т.п.
В [Башнин О.И. и др. О структуре регуляторов частоты., В кн. Системы возбуждения и регулирования мощных энергетических агрегатов. Ленинград, «Наука», Л-е отд., 1979, стр. 143.] приведена со ссылкой на рекламный бюллетень 07058 фирмы Вудворд (США) структурная схема применяемого ею для стабилизации частоты вращения гидравлических турбин регулятора, вероятно одна из первых разработок, реализующая ПИД-закон на операционных усилителях с требуемой точностью. Эта схема параллельной структуры, называемая часто «ПИД-три составляющих», представлена на фиг.2. На ней изображены: датчик 1 частоты вращения турбины, задатчик 2 частоты вращения (уставка частоты вращения), формирователь 3 сигнала статизма, элемент выявления 4 ошибки регулирования (разности между отклонением частоты вращения агрегата от уставки и положением регулирующего органа при установленном статизме, формирователи: 5 сигнала, пропорционального производной, 6 сигнала, пропорционального отклонению частоты от уставки, и 7 сигнала, пропорционального интегралу от отклонения частоты от уставки; сумматор 8 упомянутых трех сигналов, являющийся задатчиком положения регулирующего органа (органов) для исполнительной электрогидравлической системы 9. В общем случае для статизма bP≠0 в соответствии с [4] стр.143 и со схемой фиг.2:
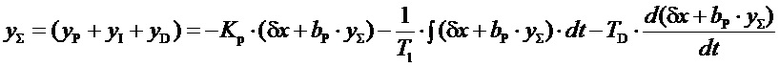 (1)
(1)
здесь:
yΣ - сигнал задания электрогидравлическому приводу положения сервомотора регулирующего органа турбины,
yP - составляющая yΣ пропорциональная ошибке регулирования,
yI - составляющая yΣ пропорциональная интегралу от ошибки регулирования,
yD - составляющая yΣ пропорциональная производной от ошибки регулирования,
KP - коэффициент усиления в канале формирования воздействия пропорционального ошибке регулирования,
Tl - постоянная времени в канале формирования воздействия пропорционального интегралу от ошибки регулирования,
TD - постоянная времени в канале воздействия по производной от ошибки регулирования,
bP - величина статизма - величина отклонения частоты от уставки в процентах (или относительных единицах) от значения ее, принятого за номинальное, вызывающее полный конструктивный ход сервомотора регулирующего органа.
При появлении цифровых регуляторов внутренние структуры ПИД-формирователей не раскрываются. Описания регуляторов, приводимые в фирменных проспектах [см. например, Буклет компании VOITH “HyCon™. Digital turbine governor”, Heidenheim. - Электронный ресурс. Режим доступа к ресурсу: https://voith.com/de/12_06_Digital_Turbine_Governor.pdf - свободный], позволяют понять только то, что для стабилизации частоты вращения гидротурбины применяется ПИД-закон, реализованный параллельно-последовательной структурной схемой.
В настоящее время инициатива в разработке и предложении новых структурных решений практически полностью исключена. В нормативных документах МЭК и России зафиксировано применение ПИД-регулятора в системе стабилизации частоты вращения гидротурбин как обязательное. Описаны два основных блока этого регулятора: пропорционально-интегрирующий и дифференцирующий. В последних изданиях: на стр. 28 в 61362 © IEC:2012 и на стр.15 в ПНСТ 49-2015 (стандарт России) рекомендованы следующие диапазоны настроек параметров регуляторов частоты вращения для работы на изолированную нагрузку для параллельной структуры (привязанной к структуре фиг.2): bp=0÷0,1; KP = 0,6÷10; Tl = 1÷20 c; K1D = 5÷10 и TD = 0÷2 c. Примечание: для большинства случаев достаточно: KP = 1,2÷10; Tl = 1÷5 c. Эти рекомендации говорят о том, что мы имеем дело, прежде всего, с ПИ-регуляторами, настраиваемыми в широком частотном и амплитудном диапазоне, и дифференциаторами, играющими вспомогательную роль и позволяющими незначительно увеличить быстродействие регулятора.
На рисунках фиг. 3 и фиг. 4 представлены две блок-схемы линейных ПИ-блоков, каждый из которых состоит из входного сумматора 4, выполняющего функцию выявления отклонения системы регулирования от статического режима; блока 7 выбора величины воздействия Kp пропорционального отклонению частоты от уставки и интегратора 6, постоянная времени которого равна Tl для параллельной структуры, представленной на фиг.3, а для параллельно-последовательной структуры - на фиг.4, равна - Ti. В обоих случаях сигнал, поступающий на вход блока 4 задания статизма, является выходным сигналом интегратора 6, который в установившихся режимах является выходным сигналом формирователя, так как в статическом режиме на входе интегратора 6, а, стало быть, и блока 7, коэффициент усиления в канале пропорциональной составляющей равен нулю.
Сравним передаточные функции каждого из представленных ПИ-формирователей. Для формирователя структуры фиг. 3. выходным сигналом внутреннего замкнутого контура является выход сумматора 4, а внешним входным - сумма всех входных сигналов, без выходного сигнала блока статизма. В обратной связи этого внутреннего контура расположены интегратор 6 и блок 3 задания статизма. В этом случае выходной сигнал сумматора 4 будет даваться выражением:
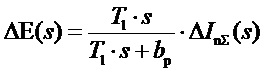 ,
,
где 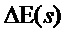 - лапласово изображение выходного сигнала сумматора 4, а
- лапласово изображение выходного сигнала сумматора 4, а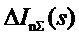 - то же самое для суммы всех входных сигналов, без выходного сигнала блока 3 статизма.
- то же самое для суммы всех входных сигналов, без выходного сигнала блока 3 статизма.
Соответственно изображение выходного сигнала ПИ-формирователя:
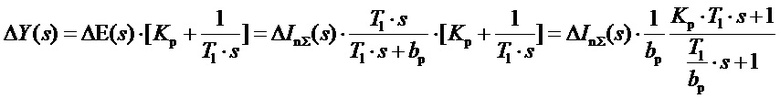 ,
,
и передаточная функция ПИ-блока регулятора фиг. 3 будет даваться выражением:
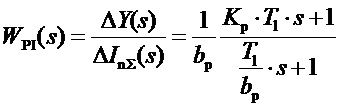 . (3)
. (3)
Для того чтобы передаточные функции (1) изодромного ПИ-блока и (3) линейного ПИ-формирователя параллельной структуры совпадали нужно, чтобы параметры определяющие их передаточные функции удовлетворяли соотношениям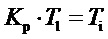 или
или 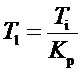 , и коэффициенты усиления пропорциональной составляющей были равны.
, и коэффициенты усиления пропорциональной составляющей были равны.
Передаточную функцию ПИ-формирователя фиг.4, можно получить аналогично предыдущему, заранее обозначив постоянную времени интегратора «Ti». В прямую цепь внутреннего замкнутого контура этого ПИ-блока входит дополнительно пропорциональный блок 7, выходной сигнал которого, поступающий на вход сумматора 8 будет даваться выражением:
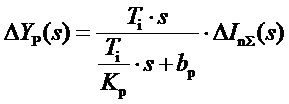
 .
.
Таким образом, передаточная функция этого линейного ПИ-формирователя фиг. 4 полностью совпадает с передаточной функцией идеального ПИ-блока изодромной структуры:
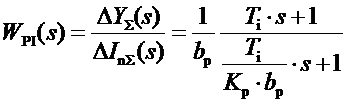 (4)
(4)
На фиг.5а представлены логарифмические асимптотические амплитудные частотные характеристики (ЛАЧХ) трех параллельно включенных каналов формирования сигналов пропорционального «P» отклонению частоты от уставки, интегралу «I» и производной «D» от него, а также результат построения асимптотической ЛАЧХ- ломаная 1-2-3-4-5-6, начинающейся на частоте ω=0, заканчивающейся на частоте ω=∞. Построение частотной характеристики параллельной структуры, требуют выполнения операций с комплексными числами. Параллельные структуры регуляторов удобны в случае анализа их по математическим описаниям движения системы регулирования нелинейными дифференциальными уравнениями во временной области.
Изодромная или полностью ее эмулирующая линейная (фиг.4) структуры имеют параметры настройки, сразу определяющие точки сопряжения асимптот результирующей частотной характеристики (фиг.5б) регулятора. Знание частотной характеристики регулятора и частотных (расчетных или экспериментальных) характеристик объекта регулирования) позволяет быстро оценить стратегию настройки на испытаниях системы.
Первоначальная идея применения изодромного регулятора частоты вращения заключается в создании дополнительной обратной связи параллельной главной обратной связи по частоте вращения турбины. Эта обратная связь, входным сигналом для которой является положение сервомотора направляющего аппарата должна быть достаточно сильной, чтобы ее действие могло подавить большое запаздывание сигнала отклонения частоты при быстрых изменениях положения сервомотора, а при медленном движении сервомотора она не должна мешать работе главной (по частоте вращения) обратной связи, так как при этом сигнал изменения частоты мало отстает от перемещения сервомотора. Это инженерное решение, получившее практическое применение в пятом десятилетии XIX века, являлось для астатических гидромеханических регуляторов единственным радикальным средством коррекции динамических характеристик для многих классов объектов: астатических (баки с жидкостями), неминимально-фазовых, с транспортным запаздыванием и реагирующим разнонаправленно на положение регулирующего органа и скорость его перемещения, к каковым и принадлежит гидротурбина как объект регулирования мощности и частоты. С течением времени применение электрических и затем электронных средств управления дали возможность введения в законы управления производных регулируемых параметров, а изучение частотных характеристик и применение правил преобразования структурных схем регуляторов, используемых в расчетах устойчивости и переходных процессов, привели к простым универсальным ПИ- и ПИД-регуляторам, выпускаемым массово. Недостатком описанных выше структур регуляторов является неэффективное использование мощности привода регулирующих органов, что увеличивает перерегулирование по частоте и длительность переходных процессов.
Для улучшения динамических характеристик контура регулирования частоты вращения в 1985 г. Г.С. Киселевым и И.И. Ляткером был предложен «Регулятор частоты вращения гидротурбины», защищенный авторским свидетельством SU 1337546. По существующей классификации регуляторов состояния предложенное устройство является «регулятором с переменной структурой». На фиг. 6 представлена блок-схема этого регулятора, где: ПИ-формирователем 6 суммируются два сигнала, поступающие на его входы: на первый из них - через устройство искусственной мертвой зоны 7 с выхода сумматора 3, на входы которого подаются выходные сигналы измерителя 1 частоты вращения, задатчика 4 ее уставки, а также выходной сигнал формирователя 6, через блок 5 задания величины статизма, а на второй - с выхода логического блока 9, на входы которого поступают выходные сигналы сумматора 3 и дифференциатора 4 сигнала частоты вращения, подключенного входом к выходу измерителя 1.
К сожалению, нет данных о применении предложенного регулятора на ГЭС. Можно предположить, что устройство реализует общий принцип, заключающийся в том, что если производная регулируемого параметра и его отклонение от уставки имеют один знак и при этом абсолютные значения каждого из них превысили некоторые контрольные значения, то коэффициент усиления в канале воздействия по производной надо установить равным TD1. В противном случае вернутся к значению TD0 проверенного устойчивого режима или, например, отключить воздействие по производной регулируемого параметра. При правильном выборе соотношения между TD0 и TD1 система регулирования переходит из устойчивого состояния с достаточным запасом устойчивости в стационарном режиме работы агрегата в состояние с малым запасом устойчивости при сопровождающих возмущение больших отклонениях частоты и ее производной в состояние с низким запасом устойчивости, что способствует быстрому выходу системы из состояния равновесия. При этом важно, чтобы система, во-первых, не слишком далеко отклонилась от точки будущего равновесия, что при не минимально-фазовой частотной характеристике объекта практически трудно достижимо и, во-вторых, чтобы не возникло в процессе нескольких переключений от режима выхода из состояния равновесия с большим коэффициентом TD1 к режиму возврата в точку равновесия с коэффициентом TD0. Для способа в случае регуляторов гидротурбин характерны: большое перерегулирование по величине перемещения регулирующего органа при реализации первой фазы с большим - TD1 и медленное приближение к точке равновесия с малым или даже равным 0 значением TD0.
Недостатком такого решения является риск: попасть в схемно-режимную ситуацию работы агрегата, в которой система регулирования окажется неустойчивой. Кроме того, для современных конструкций регуляторов нормой является несколько наборов уставок динамических параметров, переход на работу с которыми происходит автоматически по признакам, характерным для той или иной схемно-режимной ситуации, поэтому применение изобретения [6] - неактуально.
Как объект регулирования гидротурбина состоит из двух основных аккумуляторов кинетической энергии - это поле скоростей вращающихся масс ротора и поле скоростей движущихся в водоводе масс воды. Качество вырабатываемой энергии определяет частота вращения ротора агрегата, колебания которой должны быть как можно меньше. Т.е. кинетическая энергия ротора не должна изменяться при различных нагрузках генератора. Кинетическая энергия масс воды в трубопроводе необходимо изменяется в широких пределах в соответствии с расходом, обеспечивающим развитие турбиной мощности, требуемой для поддержания частоты вращения генератора в случае увеличения или уменьшения мощности потребителей. Два этих аккумулятора кинетической энергии в совокупности с главными сервомоторами (могут рассматриваться как аккумуляторы), требующими для изменения своего положения затрат энергии и при этом имеющие технологическое ограничение используемой для этого мощности образуют неизменяемую часть системы регулирования. Уравнения системы регулирования описывают процессы накопления и потери энергии в упомянутых выше аккумуляторах (см., например, В. А. Пивоваров Проектирование и расчет систем регулирования гидротурбин. Л., Машиностроение, 1973 г. стр. 184 - 199).
В чем заключается несовершенство современных регуляторов?
1. Структуры регуляторов гидротурбин, рекомендованные в нормативных документах IEC и ПНСТ, опираются на решения, получившие распространение и развитие в первой половине XX века. Синтез их, использующий метод прототипа и частотные критерии устойчивости в совокупности с расчетом переходных процессов при стандартизованных возмущениях не позволяет достигнуть высокого быстродействия регулятора. Можно сказать, что недостатком применяемых структурных решений заключается в их универсальности: они не учитывают особенностей гидротурбин как объектов регулирования. Эти решения не позволяют добиться существенного улучшения эксплуатационных характеристик агрегатов как источников электроэнергии.
2. В упомянутых рекомендуемых нормативными документами структурных схемах регуляторов не используются воздействия по полному набору сигналов пропорциональных переменным состояния (нет воздействия по динамическому отклонению напора и по отклонению положения сервомотора от положения равновесия) или по выходным сигналам устройств, позволяющих заменить их в случае недоступности прямого измерения переменных состояния, что не позволяет реализовать при компенсации возмущений в нагрузке генератора максимальное быстродействие приводов регулирующих органов.
Технической задачей настоящего изобретения является разработка способа регулирования частоты вращения гидротурбины, обеспечивающего более эффективную реакцию регулятора на изменение нагрузки и улучающего показатели качества переходных процессов (уменьшение перерегулирования по частоте и уменьшение времени переходного процесса) при сохранении требуемых запасов устойчивости без применения способов, кратковременно изменяющих структуру регулятора. В качестве прототипа принят способ, примененный в регуляторе, формирующем ПИ составляющую закона регулирования посредством охвата цепочки «усилитель-ограничитель - интегратор» гибкой отрицательной обратной связью.
Второй технической задачей изобретения является разработка структурной схемы регулятора, реализующего предлагаемый способ.
РАСКРЫТИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Задача настоящего изобретения решена предлагаемым способом формирования закона регулирования. В соответствии с сущностью изобретения в состав системы регулирования частоты вращения ротора реактивной турбины, кроме ее неизменяемой части, включающей вращающийся ротор агрегата, водоводы, подводящие воду к турбоблоку (турбина плюс отсасывающая труба), электрогидравлические приводы регулирующих органов (электро-гидравлические следящие системы), измеритель частоты вращения ротора турбины, задатчика уставки его частоты вращения, выявитель отклонения частоты от уставки, выполняющий операцию вычитания из сигнала уставки сигнал частоты, входит также используемая как основа для формирования закона регулирования цепочка: «усилитель-ограничитель - интегратор», причем выходной сигнал последнего служит заданием положения сервомотора привода регулирующих органов.
Согласно способу регулирования частоты вращения ротора реактивной турбины по настоящему изобретению формируют сигнал пропорциональный значению линейной комбинации с постоянными или зависящими от режима работы агрегата коэффициентами трех сигналов: отклонения частоты вращения от уставки, динамического отклонения напора от его статического значения и отклонения положения регулирующего органа от ожидаемого положения его в установившемся режиме, определяемого величиной мгновенной разности между моментом, развиваемым турбиной, за вычетом из него составляющих, обусловленных динамическим отклонением напора от его постоянно значения в установившихся режимах и отклонением частоты вращения ротора от уставки в ожидаемом статическом режиме, и моментом сил сопротивления полезной нагрузки, за вычетом из него составляющей, вызванной тем же отклонением частоты вращения; полученная таким образом сумма сигналов используется в качестве входного цепочки «усилитель-ограничитель - интегратор», выходной сигнал которого является входным для электрогидравлической следящей системы привода регулирующих органов.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Далее предлагаемое изобретение поясняется более подробно со ссылкой на прилагаемые чертежи, на которых:
Фиг.1 Блок-схема ПИД-регулятора изодромной структуры;
Фиг.2 Блок-схема линейного ПИД-регулятора параллельной структуры - «три составляющих»;
Фиг.3 Блок-схема линейного ПИД-регулятора параллельно-последовательной структуры с ПИ-формирователем параллельной структуры;
Фиг.4 Блок-схема линейного ПИД-регулятора параллельно-последовательной структуры с ПИ-формирователем параллельно-последовательной структуры;
Фиг.5а Асимптотическая логарифмическая амплитудная частотная характеристика линейного ПИД-регулятора «три составляющие»;
Фиг.5б. Асимптотическая логарифмическая амплитудная частотная характеристика ПИД-регуляторов изодромной и линейной параллельно-последовательной с параллельно последовательным ПИ-формирователем структур;
Фиг.6. Блок-схема «Регулятора частоты вращения гидротурбины», защищенного авторским свидетельством SU 1337546
Фиг.7. График зависимости постоянных времени двух нормированных сомножителей первого порядка при представлении нормированного квадратного трехчлена, имеющего положительный дискриминант, в виде их произведения от коэффициентов при первой и второй степени комплексной переменной, входящих в него членов.;
Фиг.8 Переходный процесс в контуре регулирования частоты вращения гидротурбины с линейным ПИД-регулятором при ступенчатом увеличении нагрузки агрегата на 20%;
Фиг.9 Переходный процесс в контуре регулирования частоты вращения гидротурбины с изодромным ПИД-регулятором при ступенчатом увеличении нагрузки агрегата на 20%;
Фиг.10 Переходный процесс в контуре регулирования частоты вращения гидротурбины с предлагаемым ПИД-СД регулятором при ступенчатом увеличении нагрузки агрегата на 20%;
Фиг.11а Исходная структурная схема контура регулирования частоты вращения турбины (неизменяемая часть системы) для применения метода структурного синтеза передаточной функции регулятора, обеспечивающего его абсолютную устойчивость;
Фиг.11б Результат первого шага структурного синтеза: полная компенсация амплитудных и фазовых искажений частотной характеристики цепи главной обратной связи, вносимые звеном, описывающим процесс накопления кинетической энергии ротором, включением в цепь главной обратной связи последовательного корректирующего частотную характеристику ПД-формирователя;
Фиг.11в Результат второго шага структурного синтеза: полная компенсация паразитной положительной гибкой обратной связи, являющейся следствием динамического отклонения напора, возникающего при движении регулирующих органов и пропорциональной скорости их перемещения, включением цепочки гибкой отрицательной обратной связи, охватывающей интегратор;
Фиг.12 Асимптотические ЛАЧХ ПИ и ПД формирователей, а также базовая ЛАЧХ ПИД-закона предлагаемого регулятора и влияние на нее коэффициентов KP и bp;
Фиг.13 Структурная схема предлагаемого регулятора;
Фиг.14 Комбинаторные характеристики турбины Новосибирской ГЭС;
Фиг.15 Зависимость расхода от положения сервомотора РК турбины Новосибирской ГЭС.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Уравнения движения неизменяемой части системы регулирования включают три дифференциальных уравнения: два из них описывают процессы накопления энергии аккумуляторами объекта регулирования: в полях скоростей ротора и трубопровода, а третье - процесс изменения положения регулирующих органов при ограниченном ресурсе мощности, который может быть использован для их перемещения. Особенностью гидротурбины как объекта регулирования частоты вращения является взаимодействие двух аккумуляторов кинетической энергии полей скоростей воды в водоводе и вращающихся масс ротора. Эта особенность заключается в том, что при перемещении регулирующего органа из одного положения «y1» в другое «y2» по разным траекториям и с разными скоростями величина кинетической энергии масс воды в трубопроводе в начальном и конечном положениях регулирующего будет одинакова. Т.е. количество энергии, отнятое из ее потока, поступающего в турбину при постоянном напоре, однозначно зависит только от начального и конечного положений регулирующих органов и не зависит от траектории их движения. При резком возрастании нагрузки в процессе перемещения регулирующих органов от одного статического режима к другому в режиме регулирования частоты вращения наблюдается небаланс между требуемой потребителями мощностью и вырабатываемой турбиной. При этом величину дефицита энергии приближенно можно оценить значением:
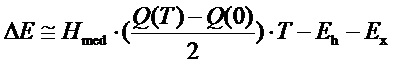 ,
,
где, ΔE - недоданная потребителям энергия, Hmed - средний напор в переходном процессе, Q(T) - расход в конце переходного процесса, Q(0) - расход в начале переходного процесса, T - время переходного процесса, Eh - энергия, затраченная на увеличение кинетической энергии движущихся в водоводе масс воды, Ex - энергия затраченная на пополнение кинетической энергии ротора (восстановление частоты вращения).
При любом законе перемещения регулирующего органа из положения «y1» в положение «y2» количество энергии Eh, которое водовод заберет из потока воды, не зависит от траектории его перемещения и будет постоянно. Поэтому переходный процесс при ступенчатом изменении нагрузки генератора должен протекать, минимизируя временный дефицит в выработке энергии, получающийся за счет длительности промежутка времени, в течение которого происходит перемещение регулирующего органа, и потере кинетической энергии ротором, также увеличивающейся при этом. Поэтому задача уменьшения промежутка времени дефицита вырабатываемой энергии, за счет которого происходит также падение частоты вращения и увеличивается риск развала энергосистемы с отключением потребителей, является актуальной. Таким образом, задача заключается в разработке способа, реализующего простой и эффективный алгоритм, реализующий близкий к оптимальному по быстродействию.
Если на ГЭС действует некоторый постоянный напор «h0», при котором положению сервомотора «y0» соответствуют неизменная частота «x0», а также момент турбины «mT=const» равен суммарному моменту сил сопротивления «mGΣ=const» на промежутке времени «T→∞», то такой режим далее называется ожидаемым установившемся для текущего значения суммарного момента сил сопротивления mGΣ(t). Обычно при анализе динамики систем регулирования частоты в энергетике считается, что уставка частоты «x0» и статизм «bp» равны нулю, т.е. «x0=0» и «δx=0» не зависит от величины момента сил сопротивления, также равным нулю предполагается и отклонение «δh» напора нетто в ожидаемом статическом режиме, т.е. считается, что изменение расхода не влияет на величину гидравлических потерь в водоводах (практика показывает, что потери в водоводах изменяются примерно на (1-3)% от номинального значения напора нетто). Таким образом, параметрами состояния системы являются отклонение «δx» частоты от уставки, динамическое отклонение напора «δh» и отклонение сервомотора от ожидаемого положения равновесия в установившемся режиме «δy=y-y0».
Если проанализировать смысловую сторону решения синтеза структуры регулятора, решающего задачу максимального быстродействия в пространстве состояния системы, то согласно алгоритму регулярного синтеза, реализующего «принцип максимума»: см., например, [Болтянский В. Г. Математические методы оптимального управления. - М.: Наука, 1969. 408 с.] для построения быстродействующего регулятора частоты вращения, необходимо использовать:
- полный набор составляющих вектора состояния системы, т.е. отклонения: частоты вращения, динамического напора и положение сервомотора от их значений в ожидаемом статическом режиме,
- ранжировать последовательность задач, решаемых в процессе управления: в первую очередь компенсировать действие возмущения, затем вернуть в состояние близкое к ожидаемому самый большой по энергоемкости аккумулятор и т.д. по очереди убывания емкости аккумуляторов, входящих в состав объекта [Болтянский В. Г. Математические методы оптимального управления. М.: Наука, 1969. 408 с.]
Следует заметить, что техническая реализация оптимального по критерию максимального быстродействия управления не нашли применения в системах с регуляторами состояния в силу, по крайней мере трех обстоятельств:
- даже для линейной системы условия переключения управления описываются нелинейными функциями переменных состояния;
- линеаризация (в случае оптимизации управления системой третьего порядка) поверхности переключения плоскостью, направление вектора нормали которой коллинеарно предельному положению векторного произведения векторов поля направлений в точке на линии переключения при управлениях разных знаков при приближении ее к цели управления, приводит к находящейся на границе устойчивости системе с ПИД-регулятором;
- нелинейность поверхности переключения и одновременно нелинейность характеристик подвода энергии к турбине и водоводу не позволяют оценить запасы устойчивости в необходимом для эксплуатации диапазоне изменения нагрузки.
В кн. «Микропроцессоры в энергетике.» Башнин О.И. и др. под ред. академика И.А Глебова, Л. «Наука», Лен. отд., 1982 г., стр. 48-52. рассмотрена проблема оптимального по быстродействию регулятора частоты вращения ротора агрегата. В ней предложено для повышения быстродействия использовать принцип Ж.-В. Понселе и ввести воздействие по нагрузке под изодром, т.е. на вход изодрома подавать дополнительно сигнал мощности генератора, таким образом, чтобы увеличение мощности генератора вызывало перемещение регулирующих органов, вызывающее увеличение мощности турбины на такую же величину. Так как мощность зависит от частоты, то возникающая при этом положительная обратная связь по частоте в высокочастотной области частотной характеристики может негативно сказаться на динамике регулирования и требует компенсации. Кроме того, электрическая мощность является системным параметром, который отражает не только нагрузку генератора, но и скоротечные электромагнитные процессы в сетях. Поэтому в предлагаемом способе регулирования частоты вращения в соответствии с положением теории оптимального управления недостающий и самый важный параметр: несоответствие положения регулирующего органа требуемому в ожидаемом установившемся режиме должен определяться по значениям доступных для измерения и вычисления параметров состояния и их производных по времени. С точки зрения теории оптимального по быстродействию регулятора устойчивого объекта управления именно возмущение со стороны нагрузки, вызывающее отклонение параметров от ожидаемых в статическом режиме должно быть скомпенсировано первым, чтобы не вызвать чрезмерное отклонение остальных переменных состояния, тем более что оно не может быть скомпенсировано иначе. Таким образом, в первую очередь надо рассмотреть управление:
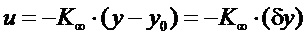 , где
, где 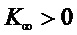 и
и 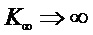
Уравнение переключающей плоскости, описываемой управлением, приведенным выше, будет «δy=0» может быть скорректировано добавлением в ее уравнение членов, содержащих отклонения других переменных состояния, взятых с определенными расчетами абсолютной устойчивости весовыми коэффициентами. При выполнении условий абсолютной устойчивости в конце переходного процесса наблюдается скольжение точки, изображающей состояние системы, по переключающей плоскости в лежащей на ней точку установившегося режима. [Уткин В. И. Скользящие режимы в задачах оптимизации и управления. М., Наука, 1981].
Заметим, что вместо отклонения текущего положения регулирующего органа от ожидаемого положения его в точке установившегося режима можно в силу однозначной монотонной зависимости момента турбины от положения регулирующего органа использовать отклонение момента турбины, вычисленного при текущем положении регулирующего органа и значениях отклонений частоты и динамического давления, равными ожидаемым в установившемся режиме, от момента сил сопротивления в нем.
ЛИНЕЙНЫЙ РЕГУЛЯТОР
Так как все нормативные документы, касающиеся структурных схем и правил настройки регуляторов частоты вращения гидротурбин, основываются на теории регулирования линейных систем вследствие отсутствия аналитического описания расходных и моментных характеристик, получаемых в численной форме, то интересно проследить к каким структурам регуляторов приводит предлагаемый способ при использовании линейных моделей объекта управления и линейных регуляторов. Линеаризованные уравнения объекта позволяют воспользоваться таким мощным аналитическим аппаратом, как преобразование Лапласа, получить явные выражения зависимости входного сигнала «u» интегратора, выходной сигнал которого является заданием положения сервомоторов регулирующих органов.
Возьмем линеаризованную в окрестности точки ожидаемого равновесия (статического режима) систему уравнений движения агрегата с одним регулирующим органом [см. Пивоваров В.А. стр. 188, ф-ла 4-16] в виде, разрешенном относительно производных, исключив из системы алгебраические уравнения и заменив обозначения оператора Лапласа «p», на «s». В результате получим систему уравнений:
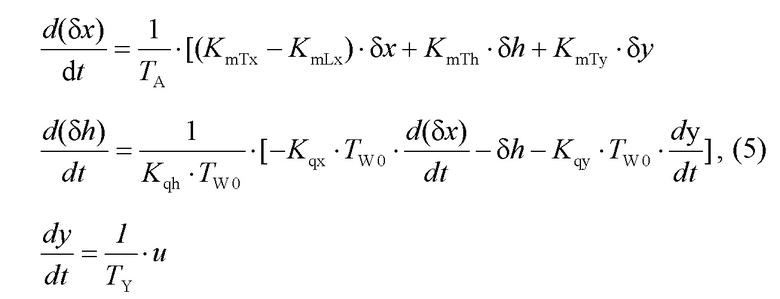
где  ,
,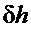 ,
, 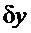 - величины отклонений переменных состояния системы: частоты вращения ротора, динамического давления и отклонения сервомотора от некоторой точки ее равновесия (x0, h0, y0), u - отклонение главного золотника от среднего положения u0=0 и -1≤ u ≤1.
- величины отклонений переменных состояния системы: частоты вращения ротора, динамического давления и отклонения сервомотора от некоторой точки ее равновесия (x0, h0, y0), u - отклонение главного золотника от среднего положения u0=0 и -1≤ u ≤1.
Уравнения (5) описывают движение неизменяемой части системы управления: объекта регулирования: ротора агрегата турбины (первое уравнение системы), движущихся масс воды в водоводах (второе уравнение системы) и главного сервомотора (третье уравнение системы), скорость перемещения которого ограничена по соображениям технологической безопасности: предотвращения амплитудой динамических отклонений напора уровней, способных привести к аварии турбины как при торможении потока, так и при его разгоне.
Замечание 1: В современных системах управления главный сервомотор не является участвующим в формировании закона управления звеном системы регулирования. Электрогидравлическая следящая система, в которой он является выходным усилителем, обладает высоким усилением в разомкнутом состоянии, что позволяет нивелировать нелинейную зависимость скорости сервомотора от отклонения главного золотника от среднего положения введением глубокой обратной связи по положению главного сервомотора, добиться большой точности слежения за командным сигналом и высокого быстродействия. Функция интегрирования выполняется в электронной части с необходимыми ограничениями величины и скорости изменения управляющего электрогидравлической следящей системой сигнала. Далее величины «y» и «δy» - выходной сигнал интегратора, функционально реализованного в электронном блоке регулятора.
В уравнениях (5):
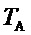 - время разгона машины;
- время разгона машины;
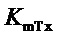 - коэффициент передачи: «отклонение частоты вращения - отклонение момента турбины» (коэффициент самовыравнивания турбины);
- коэффициент передачи: «отклонение частоты вращения - отклонение момента турбины» (коэффициент самовыравнивания турбины);
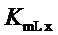 - коэффициент передачи: «отклонение частоты вращения - отклонение момента суммы сил сопротивления» (коэффициент саморегулирования момента нагрузки);
- коэффициент передачи: «отклонение частоты вращения - отклонение момента суммы сил сопротивления» (коэффициент саморегулирования момента нагрузки);
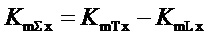 - коэффициент, учитывающий суммарное влияние отклонения частоты на изменение разности момента движущих сил и сил сопротивления, являющийся разностью коэффициентов «самовыравнивания турбины» и «саморегулирования нагрузки»;
- коэффициент, учитывающий суммарное влияние отклонения частоты на изменение разности момента движущих сил и сил сопротивления, являющийся разностью коэффициентов «самовыравнивания турбины» и «саморегулирования нагрузки»;
 - коэффициент передачи: «отклонение перепада давлений на турбине - отклонение ее момента»;
- коэффициент передачи: «отклонение перепада давлений на турбине - отклонение ее момента»;
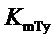 - коэффициент передачи: «отклонение положения сервомотора регулирующего органа - отклонение момента турбины»;
- коэффициент передачи: «отклонение положения сервомотора регулирующего органа - отклонение момента турбины»;
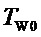 - время разгона воды в водоводе турбины;
- время разгона воды в водоводе турбины;
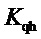 - коэффициент, определяющий скорость затухания динамического отклонения перепада давлений;
- коэффициент, определяющий скорость затухания динамического отклонения перепада давлений;
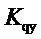 - коэффициент передачи «отклонение регулирующего органа - отклонение расхода через турбину»;
- коэффициент передачи «отклонение регулирующего органа - отклонение расхода через турбину»;
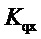 - коэффициент передачи «отклонение частоты вращения - отклонение расхода через турбину»;
- коэффициент передачи «отклонение частоты вращения - отклонение расхода через турбину»;
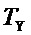 - постоянная времени сервомотора привода регулирующего органа, выбранное из условия ограничения максимального повышения давления в водоводах.
- постоянная времени сервомотора привода регулирующего органа, выбранное из условия ограничения максимального повышения давления в водоводах.
При стабилизации частоты вращения в случае достаточно больших возмущений в нагрузке необходимо обеспечить, прежде всего, компенсацию возмущения. Для системы уравнений (5) это означает, что необходимо с максимальной скоростью достигнуть равенства нулю величины:

 , (6),
, (6),
которую будем называть отклонением сервомотора от точки статического равновесия или установившегося режима в начальный момент времени, где m0(t) - значение момента нагрузки в начальный момент времени при начальных значениях отклонений частоты и напора равных нулю.
Предположим, что после действия возмущения в нагрузке в момент времени t=0 переменная (6) приняла новое значение из-за изменения величин m0(t), и далее m0=const при всех t >0. Знания координат 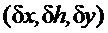 и управления «u» достаточно для определения всех составляющих вектора поля направлений системы
и управления «u» достаточно для определения всех составляющих вектора поля направлений системы 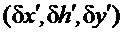 .
.
Будем рассматривать случай астатического регулирования частоты, а значит все, входящие в систему (5), отклонения переменных состояния всегда должны принимать в установившимся режиме значения равные нулю. Пусть в начальный момент времени величина m0(t) изменила ступенчато свое значение, соответственно отклонение регулирующего органа 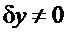 . Так как нерегулируемый объект устойчив, то, чем быстрее регулирующий орган достигнет этого, требуемого для установившегося режима положения, тем меньше будет заброс частоты вращения. Если после этого не изменять положение регулирующего органа, то в силу устойчивости объекта режим с нулевыми отклонениями режимных параметров установится без участия регулятора. В классе изучаемых управлении траектория, сформированная максимально быстрым движением регулирующего органа в точку ожидаемого равновесия, является участком оптимальной траектории управления по критерию оптимального быстродействия [Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. - М.: Наука, 1976].
. Так как нерегулируемый объект устойчив, то, чем быстрее регулирующий орган достигнет этого, требуемого для установившегося режима положения, тем меньше будет заброс частоты вращения. Если после этого не изменять положение регулирующего органа, то в силу устойчивости объекта режим с нулевыми отклонениями режимных параметров установится без участия регулятора. В классе изучаемых управлении траектория, сформированная максимально быстрым движением регулирующего органа в точку ожидаемого равновесия, является участком оптимальной траектории управления по критерию оптимального быстродействия [Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. - М.: Наука, 1976].
Таким образом, критерием оптимальности на первом отрезке траектории управления выбираем минимум времени преодоления расстояния до цели δy=0, однозначно определяемого зависимостью: 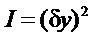 .
.
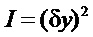 - квадрат расстояния до цели, критерий быстродействия является в данном случае одновременно и критерием оптимального демпфирования [В.И. Зубов Лекции по теории управления. М., «Наука», 1975], поэтому минимум ему будет доставлять управление, удовлетворяющее условию минимума производной в силу системы функционала I, который в данном случае является и вырожденной функцией А.М. Ляпунова:
- квадрат расстояния до цели, критерий быстродействия является в данном случае одновременно и критерием оптимального демпфирования [В.И. Зубов Лекции по теории управления. М., «Наука», 1975], поэтому минимум ему будет доставлять управление, удовлетворяющее условию минимума производной в силу системы функционала I, который в данном случае является и вырожденной функцией А.М. Ляпунова:
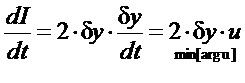 , где -1≤u≤+1.
, где -1≤u≤+1.
Решением задачи является управление u = -sign(δy).
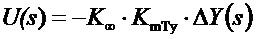 , при этом
, при этом 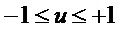 и K∞→∞. (7)
и K∞→∞. (7)
Положительность или отрицательность «u» в первой фазе управления до достижения переменной введенной формулой (6) нулевого значения, формирует в пространстве состояния системы отрезок траектории оптимального управления. Если в момент равенства нулю величины «u» зафиксировать ее, то при условии асимптотически устойчивого объекта, управление будет считаться квазиоптимальным по быстродействию, поскольку самая важная переменная состояния приняла значение, которое будет наблюдаться в ожидаемом статическом режиме. При этом остальные переменные состояния в силу устойчивости объекта и отсутствия возмущения сами собой будут асимптотически приближаться к своим нулевым значениям, скользя по плоскости, уравнение которой и системе координат 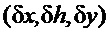 :
: 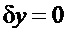 .
.
Связь между переменными системы (5) запишем в виде передаточных функций, введя символ «s» для обозначения комплексной переменной в преобразовании Лапласа и заменяя прописные буквы в обозначениях переменных на заглавные в их изображениях, например: 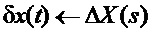 .
.
В системе (5) второе уравнение определяет величину 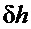 - динамического отклонения напора на турбине, зависящее от углового ускорения ротора и скорости изменения положения регулирующего органа. Его решение при нулевых начальных условиях дается выражением:
- динамического отклонения напора на турбине, зависящее от углового ускорения ротора и скорости изменения положения регулирующего органа. Его решение при нулевых начальных условиях дается выражением:
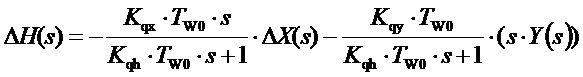 (8)
(8)
Выделением произведения  в формулах (8) и (9) подчеркивается, что скорость изменения положения сервомотора, отсчитываемая от точки полного закрытия, и ее нельзя приравнивать скорости изменения координаты состояния (6).
в формулах (8) и (9) подчеркивается, что скорость изменения положения сервомотора, отсчитываемая от точки полного закрытия, и ее нельзя приравнивать скорости изменения координаты состояния (6).
Первое уравнение системы (5), записанное в изображениях при нулевых начальных условиях и при замене изображения динамического отклонения напора выражением (8), принимает вид:
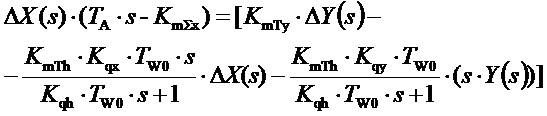 ,
,
откуда легко следует:
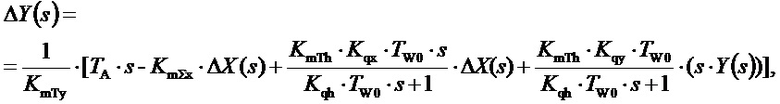 (9)
(9)
Заменим в (7) отклонение положения регулирующего органа от ожидаемого положения выражением (9), тогда получим:
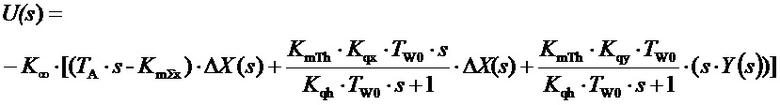 . (10)
. (10)
Заметим, что в правой части уравнения величина 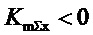 , так как с ростом частоты момент турбины падает, а момент саморегулирования нагрузки растет. Таким образом, в правой части первого уравнения системы (5) коэффициент отрицателен:
, так как с ростом частоты момент турбины падает, а момент саморегулирования нагрузки растет. Таким образом, в правой части первого уравнения системы (5) коэффициент отрицателен:
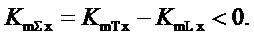
при переносе его в левую часть он примет положительное значение, т.е. все операторы в правой части (20) минимально фазовые звенья.
Замечание 2. Приведем в выражении, стоящим в правой части формулы (10) подобные члены, и выпишем множитель при 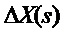 :
:
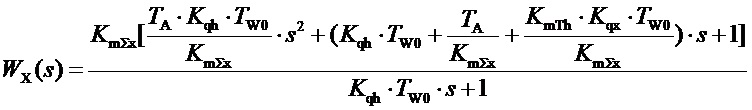 (z2.1)
(z2.1)
Расположение нулей числителя зависит от величины и знака коэффициента «Kqx» наклона характеристики расхода как функции от частоты вращения турбины. Для этого нужно рассмотреть величину известную как коэффициент демпфирования, обычно используемую для оценки расположения нулей знаменателя в случае присутствия в структуре системы колебательных звеньев. Для числителя (z2.1) он имеет вид:
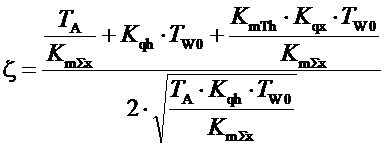 , (z2.2)
, (z2.2)
если ζ ≥1, то числитель (z2.1) представим в виде произведения двух сомножителей первого порядка:
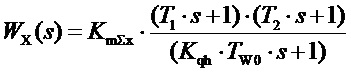 , (z2.3)
, (z2.3)
Здесь T1 и T2 - неотрицательные числа. Как будут изменяться T1 и T2 отношению к начальным их значениям при Kqx=0:
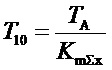 и
и  ? (z2.4)
? (z2.4)
Заметим, что произведение (T10·T20) не изменяется при изменении Kqx, а сумма (T10+T20+Kqx·KmTh·TW0·(Kqh)-1) возрастает, если Kqx>0, и уменьшается, если Kqx<0. Графики произведения постоянных времени и линий постоянных сумм их представлены в координатах (T1,T2) на рисунке фиг.6 где:
(T10·T20) = (T11·T21) = (T12·T22) = const - равнобочная гипербола, осью симметрии, которой является биссектриса угла первого квадранта, причем все искомые постоянные времени лежат на представленной гиперболе.
Σ(T10,T20,Kqx=0)=const0, Σ(T10,T20,Kqx>0)=const1, Σ(T10,T20,Kqx<0)=const2 прямые линии, отсекающие на осях «T1,T2» одинаковые отрезки равные величине суммы искомых постоянных времени, лежащих на соответствующих заданному значению Kqx линиях.
Таким образом, величины искомых постоянных времени равны координатам точек пересечения гиперболы и прямой линии их суммы.
Построенные графики дают возможность оценить, как меняются постоянные времени разложения числителя вида (z2.3). Обратимся к графикам фиг.6.
Если линия постоянной суммы проходит через точку K, то значения постоянных времени звеньев в числителе (z2.3) будут одинаковы, и величина коэффициента демпфирования «ζ» будет равна единице. Если линия постоянства суммы проходит левее точки K, то она не пересекается с гиперболой и разложение числителя (z2.3) на множители невозможно. Если линия постоянной суммы проходит правее точки K, то она дважды пересекается с гиперболой. Поскольку линия постоянства суммы, также как и гипербола, симметрична относительно биссектрисы первого квадранта, то точки пересечения ее с гиперболой будут симметричны относительно упомянутой биссектрисы. А координаты этих точек, т.е. значения искомых постоянных времени будут зеркальным отражением друг друга, что соответствует перестановке сомножителей в (z2.3) местами. Таким образом можно, рассматривать только одно решение, в частности, расположенное между осью T1 и отрезком биссектрисы KB. По мере увеличения Kqx точки пересечения линии постоянной суммы и гиперболы смещаются вправо, что соответствует увеличению большей T11 из искомых постоянных времени и уменьшению меньшей T12, при уменьшении Kqx искомые постоянные времени наоборот буду сближаться, т.е. T11 будет уменьшаться, а T12 - увеличиваться.
В результате окончательно имеем.
Пусть ζ >1, тогда (z2.1) можно представить:
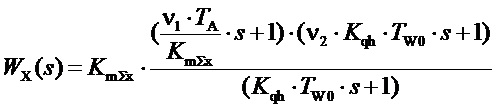 , (z2.5)
, (z2.5)
при этом: если Kqx<0, то ν1<1 и ν2>1; если Kqx=0, то ν1=1 и ν2=1; если Kqx>0, то ν1>1 и ν2<1.
Диапазон частот дифференцирования ограничивают, ввиду бессмысленности его продолжения в область частот фильтрации сигналов датчиков и полосы пропускания исполнительной следящей системы, постоянная времени которых нормируется 61362 © IEC:2012 стр.29 и для приводов направляющих аппаратов реактивных турбин должна находиться в 0,1-0,25с, а для приводов лопастей рабочего колеса 0,2-0,8с. Поэтому обычно присваивают коэффициентам значения 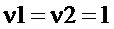 и ограничивают диапазон дифференцирования фильтром НЧ с постоянной времени T1D=0,4-0,05с.
и ограничивают диапазон дифференцирования фильтром НЧ с постоянной времени T1D=0,4-0,05с.
После чего закон регулирования по переменной (6) принимает вид:
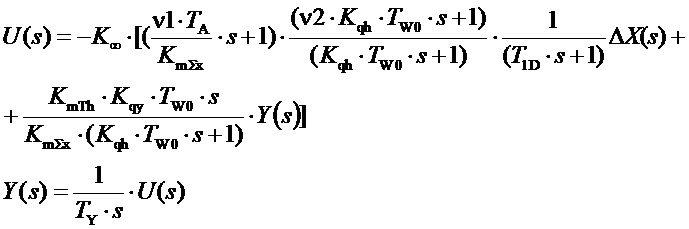 .
.
Это хорошо знакомая реализации ПИД-регулятора, блок-схема которого приведена на фиг.1 и в прямой цепи которого находятся усилитель с большим коэффициентом усиления и интегратор, охваченные гибкой отрицательной обратной связью. Передаточной функцией этого контура путем эквивалентных преобразований будет передаточная функция идеального ПИ-блока, знаменателем которой будет числитель передаточной функции звена обратной связи, а знаменателем ее - числитель. Что дает следующую передаточную функцию всего регулятора:
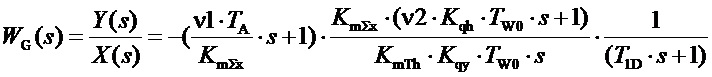 . (11)
. (11)
Полученная зависимость показывает, что влияние коэффициента 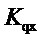 на передаточную функцию регулятора можно учесть надлежащей коррекцией величин постоянных времени дифференцирования сигнала частоты и гибкой обратной связи, т.е. не нарушая лаконичности структуры ПИД-регулятора.
на передаточную функцию регулятора можно учесть надлежащей коррекцией величин постоянных времени дифференцирования сигнала частоты и гибкой обратной связи, т.е. не нарушая лаконичности структуры ПИД-регулятора.
Что может дать введение в закон регулирования воздействия по отклонению положения регулирующего органа от ожидаемого в установившемся режиме? Оценим эффективность воздействия по координате (6) на примере регулятора частоты для турбины с параметрами близкими к машине Братской ГЭС. Параметры объекта регулирования в окрестности исследуемого режима работы при уровне нагрузки 75 % номинальной следующие:
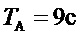 - время разгона машины;
- время разгона машины;
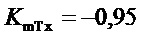 - коэффициент передачи: «отклонение частоты вращения - отклонение момента турбины»;
- коэффициент передачи: «отклонение частоты вращения - отклонение момента турбины»;
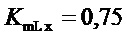 - коэффициент передачи: «отклонение частоты вращения - отклонение момента суммы сил сопротивления»
- коэффициент передачи: «отклонение частоты вращения - отклонение момента суммы сил сопротивления»
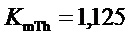 - коэффициент передачи: «отклонение перепада давлений на турбине - отклонение ее момента»;
- коэффициент передачи: «отклонение перепада давлений на турбине - отклонение ее момента»;
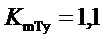 - коэффициент передачи: «отклонение положения сервомотора регулирующего органа - отклонение момента турбины».
- коэффициент передачи: «отклонение положения сервомотора регулирующего органа - отклонение момента турбины».
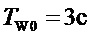 - время разгона воды в водоводе турбины;
- время разгона воды в водоводе турбины;
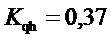 - коэффициент, определяющий скорость затухания динамического отклонения перепада давлений в зависимости от его величины;
- коэффициент, определяющий скорость затухания динамического отклонения перепада давлений в зависимости от его величины;
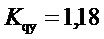 - коэффициент, передачи «отклонение регулирующего органа - отклонение расхода через турбину»;
- коэффициент, передачи «отклонение регулирующего органа - отклонение расхода через турбину»;
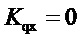 - коэффициент, передачи «отклонение частоты вращения - отклонение расхода через турбину».
- коэффициент, передачи «отклонение частоты вращения - отклонение расхода через турбину».
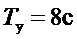 - время перемещения сервомотора на величину полного конструктивного хода при смещении главного золотника на один из упоров;
- время перемещения сервомотора на величину полного конструктивного хода при смещении главного золотника на один из упоров;
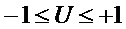 - ограничения хода главного золотника упорами;
- ограничения хода главного золотника упорами;
Величину статизма примем равной нулю bp=0. Тогда передаточная функция регулятора, представленного на фиг.1, будет даваться выражением:
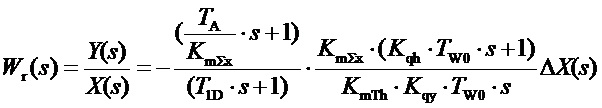
 (11)
(11)
Полученное выражение не дает представления о структуре регулятора при оценке устойчивости, например, по критерию Найквиста, поскольку частотная характеристика не изменяется, если использовать любое из представлений: либо даваемое формулой (11), где первый сомножитель соответствует пропорционально-дифференцирующему блоку ПД, а второй пропорционально-интегрирующему ПИ, либо в виде, соответствующем структуре, представленной на рисунке фиг.4:
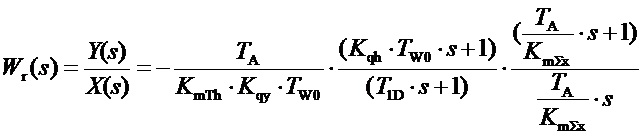 , (12)
, (12)
причем, как правило:  .
.
С точки зрения линейной теории САР формулы (11) и (12) неотличимы: у них тождественно равные нули числителей и знаменателей и одинаковый коэффициент усиления. Одинаковы и переходные функции. Однако сравним переходные процессы при ступенчатом изменении нагрузки.
На осциллограммах фиг.7, фиг.8 и фиг.9 приведены переходные процессы в контуре регулирования частоты для упомянутого числового примера и трех структур регуляторов с одинаковыми частотными характеристиками при 20% набросе нагрузки в приемной системе. Обозначения сигналов на осциллограммах соответствуют обозначениям на стр.1 и 2.
На осциллограмме фиг.7 изображен переходный процесс с линейным ПИД-регулятором частоты, структура которого изображена на фиг.4., сигналы, пропорциональные отклонению частоты и ее производной, напрямую проходят на выход регулятора, что обеспечивает быстрое перемещение сервомотора на величину примерно 0,03 (3%), а затем, поскольку скорость его движения зависит только от изменения частоты, производная которой уменьшается, движение сервомотора замедляется и длительность переходного процесса составляет приблизительно 30с. Такая же картина наблюдается (осциллограмма фиг.8) и в контуре с ПИД-регулятором, ПИ - блок которого выполнен по изодромной схеме фиг. 1. Наличие в прямой цепи формирователя интегратора, хотя и с малой постоянной времени, несколько ограничивает скорость изменения выходного сигнала регулятора, что приводит к меньшему по величине быстрому изменению величины отработки сигналов пропорциональных отклонению частоты и ее производной на выходе регулятора. Можно сказать, что переходные процессы при применении традиционных структур ПИД-регуляторов для гидротурбин неотличимы по качеству переходного процесса и имеют при одинаковых передаточных функциях одинаковые переходные процессы. Переходный процесс в контуре с регулятором, управляемым по координате отклонения положения регулирующего органа от ожидаемого положения в установившемся режиме, разительно отличается от двух предыдущих. Регулятор формирует квазиоптимальную по быстродействию траекторию первой фазы управления, когда положение золотника «u» остается постоянным до достижения выбранной координатой нулевого значения. Это иллюстрируется переходным процессом фиг.9: сервомотор движется с постоянной скоростью и останавливается в положении будущего равновесия. В этом случае говорят, что система регулирования перешла в скользящий режим по плоскости (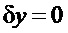 ) в пространстве параметров состояния (
) в пространстве параметров состояния (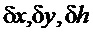 ). Перерегулирование по частоте при этом в два раза меньше, чем при применении традиционных ПИД-регуляторов, а время переходного процесса в полтора раза меньше.
). Перерегулирование по частоте при этом в два раза меньше, чем при применении традиционных ПИД-регуляторов, а время переходного процесса в полтора раза меньше.
Осциллограмма фиг.9 показывает, что в смысле критерия с функционалом «I» задача управления решена: положительно определенный функционал достиг минимума, дальнейшее движение системы продолжается в виде скольжения точки по плоскости 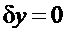 , отклонения частоты «δx» и напора «δh» уменьшаются без дополнительного воздействия со стороны регулятора до нуля, в силу асимптотической устойчивости объекта регулирования.
, отклонения частоты «δx» и напора «δh» уменьшаются без дополнительного воздействия со стороны регулятора до нуля, в силу асимптотической устойчивости объекта регулирования.
Рассмотрим пошаговые структурные преобразования, приводящие к структуре регулятора, имеющего переходный процесс фиг.9. Структурная схема неизменяемой части системы регулирования представлена на рисунке фиг. 11а. Соответствующая ей передаточная функция гидротурбины, заимствована из кн. В.А. Пивоварова «Проектирование и расчет систем регулирования гидротурбин»: стр. 195, ф-лы (4.37), (4.38) и адаптирована к системе уравнений (5). Таким образом, отклонение частоты вращения нерегулируемой системы в случае ступенчатого изменения нагрузки генератора на величину δm0 можно вычислить, используя зависимость:
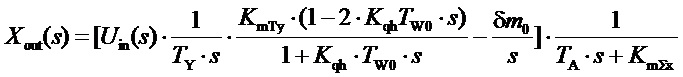
Задачей синтеза на языке структурных схем является замыкание главной обратной связи по частоте вращения, т.е. придерживаясь основных теорем теории абсолютной устойчивости регулируемых систем, сконструировать структурную схему цепи главной отрицательной обратной связи (регулятора) путем включения в нее звеньев как последовательной, так и параллельной коррекции таким образом, чтобы замкнутый контур регулирования можно было представить в виде двух блоков: один из которых это связка «главный золотник - интегратор», а второй - асимптотически устойчивый гиперустойчивый линейный блок, удовлетворяющий условию положительности реальной части его частотной характеристики [см. В.М. Попов. Теория гиперустойчивости автоматических систем», Москва, Наука, 1970]. Таким образом, необходимо создать структуру из типовых звеньев САР, которые формируют требуемую связь между xout и uin, обеспечивая асимптотическую устойчивость контура регулирования.
Сформулируем конкретную цель синтеза: главная обратная связь по частоте, после включения в ее цепь последовательных корректирующих звеньев и охвата интегратора вспомогательными цепями отрицательных обратных связей, должна быть путем эквивалентных преобразований структурных схем трансформирована в единичную отрицательную обратную связь интегратора по отклонению регулирующего органа от положения равновесия.
На фиг.11б показан первый шаг структурного синтеза: включение в последовательную цепь звеньев будущего регулятора пропорционально-дифференцирующего блока с параметрами передаточной функции, позволяющими скомпенсировать влияние инерции ротора агрегата на передачу возмущения по нагрузке на изменение положения главного золотника. В результате получается прямая передача сигнала пропорционального разности между моментом, развиваемым турбиной, и моментом сил сопротивления в качестве определяющего положение главного золотника.
На фиг.11в представлена завершающая структурный синтез операция компенсации негативного влияния на устойчивость положительной обратной связи по составляющей момента турбины, вызванной динамическим повышением давления, причиной которого является, прежде всего, движение регулирующего органа. Эта положительная обратная связь пропорциональная скорости движения регулирующего органа не может быть скомпенсирована включением звена последовательной коррекции. Она может быть скомпенсирована включением точно такой же отрицательной обратной связи, что и показано на схеме фиг.11в.
Таким образом, в рассмотренном случае синтез закона регулирования посредством эквивалентных структурных преобразований привел нас к структуре «интегратор, на входе которого предвключен пропорциональный усилитель с ограниченным выходным сигналом», охваченные жесткой обратной связью. Эта структура абсолютно устойчива при любом коэффициенте усиления линейного участка характеристики усилителя на входе интегратора. При этом интегратор будет безынерционно повторять входной сигнал, если скорость изменения последнего меньше скорости изменения выходного сигнала интегратора, развиваемой им при достижении выходным сигналом имеющего бесконечно большой коэффициент усиления усилителя-ограничителя на уровнях ограничения. Необходимо отметить, что в результате структурного синтеза получен результат, показывающий, что структура имеет большие запасы по устойчивости, потому что формулировка частотного критерия абсолютной устойчивости В.М. Попова для линейной цепи отрицательной обратной связи, охватывающей цепочку «усилитель с бесконечным коэффициентом усиления - интегратор», заключается в выполнении для нее двух условий:
- асимптотической устойчивости ее;
- положительности реальной части ее частотной характеристики.
С точки зрения обеспечения устойчивости предлагаемая структура регулятора по нечувствительности к изменчивости параметров объекта регулирования намного превосходит линейные построения. Это связано с особенностями коррекции динамических свойств, использованием в структуре регулятора коротких локальных цепей обратных связей, блокирующих влияние неблагоприятного для достижения устойчивости высокочастотных частей частотной характеристики главной отрицательной обратной связи по частоте вращения. В предлагаемой структуре комбинированное действие дифференцирования сигнала частоты в широком диапазоне частот и действие параллельной цепи коррекции (гибкой обратной связи интегратора) смещены в область высоких частот, где параллельная коррекция исключает влияние малых постоянных времени исполнительных и измерительных устройств на устойчивость, что позволяет использовать производную частоты наиболее эффективно и в области низких частот.
Выражение передаточной функции регулятора для параметров рассмотренного примера одинаково для всех трех вариантов структур регуляторов:
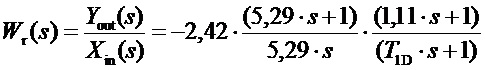 ,
,
при этом передаточная функция объекта регулирования:
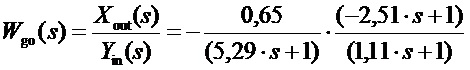 .
.
В итоге передаточная функция разомкнутой системы будет равна:
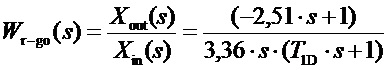
Для рассматриваемой математической модели при T1D→0 фазовая частотная характеристика разомкнутой системы при ω→∞ монотонно убывает от минус 90° и асимптотически стремится к минус 180°, аналогично ведет себя и логарифмическая частотная амплитудная характеристика, монотонно убывающая от бесконечно большой величины при ω=0 и асимптотически стремящаяся к значению ≈ минус 1,3 дБ. (0,857). При замыкании системы передаточная функция, характеризующая реакцию на изменение уставки частоты вращения, дается выражением:
 .
.
Для исключения колебательности переходного процесса при задании уставки частоты необходимо выполнить условие:

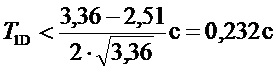
При T1D=0,232 передаточная функция замкнутой системы приобретает вид:
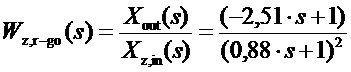 .
.
Нули знаменателя передаточной функции вещественны, следовательно, в переходном процессе не будет колебательной составляющей.
Таким образом, введение в закон регулирования частоты вращения координаты «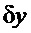 », регулирующее воздействие которой эквивалентно сумме воздействий по отклонению «
», регулирующее воздействие которой эквивалентно сумме воздействий по отклонению « » частоты, производной его и динамическому отклонению напора «
» частоты, производной его и динамическому отклонению напора «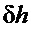 », взятых с определенными весовыми множителями, обеспечивает наибольшую скорость достижения регулирующим органом турбины положения в ожидаемом статическом режиме при компенсации возмущения со стороны нагрузки. При этом обеспечивается максимально достижимый запас абсолютной устойчивости системы. Этот запас устойчивости позволяет ввести в закон регулирование дополнительное воздействие по частоте, компенсируя усиливающееся при этом негативное влияние динамического отклонения напора на устойчивость коррекцией интенсивности воздействий по двум другим параметрам состояния.
», взятых с определенными весовыми множителями, обеспечивает наибольшую скорость достижения регулирующим органом турбины положения в ожидаемом статическом режиме при компенсации возмущения со стороны нагрузки. При этом обеспечивается максимально достижимый запас абсолютной устойчивости системы. Этот запас устойчивости позволяет ввести в закон регулирование дополнительное воздействие по частоте, компенсируя усиливающееся при этом негативное влияние динамического отклонения напора на устойчивость коррекцией интенсивности воздействий по двум другим параметрам состояния.
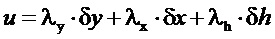 , (23)
, (23)
где λy, λx, λh - вещественные числа, полученные в результате решения поставленной задачи оптимизации.
Замечание 2. Непосредственное измерение динамического отклонения напора  «
«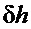 »
»  требует применения достаточно сложной и капризной аппаратуры измерения давлений перед входом в спиральную камеру и на выходе из рабочего колеса гидравлической турбины. Но не это главное, потому что полученные таким образом результаты требуют обоснования их применимости при расчете отклонений момента и мощности по статическим характеристикам турбины, которые получены при измерении напора нетто между входом в спиральную камеру и выходом из отсасывающей трубы. Поэтому при расчетах систем регулирования используют уравнения для определения динамического отклонения напора турбины, которое трактуется как отклонение действующего внешнего напора, вызывающее отклонение момента и мощности, соответствующее универсальным характеристикам. Уравнением для определения упомянутого влияния является второе уравнение системы (15). В дальнейшем будем даваемое им значение динамического отклонения напора прибавлять к напору нетто и полученную сумму, как это общепринято при исследовании динамики регулирования гидротурбин, использовать для определения расхода и момента по универсальной характеристике.
требует применения достаточно сложной и капризной аппаратуры измерения давлений перед входом в спиральную камеру и на выходе из рабочего колеса гидравлической турбины. Но не это главное, потому что полученные таким образом результаты требуют обоснования их применимости при расчете отклонений момента и мощности по статическим характеристикам турбины, которые получены при измерении напора нетто между входом в спиральную камеру и выходом из отсасывающей трубы. Поэтому при расчетах систем регулирования используют уравнения для определения динамического отклонения напора турбины, которое трактуется как отклонение действующего внешнего напора, вызывающее отклонение момента и мощности, соответствующее универсальным характеристикам. Уравнением для определения упомянутого влияния является второе уравнение системы (15). В дальнейшем будем даваемое им значение динамического отклонения напора прибавлять к напору нетто и полученную сумму, как это общепринято при исследовании динамики регулирования гидротурбин, использовать для определения расхода и момента по универсальной характеристике.
Дифференцирование, выполняемое в значимом для управления накоплением кинетической энергии ротором широком диапазоне частот, и ограничение скорости движения сервомотора, вызывающее насыщение сигнала гибкой обратной связи, имеющей к тому же постоянную времени обычно меньшую, чем постоянная времени ротора, обеспечивает длительное движение сервомотора с полной скоростью в первые секунды подавления возмущения. Эти отличительные особенности предлагаемого способа регулирования частоты вращения гидротурбины обеспечивают минимизацию отклонений частоты в первые моменты нарушения баланса «выработки - потребления» энергии и позволяют предотвратить развитие аварии в энергосистеме.
Обладая высоким быстродействием при изменении мощности со стороны нагрузки предлагаемый регулятор реагирует на изменение уставки частоты иначе, чем ПИД-регулятор традиционной структуры, так как он значительно сильнее сопротивляется отклонению положения сервомотора от точки равновесия, не обусловленного изменением нагрузки. Переходный процесс изменения частоты при ступенчатом изменении уставки и применении предлагаемого регулятора не имеет характерного для регуляторов частоты вращения гидротурбин отклонения частоты в противоположную изменению уставки сторону в первые моменты времени.
Параметры настройки
Практика настройки регуляторов предлагаемой структуры показала, что очень удобно, когда уставки постоянных времени и коэффициентов пропорциональной составляющей соответствуют идеальной изодромной структуре регулятора (1) и наглядно отображаются ЛАЧХ. Имея одинаковую с изодромным регулятором передаточную функцию, предлагаемый регулятор несколько иначе производит обработку используемых сигналов: участок пропорционального воздействия по частоте в области низких частот ЛАХ образован интегрированием в ПИ-модуле производной частоты, а воздействие по производной частоты в области высоких частот пропуском ее через формирующую пропорциональное воздействие область частот ЛАХ того же ПИ модуля. Все участки асимптот ЛАХ задаются постоянными времени, а коэффициенты усиления обратными связями ПИ-блока.
Перепишем формулу (12) следующим образом:
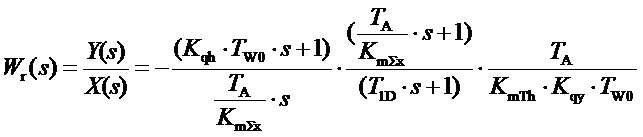 (14)
(14)
Формула состоит из трех сомножителей, каждому из которых соответствуют определенные амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) логарифмические частотные характеристики.
Первый сомножитель - ПИ-модуль:
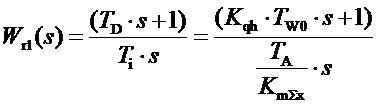 (15)
(15)
- настройка: TD - постоянная времени числителя должна совпадать с постоянной времени начала дифференцирования в передаточной функции (1) идеального изодромного регулятора, Ti - постоянная времени знаменателя с постоянной времени гибкой обратной связи (изодрома).
Низкочастотная асимптота ее ЛАЧХ, имея постоянный наклон минус 20 дБ/дек, уменьшается в диапазоне частот (0,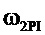 ], где
], где 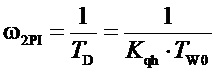 и пересекает ось частот в точке
и пересекает ось частот в точке 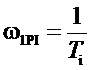 , в диапазоне частот [
, в диапазоне частот [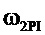 ,∞) высокочастотная асимптота ЛАЧХ идет параллельно оси «
,∞) высокочастотная асимптота ЛАЧХ идет параллельно оси «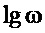 » на расстоянии от нее равном
» на расстоянии от нее равном 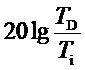 дБ. (см. фиг. 12а, красный цвет).
дБ. (см. фиг. 12а, красный цвет).
Второй сомножитель: 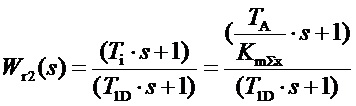 (16)
(16)
- передаточная функция ПД блока, где Ti - постоянная времени демпфирования (начало диапазона пропорциональной составляющей), T1D - постоянная времени конца диапазона дифференцирования.
Низкочастотная асимптота ее ЛАЧХ для всех частот меньших 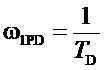 совпадает с осью ω, начинающаяся в точке
совпадает с осью ω, начинающаяся в точке  высокочастотная асимптота идет параллельно оси при всех
высокочастотная асимптота идет параллельно оси при всех 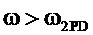 , в диапазоне средних частот [
, в диапазоне средних частот [ ,
,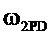 ] асимптота ЛАЧХ возрастает с наклоном 20 дБ/дек, соединяя конечную точку низкочастотной с начальной точкой высокочастотной частей асимптоты (см. фиг. 12а, синий цвет).
] асимптота ЛАЧХ возрастает с наклоном 20 дБ/дек, соединяя конечную точку низкочастотной с начальной точкой высокочастотной частей асимптоты (см. фиг. 12а, синий цвет).
Произведение передаточных функций первого и второго сомножителей образуют базовую частотную характеристику предлагаемого регулятора при коэффициенте усиления (третий сомножитель в формуле (14)) равном единице и нулевом значении статизма. Базовая ЛАХ приведена на рисунке фиг.12а (черный цвет). Ее вид однозначно определяется заданием постоянных времени: Ti, TD и T1D.
Третий сомножитель: 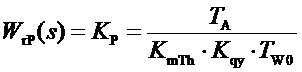 (17)
(17)
- общий коэффициент усиления регулятора, при его изменении все значения ЛАЧХ в случае астатической настройки, соответствующей передаточной функции Wr(s) (14), изменяются на одну и ту же величину, при этом сопрягающие частоты и ЛФЧХ остаются неизменными, так как это происходит в регуляторах изодромной структуры (см. фиг. 12б).
Правильное введение сигнала статизма обеспечивает ограничение усиления регулятора только в области низких частот (см. фиг. 12в).
На рисунке фиг.13 приведена структурная схема предлагаемого регулятора. На ней представлен процесс формирования управляющего воздействия: выходные сигналы измерителя 1 частоты вращения ротора турбины и задатчика 3 уставки частоты подаются на входы выявителя 2 отклонения частоты от уставки, выходной сигнал его поступает на вход пропорционально-дифференцирующего блока 4, выходной сигнал которого подается на неинвертирующий вход сумматора 5, на два инвертирующих входа которого поступают выходные сигналы формирователя 6 гибкой обратной связи и формирователя 8 величины статизма, соответственно, при этом на входы упомянутых формирователей и на вход электрогидравлической следящей системы 10 подается выходной сигнал интегратора 9, входным сигналом для которого является выходной сигнал усилителя-ограничителя 7, входным сигналом для которого служит выходной сигнал сумматора 4.
Поворотно-лопастные турбины имеют два регулирующих органа одновременно с изменением открытия направляющего аппарата (НА) изменяется и угол разворота лопастей рабочего колеса (РК). Функцию управления электрогидравлическим приводом изменения угла разворота лопастей РК выполняет комбинаторный механизм, формирующий задание положения «y2» сервомотора привода лопастей РК как функцию двух переменных; положения «y1» сервомотора (НА) и величины напора нетто. В современных регуляторах комбинаторные зависимости формируются безынерционно, используя выходной сигнал интегратора регулятора, поэтому задания сервомоторам обоих приводов подаются на входы соответствующих электрогидравлических следящих систем одновременно. В нормативных документах 61362 © IEC:2012 (стр. 29) и ПНСТ 49-2015 (стр.16) приведены требования к динамическим характеристика приводов регулирующих органов:
- постоянная времени в зоне линейности характеристики главного золотника для привода лопаток НА должна лежать в диапазоне 0,1÷0,25с и для привода лопастей РК - 0.2÷0,8с;
- мертвое время при подаче на вход ступенчатого задания на изменение положения величиной 10% от полного хода не должно быть более 0,2с.
Перечисленные параметры приводов, в случае применения в регуляторе в качестве корректирующей цепочки отрицательной гибкой обратной связи интегратора, практически не влияют на показатели устойчивости из-за шунтирующего действия коррекции этого типа, поэтому можно считать, что сервомоторы обоих приводов не имеют постоянных времени и расход через турбину вычислять, используя выходной сигнал интегратора для НА и комбинатора для РК. Эффективность действия упомянутой корректирующей цепи зависит от правильности оценки скорости изменения расхода при движении регулирующих органов, а для этого нужно располагать представлением о статических зависимостях расхода в функции от положения регулирующих органов и их движения в динамике. В работе [Б. Е. Сафаров. Расчет режимов регулирования гидроагрегатов на ЦВМ. Энергия. М., 1967] показано, что при подстановке в статические расходные и моментные характеристики значений переменных состояния, доставляемых решением дифференциальных уравнений движения системы, вместо их значений в статических режимах, траектории движения объекта регулирования в неустановившихся режимах верно отражают процессы подвода и отвода энергии, а также обмен ею между участвующими в нем аккумуляторами.
Особенность системы регулирования поворотно-лопастных турбин заключается в неодинаковости поведения приводов лопаток НА и лопастей РК при выполнении команды набора мощности, т.е. движении на увеличение расхода, и при снижении мощности - на уменьшение расхода. В первом случае движение выполняется с сохранением комбинаторной зависимости, что обеспечивает сохранение относительно высокого КПД турбины при наборе мощности, и запланированное отклонение от нее при снижении нагрузки, за счет значительного уменьшения скорости движения сервомотора привода РК на свертывание лопастей. В первом случае при окончании переходного процесса, как только спадет динамическое отклонение давления, КПД турбины установится на максимальном уровне, а во втором случае отклонение от комбинаторной зависимости обеспечивает быстрое падение КПД и, как следствие, минимальный заброс частоты вращения при сбросе нагрузки.
Расходная характеристика поворотно-лопастной турбины в комбинаторных режимах может быть приближенно представлена как функция положения сервомотора НА и напора, если воспользоваться свойством «линий угла» [Г.И. Топаж. Лопастные гидромашины и гидродинамические передачи. Уч. Пособие, С.-Пб., изд-во Политехнического университета, 2011г.]. Свойство линий (равного) угла заключается в том, что в комбинаторных режимах расход при постоянном угле разворота лопастей РК слабо зависит от напора. Если считать, что при постоянном угле разворота лопастей в статическом комбинаторном режиме расход не зависит от напора и определять его по формуле:
 ,
,
то погрешность его определения в комбинаторных режимах будет меньше 3%. Зависимость относительного расхода от положения «y2» сервомотора РК приведена на рисунке фиг. 15. Таким образом, расход однозначно определяется положением «y2» сервомотора привода лопастей РК, которое в свою очередь является функцией положения «y1» сервомотора НА и напора. На рисунке фиг.14 представлены комбинаторные зависимости турбины Новосибирской ГЭС. В результате получаем:
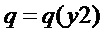 и
и 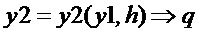 .
.
Следовательно, когда сервомоторы приводов лопаток НА и лопастей РК движутся синхронно в соответствии с комбинаторной зависимостью, расход можно определить по положению «y1» сервомотора НА и сумме статического и динамического отклонений напора от номинального, причем скорость изменения расхода в этом случае будет максимально возможной, в отличие от случаев, когда сервомотор РК отстает от сервомотора НА при сбросах нагрузки или движется в противоположную сторону при реализации программного закрытия НА. Поэтому при выборе оказывающей решающее значение на обеспечение абсолютной устойчивости контура регулирования частоты интенсивности гибкой отрицательной обратной связи интегратора следует принимать в расчеты максимальную скорость изменения расхода для случаев движения регулирующих органов при увеличении мощности турбины. Величины относительных расхода и момента для турбины с двумя регулирующими органами при необходимости учитывать большие рассогласования комбинаторных зависимостей могут быть определены методом, изложенным в статье О.И. Башнин, Н.П. Жежель, В.В. Семенов Гипотеза окружного подобия режимов поворотно-лопастных и капсульных агрегатов. Л., «Наука», Л. Отд., 1979, стр. 169-176.
Заключение
1. Законом стабилизации частоты вращения реактивных гидротурбин по критерию оптимального демпфирования с учетом ограничения на скорость перемещения регулирующего(-их) органа(-ов) в полной системе координат состояния: отклонения частоты вращения ротора, динамического (ударного) отклонения давления в водоводе агрегата и отклонения положения регулирующего(-их) органа(-ов) от положения в установившемся статическом режиме является закон регулирования с линейной переключающей плоскостью. В предыдущем разделе представлена процедура синтеза первого приближения структуры такого регулятора с вырожденной квадратичной формой по координате «отклонение регулирующего органа от положения равновесия». Уточнение структуры нужно производить методом последовательных приближений, используя математические модели турбины, учитывающие влияние нелинейности зависящих от величины нагрузки характеристик турбины и малые постоянные времени приводов регулирующих органов.
2. Показано решающее влияние на достижение абсолютной устойчивости короткой петли отрицательной гибкой обратной связи, охватывающей усилитель-ограничитель и интегратор, компенсирующей при увеличении ее интенсивности не только обусловленную гидравлическим ударом положительную обратную связь по скорости перемещения регулирующих органов, но и отрицательные фазовые сдвиги, вносимые частотными характеристиками неучтенных при анализе устойчивости элементов системы с малыми постоянными времени.
3. Существенным моментом является равенство скоростей перемещения сервомоторов регулирующих органов и интегратора регулятора, а также близкие по значению инерционные постоянные упомянутой ранее гибкой обратной связи и постоянной времени гидравлического удара, для полного подавления негативного влияния которого на устойчивость она предназначена.
4. Регулятор реализует квазиоптимальное управление с приближением к точке равновесия в скользящем режиме по ПИД-закону стабилизации частоты вращения турбины в ее окрестности. Предложены настройки пропорционально-дифференцирующего и пропорционально-интегрирующего блоков, последовательное включение которых образует структурную схему регулятора. Если обратиться к ЛЧХ, то так же, как и в регуляторах традиционной изодромной структуры постоянные времени настроек соответствуют точкам сопряжения асимптот ЛАЧХ звеньев с передаточными функциями первого порядка, произведения которых образуют числитель и знаменатель передаточной функции регулятора. Новая структура формирователя статизма позволяет исключить влияние уставки статизма на динамические свойства регулятора, так как исключает деформацию среднечастотной части его ЛАХ, характерную для изодромной и «ПИД-три составляющих» структур.
5. Рассмотрен опирающийся на свойство «линий угла» поворотно-лопастной турбины прием введения гибкой отрицательной обратной связи только по скорости изменения задания положения сервомотора НА, точно также как это выполняется в регуляторах радиально-осевых турбин.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ автоматической коррекции характеристик регулятора частоты электроэнергетического агрегата | 1981 |
|
SU1035769A1 |
| Электрогидравлический регулятор частоты вращения и мощности электроэнергетического агрегата | 1977 |
|
SU868963A1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ МОЩНОСТЬЮ ГИДРОАГРЕГАТА ГЭС | 2024 |
|
RU2830453C1 |
| СПОСОБ УПРАВЛЕНИЯ МОЩНОСТЬЮ РЕАКТИВНЫХ ГИДРАВЛИЧЕСКИХ ТУРБИН | 2017 |
|
RU2636603C1 |
| Способ автоматического регулирования частоты вращения ротора синхронного генератора и регулятор для его реализации | 2023 |
|
RU2823536C1 |
| ЭЛЕКТРОГИДРАВЛИЧЕСКАЯ СИСТЕМА АВТОМАТИЧЕСКОЙ СТАБИЛИЗАЦИИ УГЛОВОЙ СКОРОСТИ ВРАЩЕНИЯ ГИДРОАГРЕГАТА | 1993 |
|
RU2091608C1 |
| Способ резервирования электрогидравлической системы регулирования частоты вращения и устройство для его осуществления | 1983 |
|
SU1174579A1 |
| СПОСОБ УПРАВЛЕНИЯ РЕГУЛИРУЮЩИМИ ОРГАНАМИ ГИДРОТУРБИН (ВАРИАНТЫ) | 2018 |
|
RU2710944C1 |
| Устройство группового регулирования режима работы агрегатов электростанции по частоте и мощности | 1972 |
|
SU542320A1 |
| Способ управления лопастями рабочего колеса поворотно-лопастной гидротурбины | 2017 |
|
RU2674375C2 |
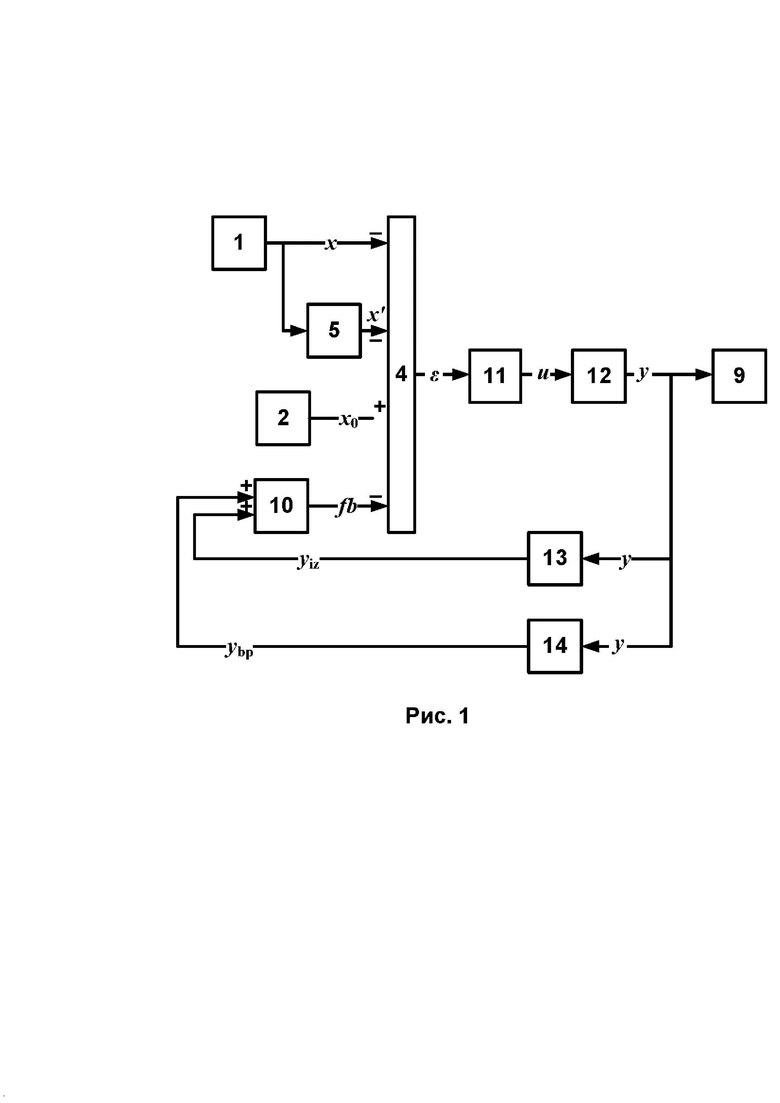


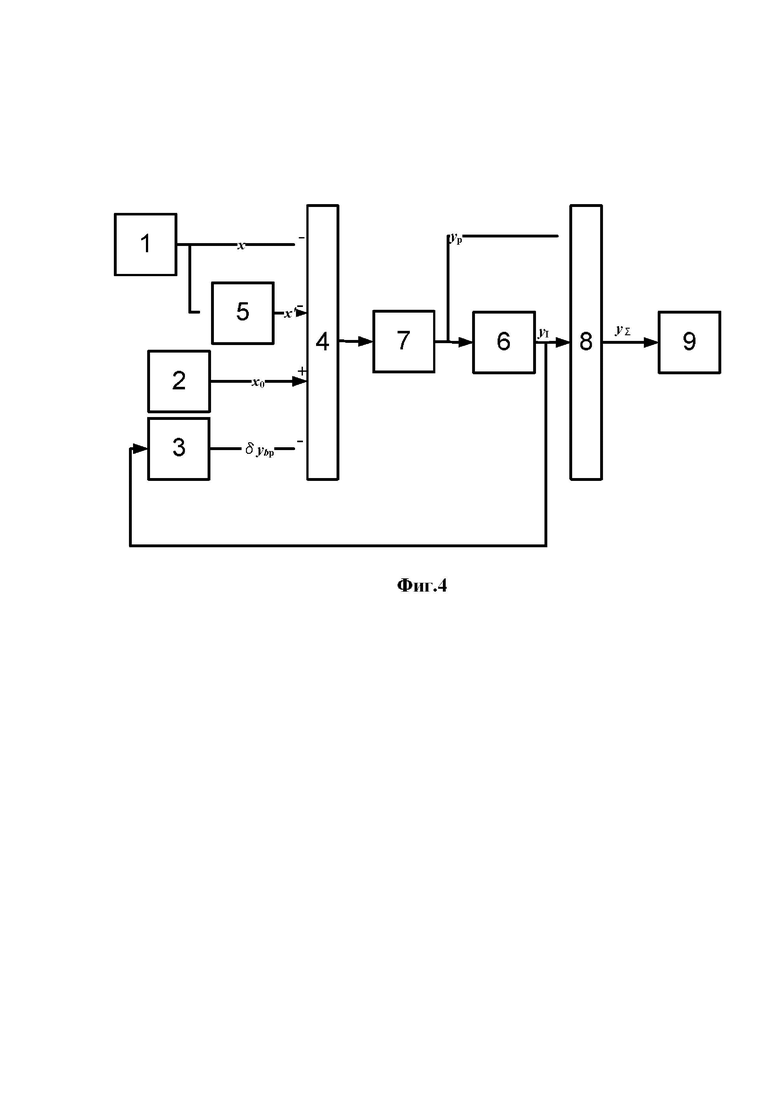
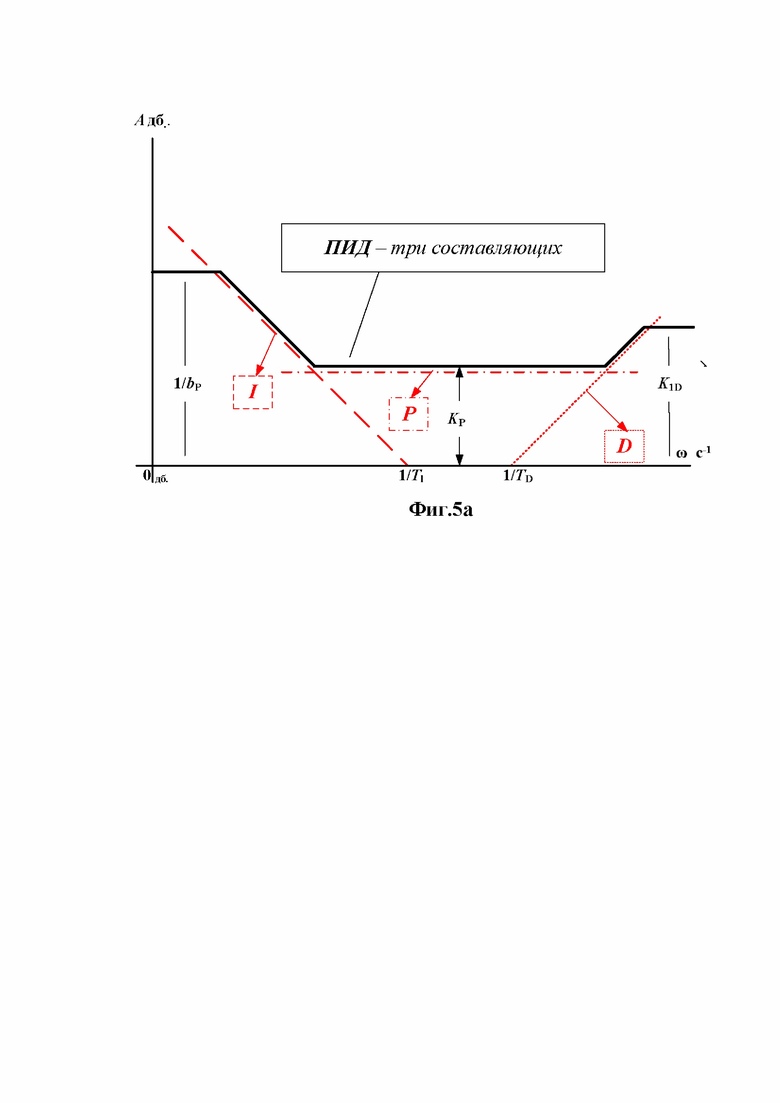
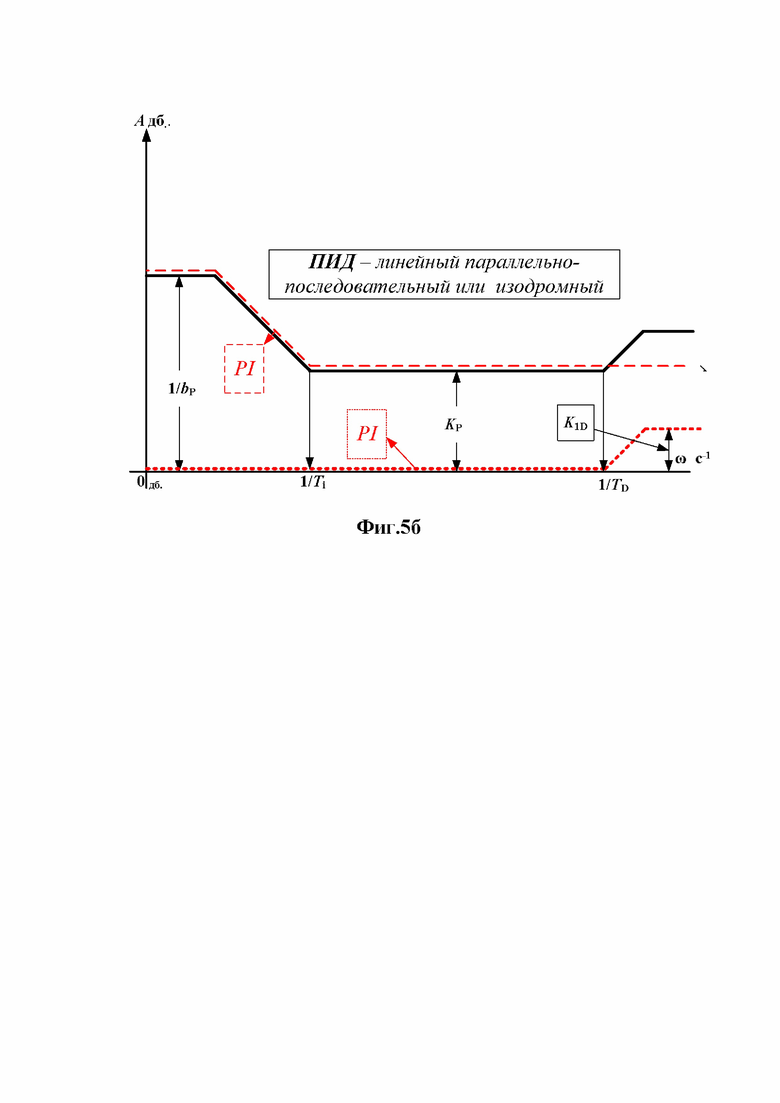
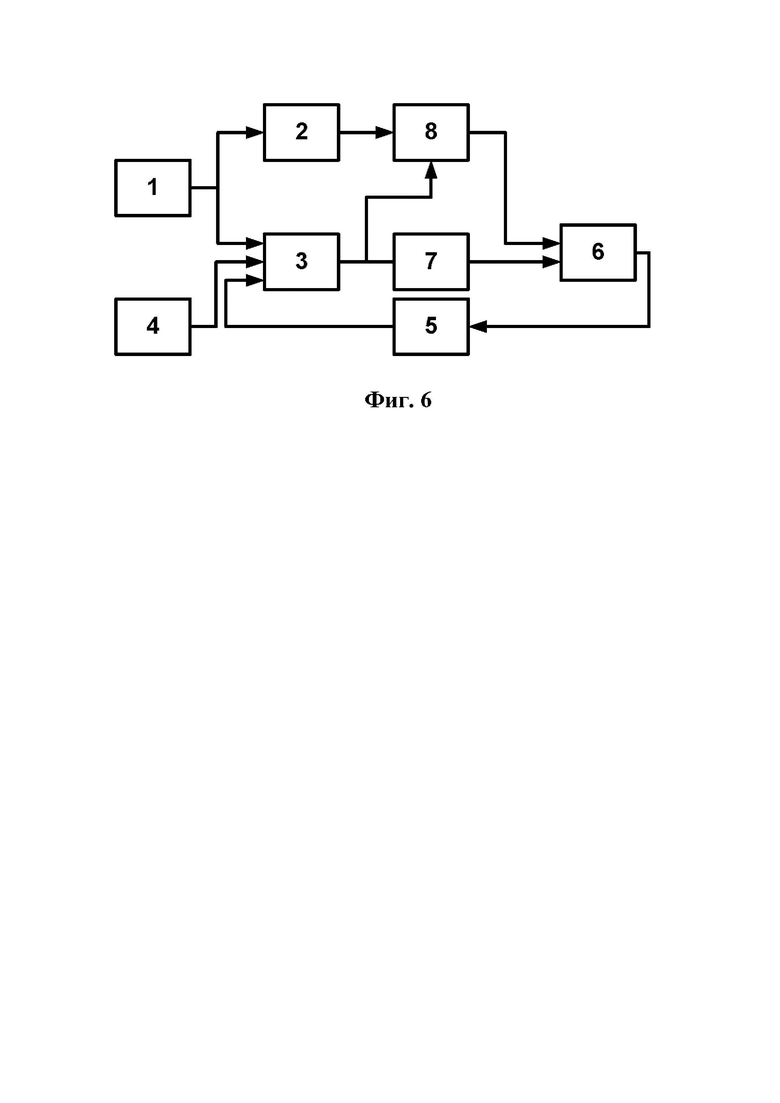


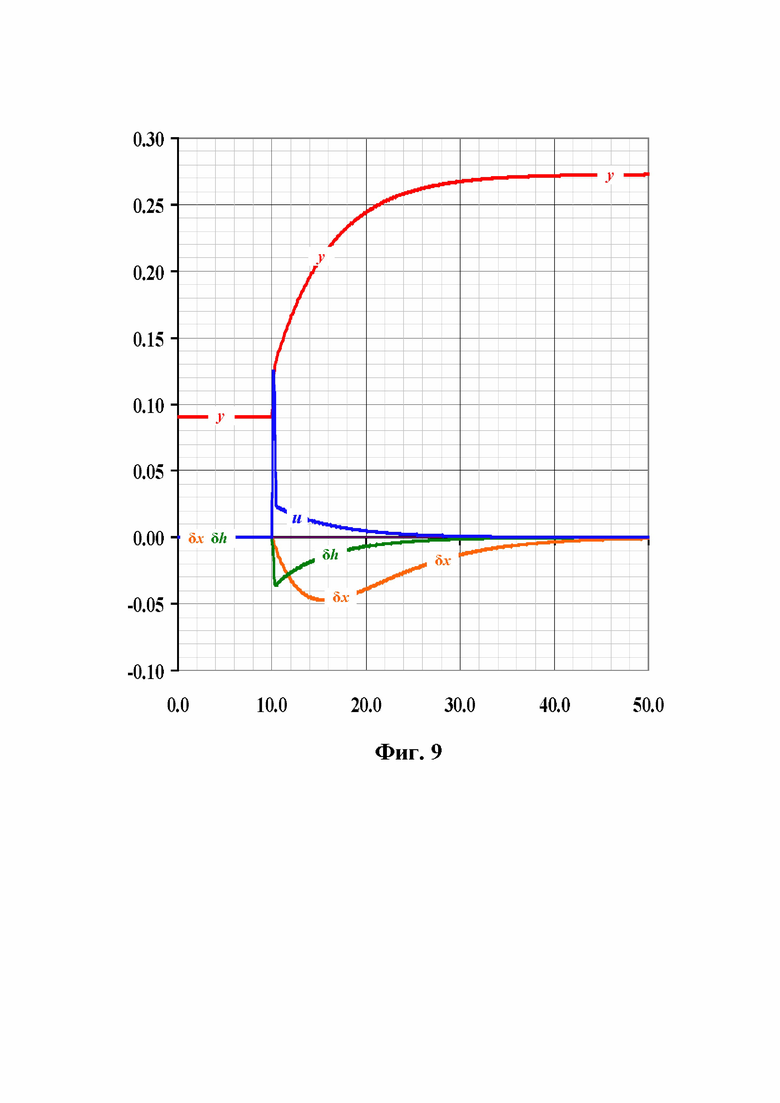
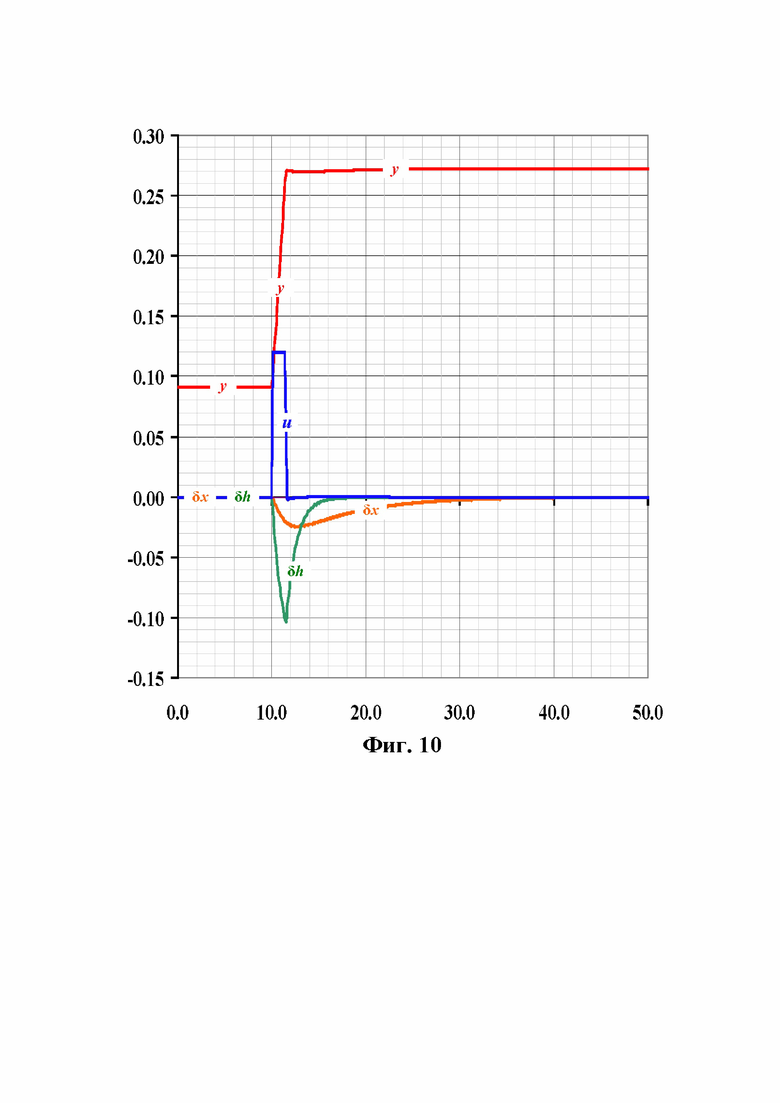
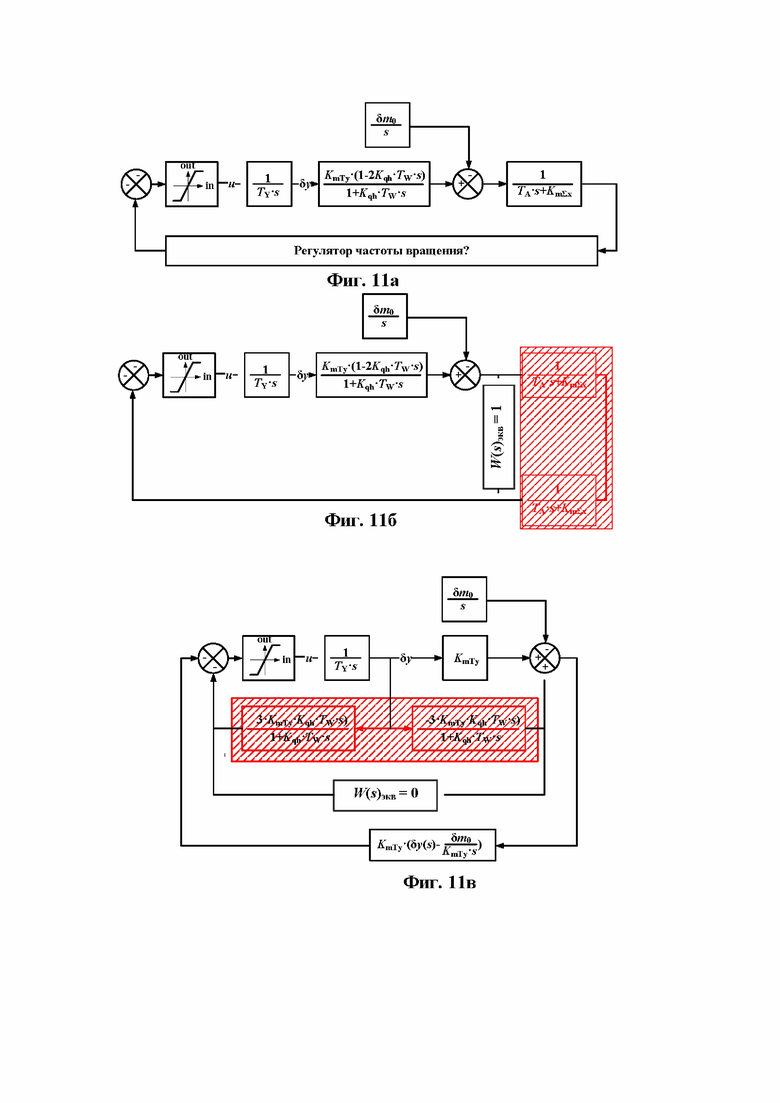
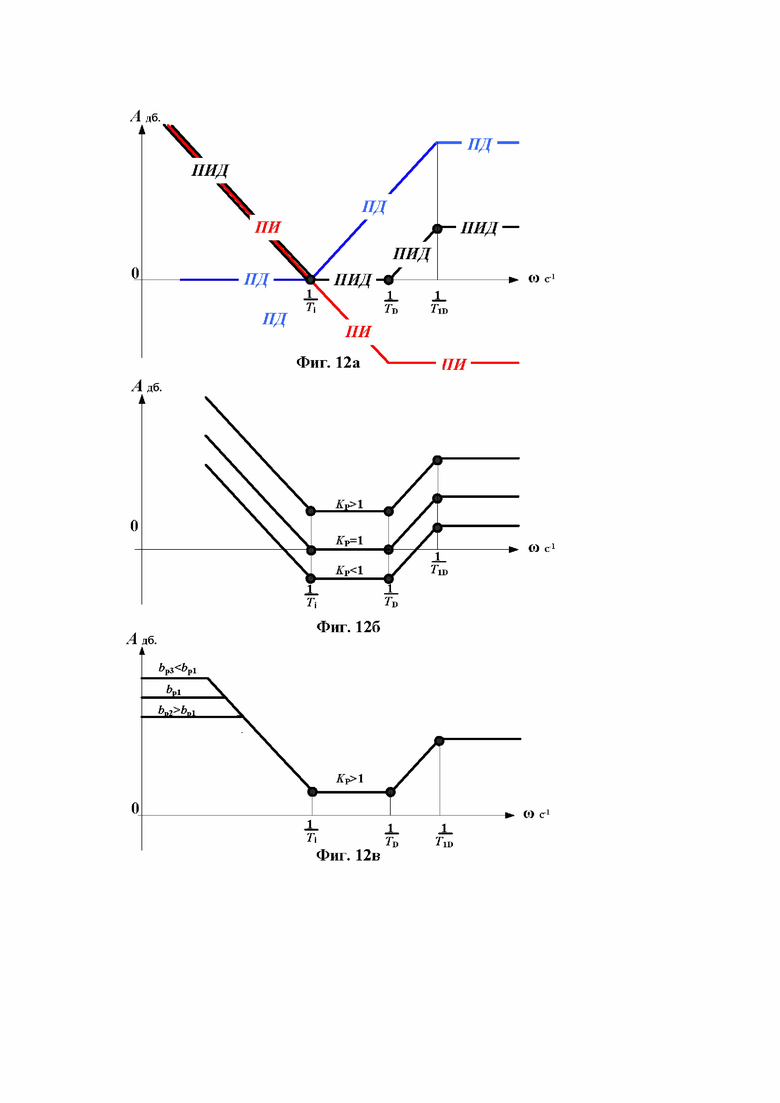
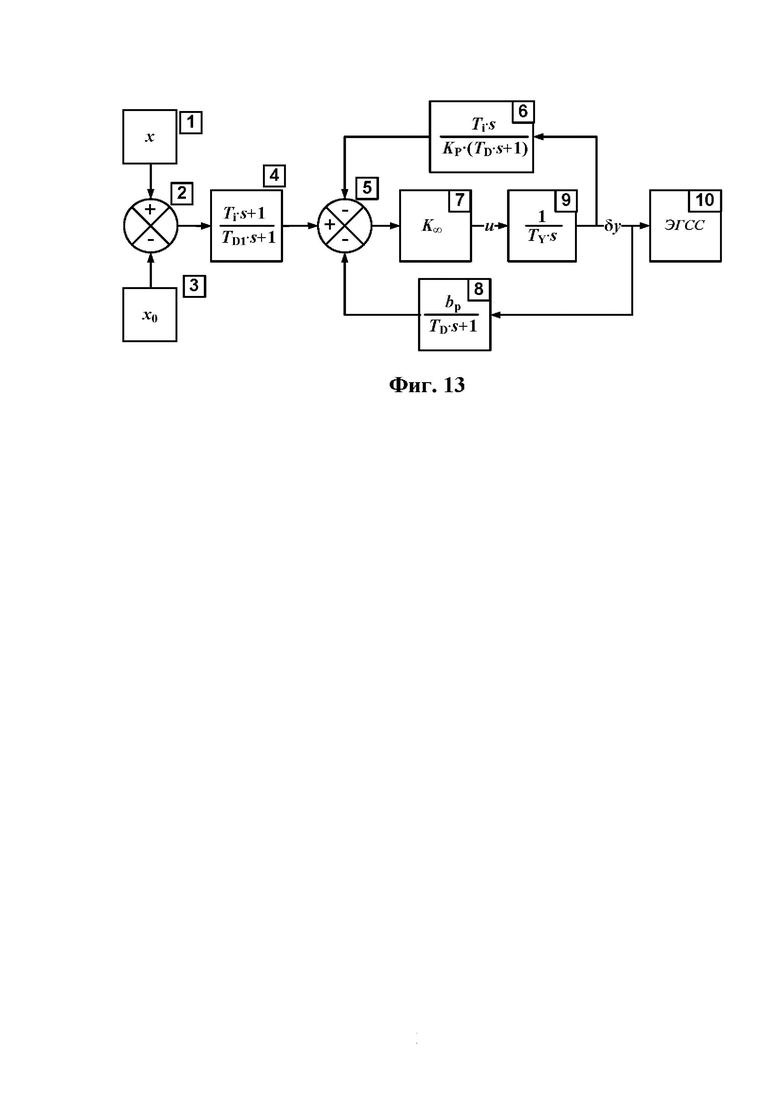
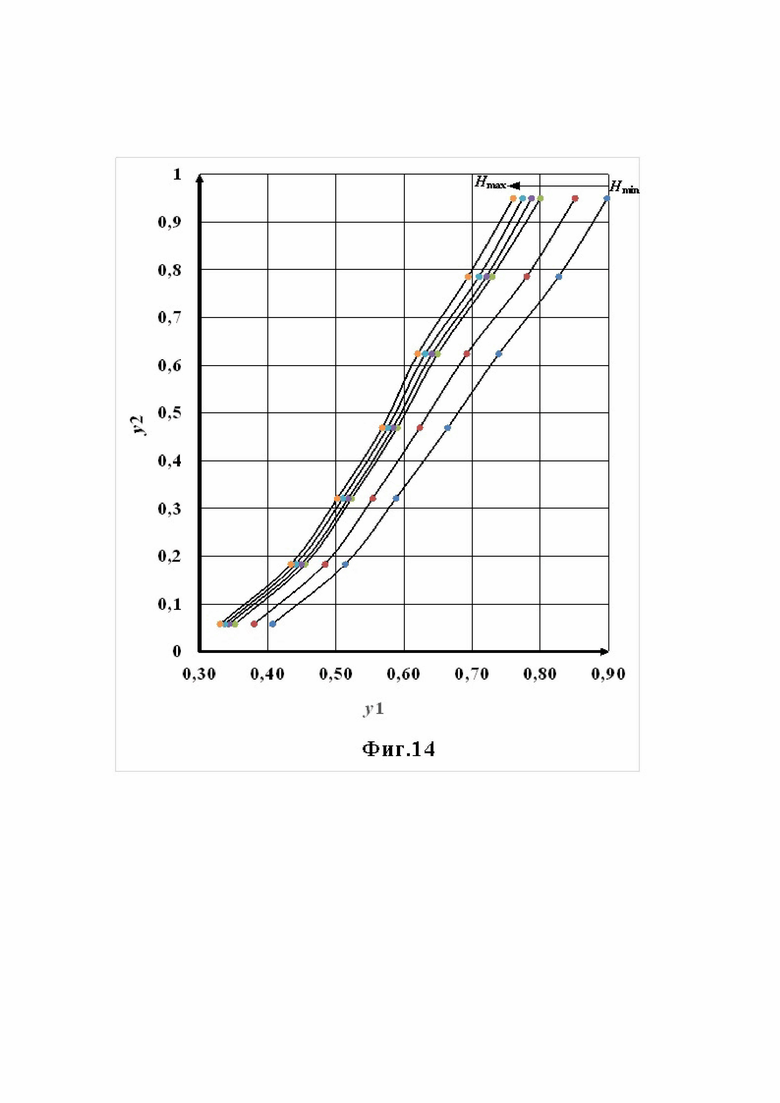
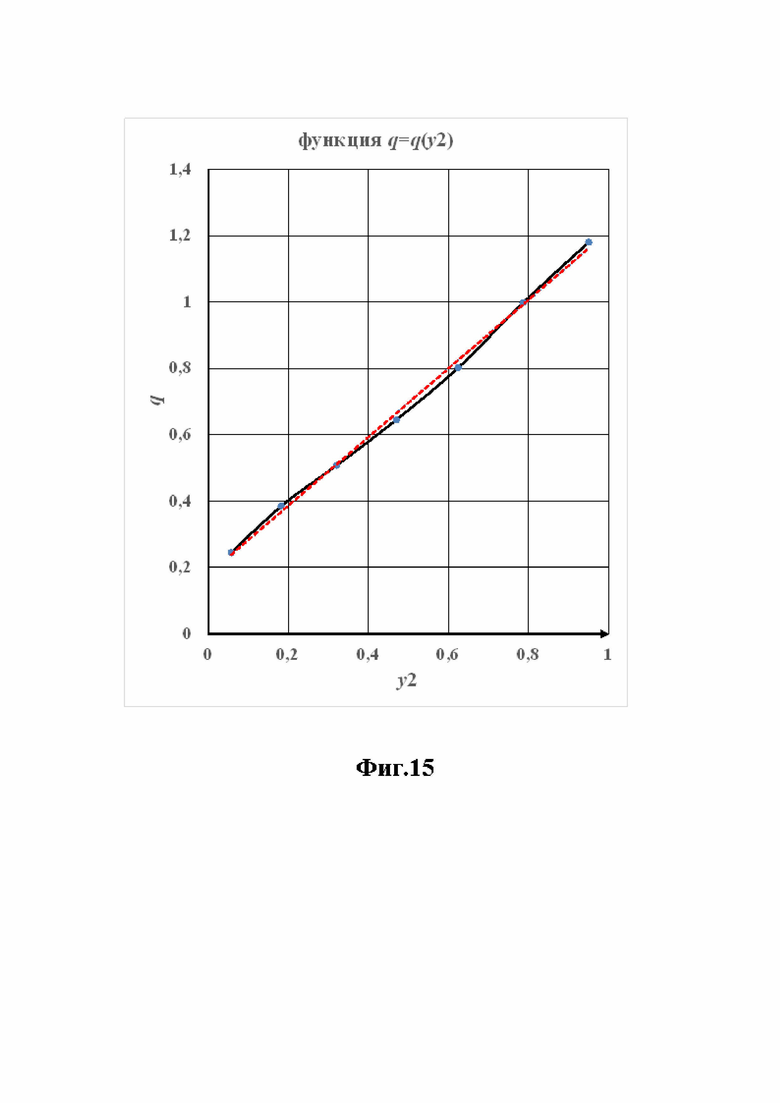
Способ регулирования частоты вращения реактивной гидравлической турбины, базирующийся на структуре «усилитель-ограничитель - интегратор», на вход которой подается сигнал, пропорциональный линейной комбинации взятых с определенными весами переменных состояния: отклонения частоты от уставки, динамического отклонения напора, вызванного перемещением регулирующего органа и упомянутым отклонением частоты вращения ротора, а также отклонением регулирующего органа от ожидаемого положения его в установившемся режиме. В линейной модели системы регулирования линейная комбинация переменных состояния представима линейной комбинацией сенсора: отклонением частоты вращения от уставки, её производной и динамическим отклонением напора, эмулируемого фантомной гибкой обратной связью с параметрами водовода. Предложен ПИД-регулятор сильного действия, использующий в качестве ПИ-блока цепочку «усилитель-ограничитель - интегратор», охваченную гибкой отрицательной обратной связью, на вход которой подается сигнал отклонения частоты с единичным усилением, просуммированный с сигналом производной частоты. Приведена схема настройки регулятора. Показано, что частотная характеристика предложенного регулятора в малом совпадает с частотной характеристикой традиционных структурных решений, при этом регулятор обладает высоким быстродействием при компенсации возмущений со стороны нагрузки, формируя квазиоптимальный закон движения регулирующего органа и переходя в режим скольжения при приближении к точке равновесия. Формирователь статизма не искажает частотную характеристику регулятора в зоне высоких частот. При правильной настройке контур регулирования частоты обладает абсолютной устойчивостью при неограниченном возрастании коэффициента усиления усилителя-ограничителя. 2 н.п. ф-лы, 20 ил.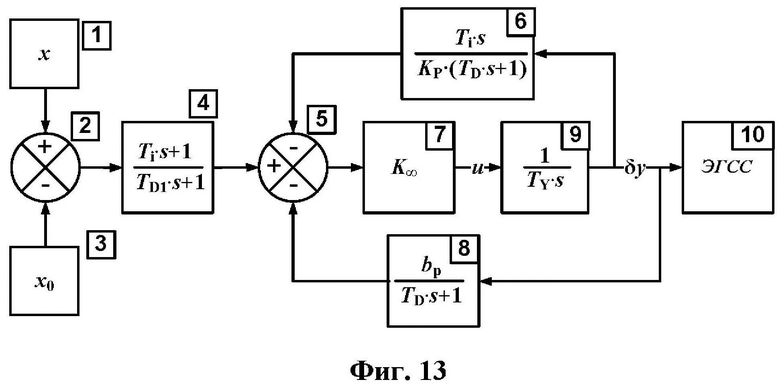
1. Способ регулирования частоты вращения ротора реактивной гидротурбины, использующий для управления электрогидравлическими приводами регулирующих органов выходной сигнал задающего их положение интегратора, на вход которого подается предварительно усиленный и затем ограниченный сигнал, пропорциональный значению линейной комбинации с постоянными или зависящими от режима работы агрегата коэффициентами трех сигналов отклонения частоты вращения от уставки, динамического отклонения напора от статического значения и отклонения текущего значения выходного сигнала интегратора от значения его в ожидаемом установившемся режиме, определяемого в линейной модели объекта регулирования суммой динамических составляющих движущего момента турбины, обусловленных отклонениями частоты вращения, ее производной и динамическим отклонением напора, уменьшенной на величину суммы отклонения момента сил сопротивления, вызванного отклонением частоты, и произведения постоянной времени разгона ротора на производную частоты вращения.
2. ПИД-регулятор сильного действия, структурная схема которого включает задатчик (3) частоты вращения и измеритель (1) частоты вращения, выходы которых подключены соответственно к суммирующему и вычитающему входам выявителя (2) отклонения частоты от уставки, выход которого через пропорционально-дифференцирующий блок (4) соединен с входом пропорционально-интегрирующего блока, являющимся одновременно неинвертирующим входом сумматора (5), на два других инвертирующих входа которого подключены выходы блока формирования сигнала гибкой обратной связи (6) и, через фильтр низкой частоты с постоянной времени гибкой обратной связи сигнала, блока формирования статизма (8), соединенные входами с являющимся выходом пропорционально-интегрирующего блока и источником сигнала задания положения регулирующих органов для их приводов (10) выходом интегратора, подключенного входом через усилитель-ограничитель (7) к выходу сумматора (5), при этом формирование закона регулирования осуществляется выбором параметров последовательно включенных пропорционально-дифференцирующего и пропорционально-интегрирующего блоков таким образом, чтобы частота начала формирования пропорционально-интегрирующим блоком пропорциональной составляющей располагалась между частотами начала и конца диапазона дифференцирования в пропорционально-дифференцирующем блоке, что обеспечивает формирование асимптот логарифмической частотной характеристики регулятора: интегрирующей в диапазоне частот меньших частоты начала дифференцирования в пропорционально-дифференцирующем блоке, пропорционального воздействия – от частоты начала дифференцирования в пропорционально-дифференцирующем блоке и до частоты начала формирования пропорционального воздействия в пропорционально-интегрирующем блоке и дифференцирующей – от частоты начала формирования пропорционального воздействия в пропорционально-интегрирующем блоке до частоты конца диапазона дифференцирования в пропорционально-дифференцирующем блоке.
| Приспособление для формования конического горла стеклянных изделий на машине Шиллера | 1936 |
|
SU51680A1 |
| СИСТЕМА РЕГУЛИРОВАНИЯ ДЛЯ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ТУРБИНЫ, А ТАКЖЕ СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ТУРБИНЫ ПРИ СБРОСЕ НАГРУЗКИ | 1996 |
|
RU2156865C2 |
| Способ регулирования турбины при сбросе нагрузки | 1983 |
|
SU1245723A1 |
Авторы
Даты
2022-10-05—Публикация
2021-04-29—Подача