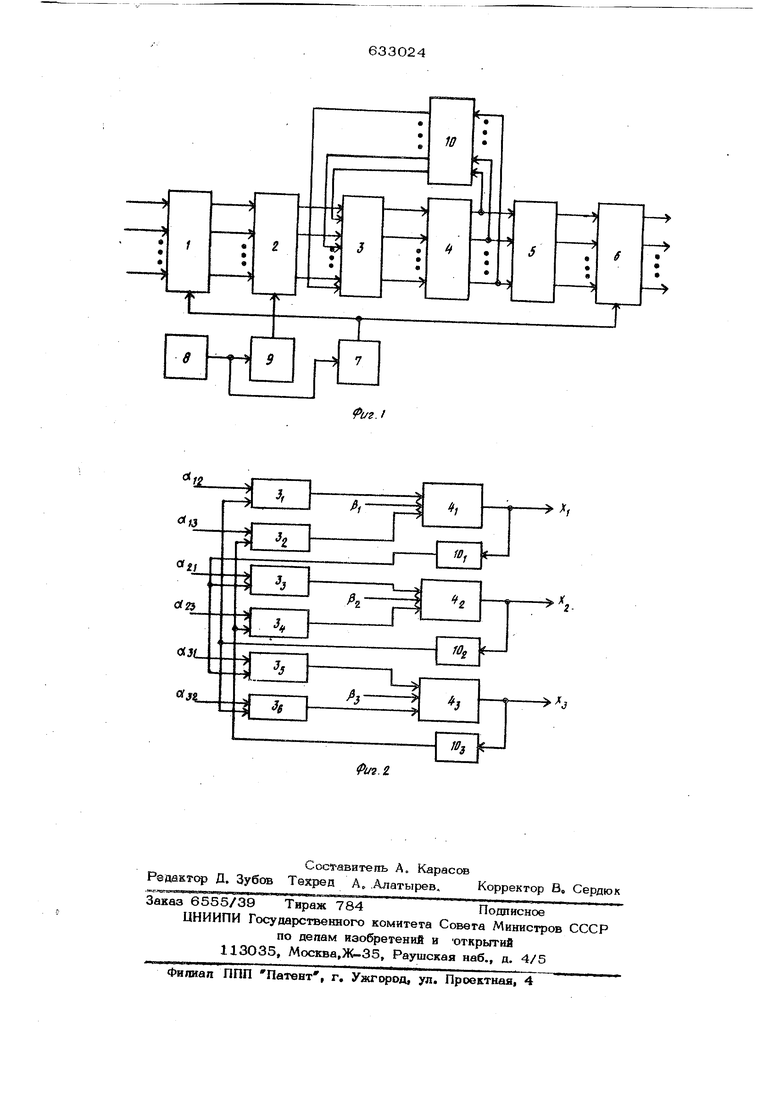
J6 pOHTHOctb 2, блок умножения 3, блок спо жения 4, блок интегрирования 5, второй бпок ключей 6, бпок управления 7, гене. ратор тактовых импульсов 8, генератор случайных чисел 9, блок задержки 10.Вы ходы первого блока ключей 1 связаны с входами блока преобразователей 2, выходы которого подключены к входам блока умножения 3. Выходы блока умножения 3 соединены с входами блока сложения 4, выходы которого подключены к входам блока.интегрирования 5 и блока задержки 10. Выходы блока задержки 1О соединены с входами блока умножения 3, а выходы блока интегрирования 5 - со вхо дами второго блока ключей 6. Управляющие входы первого и второго блоков ключей 1 и б подключены к выходу блока управления 7, вход которого соединен с выходом генератора тактовых импульсов 8 и со входом генератора слу чайных чисел 9, а выход генератора слу яайных чисел 9 подключен к управляюще му входу блока преобразователей ii, Работает устройство следукндим образом. Если задана система линейных алгебраических уравнений Sa.. X-t.- (,2...n) где X j -корни системы. Q.. - постоянные коэффициенты, то при с1 О она эквивалентна приведен ной системе (1 ,2... h) (1) ь S «- -приведенные свободные чле
приведенные коэффициенты.
X - корни системы линейных алгебраических уравнений, которая и реализуемся в схеме прототипа. При этом известные условия сходимости итерационного процесх са (1) должны быть дополнены условиями несовместности (потоков для каждого j , Физически процесс итераций (1) «в схеме прототипа обеспечивается за счет связи выходов блока ннтегрирования с входами блока умножения.
За счет этой обратной связи в данном устройстве так же как и в прототипе pea лизуется процесс последовательных приближений систем (1) в виде
хГ,. ,(2)
i lгде К - номер итерации.
T--(
(3)
где f - тактовая частота работы устройства.
По сигналу из блока управления 7 содержимое счетчиков блока интегрирования 5 при помоши второго блока ключей 6 передается на выход устройства.
Время решения Т, определяемое соотношением (3) значительно меньше времени Т ,. расходуемого на ту же операцию в схеме прототипа.
Действительно, если по исходному условию процесс последовательных приближений (2) в схеме прототипа сходится за итераций и требуемая точность вычисления приближенного значения X , на каждом щаге равна 6 , то общее время решения системы линейных апгебраичес4По сигналу из блока управления коэфициенты передаются на блок преобразователей число-вероятность 2, в котором осуществляется их преобразование в случайные двоичные последовательности с математическими ожиданиями, равными численным значениям соответст вующих коэффициентов. Все последовательности из блока преобразователей 2, а также задержанные последовательности с выхода блока сложения 4 непрерьтно поступают на входы блока умножения 3. Все (1 выходных последовательностей блока сложения 4 интегрируются при помсщи счетчиков блока интегрирования 5. Каждая новая итерация в устройстве обеспечивается за счет передачи вектора корней XI из блока сложения 4 на бпок задержки Ю (каждый вход в блоке 10 задерживаелх;я на 1 такт) и передачи этого вектора через 1 машинный такт (длительность такта задается блоком 8) на входы блока умножения. В результате на выходах блока слежения 4 в соответствии с (2) образуется новый вектору т.е. новое приближение корней X - . Таким образом, для получения каждого (по ) к) нового и точного значения л требуется лишь один машинный такт, а задача получения оценки X j с заданной точностью i ( 1 -требуемое число итераций) к накоплению символов 1 послесводится - v.()/ с довательностиX. ( S .. ,,-..-,,- , - m / ofl ) тактов. Здесь tp -параметр нормального распределения, Следовательгно, общее время решения системы линейных алгебраических уравнений в предлагаемом устройстве составит ких уравнений Т получим, воспользовавшись соотношением (3) ..(Щ V где п} -количество тактов, необходимое ппя получения результата с точность f fcp - параметр нормального распределения. .{4) Так как обычно m ), то уравнение (4) дает время решения большее в V раз чем уравнение (3), справедливое для пре лагаемого устройства. Обычно итерационный процесс завершается через нескотшко десятков итераций, т.е. Г . Это число и определяет выигрыш в быстродействии заявляемого устройства. Физически этот эффект можно объяснить тем, что если в схеме прототипа - v(K Каждое новое приближение X, должно быть выражено в форме многоразрядного кода (на что требуется TI машинных тактов), то в предлагаемом устройстве каждое новое приближение X образуется в форме вероятности появления бинарного символа и, следовательно, занимает лишь 1 такт машинного времени. Соединения выходов блока задержки Ю с выходами блока умножения 3 устанавливаются в соответствии с уравнением (2). На фиг. 2 показан пример расположе ния таких соединений применительно к решению систем линейных алгебраических уравнений третьего порядка. Анализ этой схемы показывает, что выражения для последовательных приближений значений корней X Х, Х в точности совпадают с видом уравнения (2). Например, для выхода X схемы получа- ем ,С.,,ХГ.СС,,ХГ. -16 Таким образом, для получения нового и точного значения корня (т.е. результата каждой последующей итерации) требуется только один машинный такт. Технико-экономический эффект заявляемого устройства заключается в резком (10-50 раз) сокращении времени для решения СЛАУ по методу итераций. Формула изобретения Вероятностное устройство для реше ния систем линейных алгебраических уравнений, содержащее последовательно соединенные первый блок ключей, блок преобразователей число-вероятность , блок умножения, блок сложения, блок интегрирования, второй блок ключей, управляющий вход которого соединен с управпяюшим входом первого блока к почей и с выходом блока управления,, вход которого соединен с выходом генератора тактовых импульсов и со входом генератора случайных чисел, выход которого подключен к управляющему входу блока преобразователей число-вероятность, отличаюш е е с я тем, что, с целью повьпиения быстродействия устройства, оно содержит блок задержки, входы которого соединены с выходами блока сложения, а выходы со входами блока умножения соответственно. Источники информации, принятые во внимание при экспертизе: 1. Якойлев В. В., Федоров Р. Ф. Стохастические вьпшслительные машины. Л., Машиностроение, 1974, с. 322-329. 2. Авторское свидетельство СССР 481О42, кл. Q 06 Р 15/36, 1974.


| название | год | авторы | номер документа |
|---|---|---|---|
| Цифро-вероятностное устройство для решения систем линейных алгебраических уравнений | 1980 |
|
SU993290A1 |
| Вероятностное устройство для реше-Ния СиСТЕМ лиНЕйНыХ АлгЕбРАичЕСКиХуРАВНЕНий | 1979 |
|
SU830400A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1977 |
|
SU629541A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1989 |
|
SU1688257A1 |
| Арифметическое устройство | 1979 |
|
SU773619A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1973 |
|
SU481042A1 |
| Система идентификации параметров линейных объектов | 1988 |
|
SU1534429A1 |
| Многоканальное устройство для реше-Ния иНТЕгРАльНыХ уРАВНЕНий | 1979 |
|
SU840921A1 |
| Устройство формирования оптимальных управляющих воздействий для обеспечения устойчивой работы сложных технических систем | 2017 |
|
RU2674281C1 |
| Устройство для решения систем ли-НЕйНыХ АлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU811275A1 |


Авторы
Даты
1978-11-15—Публикация
1975-12-25—Подача