В дифференцированных методах воздушной стереосъемки для вычисления превышений точек местности применяется формула, выведенная для нормального случая аэрофотосъемки, т.е. для случая, при котором составляющие стереопару аэроснимки во время фотографирования местности располагались в одной плоскости, параллельной базису фотографирования.
В полете, однако, непрерывно изменяются высота самолета, его крен и наклон его оси, а потому всегда имеют место отступления от нормального случая аэрофотосъемки. Поэтому возникают искажения стереомодели земной поверхности, вычисленной по формуле, выведенной для нормального случая аэрофотосъемки. Чтобы исключить эти искажения, необходимо ввести поправки в измеренные по аэроснимкам продольные параллаксы.
Обычно поправки к измеренным продольным параллаксам находятся как функции углов наклона аэроснимков, а углы наклона аэроснимков определяются по измеренным поперечным параллаксам. Для вычисления взаимных углов наклона аэроснимков по измеренным поперечным параллаксам, а затем для вычисления поправок в продольные параллаксы, применяются приближенные формулы. Однако и приближенная формула, определяющая зависимость между поправкой в продольный параллакс и углами наклона аэроснимка, содержит минимум три члена первого порядка.
Предметом данного изобретения является способ определения поправки для измеренной по аэрофотоснимку величины продольного параллакса, как функции величины поперечного параллакса. Согласно настоящему предложению, поправка продольного параллакса определяется непосредственно по измеренной величине поперечного параллакса, умноженной на отношение ортогональных координат точки, для которой производится определение поправки.
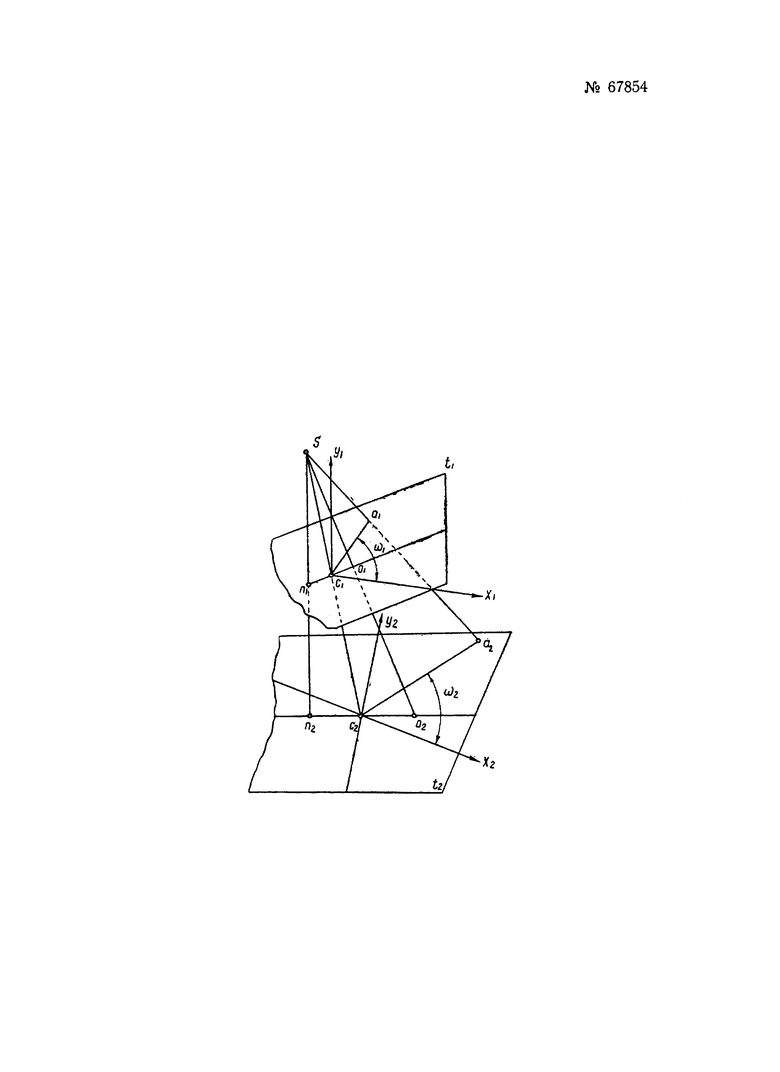
На чертеже показана плоскость аэроснимка с его главной точкой O1 и плоскость t2 с главной точкой n2, на которую должно быть спроектировано из центра проекции изображение, зафиксированное в плоскости.
Прямая Sc1c2 является биссектрисой угла nSO, а потому точки c1 и c2 являются точками нулевых искажений при проектировании изображения в плоскости t1 на плоскость t2. Таким образом, любой угол в плоскости t1 с вершиной в точке с1 будет строго равен своей проекции на плоскости t2. Выбираем взаимно-перпендикулярные оси координат в плоскости t1 с началом координат в точке c1, и обозначим через х1 и у1 координаты некоторой точки а1. Осями координат в плоскости t2 будем считать проекции соответствующих осей координат, выбранных в плоскости t1. Очевидно, что начало координат в плоскости t2 совпадает при этом с точкой с2 и оси координат в плоскости t2 будут тоже взаимно перпендикулярны. Обозначим через х2 и у2 координаты в плоскости t2 точки а2; последняя является проекцией точки а1.
Так как идентичные углы ω1 и ω2 равны между собой, то: 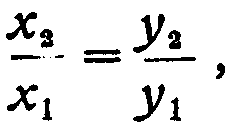
а потому: 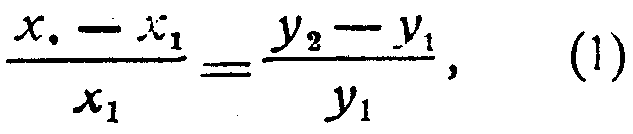
или 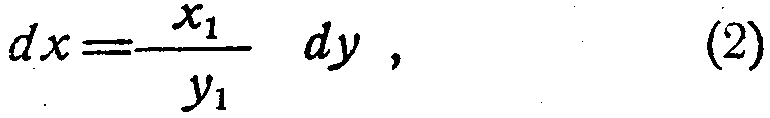
где: dx=x2-х1:dy=у2-у1.
При нормальном случае съемки плоскости левого и правого аэроснимков должны совпадать, а базис фотографирования должен быть параллелен плоскости этих аэроснимков. Здесь будет соблюдаться следующая формула
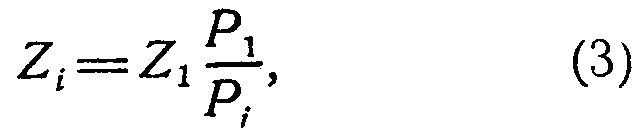
где: Z1 и Zi - аппликаты данной и определяемой точек;
P1 и Pi - продольные параллаксы данной и определяемой точек.
Ось аппликат перпендикулярна плоскости, в которой расположены аэроснимки, а ось абсцисс совпадает с базисом фотографирования.
Во всех диференцированных методах аэрофототопографической съемки, предусматривающих применение приборов типа стереокомпаратора, измеренные на аэроснимках продольные параллаксы приводятся поправками к тем значениям, которые имели бы место при нормальном случае съемки. После этого аппликаты точек вычисляют по формуле (3). Поправки к измеренным продольным параллаксам могут быть найдены, исходя из формулы (2), на основании нижеуказанных соображений.
Продольный параллакс Р некоторой точки определяется по формуле:
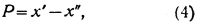
где: х′ - абсцисса изображения точки на левом аэроснимке;
х′′ - абсцисса изображения точки на правом аэроснимке.
Таким образом: 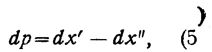
а согласно (2): 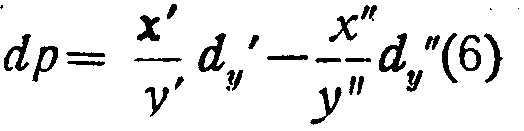
Заметим, однако, что:
dy′′=dy′-q.
где: q - поперечный паралласк данной точки;
у′ и у′′ - ординаты изображений этой точки на левом и правом аэроснимках.
Следовательно:
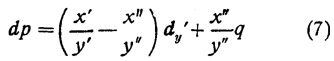
Примем теперь, что плоскость t2 совпадает с плоскостью левого аэроснимка стереопары; таким образом, для левого аэроснимка стереопары dx и dy равны нулю. Тогда, согласно (7), будем иметь:
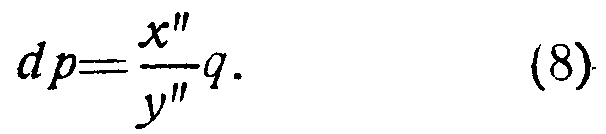
Последняя зависимость положена в основу предлагаемого способа фотограмметрического определения высот.
Новый способ несравненно проще ранее применявшихся. Помимо того, новая формула точнее ранее применявшихся, даже если в ранее применявшихся формулах при вычислениях будут сохраняться члены второго порядка малости.
Построение неискаженной стереомодели по установленной зависимости между поправками к продольным и поперечным параллаксам может осуществляться как аналитическим, так и механическим путем. При механическом решении задачи перемещение аэроснимка (в приборе типа стереокомпаратора), необходимое для устранения поперечного параллакса, нужно производить не перпендикулярно базису фотографирования, а по направлению из центра аэроснимка. Такое перемещение аэроснимка будет приводить к изменению продольного параллакса на величину dp, т.е. при указанном перемещении аэроснимка будет автоматически решаться установленная зависимость.
Преимущество предлагаемого способа по сравнению со всеми другими аналогичными способами состоит еще в том, что при пользовании им автоматически исключаются для одного из аэроснимков стереопары искажения из-за дисторсии объектива и из-за неточного выравнивания в плоскость аэропленки в аэрофотоаппарате.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОЛУЧЕНИЯ НЕПРЕРЫВНОГО СТЕРЕОИЗОБРАЖЕНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ | 2024 |
|
RU2832645C1 |
| Способ определения высоты дерева | 1989 |
|
SU1621822A1 |
| Универсальный стереоавтограф | 1960 |
|
SU134450A1 |
| Способ исправления топографической карты по аэрофотоснимкам стереопары | 1981 |
|
SU1000756A1 |
| Способ обновления карты,созданной по аэрофотоснимкам | 1984 |
|
SU1216648A1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ИЗМЕРЕНИЯ КООРДИНАТ ТОЧЕК ВНЕШНЕЙ СРЕДЫ ДЛЯ ПОСТРОЕНИЯ ЕЕ ТРЕХМЕРНОЙ МОДЕЛИ В СТЕРЕОТЕЛЕВИЗИОННОЙ СИСТЕМЕ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 1993 |
|
RU2065133C1 |
| Способ определения координат точек местности | 1977 |
|
SU705257A1 |
| Способ пространственной фототриангуляции | 1958 |
|
SU121246A1 |
| СПОСОБ УЧЕТА ГЕОМЕТРИЧЕСКИХ ИСКАЖЕНИЙ СТЕРЕОМОДЕЛИ | 1972 |
|
SU422953A1 |
| Способ связи между пересекающимися маршрутами аэрофотосъемки | 1960 |
|
SU140219A1 |
Способ определения поправки для измеренной по аэрофотоснимку величины продольного параллакса, как функции величины поперечного параллакса, отличающийся тем, что поправку продольного параллакса определяют непосредственно по измеренной величине поперечного параллакса, умноженной на отношение ортогональных координат точки, для которой производится определение поправки.
Авторы
Даты
1947-02-28—Публикация
1946-03-23—Подача