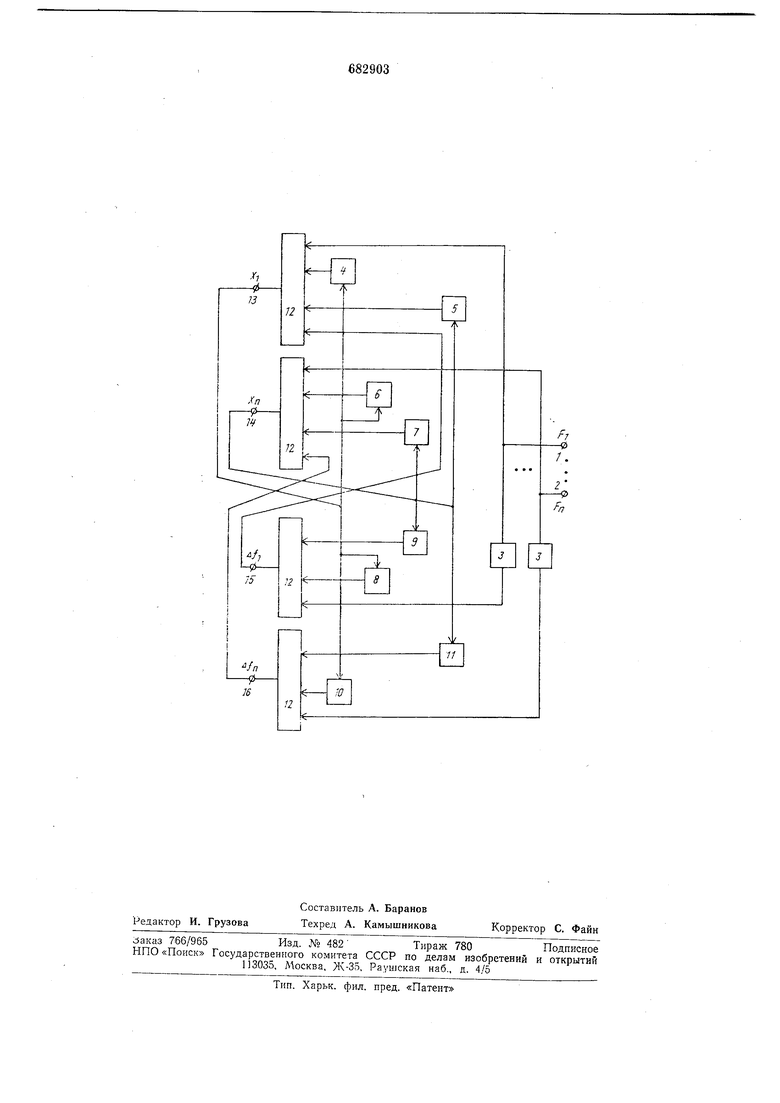
3 означающая, что вектор решений X, поданный на вход первой группы комбинационных масштабных звеньев, вызывает на (Выходах первой груплы сзмматоров вектор решений X, а он, в свою очередь, булучи поданным на вход первой группы комбинационных масштабных звеньев, - вектор решений , и т. д. Вектор решений Х вызывает вектор А , что и объясняет зацикливание решения, не позволяющее установиться схеме в устойчивое состояние. Значения компонент векторов X для рассматриваемого примера приведены в таблице. Покажем, -что вектор .решения J вызывает значения компонент вектора X (с точностью до пяти значащих разрядов). Имеем: Al 0,10000. 0,00100 + 0,10000-0,01Т11 + 0,00010 0,00111; 0,ТОООО - 0,001 ТО+ 0,ТОООО - 0,01Т11 0,ООТОО; з 0,ОТООО . 0,00110 + 0,10000 - 0,ООТОО + + 0,01000 0,010ТТ, что совпадаете приведенным во второй строке таблицы значением вектора Х. То же самое можно показать и для других значений кодов приведенной циклической цепочки несоответст.вия. Цель изобретения - расширение класса решаемых задач на замкнутых обратной связью ком-бИнационных цифровых вычислительных -структурах. Поставленная цель достигается иутем дополнительного введения второй группы сумматоров и второй группы комбинационных масштабных узлов, входы которых соединены соответственно с выходами сумМ:аторов первой группы, выходы второй группы комбинационных масштабных узлов подключены к лервой группе входов сумматоров второй группы, вторые входы которых соединены через инверторы с входами Зстройства, а выходы сумматоров второй группы соединены с третьими входами сумматоров первой группы. На чертеже представлена схема предлагаемого устройства. Устройство для решения систем алгебраических уравнений содержит входы /, 2, 682 инверторы 3, первую группу комбинационных масштабных узлов 4-7, вторую группу комбина ционных масштабных узлов 8- Il, первую и вторую группы многоразрядных сумматоров 12, .выходы 13-14. На входы /, 2 поступают значения правой части PI-F,,, заданной системы уравнений (1). Выходы 13, 14, соединенные с выходами п-ервой группы многоразрядных сумматоров, являются выходными, на которых вырабатываЕОтся значения искомого вектора неизвестных X.-X,,. На первой группе из комбинационных масштабных узлов 4-7 осуществляется умножение машинных переменных Xi-Х на постоянные коэффициенты заданной системы уравнений (1). На вто.рой группе из комбинационных масштабных узлов производится умножение машинных переменных ,, на постоянные коэффициенты, определяемые из соотношения: Л - 5, (. где А - матрица искомых коэффициентов, набираемых на второй группе комбинационных масштабных звеньев;В - матрица коэффициентов заданной системы уравнений (1); Е - единичная матрица. 1. На выходах 15, 16, соединенных с выходами второй группы многоразрядных суммато.ров и входами первой группы млогоразрядных сумматоров, выделяется значение /г младших разрядов сумм произведений искомых переменных на матрицу постоянных коэффициентов А и инвертированного значения правой части F. Работу схемы проиллюстрируем на примере, который, как было зже показано, не может быть решен на схеме прототипа. Покажем, что предложенная схема имеет одно из приведенных в таблице установившихся состояний, т. е. введение дополнительного оборудования и новых связей обрывает циклическую цеиочку несоответствия кодов. Предположим, что .на входы первой и второй групп комбинационных масштабных зсеньев постЗ пает вектор искомых неизвестных Х, т. е. А , 0,001ТО, X., ----- 0,ООТОО, J, 0,01Т11. Рассматриваемому вектору искомых неизвестных на выходах второй группы многоразрядных сумматоров 12 при /г 1 сОответствзет вспомогательный вектор с компонентами: А/1 0,ООООТ, А/2 0,00000, А/3 0,ООООТ. Тогда на выходах первой группы многоразрядных сумматоров с учетом умножения вектора, X на заданную матрицу постоянных коэффициентов и суммирования полученных произведений со значением правой части и зспомо атгльного вектора с
компонентами Afi, Д/2 и А/з, устанавливается следующий вектор неизвестных:
;«j 0,10000 0,00100+0,10000 0,01111+
+ 0,00010 + 0,00001 0,001ТО,
Л , 0,70000 . 0,001ТО + 0,ТОООО . 0.01Т11
о,оотоо,
Лз 0,ОТООО .0,001X0 + 0,10000 . 0,ООТОО + + 0,01000 + 0,00001 0,01Т11,
что соответствует вектору неизвестных X, поступающему .на входы первой и второй групн ком|бинационных масщтабных узлов. Отсюда Следует, что при замыкании обратной связи с выходов первой группы Л1НОГОразрядных сумматоров на входы первой и второй групп комбинационных масштабных узлов в схеме не возникает генерация, вызванная несоответствием кодов, и искомое рещение с некоторой степенью точности находится как установивщееся состояние всей системы. Аналогично можно рассмотреть и другие устойчивые состояния приведенной схемы устройства.
Использование дополнительных рещающих элементов и новых связей между ними выгодно отличает предлагаемое устройство для рещения систем алгебраических уравнений от прототипа, так как позволяет находить рещение для более щирокого класса задач путем устранения зацикливания в схеме, вызывающего генерацию, что увеличивает сферу применения подобного рода устройств.
Формула изобретения
Устройство для рещения систем алгебраических уравнений, содержащее первую группу сумматоров, выходы которых являются входами устройства и соединены с входами первой группы комбинационных масщтабных узлов, выходы которых соединены соответственно с пер.вой группой входов сумматоров первой группы, а вторые входы сумматоров первой группы являются входами устройства, отличающееся тем, что, с целью расщирения класса рещаемых задач, оно содержит вторую группу сумматоров и вторую группу комбинационных масштабных узлов, входы которых соединены соответственно с выходами сумматоров первой группы, а выходы второй группы комбинационных масщтабных узлов подключены соответственно к первой группе входов сумматоров второй группы, вторые входы которых соединены через инверторы с входами устройства, выходы сумматоров второй группы соединены соответственно с третьнми входами сумматоров первой группы.
Источники информации, принятые во внимание при экспертизе:
1. Авторское свидетельство СССР № 413497, кл. G 06 F 7/34, 1974.
2.Авторское свидетельство СССР До 402016, кл. Q 06 F 7/34, 1973.
3.Пухов Г. Е. и др. Принципы построения разрядных аналогов из комбинационных операционных блоков. - В кн. «Математическое моделирование и теория электрических цепей, вып. II. К-, «Наукова думка, 1973, с. 3-8, рис. 5 (прототип).


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для решения систем алгебраических уравнений | 1977 |
|
SU714405A1 |
| Устройство для решения систем алгебраи-чЕСКиХ уРАВНЕНий | 1978 |
|
SU807317A1 |
| Устройство для решения системАлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU798861A1 |
| Устройство для решения систем алгебраических уравнений | 1981 |
|
SU970381A1 |
| Устройство для решения систем линейных алгебраических уравлений | 1972 |
|
SU564638A1 |
| Устройство для решения уравнения теплопроводности | 1974 |
|
SU494751A1 |
| Устройство для вычисления функций синуса и косинуса | 1991 |
|
SU1827673A1 |
| Устройство для решения разностных уравнений задач теории поля | 1981 |
|
SU1024931A1 |
| Устройство для решения систем алгебраических уравнений | 1977 |
|
SU682902A1 |
| Модель узла сеточной области | 1974 |
|
SU510725A1 |


Авторы
Даты
1979-08-30—Публикация
1977-07-13—Подача