Изобретение относится к прецизионному станкостроению и предназначено доля определения малых погрешностей изготовления и монтажа узлов станка алмазного микроточения, влияющих на точность его работы.
Целью изобретения является повышение точности аттестации станка.
Известен способ наладки металлорежущего станка для обработки сферических поверхностей [1], согласно которому ось инструментального шпинделя (суппорта) устанавливают под углом 0о < ϕ < 90о к оси рабочего шпинделя, режущую кромку инструмента располагают от оси инструментального шпинделя на расстоянии радиуса инструмента Rи, определяемого в зависимости от радиуса кривизны Rк обрабатываемой поверхности.
Для повышения точности наладки предварительно выполняют проточку канавки инструментом заданного радиуса на плоской поверхности пробной детали, устанавливая ось инструментального шпинделя соосно с осью рабочего шпинделя, определяют линейные координаты А1, А2, А3, А4диаметрально расположенных точек на наружной и внутренней кромках канавки и среднее значение радиуса инструмента Rср. по зависимости, учитывающей упомянутые координаты. При заданном значении радиуса кривизны Rк обрабатываемой поверхности устанавливают угол наклона ϕ оси инструментального шпинделя к оси рабочего шпинделя.
Недостатком способа является то, что он учитывает при наладке станка только один фактор - радиус на вершине инструмента и не учитывает факторов, определяющих погрешности формы и размера траектории движения инструмента.
Известен способ проверки кинематической точности вертикальных станков с контурным числовым программным управлением [2].
Для обеспечения полного контроля точности всех параметров исполняемой траектории движения на столе устанавливают кольцевую оправку. Ее центрируют по внутренней поверхности относительно шпинделя посредством установленного на нем индикатора. Индикатор вводят посредством программированного движения шпинделя при его вращении во взаимодействие с наружной поверхностью оправки, предварительно сместив его по радиусу, равному сумме радиусов внутренней и наружной поверхностей оправки.
Известен также способ диагностики состояния металлорежущего станка [3], который осуществляют путем анализа частотных характеристик. С целью упрощения процесса диагностирования, осуществляют спектральный анализ профилограммы поверхности обработанной на станке детали, определяют частоты детерминированных составляющих вибрации, и при сопоставлении с расчетными частотами судят о возможных неисправностях станка.
Способ дает возможность выявить дефекты станка, проявляющиеся на вибрационных характеристиках станка и на шероховатости поверхности, но не позволяет зарегистрировать погрешности кинематики станка, влияющие на точность формы изделия.
Наиболее близким к изобретению является способ [4], заключающийся в измерении одновысотности и параллельности осей шпинделя и суппорта, регистрации и анализе результатов измерения с последующим устранением рассогласований. Для повышения точности формообразования измеряют величины перемещения оси суппорта от контрольной поверхности в середине и на максимальных удалениях контролируемого участка, для измерения используют среднее значение сигналов датчика, а ошибки рассогласования по углам определяют из математических соотношений.
При наладке на обработку изделия сферической формы устанавливают угол α, соответствующий заданному радиусу кривизны Rк, проводят контрольную проточку образца.
Недостатком способа является то, что он предусматривает измерение и устранение разновысотности и непараллельности осей шпинделя и суппорта, что позволяет ликвидировать отклонения формы обработанной поверхности от сферичности, но не позволяет определить статические погрешности кинематических параметров станка, которые приводят к отклонению от заданного значения радиуса кривизны сферической поверхности.
Целью изобретения является повышение точности аттестации станка.
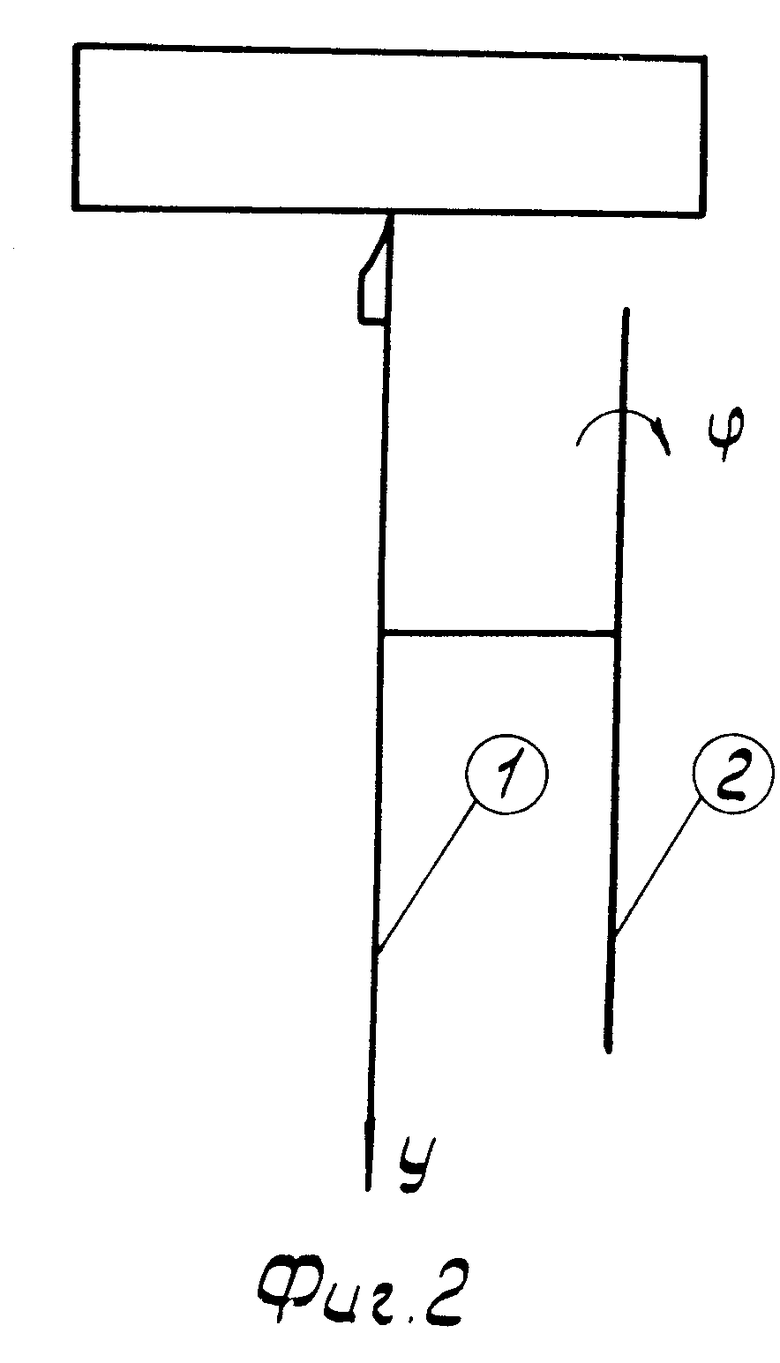
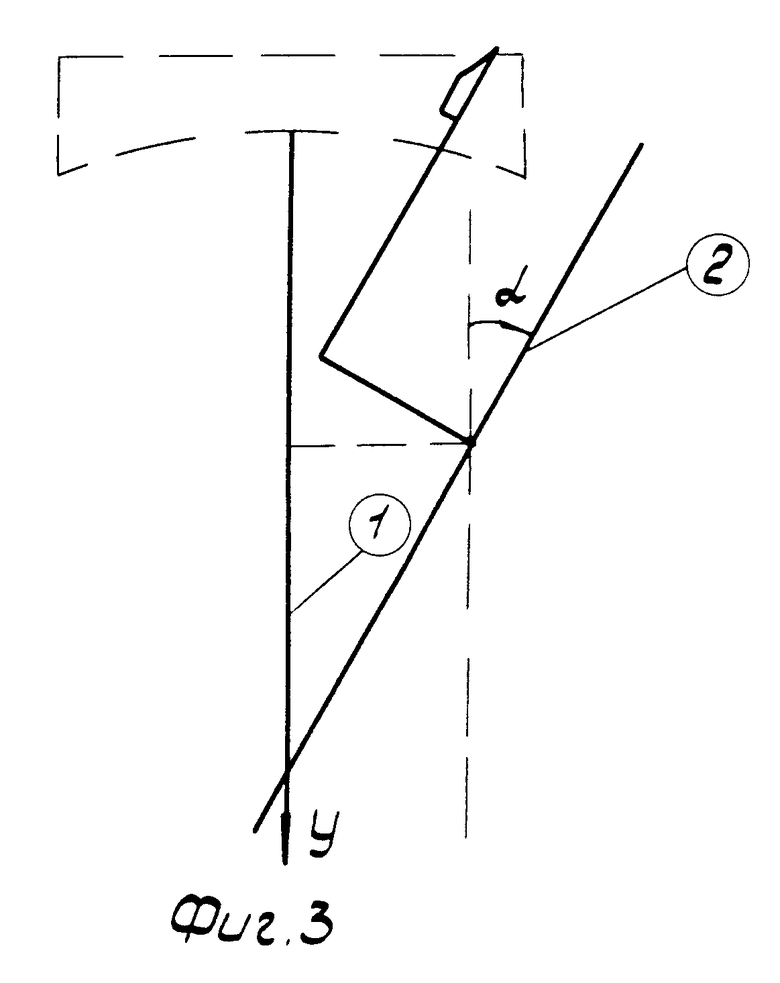
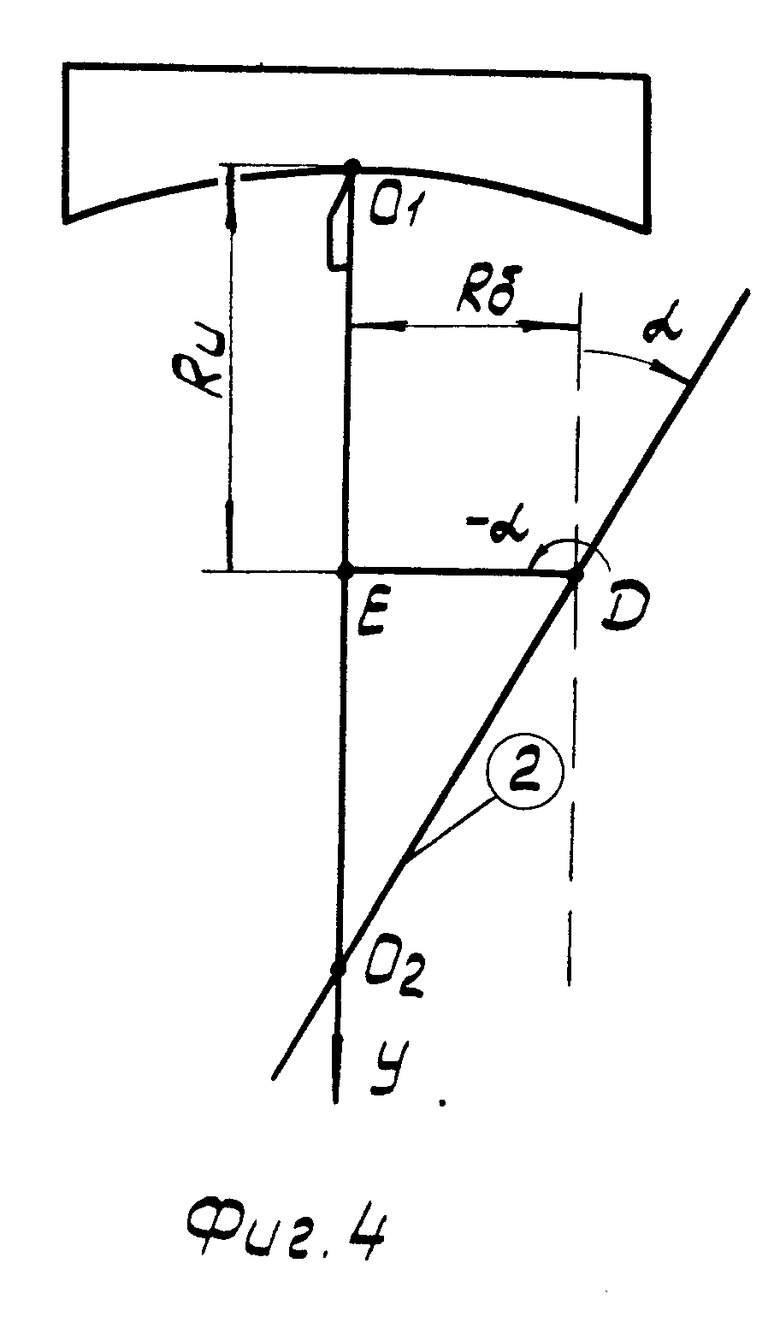
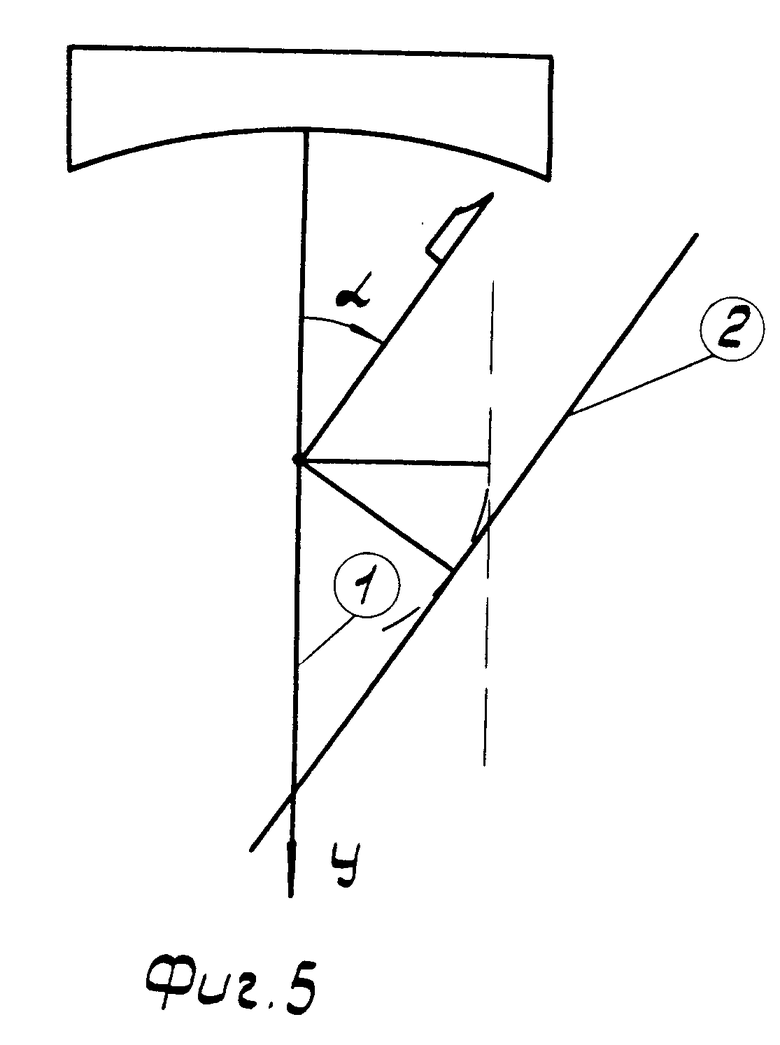
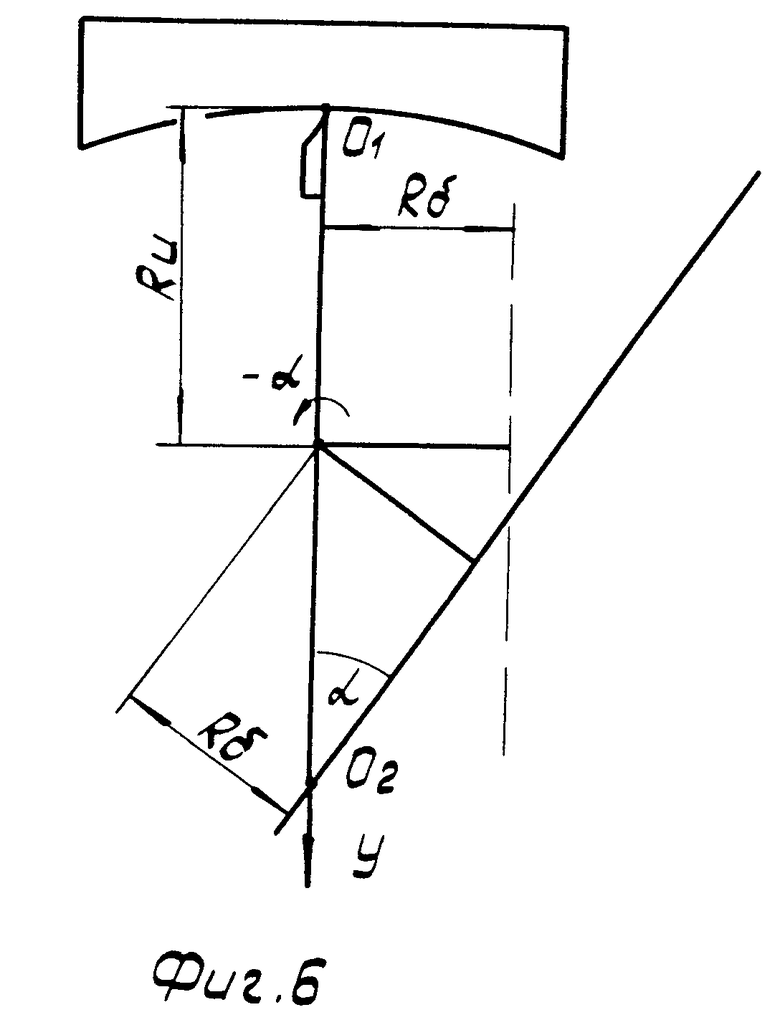
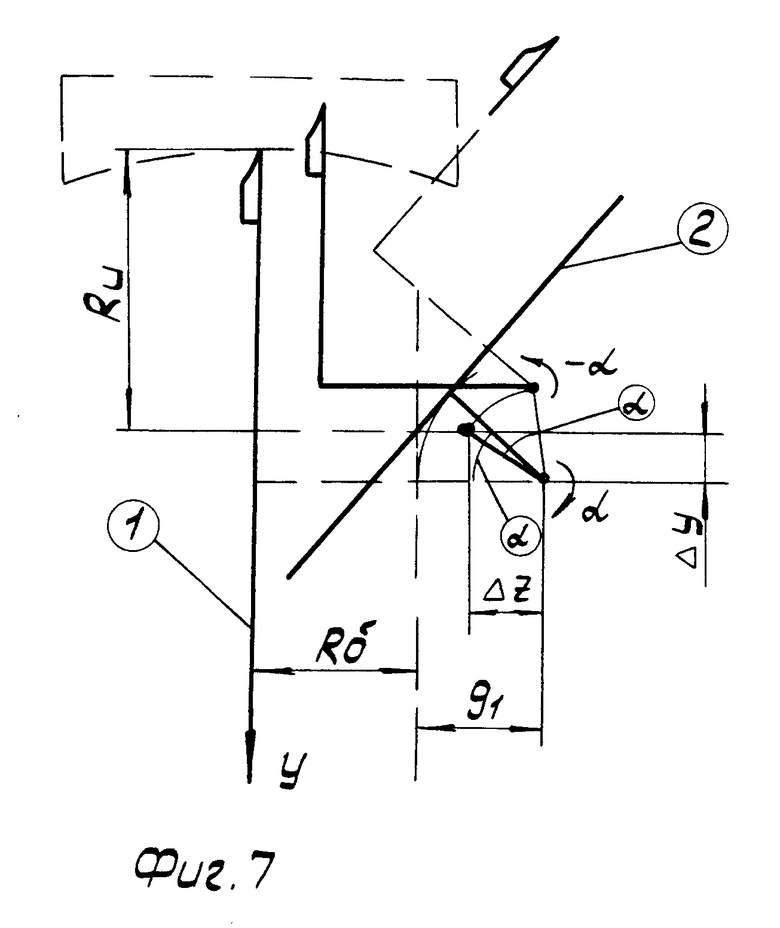
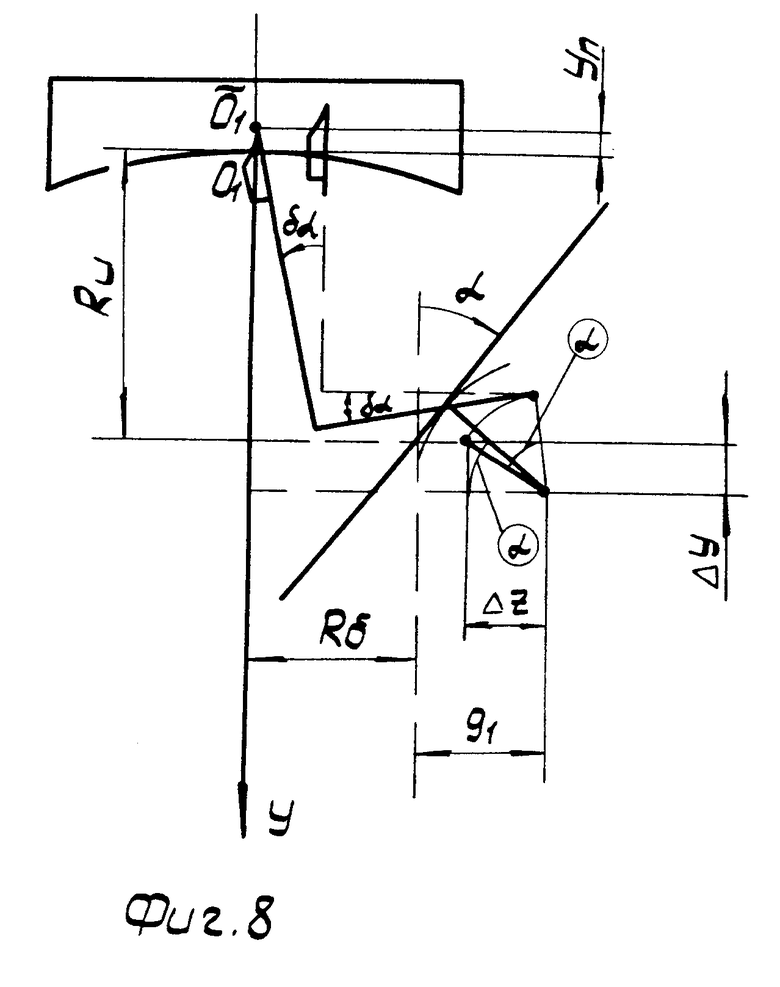
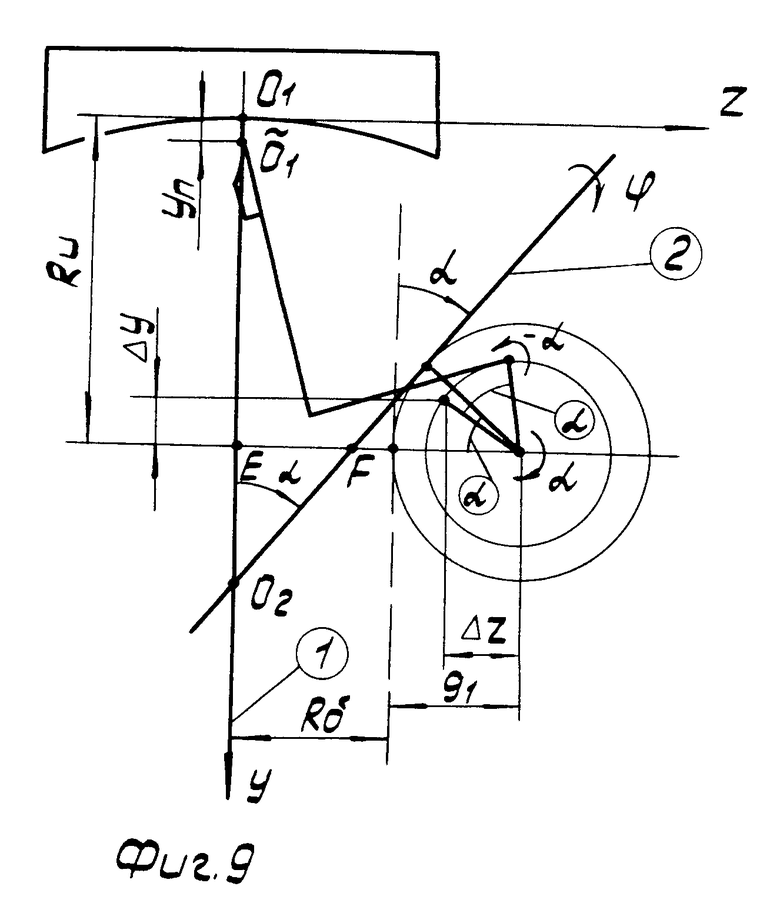
На фиг. 1 изображена схема расположения осей шпинделя и суппорта при точении сферы; на фиг. 2 - схема расположения осей шпинделя и суппорта при точении плоскости; на фиг. 3 - положение инструмента после поворота суппортной группы на угол α в случае тангенсного станка; на фиг. 4 - положение инструмента после поворота суппортной группы на угол α и резцовой каретки на угол - α; для тангенсного станка в идеальном случае; на фиг. 5 - положение инструмента после поворота суппортной группы на угол α в случае синусного станка; на фиг. 6 - положение инструмента после поворота суппортной группы на угол α и резцовой каретки на угол - α для синусного станка в идеальном случае; на фиг. 7 - положение инструмента после поворота суппортной группы на угол α и резцовой каретки на угол - α для тангенсного станка при наличии погрешностей взаимного положения осей суппортной группы и каретки; на фиг. 8 - положение инструмента после поворота суппортной группы на угол α и резцовой каретки на угол - (α + δα) для тангенсного станка при наличии погрешностей взаимного положения осей суппортной группы и каретки; на фиг. 9 - окончательное взаимное расположение оси шпинделя, оси суппорта и инструмента для установления взаимосвязи между радиусом кривизны обрабатываемой сферы и кинематическими параметрами станка.
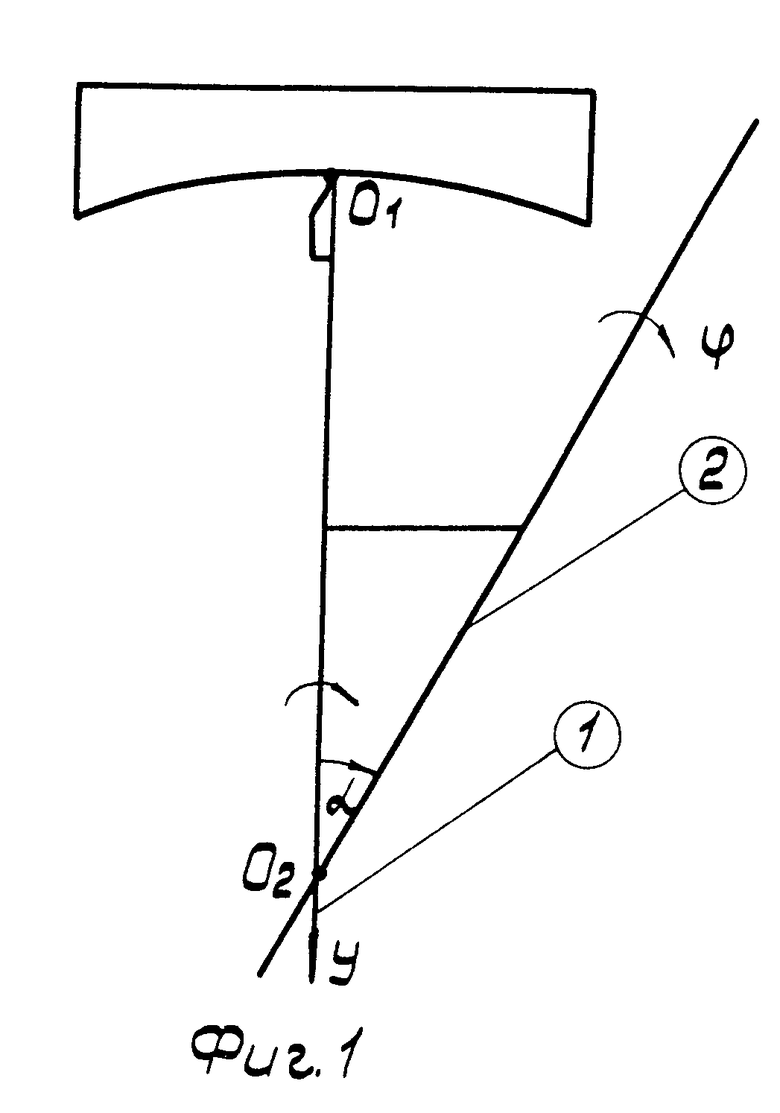
Для пояснения полученных математических зависимостей рассмотрим схему формообразования поверхности для станка алмазного микроточения. Известно, что при вращении заготовки вокруг оси шпинделя y и при вращении инструмента вокруг оси суппорта 2, лежащей в той же плоскости, что и ось y, и образующей с последней угол α (фиг. 1), формируется сферическая поверхность с радиусом кривизны, равным
Rк = О1О2, (1) где О1О2 - расстояние от точки пересечения осей шпинделя и суппорта О2до кончика резца в момент его прохождения через ось вращения заготовки О1.
Для пояснения вывода выражения для О1О2 рассмотрим последовательность операций, выполняемых при подготовке станка для точения сферической поверхности. В исходном положении ось суппорта 2 параллельна оси шпинделя 1 (фиг. 2), при этом α = 0. При повороте суппорта на угол α вокруг оси суппортной группы вершина инструмента уходит из точки пересечения оси вращения шпинделя с поверхностью заготовки (фиг. 3).
Для возвращения вершины инструмента в исходную точку выполняют поворот резцовой головки на угол - α вокруг оси каретки, совпадающей в идеальном случае с осью суппортной группы (фиг. 4). Как видно из фиг. 4 в идеальном случае расстояние О1О2 выражается через размер базы Rδ , размер инструмента Rи и угол α следующим образом:
O1O2=O1E+EO2=O1E + 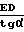 = Eи+Rδ/tgα (2)
= Eи+Rδ/tgα (2)
В случае, если ось вращения суппортной группы и каретки имеет общую точку не с осью суппорта 2, а с осью шпинделя 1, то радиус кривизны обрабатываемой сферической поверхности определяется выражением:
Rк = О1О2 = Rи + Rδ /sin α (3)
Соответственно формулам (2) и (3) станки, которым соответствуют фиг. 3 и 4, называют тангенсными, а станки, которым соответствуют фиг. 5 и 6 - синусными.
В реальном станке однако ось суппортной группы может не пересекаться с осью суппорта (для синусного станка - с осью шпинделя), а ось резцовой каретки может не совпадать с осью поворота суппортной группы. При этом если в исходном положении ( α= 0) ось каретки была смещена относительно оси поворота суппортной группы на величину Δ y по оси y и на величину Z по оси Z, то после поворота суппортной группы на угол α и поворота резца вокруг оси каретки на угол - α кончик резца окажется смещенным относительно оси вращения шпинделя (фиг. 7), и, чтобы совместить их, необходимо дополнительно довернуть резцовую головку вокруг оси каретки на некоторый угол δα. При этом кончик резца пересечет ось вращения шпинделя не в исходной точке О1, выбранной за начало координат, а в некоторой точке 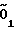 , имеющей относительно точки О1координату yn. Можно показать, рассматривая последовательно изменение координат кончика резца в результате поворотов на углы α, - α и - δα , что
, имеющей относительно точки О1координату yn. Можно показать, рассматривая последовательно изменение координат кончика резца в результате поворотов на углы α, - α и - δα , что
yn=Rи+Δy˙(1-cosα)-ΔZ˙sinα-{R42-2(Rδ+g1)[Δysinα+
+ ΔZ˙(1-cosα)]+(ΔZ2-Δy2)sin2α+2Δy˙ΔZ˙sinα˙cosα}1/2(4)
Таким образом, при наличии погрешностей взаимного расположения осей суппортной группы, суппорта и каретки после установочных движений расстояние между кончиком резца 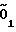 и точкой пересечения осей шпинделя и суппорта О2, задающее значение радиуса кривизны обрабатываемой сферы Rк, отличается от исходного расстояния О1О2 и, как видно из фиг. 9 равно
и точкой пересечения осей шпинделя и суппорта О2, задающее значение радиуса кривизны обрабатываемой сферы Rк, отличается от исходного расстояния О1О2 и, как видно из фиг. 9 равно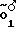 O2=
O2=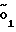 E+EO2=Rи+Δy-yn+FE·ctgα=
E+EO2=Rи+Δy-yn+FE·ctgα=
=Rи+Δy-yn+ 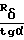 - g
- g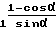 (5) В дальнейшем будем учитывать, что параметры g1, Δy, Δ Z, характеризующие погрешности взаимного расположения осей, малы по сравнению с Rδ и Rи. Разлагая (4) в ряд по g1, Δy, Δ Z, удерживая члены не выше первого порядка малости и подставляя результат в (5), находим окончательно следующее выражение для радиуса обрабатываемой сферы для тангенсного станка
(5) В дальнейшем будем учитывать, что параметры g1, Δy, Δ Z, характеризующие погрешности взаимного расположения осей, малы по сравнению с Rδ и Rи. Разлагая (4) в ряд по g1, Δy, Δ Z, удерживая члены не выше первого порядка малости и подставляя результат в (5), находим окончательно следующее выражение для радиуса обрабатываемой сферы для тангенсного станка
Rк=Rи+ 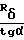 - g
- g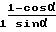 + Δy
+ Δy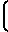 cosα -
cosα - 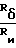 sin
sin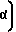 +
+
+ΔZ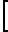 sinα -
sinα - 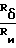 (1-cosα)
(1-cosα)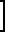 (6)
(6)
(6)
где Rδ - расстояние между осями суппорта и шпинделя при α = 0;
Rи - расстояние от оси каретки до плоскости, проходящей перпендикулярно оси шпинделя через кончик резца при α = 0;
g1 - разность расстояний от оси суппортной группы до оси шпинделя и от оси суппорта до оси шпинделя;
Δy - разность y-координат проекций осей суппортной группы и каретки на плоскость yZ;
ΔZ - разность Z-координат проекций осей суппортной группы и каретки на плоскость yZ.
Аналогичным образом для синусного станка может быть получено вместо (6) выражение:
Rк= Rи+ 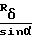 - g
- g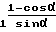 +Δycosα+ΔZ·sinα (7) где определение величин Rи, Rδ, Δy, ΔZ остается прежним, а величина g1 определяется теперь как Z-координата, проекции оси вращения суппортной группы на плоскость yZ, если ось y совпадает с осью вращения шпинделя.
+Δycosα+ΔZ·sinα (7) где определение величин Rи, Rδ, Δy, ΔZ остается прежним, а величина g1 определяется теперь как Z-координата, проекции оси вращения суппортной группы на плоскость yZ, если ось y совпадает с осью вращения шпинделя.
При изготовлении станка рассматриваемого типа в точном соответствии с проектом величины Rδ и Rи равнялись бы назначенным конструктором значениям Rδ(o) и Rи(о), а g1, Δy, ΔZ равнялись бы нулю. При этом радиус кривизны обрабатываемой сферы, в соответствии с формулами (2) и (3), имел бы значения:
Rк(о) = Rи(о) + R
Rк(о) = Rи(о) + Rδ(o)/sin α (9)
Однако вследствие погрешностей изготовления величины Rδ, Rи g1, Δy, ΔZ, в реальном станке отличаются от номинальных значений, в результате чего при том же значении α будет обрабатываться сфера с радиусом кривизны Rк, отличающимся от Rк(о) на величину Δ Rк = Rк - Rк(о), которая определяется для тангенсного станка:
ΔRк=ΔRи+ 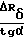 - g
- g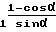 + Δy
+ Δy cosα -
cosα - 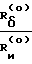 sin
sin +
+
+ ΔZ sinα -
sinα - 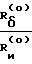 (1-cosα)
(1-cosα)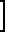 (10) для синусного станка
(10) для синусного станка
ΔRк=ΔRи + 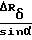 - g
- g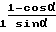 + Δycosα+ΔZ·sinα (11)
+ Δycosα+ΔZ·sinα (11)
Измерив Rк или ΔRк при пяти различных значениях α, и, подставляя соответственные пары значений ΔRк и α в формулу (10) или (11), получаем систему пяти линейных уравнений, решение которой дает значения ΔRδ ; ΔRи; g1; Δ y и ΔZ для конкретного станка.
Способ осуществляется следующим образом.
После изготовления станка перед сдачей его в эксплуатацию выполняют аттестацию станка по кинематическим параметрам, определяющим точность размера и формы изделия, в следующей последовательности.
На станок на планшайбу шпинделя устанавливают заготовку и поворачивают суппортную группу таким образом, чтобы ось суппорта 2 образовывала с вертикальной плоскостью xy, проходящей через ось шпинделя, произвольный угол α в диапазоне 0 - 90о.
Добиваются, чтобы ось шпинделя 1 и ось суппорта 2 принадлежали одной и той же горизонтальной плоскости xy. Определяют и фиксируют точное значение угла α, после чего выполняют точение заготовки.
Выполнив точение, известными способами определяют отклонения формы полученной поверхности от ближайшей сферической поверхности и определяют радиус ближайшей сферической поверхности Rк, после чего находят отклонение Rк от величины Rк(о), определяемой формулами (8) или (9), и фиксируют пару соответственных значений ΔRк и α. Затем меняют значение α, определяют соответствующее значение ΔRк и фиксируют пару значений Δ Rк и α.
Эту процедуру повторяют не менее пяти раз, поскольку при известных Δ Rк и α формула (10) или (11) содержит пять неизвестных величин Δ Rи, ΔRδ , g1, Δ y и ΔZ. Подставляя пять пар значений Rк и α в формулу (10) или (11) и решая получающуюся систему уравнений, рассчитывают величины ΔRδ, Δ Rи, g1, Δy, ΔZ, а такжеRδ = Rδ(o)+ ΔRδ и Rи = Rи(о) + Δ Rи.
Полученные значения Rδ , Rи, g1, Δ y и ΔZ заносят в паспорт станка для использования при настройке станка на требуемый радиус кривизны обрабатываемой поверхности и точность формы поверхности, при этом повышаются производительность и точность настройки.
П р и м е р. На станке алмазного микроточения МО-200 проточены изделия сферической формы. Проточку проводили в пять этапов, меняя при этом угол α. Были взяты пять значений угла α: 5, 25, 45, 65 и 85о. Измерения радиуса кривизны полученных изделий, выполненные с точностью 1 мкм, дали соответственно пяти значениям углов следующие величины: Rк = 1429,545 мм; 419,050 мм; 294,035 мм; 235,195 мм; 192,915 мм. Конструкция станка предусматривает значения размера базы и размера инструмента, равные: Rδ(o) = 110 мм; Rи(о) = 190 мм.
Определяя для каждого из пяти α по формуле (8) величины Rк(о), а затем Δ Rк = Rк - Rк(о) и, подготовляя для каждого из пяти α соответствующее значение Δ Rк, а также Rδ(o)и Rи(о), в формулу (10) и решая получающуюся систему пяти уравнений с пятью неизвестными Δ Rи, ΔRδ , g1, Δ y, ΔZ, находим
Rи = Rи(о) + ΔRи = 184,99 мм≈185,0 мм;
Rδ= Rδ(o) + ΔRδ = 108,80 мм ≈108,8 мм;
g1 = 1,93 мм ≈1,9 мм; Δy = 0,98 мм≈1,0 мм;
ΔZ = 1,40 мм ≈1,4 мм
Таким образом, предлагаемое изобретение обеспечивает возможность точной настройки станка на заданный радиус обработки сферической поверхности.
Экономическая эффективность способа может быть оценена на основании следующей информации. Без использования способа процедура аттестации станка алмазного микроточения по кинематическим параметрам, определяющим точность размера и формы поверхности изделия, требует от бригады инженеров, токарей и операторов до 30 рабочих дней с результатом, в значительной мере зависящим от интуиции и квалификации исполнителей. Способ позволяет выполнить аттестацию станка в течение двух дней с полностью детерминированным результатом.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ наладки станка для обработки поверхностей вращения | 1989 |
|
SU1839124A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ РЕЗАНИЕМ ЗЕРКАЛЬНЫХ ПОВЕРХНОСТЕЙ | 1990 |
|
RU2014964C1 |
| СПОСОБ НАЛАДКИ СТАНКА ДЛЯ ОБРАБОТКИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ | 1988 |
|
RU2028871C1 |
| СПОСОБ ФОРМООБРАЗОВАНИЯ АРОЧНЫХ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС И СТАНОК ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2070487C1 |
| Устройство для обработки криволинейных поверхностей | 1981 |
|
SU984693A1 |
| Устройство для обработки криволинейных поверхностей | 1982 |
|
SU1131602A1 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ ОБРАБОТКОЙ ВАЛОПРОВОДОВ ДВИЖИТЕЛЬНО-РУЛЕВЫХ КОЛОНОК | 2013 |
|
RU2510665C1 |
| Станок для обработки неметаллических материалов | 1987 |
|
SU1574468A1 |
| Способ накатывания профильных кругов из сверхтвердых материалов | 1990 |
|
SU1810194A1 |
| СТАНОК ДЛЯ ОБРАБОТКИ АРОЧНЫХ ЗУБЬЕВ ЗУБЧАТЫХ КОЛЕС | 1994 |
|
RU2074794C1 |
Использование: прецизионное станкостроение, для определения малых погрешностей изготовления и монтажа узлов станка алмазного микроточения. Сущность изобретения: на планшайбу шпинделя устанавливают заготовку и поворачивают суппортную группу таким образом, чтобы ось суппорта образовывала с вертикальной плоскостью XY, проходящей через ось шпинделя, произвольный угол α, в диапозоне от 0 до 90°. Добиваются, чтобы ось шпинделя и ось суппорта принадлежали одной и той же горизонтальной плоскости. Определяют и фиксируют точное значение угла α , после чего выполняют точение заготовки. Определяют отклонение формы полученной поверхности от ближайшей сферической поверхности. Определяют радиус ближайшей сферической поверхности Rк . Определяют отклонение Rк от R
СПОСОБ АТТЕСТАЦИИ СТАНКА ДЛЯ ОБРАБОТКИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ, включающий проточку изделия сферической формы, измерение величины радиуса кривизны обработанной сферической поверхности и величин угла поворота суппортной группы, по которым определяют значения кинематических параметров станка, отличающийся тем, что, с целью повышения точности аттестации, проточку изделия осуществляют в несколько этапов, изменяя на каждом этапе угол поворота суппортной группы, при этом значение радиуса кривизны обработанной поверхности измеряют на каждом этапе и используют соответствующие значения угла поворота и радиуса кривизны для определения значений кинематических параметров станка.
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Авторское свидетельство СССР N 1361840, кл | |||
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
Авторы
Даты
1995-02-20—Публикация
1990-04-16—Подача