Изобретение относится к области автоматического регулирования, а именно к регулированию выходной координаты сложных динамических объектов.
Известен способ регулирования и устройство для его реализации, содержащее объект управления, выход которого соединен с инвертирующим входом блока сравнения выходной координаты с заданным значением, выход которого соединен со входом аналогового регулятора, выход которого соединен со входом объекта управления [1, с. 269]
Недостатком указанных способа и устройства является недостаточная точность регулирования.
Наиболее близким техническим решением, выбранным за прототип, является способ регулирования путем измерения выходной координаты, сравнения измеренного значения с заданным, формирования управляющего сигнала на объект управления в соответствии с ошибкой регулирования выходной координаты [2, с. 210]
Операции этого способа осуществляются устройством [2, с. 210, рис. 7.4(б)] содержащим объект управления, выход которого соединен с инвертирующим входом блока сравнения выходной координаты с заданным значением, выход которого соединен со входом детерминированного цифрового регулятора, выход которого соединен со входом объекта управления.
Недостатком указанного способа является недостаточная точность регулирования, поскольку он не учитывает влияния случайных возмущений и флуктуаций внешней среды.
Задача изобретения повышение динамической точности регулирования выходной координаты сложных динамических объектов на установившихся режимах.
Поставленная задача решается способом регулирования динамических объектов путем измерения выходной координаты x объекта управления, сравнения измеренного значения с заданным, формирования управляющего сигнала на объект управления в соответствии с ошибкой регулирования выходной координаты εx, в отличие от прототипа формируют одномерный массив постоянных значений выходной координаты X=x} размерностью M, охватывающий весь диапазон возможных изменений величины x, одномерные массивы постоянных значений 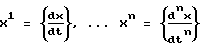 размерностью M, полностью охватывающие диапазоны возможных изменений величин первых n производных x по t соответственно, где n есть порядок дифференциального уравнения, описывающего объект управления, одномерный массив значений управляющего воздействия U=u} размерностью M. На основании этих n+2 одномерных массивов строится (n+2)-мерный массив переходных вероятностей P=p} каждый элемент которого Pkp...qj отражает вероятность перехода объекта управления из состояния
размерностью M, полностью охватывающие диапазоны возможных изменений величин первых n производных x по t соответственно, где n есть порядок дифференциального уравнения, описывающего объект управления, одномерный массив значений управляющего воздействия U=u} размерностью M. На основании этих n+2 одномерных массивов строится (n+2)-мерный массив переходных вероятностей P=p} каждый элемент которого Pkp...qj отражает вероятность перехода объекта управления из состояния 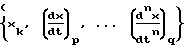 в состояние
в состояние 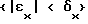 , где δx есть заданное значение точности регулирования, под действием на данном шаге управления управляющего воздействия uj. Начальные значения вероятностей P определяются из анализа априорных статистических данных о работе данного ОУ, затем на каждом последующем i-м шаге управления по величине выходной координаты OY x(ti) выбирают значение k из условия
, где δx есть заданное значение точности регулирования, под действием на данном шаге управления управляющего воздействия uj. Начальные значения вероятностей P определяются из анализа априорных статистических данных о работе данного ОУ, затем на каждом последующем i-м шаге управления по величине выходной координаты OY x(ti) выбирают значение k из условия 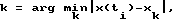 по величинам производных
по величинам производных 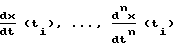 выбирают значения p, q из условий
выбирают значения p, q из условий 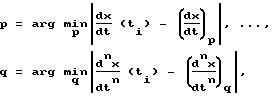 формируют управляющий сигнал, соответствующий величине uj по условию j=arg max Pkp...q(ti), пропускают его через интегратор и подают затем на ОУ, сравнивают полученную ошибку регулирования выходной координату ОУ εx(ti+1) с заданным значением точности регулирования δx
формируют управляющий сигнал, соответствующий величине uj по условию j=arg max Pkp...q(ti), пропускают его через интегратор и подают затем на ОУ, сравнивают полученную ошибку регулирования выходной координату ОУ εx(ti+1) с заданным значением точности регулирования δx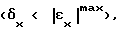 , изменяют величину вероятности Pkp...qj по формуле Pкр...qj(ti+1) = λPкр...qj(ti) + (1-λ)A(ti+1), где A(ti+1)=1 при выполнении условия
, изменяют величину вероятности Pkp...qj по формуле Pкр...qj(ti+1) = λPкр...qj(ti) + (1-λ)A(ti+1), где A(ti+1)=1 при выполнении условия 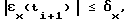 и A(ti+1)=0 во всех остальных случаях, а λ заранее заданная постоянная величина (0 < λ < 1), причем перечисленные операции повторяют на каждом шаге управления.
и A(ti+1)=0 во всех остальных случаях, а λ заранее заданная постоянная величина (0 < λ < 1), причем перечисленные операции повторяют на каждом шаге управления.
Сущность изобретения поясняется чертежом, на котором представлена блок-схем устройства, реализующего предлагаемый способ.
Устройство содержит объект управления 1, выход которого соединен с инвертирующим входом блока сравнения 2 выходной координаты x с заданным значением xзад, выход которого соединен с первым входом ЦВМ 3, реализующей вероятностный регулятор, выход которой соединен со входом интегратора 4, выход которого соединен со входом объекта управления 1, выход объекта управления 1 соединен также с соответствующим входом ЦВМ 3 и со входом блока дифференциаторов 5, выходы которого соединены с соответствующими входами ЦВМ 3.
Способ реализует следующим образом. Сигнал, соответствующий выходной координате, с объекта управления 1 поступает на блок сравнения 2 выходной координаты x с заданным значением xзад, где формируется сигнал, соответствующий ошибке регулирования выходной координаты εx, который поступает в ЦВМ 3, где заранее формируют одномерный массив постоянных значений X=x} размерностью М, охватывающий весь диапазон возможных изменений величины x, одномерные массивы постоянных значений 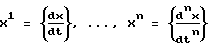 размерностью M, охватывающие полностью соответственно диапазон возможных изменении величин первых n производных x по t, где n есть порядок дифференциального уравнения, описывающего объекта управления, одномерный массив значений управляющего воздействия U=u} размерностью M, на основании этих n+2 одномерных массивов строится (n+2)-мерный массив переходных вероятностей P=P} каждый элемент которого Pkp...qj отражает вероятность перехода объекта управления из состояния
размерностью M, охватывающие полностью соответственно диапазон возможных изменении величин первых n производных x по t, где n есть порядок дифференциального уравнения, описывающего объекта управления, одномерный массив значений управляющего воздействия U=u} размерностью M, на основании этих n+2 одномерных массивов строится (n+2)-мерный массив переходных вероятностей P=P} каждый элемент которого Pkp...qj отражает вероятность перехода объекта управления из состояния  в состояние
в состояние 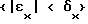 под действием на данном шаге управления уставляющего воздействия uj, начальные значения вероятностей P определяются из анализа априорных статистических данных о работе данного ОУ, затем на каждом последующем i-м шаге управления по величине выходной координату ОУ x(ti) выбирают значение k из условия
под действием на данном шаге управления уставляющего воздействия uj, начальные значения вероятностей P определяются из анализа априорных статистических данных о работе данного ОУ, затем на каждом последующем i-м шаге управления по величине выходной координату ОУ x(ti) выбирают значение k из условия 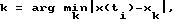 , по величинам производных
, по величинам производных 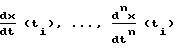 выбирают значения p, q из условий
выбирают значения p, q из условий 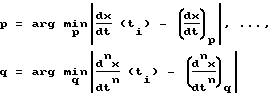 формируют управляющий сигнал на ОУ 1, предварительно пропускаемый через интегратор 4, соответствующий величине uj по условию j = arg max Pкр...qj(ti), сравнивают полученную ошибку регулирования выходной координаты ОУ εx(ti+1) с заданным значением точности регулирования
формируют управляющий сигнал на ОУ 1, предварительно пропускаемый через интегратор 4, соответствующий величине uj по условию j = arg max Pкр...qj(ti), сравнивают полученную ошибку регулирования выходной координаты ОУ εx(ti+1) с заданным значением точности регулирования 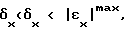 изменяют величину вероятности Pkp...qj по формуле Pкр...qj(ti+1) = λPкр...qj(ti) + (1-λ)A(ti+1), где A(ti+1)= 1 при выполнении условия
изменяют величину вероятности Pkp...qj по формуле Pкр...qj(ti+1) = λPкр...qj(ti) + (1-λ)A(ti+1), где A(ti+1)= 1 при выполнении условия 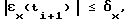 (то есть при достижении цели управления на (i+1)-ом шаге управления), и A(ti+1)=0 во всех остальных случаях, а λ -заранее заданная постоянная величина (0 < λ < 1) т.е. вероятность перехода Pkp...qj изменяется в сторону увеличения при достижении цели управления на i-м шаге или в сторону уменьшения при недостижении цели управления на i-м шаге. Затем повторяют процесс управления, выполняя на каждом его шаге описанную последовательность действий.
(то есть при достижении цели управления на (i+1)-ом шаге управления), и A(ti+1)=0 во всех остальных случаях, а λ -заранее заданная постоянная величина (0 < λ < 1) т.е. вероятность перехода Pkp...qj изменяется в сторону увеличения при достижении цели управления на i-м шаге или в сторону уменьшения при недостижении цели управления на i-м шаге. Затем повторяют процесс управления, выполняя на каждом его шаге описанную последовательность действий.
Один из возможных способов формирования начальных значений вероятностей P при отсутствии априорных статических данных о работе данного ОУ заключается в следующем. Для каждого определенного состояния 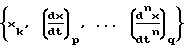 существует вектор вероятностей достижения цели управления Pj, соответствующих управляющим воздействием uj. В каждом таком векторе его элементам приписываются одинаковые значения вероятностей, превышающие ноль (например 0.1 для того, чтобы работали приведенные выше формулы), но выделяется один элемент вектора с более высоким значением, но меньше единицы (например 0.9). Если в процессе функционирования максимальные значения вероятностей имеют более чем один элемент вектора, то управляющее воздействие выбирается из максимума значения индекса j.
существует вектор вероятностей достижения цели управления Pj, соответствующих управляющим воздействием uj. В каждом таком векторе его элементам приписываются одинаковые значения вероятностей, превышающие ноль (например 0.1 для того, чтобы работали приведенные выше формулы), но выделяется один элемент вектора с более высоким значением, но меньше единицы (например 0.9). Если в процессе функционирования максимальные значения вероятностей имеют более чем один элемент вектора, то управляющее воздействие выбирается из максимума значения индекса j.
Использование предлагаемого способа регулирования динамических объектов обеспечивает по сравнению с прототипом следующие преимущества:
а) обеспечивается более высокая точность регулирования на установившихся режимах;
б) режим работы ОУ приближается к оптимальному, вследствие чего увеличивается его долговечность.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РЕГУЛИРОВАНИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ | 1995 |
|
RU2116663C1 |
| СПОСОБ ИСПЫТАНИЯ ЭЛЕКТРОННЫХ РЕГУЛЯТОРОВ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1995 |
|
RU2098790C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ВИНТОВ ТУРБОВИНТОВОГО ДВИГАТЕЛЯ | 1994 |
|
RU2078369C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ МАТРИЦЫ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2057365C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ АВИАЦИОННОГО ТУРБОВИНТОВОГО ДВИГАТЕЛЯ | 1990 |
|
RU2023897C1 |
| СПОСОБ ПОЛУНАТУРНЫХ ИСПЫТАНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ И КОНТРОЛЯ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2331054C2 |
| СПОСОБ ПОЛУНАТУРНЫХ ИСПЫТАНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ И КОНТРОЛЯ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2007 |
|
RU2340883C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ | 2000 |
|
RU2172857C1 |
| Самонастраивающаяся система управления | 1985 |
|
SU1290255A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ И ЗАДАТЧИК ПРОБНЫХ СИГНАЛОВ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2131139C1 |
Изобретение относится к области автоматического регулирования, а именно к регулированию выходной координаты динамических объектов. Задача изобретения - повышение динамической точности регулирования выходной координаты сложных динамических объектов на установившихся режимах. Существо способа заключается в формировании одномерного массива постоянных значений регулируемой величины, охватывающий весь диапазон ее возможных изменений, ее производных, одномерный массив значений управляющего воздействия, на основании которых строится массив переходных вероятностей объекта управления. На каждом шаге регулирования сравнивают полученную ошибку регулирования с заданным значением точности и изменяют величину вероятности. Устройство для реализации способа содержит последовательно соединенные блок сравнения, ЦВМ, реализующую вероятностный регулятор, интегратор и объект управления, выход которого непосредственно и через блок дифференциаторов подключен к входам ЦВМ. 1 ил.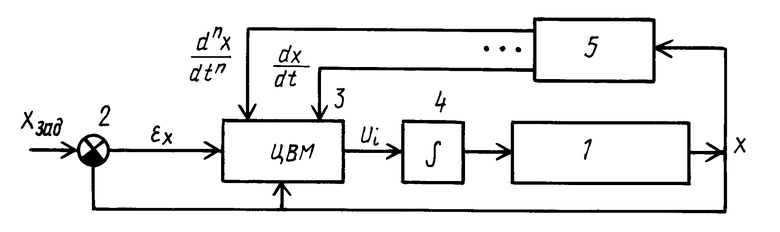
Способ регулирования сложных динамических объектов путем измерения выходной координаты х объекта управления, сравнения измеренного значения с заданным, формирования управляющего сигнала на объект управления в соответствии с ошибкой регулирования выходной координаты εx , отличающийся тем, что формируют одномерный массив постоянных значений X=x} размерностью М, охватывающий весь диапазон возможных изменений величины х, одномерные массивы постоянных значений 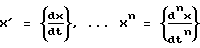 размерностью М, полностью охватывающие диапазоны возможных изменений величин первых n производных х по t соответственно, где n есть порядок дифференциального уравнения, описывающего объект управления, одномерный массив значений управляющего воздействия U=u} размерностью М, на основании этих n + 2 одномерных массивов строится (n + 2)-мерный массив переходных вероятностей P= p} каждый элемент которого Pkp ,..., qj отражает вероятность перехода объекта управления из состояния
размерностью М, полностью охватывающие диапазоны возможных изменений величин первых n производных х по t соответственно, где n есть порядок дифференциального уравнения, описывающего объект управления, одномерный массив значений управляющего воздействия U=u} размерностью М, на основании этих n + 2 одномерных массивов строится (n + 2)-мерный массив переходных вероятностей P= p} каждый элемент которого Pkp ,..., qj отражает вероятность перехода объекта управления из состояния 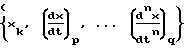 в состояние
в состояние 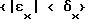 под действием на данном шаге управления управляющего воздействия Uj, начальные значения вероятностей Р определяются из анализа априорных статистических данных о работе данного объекта управления, затем на каждом последующем i-м шаге управления по величине выходной координаты объекта управления x(ti) выбирают значение k из условия
под действием на данном шаге управления управляющего воздействия Uj, начальные значения вероятностей Р определяются из анализа априорных статистических данных о работе данного объекта управления, затем на каждом последующем i-м шаге управления по величине выходной координаты объекта управления x(ti) выбирают значение k из условия 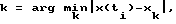 по величинам производных
по величинам производных 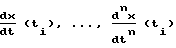 выбирают значения p, q из условий
выбирают значения p, q из условий 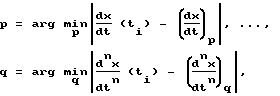 формируют управляющий сигнал, соответствующий величине Uj по условию j arg max Pkp ,..., qj(ti), пропускают управляющий сигнал через интегратор и подают его на объект управления, сравнивают полученную ошибку регулирования выходной координаты объекта управления εx(ti+1) с заданным значением точности регулирования
формируют управляющий сигнал, соответствующий величине Uj по условию j arg max Pkp ,..., qj(ti), пропускают управляющий сигнал через интегратор и подают его на объект управления, сравнивают полученную ошибку регулирования выходной координаты объекта управления εx(ti+1) с заданным значением точности регулирования 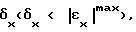 изменяют величину вероятности Pkp ,..., qj по формуле
изменяют величину вероятности Pkp ,..., qj по формуле 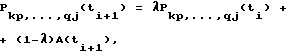
где A(ti + 1) 1 при выполнении условия 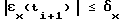 и A (ti + 1) 0 во всех остальных случаях, а λ - заранее заданная постоянная величина (0 < λ < 1) , причем перечисленные операции повторяют на каждом шаге управления.
и A (ti + 1) 0 во всех остальных случаях, а λ - заранее заданная постоянная величина (0 < λ < 1) , причем перечисленные операции повторяют на каждом шаге управления.
| Теория автоматического управления / Под ред | |||
| Нетушила А.В., ч.1 | |||
| - М.: Высшая школа, 1967, с | |||
| Нож для надрезывания подошвы рантовой обуви | 1917 |
|
SU269A1 |
| Васильев В.И | |||
| и др | |||
| Многоуровневое управление динамическими объектами | |||
| - М.: Наука, 1987, с | |||
| Стиральная машина для войлоков | 1922 |
|
SU210A1 |
Авторы
Даты
1997-10-27—Публикация
1995-02-02—Подача