Изобретение относится к области автоматического регулирования, а именно к регулированию выходной координаты сложных динамических объектов.
Известен способ регулирования и устройство для его реализации, содержащее объект управления, выход которого соединен с инвертирующим входом блока сравнения выходной координаты с заданным значением, выход которого соединен с входом аналогового регулятора, выход которого соединен с входом объекта управления [1,с.269].
Недостатком указанных способа и устройства является недостаточная точность регулирования.
Наиболее близким техническим решением, выбранным за прототип, является способ регулирования путем измерения выходной координаты, сравнения измеренного значения с заданным, формирования управляющего сигнала на объект управления в соответствии с ошибкой регулирования выходной координаты [2, с. 250].
Операции этого способа осуществляются устройством [2. с. 250, рис. 7.4(б)] , содержащим объект управления, выход которого соединен с инвертирующим входом блока сравнения выходной координаты с заданным значением, выход которого соединен с входом детерминированного цифрового регулятора, выход которого соединен с входом объекта управления.
Недостатком указанного способа является недостаточная точность регулирования, поскольку он не учитывает влияния случайных возмущений и флуктуаций внешней среды.
Недостатком указанного устройства является то, что оно не позволяет учесть случайные возмущения и получить высокую точность регулирования, так как содержит детерминированный цифровой регулятор, а не стохастический.
Задачей, на решение которой направлено заявляемое изобретение, является повышение динамической точности регулирования выходной координаты сложных динамических объектов на установившихся режимах за счет введения в контур управления адаптивного стохастического регулятора, учитывающего случайные флуктуации внешней среды и параметров объекта.
Поставленная задача решается способом регулирования динамических объектов путем измерения выходной координаты x объекта управления, сравнения измеренного значения с заданным, формирования управляющего сигнала на объект управления в соответствии с ошибкой регулирования выходной координаты εx, в отличие от прототипа сначала формируют одномерный массив постоянных значений Х={x} размерностью М, охватывающий весь диапазон возможных изменений выходной координаты объекта управления x, и одномерный массив значений управляющего воздействия U={u} размерностью N, на основании этих двух одномерных массивов строят двумерный массив переходных вероятностей P={P}, размерностью NxM, каждый элемент которого Pjk отражает оценку вероятности перехода объекта управления из состояния {xk} на i-том шаге управления в цель управления, то есть в состояние 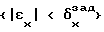 на (i+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия Uj, причем значения оценок вероятностей P определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия
на (i+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия Uj, причем значения оценок вероятностей P определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия 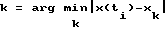 и формируют значение управляющей координаты U(ti+1)=Uj на основе метода Монте-Карло, после чего подают его на объект управления, причем на каждом (i+1)-м шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1), где A(ti+1)= 1 при выполнении условия
и формируют значение управляющей координаты U(ti+1)=Uj на основе метода Монте-Карло, после чего подают его на объект управления, причем на каждом (i+1)-м шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1), где A(ti+1)= 1 при выполнении условия 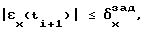 и A(tj+1)=0 во всех остальных случаях, а λ - заранее заданная постоянная величина, причем перечисленные операции повторяют на каждом шаге управления.
и A(tj+1)=0 во всех остальных случаях, а λ - заранее заданная постоянная величина, причем перечисленные операции повторяют на каждом шаге управления.
На чертеже представлена блок-схема устройства, реализующего заявляемый способ.
Устройство содержит (см. фиг. 1) объект управления 1, выход которого соединен с инвертирующим входом блока сравнения 2 выходной координаты x с заданным значением xзад, выход которого соединен с входом детерминированного регулятора 3, выход которого соединен с первым входом ключа 4, второй вход которого соединен с выходом стохастического регулятора 5, а выход соединен с входом объекта управления 1, выход которого соединен также с первым входом стохастического регулятора 5 и с входом схемы управления ключом 6, выход которой соединен с управляющим входом ключа 4, а второй вход стохастического регулятора 5 соединен с выходом генератора 7 случайных чисел.
Способ реализуют следующим образом. Сигнал, соответствующий выходной координате, с объекта управления 1 поступает на блок сравнения 2 выходной координаты x с заданным значением xзад, где формируется сигнал, соответствующий ошибке регулирования выходной координаты εx , который поступает в детерминированный регулятор 3, где формируется управляющий сигнал, который через ключ 4 подается на объект управления 1. На установившихся режимах работы объекта управления схема управления ключом 6 переключает ключ 4 и в контур управления включается стохастический регулятор 5, в котором заранее из анализа априорной информации о работе данного конкретного объекта управления на данном установившемся режиме формируют одномерный массив постоянных значений X= { x} размерностью М, охватывающий весь диапазон возможных изменений выходной координаты объекта управления x, и одномерный массив значений управляющего воздействия U= {u} размерностью N, на основании этих двух одномерных массивов строят двумерный массив переходных вероятностей P={P}, размерностью NxM, каждый элемент которого Pjk отражает оценку вероятности перехода объекта управления из состояния {xk} на i-том шаге управления в цель управления, то есть в состояние 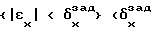 - заранее заданная постоянная величина) на (i+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия uj, причем значения оценок вероятностей P также определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта на данном установившемся режиме. Затем на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия
- заранее заданная постоянная величина) на (i+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия uj, причем значения оценок вероятностей P также определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта на данном установившемся режиме. Затем на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия 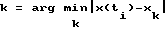 и формируют значение управляющей координаты u(ti+1)=uj на основе метода Монте-Карло [3, c.87-91], после чего подают его через ключ на объект управления. Генератор 7 случайных чисел служит для реализации метода Монте-Карло. Он генерирует на каждом шаге управления сигнал, соответствующий случайной переменной, равномерно распределенной на интервале от 0 до 1. Этот сигнал поступает в стохастический регулятор 5, где на основе величины этого сигнала и вектора оценок вероятностей PJk, с известным значением индекса k определяется значение индекса j, а по значению индекса j определяется значение управляющего воздействия на (i+1)-м шаге (u(ti+1)= uj, которое подается на объект управления. Далее на каждом (i+1)-м шаге управления обновляют оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1) , где A(ti+1)=1 при выполнении условия
и формируют значение управляющей координаты u(ti+1)=uj на основе метода Монте-Карло [3, c.87-91], после чего подают его через ключ на объект управления. Генератор 7 случайных чисел служит для реализации метода Монте-Карло. Он генерирует на каждом шаге управления сигнал, соответствующий случайной переменной, равномерно распределенной на интервале от 0 до 1. Этот сигнал поступает в стохастический регулятор 5, где на основе величины этого сигнала и вектора оценок вероятностей PJk, с известным значением индекса k определяется значение индекса j, а по значению индекса j определяется значение управляющего воздействия на (i+1)-м шаге (u(ti+1)= uj, которое подается на объект управления. Далее на каждом (i+1)-м шаге управления обновляют оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1) , где A(ti+1)=1 при выполнении условия 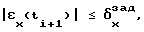 и A(ti+1)=0 во всех остальных случаях, а λ - заранее заданная постоянная величина. Затем повторяют процесс управления, выполняя на каждом его шаге описанную последовательность действий.
и A(ti+1)=0 во всех остальных случаях, а λ - заранее заданная постоянная величина. Затем повторяют процесс управления, выполняя на каждом его шаге описанную последовательность действий.
Использование предлагаемого способа регулирования динамических объектов обеспечивает по сравнению с прототипом следующие преимущества:
а) обеспечивается более высокая точность регулирования на установившихся режимах:
б) режим работы объекта управления приближается к оптимальному, вследствие чего увеличивается его долговечность.
Источники информации, принятые во внимание
1. Теория автоматического управления. Ч.1. Под ред. А.В.Нетушила. М.: Высшая шкала, 1967.
2. Многоуровневое управление динамическими объектами. Васильев В.И. и др. М.: Наука, 1987.
3. Шеннон Р. Имитационное моделирование систем - искусство и наука. М.: Мир, 1978.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИСПЫТАНИЯ ЭЛЕКТРОННЫХ РЕГУЛЯТОРОВ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1995 |
|
RU2098790C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ | 1995 |
|
RU2094837C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ ВИНТОВ ТУРБОВИНТОВОГО ДВИГАТЕЛЯ | 1994 |
|
RU2078369C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ МАТРИЦЫ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1994 |
|
RU2057365C1 |
| СПОСОБ ПОЛУНАТУРНЫХ ИСПЫТАНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ И КОНТРОЛЯ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2331054C2 |
| СПОСОБ ПОЛУНАТУРНЫХ ИСПЫТАНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ И КОНТРОЛЯ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ И СТЕНД ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2007 |
|
RU2340883C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ АВИАЦИОННОГО ТУРБОВИНТОВОГО ДВИГАТЕЛЯ | 1990 |
|
RU2023897C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ И ЗАДАТЧИК ПРОБНЫХ СИГНАЛОВ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2131139C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ | 2000 |
|
RU2172857C1 |
| Самонастраивающаяся система управления | 1985 |
|
SU1290255A1 |
Изобретение относится к области автоматического регулирования, а именно к регулированию выходной координаты динамических объектов. Цель изобретения - повышение динамической точности регулирования выходной координаты сложных динамических объектов на установившихся режимах за счет введения в контур управления стохастического регулятора, учитывающего случайные флуктуации внешней среды и параметров объекта. Сущность изобретения заключается в том, что сначала формируют одномерный массив постоянных значений X = {x} размерностью M, охватывающий весь диапазон возможных изменений выходной координаты объекта управления x, и одномерный массив значений управляющего воздействия U = {u} размерностью N, на основании этих двух одномерных массивов строят двумерный массив переходных вероятностей P = {P}, размерностью N x M, каждый элемент которого Pjk отражает оценку вероятности перехода объекта управления из состояния {xk} на i-том шаге управления в цель управления, то есть в состояние 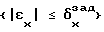 на (j+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия uj, причем значения оценок вероятностей P определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия
на (j+1)-м шаге управления под действием на i-том шаге управления управляющего воздействия uj, причем значения оценок вероятностей P определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине выходной координаты x(ti) выбирают значение k из условия 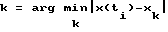 и формируют значение управляющей координаты U(ti+1) = Uj на основе метода Монте-Карло, после чего подают его на объект управления, причем на каждом (i + 1)-м шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1) , где A(ti+1) = 1 при выполнении условия
и формируют значение управляющей координаты U(ti+1) = Uj на основе метода Монте-Карло, после чего подают его на объект управления, причем на каждом (i + 1)-м шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1) , где A(ti+1) = 1 при выполнении условия 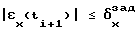 и A(ti+1) = 0 во всех остальных случаях, а λ - заранее заданная постоянная величина, причем перечисленные операции повторяют на каждом шаге управления. 1 ил.
и A(ti+1) = 0 во всех остальных случаях, а λ - заранее заданная постоянная величина, причем перечисленные операции повторяют на каждом шаге управления. 1 ил.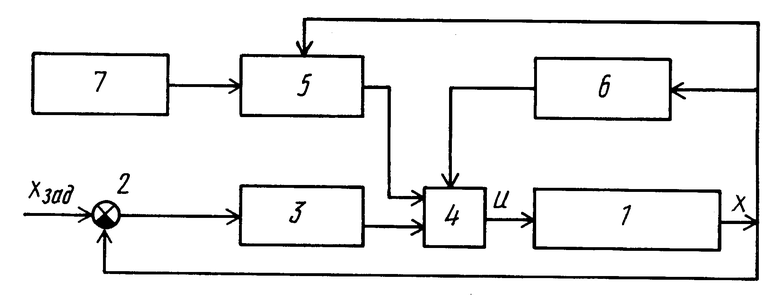
Способ регулирования динамических объектов путем измерения выходной координаты х, сравнения измеренного значения с заданным, формирования управляющего воздействия на объект управления в соответствии с ошибкой регулирования выходной координаты εx, отличающийся тем, что сначала формируют одномерный массив постоянных значений Х = {х} размерностью М, охватывающий весь диапазон возможных изменений выходной координаты объекта управления х, и одномерный массив значений управляющего воздействия U = {u} размерностью N, на основании этих двух одномерных массивов строят двумерный массив переходных вероятностей Р = {Р} размерностью N x M, каждый элемент которого Рjk отражает оценку вероятности перехода объекта управления из состояния {xk} на i-том шаге управления в состояние 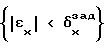 на (i + 1)-том шаге управления под действием на i-том шаге управления управляющего воздействия Uj, причем значения оценок вероятностей Р определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине измеренной выходной координаты x(ti) выбирают значение k из условия k = arg min/x(ti) - xk/ и формируют значение управляющего воздействия U(ti+1) = Uj на объект управления на основе метода Монте-Карло, причем на каждом (i+1)-том шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле
на (i + 1)-том шаге управления под действием на i-том шаге управления управляющего воздействия Uj, причем значения оценок вероятностей Р определяют из анализа априорных статистических данных о работе данного конкретного динамического объекта, затем на установившихся режимах на каждом i-том шаге управления по величине измеренной выходной координаты x(ti) выбирают значение k из условия k = arg min/x(ti) - xk/ и формируют значение управляющего воздействия U(ti+1) = Uj на объект управления на основе метода Монте-Карло, причем на каждом (i+1)-том шаге управления обновляют значение оценки вероятности Pjk по рекурентной формуле
Pjk(ti+1) = λPjk(ti)+(1-λ)A(ti+1),
где A(ti+1) = 1 при выполнении условия 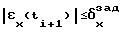 и A(ti+1) = 0 во всех остальных случаях;
и A(ti+1) = 0 во всех остальных случаях;
λ - заранее заданная постоянная величина.
| Васильев В.И | |||
| и др | |||
| Многоуровневое управление динамическими объектами | |||
| - М.: Наука, 1987, с | |||
| Катодное реле | 1921 |
|
SU250A1 |
Авторы
Даты
1998-07-27—Публикация
1995-10-10—Подача