Настоящее изобретение относится к паре сопряженных роторов.
Сопряженные роторы могут быть применены в жидкоструйных насосах, вакуумных насосах и/или в гидро- или пневмодвигателях, а также в роторных двигателях внутреннего сгорания.
Существующие шестеренчатые насосы конструктивно состоят из пары зубчатых колес, называемых роторами, которые находятся в зацеплении друг с другом и вращаются внутри кожуха. Такого рода насосы закачивают или выкачивают жидкость через полость не является сплошной, ее емкость недостаточно велика, а между зацепленными зубьями всегда остается какое-то количество сжатой жидкости, шестеренчатый насос не пригоден для перекачивания газа.
В заявке на роторный двигатель внутреннего сгорания (WO90/02888, кл. F 16 F 9/02, 1991) раскрыт ротор, применяемый в роторном двигателе внутреннего сгорания. Такой ротор, однако, не снабжен эвольвентными зубьями, входящими в зацепление при вращении зубчатых колес, а в самой заявке не приведена расчетная формула, описывающая форму рабочего зуба и соответствующей ему впадины.
В германской заявке N DT 2330992, кл. F 01 C 1/14, 1975 раскрыт ротор, снабженный эвольвентными зубьями, входящими в зацепление при вращении зубчатых колес, рабочим зубом и взаимодействующей с ним впадиной. Однако подобно международной заявке, в ней не приведена расчетная формула, описывающая форму рабочего зуба и соответствующей ему впадины. В ней также не содержится подробной информации о конструкции рабочего зуба и впадины. Кроме того при их зацеплении друг с другом не обеспечивается равномерность скорости вращения.
Технической задачей настоящего изобретения является создание пары взаимодействующих роторов, вдоль внешних окружностей которых расположены эвольвентные зубья, рабочие зубья и соответствующие впадины, входящие в зацепление друг с другом при вращении роторов, а форма зубьев и впадин определяется согласно особым расчетным формулам, когда при вращении роторов рабочий зуб входит в зацепление с сопряженной с ним впадиной, при этом характеристика их равномерного вращения по окружности совпадает с характеристиками вращения эвольвентного зуба, чем достигается равномерность скорости вращения.
Указанная задача достигается тем, что сопряженные роторы, состоящие из взаимодействующих друг с другом и вращающихся внутри кожуха рабочего колеса и колеса, сопряженного с ним, вдоль внешних окружностей которых выполнены эвольвентные зубья и впадины между ними, при этом вдоль внешних окружностей рабочего колеса также выполнены рабочие зубья, а на другом колесе - впадины, сопряженные с рабочими зубьями рабочего колеса, высота рабочего зуба выполнена превышающей высоту эвольвентного зуба, а глубина указанной сопряженной впадины между зубьями выполнена превышающей глубины впадины между эвольвентными зубьями, форма рабочего зуба задана следующей параметрической зависимостью: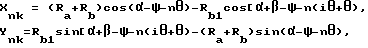
где
n - целые числа;
a - расстояние между точкой пересечения линии, проходящей через точку Rd, с перпендикулярной ей линией OO' и точкой касания окружности радиусом Ra с окружностью радиусом Ro;
Ra - радиус базовой окружности эвольвентного зуба рабочего колеса;
Rd - точка пересечения линии R2 рабочего колеса с наружной окружностью эвольвентного зуба сопряженного колеса;
К2 - радиус внешней окружности рабочего зуба рабочего колеса:
OO' - линия, соединяющая центр O' рабочего колеса и центр O сопряженного колеса;
Rb - радиус базовой окружности эвольвентного зуба сопряженного колеса;
Rb1 - радиус внешней окружности эвольвентного зуба сопряженного колеса;
α - угол, образованный линией R2 и линией OO', при этом O является центром окружности;
ORd - линия, соединяющая точку Rd с центром O сопряженного колеса;
β - угол, образованный линией OR и линией OO', при этом O является центром окружности;
i - передаточное число;
ψ - половина угловой толщины рабочего зуба;
θ - заданная константа,
причем толщина рабочего зуба по дуге внешней окружности определена дугой, соответствующей внутреннему углу 2ψ , а центр рабочего колеса - центр окружности, где R2 - ее радиус, при этом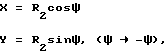
а форма сопряженной впадины задана следующей параметрической зависимостью: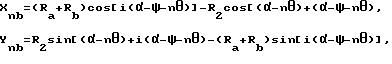
нижняя кривая сопряженной впадины ограничена дугой, образованной углом 2iψ , соответствующим внутреннему углу 2ψ окружной толщины рабочего зуба, причем центр сопряженного колеса - это центр окружности, а его радиус (Ra + Rb - R2) - это радиус окружности, при этом
по окружности сопряженного колеса равномерно распределено nb впадин, а по окружности рабочего колеса na рабочих зубьев, длина дуги, ограниченной углом ωna , образованным между рабочими зубьями и радиусом Ra базовой окружности эвольвентного зуба рабочего колеса, равна длине дуги, ограниченной углом ωnb , образованным сопряженными впадинами и радиусом Rb базовой окружности эвольвентного зуба сопряженного колеса, при этом: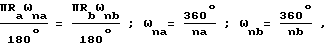
где
na и nb - целые положительные числа.
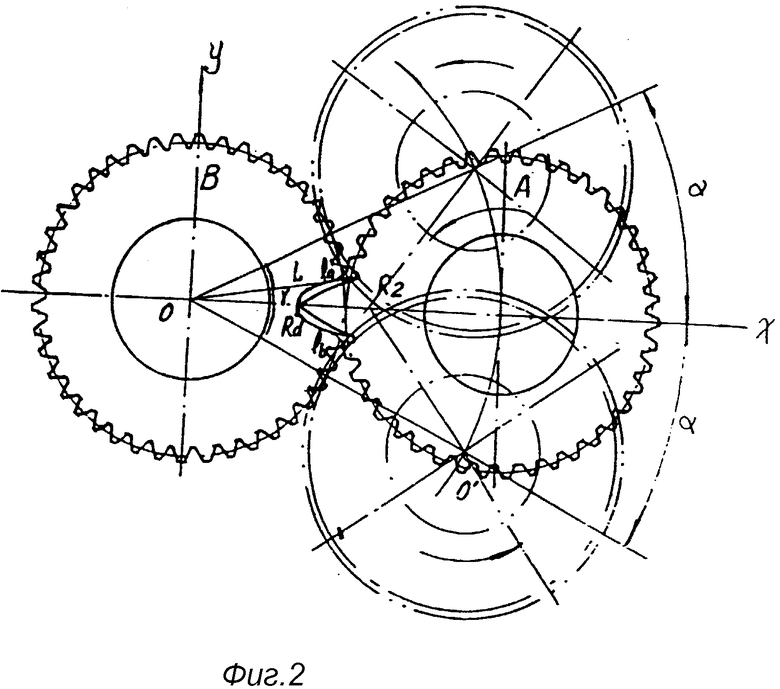
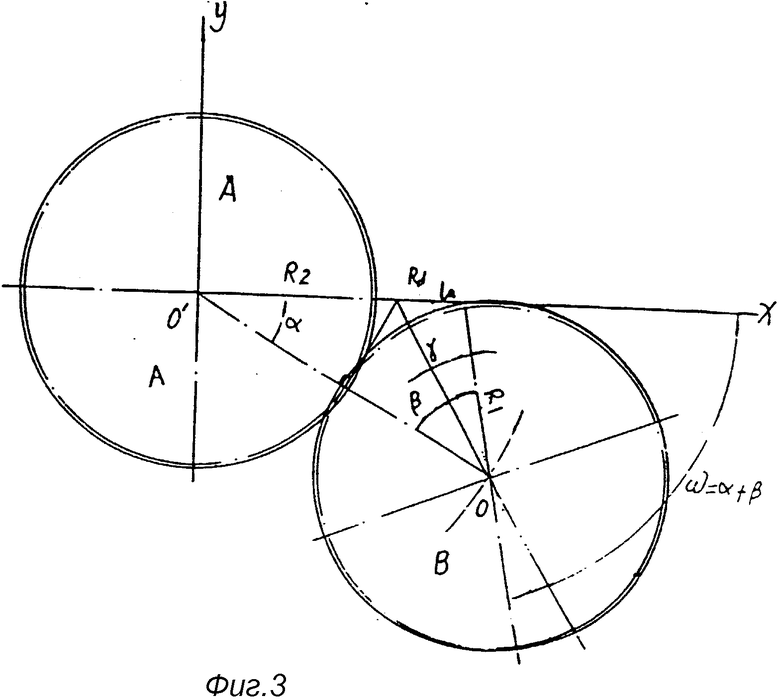
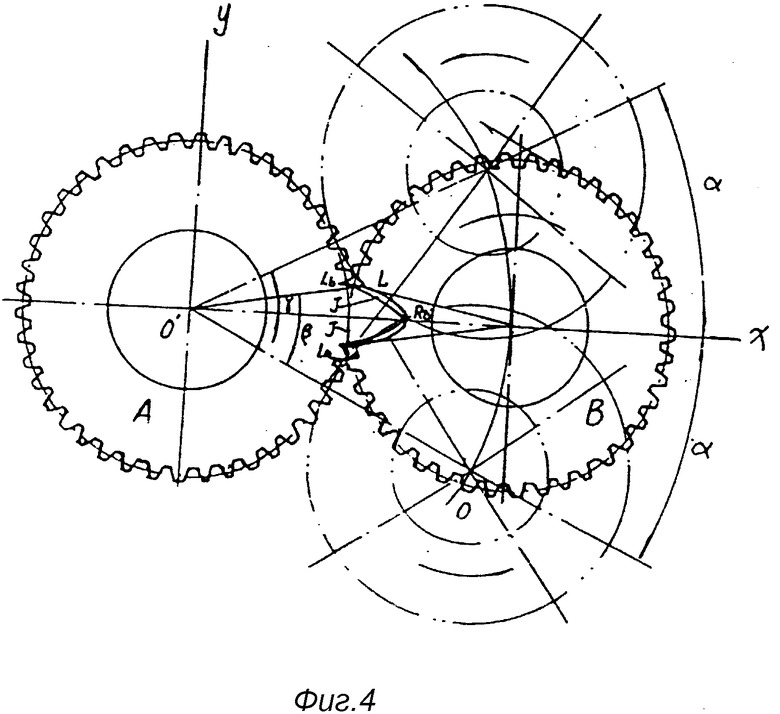
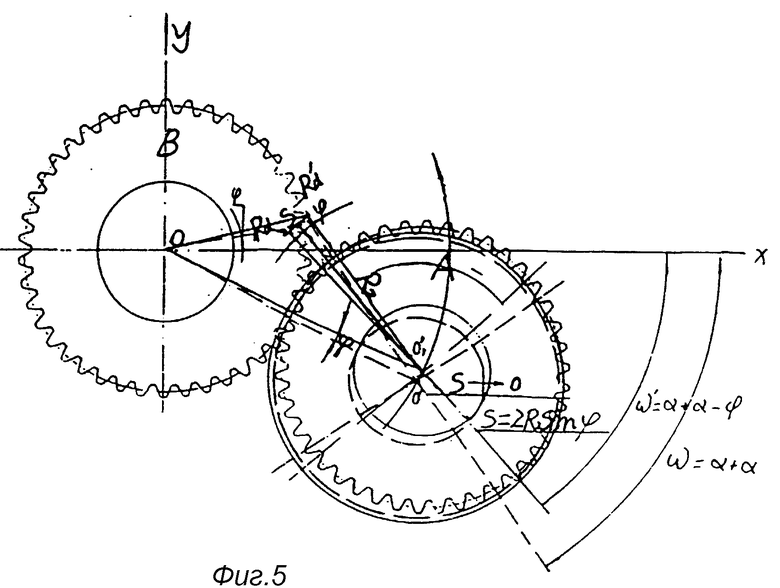
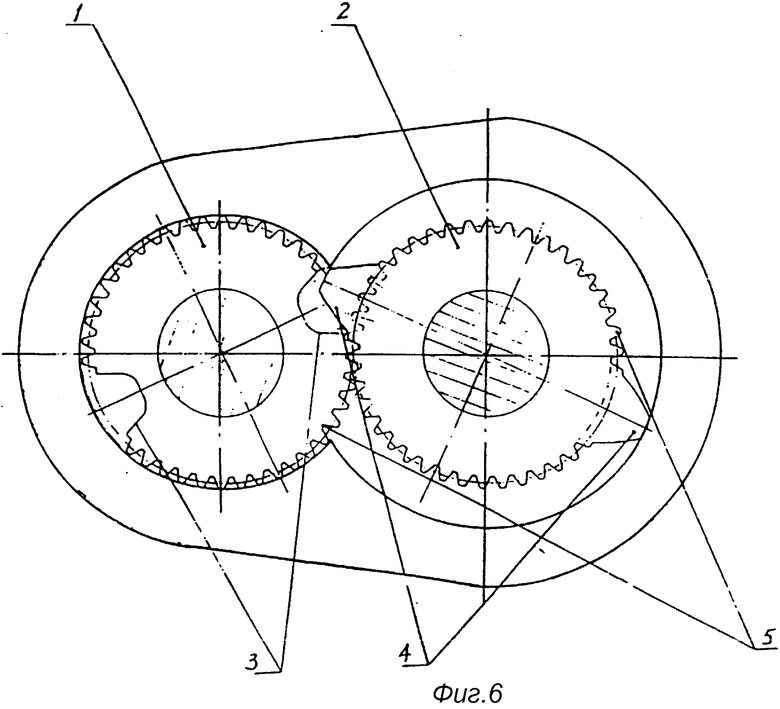
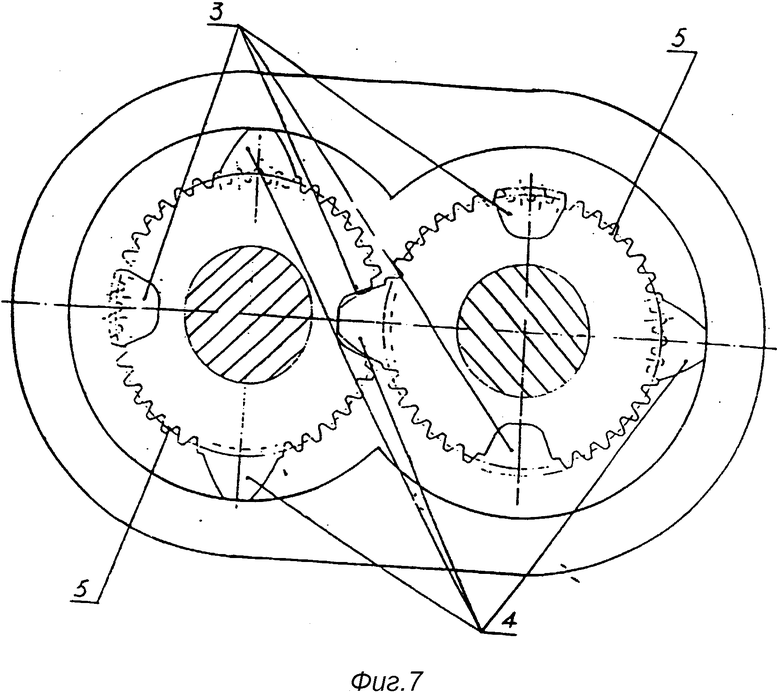
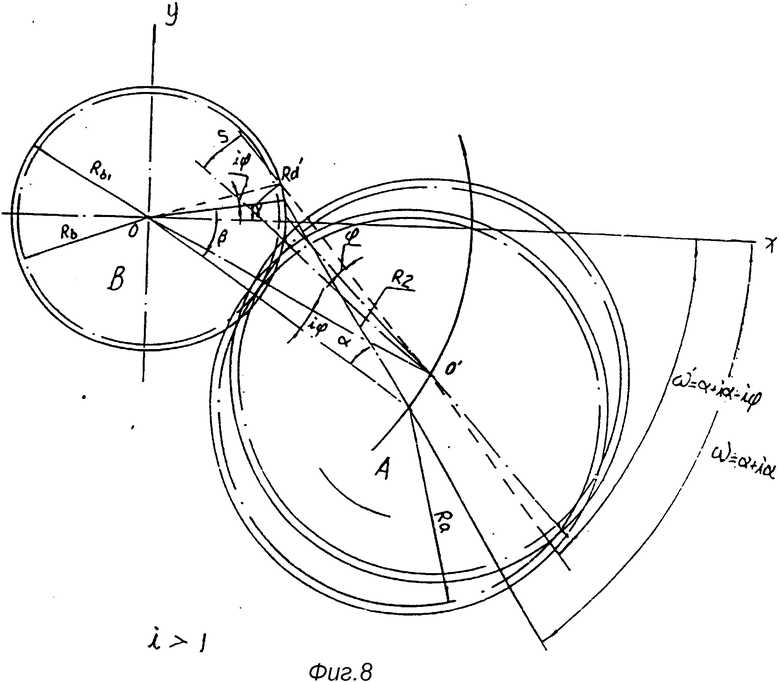
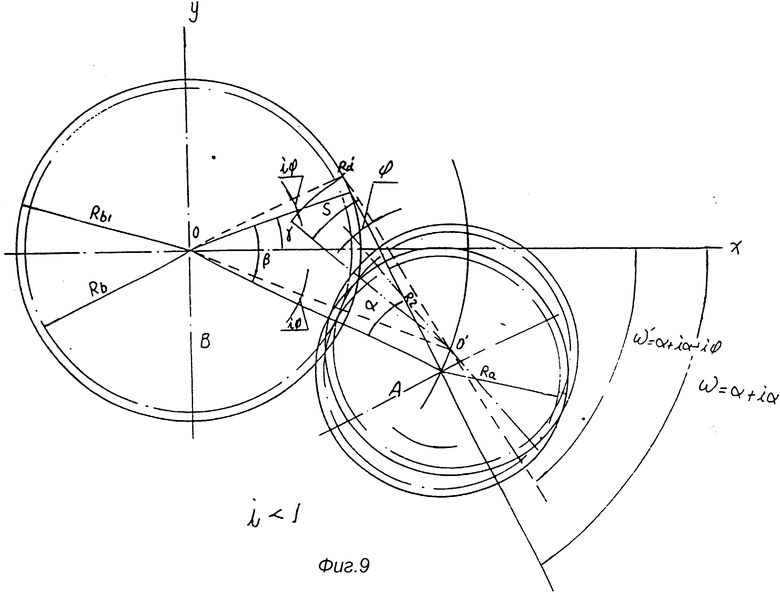
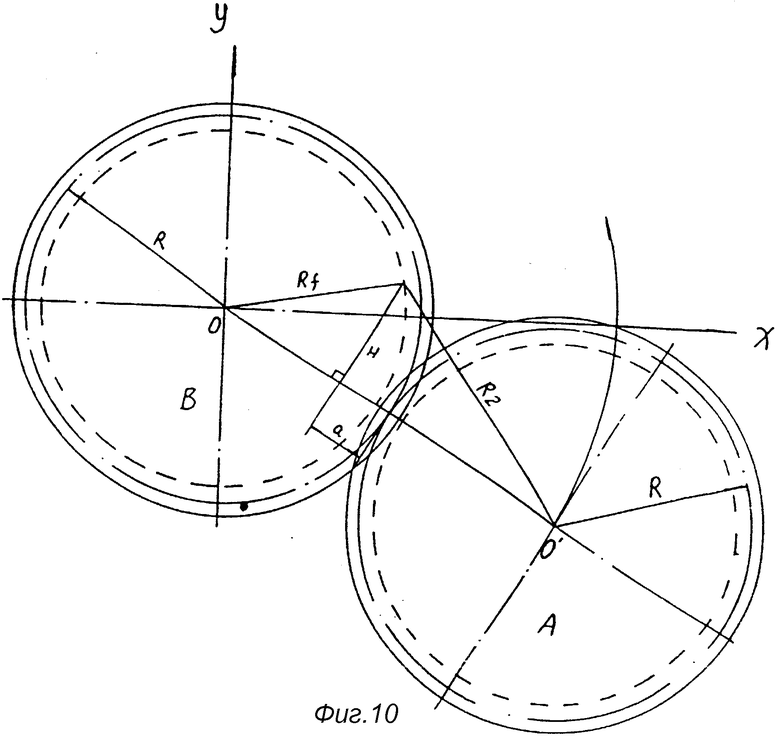
На фиг. 1 показана принципиальная схема, иллюстрирующая образование кривой сопряженной впадины; на фиг. 2 - схематический чертеж кривой сопряженной впадины; на фиг. 3 - принципиальная схема, иллюстрирующая образование кривой рабочего зуба; на фиг. 4 - схематический чертеж кривой рабочего зуба; на фиг. 5 - принципиальная схема, иллюстрирующая толщину рабочего зуба по дуге окружности; на фиг. 6 - первый вариант основной конструкции механизма сопряженного ротора (ERM) (1 - сопряжение зубчатое колесо; 2 - рабочее зубчатое колесо; 3 - сопряженная впадина; 4 - рабочий зуб; 5 - эвольвентный зуб); на фиг. 7 - второй вариант основной конструкции ERM (3 - сопряженная впадина; 4 - рабочий зуб; 5 - эвольвентный зуб); на фиг. 8 - принципиальная схема, иллюстрирующая соотношение параметров, возникающих при сопряжении рабочего зуба и сопряженной впадины в процессе вращения роторов, когда i больше 1; на фиг. 9 - принципиальная схема, иллюстрирующая соотношение параметров, возникающих при сопряжении рабочего зуба и сопряженной впадины в процессе вращения роторов, когда i меньше 1; на фиг. 10 - принципиальная схема, иллюстрирующая соотношение между H, R, Rf и a; на фиг. 11 - вариант осуществления конструкции и размеры сопряженного зубчатого колеса; на фиг. 12 - вариант осуществления конструкции и размеры рабочего зубчатого колеса.
В первую очередь следует пояснить происхождение формы и математический расчет кривых сопряженной впадины и рабочего зуба. Предположим, что имеется пара сопряженных зубчатых колес (A и B), рабочего колеса и сопряженного с ним колеса, находящихся в сопряженном вращении и имеющих одинаковые модули и равное число зубьев, а их передаточное число i равно 1; в целях удобства выведения формулы мы упрощаем пару колес до одного колеса, закрепленного в прямоугольной системе координат, где точка O является центральной точкой, а другое колесо вращается вокруг закрепленного колеса и одновременно вокруг собственной оси.
В прямоугольной системе координат, показанной на фиг. 1, точка O является центром колеса B: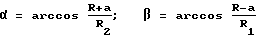
Пусть γ = β - α ,
при этом
R - радиус базовой окружности эвольвентного зубчатого колеса;
R2 - радиус внешней окружности рабочего зуба Колеса A (рабочего колеса);
R1 - радиус внешней окружности эвольвентного зуба;
γ - половина центрального угла сопряженной впадины.
Линия R2 колеса A, превышающая R1, пересекает внешнюю окружность эвольвентного зуба колеса B в точке Rd.
Предположим, что угол, образованный линией O'Rd и осью X, равен ω , тогда ω = β - γ + α = 2α.
Центральное соединение колеса A и колеса B OO' равно 2R, а угол, образованный линией OO' и осью X, равен β - γ = α.
Если колесо A вращается против часовой стрелки вокруг колеса B под углом θ , тогда угол, образованный линией OO' и осью X, равен α - θ , а колесо A при этом вращается вокруг собственной оси под углом θ .
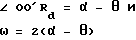
По мере вращения колеса A вокруг колеса B и вокруг собственной оси под углом nθ , расчет геометрического места точек α , образованного, когда вершина линии R2 колеса A, точка Rd, пересекает плоскость колеса B, должен подчиняться следующей формуле: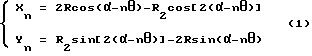
где
R2 - радиус внешней окружности рабочего зуба;
R1 - радиус внешней окружности эвольвентного зубчатого колеса;
R - радиус базовой окружности эвольвентного зубчатого колеса;
θ - соответствует заданной константе, а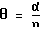 (n = 0, 1, 2,... k, где k является натуральным числом).
(n = 0, 1, 2,... k, где k является натуральным числом).
В формуле (I), если n = 0, nθ = 0, тогда точка Rd линии R2 на колесе A совпадает с исходной точкой La геометрического места точек L на колесе B.
Если nθ = α , тогда линия R2 совпадает с осью X, а точка Rd становится средней точкой геометрического места точек L.
Если nθ = -α тогда точка Rd линии R2 на колесе A совпадает с конечной точкой Lb геометрического места точек L, а линия R2 заканчивается, пересекая плоскость колеса B (см. фиг. 2).
Как показано на фиг. 3, предположим, что колесо A закреплено в прямоугольной системе координат. Точка O является его центром, линия R2(RdO' = R2) совпадает с осью X, угол, образованный линией OO' и осью X, равен α . Точка Rd совпадает с точкой La (точка на радиусе R1 наружной окружности колеса B), угол, образованный OLa и осью X, равен ω(ω = α+β) , а когда колесо B начинает вращаться вокруг колеса A и вокруг собственной оси под углом nθ , ω′= α-nθ+β-nθ = α+β-2nθ , тогда мы получаем: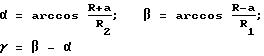
По мере вращения колеса B вокруг колеса A и вокруг собственной оси, линия R2 пересекает плоскость колеса B, а геометрическое место точек L на колесе B (причем La и Lb являются начальной и конечной точкой, соответственно) начинает проецировать на плоскость колеса A два геометрических места точек I и I' (как показано на фиг. 4), что описывается следующей формулой: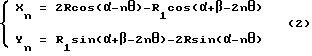
где
R1 - радиус внешней окружности эвольвентного зубчатого колеса;
R - радиус базовой окружности эвольвентного зубчатого колеса;
θ соответствует заданной константе, а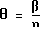 (n = 0, 1, 2...k, где k является натуральным числом).
(n = 0, 1, 2...k, где k является натуральным числом).
В формуле (2): если n = 0, 1, nθ = 0 , тогда точка Rd совпадает с исходной точкой La геометрического места точек L на колесе B; если nθ = α , тогда средняя точка геометрического места точек L находится на линии R2, т. е. на оси X.
Когда α = β - γ ( γ является исходным полууглом сопряженной впадины), формула (2) изменяется на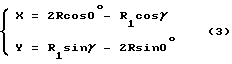
Когда исходная точка La геометрического места точек L доходит до наружной окружности R1 на колесе A, nθ = β , формула (2) изменяется следующим образом: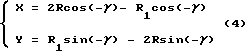
На этом этапе геометрическое место точек L на колесе B проецируется на плоскость колеса A.
Вкратце, ERM (сопряженный роторный механизм) имеет в основе два колеса - колесо A и колесо B. По мере вращения колеса A как вокруг колеса B, так и вокруг собственной оси, вершина линии R2 на колесе A, точка Rd пересекает плоскость колеса B и образует геометрическое место точек L, называемое "кривой сопряженной впадины" (см. формулу 1); и, соответственно, по мере вращения колеса B вокруг колеса A и вокруг собственной оси, кривая сопряженной впадины L проецирует на плоскость колеса A две кривые, при этом La является их начальной точкой, а Lb - конечной точкой; указанные две проецированные кривые I и I' образуют кривую рабочего зуба (см. формулу 2).
Предположим, что в формуле 2 I и I' пересекаются в точке Rd (как показано на фиг. 4), когда высота головки зуба S приближается к нулю. Поскольку сопряженный роторный механизм главным образом применяется для сжатия газов и жидкостей или для преобразования энергии сжатого газа или жидкости в крутящий момент, большая поверхность трения головки зуба S и кожуха обеспечивает более высокую степень герметизации. Для достижения этого предполагаем, что I и I' по отдельности развернуты назад на величину одного угла ψ , после чего мы можем получать хордальную толщину зуба S = 2R2sinψ (где R2 - расстояние между внешней окружностью рабочего зуба и центром колеса). Одновременно к соответствующему половине главного угла ψ сопряженной впадины добавляется величина угла γ . В прямоугольной системе координат, показанной на фиг. 5, по мере вращения колеса A вокруг колеса B на величину угла ψ . Точка Rd линии R2 на колесе A перемещается в 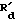 , когда угол, образованный линией O'R'd и осью X равен
, когда угол, образованный линией O'R'd и осью X равен 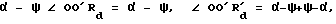 , а угол, образованный линией O'Rd и осью X, равен ω = α+α-ψ = 2α - ψ. Если подставить эти величины в формулу 1, формула расчета кривой сопряженной впадины будет следующей:
, а угол, образованный линией O'Rd и осью X, равен ω = α+α-ψ = 2α - ψ. Если подставить эти величины в формулу 1, формула расчета кривой сопряженной впадины будет следующей: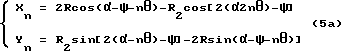
Нижняя кривая сопряженной впадины, т.е. дуга, соответствующая величине ψ , равной угловой толщине зуба по внешней окружности 2ψ , где центр сопряженного колеса является центром окружности, а 2R - 2R2 является радиусом, определяется по следующей формуле: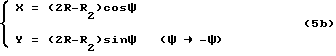
Формула расчета кривой рабочего зуба выводится из формулы 2 следующим образом: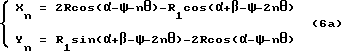
Кривая рабочего зуба по толщине наружной окружности, т.е. дуга, соответствующая угловой толщине зуба по наружной окружности 2ψ , где центр рабочего колеса совпадает с центром окружности, а R2 является радиусом, определяется по нижеследующей формуле: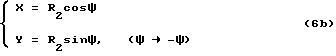
Таким образом, мы получили математические модели сопряженной впадины (формулы 5A и 5B) и рабочего колеса (формулы 6A и 6B), где глубина сопряженной впадины равна (R2 - R), высота рабочего зуба - (R2 - R), а толщина рабочего зуба по наружной окружности равна S = 2R2sinψ . Указанная сопряженная впадина и рабочий зуб, которые могут входить зацепление друг с другом при равномерном вращении роторов по окружности со скоростью 2Rπ , сочетаются с эвольвентными зубьями, образуя практически применим механизм (показанный на фиг. 6 и 7).
Сопряженный роторный механизм является разновидностью вращающегося механизма. Для балансировки его массы, предпочтительно, чтобы он обладал идеальной центральной симметрией, т.е. равномерными интервалами по окружности. (Его базовая конструкция проиллюстрирована на фиг. 6 и 7).
Если передаточное число i ≠ 1, нижеследующая формула должна оставаться неизменной, чтобы обеспечить обращение колеса A вокруг колеса B за счет равномерного вращения зацепленных зубчатых колес;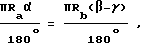
из чего мы выводим (см. фиг. 8 и 9).
Raα = Rb(β-γ)
Когда угол вращения β - γ = 0, а угол вращения колеса A вокруг собственной оси α = 0. Линия R2 на колесе A совпадает с осью X.
Если 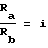
тогда iα = β - γ
или 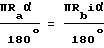
Как показано на фиг. 8 и фиг. 9, если i ≠ 1 , чтобы толщина рабочего зуба по наружной окружности была равна S = 2R2sinψ. Колесо A должно поворачиваться вокруг колеса B на величину одного угла iψ , а в исходный угол γ сопряженной впадины должен быть увеличен на величину одного угла iψ , чтобы Rd' пересекалась с внешним радиусом Rb1 колеса B. При этом угол, образованный линией OO' и осью X будет равен: iα - iψ = i(α - ψ) . Поскольку ∠ 00′Rd = α - ψ, 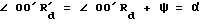 , угол, образованный линией
, угол, образованный линией 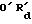 и осью X равен ω = α + i(α - ψ), т.е.
и осью X равен ω = α + i(α - ψ), т.е.
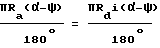
где
Ra - радиус базовой окружности эвольвентного зуба колеса A (рабочего колеса);
Rb - радиус базовой окружности эвольвентного зуба колеса B (сопряженного колеса);
γ - половина центрального угла сопряженной впадины;
iψ - половина угла сопряженной впадины, соответствующего половине угловой толщины рабочего зуба по внешней окружности;
ψ - половина угловой толщины рабочего зуба по внешней окружности.
При повороте колеса A вокруг колеса B на величину одного угла iθ , угол, образованный линией OO' и осью X, будет равен i(α - ψ - θ) , а при повороте колеса A вокруг собственной оси на величину одного угла 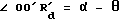 , линия
, линия 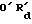 образует с осью X угол ω = (α - θ) + i(α - ψ - θ). . Таким образом, если i ≠ 1 , формула расчета кривой сопряженной впадины выводится из формулы 5a следующим образом:
образует с осью X угол ω = (α - θ) + i(α - ψ - θ). . Таким образом, если i ≠ 1 , формула расчета кривой сопряженной впадины выводится из формулы 5a следующим образом: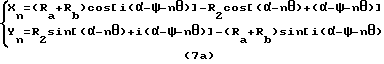
Нижняя кривая сопряженной впадины рассчитывается по формуле 7B: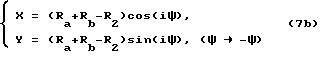
Координаты кривой рабочего зуба можно вывести из формулы 6A следующим образом: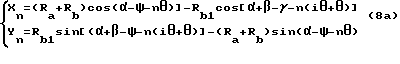
Кривая рабочего зуба по толщине наружной окружности рассчитывается по следующей ниже формуле 8B: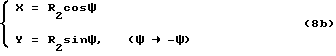
Передаточное число i > 1 или i < 1, относящееся к фиг. 8 и 9, а также к формулам 7A и 8A, должно отвечать следующим требованиям:
По окружности одного из эвольвентных зубчатых колес. Колеса A, должны быть равномерно распределено na рабочих зубьев, а по окружности другого зубчатого колеса (колеса B) должно быть равномерно распределено nb сопряженных впадин;
Длина дуги, ограниченной углом ωna , образованным рабочими зубьями и радиусом Ra базовой окружности эвольвентного зуба колеса A, должна равняться длине дуги, ограниченной углом ωnb , образованным сопряженными впадинами и радиусом Rb базовой окружности эвольвентного зуба колеса B: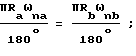
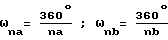
Ниже следует подробное описание варианта осуществления сопряженных роторов (ER), которые могут применяться, например, в компрессорах холодильных установок.
Предположим, что рабочее колесо A и сопряженное колесо B имеют равное число зубьев, одинаковые модули и углы зацепления, а передаточное число i = 1.
Эвольвентное зубчатое колесо имеет следующие характеристики:
число зубьев Z = 40;
модуль m = 0,5;
угол зацепления α = 20o;
радиус базовой окружности 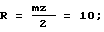
радиус окружности выступов 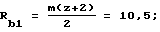
радиус окружности впадин 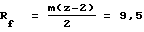
с целью снизить размер допуска между зубьями, радиальный зазор C в данном случае не принимается во внимание;
радиус окружности рабочего зуба R2 = 13,6.
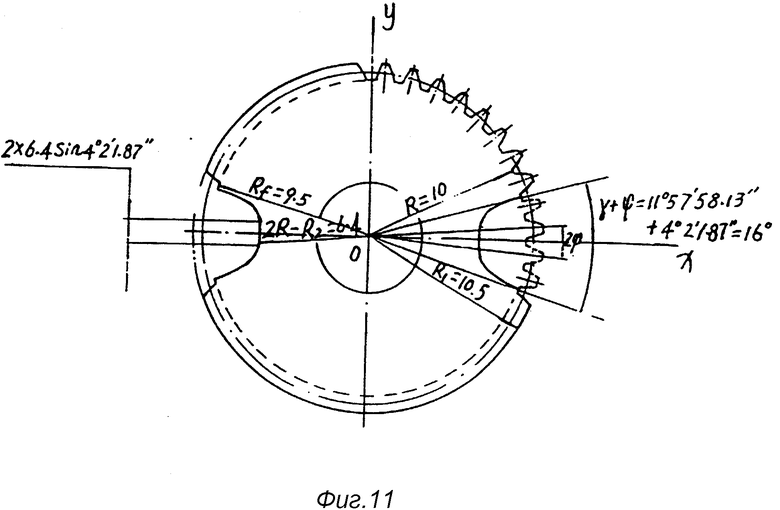
С учетом числа и прочности эвольвентных зубьев на колесе B кривая сопряженной впадины рассчитана таким образом, чтобы в нее вписывались четыре зуба, а наружная окружность рабочего зуба рассчитана таким образом, чтобы ее радиус выходил радиус Rb1 внешней окружности эвольвентного зуба и непосредственно рассекал радиус Rf окружности впадин колеса B (см. фиг. 11).
Проведем линию, перпендикулярную линии OO' и пересекающую ее, от точки пересечения D точкой R2 (радиус внешней окружности рабочего зуба) с Rf (радиус окружности впадин колеса B), при этом H является высотой от точки D до линии OO' (см. фиг. 10). Тогда мы получим: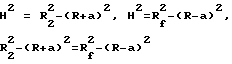
в результате a = 2,36775.
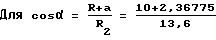
тогда α = 24o34'42,04".
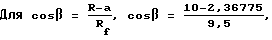
тогда β = 36o32'40,17".
Пусть θ = 4o5'47,01",
тогда k = 6, n = 0, 1, 2, ... r, γ = β - α, γ = 11o57'58,13".
Допустим, что угловая толщина рабочего зуба по наружной окружности равна ψ = 4o2'1,87", а половина угла сопряженной впадины равна γ + ψ = 11o57'5,13" + 4o2'1,7" = 16o
Подставим эти данные в формулу 7A расчета кривой сопряженной впадины: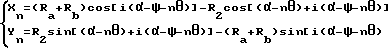
тогда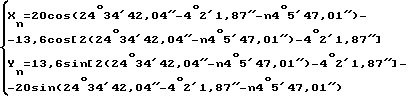
Если n = 0, тогда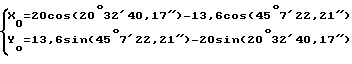
Если n = 1, тогда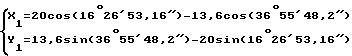
.......... (опускается)
Если n = 6, тогда
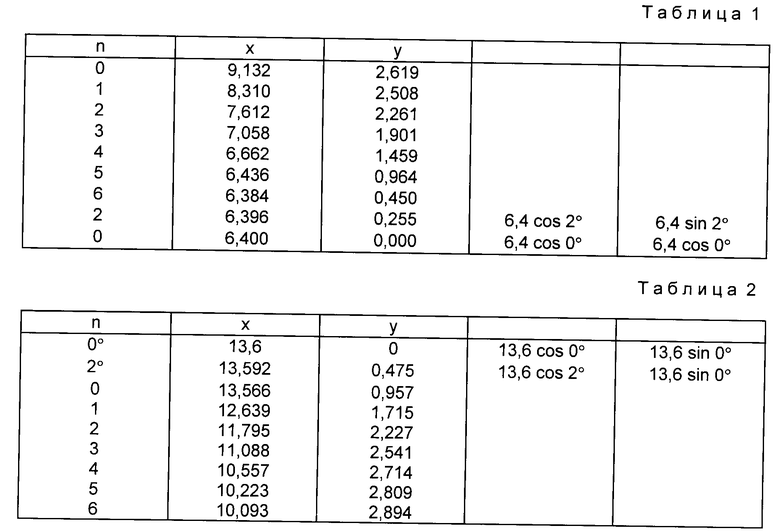
Остальные координаты угла ψ , соответствующего угловой толщине зуба по внешней окружности, основаны на окружности, центром которой является точка O, а радиус 2R - R2 = 6,4, и приведены в табл. 1.
Поскольку кривая сопряженной впадины L состоит из точек, абсолютно симметричных оси X, соединив вышеназванные точки и прочертив симметричную кривую, можно получить полную впадину, воссоздав впадину на эвольвентном зубчатом колесе, затем можно получить так называемое сопряженное колесо, как это показано на фиг. 11.
А теперь обратимся к кривой рабочего зуба.
В формуле 8A, где 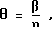
допустим, что = 6o5'26,69", когда n = 1, 2, ... k, (k = 6), а Rb1 заменено на Rf.
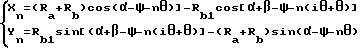
Подставим эти данные в формулу 8A и получим:
Если n = 0, тогда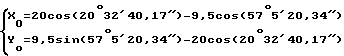
Если n = 1, тогда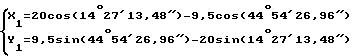
............ (опускается)
Если n = 6, тогда
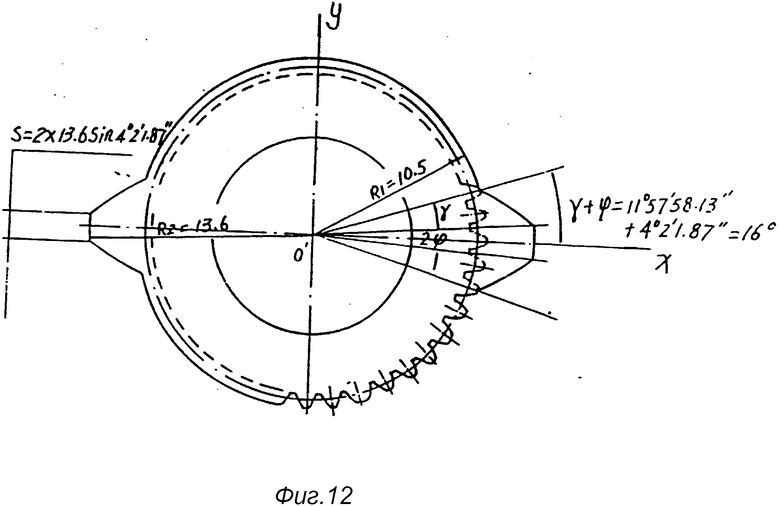
Координаты толщины зуба по внешней окружности S = 2R2sinψ описываются окружностью с центром O' и радиусом, равным 13,6 (см. табл. 2).
Поскольку кривые рабочего зуба I и I', абсолютно симметричны оси X соединив вышеназванные точки и прочертив симметричную кривую, можно получить рабочий зуб. Восстановив рабочий зуб в эвольвентном зубчатом колесе, затем можно получить рабочее колесо.
Эвольвентному зубчатому колесу может быть придана его форма с помощью традиционной технологии, поэтому здесь она опускается. Величина заданной константы θ зависит от точности механической обработки. Чем более точная требуется обработка, тем больше будет точек; чем меньше величина θ , тем больше будет значение натурального числа k.
Сопряженный роторный механизм (ERM) состоит из кожуха, двух боковин, замкнутых дугообразных полостей, образованных сопряженным колесом и рабочим колесом, причем кольцевая полость сопряженного колеса служит опорной поверхностью. Когда рабочее колесо начинает вращаться, объем двух дугообразных полостей, разделенных рабочим зубом, периодически варьируется от большего к меньшему, что удовлетворяет основное требование при производстве насосов, моторов и двигателей внутреннего сгорания.
За счет сочетания представленных в настоящем изобретении пары роторов, снабженных кожухом, имеющим впускное и выпускное отверстия, соответственно, и торцевые крышки, возможно производить различные газожидкостные насосы, например, насосы для жидкостей и газа, а также вакуумные насосы и дозирующие насосы. Указанные роторы могут также применяться для производства жидкостных двигателей или особых роторных двигателей внутреннего сгорания. Поскольку формы рабочего зуба и сопряженной впадины роторов, согласно настоящему изобретению, рассчитываются по особым формулам, что вытекает из сопряженного характера вращения эвольвентного зубчатого колеса, в процессе сопряженного вращения характеристики эвольвентных зубьев точно соответствует характеристикам рабочего зуба и сопряженной впадины.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО С АВТОМАТИЧЕСКОЙ КОМПЕНСАЦИЕЙ НЕПАРАЛЛЕЛЬНОСТИ ОСЕЙ | 1991 |
|
RU2025616C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС С АРОЧНЫМИ ЗУБЬЯМИ | 2011 |
|
RU2467838C2 |
| Способ нарезания выпуклых и вогнутых сторон арочных зубьев цилиндрических зубчатых колес | 1989 |
|
SU1722719A1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ЦИЛИНДРИЧЕСКИХ КОЛЕС С АРОЧНЫМИ ЗУБЬЯМИ | 2009 |
|
RU2404030C1 |
| СПОСОБ ЭЛЕКТРОЭРОЗИОННОЙ ОБРАБОТКИ МАТРИЦ ДЛЯ ИЗГОТОВЛЕНИЯ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1998 |
|
RU2147497C1 |
| ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ КОРРИГИРОВАННАЯ ПЕРЕДАЧА ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ | 1991 |
|
RU2025614C1 |
| ПРОФИЛЬ РОТОРА ВИНТОВОГО КОМПРЕССОРА | 2010 |
|
RU2457362C1 |
| СПОСОБ ОБРАБОТКИ ЭВОЛЬВЕНТНЫХ ПРОФИЛЕЙ КРУГОВЫХ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ КОЛЕС | 1992 |
|
RU2049608C1 |
| АРОЧНАЯ ЦИЛИНДРИЧЕСКАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 2011 |
|
RU2469230C1 |
| ЗУБЧАТОЕ КОЛЕСО | 2009 |
|
RU2491458C2 |
Сопряженные роторы могут быть использованы в жидкоструйных насосах, вакуумных насосах, в гидро- или пневмодвигателях, а также в роторных двигателях внутреннего сгорания. Вдоль внешних окружностей сопряженных роторов расположены эвольвентные зубья 5, рабочие зубья 4 и соответствующие им впадины 3, входящие в зацепление друг с другом при вращении роторов. Форма рабочих зубьев 4 и впадин 3 определяется согласно особым расчетным формулам. При вращении роторов рабочий зуб 4 входит в зацепление с сопряженной с ним впадиной 3. При этом характеристики их равномерного вращения по окружности совпадают с характеристиками вращения эвольвентного зуба 5, что обеспечивает равномерность скорости вращения. 2 табл. 12 ил.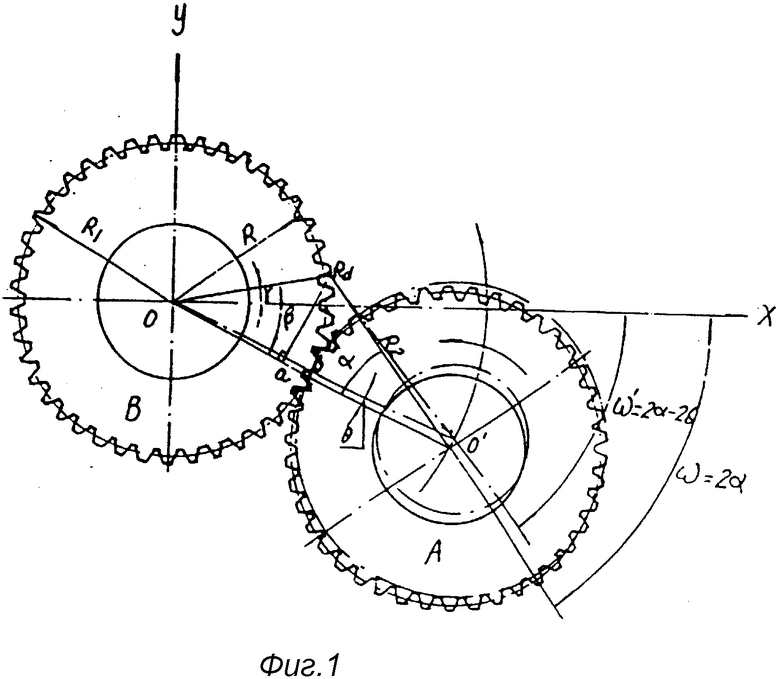
Сопряженные роторы, состоящие из взаимодействующих друг с другом и вращающихся внутри кожуха рабочего колеса и колеса, сопряженного с ним, вдоль внешних окружностей которых выполнены эвольвентные зубья и впадины между ними, при этом вдоль внешних окружностей рабочего колеса также выполнены рабочие зубья, а на другом колесе - впадины, сопряженные с рабочими зубьями рабочего колеса, высота рабочего зуба выполнена превышающей высоту эвольвентного зуба, а глубина указанной сопряженной впадины между зубьями выполнена превышающей глубину впадины между эвольвентными зубьями, отличающиеся тем, что форма рабочего зуба задана следующей параметрической зависимостью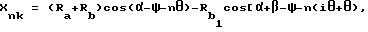
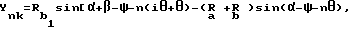
где n - целые числа;
a - расстояние между точкой пересечения линии, проходящей через точку Rd, с перпендикулярной ей линией 00' и точкой касания окружности радиусом Ra с окружностью радиусом Rb;
Ra - радиус базовой окружности эвольвентного зуба рабочего колеса;
Rd - точка пересечения линии R2 рабочего колеса с наружной окружностью эвольвентного зуба сопряженного колеса;
R2 - радиус внешней окружности рабочего зуба рабочего колеса;
OO' - линия, соединяющая центр O' рабочего колеса и центр O сопряженного колеса;
Rb - радиус базовой окружности эвольвентного зуба сопряженного колеса;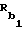 - радиус внешней окружности эвольвентного зуба сопряженного колеса;
- радиус внешней окружности эвольвентного зуба сопряженного колеса;
α - угол, образованный линией R2 и линией OO', при этом O' является центром окружности;
ORd - линия, соединяющая точку Rd с центром O сопряженного колеса;
β - угол, образованный линией ORd и линией OO', при этом O является центром окружности;
i - передаточное число;
ψ - половина угловой толщины рабочего зуба;
θ - заданная константа,
причем толщина рабочего зуба по дуге внешней окружности определяется дугой, соответствующей внутреннему углу 2ψ, а центр рабочего колеса - центр окружности, где R2 - ее радиус, при этом
X = R2cosψ, (ψ → -ψ);
Y = R2sinψ,
где форма сопряженной впадины задана следующей параметрической зависимостью:
Xnb=(Ra+Rb)cos[i(α-ψ-nθ)]-R2cos[(α-nθ)+(α-ψ-nθ)],
Ynb=R2sin[(α-nθ)+i(α-ψ-nθ)]-(Ra+Rb)sin[i(α-ψ-nθ)],
нижняя кривая сопряженной впадины ограничена дугой, образованной углом 2iψ, соответствующим внутреннему углу 2ψ окружной толщины рабочего зуба, причем центр сопряженного колеса - это центр окружности, а его радиус (Ra + Rb - R2) - это радиус окружности, при этом
X = (Ra+Rb-R2)cos(iψ),
Y = (Ra+Rb-R2)sin(iψ), (ψ → -ψ),
по окружности сопряженного колеса равномерно распределено nb впадин, а по окружности рабочего колеса na рабочих зубьев, длина дуги, ограниченной углом 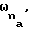 образованным рабочими зубьями и радиусом Ra базовой окружности эвольвентного зуба рабочего колеса, равна длине дуги, ограниченной углом
образованным рабочими зубьями и радиусом Ra базовой окружности эвольвентного зуба рабочего колеса, равна длине дуги, ограниченной углом 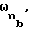 образованным сопряженными впадинами и радиусом Rb базовой окружности эвольвентного зуба сопряженного колеса, при этом
образованным сопряженными впадинами и радиусом Rb базовой окружности эвольвентного зуба сопряженного колеса, при этом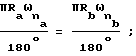
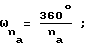
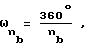
где na и nb - целые положительные числа.
Авторы
Даты
1998-06-10—Публикация
1996-03-15—Подача