Ожидаемое время разворота tk определяется путем математического моделирования свободного движения КА (при 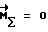 , где
, где 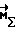 - главный момент всех внешних сил, действующих на КА) при начальных условиях
- главный момент всех внешних сил, действующих на КА) при начальных условиях 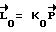 (
( 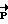 найдено из решения краевой задачи Λ(0) = Λн,Λ(tк) = Λк). В общем случае может получиться tk ≠ Tзад. Поэтому и необходима корректировка расчетного значения кинетического момента
найдено из решения краевой задачи Λ(0) = Λн,Λ(tк) = Λк). В общем случае может получиться tk ≠ Tзад. Поэтому и необходима корректировка расчетного значения кинетического момента 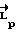 . Величина кинетического момента определяется управляющими возможностями системы исполнительных органов m0, моментом инерции относительно поперечной оси J, углом поворота ψ и заданным временем разворота Tзад:
. Величина кинетического момента определяется управляющими возможностями системы исполнительных органов m0, моментом инерции относительно поперечной оси J, углом поворота ψ и заданным временем разворота Tзад: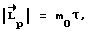
где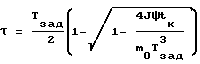 - расчетное время разгона.
- расчетное время разгона.
Таким образом, управление программным разворотом в предлагаемом способе сводится к следующему:
1) прогнозу ожидаемого времени окончания маневра tk путем математического моделирования свободного движения КА при известной величине кинетического момента: K0= Jψ/Tзад ;
2) если tk ≠ Tзад, то корректируем величину K0 умножением ее на коэффициент tk/Tзад, расчетное значение кинетического момента станет равно 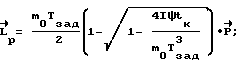
3) разгону КА с максимальным управляющим моментом 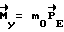 до кинетического момента
до кинетического момента 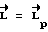 , т.к. mо>>Mвн, то
, т.к. mо>>Mвн, то 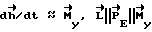 ;
;
4) движению КА с постоянным в абсолютном пространстве кинетическим моментом 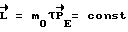 до момента времени, когда τд= τг , при этом
до момента времени, когда τд= τг , при этом 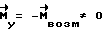 ,
,
где τг - время гашения текущего кинетического момента; τд - время на доворот КА до конечного положения Λк , производимого при торможении, времена τг и τд определяются по выражениям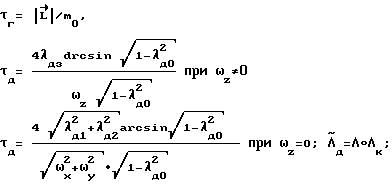
5) торможению КА с максимальным управляющим моментом 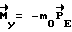 до момента, когда
до момента, когда 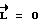 .
.
Временные диаграммы приведены на фиг. 2.
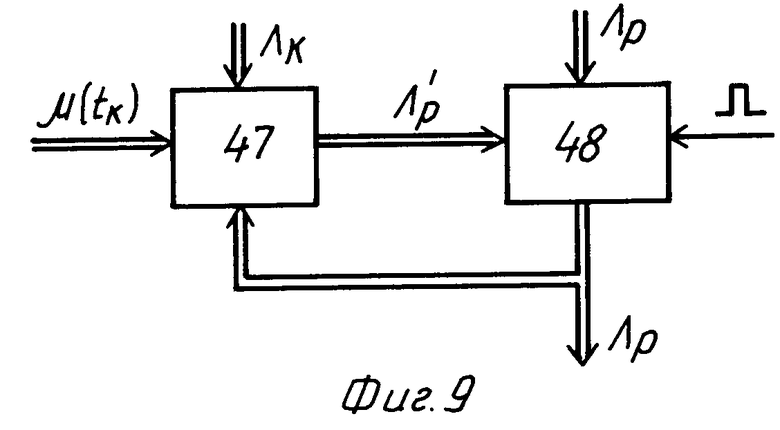
Отличительной особенностью предложенных технических решений являются непрерывный контроль фактического движителя КА в процессе разворота и управление им на всем интервале времени. При этом вращение КА происходит по траектории свободного движения, что обеспечивает разворот с минимальными энергозатратами. Расчет требуемого кинетического момента 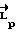 носит итерационный характер и описывается алгоритмом
носит итерационный характер и описывается алгоритмом 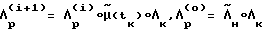 , где μ(tк) - прогнозируемое угловое положение КА на момент времени tk, полученное моделированием движения КА. Отличием являются определение прогнозируемого времени окончания маневра tk, полученное моделированием движения КА, запоминание значения tk и дальнейшее его использование с целью более точного, чем в прототипе, определения времени разгона КА τ и расчетного значения кинетического момента
, где μ(tк) - прогнозируемое угловое положение КА на момент времени tk, полученное моделированием движения КА. Отличием являются определение прогнозируемого времени окончания маневра tk, полученное моделированием движения КА, запоминание значения tk и дальнейшее его использование с целью более точного, чем в прототипе, определения времени разгона КА τ и расчетного значения кинетического момента 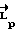 .
.
В предлагаемых способе и системе управляющие моменты формируются не только при разгоне и торможении объекта, но и в процессе вращения его по траектории свободного движения. В системе автоматически определяется такой требуемый импульс кинетического момента 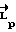 , сообщение которого корпусу КА гарантирует достижение через заданное время требуемого углового положения с любыми наперед заданными точностями как по положению, так и по времени окончания маневра. С момента окончания действия разгонного импульса (когда аппарату сообщили расчетное значение кинетического момента) к КА прикладывают управляющий момент, обеспечивающий движение аппарата с расчетным кинетическим моментом
, сообщение которого корпусу КА гарантирует достижение через заданное время требуемого углового положения с любыми наперед заданными точностями как по положению, так и по времени окончания маневра. С момента окончания действия разгонного импульса (когда аппарату сообщили расчетное значение кинетического момента) к КА прикладывают управляющий момент, обеспечивающий движение аппарата с расчетным кинетическим моментом 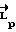 . При этом управляющий момент формируется комбинацией программного управления с управлением по отклонению
. При этом управляющий момент формируется комбинацией программного управления с управлением по отклонению  . Программное управление (прогнозируемый момент
. Программное управление (прогнозируемый момент 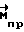 ) строится исходя из того, что КА движется по номинальной (рассчитанной заранее) траектории и определяется решением обратной задачи динамики. Однако одной этой составляющей управляющего момента недостаточно, т.к. она не обеспечивает возвращение на номинальный режим вращения при наличии возможных отклонений
) строится исходя из того, что КА движется по номинальной (рассчитанной заранее) траектории и определяется решением обратной задачи динамики. Однако одной этой составляющей управляющего момента недостаточно, т.к. она не обеспечивает возвращение на номинальный режим вращения при наличии возможных отклонений 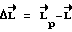 и внешних возмущающих факторов. Поэтому необходима составляющая управляющего момента, формируемая по отклонению фактического кинетического момента от расчетного значения (компенсационный момент
и внешних возмущающих факторов. Поэтому необходима составляющая управляющего момента, формируемая по отклонению фактического кинетического момента от расчетного значения (компенсационный момент  ), которая компенсирует возникающее рассогласование
), которая компенсирует возникающее рассогласование 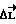 . Компенсация
. Компенсация  зависит только от отклонения
зависит только от отклонения 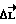 и является некоторым его оператором
и является некоторым его оператором 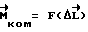 . Простейшим является линейный оператор F, а главной его частью служит пропорциональная компенсация
. Простейшим является линейный оператор F, а главной его частью служит пропорциональная компенсация 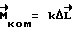 (k>0 - коэффициент усиления). Вид оператора F определяет такие важнейшие характеристики контура управления, как устойчивость, время затухания переходных процессов, качество регулирования, порядок астатизма, чувствительность к случайным воздействиям, помехам и ошибкам измерений. Наличие компенсационной составляющей приводит к тому, что при малейшем отклонении
(k>0 - коэффициент усиления). Вид оператора F определяет такие важнейшие характеристики контура управления, как устойчивость, время затухания переходных процессов, качество регулирования, порядок астатизма, чувствительность к случайным воздействиям, помехам и ошибкам измерений. Наличие компенсационной составляющей приводит к тому, что при малейшем отклонении  от расчетного
от расчетного 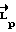 возникает управляющий момент, возвращающий КА в номинальный режим движения.
возникает управляющий момент, возвращающий КА в номинальный режим движения.
Повышенные требования к управлению кинетическим моментом  в процессе разворота приводит к необходимости расчета
в процессе разворота приводит к необходимости расчета 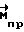 по фактическим параметрам углового движения КА:
по фактическим параметрам углового движения КА: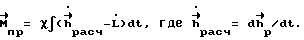
При наличии отклонения фактического кинетического момента  от расчетного значения
от расчетного значения 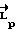 желаемое движение задаем дифференциальным уравнением
желаемое движение задаем дифференциальным уравнением 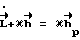 , где κ > 0 - коэффициент апериодичности. Тогда расчетное изменение кинетического момента определяется выражением
, где κ > 0 - коэффициент апериодичности. Тогда расчетное изменение кинетического момента определяется выражением 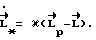 Управляющие моменты формируем алгоритмически согласно уравнению
Управляющие моменты формируем алгоритмически согласно уравнению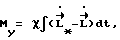
где
χ > 0 - коэффициент усиления.
Подставляя 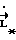 и интегрируя, получим общий вид закона управления:
и интегрируя, получим общий вид закона управления: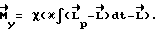
Интегрирование производится с момента окончания участка разгона. Коэффициент κ определяет быстродействие, а χ - степень приближения 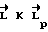 . Чем больше κ , тем быстрее
. Чем больше κ , тем быстрее  сходится к заданному значению
сходится к заданному значению 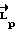 . Чем больше χ , тем ближе реальное движение
. Чем больше χ , тем ближе реальное движение 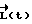 к расчетному. Отдельной компенсации в этом случае не требуется, т.к. управляющий момент формируется по принципу обратной связи, т.е. реализуется управление по отклонению, учитывающее фактическое движение КА.
к расчетному. Отдельной компенсации в этом случае не требуется, т.к. управляющий момент формируется по принципу обратной связи, т.е. реализуется управление по отклонению, учитывающее фактическое движение КА.
Для улучшения качества переходных процессов необходимо учитывать начальные условия на начало регулирования, для чего в выражение для 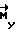 вводим значение
вводим значение 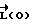 . В результате получаем
. В результате получаем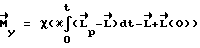 .
.
Рассмотрим случай, когда управляющий момент на этапе между разгоном и торможением формируется по отклонению кинетического момента от расчетного значения 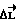 . Задача управления состоит в стабилизации вектора кинетического момента
. Задача управления состоит в стабилизации вектора кинетического момента  в инерциальном пространстве в окрестности зафиксированного значения
в инерциальном пространстве в окрестности зафиксированного значения 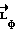 . Направление кинетического момента в процессе разворота представим в инерциальной системе координат (ИСК)
. Направление кинетического момента в процессе разворота представим в инерциальной системе координат (ИСК) 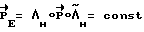 , где
, где 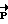 - вектор разворота в связанной системе координат (ССК) на начало разворота. Тогда имеем
- вектор разворота в связанной системе координат (ССК) на начало разворота. Тогда имеем 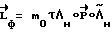 - зафиксированный в ИСК вектор кинетического момента. Расчетное значение кинетического момента в ИСК постоянно и известно:
- зафиксированный в ИСК вектор кинетического момента. Расчетное значение кинетического момента в ИСК постоянно и известно: 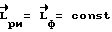 (индекс "и" означает, что вектор представлен в ИСК). Фактический кинематический момент КА
(индекс "и" означает, что вектор представлен в ИСК). Фактический кинематический момент КА  измеряется в ССК. Тогда
измеряется в ССК. Тогда 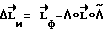 . Пусть
. Пусть 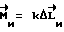 , где k>0 - коэффициент усиления, определяющий скорость компенсации.
, где k>0 - коэффициент усиления, определяющий скорость компенсации.
В итоге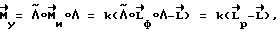
где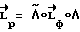 - расчетное значение кинетического момента.
- расчетное значение кинетического момента.
Выражение для управляющего момента с учетом интегральной компенсации принимает вид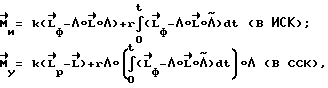 ,
,
где
k, r - коэффициенты усиления (k = const, r = const).
Принимаем 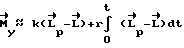
(в предположении, что за малое время 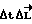 повернется незначительно).
повернется незначительно).
Момент управления может быть сформирован по принципам инвариантного управления, сочетающего программное управление с управлением по отклонению: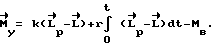
Та часть управляющего момента, которая пропорциональна отклонению 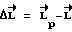 , является основной в компенсационном моменте
, является основной в компенсационном моменте  . Интегральная компенсация, с одной стороны, улучшает качество регулирования (повышает быстроту и точность отработки
. Интегральная компенсация, с одной стороны, улучшает качество регулирования (повышает быстроту и точность отработки  ) и повышает астатизм контура управления, а с другой - позволяет компенсировать внешние возмущения и случайные факторы. Интегральная составляющая управляющего момента позволяет обеспечить
) и повышает астатизм контура управления, а с другой - позволяет компенсировать внешние возмущения и случайные факторы. Интегральная составляющая управляющего момента позволяет обеспечить 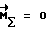 при
при 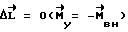 в случае медленно меняющихся внешних воздействий. Здесь
в случае медленно меняющихся внешних воздействий. Здесь 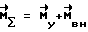 - момент всех сил, действующих на КА,
- момент всех сил, действующих на КА, 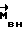 - внешний возмущающий момент. Значения коэффициентов усиления k, r выбираются из условий обеспечения устойчивости, точности поддержания
- внешний возмущающий момент. Значения коэффициентов усиления k, r выбираются из условий обеспечения устойчивости, точности поддержания  и помехозащищенности. Чем больше k, тем больше быстродействие контура стабилизации, тем меньше возможная ошибка управления
и помехозащищенности. Чем больше k, тем больше быстродействие контура стабилизации, тем меньше возможная ошибка управления 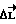 но, с другой стороны, повышается чувствительность к ошибкам измерения. Отношение k/r определяет запас устойчивости (чем оно больше, тем более устойчива система). Конкретные величины коэффициентов зависят только от технических данных элементов системы управления.
но, с другой стороны, повышается чувствительность к ошибкам измерения. Отношение k/r определяет запас устойчивости (чем оно больше, тем более устойчива система). Конкретные величины коэффициентов зависят только от технических данных элементов системы управления.
Введение в 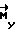 расчетного значения возмущающего момента
расчетного значения возмущающего момента 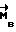 существенно снижают ошибку
существенно снижают ошибку 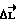 . Так, в частном случае, когда на КА действуют внешние моменты расчетной величины, обеспечивается движение с
. Так, в частном случае, когда на КА действуют внешние моменты расчетной величины, обеспечивается движение с 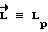 . Статическая составляющая разности
. Статическая составляющая разности 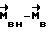 полностью парируется интегральной компенсацией и ошибка
полностью парируется интегральной компенсацией и ошибка 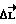 при этом сводится к нулю.
при этом сводится к нулю.
Повышение точности разворота обеспечивается и тем, что момент начала торможения определяется исходя из фактических параметров движения КА 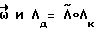 путем сравнения времени τд c τг .
путем сравнения времени τд c τг .
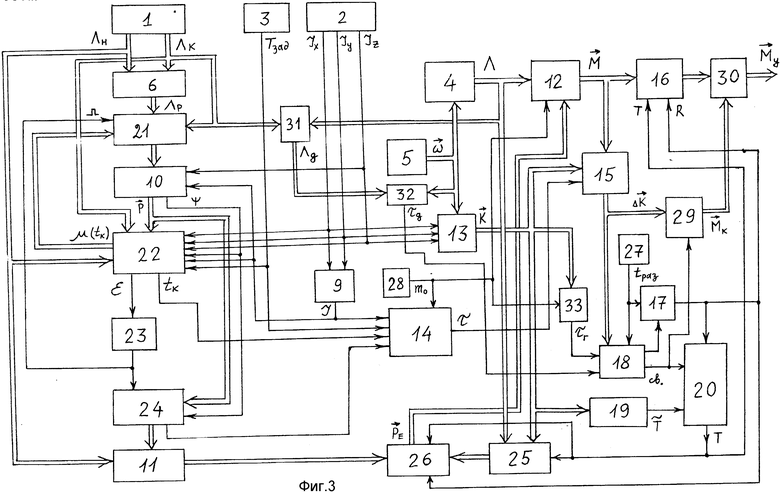
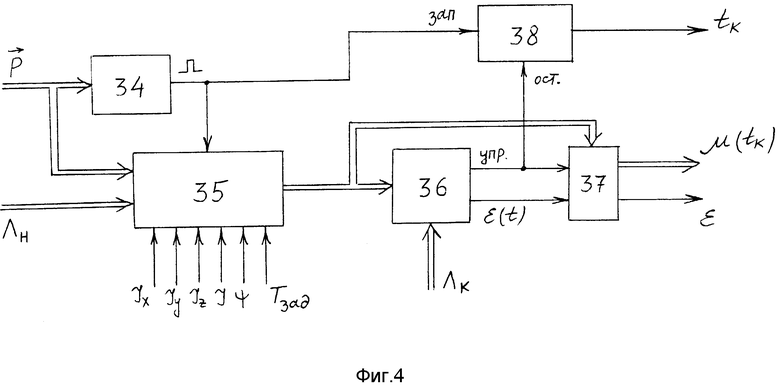
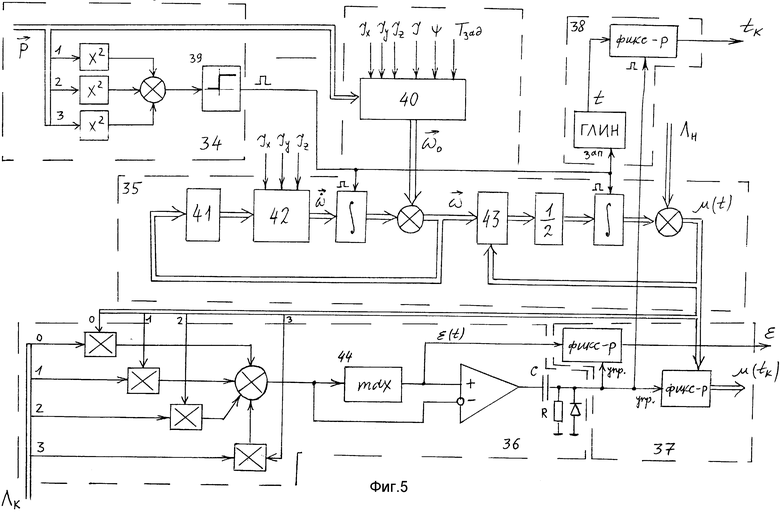
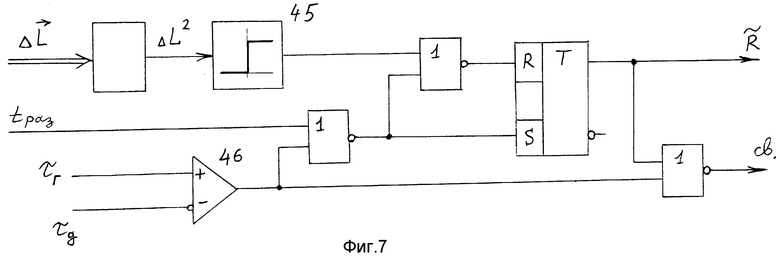
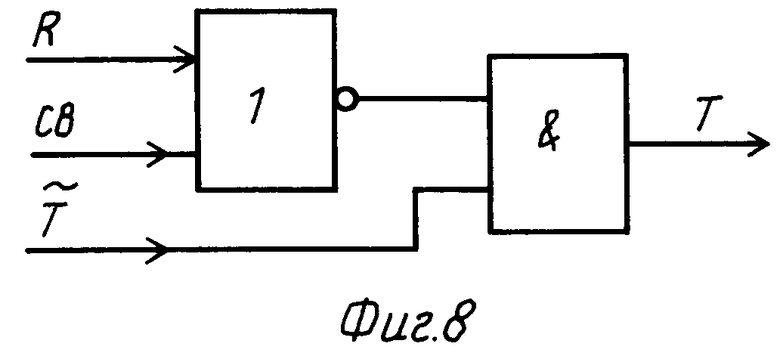
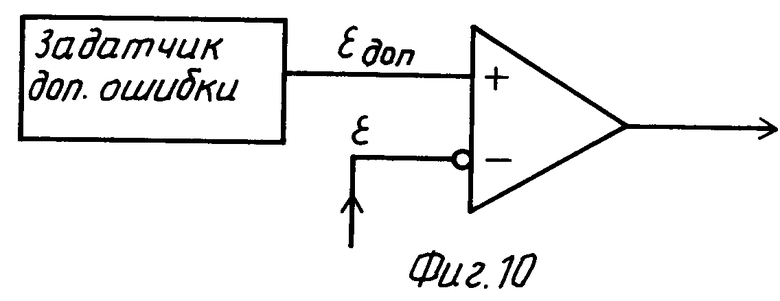
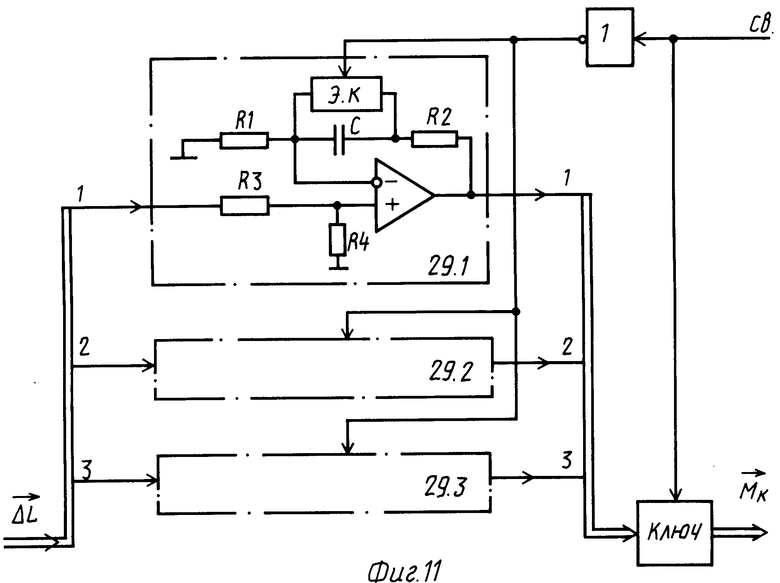
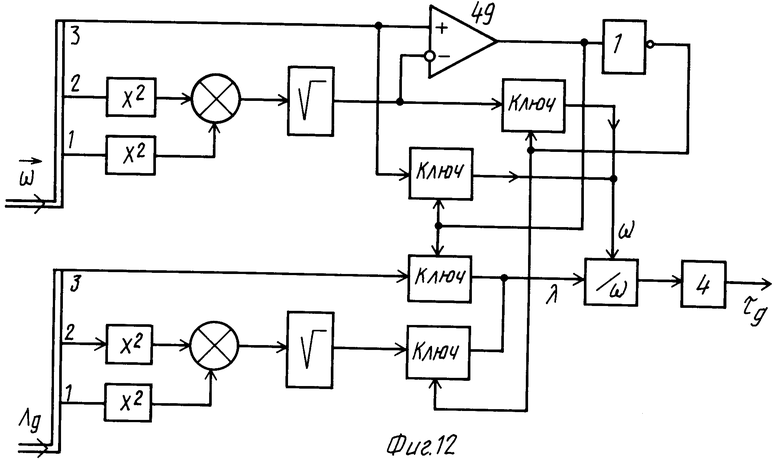
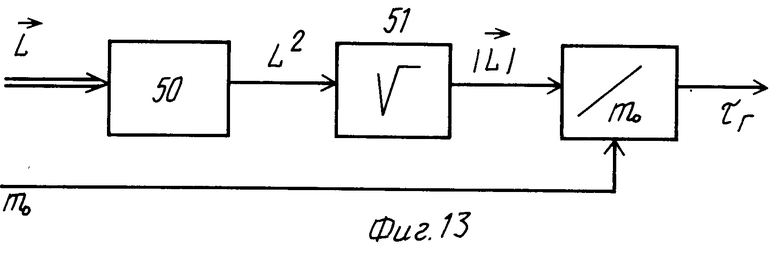
На фиг. 1 представлена функциональная схема системы-аналога; на фиг. 2 показаны временные диаграммы для способа и системы-прототипа и предлагаемых способа и системы; на фиг. 3 изображена функциональная схема предлагаемой системы; на фиг. 4 - функциональная схема БОПрР (22); на фиг. 5 - схема реализации БОПрР (22); на фиг. 6 - схема реализации БОВР (14); на фиг. 7 - схема выполнения БФКСВ (18); на фиг. 8 - схема выполнения БФКТ (20); на фиг. 9 - схема реализации БКОПР (21); на фиг. 10 - схема реализации БСПР (23); на фиг. 11 - схема реализации БФКМ (29); на фиг. 12 - схема реализации БФВД (32); на фиг. 13 - схема реализации БФВГКМ (33).
Функциональная схема предлагаемой системы представлена на фиг. 3, 4, где 1 - блок задания начального и конечного положений аппарата (БЗНКП), 2 - блок задания моментов инерции (БЗМИ), 3 - задатчик времени разворота (ЗВР), 4 - бесплатформенная инерционная навигационная система (БИНС), 5 - блок датчиков угловых скоростей (БДУС), 6 - блок определения параметров разворота (БОПР), 9 - блок определения момента инерции вокруг поперечной оси (БОМИПО), 10 - блок прогноза вектора разворота (ВПВР), 11 - блок определения направления разгонного импульса (БОНРИ), 12 - блок формирования момента управления (БФМУ), 13 - блок определения кинетического момента (БОКМ), 14 - блок определения времени разгона (БОВР), 15 - блок определения отклонения кинетического момента от расчетного (БООКМ), 16 - блок формирования разгонного и тормозного импульсов (БФРТИ), 17 - блок формирования команды на разгон (БФКР), 18 - блок формирования команды на свободное вращение (БФКСВ), 19 - блок определения момента остановки аппарата (БОМО), 20 - блок формирования команды на торможение (БФКТ), 21 - блок коррекции и обновления параметров разворота (БКОПР), 22 - блок определения промаха разворота (БОПрР), 23 - блок сравнения промаха разворота с заданной величиной (БСПР), 24 - блок запоминания вектора разворота (БЗВР), 25 - блок определения направления тормозного импульса (БОНТИ), 26 - блок определения направления разворота (БОНР), 27 - задатчик команды на начало разворота (ЗНКР), 28 - задатчик максимальной величины управляющего момента (ЗМВУМ), 29 - блок формирования корректирующего момента (БФКМ), 30 - блок суммирования управляющего момента (БСУМ), 31 - блок определения параметров доворота (БОПД), 32 - блок формирования времени на доворот до конечного углового положения (БФВД), 33 - блок формирования времени гашения текущего кинетического момента (БФВГКМ). При этом выход задания начального положения БЗНКП связан с соответствующим входом БОПР, БОПрР и информационным входом БОНРИ. Выход задания конечного положения БЗНКП связан с соответствующим входом БОПР, БКОПР, БОПрР и БОПД. Первый, второй и третий выходы БЗМИ связаны соответственно с первым, вторым и третьим параметрическими входами БОКМ и первым, вторым и третьим входами задания моментов инерции БРПрР. Первый и второй входы БОМИПО связаны соответственно с первым и вторым выходами БЗМИ, третий выход которого связан с входом ввода момента инерции относительно продольной оси БПРВ, скалярный выход которого связан с входом ввода угла разворота БОПрР и со скалярным входом БЗВР. Выход связан с входами задания времени разворота БОВР и БОПрР. Выход БИНС связан с входами задания углового положения БФМУ, БОНТИ и входом ввода текущего углового положения БОПД, выход которого связан с информационным входом БФВД. Выход БДУС связан с входом БИНС и векторным входом БОКМ, выход которого связан с входом ввода кинетического момента БООКМ, входом БОМО, векторным входом БОНТИ и БФВГКМ, выход которого связан с входом ввода времени гашения угловой скорости БФКСВ. Выход ввода времени доворота БФКСВ связан с выходом БФВД, векторный вход которого связан с выходом БДУС. Выход БОПР связан с входом ввода исходных параметров разворота БКОПР. Выход БОМИПО связан с входами ввода моментов инерции вокруг поперечной оси БОВР, БОПрР и БПВР, векторный выход которого связан с входами ввода вектора разворота БОПрР и БЗВР. Выход БОНРИ связан с входом ввода направления разгонного импульса БОНР. Выход БФМУ связан с входом задания момента управления БООКМ и векторным входом БФРТИ. Вход ввода прогнозируемого времени разворота БОВР связан с одноименным выходом БОПрР. Логический выход БФКСВ связан с управляющим входом БФКР, выход которого связан с входами разрешения разгона БФРТИ, БФКТ и БОНР. Командный выход БФКСВ связан с входом разрешения свободного движения БФКТ. Выход БОМО связан с входом ввода сигнала на остановку аппарата БФКТ, выход которого связан с входами ввода команды на торможение БФРТИ, БОНР и БОНТИ, выход которого связан с входом ввода направления тормозного импульса БОНР, выход которого связан с векторным входом БФМУ. Выход БКОПР связан с входом задания параметров разворота БПВР. Выход прогнозируемого углового положения БОПрР связан с соответствующим входом БКОПР, информационный выход БОПрР связан с входом БСПР, выход которого связан с управляющими входами БКОПР и БЗВР, векторный выход которого связан с векторным входом БОНРИ. Скалярный выход БЗВР связан с входом задания угла разворота БОВР, выход которого связан с входом задания времени разгона БООКМ, выход которого связан с векторным входом БФКСВ и с информационным входом БФКМ, управляющий вход которого связан с выходом разрешения свободного движения БФКСВ. Выход ЗКНР связан с входом наличия разворота БФКР и БФКСВ. Выход ЗМВУМ связан с параметрическими входами БФМУ, БОВР и БФВГКМ. Первый вход БСУМ связан с выходом БФРТИ , второй вход БСУМ связан с выходом БФКМ, выход БСУМ является выходом системы.
Реализация отдельных блоков и элементов предлагаемой системы выполнена на интегральных схемах и стандартных аналоговых модулях и представлена фиг. 5-13.
БОПР 6 вычисляет кватернион разворота по формуле 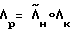 и состоит из блока взятия сопряженного кватерниона и блока перемножения кватернионов.
и состоит из блока взятия сопряженного кватерниона и блока перемножения кватернионов.
БОМИПО 9 усредняет моменты инерции вокруг поперечных осей Jx и Jy по выражению J = (Jx + Jy)/2.
БПВР 10 как и в прототипе определяет вектор разворота 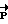 и угол поворота КА вокруг него ψ (угол прецессии), соответствующие развороту динамически симметричного тела с моментами инерции J, Jz на кватернион Λр .
и угол поворота КА вокруг него ψ (угол прецессии), соответствующие развороту динамически симметричного тела с моментами инерции J, Jz на кватернион Λр .
БОНРИ 11 реализует соотношение 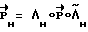 .
.
БФМУ 12 вычисляет потребный момент управления  исходя из фактического углового положения Λ и вектора разворота
исходя из фактического углового положения Λ и вектора разворота 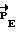 и реализует функцию
и реализует функцию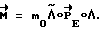
БОКМ 13 осуществляет умножение вектора на диагональную матрицу по выражению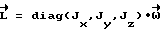
БОВР 14 представлен на фиг. 6 и вычисляет время разгона τ по формуле 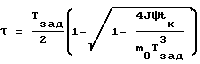
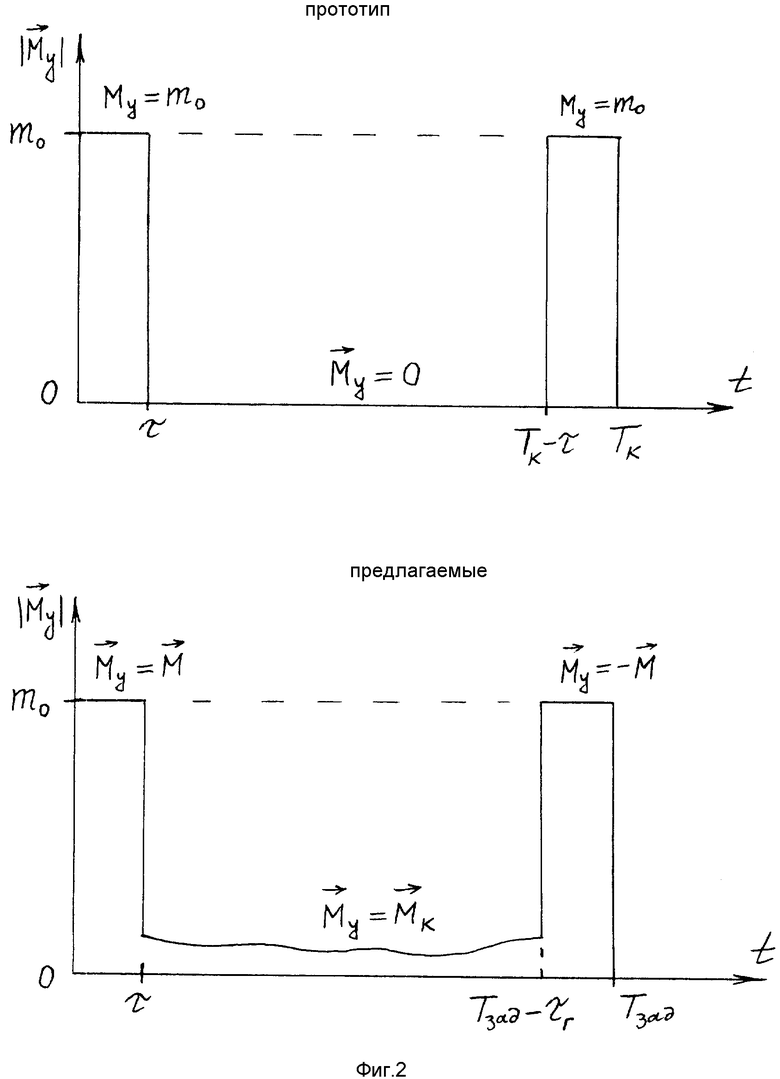
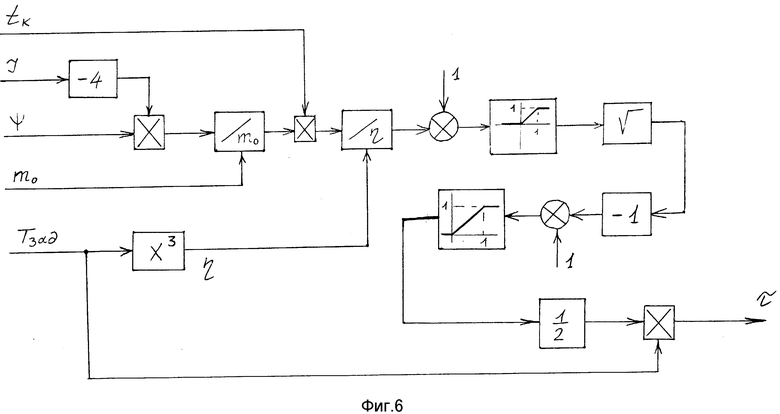
Способ управления разворотом космического аппарата (КА) и система для его реализации предназначены для перевода КА из произвольного начального углового положения в заданное конечное угловое положение за фиксированное время. Предлагаемый способ реализует разворот КА по траектории свободного движения. При этом направление кинетического момента КА остается постоянным относительно абсолютного пространства во все время разворота. Высокие точности по положению и времени окончания разворота обеспечиваются тем, что определяют прогнозируемое время окончания маневра, сравнивают его с заданным временем разворота, по результатам сравнения корректируют расчетное значение вектора кинетического момента и фиксируют его в инерциальном базисе, по окончании действия разгонного импульса по измеренным параметрам углового движения аппарата формируют и прикладывают к аппарату управляющий момент, обеспечивающий движение КА с расчетным кинетическим моментом, а торможение КА начинают с момента, когда время на доворот аппарата до конечного углового положения станет равным времени гашения текущего кинетического момента. Система, реализующая разворот КА по этому способу, производит автоматическое определение параметров попадающей траектории. 2 с. и 3 з.п. ф-лы, 13 ил.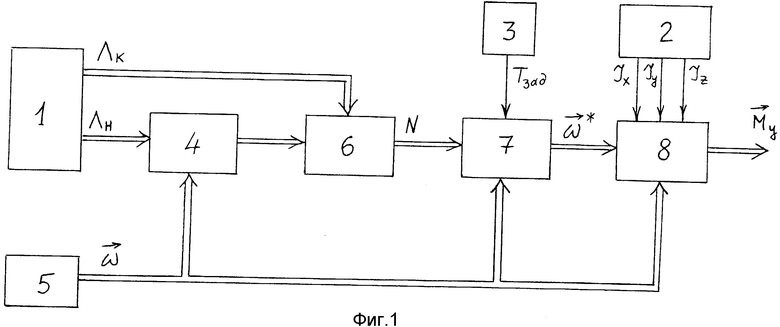
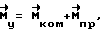
где  компенсационный момент;
компенсационный момент;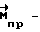 прогнозируемый момент,
прогнозируемый момент,
до тех пор, пока время на доворот аппарата до конечного углового положения τд не станет равным времени гашения текущего кинетического момента τг.
2. Способ по п.1, отличающийся тем, что управляющий момент, прикладываемый к аппарату на этапе между разгоном и торможением, определяют по выражению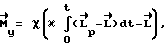
где 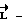 фактический кинетический момент аппарата;
фактический кинетический момент аппарата;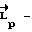 расчетное значение кинетического момента;
расчетное значение кинетического момента;
t - время с момента окончания участка разгона;
χ - коэффициент усиления;
κ - коэффициент апериодичности (1 ≤ κ ≤ 1000 c-1, χ > 4κ).
3. Способ по п.1 и 2, отличающийся тем, что управляющий момент, прикладываемый к аппарату на этапе между разгоном и торможением, определяют по выражению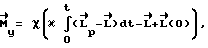
где 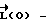 значение кинетического момента аппарата на момент окончания участка разгона.
значение кинетического момента аппарата на момент окончания участка разгона.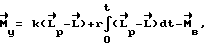
где 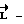 фактический кинетический момент аппарата;
фактический кинетический момент аппарата;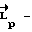 расчетное значение кинетического момента;
расчетное значение кинетического момента;
k, r - коэффициенты усиления;
t - время с момента окончания участка разгона;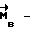 расчетное значение возмущающего момента, (0,01 ≤ k ≤ 1000 c-1, 0 ≤ r/k < 2c-1).
расчетное значение возмущающего момента, (0,01 ≤ k ≤ 1000 c-1, 0 ≤ r/k < 2c-1).
| RU, патент, 2006431, кл | |||
| Нефтяной конвертер | 1922 |
|
SU64A1 |
Авторы
Даты
1998-07-10—Публикация
1997-06-24—Подача