Изобретение относится к космической технике и может быть использовано для эффективного управления угловым положением космических аппаратов и орбитальных станций.
Наиболее известным способом управления пространственным разворотом космического аппарата (КА) является изменение углового его положения путем выполнения последовательных поворотов на определенные углы вокруг осей, жестко связанных с аппаратом [1] . Возможен следующий порядок разворотов (поворотов) - поворот КА вокруг продольной его оси X до совмещения одной из связанных с КА поперечных осей Y или Z с требуемым ее положением в пространстве Yк (или Zк соответственно), а затем поворот вокруг этой поперечной оси до совмещения продольной оси X с заданным положением X [2]. Системы управления, реализующие развороты вокруг связанных осей КА, широко известны и хорошо изучены. При многих достоинствах подобных систем, включая их простоту и надежность, они имеют один существенный недостаток - такие поворотные маневры имеют большую продолжительность и требуют значительных энергозатрат.
Ближайшим по технической сущности является способ управления пространственным разворотом динамически симметричного КА [3], включающий разгон космического аппарата, свободное его вращение и торможение космического аппарата.
Его и принимаем в качестве прототип. При этом способе управления предлагается, что космический аппарат движется по коническим траекториям, совершая при этом регулярную прецессию. Движение состоит из участков, где действует максимальный момент m0 (участки разгона и торможения КА), и участка свободного движения, на котором управляющий момент равен нулю.
Определяющими характеристиками процесса разворота являются время разгона (торможения) τ и время свободного движения tсв, которые вычисляются по соотношениям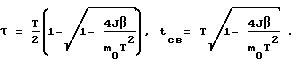
где
J = 0,5 (J2 + J3) - момент инерции КА относительно поперечной оси;
m0 - величина максимального момента управления;
T - заданное время разворота;
β - угол поворота КА вокруг оси прецессии.
Управляющие моменты формируются на участках разгона и торможения исходя из выражения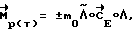
где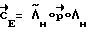 - направление разворота (направление кинетического момента в инерциальном базисе),
- направление разворота (направление кинетического момента в инерциальном базисе),
Λн - кватернион начального положения КА,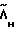 - кватернион текущего положения КА.
- кватернион текущего положения КА.
Знак "+" соответствует участку разгона, а знак "-" - участку торможения. Вектор разворота 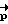 однозначно определяется начальным Λн и конечным Λк положениями КА. Символ "o" обозначает операцию умножения кватернионов, а
однозначно определяется начальным Λн и конечным Λк положениями КА. Символ "o" обозначает операцию умножения кватернионов, а  - кватернион, сопряженный кватерниону Λ.
- кватернион, сопряженный кватерниону Λ.
Приведение КА из начального углового положения Λн в требуемое конечное положение Λк, производится следующим образом. Прежде всего определяется кватернион разворота 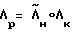 , исходя из которого вычисляют орт
, исходя из которого вычисляют орт 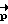 (вектор разворота) и угол поворота β с учетом инерционных характеристик КА J, J1; где J1 - момент инерции КА относительно продольной оси, Λк - кватернион конечного положения КА.
(вектор разворота) и угол поворота β с учетом инерционных характеристик КА J, J1; где J1 - момент инерции КА относительно продольной оси, Λк - кватернион конечного положения КА.
По заданному времени разворота T и углу поворота β определяют время разгона τ. Требуемая величина кинетического момента K0 определяется по соотношению: K0= m0τ. С момента поступления команды на разворот к КА прикладывают управляющий момент 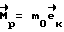 до тех пор, пока величина фактического кинетического момента
до тех пор, пока величина фактического кинетического момента  не станет равна расчетному значению K0. Здесь
не станет равна расчетному значению K0. Здесь 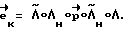 В момент времени, когда
В момент времени, когда 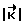 = K0, начинается участок свободного движения КА, на котором управляющий момент отсутствует
= K0, начинается участок свободного движения КА, на котором управляющий момент отсутствует 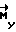 = 0. Через время T-τ с начала разворота производят торможение КА по закону
= 0. Через время T-τ с начала разворота производят торможение КА по закону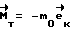 .
.
В момент времени, когда  = 0, разворот КА будет завершен.
= 0, разворот КА будет завершен.
Недостатком способа-прототипа является низкая точность разворота в случае несимметричного КА и при разворотах на большие углы, так как на участке свободного движения не производится контроль кинематических параметров.
Техническим результатом данного изобретения является существенное повышение точности разворота произвольного КА при относительно низких энергетических затратах.
Указанный технический результат достигается тем, что в предлагаемом способе управления пространственным разворотом космического аппарата, включающем определение параметров разворота, формирование и с заданного момента времени приложение разгонного импульса, свободное вращение аппарата, формирование и приложение тормозного импульса, в отличие от прототипа на этапе между разгоном и торможением в определенные дискретные моменты времени ti
ti > ti-1 + tсч, i = 1, 2, 3, 4, ...,
где
tсч - время расчета кинетического момента  , необходимого для приведения космического аппарата при свободном его вращении из текущего углового положения в заданное конечное угловое положение; сравнивают угол доворота аппарата до конечного углового положения νост с расчетным углом поворота аппарата при торможении ψрас , в случае выполнения условия νост>ψрас определяют кинетический момент
, необходимого для приведения космического аппарата при свободном его вращении из текущего углового положения в заданное конечное угловое положение; сравнивают угол доворота аппарата до конечного углового положения νост с расчетным углом поворота аппарата при торможении ψрас , в случае выполнения условия νост>ψрас определяют кинетический момент 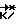 , сравнивают его с фактическим кинетическим моментом аппарата
, сравнивают его с фактическим кинетическим моментом аппарата 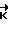 и в случае
и в случае 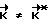 прикладывают к аппарату управляющий момент, вычисляемый, например, по формуле
прикладывают к аппарату управляющий момент, вычисляемый, например, по формуле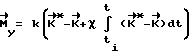
где
k - коэффициент усиления (k > 0); [k] = с-1;
χ - коэффициент апериодичности 0 ≤ χ ≤ 1.5; [χ] = c-1
до момента выполнения равенства 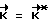 , а с момента выполнения равенства: νост= ψрас прикладывают тормозной импульс.
, а с момента выполнения равенства: νост= ψрас прикладывают тормозной импульс.
Указанный технический результат достигается и тем, что в предлагаемом способе по пункту 1 дискретные моменты времени ti определяют условием
ti= ti-1+Δt,
где
Δt = const - принятая дискретность по времени;
max{τ,tcч+τ/2} ≤ Δt ≤ T/3 ,
τ - время разгона аппарата;
T - заданное время разворота.
Указанный технический результат достигается и тем, что в предлагаемом способе по пункту 1 дискретные моменты времени ti определяются как соответствующие моментам времени, в которые выполняется условие
ϕi= ϕi-1-Δϕ,
где
Δϕ = const - принятая дискретность по углу;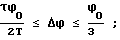
ϕ0 - величина угла разворота, определенная на начало разворота;
ϕi - величина угла разворота в i-й дискретный момент времени ti;
τ - время разгона аппарата;
T - заданное время разворота.
Указанный технический результат достигается и тем, что в предлагаемом способе дискретные моменты времени ti определяются условием
ti= ti-1+Δt1-d(i-1),
где
d = const - разность арифметической прогрессии;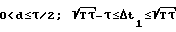
Указанный технический результат достигается и тем, что в предлагаемом способе дискретные моменты времени ti определяются как соответствующие моментам времени, в которые выполняется условие
ϕi= ϕi-1-Δϕ1+dϕ•(i-1),
где
dϕ = const - разность арифметической прогрессии по углу;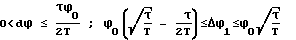
Указанный технический результат достигается и тем, что в предлагаемом способе дискретные моменты времени ti определяются условием
ti= ti-1+Δt1•q
где
q = const - знаменатель геометрической прогрессии;
1,05 ≤ q ≤ 2,5; Δt1 = T(1-q-1).
Указанный технический результат достигается и тем, что в предлагаемом способе дискретные моменты времени ti определяются как соответствующие моментам времени, в которые выполняется условие
ϕi= ϕi-1-Δϕ1•q
где
q = const - знаменатель геометрической прогрессии;
1,05 ≤ q ≤ 2,5;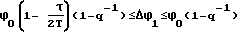
Указанный технический результат достигается и тем, что в предлагаемом способе величины углов разворота, соответствующие дискретным моментам времени ti образуют убывающую геометрическую прогрессию
ϕi= ϕ0•a-1,
где
ϕ0 - величина угла разворота до начала разворота;
ϕi - величина угла разворота в i-й дискретный момент времени ti;
а - постоянное число (1,1 ≤ а ≤ 4).
Сущность предлагаемого способа заключается в управлении угловым движением КА по методу свободных траекторий. Однако при отсутствии контроля фактического вращения КА до самого начала торможения ошибка переориентации может оказаться недопустимо большой. Уменьшить величину ошибки переориентации возможно за счет приложения импульсов коррекции внутри неуправляемого участка вращения КА. Учитывая, что фактическое движение КА отличается от прогнозируемого незначительно, применяем следующий принцип формирования управляющих моментов в процессе разворота. Он состоит в коррекции траектории движения КА в определенные дискретные моменты времени. Коррекция сводится к определению требуемого для попадания КА в конечное положение Λк кинетического момента 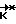 и сообщения поправочного импульса
и сообщения поправочного импульса 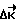 к имеющемуся кинетическому моменту КА
к имеющемуся кинетическому моменту КА  . Вся траектория движения будет состоять из чередующихся управляемых и неуправляемых участков и включать в себя участки разгона и торможения, участки свободного движения
. Вся траектория движения будет состоять из чередующихся управляемых и неуправляемых участков и включать в себя участки разгона и торможения, участки свободного движения 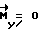 и кратковременные участки коррекции траектории. Задача управления состоит в обеспечении для неуправляемых участков таких начальных условий, при которых движение по прогнозу проходит через конечное положение Λк. Для этого на начало каждого участка ti определяется кватернион разворота
и кратковременные участки коррекции траектории. Задача управления состоит в обеспечении для неуправляемых участков таких начальных условий, при которых движение по прогнозу проходит через конечное положение Λк. Для этого на начало каждого участка ti определяется кватернион разворота 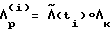 , по которому определяются требуемые начальные условия ω10,ω20,ω30 для следующего участка.
, по которому определяются требуемые начальные условия ω10,ω20,ω30 для следующего участка.
Необходимо заметить, что движение КА существенно отличается, от регулярной прецессии (т.к. КА не обладает динамический симметрией) и вектор разворота 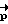 не может быть найден аналитически. Однако, имея математическую модель фактического КА и применяя метод последовательных приближений, можно определить для любых начального Λ0 и конечного Λк положений КА и времени разворота T направление вектора кинетического момента
не может быть найден аналитически. Однако, имея математическую модель фактического КА и применяя метод последовательных приближений, можно определить для любых начального Λ0 и конечного Λк положений КА и времени разворота T направление вектора кинетического момента 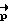 , соответствующего траектории свободного движения КА, проходящей через Λ0 и Λк.
, соответствующего траектории свободного движения КА, проходящей через Λ0 и Λк.
Космический аппарат характеризуется прежде всего инерционными характеристиками J1, J2, J3. Начальное и конечное угловые положения задаются кватернионами Λн и Λк. Определение орта 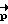 -вектора разворота, соответствующего полодии, проходящей через начальное и конечное угловые положения, и обеспечивающего перевод КА в заданное положение Λк при свободном его вращении, осуществляется методом последовательных приближений. В качестве первого приближения
-вектора разворота, соответствующего полодии, проходящей через начальное и конечное угловые положения, и обеспечивающего перевод КА в заданное положение Λк при свободном его вращении, осуществляется методом последовательных приближений. В качестве первого приближения 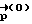 принимается значение вектора разворота, соответствующего развороту динамически симметричного тела на кватернион Λp, которое вычисляется в результате решения системы уравнений
принимается значение вектора разворота, соответствующего развороту динамически симметричного тела на кватернион Λp, которое вычисляется в результате решения системы уравнений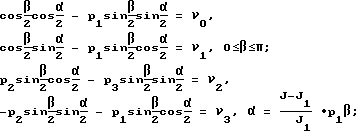
где
J, J1 - моменты инерции КА,
ν0,ν1,ν2,ν3 - компоненты кватерниона разворота 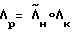 .
.
Математическая модель вращательного движения КА имеет вид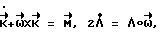
где = {M1, M2, M3] - момент внешних сил,
= {M1, M2, M3] - момент внешних сил,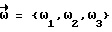 - вектор угловой скорости,
- вектор угловой скорости,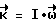 - кинетический момент КА,
- кинетический момент КА,
Ι - тензор инерции КА.
Здесь "x" означает векторное произведение векторов.
Моделируя движение КА с начальными условиями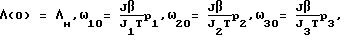
где
β - угол поворота, соответствующий вектору разворота 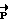 ;
;
J - момент инерции КА относительно поперечной оси;
T - время разворота;
и учитывая, что 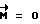 , определим промах разворота
, определим промах разворота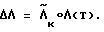 .
.
Введя полученный промах ΔΛ в качестве поправки к предыдущему кватерниону разворота, определим новые параметры разворота 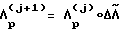 и соответствующие ему
и соответствующие ему 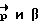 . Схема итерационного процесса проста
. Схема итерационного процесса проста 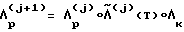 . Вектор
. Вектор 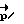 будет определен, когда Sqαl(ΔΛ)>εдоп. Направление разворота
будет определен, когда Sqαl(ΔΛ)>εдоп. Направление разворота 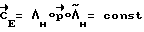 . Величина кинетического момента определяется управляющими возможностями системы исполнительных органов m0, моментом инерции относительно поперечной оси J, углом поворота β и заданным временем разворота T.
. Величина кинетического момента определяется управляющими возможностями системы исполнительных органов m0, моментом инерции относительно поперечной оси J, углом поворота β и заданным временем разворота T.
K0= m0τ ,
где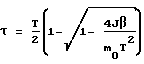 .
.
На участках разгона и торможения управляющие моменты максимальны, а на участках коррекции траектории углового движения КА управляющий момент носит импульсный характер.
На участке неуправляемого движения КА (на этапе между разгоном и торможением КА) контроль движения КА осуществляют лишь в определенные дискретные моменты времени ti. Прежде всего сравнивают угол доворота νост с расчетной величиной ψрас , где νост= 2arccosλg0,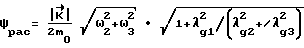
λд0,λд1,λд2,λд3 - компоненты кватерниона доворота.
Если νост> ψрас, то производят коррекцию углового движения КА путем целенаправленного изменения его кинетического момента. Для этого определяют такое расчетное значение вектора кинетического момента 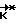 , при котором КА при свободном его вращении из текущего углового положения Λ(ti) перейдет в заданное конечное угловое положение Λк , и затем прикладывают к корпусу КА управляющий момент
, при котором КА при свободном его вращении из текущего углового положения Λ(ti) перейдет в заданное конечное угловое положение Λк , и затем прикладывают к корпусу КА управляющий момент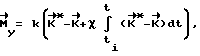
до установления равенства 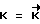 . Как только фактический кинетический момент
. Как только фактический кинетический момент  станет равен расчетному значению
станет равен расчетному значению 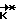 , аппарат предоставляют самому себе до следующей коррекции (до наступления следующего момента времени ti). Последовательность времен ti определяется программой полета, исходя из приоритета решаемых параллельно с разворотом задач, и может задаваться как исходные данные в виде цифрового массива в программно-временном устройстве.
, аппарат предоставляют самому себе до следующей коррекции (до наступления следующего момента времени ti). Последовательность времен ti определяется программой полета, исходя из приоритета решаемых параллельно с разворотом задач, и может задаваться как исходные данные в виде цифрового массива в программно-временном устройстве.
Расчетное значение вектора кинетического момента 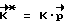 , где
, где 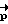 - вектор разворота, K - величина фактического кинетического момента на время ti.
- вектор разворота, K - величина фактического кинетического момента на время ti.
Определение вектора разворота 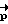 сводится к решению краевой задачи: Λ0= Λ(ti),Λ(T) = Λк при имеющихся дифференциальных связях, накладываемых на движение КА
сводится к решению краевой задачи: Λ0= Λ(ti),Λ(T) = Λк при имеющихся дифференциальных связях, накладываемых на движение КА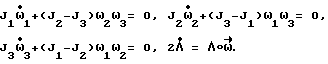
Таким образом, управление программным разворотом КА в предлагаемом способе сводится к следующему:
1) расчет требуемого значения вектора разворота 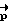 и сообщение корпусу КА кинетического момента расчетной величины (разгон КА); момент управления формируется по закону
и сообщение корпусу КА кинетического момента расчетной величины (разгон КА); момент управления формируется по закону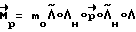
2) свободное вращение КА по падающей траектории 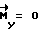 ;
;
3) в дискретные моменты времени ti, задаваемые программно-временным устройством по какой-либо программе, проверяют условие
νост> ψрас ,
где
νост - угол доворота космического аппарата до конечного углового положения;
ψрас - расчетный угол поворота космического аппарата при торможении;
и в случае его выполнения производят коррекцию траектории вращения КА, которая заключается в определении расчетного значения вектора кинетического момента 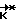 , необходимого для приведения КА при свободном его вращении из текущего углового положения
, необходимого для приведения КА при свободном его вращении из текущего углового положения 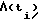 в заданное конечное угловое положение Λк, и приложении к космическому аппарату управляющего момента
в заданное конечное угловое положение Λк, и приложении к космическому аппарату управляющего момента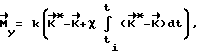
где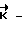 - фактический кинетический момент аппарата;
- фактический кинетический момент аппарата;
k - коэффициент усиления (k > 0);
χ - - коэффициент апериодичности, 0 ≤ χ ≤ 1,5;
до совмещения фактического кинетического момента аппарата с расчетным его значением 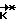 . После выполнения условия
. После выполнения условия 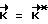 происходит свободное движение КА (
происходит свободное движение КА ( 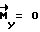 );
);
4) в момент выполнения равенства νост= ψрас начинают гашение угловой скорости КА (торможение КА);
момент управления формируется по закону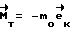 ,
,
где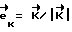 .
.
Отличительной особенностью предложенных технических решений является наличие математической модели фактически несимметричного КА, а также организация и выполнение на этапе между разгоном и торможением импульсных коррекций движения КА. Расчет требуемого кинетического момента 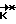 носит итерационный характер и описывается алгоритмом
носит итерационный характер и описывается алгоритмом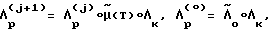
где
μ(T) - прогнозируемое угловое положение КА на момент времени T, полученное моделированием движения КА.
При проведении коррекции свободного вращения аппарата момент управления 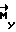 формируется по отклонению кинетического момента
формируется по отклонению кинетического момента 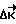 . Линейная часть управляющей функции обеспечивает уменьшение отклонения
. Линейная часть управляющей функции обеспечивает уменьшение отклонения 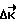 до нуля, а введение в управляющую функцию интегральной составляющей повышает быстродействие коррекции.
до нуля, а введение в управляющую функцию интегральной составляющей повышает быстродействие коррекции.
Предлагаемое сочетание свободного разворота с кратковременными коррекциями позволяет при довольно низком расходе топлива добиваться большой точности разворота при любых неизвестных возмущениях. Экономичность разворота достигается тем, что на большей части траектории управление отсутствует (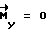 ), а повышение точности обеспечивается организацией и проведением в определенные дискретные моменты времени ti кратковременных коррекций углового движения аппарата.
), а повышение точности обеспечивается организацией и проведением в определенные дискретные моменты времени ti кратковременных коррекций углового движения аппарата.
Приводим перечень фигур.
Фиг. 1 - функциональная схема системы для реализации способа;
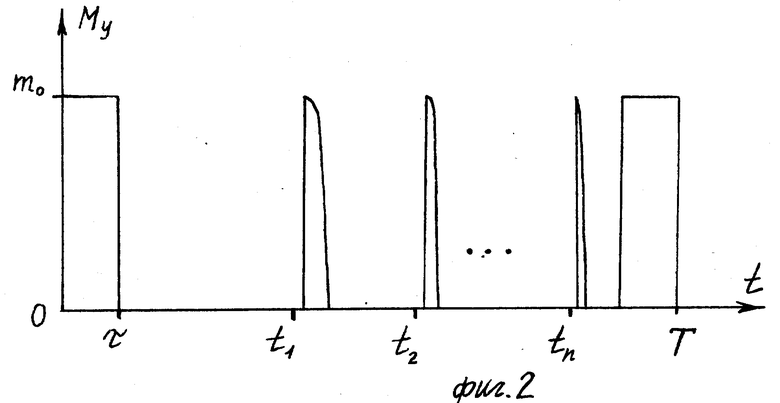
фиг. 2 - временные диаграммы управляющих воздействий.
Пример реализации предложенного способа представлен фиг. 1, где обозначено 1 - устройство ввода и хранения начального и коечного положений КА (УВХНКП), 2 - блок задатчиков моментов инерции КА (БЗМИ), 3 - устройство ввода времени разворота (УВВР), 4 - бесплатформенная инерциальная навигационная система (БИНС), 5 - блок датчиков угловых скоростей (БДУС), 6 - вычислительное устройство (ВУ), 7 - блок хранения коэффициентов закона управления (БХКЗУ), 8 -программно-временное устройство (ПВУ), 9 - согласующе-преобразующее устройство (СПУ), 10 - исполнительные органы (ИО), при этом первый выход УВХНКП-1 связан с первым входом ВУ-6, второй выход УВХНКП-1 связан с вторым входом ВУ-6, выход БЗМИ-2 связан с третьим входом ВУ-6, выход УВВР-3 связан с четвертым входом ВУ-6, выход БИНС-4 связан с пятым входом ВУ-6, выход БДУС-5 связан с входом БИНС-4 и с шестым входом ВУ-6, выход ВУ-6 связан с входом СПУ-9, первый выход БХКЗУ-7 связан с седьмым входом ВУ-6, второй выход БХКЗУ-7 связан с восьмым входом ВУ-6, выход ПВУ-8 связан с девятым входом ВУ-6, первый выход СПУ-9 связан с исполнительными органами первого канала, второй выход СПУ-9 связан с исполнительными органами второго канала, третий выход СПУ-9 связан с исполнительными органами третьего канала.
В системе автоматически определяется и фиксируется направление кинетического момента в инерциальном базисе 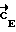 , обеспечивающего перевод КА из положения Λн в требуемое положение Λк за время T с допустимой точностью εдоп.
, обеспечивающего перевод КА из положения Λн в требуемое положение Λк за время T с допустимой точностью εдоп.
Отметим, что вычислительное устройство производит все математические операции, необходимые для реализации способа, и содержит в себе математическую модель углового движения КА. По начальному и конечному положениям КА и его инерционным характеристикам ВУ-6 осуществляет расчет требуемого кинетического момента 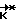 по методу итераций. Отклонение прогнозируемого положения КА μ(T) от требуемого Λк определяется путем математического моделирования в ВУ-6. Итерационный процесс
по методу итераций. Отклонение прогнозируемого положения КА μ(T) от требуемого Λк определяется путем математического моделирования в ВУ-6. Итерационный процесс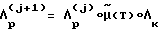
повторяется пока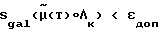
где
Λ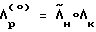 ;
;
Λ
В качестве вычислительного устройства может быть использована БЦВМ, но тогда в систему необходимо ввести интерфейс сопряжения и обмена информацией с измерительными приборами и исполнительными органами.
Моменты времени ti, в которые производят коррекцию углового движения КА, задаются программно-временным устройством.
Работает система, реализующая предлагаемый способ управления пространственным разворотом КА, следующим образом. По значениям моментов инерции КА J1, J2, J3 ВУ-6 вычисляет значение момента инерции вокруг поперечной оси J согласно выражению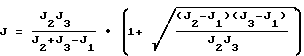 .
.
далее по начальному Λн = и конечному Λк положениям КА, заданному времени разворота T и инерционным характеристикам J1, J2, J3 в ВУ-6 осуществляется расчет вектора разворота 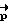 (путем решения краевой задачи) и соответствующего ему угла поворота β . Исходя из него ВУ-6 определяет время разгона τ по выражению:
(путем решения краевой задачи) и соответствующего ему угла поворота β . Исходя из него ВУ-6 определяет время разгона τ по выражению: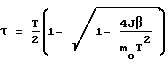
и расчетную величину кинетического момента K0= m0τ .
В исходном состоянии 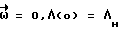 выход вычислительного устройства замаскирован и
выход вычислительного устройства замаскирован и 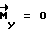 . В момент поступления команды на разворот ВУ-6 формирует управляющий момент
. В момент поступления команды на разворот ВУ-6 формирует управляющий момент 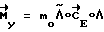 , который прикладывают к КА посредством ИО-10. Расчет текущего кинетического момента
, который прикладывают к КА посредством ИО-10. Расчет текущего кинетического момента  ВУ-6 производит непрерывно по показаниям ДУС-5
ВУ-6 производит непрерывно по показаниям ДУС-5  и моментам инерции Jj:Kj= Jjωj . Как только КА будет сообщен кинетический момент расчетной величины K0, выход ВУ-6 маскируется, управляющие моменты отсутствуют
и моментам инерции Jj:Kj= Jjωj . Как только КА будет сообщен кинетический момент расчетной величины K0, выход ВУ-6 маскируется, управляющие моменты отсутствуют 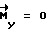 и КА производит свободное вращение. В момент времени ti, определяемый тактовым импульсом с выхода ПВУ-8, ВУ-6 определяет величину угла доворота νост= arccosλgo и сравнивает его с расчетной величиной
и КА производит свободное вращение. В момент времени ti, определяемый тактовым импульсом с выхода ПВУ-8, ВУ-6 определяет величину угла доворота νост= arccosλgo и сравнивает его с расчетной величиной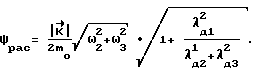
Если νост> ψрас , то ВУ-6 фиксирует кватернион разворота из текущего углового положения в заданное конечное Λк , исходя из которого методом последовательных приближений рассчитывает вектор разворота 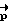 и расчетное значение вектора кинетического момента
и расчетное значение вектора кинетического момента 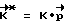 , где K - величины фактического кинетического момента на момент времени ti. ИО-10 сообщают КА корректирующий импульс
, где K - величины фактического кинетического момента на момент времени ti. ИО-10 сообщают КА корректирующий импульс 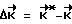 путем приложения управляющего момента
путем приложения управляющего момента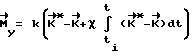 ,
,
рассчитываемого в ВУ-6.
Как только 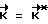 , выход ВУ-6 маскируется, управляющие моменты отсутствуют
, выход ВУ-6 маскируется, управляющие моменты отсутствуют 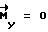 и КА производит свободное вращение до следующего момента времени ti. В момент равенства углов νост= ψрас производят торможение КА; управляющие моменты формируются исходя из выражения
и КА производит свободное вращение до следующего момента времени ti. В момент равенства углов νост= ψрас производят торможение КА; управляющие моменты формируются исходя из выражения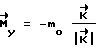 .
.
Когда 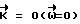 , выход ВУ-6 маскируется, исполнительные органы отключены, разворот завершен. Система готова к следующему развороту КА.
, выход ВУ-6 маскируется, исполнительные органы отключены, разворот завершен. Система готова к следующему развороту КА.
Временные диаграммы приведены на фиг. 2.
Данная схема разворота снижает влияние внешних возмущающих моментов на точность разворота. Расход рабочего тела на корректирующие импульсы незначителен.
Моменты проведения коррекций ti могут определяться и автоматически самой системой управления по какому-нибудь закону (или рекурентному соотношению). Простейшим является случай, когда коррекции следуют с равной частотой, т.е. интервал между соседними дискретными моментами времени ti постоянный Δt = t1 - ti-1 = const. Принятая дискретность по времени Δt ограничена снизу не только быстродействием ВУ-6, характеризующимся временем расчета tcч, но и временем разгона τ (т.к. за меньшее время отклонение фактического движения КА от расчетного незначительно и расчет 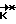 будет бессмысленным). Но Δt/ ограничена и сверху заданным временем разворота T. Исходя из того, что одной коррекции свободного вращения КА, как правило, недостаточно для обеспечения приемлемой точности разворота, минимальное число коррекций принимаем равным 2. Отсюда
будет бессмысленным). Но Δt/ ограничена и сверху заданным временем разворота T. Исходя из того, что одной коррекции свободного вращения КА, как правило, недостаточно для обеспечения приемлемой точности разворота, минимальное число коррекций принимаем равным 2. Отсюда
max{τ,tcч+τ/2} ≤ Δt≤T/3,
где
t0 - время окончания участка разгона КА.
Для этого случая реализации в качестве ПВУ-8 может выступать генератор тактовых импульсов (с заданной частотой их выдачи f = Δt-1 ).
Иногда желательно контролировать движение КА по угловому рассогласованию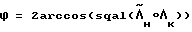 .
.
Пусть Δϕ = ϕi-ϕi-1= const , где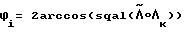
величина угла разворота в момент времени ti. Повышение точности разворота может быть достигнуто путем увеличения числа коррекций траектории движения КА. В этом случае Δϕ не превышает ϕ0/3 ; 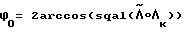 . С другой стороны, независимо от заданного времени разворота T дискретность по углу Δϕ должна быть не менее угла поворота КА на этапе разгона ϕраз , который связан с временем разгона τ соотношением ϕраз= ωpτ/2 , где средняя угловая скорость ωp оценивается величиной ωp≈ ϕ0/T . Таким образом,
. С другой стороны, независимо от заданного времени разворота T дискретность по углу Δϕ должна быть не менее угла поворота КА на этапе разгона ϕраз , который связан с временем разгона τ соотношением ϕраз= ωpτ/2 , где средняя угловая скорость ωp оценивается величиной ωp≈ ϕ0/T . Таким образом,
0,5τϕ0/T≤Δϕ≤ϕ0/3.
Для повышения точности управления формирование управляющих моментов с целью коррекции вращательного движения КА следует производить несколько чаще по мере приближения КА к требуемому положению Λк . Например, длительность интервала между соседними моментами времени уменьшаем по арифметической прогрессии:
Δti= Δti-1-d ,
где
Δti = ti - ti-1; d = const.
Аналогичный принцип определения моментов проведения коррекции возможен и по шкале углов:
Δϕi= Δϕi-1-dϕ ,
где
Δϕi= ϕi-ϕi-1;ϕ = const
Величину d и время неуправляемого участка (время до первой коррекции Δt1 выбираем из требования, чтобы время между последними коррекциями было не меньше времени разгона τ .
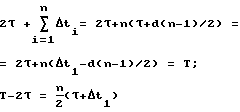
Для угловых величин условия реализуемости будут следующими: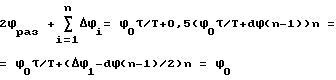
Обычно число коррекций n пропорционально углу разворота ϕ0 , поэтому dϕ ≤ 0,5ϕ0τ/T . Величина Δϕ1 определяется из предположения, что dϕ максимально dϕmax= 0,5ϕ0τ/T , откуда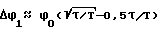 .
.
Значение d определяется из пропорции d : T = dϕ:ϕ0, откуда 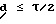 . Для предельного dmax = dτ/2 получим
. Для предельного dmax = dτ/2 получим 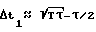 .
.
При d = 0 или dϕ = 0 получим частный случай равномерной последовательности чисел ti (или ϕi ).
Представляется возможным задать и более сложный закон формирования моментов выдачи корректирующих импульсов ti, который учитывает фазу разворота (по времени с окончания разгона КА или по оставшемуся углу до конечного положения). Принимаем, что длительность интервала между соседними моментами времени ti уменьшается по геометрической прогрессии
Δti= Δti-1/q , q = const, q > 1.
Условием осуществимости разворота в этом случае будет
τ+Δt1/(1-q-1)≥T
для чего достаточно положить Δt1= T(1-q-1) . Аналогично можно потребовать, чтобы разность углов разворота ϕi , соответствующих соседним дискретным моментам времени ti, уменьшалась по геометрической прогрессии
Δϕi= Δϕi-1/q , q = const.
Для угловых величин получим аналогичные соотношения:
ϕ0≤ ϕраз+Δϕ1/(1-q-1) или Δϕ1/(1-q-1)≤ϕ0 ;
откуда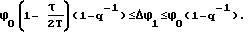 .
.
Постоянная q всегда больше 1. Зададим Δϕ1≤ 0,6ϕ0 (или Δt1≤ 0,6T) и получим верхнюю границу qmax = 2,5.
Рассмотренные схемы разворота снижают влияние случайных факторов на точность разворота.
В ряде случаев оказывается предпочтительным логарифмический (или показательный) закон изменения углов ϕi , при котором ϕi= ϕi-1/a , где а - некоторое постоянное число (а > 1). Чтобы коррекции свободного движения КА не были слишком частыми аmin = 1,1. Максимальное его значение выбираем с помощью численного эксперимента аmax ≈ 4.В результате d∈ [1,1; 4], при котором происходит несколько коррекций и обеспечивается необходимая степень точности разворота КА.
Эффективность предлагаемого способа определяется прежде всего тем, что на большей части траектории движения управляющий момент равен нулю, что экономит топливо. Вместе с тем способ предполагает принцип управления по отклонению при подходе к заданному угловому положению Λк , чем и обеспечивает высокую точность разворота в условиях действия значительных внешних возмущающих моментов.
Изобретение относится к средствам эффективного управления угловым положением космических аппаратов (КА) и орбитальных станций. Сущность предлагаемого способа состоит в определении параметров разворота КА (на этапах разгона, свободного вращения и торможения) в требуемое угловое положение за заданное время, причем в свободном вращении КА сравнивают требуемый угол его доворота с расчетным углом поворота КА при торможении и в случае превышения первым расчетного значения импульсно корректируют угловое движение КА, определяя расчетный кинетический момент, необходимый для приведения КА при свободном вращении в заданное угловое положение, прикладывают к КА управляющий момент до совмещения фактического кинетического момента с расчетным. Торможение КА начинают при равенстве угла его доворота расчетному углу поворота КА при торможении. В результате повышается точность разворота КА при пониженных энергозатратах. 7 з.п. ф-лы, 2 ил.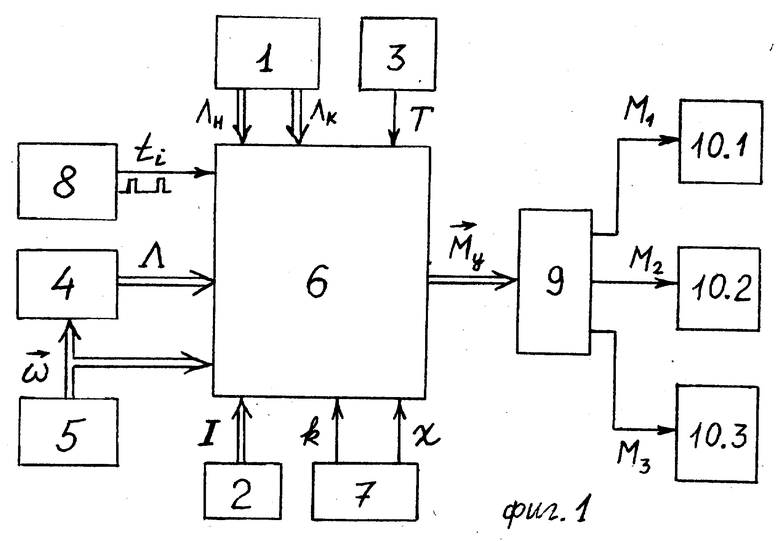
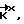 необходимого для приведения космического аппарата при свободном вращении из текущего углового положения в заданное конечное угловое положение, в случае выполнения условия ϑост > Ψрас рассчитывают указанный кинетический момент
необходимого для приведения космического аппарата при свободном вращении из текущего углового положения в заданное конечное угловое положение, в случае выполнения условия ϑост > Ψрас рассчитывают указанный кинетический момент 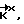 сравнивают его с фактическим кинетическим моментом
сравнивают его с фактическим кинетическим моментом  аппарата и при несовпадении указанных кинетических моментов прикладывают к космическому аппарату управляющий момент коррекции до выполнения равенства
аппарата и при несовпадении указанных кинетических моментов прикладывают к космическому аппарату управляющий момент коррекции до выполнения равенства 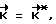 а с момента выполнения равенства ϑост = Ψрас прикладывают тормозной импульс.
а с момента выполнения равенства ϑост = Ψрас прикладывают тормозной импульс.
ti = ti-1+Δt,
где Δt = const - принятая дискретность по времени max{τ,tcч+τ/2} ≤ Δt ≤ T/3;
τ - время разгона аппарата;
T - заданное время разворота.
ϕi= ϕi-1-Δϕ,
где Δϕ = const - принятая дискретность по углу,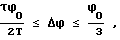
ϕ0 - величина угла разворота, определенная на начало разворота;
ϕi - величина угла разворота в i-й дискретный момент времени ti;
τ - время разгона аппарата;
T - заданное время разворота.
ti= ti-1+Δt1-d•(i-1),
где d = const - разность арифметической прогрессии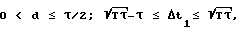
τ, T - время разгона и заданное время разворота аппарата.
ϕi= ϕi-1-Δϕi+dϕ•(i-1),
где dϕ = const - разность арифметической прогрессии по углу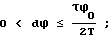
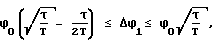
ϕ0 - величина угла разворота, определенная на начало разворота;
ϕi - величина угла разворота в момент времени ti;
τ - время разгона аппарата;
T - заданное время разворота.
ti= ti-1+Δt1•q1-i,
где q = const - знаменатель геометрической прогрессии
1,05 ≤ q ≤ 2,5;
Δt1= T(1-q-1);
τ, T - время разгона и заданное время разворота аппарата.
ϕi= ϕi-1Δϕiq1-i,
где q = const - знаменатель геометрической прогрессии
1,05 ≤ q ≤ 2,5; 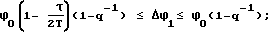
ϕ0 - величина угла разворота, определенная на начало разворота;
ϕi - величина угла разворота в момент времени ti;
τ, T - время разгона и заданное время разворота аппарата.
ϕi = ϕ0a-i,
где ϕ0 - величина угла разворота, определенная на начало разворота;
ϕi - величина угла разворота в i-й дискретный момент времени ti;
a - постоянное число (1,1 ≤ a ≤ 4).
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Раушенбах Б.В., Токарь Е.Н | |||
| ПРИБОР ДЛЯ ЗАПИСИ И ВОСПРОИЗВЕДЕНИЯ ЗВУКОВ | 1923 |
|
SU1974A1 |
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Алексеев К.Б., Бебенин Г.Г | |||
| Управление космическими ЛА | |||
| ПРИБОР ДЛЯ ЗАПИСИ И ВОСПРОИЗВЕДЕНИЯ ЗВУКОВ | 1923 |
|
SU1974A1 |
| Машина для добывания торфа и т.п. | 1922 |
|
SU22A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Бранец В.Н., Черток М.Б., Казначеев Ю.В | |||
| Оптимальный разворот твердого тела с одной осью симметрии // Космические исследования, 1984, т | |||
| Машина для добывания торфа и т.п. | 1922 |
|
SU22A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Судно | 1918 |
|
SU352A1 |
Авторы
Даты
1998-08-10—Публикация
1996-03-22—Подача