Изобретение относится к области космической техники и может использоваться для эффективного управления угловым положением космических аппаратов и орбитальных станций.
Наиболее известным способом управления пространственным разворотом космического аппарата (КА) является изменение углового его положения путем выполнения последовательных поворотов на определенные углы вокруг осей, жестко связанных с аппаратом [1, с. 85-92, 139-143]. Возможен следующий порядок разворотов - поворот КА вокруг продольной его оси X до совмещения одной из связанных с КА поперечных осей Y или Z с требуемым ее положением в пространстве Yk (или Zk соответственно), а затем поворот вокруг этой поперечной оси до совмещения продольной оси X с заданным положением Xk [2]. Системы управления, реализующие развороты вокруг связанных осей КА, широко известны и хорошо изучены. При многих достоинствах подобных систем, включая их простоту и надежность, они имеют один существенный недостаток - такие поворотные маневры имеют большую продолжительность и требуют значительных энергозатрат.
Ближайшим по технической сущности является способ управления пространственным разворотом динамически симметричного КА [3], включающий разгон космического аппарата, свободное его вращение и торможение космического аппарата (прототип).
При этом способе управления предполагается, что космический аппарат движется по космическим траекториям, совершая при этом регулярную прецессию. Движение состоит из участков, где действует максимальный момент mo (участки разгона и торможения КА) и участка свободного движения, на котором управляющий момент равен нулю.
Определяющими характеристиками процесса разворота являются время разгона (торможения) τ и время свободного движения tсв, которые вычисляются по соотношениям: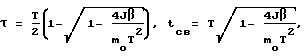
где
J=0,5(J2+J3) - момент инерции КА относительно поперечной оси;
mo - величина максимального момента управления;
T - заданное время разворота;
β - угол поворота КА вокруг оси прецессии.
Управляющие моменты формируются на участках разгона и торможения исходя из выражения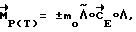
где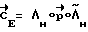 - направление разворота (направление кинетического момента в инерциальном базисе);
- направление разворота (направление кинетического момента в инерциальном базисе);
Λн - кватернион начального положения КА;
Λ - кватернион текущего положения КА.
Знак "+" соответствует участку разгона, а знак "-" - участку торможения. Вектор разворота 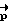 однозначно определяется начальным Λн и конечным Λк положениями КА. Символ "°" обозначает операцию умножения кватернионов, а
однозначно определяется начальным Λн и конечным Λк положениями КА. Символ "°" обозначает операцию умножения кватернионов, а 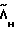 - кватернион, сопряженный кватерниону Λн .
- кватернион, сопряженный кватерниону Λн .
Приведение КА из начального углового положения Λн в требуемое конечное положение Λк производится следующим образом. Прежде всего определяется кватернион разворота 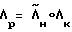 , исходя из которого вычисляют орт
, исходя из которого вычисляют орт 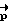 (вектор разворота) и угол поворота β с учетом инерционных характеристик КА J, J1, где
(вектор разворота) и угол поворота β с учетом инерционных характеристик КА J, J1, где
J1 - момент инерции КА относительно продольной оси;
Λк - кватернион конечного положения КА.
По заданному времени разворота T и углу поворота β определяют время разгона τ . Требуемая величина кинетического момента Ko определяется по соотношению: Ko = mo τ . Расчетное значение вектора кинетического момента  определяется следующим образом:
определяется следующим образом: 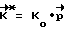 . С момента поступления команды на разворот к КА прикладывают управляющий момент
. С момента поступления команды на разворот к КА прикладывают управляющий момент 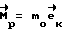 до тех пор, пока величина фактического кинетического момента
до тех пор, пока величина фактического кинетического момента 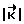 не станет равна расчетному значению Ko. Здесь
не станет равна расчетному значению Ko. Здесь 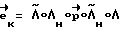 . В момент времени, когда
. В момент времени, когда 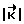 = Ko, начинается участок свободного движения КА, на котором управляющий момент отсутствует
= Ko, начинается участок свободного движения КА, на котором управляющий момент отсутствует 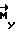 = 0. Через время T - τ с начала разворота производят торможение КА по закону:
= 0. Через время T - τ с начала разворота производят торможение КА по закону: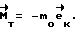
В момент времени, когда  = 0, разворот КА будет завершен.
= 0, разворот КА будет завершен.
Недостатком способа-прототипа является низкая точность разворота в случае несимметричного КА и при разворотах на большие углы, так как на участке свободного движения не производится контроль углового движения аппарата.
Техническим результатом данного изобретения является существенное повышение точности разворота произвольного КА при относительно низких энергетических затратах.
Указанный технический результат достигается тем, что в предлагаемом способе управления пространственным разворотом космического аппарата, включающем определение параметров разворота, определение кинетического момента 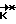 , требуемого для приведения космического аппарата при свободном его вращении в заданное угловое положение, формирование и с заданного момента времени приложение разгонного импульса, свободное вращение аппарата, формирование и приложение тормозного импульса, в отличие от прототипа, на этапе между разгоном и торможением определяют величину отклонения фактического кинетического момента от расчетного его значения
, требуемого для приведения космического аппарата при свободном его вращении в заданное угловое положение, формирование и с заданного момента времени приложение разгонного импульса, свободное вращение аппарата, формирование и приложение тормозного импульса, в отличие от прототипа, на этапе между разгоном и торможением определяют величину отклонения фактического кинетического момента от расчетного его значения 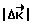 , в момент выполнения условия:
, в момент выполнения условия: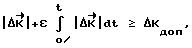
где Δ Kдоп - заданная величина допустимого отклонения кинетического момента;
t - время с начала участка неуправляемого движения;
ε - коэффициент пропорциональности, 0≤ ε ≤1; [ε] = c-1,
определяют расчетное значение кинетического момента 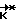 , при котором аппарат переходит при свободном своем вращении из текущего углового положения в заданное конечное угловое положение, и прикладывают к аппарату управляющий момент, например, по закону:
, при котором аппарат переходит при свободном своем вращении из текущего углового положения в заданное конечное угловое положение, и прикладывают к аппарату управляющий момент, например, по закону: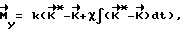
где  - фактический кинетический момент аппарата;
- фактический кинетический момент аппарата;
k - коэффициент усиления (k>0); [k] = c-1;
χ - коэффициент апериодичности (0≤ χ ≤1,5 c-1),
до совмещения фактического кинетического момента аппарата  с расчетным его значением
с расчетным его значением 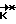 .
.
Указанный технический результат достигается и тем, что в предлагаемом способе по пункту 1 Δ Kдоп определяется углом доворота космического аппарата до конечного углового положения ϕост:
ΔKдоп= f(ϕост),
где f - монотонно-возрастающая функция.
Сущность предлагаемого способа заключается в управлении угловым движением КА по методу свободных траекторий. Однако, при отсутствии контроля фактического вращения КА вплоть до начала торможения ошибка переориентации может оказаться недопустимо большой. Уменьшить величину ошибки переориентации возможно за счет приложения импульсов коррекции внутри неуправляемого участка вращения КА. Учитывая, что фактическое движение КА отличается от прогнозируемого незначительно, применяют следующий принцип формирования управляющих моментов в процессе разворота. Он состоит в коррекции траектории движения КА в определенные дискретные моменты времени. Коррекция сводится к определению требуемого для попадания КА в конечное положение Λк кинетического момента 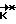 и сообщения поправочного импульса
и сообщения поправочного импульса 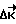 к имеющемуся кинетическому моменту КА
к имеющемуся кинетическому моменту КА  . Вся траектория движения будет состоять из чередующихся управляемых и неуправляемых участков и включать в себя участки разгона и торможения, участки свободного движения (
. Вся траектория движения будет состоять из чередующихся управляемых и неуправляемых участков и включать в себя участки разгона и торможения, участки свободного движения (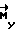 = 0) и кратковременные участки коррекции траектории. Задача управления состоит в обеспечении для неуправляемых участков таких начальных условий, при которых движение по прогнозу проходит через конечное положение Λк. Для этого на начало каждого участка ti определяется кватернион разворота
= 0) и кратковременные участки коррекции траектории. Задача управления состоит в обеспечении для неуправляемых участков таких начальных условий, при которых движение по прогнозу проходит через конечное положение Λк. Для этого на начало каждого участка ti определяется кватернион разворота 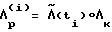 , по которому определяются требуемые начальные условия ω10, ω20, ω30 для следующего участка. Моменты проведения коррекции ti определяются условием:
, по которому определяются требуемые начальные условия ω10, ω20, ω30 для следующего участка. Моменты проведения коррекции ti определяются условием: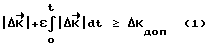 .
.
Величина ΔKдоп выбирается из соображения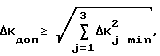
где ΔKjmin - минимально возможный импульс кинетического момента по j-му каналу управления (он определяется характеристиками исполнительных органов - номинальной тягой реактивных двигателей, плечом его установки и минимальным временем его включения τmin, [1, с. 116, 190, 219]).
По мере неуправляемого движения КА (например, после разгона КА) в силу действия на него внешних возмущающих моментов фактический кинетический момент КА  будет отличаться от расчетного его значения
будет отличаться от расчетного его значения 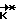 , и соответственно величина отклонения
, и соответственно величина отклонения 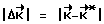 будет увеличиваться с течением времени. Пока
будет увеличиваться с течением времени. Пока 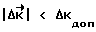 управляющие моменты не формируются и не прикладываются к корпусу КА (
управляющие моменты не формируются и не прикладываются к корпусу КА ( = 0), так как нет смысла в коррекции траектории его вращения (из-за неидеальности исполнительных органов - релейности их характеристики - реализация такой коррекции даст большую ошибку кинетического момента, чем та, что уже имеется). Введение интегрального члена учитывает факт накопления ошибки управления по угловым (а не скоростным) координатам даже при незначительных отклонениях кинетического момента от требуемого значения. Настройкой величин ε и ΔKдоп обеспечивается оптимизация программы коррекции углового движения КА в процессе разворота.
= 0), так как нет смысла в коррекции траектории его вращения (из-за неидеальности исполнительных органов - релейности их характеристики - реализация такой коррекции даст большую ошибку кинетического момента, чем та, что уже имеется). Введение интегрального члена учитывает факт накопления ошибки управления по угловым (а не скоростным) координатам даже при незначительных отклонениях кинетического момента от требуемого значения. Настройкой величин ε и ΔKдоп обеспечивается оптимизация программы коррекции углового движения КА в процессе разворота.
В отличие от ближайшего аналога (прототипа) расчетное значение 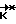 определяется неоднократно. Обусловлено это тем, что в силу действия на аппарат различных возмущающих факторов условие (1) выполняется не менее одного раза.
определяется неоднократно. Обусловлено это тем, что в силу действия на аппарат различных возмущающих факторов условие (1) выполняется не менее одного раза.
Необходимо заметить, что движение КА существенно отличается от регулярной прецессии (так как КА не обладает динамической симметрией) и вектор разворота 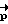 не может быть найден аналитически. Однако, имея математическую модель фактического КА и применяя метод последовательных приближений, можно определить для любых начального Λo/ и конечного Λк положений КА и времени разворота T направление вектора кинетического момента
не может быть найден аналитически. Однако, имея математическую модель фактического КА и применяя метод последовательных приближений, можно определить для любых начального Λo/ и конечного Λк положений КА и времени разворота T направление вектора кинетического момента 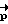 , соответствующего траектории свободного движения КА, проходящей через Λo и Λк.
, соответствующего траектории свободного движения КА, проходящей через Λo и Λк.
Космический аппарат характеризуется прежде всего инерционными характеристиками J1, J2, J3. Начальное и конечное угловые положения задаются кватернионами Λн и Λк. Определение орта 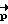 - вектора разворота, соответствующего полодии, проходящей через начальное и конечное угловые положения, и обеспечивающего перевод КА в заданное положение Λк при свободном его вращении, осуществляется методом последовательных приближений. В качестве первого приближения
- вектора разворота, соответствующего полодии, проходящей через начальное и конечное угловые положения, и обеспечивающего перевод КА в заданное положение Λк при свободном его вращении, осуществляется методом последовательных приближений. В качестве первого приближения 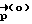 принимается значение вектора разворота, соответствующего развороту динамически симметричного тела на кватернион Λp, которое вычисляется в результате решения системы уравнений:
принимается значение вектора разворота, соответствующего развороту динамически симметричного тела на кватернион Λp, которое вычисляется в результате решения системы уравнений: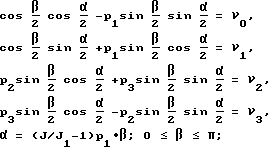
где J, J1 - моменты инерции КА;
ν0,ν1,ν2,ν3 - компоненты кватерниона разворота 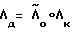 .
.
Математическая модель вращательного движения КА имеет вид: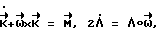
где 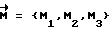 - момент внешних сил;
- момент внешних сил;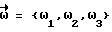 - вектор угловой скорости;
- вектор угловой скорости;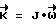 - кинетический момент КА; J - тензор инерции КА.
- кинетический момент КА; J - тензор инерции КА.
Здесь x означает векторное произведение векторов.
Моделируя движение КА с начальными условиями Λ(0) = Λo,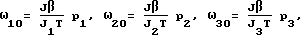
где β - угол поворота, соответствующий вектору разворота 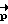 ;
;
J - момент инерции КА относительно поперечной оси;
T - время разворота,
и учитывая, что  = 0, определяют промах разворота
= 0, определяют промах разворота 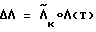 .
.
Введя полученный промах ΔΛ в качестве поправки к предыдущему кватерниону разворота, определяют новые параметры разворота 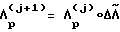 и соответствующие ему
и соответствующие ему 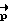 и β. Схема итерационного процесса проста
и β. Схема итерационного процесса проста 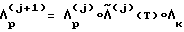 . Вектор
. Вектор 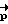 будет определен, когда Sqal(ΔΛ) > εдоп. Направление разворота
будет определен, когда Sqal(ΔΛ) > εдоп. Направление разворота 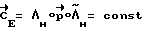 .
.
Величина кинетического момента определяется управляющими возможностями системы исполнительных органов m0, моментом инерции относительно поперечной оси J, углом поворота 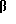 и заданным временем разворота T.
и заданным временем разворота T.
K0=m0 τ, где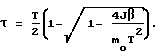
На участках разгона и торможения управляющие момента максимальны, а на участках коррекции траектории углового движения КА управляющий момент носит импульсный характер.
На участке неуправляемого движения КА (на этапе между разгоном и торможением КА) контроль движения КА осуществляют лишь в некоторые дискретные моменты времени ti, определяемые условием (1). В момент его выполнения производят коррекцию углового движения КА путем целенаправленного изменения его кинетического момента. Для этого определяют такое расчетное значение вектора кинетического момента 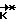 , при котором КА при свободном его вращении из текущего углового положения Λ (ti) перейдет в заданное конечное угловое положение Λк, и затем прикладывают к корпусу КА управляющий момент
, при котором КА при свободном его вращении из текущего углового положения Λ (ti) перейдет в заданное конечное угловое положение Λк, и затем прикладывают к корпусу КА управляющий момент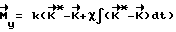
до установления равенства 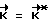 . Как только фактический кинетический момент
. Как только фактический кинетический момент  станет равен расчетному значению
станет равен расчетному значению 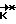 , аппарат предоставляют самому себе до следующей коррекции (до очередного выполнения условия (1)). Расчетное значение вектора кинетического момента
, аппарат предоставляют самому себе до следующей коррекции (до очередного выполнения условия (1)). Расчетное значение вектора кинетического момента 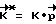 , где
, где 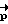 - вектор разворота, K - величина фактического кинетического момента на момент выполнения условия (1).
- вектор разворота, K - величина фактического кинетического момента на момент выполнения условия (1).
Определение вектора разворота  сводится к решению краевой задачи: Λo= Λ(ti), Δ(T) = Λк при имеющихся дифференциальных связях, накладываемых на движение КА:
сводится к решению краевой задачи: Λo= Λ(ti), Δ(T) = Λк при имеющихся дифференциальных связях, накладываемых на движение КА: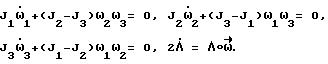
Таким образом, управление программным разворотом КА в предлагаемом способе сводится к следующему:
1) расчет требуемого значения вектора разворота 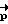 и сообщение корпусу КА расчетного кинетического момента (разгон КА); момент управления формируется по закону:
и сообщение корпусу КА расчетного кинетического момента (разгон КА); момент управления формируется по закону: 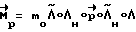 .
.
2) свободное вращение КА по попадающей траектории (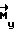 = 0);
= 0);
3) определяют величину отклонения фактического кинетического момента от расчетного его значения 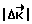 и проверяют условие (1); в момент его выполнения производят коррекцию траектории вращения КА, которая заключается в определении расчетного значения вектора кинетического момента
и проверяют условие (1); в момент его выполнения производят коррекцию траектории вращения КА, которая заключается в определении расчетного значения вектора кинетического момента 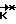 , необходимого для приведения КА при свободном его вращении из текущего углового положения Λ(ti) в заданное конечное угловое положение Λк, и приложении к космическому аппарату управляющего момента
, необходимого для приведения КА при свободном его вращении из текущего углового положения Λ(ti) в заданное конечное угловое положение Λк, и приложении к космическому аппарату управляющего момента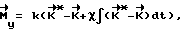
где - фактический кинетический момент аппарата;
- фактический кинетический момент аппарата;
k - коэффициент усиления (k>0);
χ - коэффициент апериодичности, 0 ≤ χ ≤ 1,5;
до совмещения фактического кинетического момента аппарата с расчетным его значением 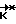 . После выполнения условия
. После выполнения условия 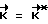 происходит свободное движение КА (
происходит свободное движение КА (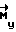 = 0);
= 0);
4) в момент выполнения равенства: 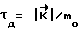 начинают гашение угловой скорости КА (торможение КА);
начинают гашение угловой скорости КА (торможение КА);
момент управления формируется по закону: 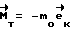 , где
, где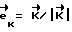 .
.
Время τд = вычисляется по выражению:
где
ϕост= 2arccosλд0,
λд0, λд1, λд2, λд3 - компоненты кватерниона доворота 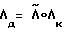 .
.
Отличительной особенностью предложенных технических решений является наличие математической модели фактически несимметричных КА, а также организация и выполнение на этапе между разгоном и торможением импульсных коррекций движения КА. Расчет требуемого кинетического момента 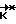 носит итерационный характер и описывается алгоритмом
носит итерационный характер и описывается алгоритмом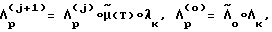
где
μ(T) - прогнозируемое угловое положение КА на момент времени T, полученное моделированием движения КА.
При проведении коррекции свободного вращения аппарата момент управления 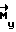 формируется по отклонению кинетического момента
формируется по отклонению кинетического момента 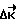 . Линейная часть управляющей функции обеспечивает уменьшение отклонения
. Линейная часть управляющей функции обеспечивает уменьшение отклонения 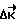 до нуля, а введение в управляющую функцию интегральной составляющей повышает быстродействие коррекции.
до нуля, а введение в управляющую функцию интегральной составляющей повышает быстродействие коррекции.
Предлагаемое сочетание свободного разворота с кратковременными коррекциями позволяет при довольно низком расходе топлива добиваться большой точности разворота при любых неизвестных возмущениях. Экономичность разворота достигается тем, что на большей части траектории управление отсутствует (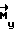 = 0), а повышение точности обеспечивается организацией и проведением в определенные дискретные моменты времени кратковременных коррекций углового движения аппарата.
= 0), а повышение точности обеспечивается организацией и проведением в определенные дискретные моменты времени кратковременных коррекций углового движения аппарата.
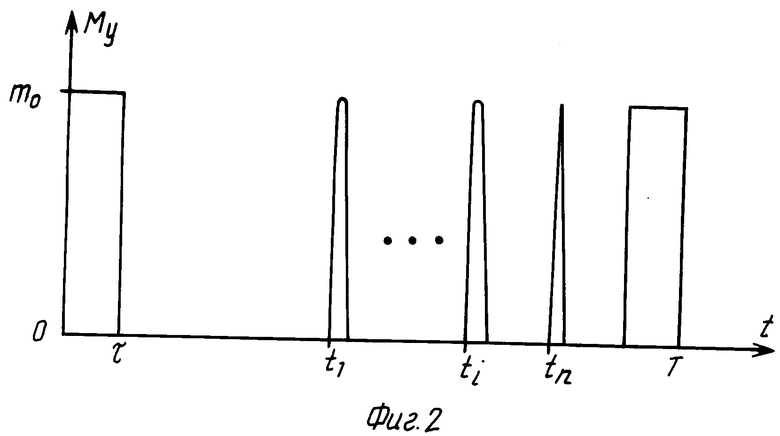
На фиг. 1 дана функциональная схема системы для реализации способа; на фиг.2 - временные диаграммы управляющих воздействий.
Пример реализации предложенного способа представлена фиг.1, где обозначено: 1 - устройство ввода и хранения начального и конечного положений КА (УВХНКП); 2 - блок задатчиков моментов инерции КА (БЗМИ); 3 - устройство ввода времени разворота (УВВР); 4 - бесплатформенная инерциальная навигационная система (БИНС); 5 - блок датчиков угловых скоростей (БДУС); 6 - вычислительное устройство (ВУ); 7 - блок хранения коэффициентов закона управления (БХКЗУ); 8 - задатчик допустимого отклонения кинетического момента (ЗДОКМ); 9 - согласующе-преобразующее устройство (СПУ); 10 - исполнительные органы (ИО), при этом первый выход УВХНКП 1 связан с первым входом ВУ 6, второй выход УВХНКП 1 связан с вторым входом ВУ 6, выход БЗМИ 2 связан с третьим входом ВУ 6, выход УВВР 3 связан с четвертым входом ВУ 6, выход БИНС 4 связан с пятым входом ВУ 6, выход БДУС 5 связан с входом БИНС 4 и с шестым входом ВУ 6, выход ВУ 6 связан с входом СПУ 9, первый выход БХКЗУ 7 связан с седьмым входом ВУ 6, второй выход БХКЗУ 7 связан с восьмым входом ВУ 6, третий выход БХКЗУ 7 связан с девятым входом ВУ 6, выход ЗДОКМ 8 связан с десятым входом ВУ 6, первый выход СПУ 9 связан с исполнительными органами первого канала, второй выход СПУ 9 связан с исполнительными органами второго канала, третий выход СПУ 9 связан с исполнительными органами третьего канала.
В системе автоматически определяется и фиксируется направление кинетического момента в инерциальном базисе 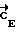 , обеспечивающего перевод КА из положения Λн в требуемое положение Λк за время T с допустимой точностью εдоп.
, обеспечивающего перевод КА из положения Λн в требуемое положение Λк за время T с допустимой точностью εдоп.
Отметим, что вычислительное устройство производит все математические операции, необходимые для реализации способа, и содержит в себе математическую модель углового движения КА. По начальному и конечному положениям КА и его инерционным характеристикам ВУ 6 осуществляет расчет кинетического момента 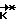 по методу итераций. Отклонение прогнозируемого положения КА μ(T) от требуемого Λк определяется путем математического моделирования в ВУ 6. Итерационный процесс
по методу итераций. Отклонение прогнозируемого положения КА μ(T) от требуемого Λк определяется путем математического моделирования в ВУ 6. Итерационный процесс 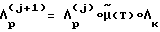 повторяется, пока
повторяется, пока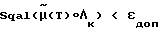 ,
,
Λ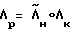 ;
;
Λ
В качестве вычислительного устройства может быть использована БЦВМ, но тогда в систему необходимо ввести интерфейс сопряжения и обмена информацией с измерительными приборами и исполнительными органами.
Моменты времени ti, в которые производят коррекцию углового движения КА, определяются ВУ 6 логической проверкой условия (1).
Работает система, реализующая предлагаемый способ управления пространственным разворотом КА, следующим образом. По значениям моментов инерции КА J1, J2, J3 ВУ 6 вычисляет значение момента инерции вокруг поперечной оси J согласно выражению: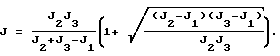
Далее по начальному Λн и конечному Λк положениям КА, заданному времени разворота T и инерционным характеристикам J1, J2, J3 в ВУ 6 осуществляется расчет вектора разворота 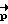 (путем решения краевой задачи) и соответствующего ему угла поворота β. Исходя из него ВУ 6 определяет время разгона τ по выражению:
(путем решения краевой задачи) и соответствующего ему угла поворота β. Исходя из него ВУ 6 определяет время разгона τ по выражению: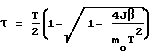 .
.
и расчетную величину кинетического момента 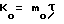 .
.
В исходном состоянии 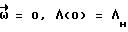 , выход вычислительного устройства замаскирован и
, выход вычислительного устройства замаскирован и 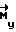 =0. В момент поступления команды на разворот ВУ 6 формирует управляющий момент
=0. В момент поступления команды на разворот ВУ 6 формирует управляющий момент 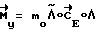 , который прикладывают к КА посредством ИО 10. Расчет текущего кинетического момента
, который прикладывают к КА посредством ИО 10. Расчет текущего кинетического момента  ВУ 6 производит непрерывно по показаниям БДУС 5
ВУ 6 производит непрерывно по показаниям БДУС 5  и моментам инерции Jj : Kj=Jjωj. Как только КА будет сообщен кинетический момент расчетной величины K0, выход ВУ 6 маскируется, управляющие моменты отсутствуют
и моментам инерции Jj : Kj=Jjωj. Как только КА будет сообщен кинетический момент расчетной величины K0, выход ВУ 6 маскируется, управляющие моменты отсутствуют 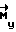 = 0 и КА производит свободное вращение. Одновременно определяется величина отклонения кинетического момента от расчетного его значения
= 0 и КА производит свободное вращение. Одновременно определяется величина отклонения кинетического момента от расчетного его значения 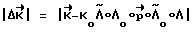 и по нему вычисляется функция
и по нему вычисляется функция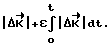
В момент, когда ее значение превысит допустимую величину ΔKдоп, ВУ 6 фиксирует кватернион разворота из текущего углового положения в заданное конечное Λк, исходя из которого методом последовательных приближений рассчитывают вектор разворота 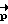 и расчетное значение вектора кинетического момента
и расчетное значение вектора кинетического момента 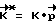 , где
, где
K - величина фактического кинетического момента на момент времени ti.
ИО 10 сообщают КА корректирующий импульс 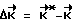 путем приложения управляющего момента
путем приложения управляющего момента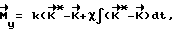
рассчитываемого в ВУ 6.
Как только 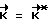 , выход ВУ 6 маскируется, управляющие моменты отсутствуют
, выход ВУ 6 маскируется, управляющие моменты отсутствуют 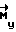 = 0 и КА производит свободное вращение до следующего момента времени ti. Расчетное значение вектора кинетического момента в связанной системе координат будет равно:
= 0 и КА производит свободное вращение до следующего момента времени ti. Расчетное значение вектора кинетического момента в связанной системе координат будет равно: ,
,
где
Λ - кватернион текущего углового положения КА;
Λ (ti) - кватернион углового положения КА на момент коррекции ti.
В момент равенства 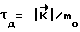 производят торможение КА; управляющие моменты формируются исходя из выражения:
производят торможение КА; управляющие моменты формируются исходя из выражения: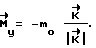
Когда 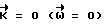 , выход ВУ 6 маскируется, исполнительные органы отключены, разворот завершен. Система готова к следующему развороту КА.
, выход ВУ 6 маскируется, исполнительные органы отключены, разворот завершен. Система готова к следующему развороту КА.
Временные диаграммы приведены на фиг.2.
Данная схема разворота снижает влияние внешних возмущающих моментов на точность разворота. Расход рабочего тела на корректирующие импульсы незначителен. Моменты проведения коррекций ti определяются автоматически самой системой управления.
Для повышения точности управления формирования управляющих моментов с целью коррекции вращательного движения КА желательно производить несколько чаще по мере приближения к требуемому положению Λк. Для обеспечения этого требования достаточно принять непостоянной величину ΔKдоп и уменьшать ее одновременно с уменьшением в процессе разворота оставшегося угла доворота аппарата до конечного углового положения ϕост. Другими словами следует положить: ΔKдоп= f(ϕост), где f - монотонно-возрастающая функция.
Конкретный вид функции f может быть легко определен путем математического моделирования большого числа разворотов КА, а простейшей ее формой служит линейная функция угла ϕост.
В результате получают более гибкое управление, при котором происходит несколько коррекций и обеспечивается необходимая степень точности разворота КА.
Эффективность предлагаемого способа определяется прежде всего тем, что на большей части траектории движения управляющий момент равен нулю, что экономит топливо. Вместе с тем способ предполагает принцип управления по отклонению при подходе к заданному угловому положению, чем и обеспечивает высокую точность разворота в условиях действия значительных внешних возмущающих моментов.
Литература.
1. Раушенбах Б.В., Токарь Е.Н. Управление ориентацией КА. -М., 1974.
2. Алексеев К.Б., Бебенин Г.Г. Управление космическими ЛА. -М., 1974, с. 22.
3. Бранец В.Н., Черток М.Б., Казначеев Ю.В. Оптимальный разворот твердого тела с одной осью симметрии. // Космические исследования, 1984, т. 22, вып. 3, с. 352-360.
Изобретение относится к области космической техники и может использоваться для эффективного управления ориентацией космических аппаратов (КА) и орбитальных станций. Предлагаемый способ включает этапы разгона, свободного вращения и импульсного торможения вращения КА, причем на среднем этапе определяют отклонение текущего кинетического момента КА от его расчетного значения, при котором КА переходит в свободном вращении из текущего в заданное конечное угловое положение, импульсно корректируют вращение КА, устраняя указанное отклонение. Расчетное значение кинетического момента КА автоматически определяется системой управления из решения краевой кинематической задачи ориентации твердого тела методом последовательных приближений с прогнозированием. Способ позволяет снизить энергозатраты и повысить точность маневра переориентации широкого класса КА. 1 з.п. ф-лы, 2 ил.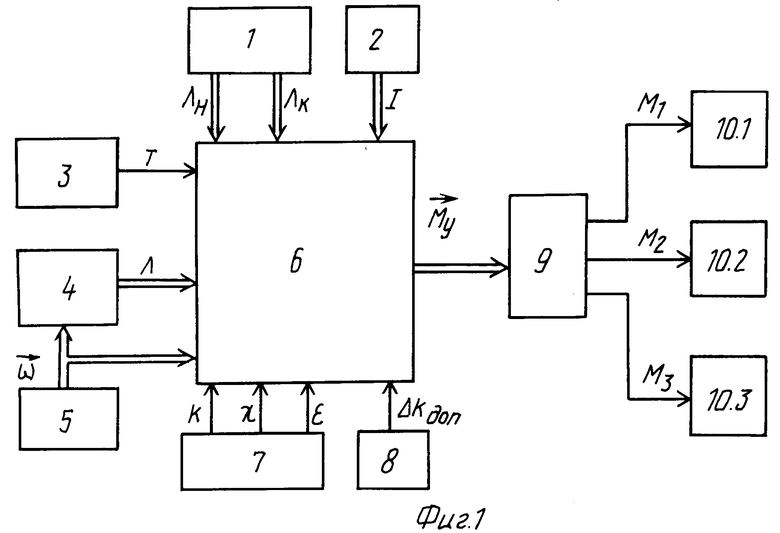
 требуемого для приведения космического аппарата при его свободном вращении в заданное угловое положение, формирование и с заданного момента времени приложение разгонного импульса, свободное вращение аппарата, формирование и приложение тормозного импульса, отличающийся тем, что на этапе между разгоном и торможением определяют величину отклонения фактического кинетического момента аппарата от его расчетного значения
требуемого для приведения космического аппарата при его свободном вращении в заданное угловое положение, формирование и с заданного момента времени приложение разгонного импульса, свободное вращение аппарата, формирование и приложение тормозного импульса, отличающийся тем, что на этапе между разгоном и торможением определяют величину отклонения фактического кинетического момента аппарата от его расчетного значения 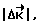 в момент выполнения условия
в момент выполнения условия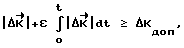
где ΔKдоп - заданная величина допустимого отклонения кинетического момента;
t - время с начала участка неуправляемого движения;
ε - коэффициент пропорциональности, 0 ≤ ε ≤ 1;
определяют указанное расчетное значение кинетического момента 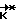 и прикладывают к аппарату управляющий момент до совмещения фактического кинетического момента
и прикладывают к аппарату управляющий момент до совмещения фактического кинетического момента  аппарата с его расчетным значением
аппарата с его расчетным значением 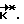
2. Способ по п.1, отличающийся тем, что величина ΔKдоп определяется углом доворота ϕост космического аппарата до конечного углового положения по выражению
ΔKдоп= f(ϕост),
где f - монотонно возрастающая функция.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Раушенбах Б.В., Токарь Е.Н | |||
| Управление ориентацией космических аппаратов | |||
| - М.: Машиностроение, 1974, с.85 - 92, 139 - 143 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Бранец В.Н., Черток М.Б | |||
| и др | |||
| Оптимальный разворот твердого тела с одной осью симметрии | |||
| Космич.исследования, т.22, вып.3, с.352 - 360. | |||
Авторы
Даты
1998-07-20—Публикация
1996-06-06—Подача