Изобретение относится к медицине и биологии, точнее к лабораторной диагностике, и может быть использовано для оценки количественного состава клеточных популяций (кровь, клеточные культуры).
Известна счеткая камера с сетками Бюркера [1]. Сетка Бюркера состоит из 9 одинаковых квадратных полей, которые разделены тройными линиями. Внутри каждого поля с помощью взаимно пересекающихся двойных линий выделены 12 больших квадратов и малые квадраты (по 4 у углов каждого большого квадрата). Площадь одного большого квадрата 1/25 мм2, площадь одного малого квадрата 1/400 мм2. Всего сетка содержит 144 больших квадрата. На долю этих квадратов в пределах каждого из 9 полей приходятся 0,64 мм2, на долю малых квадратов, промежутков между большими квадратами и обрамления полей - 0,36 мм2. Площадь сетки Бюркера - 9,0 мм2, объем камеры - 0,9 мм3. Существенные признаки счетной камеры с сетками Бюркера, совпадающие с таковыми заявляемого изобретения, следующие: предметное стекло, в котором имеются углубления с сетками, выгравированными на их дне; площадь большого и малого квадратов, площадь сетки, объем камеры.
Вероятность попадания клеток в квадраты сетки счетной камеры подчиняется распределению Пуассона [2, 3]. Метрологической основой установления числа частиц, в том числе числа клеток в суспензии, является свойство распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего [4 - 9]. У счетной камеры с сетками Бюркера отсутствуют элементы, способствующие нахождению средних, которые удовлетворяют свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, при подсчете эритроцитов, лейкоцитов, тромбоцитов и культивируемых клеток.
Известна счетная камера с сетками Нейбауэра [1]. Сетка Нейбауэра состоит из 9 по-разному разграфленных полей. Центральное поле содержит 25 больших квадратов, в каждом из которых имеются 16 малых квадратов. Четыре боковых поля пересечены в одном направлении. Каждое из угловых полей разделено на 16 пустых квадратов. Площадь одного большого квадрата 1/25 мм2, площадь одного малого квадрата 1/400 мм2, площадь сетки Нейбауэра 9,0 мм2, объем камеры 0,9 мм3. Существенные признаки счетной камеры с сетками Нейбауэра, совпадающие с таковыми заявляемого изобретения, следующие: предметное стекло, в котором имеются углубления с сетками, выгравированными на их дне; площадь большого и малого квадратов, площадь сетки, объем камеры. У счетной камеры с сетками Нейбауэра отсутствуют элементы, способствующие нахождению средних, которые удовлетворяют свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, при подсчете эритроцитов, лейкоцитов, тромбоцитов и культивируемых клеток.
Известна счетная камера с сетками Горяева [1]. Сетка Горчяева состоит из 225 больших квадратов. Среди них 100 квадратов пустых, 100 - пересеченных в одном направлении, 25 - пересеченных в двух взаимно перпендикулярных направлениях. В каждом из указанных 25 больших квадратов содержатся 16 малых квадратов. Площадь одного большого квадрата 1/25 мм2, площадь одного малого квадрата 1/400 мм2, площадь сетки Горяева 9,0 мм2, объем камеры 0,9 мм3. Существенные признаки счетной камеры с сетками Горяева, совпадающие с таковыми заявляемого изобретения, следующие: предметное стекло, в котором имеются углубления с сетками, выгравированными на их дне; площадь большого и малого квадратов, площадь сетки, объем камеры. У счетной камеры с сетками Горяева отсутствуют элемены, способствующие нахождению средних, которые удовлетворяют свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, при подсчете эритроцитов, лейкоцитов, тромбоцитов и культивируемых клеток. Последнее устройство взято за прототип.
Предложенное устройство позволяет повысить точность оценки плотности клеточной суспензии за счет введения элементов, способствующих нахождению средних, удовлетворяющих свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, и соответствующего изменения методики подсчета клеток. Повышение точности оценки плотности клеточной суспензии в результате нахождения указанных средних основана на возможности легко определить доверительные пределы среднего при заданном уровне значимости и сравнить два средних. Этот технический результат достигается тем, что рядом с сеткой Горяева выгравировываются квадраты (пуассоновские единицы), площадь которых в 10 раз меньше той, на которой подсчитывают эритроциты, лейкоциты, тромбоциты и культивируемые клетки.
На фиг. 1 изображена счетная камера с сеткой Горяева и элементами, способствующими нахождению средних, удовлетворяющих свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего (пуассоновскими единицами).
Счетная камера состоит из толстого предметного стекла (1), в центре которого имеется средняя пластинка (2), разделенная на две половины поперечной канавкой (3). Каждая половина содержит углубление с сеткой Горяева (4). С каждой стороны средней пластинки располагаются краевые пластинки (5), отделенные от средней пластинки канавками (6) и предназначенные для притирания покровного стекла. Высота краевых пластинок на 0,1 мм меньше, чем высота углублений с сетками средней пластинки. Рядом с сетками выгравированы квадраты (пуассоновские единицы), маркированные буквами Э (эритроциты), Т (тромбоциты), Л (лейкоциты) и КК (культивируемые клетки) (7). Площади пуассоновских единиц для определения средних в случаях подсчета эритроцитов, тромбоцитов и лейкоцитов и культивируемых клеток равны соответственно 0,02, 0,1, 0,4 и 1,8 мм2. Стороны квадратов для эритроцитов, тромбоцитов, лейкоцитов и культивируемых клеток, с точностью до 0,01 мм, равны соответственно 0,14, 0,32, 0,63 и 1,34 мм. Обоснование установления размеров пуассоновских единиц дано ниже.
Счетную камеру заполняют общепринятыми способами.
Наиболее часто подсчитывают эритроциты, лейкоциты и тромбоциты периферической крови, а также культивируемые клетки человека и животных (клетки однослойных и суспензионных культур).
Для подсчета эритроцитов, лейкоцитов и тромбоцитов периферической крови человека существуют стандартные методики применительно к счетной камере с сеткой Горяева [10]. Согласно этим методикам подсчет эритроцитов осуществляют в 5, тромбоцитов в 25, лейкоцитов в 100 больших квадратах сетки счетной камеры. Таким образом, учитывая то, что площадь большого квадрата равна 0,04 мм2, эритроциты подсчитывают на площади 0,2мм2, тромбоциты - на площади 1,0 мм2, лейкоциты - на площади 4,0 мм2. В опытах с культурами клеток удобно подсчитывать клетки на поверхности обеих сеток (в 450 больших квадратах), то есть на площади 18,0 мм2. Опытами с культурами клеток установлено, что если принять за единицу подсчета 1/5 часть сетки Горяева (1,8 мм2; 45 больших квадратов) и произвести подсчет клеток в 10 таких единицах, то полученное среднее из этих 10 подсчетов позволяет обеспечить удовлетворительное соответствие равенству стандартного отклонения квадратному корню из среднего. Для такого соответствия достаточно в целом подсчитать в указанных 10 единицах сетки счетной камеры примерно 200 клеток. Дальнейшее увеличение числа сосчитанных клеток не повышает точности подсчета. Нахождение среднего указанным способом и общее число сосчитанных клеток дают возможность аппроксимировать распределение Пуассона нормальным распределением [9]. Таким образом, использование 1/5 части сетки Горяева в качестве единицы подсчета позволяет легко определять среднее, обеспечивающее соответствие данных подсчета свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего и аппроксимировать распределение Пуассона нормальным распределением.
Методика определения среднего с использованием пуассоновских единиц заключается в следующем. Суспензии эритроцитов, лейкоцитов и тромбоцитов разводят в соответствии со стандартными методиками (суспензии эритроцитов и тромбоцитов в 200 раз, суспензию лейкоцитов в 20 раз).
В случаях суспензий культивируемых клеток сначала проводят ориентировочный подсчет клеток на площади, равной двум большим квадратам, а затем разводят суспензию с таким расчетом, чтобы общее число клеток над сеткой счетной камеры было равно 100.
Для получения среднего, соответствующего свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, полученные числа делят на 10. При работе с культивируемыми клетками, где разведения исходной суспензии относительно невелики (обычно не более чем в 4 раза), можно умножить предварительно число сосчитанных клеток на величину разведения. При работе с клетками крови, где величины разведения велики (20 и 200 раз), целесообразно оперировать непосредственно с числами сосчитанных клеток.
Таким образом, подсчет клеток осуществляется не в самих пуассоновских единицах сетки счетной камеры, а эти единицы являются ориентирами для нахождения среднего.
Использование пуассоновских единиц сетки счетной камеры позволяет найти среднее, соответствующее свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, и доверительные пределы для среднего; осуществить сравнение двух средних; определить время удвоения популяции клеток при увеличении размеров этой популяции; определить конечные точки при воздействии на клетки статических и токсических агентов.
Примеры использования пуассоновских единиц.
Определение среднего и его доверительных пределов.
При подсчете лейкоцитов в 5 больших квадратах сетки Горяева получено число 150, что соответствует 7500 лейкоцитов в 1 мкл или 7,5 • 109/л. Среднее, по данным соотнесения с пуассоновской единицей для лейкоцитов, равно 15 лейкоцитам. Квадратичную ошибку среднего, 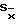 , исходя из аппроксимации распределения Пуассона нормальным распределением, вычисляют по формуле
, исходя из аппроксимации распределения Пуассона нормальным распределением, вычисляют по формуле 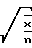 , где
, где 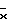 - выборочное среднее для распределения Пуассона (в данном случае - 15 лейкоцитов), а n - число подсчетов (в данном случае 10).
- выборочное среднее для распределения Пуассона (в данном случае - 15 лейкоцитов), а n - число подсчетов (в данном случае 10).
Следовательно, при 5,2 и 1% уровнях значимости истинное среднее (m) будет находиться соответственно в следующих доверительных пределах: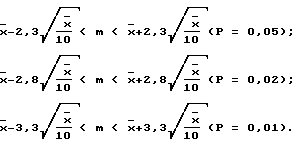
Таким образом, в данном случае при 5,2 и 1% уровнях значимости m будет находиться в следующих доверительных пределах:
15 - 2,3 • 1,22 < 15 < 15 + 2,3 • 1,22 или, округляя до 0,1, 12,2 < 15 < 17,8 (Р = 0,05);
15 - 2,8 • 1,22 < 15 < 15 + 2,8 • 1,22 или, округляя до 0,1, 11,6 < 15 < 18,4 (Р = 0,02);
15 - 3,3 • 1,22 < 15 < 15 + 3,3 • 1,22 или, округляя до 0,1, 11,0 < 15 < 19,0 (Р = 0,01).
Сравнение плотностей двух суспензий
При определении плотностей неразведенных суспензий клеток Hela (культивируемая постоянная линия клеток карциномы матки человека) с интервалом в 1 сут в первый раз в 2 сетках Горяева оказалось 280 клеток, а во второй раз - 198 клеток (в перерасчете на 1 мл соответственно 1,6 • 105 и 1.5 • 105 клеток). Средние, 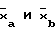 , по данным соотнесения с пуассоновской единицей для культивируемых клеток равны соответственно 28,0 и 19,8 клетки. Сравнение двух средних для совокупностей, подчиняющихся распределению Пуассона, с учетом аппроксимации этого распределения нормальным распределением осуществляют по формуле
, по данным соотнесения с пуассоновской единицей для культивируемых клеток равны соответственно 28,0 и 19,8 клетки. Сравнение двух средних для совокупностей, подчиняющихся распределению Пуассона, с учетом аппроксимации этого распределения нормальным распределением осуществляют по формуле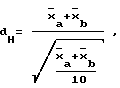
где dH - найденное значение квантиля уровня 1 - α(1 - α, или Р - доверительная вероятность) для нормального распределения, сравниваемое с табличным значением этой величины (dT) при заданной доверительной вероятности (уровне значимости).
В данном случае
Различие между 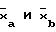 следует признать статически значимым.
следует признать статически значимым.
Определение времени удвоения популяции культивируемых клеток
Клетки постоянной линии Hela выращивали при 36oС во флаконах Карреля, используя смесь среды 199 и 20% сыворотки крупного рогатого скота. Каждые 5 сут удаляли кондиционированную среду и вносили свежую питательную смесь. Клетки отслаивали смесью 0,25% раствора трипсина и 0,02% раствора версена (1: 1). В этих условиях суспензии, используемые для подсчета, были однородными, и клетки почти не образовывали конгломератов. Клетки подсчитывали обычно каждые 2 сут. Исходное среднее и его доверительные пределы при 1% уровне значимости, по данным соотнесения с пуассоновской единицей для культивируемых клеток, оказались равными 15,2 ± 4,1 клетки. На 2-е, 4-е, 6-е, 9-е, 11-е и 13-е сут средние и их доверительные пределы равнялись соответственно 26,7 ± 5,4; 29,4 ± 5,7; 53,1 ± 7,6; 106,0 ± 10,1; 161,6 ± 13,3 и 140,8 ± 12,4 клетки. Время удвоения популяции определяли аналитически и графически. При аналитическом способе использовали формулу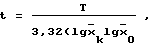
где t - время удвоения популяции, сут;
T - длительность логарифмической фазы роста, сут;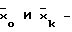 средние соответственно для исходной и конечной суспензий, полученные путем соотнесения с пуассоновской единицей для культивируемых клеток.
средние соответственно для исходной и конечной суспензий, полученные путем соотнесения с пуассоновской единицей для культивируемых клеток.
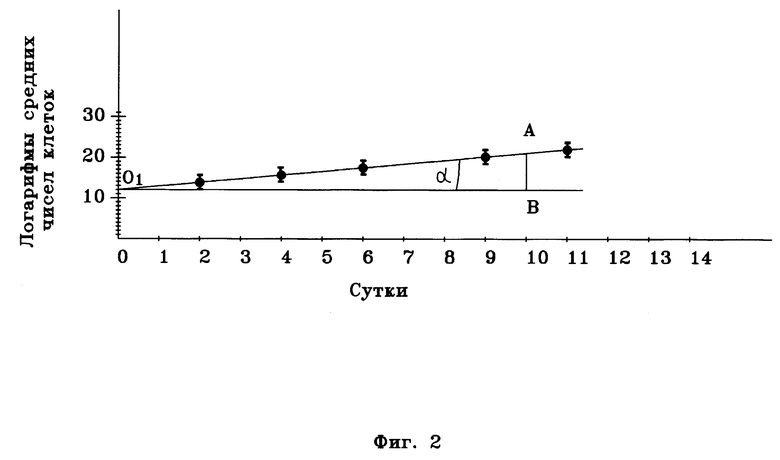
При графическом способе логарифмы средних и доверительных пределов наносили на ось ординат, сутки - на ось абсцисс (фиг. 2). Время удвоения популяции определяли по формуле
t = lg2/tgα,
где t - время удвоения популяции, сут;
α - угол между экспериментальной прямой и осью абсцисс.
По данным аналитического метода время удвоения популяции оказалось равным 3,31 сут (~79,4 ч). Отмечено почти полное отсутствие разброса точек на графике, что позволило легко провести через них прямую. Величина tg α = 0,09. Согласно формуле для графического метода t = 3,34 сут (~80,2 ч).
Таким образом, использование пуассоновской единицы позволило с высокой точностью определить время удвоения популяции клеточной культуры.
Определение 50% конечной точки при действии токсического агента на культуру клеток
На однослойные культуры клеток HeLa воздействовали метилртутьйодидом в концентрациях 14,6; 7,3; 3,65; 1,8; 0,9 и 0,45 мкмоль. Спустя 24 ч после внесения препарата клетки отслаивали смесью 0,25% раствора трипсина и 0,02% раствора версена (1:1) и осуществляли подсчет. Исходное среднее число клеток, по соотнесению с пуассоновской единицей для культивируемых клеток, оказалось равным 41,4 клетки; средние для культур, в которые вносили метилртутьйодид, равнялись соответственно 0,0; 3,2; 17,0; 19,6; 31,6 и 40,6 клетки (1-я серия опытов); 0,0; 11,0; 16,5; 20,7; 26,8 и 41,8 клетки (2-я серия опытов); 0,0; 6,8; 9,7; 13,2; 15,3 и 23,2 клетки (3-я серия опытов).
Логарифм средней летательной дозы для клеток в культуре тканей (LTCD50) определяли по формуле lg LTCD50 = 1/2 (lgDn + lgDn+1) - 1/2 [h1(lgD2 - lgD0 + h2(lgD3 - lgD1) + , ... , + hn (lgDn+1 - lgDn-1)] , где
D0 - доза, при которой гибель клеток не наблюдается; D1,2, 3,...,n - нарастающие дозы, при которых гибель клеток увеличивается; Dn+1 - доза, при которой погибают все клетки; h1,2,...,n - соответствующие нарастающим дозам доли погибщих клеток (отношение чисел погибших клеток к исходному числу клеток) [11].
Числа клеток определяются как выборочные средние  . Из величин логарифмов LTCD50 определяли LTCD50. В указанных сериях опытов LTCD50 оказались равными 2,48; 2,52 и 2,89 мкмоль.
. Из величин логарифмов LTCD50 определяли LTCD50. В указанных сериях опытов LTCD50 оказались равными 2,48; 2,52 и 2,89 мкмоль.
Таким образом, определение средней летальной дозы при воздействии токсического агента на культуру клеток с использованием при подсчете клеток пуассоновской единицы позволило получить близко совпадающие величины этой дозы.
Источники информации:
1. Альперин П. Камеры счетные // Большая медицинская энциклопедия. Т. 12. 2-е изд. - М.: 1959 с.57 - 65.
2. Student. On the error of counting with a haemocytometer // Biometrica. - 1907. - V. 5. - Part 3. - P. 351 - 360.
3. Student. An explanation of deviations from Poisson's law in practice // Biometrica. - 1919. - V. 12. - Parts 3 - 4. - P. 211 - 215.
4. Abbe E. Uber Blutkorperchenzahlung // Sitzungsberichte der Gesellsch. f. Med. Und Naturwissensch. in Jena. - Jg. 1878. - N 29. - S. 98 - 105.
Reichel J. Blutkorperchenzahlung. Experimentelle Studien der Berechnung der Fehler der Menhodik und die Bewertung der Fehler bei Einzel- und Serienzahlungen // Fol. Haematol. - 1930. - B. 41. - N. 41. - S. 307 - 332.
6. Berkson J., Magath Th.B., Hurn M. Laboratory standards in relation to chance, fluctuations of the erytrocyte count as estimated with the hemocytometer // J.Am. Statist. Assoc. - 1935. - V. 30. - N. 190. - P. 414 - 426.
7. Berkson J., Magath Th.B., Hurn M. Error of estimate of blood cell count as made with the hemocytometer. - Am. J. Physiol. - 1940. - V. 128. - N. 2. - P. 309 - 323.
8. Налимов В.В. Применение математической статистике при анализе вещества. - М.: Физматгиз, 1960, 431 с.
9. Бенюмович М.С. Статистическое обоснование оптимальных условий подсчета клеток в однослойных культурах. Лаб. Дело. - 1965 N 10, с. 609 - 614.
10. Золотницкая Р.П. Методы гематологических исследований. Лабораторные методы исследования в клинике. Справочник / Под ред. В.В.Меньшикова. - М.: Медицина. 1987 с. 106 - 148.
11. [Waerden van der B.L.] Варден ван дер Б.Л. Математическая статистика // Пер. с нем. - М.: Иностранная литература, 1960, 434 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ комбинированного измерения концентрации пероксидазо-положительных клеток (нейтрофильных гранулоцитов) и сперматозоидов в эякуляте человека с использованием вариаций на основе цитохимического окрашивания | 2019 |
|
RU2726207C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕМОГЛОБИНА, КОЛИЧЕСТВА ЭРИТРОЦИТОВ, ЛЕЙКОЦИТОВ, ТРОМБОЦИТОВ, ГЕМАТОКРИТА И СКОРОСТИ ОСЕДАНИЯ ЭРИТРОЦИТОВ В ЦЕЛЬНОЙ КРОВИ | 2005 |
|
RU2289133C1 |
| МЕТОД МОРФОФУНКЦИОНАЛЬНОЙ ОЦЕНКИ КЛЕТОЧНОГО КОМПОНЕНТА БИОТРАНСПЛАНТАТОВ | 2012 |
|
RU2484472C1 |
| СПОСОБ ОДНОВРЕМЕННОГО ОПРЕДЕЛЕНИЯ КЛЕТОК С РЕЦЕПТОРАМИ К БИОЛОГИЧЕСКИ АКТИВНЫМ ВЕЩЕСТВАМ И ИХ ПОПУЛЯЦИОННОЙ ПРИНАДЛЕЖНОСТИ | 1994 |
|
RU2081418C1 |
| СПОСОБ ОЦЕНКИ СОДЕРЖАНИЯ ЛЕЙКОЦИТОВ, ЭРИТРОЦИТОВ И ТРОМБОЦИТОВ В КРОВИ С УЧЕТОМ ГЕМОКОНЦЕНТРАЦИИ | 2002 |
|
RU2232988C2 |
| Способ и приспособление для подсчета лейкоцитов на сухом мазке крови | 1936 |
|
SU49027A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФАГОЦИТАРНОЙ АКТИВНОСТИ ЛЕЙКОЦИТОВ | 1999 |
|
RU2143693C1 |
| СПОСОБ ОЦЕНКИ РЕОЛОГИЧЕСКИХ СВОЙСТВ КРОВИ | 2009 |
|
RU2393475C1 |
| Способ определения внутрисосудистого свертывания крови | 1985 |
|
SU1288608A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ СТЕНКИ КРОВЕНОСНЫХ СОСУДОВ | 2011 |
|
RU2453845C1 |
Изобретение предназначено для введения в конструкцию счетной камеры с сетками Горяева элементов, способствующих нахождению средних, которые удовлетворяют свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, при подсчете эритроцитов, лейкоцитов, тромбоцитов и культивируемых клеток. Рядом с сетками выгравировываются квадраты (пуассоновские единицы), площадь которых составляет 1/10 площадей, на которых подсчитывают эритроциты, тромбоциты и лейкоциты по стандартным методикам (соответственно 0,02, 0,1 и 0,4 мм2, а площадь квадрата (пуассоновской единицы) для культивируемых клеток равна 1,8 мм2, что составляет 1/10 площади, на которой удобно подсчитывать культивируемые клетки (18,0 мм2). Числа клеток, установленные по принятым методикам, делят на 10, получая таким образом искомые средние. Пуассоновские единицы служат индикаторами для осуществления этого деления. Нахождение средних, удовлетворяющих свойству распределения Пуассона о равенстве стандартного отклонения квадратному корню из среднего, с последующей аппроксимацией распределения Пуассона нормальным распределением позволяет легко вычислять доверительные пределы среднего, сравнивать средние, определять время удвоения клеточной популяции, устанавливать конечные точки при воздействии на клетки статических и токсических агентов. 1 з.п.ф-лы, 2 ил.
| Краткая медицинская энциклопедия | |||
| Т | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Большая медицинская энциклопедия | |||
| Т | |||
| Способ гальванического снятия позолоты с серебряных изделий без заметного изменения их формы | 1923 |
|
SU12A1 |
Авторы
Даты
1999-02-20—Публикация
1997-05-29—Подача