Предлагаемое изобретение относится к области систем автоматического управления динамическими объектами широкого класса с неизвестными переменными параметрами и неконтролируемыми возмущениями.
Прототипом предлагаемого изобретения является беспоисковая адаптивная система управления с идентификатором и неявной эталонной моделью, описанная в изобретении [1]. Структурная схема адаптивной системы управления для объектов с неконтролируемыми возмущениями включает в себя сумматор, два регулятора (один в прямой и один в обратной связи), фильтр низких частот, объект управления и контур адаптации. Последний, в свою очередь, состоит из блока текущей идентификации, блока априорной информации о матрице эффективности управления объекта и блока настройки регуляторов.
Рассмотрим построение такой системы управления для следующей задачи. Пусть объект управления (ОУ) описывается следующим матричным дифференциальным уравнением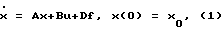
где где x∈Rn - непосредственно измеряемый вектор состояния ОУ; u∈Rm - вектор управления (в дальнейшем - закон управления); f - вектор неконтролируемых внешних возмущений, ограниченный по норме; А, В и D - матрицы неизвестных параметров ОУ с соответствующими размерностями, в общем случае переменные;  - непосредственно измеряется или аналитически вычисляется по x.
- непосредственно измеряется или аналитически вычисляется по x.
Адаптивная система должна формировать такой закон управления, чтобы ОУ вел себя подобно эталонной модели, которая задана неявным образом в виде следующего дифференциального уравнения
где хм - вектор состояния модели; uм - ограниченное по норме входное воздействие модели; размерности соответствуют уравнению (1); Ам и Вм - матрицы параметров модели в общем случае переменные, причем оператор Ам - асимптотически устойчивый.
Точный закон управления можно найти только тогда, когда выполнено условие полного соответствия моделей [2]
rankB=rank(B,Aм-А)=rank(B,Bм)=rank(B,D)
или, что тождественно
ВВ+(Ам-А)=Ам-А; ВВ+Вм=Вм; ВВ+D=D, (3)
где В+ - псевдообратная матрица к В. При выполнении условия (3) управление, которое назовем точным,
и*=В+[(Ам-А)х+Вмим-Df] (4)
обеспечит асимптотические свойства ошибки адаптации е=х-хм. Действительно, подставляя закон (4) в уравнение (1), учитывая (3) и вычитая из результата уравнение (2), получим уравнение ошибки адаптации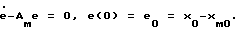
Однако по условию матрицы А, В и D неизвестны и внешние возмущения не измеряются, поэтому вместо (4) используется закон управления
 - оценки матриц А и В, доставляемые блоком текущей идентификации.
- оценки матриц А и В, доставляемые блоком текущей идентификации.
В работах [1, 5] сформулированы условия, при которых достигается цель адаптации (е-->0 с течением времени) при использовании закона (5). При этом требования асимптотической точности выдаваемых идентификатором оценок  и отсутствия неконтролируемых внешних возмущений (Df ≡ 0) являются необязательными.
и отсутствия неконтролируемых внешних возмущений (Df ≡ 0) являются необязательными.
Остановимся на условиях, сформулированных в работах [1, 5], рассматривая вопрос адаптации в непрерывной постановке при наличии неконтролируемых внешних возмущений. В качестве алгоритма текущей идентификации будем использовать алгоритм типа стохастической аппроксимации, который в непрерывной постановке описывается следующим образом [6]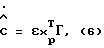
 - невязка, называемая в дальнейшем ошибкой идентификации (не путать с ошибкой оценивания параметров системы); хр Т=[хТ,иТ] - расширенный вектор состояния ОУ; Г - в общем случае переменная положительно определенная квадратная матрица размерностью (n+m) или скаляр; следующие нормы векторов и матриц ограничены
- невязка, называемая в дальнейшем ошибкой идентификации (не путать с ошибкой оценивания параметров системы); хр Т=[хТ,иТ] - расширенный вектор состояния ОУ; Г - в общем случае переменная положительно определенная квадратная матрица размерностью (n+m) или скаляр; следующие нормы векторов и матриц ограничены  , что справедливо для подавляющего большинства прикладных задач. В работе [1] показано, что при достаточно большой норме матрицы Г с течением времени ε → 0, причем без каких-либо дополнительных условий, в отличии от оценок параметров, сходимость которых к истинным значениям требует соблюдения целого ряда условий, в том числе отсутствия неконтролируемых внешних возмущений [6].
, что справедливо для подавляющего большинства прикладных задач. В работе [1] показано, что при достаточно большой норме матрицы Г с течением времени ε → 0, причем без каких-либо дополнительных условий, в отличии от оценок параметров, сходимость которых к истинным значениям требует соблюдения целого ряда условий, в том числе отсутствия неконтролируемых внешних возмущений [6].
В связи с указанным свойством ошибки идентификации в работах [1, 5] предлагается найти зависимость ошибки адаптации е от ошибки идентификации ε. Пропуская промежуточные преобразования, приведем выражения, полученные в [1, 5], справедливые для управления, определяемого по закону (5)

Уравнение (8) показывает, что его выражение в квадратных скобках всегда ортогонально строкам матрицы  или согласно свойствам псевдообратной матрицы - столбцам матрицы
или согласно свойствам псевдообратной матрицы - столбцам матрицы  [7]. При выполнении условий [1]
[7]. При выполнении условий [1]
или
из выражения (8) следует
B(u-u*) = Kε, (11)
где матрица К имеет ограниченную норму.
Для того чтобы доказать это утверждение, предположим, что rankB=k≤min(n, m). Тогда матрицу В можно представить через скелетное разложение в виде [7]
B=FL,
где F и L - матрицы размерностью n•k и k•m соответственно такие, что rankF=rankL=k. В этом случае равенство (9) влечет за собой выполнение условия  или согласно свойствам псевдообратной матрицы
или согласно свойствам псевдообратной матрицы  . Последнее обуславливает то, что
. Последнее обуславливает то, что  , где Ek - единичная k•k матрица [7]. Следовательно, умножение уравнения (8) слева на матрицу
, где Ek - единичная k•k матрица [7]. Следовательно, умножение уравнения (8) слева на матрицу  ограниченной нормы дает
ограниченной нормы дает
При этом матрица  . Условие (10) является частным к условию (9), когда столбцы матрицы В линейно зависимы со столбцами
. Условие (10) является частным к условию (9), когда столбцы матрицы В линейно зависимы со столбцами  .
.
Из выражений (7), (11) следует, что при выполнении хотя бы одного из условий (9), (10) искомое уравнение связи ошибки адаптации и ошибки идентификации имеет вид
Уравнение (13) - устойчивое дифференциальное уравнение с возмущением Kε и при ε → 0 достигается цель адаптации (-->0).
В изобретении [1] отмечается, что для выполнения условия ε → 0 требуется  , но последнее согласно свойствам уравнения (6) приводит к увеличению скорости изменения оценок, возрастанию норм
, но последнее согласно свойствам уравнения (6) приводит к увеличению скорости изменения оценок, возрастанию норм  , что препятствует сходимости ошибки идентификации и может привести к возникновению высокочастотных резонансных явлений. Рабочие частоты объекта управления находятся, как правило, в низкочастотной области, рабочие же частоты алгоритма текущей идентификации (они определяются нормой матрицы Г) лежат выше рабочих частот объекта. Поэтому в изобретении [1] предлагается для устранения неблагоприятных резонансных явлений управление (5) пропускать через фильтр низких частот с частотой среза, меньшей, чем частота алгоритма идентификации, но превышающей диапазон рабочих частот ОУ.
, что препятствует сходимости ошибки идентификации и может привести к возникновению высокочастотных резонансных явлений. Рабочие частоты объекта управления находятся, как правило, в низкочастотной области, рабочие же частоты алгоритма текущей идентификации (они определяются нормой матрицы Г) лежат выше рабочих частот объекта. Поэтому в изобретении [1] предлагается для устранения неблагоприятных резонансных явлений управление (5) пропускать через фильтр низких частот с частотой среза, меньшей, чем частота алгоритма идентификации, но превышающей диапазон рабочих частот ОУ.
Так как для справедливости в замкнутой системе выражения (12) является необходимым соблюдение условий (9) или (10), то в изобретении [1] предлагается внести в структурную схему адаптивной системы блок априорной информации о матрице эффективности управления объекта, который выдает в блок текущей идентификации информацию о матрице В0 с размерностью n•m. Эта матрица учитывает априорную информацию о матрице эффективности управления в виде соблюдения равенства [1]
rank(B0 TB)=rankB
В блоке текущей идентификации матрица B0 используется для коррекции оценки матрицы  с целью, чтобы скорректированная оценка
с целью, чтобы скорректированная оценка 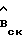 удовлетворяла условию (9).
удовлетворяла условию (9).
Таким образом, предложенная в изобретении [1] схема адаптивного управления с идентификатором и эталонной моделью позволяет упростить условия адаптируемости замкнутой системы. Основные результаты, полученные в [1], можно сформулировать следующим образом:
- требование асимптотической точности оценок параметров ОУ является лишь частным случаем требований достижения цели адаптации;
- цель адаптации можно достигнуть, если обеспечить малую норму ошибки идентификации и наложить ограничения (9) или (10) на оценку матрицы эффективности управления; эти ограничения могут быть выполнены при использовании небольшого объема априорной информации об управляемом объекте; для выполнения условия (9) или (10) в структурной схеме системы используется блок априорной информации о матрице эффективности управления объекта; по сигналам с этого блока производится коррекция текущей оценки  ;
;
- выбором матрицы Г алгоритма идентификации (6) можно всегда добиться требуемой скорости сходимости ошибки идентификации ε, что дает возможность увеличения скорости адаптации в системе и устранение цикличности ее работы (цикл идентификации и цикл настройки регулятора [3]); однако при возрастании нормы матрицы Г увеличивается скорость изменения оценок и для устранения возможного возникновения резонансных явлений в замкнутой системе используется фильтр низких частот с частотой среза выше верхней границы диапазона рабочих частот объекта управления, но ниже собственной частоты идентификатора;
- нет никаких дополнительных требований к входному сигналу ОУ, поэтому адаптивная система управления может функционировать на фоне естественных управляющих сигналов;
- возможно расширение области применения адаптивной системы на класс существенно нестационарных и нелинейных ОУ, у которых скорость изменения параметров ограничена;
- возможно использование системы при воздействии на ОУ неконтролируемых внешних возмущений, ограниченных по норме.
Однако раскрытый в изобретении [1] подход содержит ряд недостатков. Проанализируем их.
Условие (9) показывает, что для справедливости выражения (13), описывающего динамику ошибки адаптации в замкнутой системе, необходимо, чтобы все столбцы матрицы  не были ортогональны столбцам матрицы В. Для контроля этого условия необходима априорная информация о расположении столбцов матрицы В в пространстве в виде выполнения равенства rank(B0 TB)=rankB. Получение такой информации в ряде случаев не вызывает трудностей. Однако для целого ряда ОУ (например, самолета на критических режимах полета - полет на закритических углах атаки, штопор и др.) получение достоверной априорной информации о параметрах матрицы эффективности управления чрезвычайно затруднено или невозможно. В этом случае вполне вероятным является случай, когда в заданной априорно матрице B0 часть столбцов окажется ортогональной столбцам матрицы В. Очевидно в этом случае полученная при коррекции матрицы
не были ортогональны столбцам матрицы В. Для контроля этого условия необходима априорная информация о расположении столбцов матрицы В в пространстве в виде выполнения равенства rank(B0 TB)=rankB. Получение такой информации в ряде случаев не вызывает трудностей. Однако для целого ряда ОУ (например, самолета на критических режимах полета - полет на закритических углах атаки, штопор и др.) получение достоверной априорной информации о параметрах матрицы эффективности управления чрезвычайно затруднено или невозможно. В этом случае вполне вероятным является случай, когда в заданной априорно матрице B0 часть столбцов окажется ортогональной столбцам матрицы В. Очевидно в этом случае полученная при коррекции матрицы  матрица
матрица  не будет удовлетворять условию (9). В статье [5] анализируется решение, которое получается в этом случае. Показано, что при нарушении условия (9) независимо от оценок
не будет удовлетворять условию (9). В статье [5] анализируется решение, которое получается в этом случае. Показано, что при нарушении условия (9) независимо от оценок  и
и  , а также от выбора Ам ошибка адаптации может изменяться произвольным образом, т.е. система перестанет выполнять возложенные на нее функции.
, а также от выбора Ам ошибка адаптации может изменяться произвольным образом, т.е. система перестанет выполнять возложенные на нее функции.
Другим недостатком изобретения [1] является допущение о выполнении условия полного соответствия моделей (3). Однако выполнение этого условия в ряде случаев представляет серьезную проблему. Условия (3) требуют, чтобы все столбцы матриц (Ам-А), Вм, D лежали в подпространстве, образованном столбцами матрицы В. Если rankB<n, то для контроля за выполнением условия (3) необходимо иметь достоверную априорную информацию о расположении столбцов матрицы В в пространстве. При этом для контроля выполнения условия
rankB=rank(B, Ам-A)=rank(B, Вм)
нужно иметь априорную информацию о матрицах А, В. Восстановить нарушенное условие можно только путем изменения матриц Ам, Вм. Для контроля за условием
rankB=rank(B,D)
необходимо иметь информацию о подпространстве, образованном столбцами матрицы D. Восстановить последнее условие при его нарушении невозможно. Если не выполняется условие полного соответствия моделей (3), то не существует управления, обеспечивающего точное слежение ОУ (1) за эталонной моделью (2). В этом случае согласно свойствам нормального решения [7] законы управления (4) или (5) будут обеспечивать минимально возможную невязку между движениями ОУ и эталонной модели. Однако в этом случае качество управления может значительно ухудшаться, так как устойчивость замкнутой системы по ошибке адаптации нарушается.
Задачей данного изобретения является улучшение качества управления в адаптивной системе и расширение области ее применения путем устранения указанных недостатков. Для достижения данной задачи предлагается изменить структуру системы. Обоснуем изменения, которые необходимо внести.
Заметим, что если rankB=n, то условие полного соответствия моделей (3) выполняется всегда и не нуждается в контроле. Действительно, в этом случае матрица В имеет полный строковый ранг (n - размерность вектора состояния) и ранг блочной матрицы (B, H), где Н - любая матрица из n строк и произвольного количества столбцов будет всегда равна n. В этом случае от оценки матрицы  также целесообразно потребовать
также целесообразно потребовать
Тогда из выражений (7) и (8) следует
Для доказательства справедливости уравнения (15) умножим уравнение (8) слева на матрицу 

 . С учетом выражения (7) получаем уравнение (15). Если оценка матрицы эффективности управления такова, что условие (14) не выполняется, то матрицу
. С учетом выражения (7) получаем уравнение (15). Если оценка матрицы эффективности управления такова, что условие (14) не выполняется, то матрицу  необходимо скорректировать, т.е. заменить ее на матрицу
необходимо скорректировать, т.е. заменить ее на матрицу  , удовлетворяющую условию (14). Очевидно, что такая коррекция не требует какой-либо априорной информации о матрице эффективности управления. В связи с этим необходимость использования в системе блока априорной информации о матрице эффективности управления объекта отпадает и его предлагается исключить из структурной схемы. Коррекция матрицы
, удовлетворяющую условию (14). Очевидно, что такая коррекция не требует какой-либо априорной информации о матрице эффективности управления. В связи с этим необходимость использования в системе блока априорной информации о матрице эффективности управления объекта отпадает и его предлагается исключить из структурной схемы. Коррекция матрицы  не должна вызывать значительного приращения ошибки идентификации в замкнутой системе
не должна вызывать значительного приращения ошибки идентификации в замкнутой системе
Из последнего выражения следует требование, предъявляемое к алгоритму коррекции, обеспечивать малую норму  . Для контроля за соблюдением условия (14) и коррекции при необходимости матрицы
. Для контроля за соблюдением условия (14) и коррекции при необходимости матрицы  в структурную схему адаптивной системы предлагается внести блок коррекции оценки матрицы эффективности управления объекта.
в структурную схему адаптивной системы предлагается внести блок коррекции оценки матрицы эффективности управления объекта.
В случае, если структура матрицы эффективности управления такова, что  , то условия полного соответствия моделей можно выполнить для части объекта управления (1). Это достигается умножением уравнения (1) слева на матрицу выделения Q размерностью k•n, которая содержит k столбцов, образующих единичную матрицу, и остальные (n-k) столбцов нулевые. Введем обозначения
, то условия полного соответствия моделей можно выполнить для части объекта управления (1). Это достигается умножением уравнения (1) слева на матрицу выделения Q размерностью k•n, которая содержит k столбцов, образующих единичную матрицу, и остальные (n-k) столбцов нулевые. Введем обозначения
Уравнение объекта после его умножения на матрицу Q слева принимает вид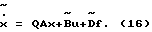
Полученное матричное уравнение является частью из k строк исходного уравнения (1) и описывает динамику k выбранной координаты состояния ОУ. Матрица Q назначается такой, чтобы  , тогда условие полного соответствия моделей для части объекта
, тогда условие полного соответствия моделей для части объекта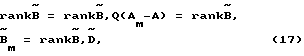
 выполняется всегда.
выполняется всегда.
Отсюда следует, что устойчивость замкнутой системы по ошибке адаптации может быть достигнута для выделенной части объекта. Это не трудно показать. Вычитая из уравнения (16) уравнение эталонной модели (2), умноженное слева на матрицу Q и добавляя и вычитая из результата  , получаем
, получаем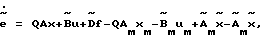
 - квадратная матрица, образованная пересечением выбранных k строк и k столбцов матрицы Ам. Аналогично обозначим
- квадратная матрица, образованная пересечением выбранных k строк и k столбцов матрицы Ам. Аналогично обозначим  , а матрицы из оставшихся (n-k) столбцов матриц QA и QAм после выделения из них матриц
, а матрицы из оставшихся (n-k) столбцов матриц QA и QAм после выделения из них матриц  соответственно. Компоненты
соответственно. Компоненты 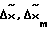 - оставшиеся компоненты векторов х и хм после выделения из них компонент
- оставшиеся компоненты векторов х и хм после выделения из них компонент 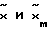 .
.
Преобразуем с учетом введенных обозначений выражения для 

Отсюда видно, что справедливость уравнения
обеспечивает ЗУ
Этот закон обеспечивает цель 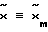 , поведение оставшейся части координат вектора х в этом случае подчинено указанной цели. Реализация закона требует использования явной ЭМ для формирования сигнала
, поведение оставшейся части координат вектора х в этом случае подчинено указанной цели. Реализация закона требует использования явной ЭМ для формирования сигнала  . Таким образом, в структурную схему системы необходимо внести блок явной эталонной модели, в котором будут интегрироваться в реальном масштабе времени дифференциальные уравнения эталонной модели (2) с целью вычисления значения вектора
. Таким образом, в структурную схему системы необходимо внести блок явной эталонной модели, в котором будут интегрироваться в реальном масштабе времени дифференциальные уравнения эталонной модели (2) с целью вычисления значения вектора 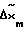 в текущий момент времени. В адаптивной системе используется закон
в текущий момент времени. В адаптивной системе используется закон
где верхний индекс"∧" обозначает выдаваемые идентификатором оценки соответствующих матриц. Структура закона (18) показывает, что для его реализации требуется идентификация только выбранных k строк объекта (1).
При использовании ЗУ (18) (случай выполнения условий ПСМ для части объекта) по представленной в работах [1, 5] методике легко получить, что в замкнутой системе справедливы следующие уравнения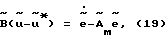

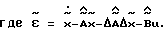
Используя приведенную выше методику, получаем, что при выполнении условия
из уравнений (19)-(20) следует следующее дифференциальное уравнение, описывающее закон изменения ошибки адаптации в замкнутой системе при законе управления (18)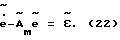
Следовательно, в замкнутой системе  , если оценка матрицы
, если оценка матрицы 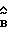 имеет полный строковый ранг (условие (21)) и
имеет полный строковый ранг (условие (21)) и  . Так как выдаваемая идентификатором оценка
. Так как выдаваемая идентификатором оценка  может не удовлетворять условию (21), здесь также необходимо использовать блок коррекции оценки матрицы эффективности управления объекта, который обеспечивает контроль за выполнением условия (21) и при необходимости корректирует оценку
может не удовлетворять условию (21), здесь также необходимо использовать блок коррекции оценки матрицы эффективности управления объекта, который обеспечивает контроль за выполнением условия (21) и при необходимости корректирует оценку  , т.е. заменяет ее на матрицу
, т.е. заменяет ее на матрицу  , удовлетворяющую условию (21) и обеспечивающую малую норму
, удовлетворяющую условию (21) и обеспечивающую малую норму 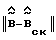 .
.
Из изложенного следует ряд выводов:
1. Предлагаемое в изобретении [1] решение содержит недостатки, приводящие к снижению качества управления в адаптивной системе. Во-первых, делается допущение о выполнении условия полного соответствия моделей (3), выполнение которого в случае, если rankB<n, представляет серьезную проблему. Решение этой проблемы в изобретении [1] не рассматривается. Во-вторых, в случае, если матрица В0 не удовлетворяет условию rank(B0 TB)=rankB (что вполне может оказаться на практике), то ошибка адаптации в замкнутой системе ведет себя произвольным образом.
2. Для снятия указанных недостатков предлагается в случае, если rankB<n, выполнять условие полного соответствия моделей (условие (17)) для части объекта из k строк путем выбора матрицы выделения Q такой, что 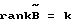 . В этом случае слежение за эталонной моделью обеспечивается по выбранной части из k компонент вектора состояния. Для реализации закона управления в этом случае (выражение (18)) требуется информация о части вектора состояния эталонной модели. В связи с этим в структурную схему системы необходимо внести блок явной эталонной модели. В качестве условия устойчивости замкнутой системы по ошибке адаптации предлагается использовать не условия (9) или (10), так как они требуют априорной информации о матрице эффективности управления, а условие (14) при rankB=n и условие (21) при rankB=k. Контроль за условиями (14) или (21) не требует априорной информации о матрице эффективности управления, поэтому из структурной схемы системы предлагается убрать блок априорной информации о матрице эффективности управления объекта. За контролем за выполнением условий (14) или (21) и при необходимости коррекции оценки матрицы
. В этом случае слежение за эталонной моделью обеспечивается по выбранной части из k компонент вектора состояния. Для реализации закона управления в этом случае (выражение (18)) требуется информация о части вектора состояния эталонной модели. В связи с этим в структурную схему системы необходимо внести блок явной эталонной модели. В качестве условия устойчивости замкнутой системы по ошибке адаптации предлагается использовать не условия (9) или (10), так как они требуют априорной информации о матрице эффективности управления, а условие (14) при rankB=n и условие (21) при rankB=k. Контроль за условиями (14) или (21) не требует априорной информации о матрице эффективности управления, поэтому из структурной схемы системы предлагается убрать блок априорной информации о матрице эффективности управления объекта. За контролем за выполнением условий (14) или (21) и при необходимости коррекции оценки матрицы  или
или  в структурную схему системы предлагается внести блок коррекции оценки матрицы эффективности управления.
в структурную схему системы предлагается внести блок коррекции оценки матрицы эффективности управления.
Подробное описание устройства предлагаемой адаптивной системы и принципа ее действия приведено ниже.
Для подтверждения полученных выводов приводятся численные исследования на одном из возможных приложений рассматриваемой системы управления.
Рассмотрим упрощенную модель бокового движения гипотетического самолета
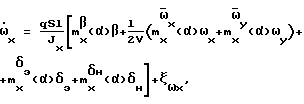


где α,β - углы атаки и скольжения; ωx,ωy - угловые скорости крена и рыскания; γ - угол крена; q = ρV2/2 - скоростной напор, ρ - плотность воздуха; V - воздушная скорость; δэ,δн - отклонения элеронов и руля направления соответственно; S, l - площадь и размах крыла; Jx, Jy - моменты инерции относительно осей связанной системы координат; m - масса; C
Запишем первые три уравнения системы (23) в матричной форме
где xT = [β,ωx,ωy];uT = [δэ,δн];
где ai j - неизвестные параметры модели объекта управления, подлежащие определению с помощью алгоритма текущей идентификации,

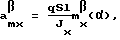


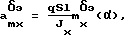






Пусть требуемые характеристики устойчивости и управляемости в боковом канале задает следующая ЭМ
где βм,ωxм,ωxм - соответствующие компоненты вектора состояния эталонной модели; δэм,δнм - задающие воздействия (преобразованные управляющие воздействия летчика или системы автоматического управления).
Как видно из структуры математических моделей объекта управления (24) и эталонной модели (25), условия полного соответствия моделей (3) здесь не выполняются. Поэтому не существует управления, обеспечивающего точное слежение объекта управления за эталонной моделью по всему вектору состояния. Из структуры матрицы эффективности управления видно, что здесь rankB=2. Следовательно, можно обеспечить слежение за эталонной моделью по каким-либо двум компонентам вектора состояния. Из практических соображений в качестве этих компонент выберем угол β и угловую скорость ωx, так как именно они больше всего влияют на оценку пилотажных характеристик самолета в боковом канале. Матрица выделения имеет вид
При решении задачи идентификации в качестве настраиваемой модели принималась следующая система


Ошибка идентификации для каждого из уравнений настраиваемой модели равна 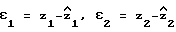 .
.
Так как набор факторов (термин регрессионного анализа) для каждой из строк объекта различен, то идентификация параметров уравнений проводится построчно. В качестве алгоритма текущей идентификации используем рекуррентный метод наименьших квадратов с фактором забывания [9], уравнения которого для j-й строки математической модели объекта имеют вид


Г10 = 50E3; Г20 = 50E5; λ = 0.99,
где
y
y
Начальные значения всех оценок параметров задаются нулевыми.
Алгоритмы идентификации и управления работают дискретно. Ниже для сокращения записи индекс i пропущен.
Переходим к алгоритму коррекции оценки матрицы эффективности управления. Матрица
Условие (21) для рассматриваемого случая тождественно
Заметим, что если условие (26) выполняется, но 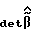 мал, то норма
мал, то норма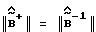
велика. Это соответствует возрастанию коэффициента усиления в замкнутой системе (см. структуру закона управления (18)), что ведет к снижению запаса устойчивости. Поэтому на практике условие (26) целесообразно заменить на более жесткое
где l - граница коридора минимальных значений определителя, соблюдение которой обеспечивает требуемую степень устойчивости системы управления. Значение l выбирается экспериментально.
Контроль за соблюдением условия (27) возлагается на блок коррекции оценки матрицы эффективности управления, алгоритм работы которого имеет вид
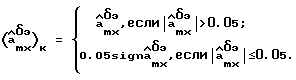
 - скорректированные значения оценок соответствующих параметров эффективности управления. Граничные значения 0,001 и 0,05 были выбраны экспериментально из анализа качества управления в замкнутой системе. При этом l=5•10-5.
- скорректированные значения оценок соответствующих параметров эффективности управления. Граничные значения 0,001 и 0,05 были выбраны экспериментально из анализа качества управления в замкнутой системе. При этом l=5•10-5.
Закон управления имеет вид
Для фильтрации управления используется апериодическое звено с единичным коэффициентом управления и постоянной времени 0,05 с, которое обеспечивает устранение высокочастотной составляющей (по отношению к рабочим частотам объекта) в управлении.
Зависимости изменения аэродинамических коэффициентов были аппроксимированы степенными полиномами до восьмого порядка с погрешностью не хуже 5%. Дифференциальные уравнения (23) и (25) решались методом Рунге-Кута четвертого порядка с шагом 0,01 с. Дискретность алгоритма идентификации и формирования управления та же.
При проведении исследований в продольном канале моделировался выход самолета на угол атаки 20 град. Изменения угла атаки и скорости полета, соответствующие проводимым исследованиям, приведены на фиг.1.
Реакция исходного объекта и заданной эталонной модели на один и тот же входной сигнал δэм(δэ = δэм,δн = 0) показана на фиг.2. Как видно, на исходном объекте в рассматриваемых условиях возникает обратная реакция по крену (противоположная навыкам летчика) на отклонение элеронов. Поведение замкнутой адаптивной системы представлено на фиг.3. Как видно, обратная реакция по крену не только устранена, но и обеспечен переходный процесс по угловой скорости крена, близкий к заданному эталонной моделью. Скольжение в отличие от фиг. 2 также автоматически поддерживается близким к эталонному значению. На фиг.3 для сравнения синтезированного управления пунктирными линиями приведены точные значения управлений  . На фиг.4 представлено поведение выдаваемых идентификатором оценок параметров
. На фиг.4 представлено поведение выдаваемых идентификатором оценок параметров  , модуля определителя
, модуля определителя  , евклидовой нормы относительной ошибки идентификации
, евклидовой нормы относительной ошибки идентификации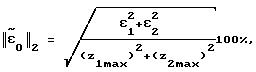
где z1max, z2max - максимальное значение откликов z1, z2 на рассматриваемом интервале времени. Из представленных графиков видно, что скорректированные значения оценок 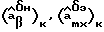 и модуль определителя
и модуль определителя  удовлетворяют условию (27), норма ошибки идентификации мала, оценки параметров неточные (изменения точных значений параметров показаны пунктирными линиями), но цель управления выполняется: движение объекта по угловой скорости крена и углу скольжения близко к эталонному. Причем при нулевых шумах ξβ,ξωx,ξωy движение объекта по контролируемым компонентам вектора состояния практически точно совпадает с эталонными (результаты не приведены). Приведенные численные исследования полностью подтверждают справедливость теоретических выводов.
удовлетворяют условию (27), норма ошибки идентификации мала, оценки параметров неточные (изменения точных значений параметров показаны пунктирными линиями), но цель управления выполняется: движение объекта по угловой скорости крена и углу скольжения близко к эталонному. Причем при нулевых шумах ξβ,ξωx,ξωy движение объекта по контролируемым компонентам вектора состояния практически точно совпадает с эталонными (результаты не приведены). Приведенные численные исследования полностью подтверждают справедливость теоретических выводов.
Таким образом, предлагаемое техническое решение позволяет расширить область применения адаптивной системы на объекты управления, для которых условия полного соответствия моделей (3) не выполняются, а также снизить объем требуемой для работы системы априорной информации о ее параметрах и обеспечить гарантированный уровень качества управления на всем промежутке времени работы системы.
На фиг.1...4 приводятся результаты, полученные при проведении численных исследований.
На фиг.1 приведены условия проведения численных исследований - изменение угла атаки α и воздушной скорости полета V во времени.
На фиг. 2 показано поведение разомкнутой системы управления.
На фиг. 3 показано поведение замкнутой системы управления.
На фиг.4 показаны изменения во времени нормы относительной ошибки идентификации, модуля определителя матрицы 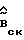 , выдаваемых идентификатором оценок параметров и их точных значений.
, выдаваемых идентификатором оценок параметров и их точных значений.
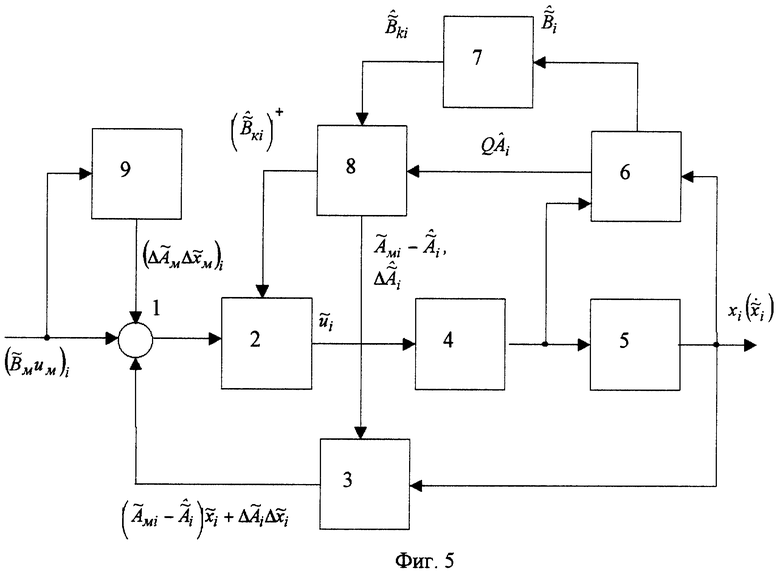
На фиг. 5 представлена структурная схема дискретной адаптивной системы управления с идентификатором и эталонной моделью.
Структурная схема содержит сумматор 1, первый 2 и второй 3 регуляторы, фильтр 4 низких частот, объект 5 управления, блок 6 текущей идентификации, блок 7 коррекции оценки матрицы эффективности управления объекта, блок 8 настройки регулятора, блок 9 явной эталонной модели.
Адаптивная система работает следующим образом. Задающее воздействие в виде 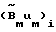 подается на первый вход сумматора 1 и на вход явной эталонной модели 9, в котором происходит интегрирование в реальном масштабе времени дифференциальных уравнений эталонной модели с известными начальными условиями и задающим воздействием. На второй вход сумматора поступает сигнал с выхода второго регулятора 3. На третий вход сумматора поступает с выхода блока эталонной модели сигнал
подается на первый вход сумматора 1 и на вход явной эталонной модели 9, в котором происходит интегрирование в реальном масштабе времени дифференциальных уравнений эталонной модели с известными начальными условиями и задающим воздействием. На второй вход сумматора поступает сигнал с выхода второго регулятора 3. На третий вход сумматора поступает с выхода блока эталонной модели сигнал 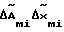 . Выход сумматора связан с первым входом первого регулятора 2. Этот регулятор окончательно формирует управление в соответствие с зависимостью
. Выход сумматора связан с первым входом первого регулятора 2. Этот регулятор окончательно формирует управление в соответствие с зависимостью
Выход первого регулятора связан со входом фильтра низких частот 4, пропускающего рабочие частоты объекта управления. Выход фильтра связан со входом объекта управления 5 и с первым входом блока 6 текущей идентификации. Выход объекта управления связан с первым входом второго регулятора 3, преобразующего входной сигнал хi в виде
и со вторым входом блока текущей идентификации. Блок текущей идентификации по входным и выходным сигналам с объекта управления:  формирует текущие оценки параметров объекта управления. Вектор
формирует текущие оценки параметров объекта управления. Вектор  может либо непосредственно изменяться, либо аналитически вычисляться в блоке текущей идентификации по текущим значениям
может либо непосредственно изменяться, либо аналитически вычисляться в блоке текущей идентификации по текущим значениям 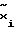 , например, на основе полиномиальной или тригонометрической аппроксимации на скользящем интервале [10]. Алгоритм текущей идентификации блока 6 относится к классу алгоритмов типа стохастической аппроксимации (например, рекуррентный метод наименьших квадратов (см. пример) и др. ). Алгоритм текущей идентификации должен быть настроен так, чтобы его собственная частота превышала верхнюю границу диапазона рабочих частот объекта управления. Основным требованием к алгоритму текущей идентификации является обеспечение им малой нормы невязки
, например, на основе полиномиальной или тригонометрической аппроксимации на скользящем интервале [10]. Алгоритм текущей идентификации блока 6 относится к классу алгоритмов типа стохастической аппроксимации (например, рекуррентный метод наименьших квадратов (см. пример) и др. ). Алгоритм текущей идентификации должен быть настроен так, чтобы его собственная частота превышала верхнюю границу диапазона рабочих частот объекта управления. Основным требованием к алгоритму текущей идентификации является обеспечение им малой нормы невязки 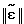 на всем промежутке времени работы системы.
на всем промежутке времени работы системы.
Через первый выход блока текущей идентификации выдается информация об оценке  в блок 7 коррекции матрицы эффективности управления объекта. Через второй выход блока 6 поступает оценка
в блок 7 коррекции матрицы эффективности управления объекта. Через второй выход блока 6 поступает оценка 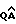 на первый вход блока 8 настройки регулятора. В блоке 7 проверяется полнота ранга матрицы
на первый вход блока 8 настройки регулятора. В блоке 7 проверяется полнота ранга матрицы 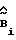 (условие (21)), обеспечение которого гарантирует асимптотические свойства координатной невязки
(условие (21)), обеспечение которого гарантирует асимптотические свойства координатной невязки  . При нарушении условия (21) матрица
. При нарушении условия (21) матрица  корректируется. В результате коррекции матрица
корректируется. В результате коррекции матрица 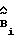 преобразуется в матрицу
преобразуется в матрицу  , такую, что для матрицы
, такую, что для матрицы 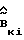 выполняется условие (21) при "минимальном" изменении исходной матрицы. Выход блока коррекции оценки матрицы эффективности управления связан со вторым входом блока 8 настройки регулятора, через который поступает оценка
выполняется условие (21) при "минимальном" изменении исходной матрицы. Выход блока коррекции оценки матрицы эффективности управления связан со вторым входом блока 8 настройки регулятора, через который поступает оценка 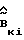 . Этот блок вычисляет
. Этот блок вычисляет  . Для реализации псевдообращения можно использовать последовательный метод Гревилля [7]. Первый выход блока 8 связан со вторым входом второго регулятора, по нему передается информация о
. Для реализации псевдообращения можно использовать последовательный метод Гревилля [7]. Первый выход блока 8 связан со вторым входом второго регулятора, по нему передается информация о  . Второй выход блока 8 связан со вторым входом второго регулятора, по нему передается информация о матрицах
. Второй выход блока 8 связан со вторым входом второго регулятора, по нему передается информация о матрицах 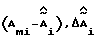 .
.
ЛИТЕРАТУРА
1. Буков В. Н., Круглов С.П. Адаптивная система управления с идентификатором и неявной эталонной моделью. - Патент 2108612 от 14.09.94г. (прототип).
2. Уткин В.Н. Скользящие режимы в задачах оптимизации и управления. - М. : Наука, 1981.
3. Справочник по теории автоматического управления. / Под ред. А.А. Красовского. - М.: Наука, Гл. ред. физ. мат. лит., 1987.
4. Изерман Р. Цифровые системы управления: Пер. с англ. - М.: Мир, 1984.
5. Буков В.Н., Круглов С.П., Решетняк Е.П. Адаптируемость линейной динамической системы с идентификатором и эталонной моделью. // Автоматика и телемеханика, 1994. - 3, с. 99...107.
6. Цыпкин Я.З. Основы информационной теории идентификации. - М.: Наука, Гл. ред. физ.-мат. лит., 1984.
7. Гантмахер Ф.Р. Теория матриц. - М.: Наука, Гл. ред. физ. мат. лит., 1988.
8. Летно-технические характеристики самолета Су-27. // Под ред. А.И. Нелюбова. М.: ВВИА, 1988.
9. Гроп Д. Методы идентификации систем: Пер. с англ. - М.: Мир, 1979.
10. Пашковский И.М., Леонов В.А., Поплавский Б.К. Летные испытания самолетов и обработка результатов испытаний. - М.: Машиностроение, 1985.



Изобретение относится к области систем автоматического управления динамическими объектами широкого класса с неизвестными переменными параметрами и неконтролируемыми возмущениями. Технический результат изобретения заключается в упрощении условий для достижения цели адаптации замкнутой системы управления, снижении объема требуемой априорной информации, необходимой для синтеза системы. Система содержит сумматор, первый и второй регуляторы, фильтр низких частот, объект управления, блок текущей идентификации, блок коррекции оценки матрицы эффективности управления объекта, блок настройки регуляторов, блок эталонной модели. 5 ил.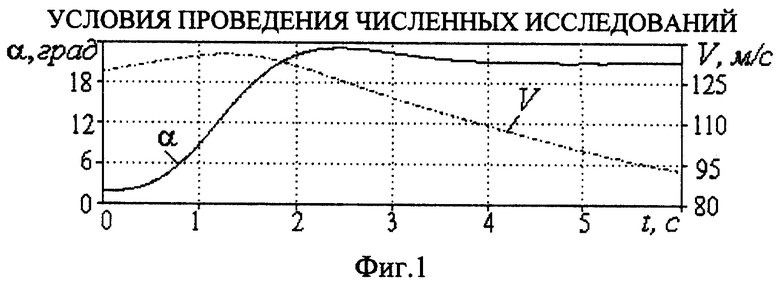
Адаптивная система управления с идентификатором и эталонной моделью, содержащая сумматор, первый вход которого подключен к задающему воздействию, а выход - к первому входу первого регулятора, выход первого регулятора подключен к входу фильтра низких частот, выход фильтра низких частот подключен к входу объекта управления и к первому входу блока текущей идентификации, выход объекта управления подключен к первому входу второго регулятора и ко второму входу блока текущей идентификации, выход второго регулятора подключен ко второму входу сумматора, второй выход блока текущей идентификации подключен к первому входу блока настройки регуляторов, первый выход которого подключен ко второму входу первого регулятора, а второй выход - ко второму входу второго регулятора, отличающаяся тем, что она дополнительно содержит блок явной эталонной модели, вход которого подключен к задающему воздействию, а выход - к третьему входу сумматора, блок коррекции оценки матрицы эффективности управления объекта, вход которого подключен к первому выходу блока текущей идентификации, а выход - ко второму входу блока настройки регуляторов.
| RU 96120056 A, 10.01.1999 | |||
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ИДЕНТИФИКАТОРОМ И НЕЯВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ | 1994 |
|
RU2108612C1 |
| US 4407013 A, 27.09.1983 | |||
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
| Справочник по теории автоматического управления | |||
| /Под ред | |||
| КРАСОВСКОГО А.А | |||
| - М.: Наука, 1987, с.492-495, рис.10.5.1. | |||
Авторы
Даты
2002-10-20—Публикация
2001-02-05—Подача