Настоящее изобретение относится к компьютерной графике, более конкретно к представлению трехмерных неподвижных и анимированных объектов, полученному с использованием фотографий реальных объектов и их геометрических представлений, и к способу и устройству для представления и визуализации, использующим бинарное волюметрическое октодерево.
В ближайшее время основной упор в современных графических системах будет сделан на высококачественную интерактивную визуализацию трехмерных объектов в реальном времени. Требование высокого качества визуализации техмерных объектов ведет к необходимости построения эффективных алгоритмов сжатия этих объектов и передачи по сетям связи в таких областях, как электронная коммерция, компьютерные игры, научные области, техника, медицина. Использование традиционных полигональных моделей трехмерных объектов для одновременного достижения всех этих требований в течение последних десятилетий не привело к желаемому результату. Полигональные модели имеют два основных недостатка: большой объем (т. е. реалистические модели требуют десятки миллионов треугольников) и трудность построения. Чтобы преодолеть эти трудности, в последние годы предложено несколько подходов к трехмерной графике. Наиболее перспективными из них являются способы, основанные на использовании изображений объектов, и способы, основанные на использовании точек вместо треугольников в трехмерном пространстве.
Способы, основанные на использовании изображений объектов, представляют данный объект в качестве набора изображений - "фотографий" объекта, полностью покрывающих его видимую поверхность и полученных с нескольких различных положений камеры. Помимо этого, каждое такое изображение рассматривается совместно с соответствующей картой глубины, которая является матрицей расстояний от пикселов в плоскости изображения до поверхности объекта. Преимущество такого представления состоит в том, что опорные изображения могут обеспечить высокое качество визуализации объекта независимо от сложности его многоугольной модели и могут быть сжаты обычными методами сжатия изображений без больших потерь качества. В дополнение к этому, время визуализации пропорционально числу пикселов в опорном и выходном изображениях, а не сложности объекта.
Недостатки состоят в том, что получение карт глубины для реальных объектов (например, скульптур) представляет собой довольно сложную работу. Кроме того, методы обращения с такими представлениями еще недостаточно развиты.
Способы, основанные на использовании точек, представляют объект как "облако точек" без наложения точной локальной многоугольной структуры. В этом способе набор изображений с глубиной определяет набор точек (имеющих соответствующие цвета) на поверхности объекта путем переноса каждого пиксела каждого опорного изображения посредством соответствующего значения глубины в направлении, перпендикулярном плоскости изображения. Следовательно, основанные на изображениях представления являются частным случаем представлений, основанных на точках. В последующем мы сосредоточимся на представлениях, основанных на изображениях, т.к. они ближе к нашему подходу.
В литературе два вышеуказанных направления описаны в источниках [1]-[13] , описывающих такое представление трехмерных объектов и способы визуализации, как метод рельефных текстур [1], многослойные изображения с глубиной [2] , дерево из многослойных изображений с глубиной [3], Q-сплаты [4], метод поверхностных элементов (ПЭ)[5] и некоторые иные, которые известны в существующем уровне техники. В нижеследующем обсуждении подходов существующего уровня техники будут делаться ссылки на следующие публикации (см. в конце описания).
Общая проблема для основанных на изображениях способов состоит в появлении дырок в результирующем изображении. В отличие от многоугольных моделей, которые являются "непрерывными" в том смысле, что поверхность объекта линейно интерполируется во внутренность всех многоугольников (как правило, треугольников), основанные на изображениях и основанные на точках представления, создают "дискретные" аппроксимации объектов. В случае основанных на изображениях представлений поверхность объекта фактически аппроксимируется малыми цветными квадратами, т.е. сдвинутыми пикселами опорных изображений. Когда направление взгляда значительно отличается от нормального направления к каждой из плоскостей опорного изображения, проекции аппроксимирующих квадратов в общем случае не полностью покрывают проекцию поверхности объекта. Назовем такие дырки дырками первого типа. Другим источником дырок в результирующем изображении для основанных на изображениях представлений является то, что некоторая часть поверхности может быть не видна на всех опорных изображениях, но становится видимой для некоторых точек зрения (дырки второго типа). Эти дырки появляются из-за недостаточной информации, содержащейся в конкретном основанном на изображениях представлении.
Способ рельефной текстуры [1] подавляет дырки первого типа с помощью аналога линейной интерполяции, что может привести к искажениям и артефактам, поскольку интерполяция выполняется на двумерной проекции объекта, а не в трехмерном пространстве. Более важно то, что при этом подходе дырки второго типа могут быть обработаны лишь тем же методом. Поскольку способ [1] использует только 6 опорных изображений, т.е. проекций объекта на грани описанного куба, это налагает серьезные ограничения на применение данного способа к сложным формам, когда имеются точки, невидимые со всех шести граней куба. Этот подход выбирался для максимизации скорости визуализации, а именно путем использования быстрой предварительной деформации (геометрическое преобразование, эквивалентное смене направления взгляда при ортографической проекции), но он ведет к ухудшению качества.
Многослойные изображения с глубиной (МИГ) [2] являются структурой данных, созданной для того, чтобы избежать проблемы с дырками второго типа. МИГ представляет собой изображение, пикселы которого содержат все точки объекта, проецирующиеся на фиксированное местоположение плоскости опорного изображения. Быстрый алгоритм деформации из [1] применим также и здесь. Однако остаются проблемы с дырками первого типа. Для решения проблемы дырок первого типа используют cплаты (введенные в [10]). Сплаты являются маленьким двумерным участком поверхности прямоугольной или эллиптической формы, наделенным некоторым распределением цвета, например, гауссовым, с центром в центре этого участка или с постоянным распределением цвета. Недостаток метода МИГ состоит в его несимметрии, поскольку данное представление основано на проекции с определенным фиксированным направлением. Это приводит к трудностям заполнением дырок для направлений зрения, сильно отличающихся от указанного фиксированного направления.
Дерево МИГ [3] является октодеревом с МИГ в каждой ячейке (узле) октодерева. Преимущество использования иерархической модели состоит в том, что не каждое МИГ в октодереве должно быть визуализировано. Те ячейки, которые удалены дальше, визуализируются менее подробно с помощью отфильтрованных точек, которые хранятся в более высоких по иерархии МИГ. Данное представление было разработано для преодоления несимметрии МИГ за счет использования многих опорных изображений. Однако объем запоминания становится очень большим: дерево МИГ для изображения 512 х 512 (полученное из 36 опорных изображений) занимает 30 Мбайт [3], и примерно половина этого объема содержит структуру дерева. Согласно [3], время визуализации для данного объекта также велико: 2-3 секунды на кадр на Silicon Graphics Onyx2 с процессорами MIPS R10000 с частотой 32250 МГц (без использования параллелизма).
Еще одним представлением, объединяющим основанные на изображениях данные в структуру дерева, является недавно предложенный способ ПЭ [5]. Он имеет дело со специальным деревом [8], представляющим собой многослойный по глубине куб (МГК), где вместо единственного дерева МИГ узлы содержат три МИГ, соответствующие трем ортогональным плоскостям. Результаты, представленные в [5] , получены для исходной модели, содержащей 81000 треугольников. При использовании выходного буфера 256 х 256 была получена скорость в 11 кадров/сек на процессоре Pentium III 700 МГц. ПЭ представляют собой пикселы опорных изображений, сдвинутые в соответствии с вектором глубины. Структура дерева используется для ускорения вычислений отбора видимых элементов. Заполнение дырок достигается методом фильтрации ближайшего соседа или гауссовой фильтрацией. В этой работе используются оплаты. Высокое качество результирующего изображения достигается за счет ограничений по объему данных и скорости вычислений.
Следует также упомянуть недавно введенное представление Q-сплатов [4], основанное на точечном представлении, а не на изображениях. Этот подход использует иерархическую структуру точек, основанную на вложенных шарах. На стадии визуализации используются эллиптические сплаты требуемого размера. В [4] используется сложный и занимающий большое время усеченный отбор. Структура данных также достаточно сложная и требует большого времени для обработки.
Идея и различные способы воплощения для получения трехмерной модели со структурированным октодеревом из таких данных диапазона, как наборы изображений с глубиной, разрабатывались в [11]-[12]. Источник [13] имеет дело с конструкцией полигональной модели из исходных данных с помощью октодерева.
Все вышеописанное относится к неподвижным трехмерным представлениям, основанным на изображениях. Говоря об анимированных трехмерных объектах, следует отметить, что до сих пор известно очень мало основанных на изображениях способов для решения этой проблемы. В [14] предложена идея модификации изображения лица для мало изменяющейся трехмерной геометрии лица. Она применима только к ограниченному классу анимированных объектов и не является анимацией действительного трехмерного объекта. В [15] предложено анимировать архитектурные виды с помощью зависящего от взгляда текстурного отображения, реконструирующего архитектурные виды с разных точек зрения на основе нескольких фотографий.
Таким образом, ясно, что существует необходимость в основанном на изображениях представлении, обеспечивающем компактное хранение, быструю визуализацию с высоким качеством выходного изображения и пригодном для целей анимации.
Задачей изобретения является получение представления трехмерных объектов, основанного на изображениях с глубиной, требующего относительно малого пространства для хранения и обеспечивающего быструю и высококачественную визуализацию, в котором снижены или исключены недостатки рассмотренных выше способов.
Кроме того, задачей изобретения является создание способа и устройства представления и визуализации трехмерного объекта, обеспечивающих быстрое вычисление преобразования координат, автоматическое вычисление порядка наложения элементов бинарного волюметрического октодерева (БВО) и формирование сплатов точно определенного размера.
Кроме того, задачей изобретения является создание способа компактного представления анимированного трехмерного объекта, обеспечивающего быструю и корректную визуализацию.
Компактное представление потока данных осуществляется путем разделения геометрической и цветовой составляющей БВО и использования для сжатия геометрической части бинарного представления октодерева, а для сжатия цветовой составляющей - алгоритмов сжатия двумерных изображений.
Указанный результат достигается тем, что способ представления и визуализации трехмерного объекта в соответствии с изобретением включает этапы, при которых преобразуют исходные данные трехмерного объекта в представление в виде бинарного волюметрического октодерева (БВО), при этом с каждой вершиной БВО, соответствующей координатам точек поверхности объекта, сопоставляют усредненный цвет точек поверхности объекта, координаты которых находятся внутри куба, представляющего собой элемент трехмерного изображения - воксела, соответствующего данной вершине БВО, визуализируют БВО путем иерархического прохождения октодерева от корневой вершины до листьев, при этом получают локальные трехмерные координаты центров вокселов, соответствующих листьям БВО, преобразуют полученные трехмерные координаты в двумерные координаты центра воксела и информацию о размере изображения спроецированного воксела и формируют для каждого листа БВО и отображают соответствующий сплат, перекрывающий область изображения спроецированного воксела и использующий информацию о цвете, причем множество отображенных сплатов визуализируют трехмерный объект.
При этом исходные данные трехмерного объекта представляют собой набор изображений с глубиной либо данные многоугольной модели, либо набор точек с цветом.
Кроме того, иерархическое прохождение октодерева предпочтительно осуществляют в порядке от вокселов БВО, более удаленных от наблюдателя, к вокселам БВО, менее удаленным от наблюдателя.
Для обеспечения минимальной вычислительной сложности процесса преобразования перед прохождением октодерева вычисляют
fT(i,σi) = T2i-1σi,
где Т - матрица 4 х 4 видового преобразования координат;
σi - любой четырехмерный вектор, элементы которого принимают значение 0 или 1;
i - целое число, принимающее значения от 0 до высоты рассматриваемого БВО, и используют полученные результаты при иерархическом преобразовании трехмерных координат в двумерные координаты, при этом на каждой вершине БВО вычисляют Fi: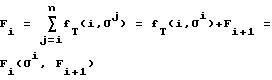
и в результате после прохождения всего пути от корневой вершины до листьев БВО, для каждого листа БВО, задаваемого локальными координатами (х, у, z), получают
Tv = F1(σ1, F2(σ2..Fn(σn)..)),
где σi определяется выражением, использующим бинарную запись координат:
Указанный выше технический результат достигается также тем, что устройство для представления и визуализации трехмерного объекта содержит средство для формирования исходных данных трехмерного объекта, средство для преобразования исходных данных трехмерного объекта в представление в виде бинарного волюметрического октодерева (БВО), связанное со средством для формирования исходных данных трехмерного объекта, при этом с каждой вершиной БВО, соответствующей координатам точек объекта, сопоставлен усредненный цвет точек объекта, координаты которых находятся внутри куба, представляющего собой элемент трехмерного изображения - воксела, соответствующего данной вершине БВО, средство для визуализации БВО, связанное со средством для преобразования исходных данных трехмерного объекта в представление в виде БВО.
При этом средство для формирования исходных данных трехмерного объекта выполнено в виде трехмерного сканера реального трехмерного объекта, обеспечивающего формирование на выходе множества трехмерных координат точек, либо представляет собой средство для формирования полигональной модели трехмерного объекта или средство для формирования изображения с глубиной.
Кроме того, указанный технический результат достигается тем, что способ представления анимированного трехмерного объекта включает этапы, при которых преобразуют исходные данные для каждого трехмерного объекта в последовательности трехмерных объектов в представление в виде бинарного волюметрического октодерева (БВО), при этом с каждой вершиной БВО, соответствующей координатам точек поверхности объекта, сопоставляют усредненный цвет точек поверхности объекта, координаты которых находятся внутри куба, представляющего собой элемент трехмерного изображения - воксела, соответствующего данной вершине БВО, в результате чего формируют последовательность БВО для последовательности трехмерных объектов, соответствующей анимированному трехмерному объекту.
При этом проецируют каждый БВО в последовательности БВО на грани куба, соответствующего корневой вершине БВО, в результате чего для каждой грани куба получают поток видеоданных, соответствующих изображениям анимированного объекта, и формируют байтовый поток октодеревьев, каждый байт в котором соответствует вершине октодерева, а каждый бит в байте указывает на наличие или соответственно отсутствие поддерева для данной вершины октодерева, при этом шесть потоков видеоданных и байтовый поток октодеревьев совместно образуют представления анимированного трехмерного объекта, причем для хранения шести потоков видеоданных в компактной форме используют формат сжатия видеоданных группы стандартов MPEG, а для хранения байтового потока октодеревьев используют энтропийное сжатие.
Кроме того, анимированный трехмерный объект визуализируют путем проецирования шести потоков опорных изображений на БВО для определения цвета для каждой вершины БВО и проецирования полученного окрашенного БВО для визуализации анимированного трехмерного объекта.
Изобретение поясняется на примерах осуществления, иллюстрируемых чертежами, на которых представлено следующее:
фиг. 1 - функциональная схема устройства представления и визуализации трехмерного объекта из различных типов исходных данных;
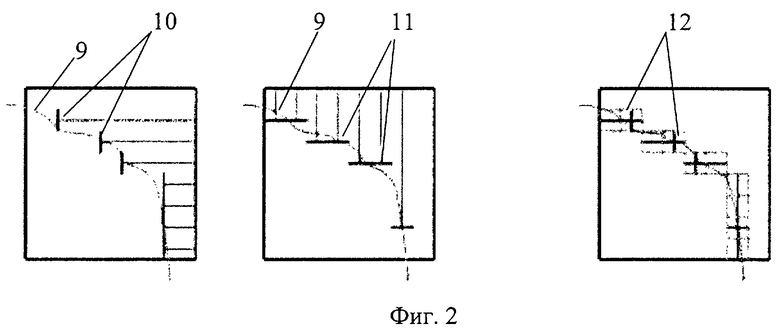
фиг.2 - схема получения БВО из пары изображений с глубиной, полученных с использованием ортогональных камер (двумерный вид);
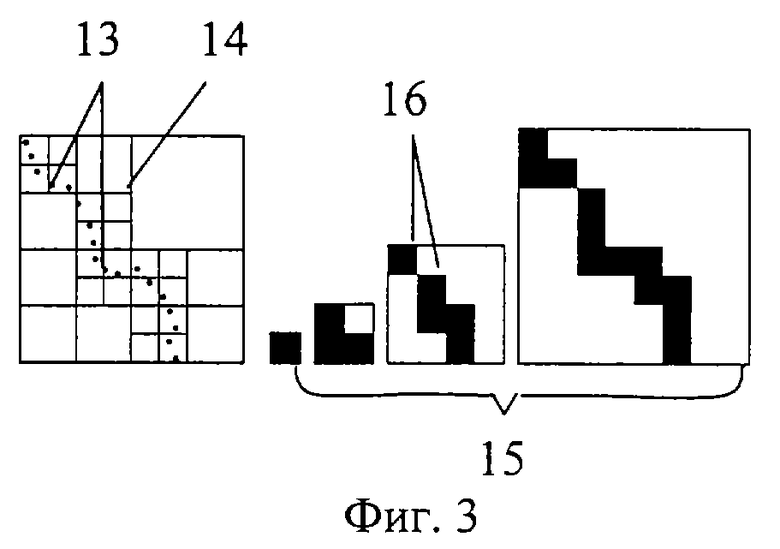
фиг. 3 - представление схем соответствия трехмерных точек различным иерархическим уровням БВО (двумерный вид);
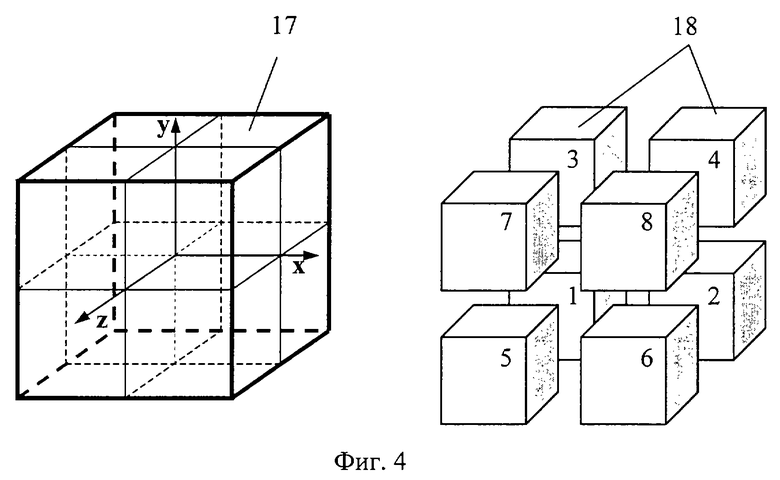
фиг.4 - иллюстрация куба БВО и его подразделения на 8 подкубов;
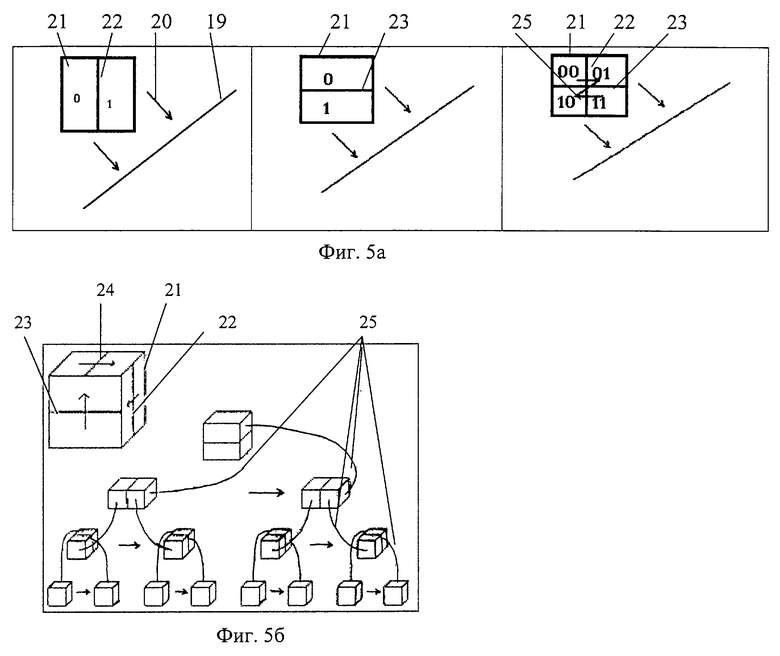
фиг.5а,б - двумерная и трехмерная иллюстрация способа определения порядка прохождения вершин БВО на одном иерархическом уровне;
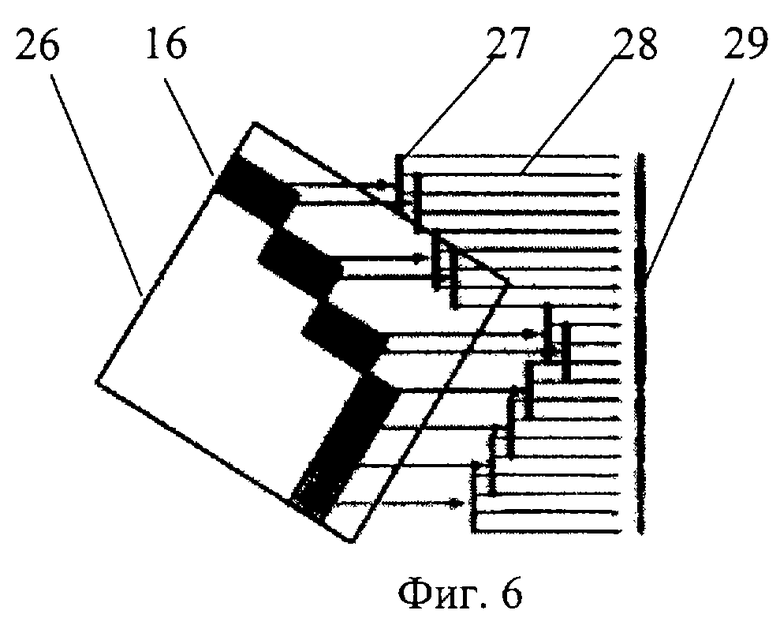
фиг.6 - иллюстрация процесса проецирования сплатов во времени и в пространстве и геометрические условия определения размера оплата;
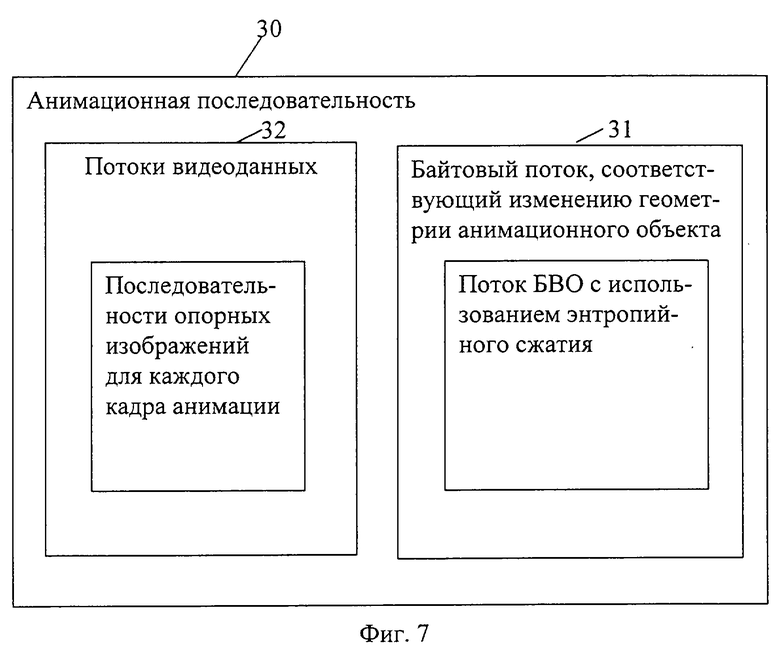
фиг.7 - структура потока данных, представляющего анимированный трехмерный объект;
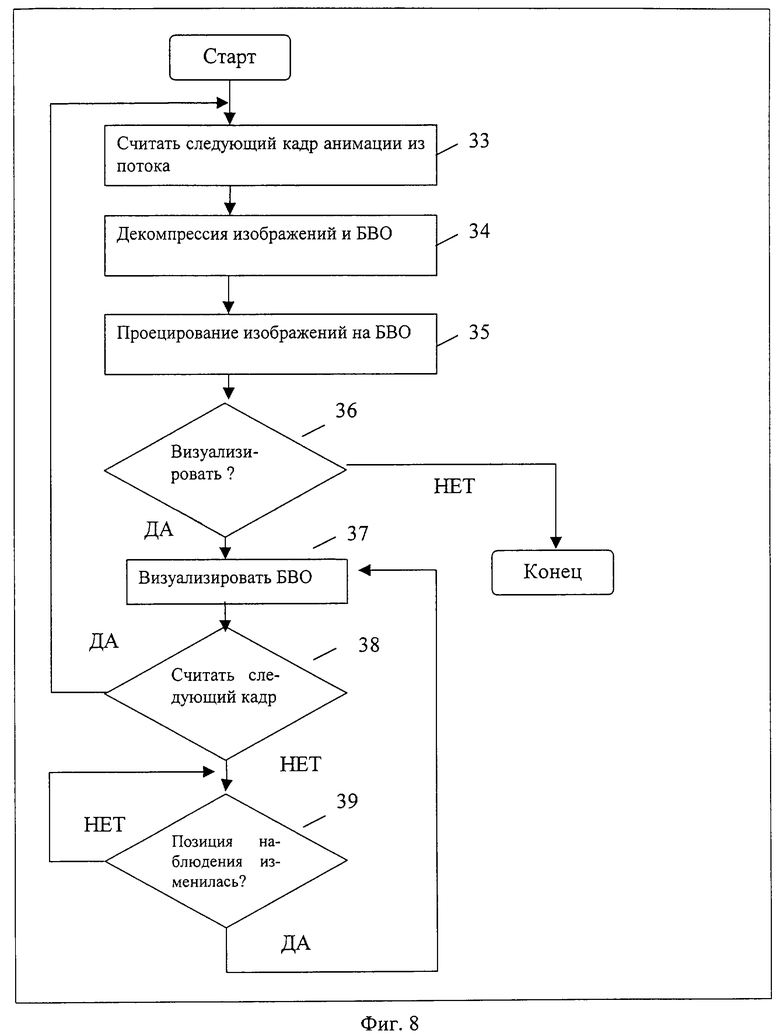
фиг.8 - блок-схема процесса визуализации анимационного трехмерного объекта, представленного потоком данных.
Как показано на фиг.1, устройство представления и визуализации трехмерного объекта из различных типов исходных данных содержит средство для формирования исходных данных трехмерного объекта, выполненное в виде трехмерного сканера 1 реального трехмерного объекта, обеспечивающего формирование на выходе множества трехмерных координат точек, или средства 2 для формирования полигональной модели трехмерного объекта, или средства 3 для формирования изображения с глубиной, средство 4 для преобразования исходных данных трехмерного объекта в представление в виде БВО, которое включает в себя средство 5 формирования множества шестимерных векторов, элементами которого являются три декартовых координаты х, у, z и три цветовых координаты, например RGB, и средство 6 построения БВО. Средство 6 построения БВО связано со средством 7 визуализации БВО, включающим в себя буфер изображения, и со средством 8 получения матрицы преобразования координат.
На фиг. 2 показано, каким образом из реальной поверхности создаются изображения с глубиной и каким образом они объединяются для получения вокселов для случая двух ортогональных камер. На фиг.2 обозначено: 9 - разрез поверхности реального объекта; 10 - проекции прямоугольников, аппроксимирующих поверхность реального объекта, соответствующие дискретным значениям пикселов изображения с глубиной, снятого первой камерой (не показана); 11 - дискретизированные значения глубин поверхности 9, снятой второй камерой (не показана); 12 - вокселы, которым соответствуют объединенные значения глубин поверхности, снятых обеими камерами.
На фиг.3 представлены схемы соответствия трехмерных точек различным масштабным уровням БВО (двумерный вид). На фиг.3 обозначено: 13 - множество точек с трехмерными координатами, 14 - структура БВО, соответствующая точкам 13; 15 - масштабные уровни БВО с выделенными вокселами 16, содержащими цветовую информацию и находящимися в узлах БВО.
На фиг. 4 представлен вид куба БВО 17 и его подразделения на 8 подкубов 18.
На фиг.5 а,б иллюстрируется метод нахождения порядка прохождения вершин БВО на одном иерархическом уровне. На фиг.5 а, б обозначено: 19 - плоскость проецирования; 20 - направление проекции; 21 - куб, соответствующий одной из вершин БВО, разбитый на части плоскостями 22, 23, 24, параллельными граням куба 21; 25 - порядок прохождения (проецирования) каждого из восьми подкубов рассматриваемого куба.
На фиг. 6 иллюстрируется процесс проецирования сплатов во времени и в пространстве и геометрические условия определения размера сплата. На фиг.6 обозначено: 26 - полное БВО 8 х 8, 16 - воксел, 27 - сплат, 28 - направление ортогональной проекции, 29 - буфер изображения.
На фиг.7 показана структура анимационной последовательности 30 БВО, состоящей из последовательности 31 байтовых потоков БВО, соответствующей изменению геометрии анимированного объекта, и из потоков 32 видеоданных (последовательности опорных изображений для каждого кадра анимации).
На фиг. 8 представлены этапы 33-39 процесса визуализации анимационного трехмерного объекта, представленного потоком данных.
Требуемое представление трехмерного объекта, БВО, может быть получено из большинства используемых в настоящее время представлений трехмерных моделей. На фиг. 1 показаны известные средства для получения входных представлений в виде данных трехмерного сканера 1, полигональных моделей, формируемых средством 2, наборы изображений с глубиной, формируемые средством 3. Основная область применения БВО нацелена на использование в качестве входного представления наборов изображений с глубиной. Достоинством представления моделей изображениями с глубиной является возможность создания трехмерных моделей не путем трудоемкого процесса моделирования моделей, а путем непосредственного их получения из фотографий моделей реального мира.
Для получения БВО входное представление, сформированное любым из средств 1, 2, 3, переводят в промежуточное представление с помощью средства 5 формирования множества шестимерных векторов, элементами которого являются три декартовых координаты х, у, z и три цветовых координаты RGB. Для создания БВО следует задать его высоту n, тогда длина ребра куба БВО в локальных координатах БВО будет равна L= 2n. Промежуточное представление строится средством 5 следующим образом:
Для полигональной модели:
Используя преобразования переноса и масштабирования, добиваются помещения всех вершин полигонов модели в куб, одна из вершин которого расположена в начале координат, а противоположная вершина - в точке с координатами (L, L, L). Используя методы подразбиения полигонов, добиваются, чтобы расстояние между любыми двумя соседними вершинами любого полигона было не более 1. Каждой вершине полигона сопоставляют цвет, используя текстуры и текстурные координаты исходной полигональной модели.
Для изображений с глубиной:
Изображения с глубиной масштабируют и переносят таким образом, чтобы в пересчете в общую для изображений систему координат линейные размеры соответствующего пикселу прямоугольника не превышали 1, и все эти прямоугольники были помещены в пространство, ограниченное кубом БВО. При пересчете в общую систему координат используется информация о расположении камер, с помощью которых были получены изображения, и значения глубины, соответствующие пикселам на изображении. В результате получают множество точек с цветовыми координатами и координатами в общей для всех изображений декартовой системе координат. Цветовые координаты точки соответствуют цвету пиксела исходного масштабированного изображении.
Для данных трехмерного сканирования модели:
Используя преобразования переноса и масштабирования, добиваются помещения всех точек сканированной модели в пространство, ограниченное кубом БВО, одна из вершин которого расположена в начале координат, а противоположная вершина - в точке с координатами (L, L, L).
После получения промежуточного представления в виде множества точек {x, y, z, R, G, B}, где координаты х, у, z вмещаются в куб БВО, средство 6 осуществляет построение БВО, иллюстрируемое с помощью фиг.3. Иерархически подразделяют куб 17 (фиг. 4) на 8 подкубов 18, соответствующих вершинам, находящимся на следующем иерархическом уровне после корневой вершины, при этом получают БВО первого масштабного уровня. БВО можно рассматривать как последовательность масштабных уровней 15 (фиг.3) БВО с увеличивающейся высотой, при этом использование деревьев с меньшей высотой не влечет необходимости обработки деревьев с большей высотой для всех перечисляемых ниже алгоритмов. Для последующей обработки сохраняются поддеревья БВО тогда и только тогда, когда соответствующий этому поддереву куб содержит хотя бы одну точку 13. Из множества точек 13 получают структуру БВО 14. При этом каждой вершине (не только концевой) БВО приписывается цвет. Цвет, приписанный вершине, равен усредненному цвету точек, принадлежащих кубу, соответствующему данной вершине.
Средство 7 визуализации БВО использует трехмерное видовое преобразование системы координат, задаваемое средством 8 получения матрицы Т 4 х 4 видового преобразования координат. Координаты, полученные в результате видового преобразования, задают расположение точки наблюдения относительно БВО.
Для визуализации БВО необходим проход по всем его вершинам, от корневой вершины до листьев дерева. При прохождении листьев в буфер 29 изображения (фиг. 6) заносится специального вида рисунок, называемый сплатом. Как показано на фиг. 6, сплат 27 рассматриваемой вершины должен покрывать пространство спроецированного куба 26, соответствующего рассматриваемой вершине. Цвет сплата должен соответствовать цвету рассматриваемой вершины БВО. Форма оплата выбирается из соображения быстроты наложения в буфер изображения и обычно представляет из себя квадрат или круг. Координаты центра оплата 27 должны соответствовать координате центра спроецированого куба 26, соответствующего данной вершине.
Для корректной визуализации БВО, учитывающей расположения кубов относительно точки наблюдения, необходимо в процессе визуализации следить за тем, чтобы в каждой точке буфера изображения оплаты, спроецированные последними, были расположены по отношению к наблюдателю ближе, чем остальные сплаты, ранее спроецированные на рассматриваемую точку буфера изображения. Скорость визуализации БВО во многом зависит от скорости выполнения видовых преобразований координат точек, соответствующих центрам кубов. При наличии аппаратного графического ускорителя перечисленные проблемы можно решить, используя аппаратный z-буфер для решения проблемы корректной визуализации и аппаратное ускорение операции умножения на матрицу при вычислении преобразования точек центров кубов.
Способ визуализации БВО, не использующий специальных графических ускорителей, включает способ определения корректного порядка прохождения БВО и способ быстрого иерархического видового преобразования координат центров кубов. Использование предложенного порядка прохождения БВО позволяет корректно проецировать оплаты без использования z-буфера.
Способ определения порядка прохождения БВО, при котором осуществляется корректное проецирование сплатов, основан на определении на каждой вершине БВО порядка обхода поддеревьев, корневые вершины которых исходят из этой вершины. Как показано на фиг.5, для определения порядка прохождения вершин куба 21, соответствующего рассматриваемой вершине БВО, куб 21 разделяют плоскостью на два равных параллелепипеда всеми из трех возможных способов. На фиг.5 а, б эти плоскости изображены линиями 22, 23, 24. Для каждого из разрезов определяют порядок корректного проецирования, что можно сделать путем определения направления угла между нормалью к общей грани параллелепипеда 22 (23) и направлением 19 проекции. После выполнения этой операции в каждом из трех случаев получаем порядок прохождения 25 каждого из восьми подкубов рассматриваемого куба 21.
Описанный процесс определения порядка проецирования кубов осуществляют рекурсивно, согласно следующему описанию общего процесса визуализации, включающего определение порядка прохождения БВО и быстрое иерархическое преобразование:
а) осуществить препроцессинг при каждом изменении положения наблюдения;
б) принять корневую вершину в качестве текущей вершины;
в) определить корректный порядок проецирования всех восьми подкубов, соответствующих текущей вершине. Для ортографической проекции все узлы наследуют этот порядок из подразделения куба соответствующей корневой вершины;
г) для всех подкубов текущей вершины выполнить следующее:
1) вычислить необходимые для данной вершины преобразования координат центра куба;
2) если текущая вершина является листом дерева, спроецировать сплат, как описано выше (фиг.6);
3) если текущая вершина не является листом дерева, принять вершину, соответствующую этому подкубу, в качестве текущей и рекурсивно перейти к этапу в).
Действия, проводимые на этапах а) и г), осуществляются следующим образом. Обозначим матрицу 4 х 4 видового преобразования Т. Оно описывает линейное преобразование в четырехмерном пространстве. Пусть n - высота БВО, v - локальные нормальные координаты воксела. Предположим, что координаты вокселов хранятся в стандартной неявной бинарной подразумеваемой форме (стандартная двоичная запись представления БВО, где каждый байт соответствует внутренней вершине октодерева (в том числе корневой вершине), а каждый бит в байте указывает на наличие или соответственно отсутствие поддерева для данной вершины октодерева), и перепишем координаты узла как (1):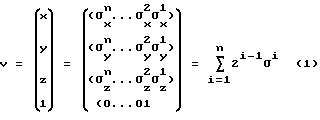
Тогда требуемое преобразование координаты вершины имеет вид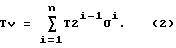
Здесь σ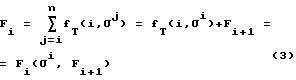
Для фиксированного Т элементы выражения (3) вычисляются на этапе а) препроцессинга:
fT(i,σi) = T2i-2σi. (4)
Эти выражения заносятся в таблицу размером n на 8, и затем выполняется вычисление преобразования с помощью формулы (3) для всех вершин с использованием только табличного просмотра и суммирования. В результате после прохождения всего пути от корневой вершины до листьев БВО, для каждого листа БВО, задаваемого локальными координатами (х, у, z), получают
Tv = F1(σ1, F2(σ2..Fn(σn)..)).
Данный способ преобразования координат обеспечивает на порядок меньшую вычислительную емкость, нежели при прямом умножении на матрицу каждого листа дерева.
Следует отметить, что упомянутое свойство многомасштабности БВО обеспечивает возможность непосредственного подбора конкретного многомасштабного уровня БВО соразмерно с необходимым уровнем детализации трехмерной модели, представляемой в виде БВО, и расстоянием от этой модели до наблюдателя.
Способ представления анимированного трехмерного объекта выполняется следующим образом. Исходные данные для каждого трехмерного объекта в последовательности трехмерных объектов преобразуют в представление в виде БВО. Для каждого кадра трехмерной анимации строится 6 изображений с глубиной, соответствующих проекциям объекта на грани куба. Таким образом формируются потоки видеоданных, по одному на каждую грань куба, а также шесть карт глубины на кадр. Для каждого кадра строится представление БВО в виде байтового потока, как пояснено выше. Потоки видеоданных сжимаются с помощью любого эффективного способа сжатия, такого как MPEG 2. Как показано на фиг.8, анимационная последовательность 30 БВО состоит из последовательности 31 байтовых потоков БВО, соответствующей изменению геометрии анимированного объекта, и из 6 упомянутых выше потоков 32 видеоданных (последовательности опорных изображений для каждого кадра анимации).
Способ визуализации анимированного трехмерного объекта иллюстрируется с помощью блок-схемы алгоритма, представленного на фиг. 9. На этапе 33 из анимационной последовательности извлекаются данные о шести опорных изображениях и данные байтового потока, сформированные, как описано выше. На этапе 34 осуществляют декомпрессию шести изображений и строится структура БВО. На этапе 35 полученные шесть потоков опорных изображений проецируются на БВО для определения цвета для каждой вершины БВО. На этапе 36 принимают решение о необходимости визуализации демпрессированного БВО. При положительном решении на этапе 37 визуализируют полученное БВО, соответствующее кадру анимационного объекта. На этапе 38 принимают решение о необходимости считывания следующего кадра. При положительном решении осуществляется переход к этапу 33, а при отрицательном решении - переход к этапу 39, с которого осуществляется переход к этапу 37 визуализации при изменении позиции наблюдения.
Эксперименты показывают, что объем одного кадра БВО представления, полученного заявленным способом, в 4-10 раз ниже, чем для наиболее близкого известного ортогонального МИГ представления. Скорость визуализации БВО для разрешения опорного и выходного изображений 256 х 256 составляет порядка 20 кадров/сек, на компьютере Pentium Celeron 500 МГц (без использования аппаратного ускорения, при фиксированом масштабном уровне), что в 2-3 раза превышает скорость визуализации в известных способах, также не использующих аппаратное ускорение.


Изобретение относится к представлению трехмерных объектов, полученному с использованием фотографий реальных объектов. Его применение при визуализации трехмерного изображения позволяет получить технический результат в виде обеспечения компактности хранения информации об изображении, быстрой визуализации с высоким качеством выходного изображения. Этот результат достигается благодаря тому, что устройство содержит средство для формирования исходных данных трехмерного объекта, средство для преобразования исходных данных трехмерного объекта в представление в виде бинарного волюметрического октодерева (БВО), средство для визуализации БВО. 6 с. и 9 з.п.ф-лы, 8 ил.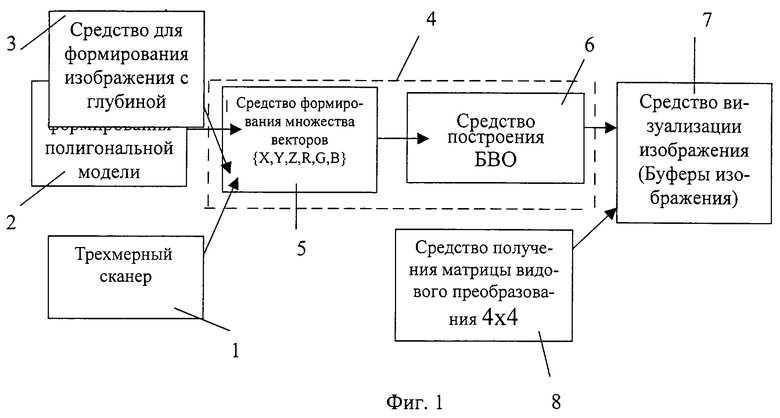
fT(i,σi) = T2i-1σi,
где Т - матрица 4х4 видового преобразования координат;
σi - любой четырехмерный вектор, элементы которого принимают значение 0 или 1;
i - целое число, принимающее значения от 0 до высоты рассматриваемого БВО,
и используют полученные результаты при иерархическом преобразовании трехмерных координат в двумерные координаты, при этом на каждой вершине БВО вычисляют Fi: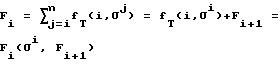
и в результате после прохождения всего пути от корневой вершины до листьев БВО для каждого листа БВО, задаваемого локальными координатами (x, y, z), получают
Tv = F1(σ1, F2(σ2..Fn(σn)..)),
где σi определяется выражением, использующим бинарную запись координат: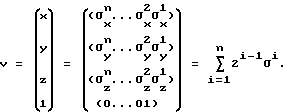
5. Устройство для представления и визуализации трехмерного объекта, содержащее средство для формирования исходных данных трехмерного объекта, средство для преобразования исходных данных трехмерного объекта в представление в виде бинарного волюметрического октодерева (БВО), связанное со средством для формирования исходных данных трехмерного объекта, при этом с каждой вершиной БВО, соответствующей координатам точек объекта, сопоставлен усредненный цвет точек объекта, координаты которых находятся внутри куба, представляющего собой элемент трехмерного изображения - воксела, соответствующего данной вершине БВО, средство для визуализации БВО, связанное со средством для преобразования исходных данных трехмерного объекта в представление в виде БВО.
| СПОСОБ АВТОМАТИЗИРОВАННОГО ИЗМЕРЕНИЯ С ИСПОЛЬЗОВАНИЕМ МОДЕЛИ ВНЕШНЕЙ СРЕДЫ В СТЕРЕОТЕЛЕВИЗИОННОЙ СИСТЕМЕ ТЕХНИЧЕСКОГО ЗРЕНИЯ | 1997 |
|
RU2148794C1 |
| Печь-кухня, могущая работать, как самостоятельно, так и в комбинации с разного рода нагревательными приборами | 1921 |
|
SU10A1 |
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| US 5708764 А, 13.01.1998 | |||
| Бесколесный шариковый ход для железнодорожных вагонов | 1917 |
|
SU97A1 |
Авторы
Даты
2003-10-27—Публикация
2001-06-29—Подача