Изобретение относится к области радиолокации, в том числе и к пассивной радиолокации. Использование изобретения позволит по угломерным данным в однопозиционных радиолокационных системах (РЛС) измерять дальность до движущихся источников радиоизлучения (ИРИ), в том числе и постановщиков помех, и скорость сближения с ними.
Основным источником информации о воздушной и наземной обстановке на летательных аппаратах (ЛА) являются бортовые РЛС, от качества функционирования которых существенно зависит эффективность авиации. С развитием техники радиолокации одновременно происходит совершенствование средств радиоэлектронной борьбы и их возможностей по подавлению РЛС [1]. В связи с чем в процессе работы РЛС с высокой степенью вероятности возможна ситуация, когда в ней каналы измерения дальности и скорости будут подавлены радиопомехами, создаваемыми станциями активных помех, размещенными на лоцируемых объектах [2, 3]. В такой ситуации определение дальности до лоцируемого объекта, который в рассматриваемом случае становится ИРИ, и скорости сближения с ним может быть осуществлено по его угломерным данным - пеленгу и угловой скорости линии визирования, измеренных РЛС по помеховым сигналам пассивными способами [4-11], поскольку измерение пеленгов и угловых скоростей линии визирования ИРИ может быть осуществлено известными в радиотехнике способами и не вызывает особых трудностей.
Для определения дальности до ИРИ и скорости сближения с ним известны различные способы, среди которых наибольшее распространение получили статические способы, включающие азимутально-угломестный, триангуляционный и кинематический, и позиционно-скоростные способы, включающие псевдотриангуляционный и динамико-кинематический [12].
Азимутально-угломестный способ использует результаты одновременного измерения азимута и угла места неподвижного наземного ИРИ [4], однако сфера его применения ограничена только неподвижными ИРИ [12].
Триангуляционный способ определения положения ИРИ использует формульные зависимости между сторонами и углами треугольника, вершины которых связаны с ИРИ и ЛА. Однако сфера его применения ограничена также только неподвижными наземными ИРИ [12].
Кинематические способы опираются на знание уравнений, описывающих процесс взаимного перемещения ЛА и ИРИ, в том числе и движущегося. В литературе [12] показано, что основным недостатком известных кинематических способов является достаточно низкая точность определения дальности до подвижных ИРИ и скорости сближения с ними, повышение которой можно обеспечить лишь за счет увеличения тангенциальной составляющей скорости движения ИРИ Vтан относительно ЛА в результате маневра ЛА с отворотом от ИРИ, что вступает в противоречие с необходимостью выдерживания определенной траектории полета ЛА.
Псевдотриангуляционный способ определения дальности и скорости сближения с подвижным ИРИ по угломерным данным РЛС, функционирующей в пассивном режиме, разработан как альтернатива триангуляционному способу, но во многом схож с ним [13, 14]. Основное достоинство данного способа состоит в относительной простоте его реализации. В [13] показано, что с помощью данного способа можно достаточно точно оценивать дальность до ИРИ и скорость сближения с ним, однако высокая точность оценивания может быть достигнута лишь при выполнении ЛА отворота от ИРИ на достаточно большой угол. Кроме этого, при определении координат движущихся ИРИ данным способом необходимо использовать производные от измеренных координат до 3-го порядка включительно, что накладывает на данный способ существенные ограничения.
Динамико-кинематические способы основаны на математическом описании в пространстве состояний собственного или относительного движения ИРИ и ЛА - носителя РЛС. В литературе [12] дано достаточно подробное описание данных способов и показано, что такой подход к решению задачи определения дальности и скорости сближения с неманеврирующим ИРИ позволяет использовать их на практике. Однако в реальных условиях, с достаточно большой степенью вероятности, ИРИ будет маневрировать. В этом случае алгоритмы оценивания фазовых координат, так же как и движение ЛА-носителя РЛС, усложняются, что достаточно часто приводит к формированию расходящихся оценок дальности до ИРИ и скорости сближения с ним [12].
Из известных технических решений наиболее близким является способ определения дальности до ИРИ и скорости сближения с ним, описанный в литературе [12, стр. 79-81] на основе материалов, изложенных в [15]. Суть способа заключается в том, что на первом предварительном этапе в момент времени k-1 на летательном аппарате, отображенном на фиг.1 символами “ЛА” и движущемся со скоростью Vлa, измеряют xла(k-1), zла(k-1), yла(k-1) - координаты собственного местоположения в неподвижной земной системе координат OXYZ и запоминают их.
В этот же момент времени на ЛА принимают радиосигналы от ИРИ, отображенного на фиг.1 символами “ИРИ” и движущегося со скоростью Vири. По этим радиосигналам измеряют азимут α(k-1) и угол места β(k-1) ИРИ, значения которых запоминают.
Поскольку любой измеритель осуществляет измерения с ошибками, дисперсия которых для любого измерителя известна, то для учета в дальнейшем ошибок измерения азимута и угла места, дисперсии ошибок измерения азимута  и угла места
и угла места 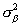 запоминают в виде значений сооответствующих компонент матрицы
запоминают в виде значений сооответствующих компонент матрицы
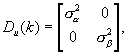
называемой матрицей дисперсий шумов измерения.
По упомянутым запомненным значениям координат местоположения ЛА, азимута и угла места ИРИ вычисляют значения координат местоположения ИРИ в той же системе координат (см. фиг.1) в соответствии с формулами
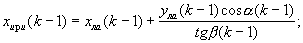

где xири(k-1), zири(k-1) - значения координат ИРИ по осям Х и Z.
Кроме этого, исходя из диапазона возможных скоростей и ускорений заданных типов движущихся ИРИ, задают значения Vxири, Vzири - скоростей и ахири, аzири - ускорений движения ИРИ, по соответствующим осям упомянутой системы координат.
Вычисленные значения xири(k-1), zири(k-1) и заданные значения Vхири, Vzири, ахири, аzири запоминают в виде соответствующих значений компонент вектора
Rири(k-1)=[xири(k-1)axири(k-1)zири(k-1)Vzири(k-1)azири(k-1)]T,
называемого вектором состояния ИРИ, где символ “т” определяет операцию транспонирования.
Поскольку вычисление значений координат ИРИ сопровождается случайными ошибками, дисперсии которых известны, и задание скоростей и ускорений движения ИРИ осуществляется также с большими ошибками, то для учета в дальнейшем этих ошибок, наиболее весомыми из которых являются ошибки определения ускорений ИРИ, дисперсии шумов ускорений ИРИ 
 по осям Х и Z соответственно запоминают в виде соответствующих значений компонент матрицы
по осям Х и Z соответственно запоминают в виде соответствующих значений компонент матрицы
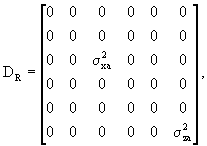
называемой матрицей дисперсий шумов состояния. Размерность упомянутой матрицы определяют в соответствии с размерностью n вектора состояния: поскольку в состав вектора состояния ИРИ входят шесть компонент, т.е. n=6, то размерность матрицы dr n×n=6×6.
Перевод всех упомянутых выше значений координат и параметров движения ЛА и ИРИ в векторно-матричную форму обусловлен тем, что современные вычислители способны выполнять обработку представленных в такой, более удобной для программирования и хранения данных форме.
Упомянутые значения координат местоположения ИРИ и параметров их движения, запомненных в виде значений компонент вектора Rири(k-1), экстраполируют на следующий k-ый момент измерений по формуле
Rэири(k)=Ф(k,k-1)Rири(k-1),
где
Rэири(k)=[xэири(k) Vхэири(k) aхэири(k) zэири(k) Vzириу (k) azэири (k)]T
- вектор, компоненты которого xэири(k), Vxэири(k), аxири(k), zэири(k), Vzэири(k),
аzэири(k) - экстраполированные на следующий момент измерений значения координат местоположения ИРИ xири(k), zири(k), скорости Vхири(k), Vzири(k) и ускорения ахири(k) аzири(k) его движения по соответствующим осям упомянутой выше системы координат;

- матрица, называемая в литературе переходной или фундаментальной, в которой λх и λz - считающиеся известными константы, определяющие постоянные времени маневра ИРИ по соответствующей координате, зависящие от его характера и задаваемые исходя из априорных сведений о типе ИРИ;
τ - интервал дискретизации.
Экстраполированные значения координат местоположения ИРИ и параметров их движения запоминают в виде соответствующих значений компонент вектора состояния Rэири(k).
Кроме этого, для следующего k-го момента времени вычисляют экстраполированные значения апостериорных дисперсий и взаимных дисперсий ошибок фильтрации Dэ(k) компонент вектора состояния в соответствии с формулой
Dэ(k)=Ф(k,k-1)D(k-l)ФT(k,k-1)+DR,
где

- матрица экстраполированных апостериорных значений дисперсий и взаимных дисперсий ошибок фильтрации, в которой значения ее компонент dэij, где 
 представляют собой экстраполированные апостериорные дисперсии и взаимные дисперсии ошибок фильтрации соответствующих значений компонент вектора состояния Rэири;
представляют собой экстраполированные апостериорные дисперсии и взаимные дисперсии ошибок фильтрации соответствующих значений компонент вектора состояния Rэири;

- матрица апостериорных дисперсий и взаимных дисперсий ошибок фильтрации, значения компонент которой dij, где 
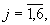 в начальный момент времени задают исходя из априорных сведений о корреляционной матрице распределения соответствующих значений плотности вероятности соответствующих компонент вектора состояния ИРИ Rири, а в дальнейшем вычисляют.
в начальный момент времени задают исходя из априорных сведений о корреляционной матрице распределения соответствующих значений плотности вероятности соответствующих компонент вектора состояния ИРИ Rири, а в дальнейшем вычисляют.
Вычисленные экстраполированные значения апостериорных дисперсий и взаимных дисперсий ошибок фильтрации dэij запоминают в виде соответствующих значений компонент матрицы Dэ(k).
На втором основном этапе, в момент времени k, отстоящего от момента времени k-1 на τ - интервал дискретизации, измеряют скорость ЛА Vлa(k), координаты его местоположения xла(k), zлa(k) и yла(k) и принимают радиосигналы от ИРИ, по которым измеряют значения азимута α(k) и угла места β(k) ИРИ. Измеренные значения азимута α(k) и угла места β(k) ИРИ запоминают в виде соответствующих значений компонент вектора
z(k)=[α(k)((k)]T,
называемого вектором измерений.
По измеренным значениям местоположения ЛА xлa(k), zлa(k), yлa(k), азимута α(k), угла места β(k) ИРИ и запомненным экстраполированным значениям апостериорных дисперсий и взаимных дисперсий ошибок фильтрации dэij вычисляют значения компонент матрицы D(k) - апостериорных дисперсий и взаимных дисперсий ошибок фильтрации в соответствии с формулой

где  - представляет собой матрицу производных, в которой
- представляет собой матрицу производных, в которой
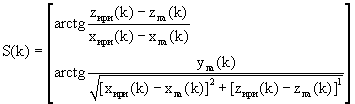
- вектор, компоненты которого представляют собой азимут и угол места ИРИ, соответственно.
Кроме этого, по измеренным значениям местоположения ЛА xла(k), zлa(k), ула(k), азимута α(k), угла места β(k) ИРИ, запомненным экстраполированным значениям координат местоположения ИРИ, скорости и ускорения его движения и вычисленным значениям компонент матрицы D(k) оценивают значения компонент вектора состояния ИРИ Rири(k) в соответствии формулой
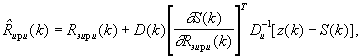
где

- вектор, компоненты которого представляют собой оцененные значения соответствующих компонент вектора состояния; символ “^” означает, что используются оцененные значения компонент соответствующей компоненты вектора или матрицы.
По оцененным значениям 
 - координат ИРИ,
- координат ИРИ, 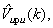

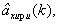
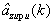 - скоростей и ускорений ИРИ по соответствующим осям земной системы координат вычисляют дальность до ИРИ Дири и скорости сближения с ним Vxcб, Vzcб по соответствующим осям по формулам
- скоростей и ускорений ИРИ по соответствующим осям земной системы координат вычисляют дальность до ИРИ Дири и скорости сближения с ним Vxcб, Vzcб по соответствующим осям по формулам
Д(k)=улa(k)/sinβ(k);
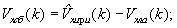

Далее описанный выше процесс, начиная со второго этапа, повторяют.
Недостатком прототипа является ограничение в применении только наземными малоподвижными ИРИ [12]. В случае использования данного способа по интенсивно маневрирующим ИРИ, процедура оценивания дальности до ИРИ и скорости сближения с ним значительно усложняется, и способ становится практически неработоспособным из-за низкой устойчивости процесса оценивания компонент вектора состояния ИРИ [12].
Таким образом, задачей изобретения является разработка высокоточного способа определения дальности до маневрирующих ИРИ и скорости сближения с ними в однопозиционных радиолокационных системах.
Принципиальное отличие заявленного изобретения от прототипа заключается в том, что в прототипе неизвестные значения компонент вектора состояния Rири ИРИ, т.е. координаты местоположения ИРИ, скорости и ускорения его движения, оцениваются с учетом считающихся полностью известными параметрами маневра ИРИ, задаваемыми посредством констант λх и λz, входящих в соответствующие компоненты фундаментальной матрицы Ф(k,k-1), а в предлагаемом способе оцениваются значения неизвестных компонент фундаментальной матрицы Ф(k,k-1) по вычисляемым значениям компонент вектора состояния ИРИ при условии, что компоненты фундаментальной матрицы являются функциями Дири - дальности до ИРИ и Vcб - скорости сближения с ним, и затем по этим компонентам вычисляют значения дальности до ИРИ и скорости сближения с ним.
Ниже, прежде чем будет описана сущность изобретения, для облегчения понимания последующего материала, рассмотрим решение поставленной задачи в математическом аспекте.
Заявляемый способ определения дальности до ИРИ и скорости сближения с ним был получен на основе одного из наиболее простых из известных [16, 17] методов идентификации, называемым в литературе в честь его разработчика методом Мейна [16]. Алгоритм идентификации параметров модели состояния, предложенный Мейном, по своей сути представляет алгоритм линейной фильтрации, в котором оценивается не значения компонент вектора состояния, а значения компонент вектора параметров модели состояния.
Пусть процесс изменения ϕ - угла визирования ИРИ в одной из плоскостей, ω - угловой скорости линии визирования ИРИ и jп -поперечного ускорения ЛА, записан в векторной форме посредством изменения вектора состояния
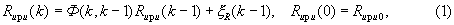
где Rири(k), Rири(k-1), Rири(0) - n-мерный вектор состояния в k-й, (k-1)-й и начальный моменты времени, компонентами которого в общем случае могут быть углы визирования ИРИ ϕ, угловые скорости линии визирования ИРИ ω в различных плоскостях и поперечные ускорение ЛA jп (n - определяется общим количеством компонент, входящих в его состав);
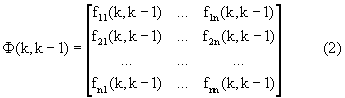
- переходная матрица вектора состояния, компоненты fij(k,k-1) которой в общем случае являются функциями, зависящими от дальности до ИРИ Дири и скорости сближения с ним Vcб, причем имеются обратные функции ηm (m=1, 2), позволяющие по ним вычислить Дири и Vcб по формулам
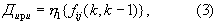
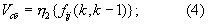
ξr - n-мерный вектор шумов состояния с известной дисперсией, определяемой матрицей дисперсий шумов вектора состояния dr;
запись “k,k-1” означает, что с помощью компонент переходной матрицы fij(k,k-1), определяющих степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ, однозначно определяется связь между значениями компонент вектора состояния с момента времени k-1 на момент k.
Все компоненты fij(k,k-1) переходной матрицы состояния Ф(k,k-1) (2) объединяют в вектор

называемый вектором параметров модели состояния, компоненты al(k) которого находят по компонентам fij(k,k-1) по формулам

где n - общее количество фазовых координат, входящих в вектор состояния.
Пусть имеется возможность измерять значения всех или части параметров вектора состояния Rири(k) (1). Процесс измерений записывают в виде вектора измерений

где H(k) - переходная матрица вектора измерений, посредством которой определяют измеряемые компоненты вектора состояния; ξи - вектор шумов измерений с известной дисперсией, определяемой матрицей дисперсий шумов измерений Dи.
Оценку 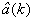 вектора параметров модели состояния a(k) (5) осуществляют, используя алгоритм Мейна [12]:
вектора параметров модели состояния a(k) (5) осуществляют, используя алгоритм Мейна [12]:


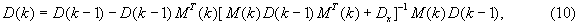
В выражениях (8)-(10) обозначено:
а0 - значение вектора параметров модели состояния в начальный момент времени, компоненты которого определяют по априорным данным о дальности до ИРИ и скорости сближения с ним;
K(k) - матричный коэффициент усиления;

- переходная матрица вектора параметров модели состояния размером n×n2;
D(k) - матрица дисперсий и взаимных дисперсий ошибок оценивания компонент вектора параметров модели состояния, значения компонент которой в начальный момент времени задают исходя из априорных сведений о корреляционной матрице распределения значений компонент вектора состояния;
0 - n-мерные нулевые векторы.
Поскольку имеется однозначное соответствие между полученными оценками вектора параметров модели состояния 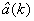 и дальностью до ИРИ Дири и скоростью сближения с ним Vcб, то по формулам (3) и (4) вычисляют дальность до ИРИ и скорость сближения с ним.
и дальностью до ИРИ Дири и скоростью сближения с ним Vcб, то по формулам (3) и (4) вычисляют дальность до ИРИ и скорость сближения с ним.
Таким образом, поставленная задача достигается тем, что на первом предварительном этапе выполняют следующее.
1. В момент времени k-2 на летательном аппарате (ЛА) измеряют ϑ(k-2) - тангаж, ψ(k-2) - угол рыскания и yла(k-2) - высоту ЛА. В этот же момент времени на ЛА принимают радиосигналы от ИРИ, по которым любым из известных способов [4-6] измеряют значения ϕг(k-2), ϕв(k-2) - пеленгов ИРИ в горизонтальной и вертикальной плоскостях соответственно. Измеренные значения ϑ(k-2), ψ(k-2), yла(k-2), ϕг(k-2), ϕв(k-2) запоминают.
2. В следующий момент времени k-1, отстоящий от момента времени k-2 на τ - интервал дискретизации, измеряют значения высоты yла(k-1) ЛА, его тангажа ϑ(k-1) и угла рыскания ψ(k-1), а также поперечных ускорений jг(k-1), jв(k-1) ЛА в горизонтальной и вертикальной плоскостях соответственно. Принимают радиосигналы от ИРИ, по которым измеряют значения пеленгов ϕг(k-1), ϕв(k-1) ИРИ и угловых скоростей линии визирования ωг(k-1), ωв(k-1) ИРИ в горизонтальной и вертикальной плоскостях соответственно. Измеренные значения yла(k-1), ϑ(k-1) и ψ(k-1) запоминают. Измеренные значения ϕг(k-1), ωг(k-1), jг(k-1), ϕв(k-1), ωв(k-1), jв(k-1) запоминают как значения соответствующих компонент вектора
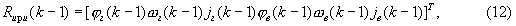
называемого вектором состояния.
Заявленный способ не накладывает ограничений на вектор состояния. Если какие-либо из упомянутых выше его компонент не будут доступны измерению, или, наоборот, будет иметься возможность измерять другие координаты или параметры движения ИРИ, то состав вектора состояния может быть изменен.
3. По запомненным в (k-2)-oй и (k-1)-ый моменты времени значениям высоты yла, угла пеленга ϕв и тангажа ϑ вычисляют приблизительные значения дальности до ИРИ Дири, имевшие место в моменты времени k-2 и k-1, по формулам

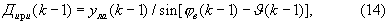
4. По вычисленным значениям дальности до ИРИ Дири и запомненным значениям ϕг, ϕв, ϑ и ψ вычисляют приблизительные значения проекций скорости сближения с ИРИ Vycб, Vzcб и Vxcб на оси Y, Z и X соответственно неподвижной земной прямоугольной системы координат OYZX по формулам



по которым вычисляют приблизительные значения скорости сближения с ИРИ Vcб по формуле

5. Поскольку измерения угловых координат ИРИ и параметров их изменения сопровождаются случайными ошибками, дисперсии которых известны, то для учета их в дальнейшем, дисперсии ошибок измерений пеленгов ИРИ 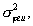
 угловых скоростей линии визирования ИРИ
угловых скоростей линии визирования ИРИ 
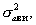 поперечных ускорений
поперечных ускорений 
 в горизонтальной и вертикальной плоскостях соответственно запоминают в виде значений соответствующих компонент матрицы
в горизонтальной и вертикальной плоскостях соответственно запоминают в виде значений соответствующих компонент матрицы

называемой матрицей дисперсий шумов измерений, недиагональные компоненты которой равны нулю. Заявленный способ не накладывает ограничений на матрицу дисперсий шумов измерений: если состав измерителей будет другим, то состав ее компонент может быть изменен.
6. По запомненным значениям компонент ϕг(k-1), ωг(k-1), jг(k-1), ϕв(k-1), ωв(k-1), jв(k-1) вектора состояния Rири(k-1) (12) и вычисленным значениям дальности до ИРИ Дири(k-1) (14) и скорости сближения ЛА с ИРИ Vcб(k-1) (16) осуществляют экстраполяцию на k-й момент времени всех упомянутых значений компонент вектора состояния по формуле

где
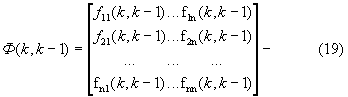
переходная матрица вектора состояния, компоненты fij(k,k-1) которой представляют собой известные функции [18, стр. 285, 291, 305, 332], посредством которых связаны ϕг, ωг, jг, ϕв, ωв, jв с Дири и Vсб. Например, для вектора состояния Rири(k-1) (12) переходная матрица Ф(k,k-1) может иметь следующий вид:

в которой
f11(k,k-1)=1, f12=(k,k-1)=τ, 

f33(k,k-1)=1, f44(k,k-1)=1, 

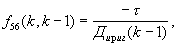 f66(k,k-2)=1,
f66(k,k-2)=1,
а остальные функции - нулевые; Дириг, Дирив, Vсбг, Дсбв - значений проекций дальности до ИРИ и скорости сближения с ним на горизонтальную и вертикальную плоскости соответственно.
На конкретный вид функций fij(k,k-1), определяемых при разработке конкретных устройств измерения дальности до ИРИ и скоростей сближения с ними в однопозиционных РЛС, способ не накладывает никаких ограничений.
Количество упомянутых функций также зависит от конкретного устройства: оно равно квадрату числа компонент n, входящих в состав вектора состояния.
Экстраполированные значения компонент ϕэг(k), ωэг(k), jэг(k), ϕэв(k), ωэв(k), jэв(k) вектора состояния Rэири(k) (18) запоминают.
7. По вычисленным значениям дальности до ИРИ Дири(14) и скорости сближения с ним Vсб (16) вычисляют значения функций fij(k,k-1) (19) и по формулам
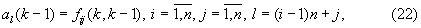
присваивают их значения соответствующим компонентам  вектора
вектора
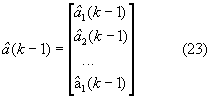
называемого вектором параметров модели состояния, которые запоминают. Значение каждой из компонент  данного вектора, как и значение соответствующей ей функции fij(k,k-1), определяет степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ.
данного вектора, как и значение соответствующей ей функции fij(k,k-1), определяет степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ.
Поскольку на данный момент времени k-1 вычисления значений компонент al(k-1) вектора параметров модели состояния было проведено по приблизительным значениям дальности до ИРИ и скорости сближения с ним, то их значения имеют достаточно большие ошибки. Поэтому для учета в дальнейшем этих ошибок задают и запоминают начальные значения компонент матрицы

называемой матрицей апостериорных дисперсий и взаимных дисперсий ошибок оценивания вектора параметров модели состояния, значения компонент которой dij(k-1)=0, при i≠j, где 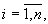
 а диагональные значения компонент dij(k-1), при i=j, заданы исходя из априорных сведений о корреляционных функциях распределения значений плотности вероятности соответствующих компонент вектора состояния ИРИ Rири.
а диагональные значения компонент dij(k-1), при i=j, заданы исходя из априорных сведений о корреляционных функциях распределения значений плотности вероятности соответствующих компонент вектора состояния ИРИ Rири.
Поскольку нельзя точно описать связь между компонентами вектора состояния в соседние моменты времени, так как ИРИ может двигаться произвольно, то всегда вычисления значений компонент fij(k,k-1) и соответствующих компонент  будут сопровождаться ошибками, поэтому для учета в дальнейшем и этих ошибок задают и запоминают значения компонент матрицы
будут сопровождаться ошибками, поэтому для учета в дальнейшем и этих ошибок задают и запоминают значения компонент матрицы
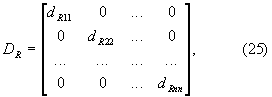
называемой матрицей дисперсий вектора состояния, компоненты которой dij=0, при i≠j, где 
 a dij при i=j, задают исходя из конкретной структуры вектора состояния Rири и априорных сведений о корреляционных функциях распределения значений плотности вероятности его компонент.
a dij при i=j, задают исходя из конкретной структуры вектора состояния Rири и априорных сведений о корреляционных функциях распределения значений плотности вероятности его компонент.
8. По запомненным значениям компонент вектора состояния Rэири(k) формируют и запоминают соответствующие значения переходной матрицы вектора параметров модели состояния M(k) по формуле
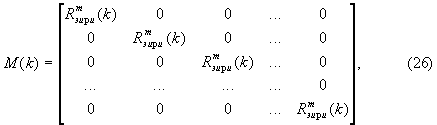
где 0 - n-мерные нулевые векторы.
На втором основном этапе, начиная с момента времени k, выполняют следующее.
1. Измеряют значения jг, jв. Принимают радиосигналы от ИРИ, по которым измеряют значения ϕг, ϕв, ωг и ωв. Измеренные значения ϕг, ωг, jг, ϕв, ωв и jв запоминают в виде значений соответствующих компонент вектора
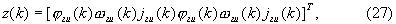
называемого вектором измерений, где ϕги(k)=ϕг(k), ωги(k)=ωг(k), jги(k)=jг(k), ϕви(k)=ϕв(k), ωвн(k)=ωв(k), jви(k)=jв(k).
Заявленный способ не накладывает ограничений на вектор измерений. Если какие-либо из упомянутых выше его компонент не будут доступны измерению, то состав вектора состояния может быть изменен.
2. По запомненным значениям компонент матриц D(k-1) (24), DR (25) и M(k) (26) по формуле

вычисляют и запоминают текущие значения компонент dij(k) матрицы D(k).
3. По запомненным значениям компонент матриц D(k) (28), M(k) (26) и Dи (17) по формуле

вычисляют и запоминают значения компонент кij(k), где 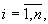
 матричного коэффициента усиления K(k).
матричного коэффициента усиления K(k).
4. По запомненным значениям компонент векторов  (23), z(k) (27) и матриц M(k) (26), K(k) (29) по формуле
(23), z(k) (27) и матриц M(k) (26), K(k) (29) по формуле
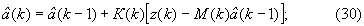
оценивают текущие значения компонент  вектора параметров модели состояния
вектора параметров модели состояния 
5. Поскольку имеется однозначное соответствие между оцененными значениями компонент 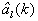 и значениями компонент fij(k+1,k) переходной матрицы вектора состояния, то по формулам
и значениями компонент fij(k+1,k) переходной матрицы вектора состояния, то по формулам

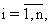
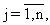

присваивают значения соответствующим компонентам fij(k+1,k) переходной матрицы вектора состояния и запоминают их в виде
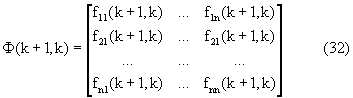
6. Поскольку имеется известное однозначное соответствие между полученными значениями fij(k+1,k) и дальностью до ИРИ Дири и скоростью сближения с ним Vcб, то по формулам


вычисляют дальность до ИРИ Дири(k) и скорость сближения с ним Vcб(k), которые выдают различным потребителям информации, например на индикатор летчику.
На конкретный вид функций η1{fij(k+1,k)} и η2{fij(k+1,k)}, определяемых при разработке конкретных устройств измерения дальности до ИРИ и скоростей сближения с ними в однопозиционных РЛС на основе известных кинематических уравнений, например, приведенных в литературе [18, стр. 178, 184], способ не накладывает никаких ограничений. Например, в случае использования переходной матрицы Ф(k,k-1) вида (20) с компонентами fij(k+1,k) вида (21) упомянутые функции, полученные по функциям f22(k+1,k), f23(k+1,k), f55(k+1,k) и f56(k+1,k), имеют вид:
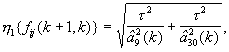

7. По запомненным значениям компонент ϕг(k), ωг(k), jг(k), ϕв(k), ωв(k), jв(k) вектора состояния Rири(k) и полученным значениям компонент матрицы
Ф(k+1,k) no формуле

экстраполируют на следующий k+1-ый шаг измерений и запоминают значения компонент вектора состояния Rэири(k+1).
8. По запомненным значениям компонент вектора состояния Rэири(k+1) по формуле

формируют и запоминают значения компонент переходной матрицы вектора параметров модели состояния M(k+1) для следующего шага измерений.
Далее, описанный выше процесс, начиная со второго этапа, повторяют.
На фиг.1 приведено пространственное положение ИРИ и ЛА, где обозначено:
OXYZ - неподвижная земная система координат;
xла, zла, yла, Vла - координаты ЛА по осям Х и Z, высота ЛА и его воздушная скорость соответственно;
rпрод, rхпрод, rпоп - орт продольной оси ЛА, его проекция на ось Х и орт поперечной оси ЛА соответственно;
ϑ, ψ - тангаж и угол рыскания ЛА;
ϕг, ϕв, ωг, ωв - пеленги ИРИ и угловые скорости линии визирования ИРИ в горизонтальной и вертикальной плоскостях соответственно;
α, β - азимут и угол места ИРИ;
xири, zири, Vири - координаты ИРИ по осям Х и Z и скорость его движения соответственно;
Дири - дальность до ИРИ.
На фиг.2 приведена упрощенная структурная схема измерителя дальности до ИРИ и скорости сближения с ними в однопозиционных радиолокационных системах, в котором реализован заявленный способ, где:
1 - автономные измерители, в состав которых входят датчики углов тангажа и рыскания, скорости ЛА, доплеровские измерители скорости и угла сноса, акселерометры и др.;
2 - запоминающее устройство (ЗУ);
3 - первый вычислитель;
4 - второй вычислитель;
5 - третий вычислитель;
6 - радиолокационная система (РЛС);
7 - четвертый вычислитель;
8 - пятый вычислитель;
9 - шестой вычислитель;
10 - источник радиоизлучения (ИРИ);
11 - седьмой вычислитель;
12 - восьмой вычислитель.
Цифрами у измерителей 1, РЛС 6 и ЗУ 2 условно обозначены номера соответствующих входов и выходов.
На фиг.3 приведены графики текущих ошибок оценивания дальности до маневрирующего ИРИ, где обозначено: Дириист - истинное значение дальности до ИРИ; Дири - вычисленное в соответствии с заявленным способом значение дальности до ИРИ.
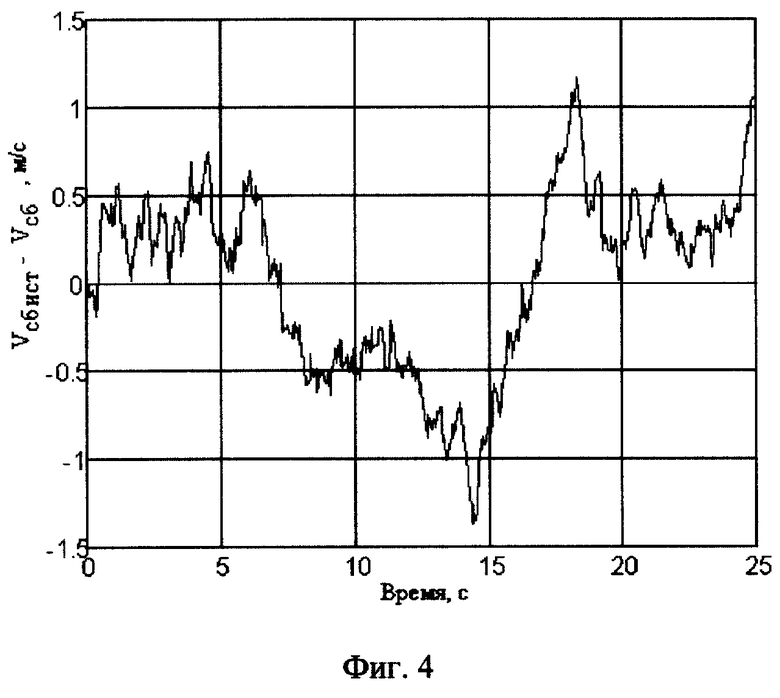
На фиг.4 приведены графики текущих ошибок оценивания скорости сближения с маневрирующим ИРИ, где обозначено: Усбист - истинное значение скорости сближения с ИРИ; Vcб - значение скорости сближения с ИРИ, вычисленное в соответствии с заявленным способом.
В качестве примера реализации способа измерения дальности до ИРИ и скорости сближения с ними в однопозиционных радиолокационных системах рассмотрим измеритель, при разработке которого полагалось, что:
1) вертикальный и горизонтальный каналы измерения не влияют друг на друга, в связи с чем рассматривается принцип функционирования измерителя только для одной вертикальной плоскости;
2) кинематические уравнения, связывающие координаты абсолютного и относительного движения ЛА и ИРИ, в дискретном виде, полученные на основе известных аналоговых соотношений [18, стр. 178], определяются формулами
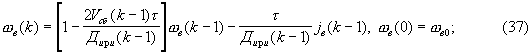

где ωв, ωв0 - угловая скорость линии визирования ИРИ в вертикальной плоскости и ее значение в начальный момент времени соответственно; jв, jв0 - ускорение ЛА в вертикальной плоскости и его значение в начальный момент времени соответственно; Дири и Vcб - дальность до ИРИ и скорость сближения с ним соответственно; τ - интервал дискретизации; ξj - шум ускорения ЛА с известной дисперсией 
3) угловая скорость линии визирования ИРИ измеряется угломером РЛС
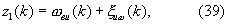
где ξиω - шум измерений угловой скорости линии визирования ИРИ с известной дисперсией 
4) ускорение ЛА jв измеряется акселерометром

ξиj - шум измерений ускорения с известной дисперсией 
5) вектор состояния Rири(k) (12), вектор измерений z(k) (27) и соответствующие им матрицы дисперсий шумов вектора состояния DR (25) и вектора измерений Dи (17), определяемые на основе формул (37)-(40), имеют следующий вид




7) компоненты fij(k,k-1) переходной матрицы состояния Ф(k,k-1) (19) определены на основе уравнений (18), (37), (38):

8) на основе вектора состояния Rири (41) вектор параметров модели состояния а (5) для момента времени k-1 будет иметь вид:

компоненты которого найдены в соответствии с выражениями (22) и (43), (45)

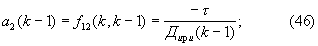


9) в соответствии с векторами Rири(k) (41) и Rэири(k) (18) переходная матрица вектора параметров модели состояния M(k) (26) имеет вид:

10) решив систему уравнений (45) и (46) относительно Дири и Vсб, получим обратные функции ηm{fij(k,k-1)}, входящие в уравнения (33) и (34):
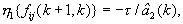
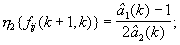
откуда в соответствии с формулами (33) (34) имеем, что
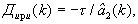

Рассматриваемый измеритель дальности до ИРИ и скорости сближения с ними в однопозиционных радиолокационных системах функционирует следующим образом.
На первом предварительном этапе выполняют следующее.
В момент времени k-2 на летательном аппарате с помощью установленных на нем автономных измерителей 1 измеряют ϑ(k-2) - тангаж, ψ(k-2) - угол рыскания и ула(k-2) - высоту ЛА, которые с первого выхода автономных измерителей 1 подают на первый вход ЗУ 2. В этот же момент времени с помощью РЛС 6 работающей в пассивном режиме, принимают радиосигналы от ИРИ 10 и по ним любым из известных способов [4-6] измеряют значения ϕг(k-2), ϕв(k-2) - пеленгов ИРИ в горизонтальной и вертикальной плоскостях, которые с первого выхода РЛС 6 подают на четвертый вход ЗУ 2. В ЗУ 2 все измеренные значения упомянутых координат ЛА и ИРИ запоминают.
В следующий момент времени k-1 автономными измерителями 1 измеряют значения yлa(k-1), ϑ(k-1) и ψ(k-1), которые с первого выхода автономных измерителей 1 подают на первый вход ЗУ 2. Кроме этого, измеренное в этот же момент времени автономными измерителями 1 ускорение ЛА в вертикальной плоскости jв(k-1) со второго выхода автономных измерителей 1 подают на второй вход ЗУ 2. В этот же момент времени с помощью РЛС 6 принимают радиосигналы от ИРИ 10 и по ним измеряют значения пеленгов ИРИ ϕг(k-1), ϕв(k-1) в соответствующих плоскостях и угловую скорость линии визирования ИРИ ωв(k-1) в вертикальной плоскости. Измеренные значения ϕг(k-1), ϕв(k-1) с первого выхода РЛС 6 подают на четвертый вход ЗУ 2. Измеренное значение ωв(k-1) со второго выхода РЛС 6 подают на пятый вход ЗУ 2. В ЗУ 2 измеренные значения yла(k-1), ϑ(k-1) и ψ(k-1) запоминают. Кроме этого, в ЗУ 2 измеренные значения ϕв(k-1) и jв(k-1) запоминают как значения соответствующих компонент вектора Rири(k-1) (41).
С восьмого выхода ЗУ 2 запомненные в (k-2)-ой и (k-1)-ый моменты времени значения высоты yла, пеленгов ϕг, ϕв, тангажа ϑ и угла рыскания ψ подают в первый вычислитель 3, где по ним вычисляют приблизительные значения дальности до ИРИ Дири, имевшие место в моменты времени k-2 и k-1, по формулам (13) и (14) и приблизительное значение скорости сближения с ИРИ Vсб по формулам (15) и (16). Вычисленные значения Дири и Vсб с выхода первого вычислителя 3 подают на пятнадцатый вход ЗУ 2, где их запоминают.
Поскольку и РЛС 6 и автономные измерители 1 осуществляют измерения, соответственно ωв(k-1) и jв(k-1), с ошибками, дисперсии которых известны, то для их учета, дисперсии ошибок измерений угловой скорости линии визирования ИРИ  и поперечного ускорения ЛА
и поперечного ускорения ЛА  с третьих выходов РЛС 6 и автономных измерителей 1 соответственно подают на шестой и третий входы ЗУ 2, где их запоминают в виде значений соответствующих компонент матрицы дисперсий шумов измерений Dи (42).
с третьих выходов РЛС 6 и автономных измерителей 1 соответственно подают на шестой и третий входы ЗУ 2, где их запоминают в виде значений соответствующих компонент матрицы дисперсий шумов измерений Dи (42).
С седьмого выхода ЗУ 2 запомненные значения компонент ωв(k-1) и jв(k-1) вектора состояния Rири(k-1) и вычисленные значениям дальности до ИРИ Дири(k-1) и скорости сближения Vсб(k-1) подают во второй вычислитель 4, где по ним осуществляют прогноз на k-й момент времени всех значений компонент вектора состояния Rири(k) по формуле (18), где компоненты fij(k,k-1) переходной матрицы вектора состояния определяют по формуле (43). Спрогнозированные значения компонент ωэв(k) и jэв(k) вектора состояния Rэири(k) с выхода второго вычислителя 4 подают на четырнадцатый вход ЗУ 2, где их запоминают.
С шестого выхода ЗУ 2 запомненные значения дальности до ИРИ Дири и скорости сближения с ним Vсб подают в третий вычислитель 5, где по формулам (45)-(48) вычисляют значения компонент a1(k-1), a2(k-1), а3(k-1), a4(k-1) вектора параметров модели состояния a(k-1) (44), которые с выхода третьего вычислителя 5 подают на тринадцатый вход ЗУ 2, где их запоминают в виде оцененных значений компонент вектора параметров модели состояния  (44).
(44).
На седьмой вход ЗУ 2, исходя из априорных сведений о корреляционных функциях распределения значений плотности вероятности ωв(k) и jв(k), подают значения дисперсий ошибок оценивания вектора параметров модели состояния d11(k-1) и d12(k-1), по которым в ЗУ 2 присваивают и запоминают начальные значения соответствующим компонентам матрицы апостериорных дисперсий и взаимных дисперсий ошибок оценивания вектора параметров модели состояния

значения компонент которой d12(k-1)=0, d21(k-1)=0.
На этот же седьмой вход ЗУ 2, исходя из априорных сведений о корреляционной функции распределения значений плотности вероятности поперечного ускорения, вводят значения дисперсии этого распределения ускорения ЛА 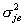 , по которому в ЗУ 2 формируют и запоминают значения компонент матрицы дисперсий шумов вектора состояния DR (41).
, по которому в ЗУ 2 формируют и запоминают значения компонент матрицы дисперсий шумов вектора состояния DR (41).
В ЗУ 2 по запомненным значениям компонент вектора состояния Rэири(k) по формуле (49) формируют и запоминают значения переходной матрицы вектора параметров модели состояния M(k).
На втором основном этапе, начиная с момента времени k, выполняют следующее.
Автономными измерителями 1 измеряют значение jв, которое со второго выхода измерителей 1 подают на второй вход ЗУ 2.
С помощью РЛС 6 принимают радиосигналы от ИРИ, по которым измеряют значение ωв. Измеренное значение ωв со второго выхода РЛС 6 подают на пятый вход ЗУ 2, где его и значение jв запоминают в виде значений соответствующих компонент вектора измерений z(k) (42).
С пятого выхода ЗУ 2 запомненные значения компонент матриц D(k-1) (51), M(k) (49) и DR (41) подают на вход четвертого вычислителя 7, где по формуле (28) вычисляют текущие значения компонент d11(k), d12(k), d21(k), d22(k) матрицы D(k), которые с его выхода подают на двенадцатый вход ЗУ 2, где их запоминают.
С четвертого выхода ЗУ 2 запомненные значения компонент матриц D(k) (28), M(k) (49) и Dи (42) подают на вход пятого вычислителя 8, где по формуле (29) вычисляют значения компонент к11(k), к12(k), к21(k), к22(k) матричного коэффициента усиления K(k), которые с его выхода подают на одиннадцатый вход ЗУ 2, где их запоминают.
С третьего выхода ЗУ 2 запомненные значения компонент векторов  (44), z(k) (42) и матриц M(k) (49), K(k) (29) подают на вход шестого вычислителя 9, где по формуле (30) оценивают текущие значения компонент
(44), z(k) (42) и матриц M(k) (49), K(k) (29) подают на вход шестого вычислителя 9, где по формуле (30) оценивают текущие значения компонент 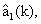

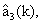
 вектора параметров модели состояния
вектора параметров модели состояния  которые с его выхода подают на десятый вход ЗУ 2, где их запоминают.
которые с его выхода подают на десятый вход ЗУ 2, где их запоминают.
В ЗУ 2 по полученным оцененным значениям компонент 

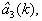
 вектора параметров модели состояния по формулам (31) присваивают значения соответствующим компонентам f11(k+1,k), f12(k+1,k), f21(k+1,k), f22(k+1,k) переходной матрицы вектора состояния и запоминают их в виде значений компонент матрицы Ф(k+1,k) (32).
вектора параметров модели состояния по формулам (31) присваивают значения соответствующим компонентам f11(k+1,k), f12(k+1,k), f21(k+1,k), f22(k+1,k) переходной матрицы вектора состояния и запоминают их в виде значений компонент матрицы Ф(k+1,k) (32).
Со второго выхода ЗУ 2 запомненные значения компонент 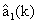 и
и  подают на вход седьмого вычислителя 11, где по формулам (50) вычисляют дальность до ИРИ Дири(k) и скорость сближения с ним Vсб(k), которые с его выхода подают на девятый вход ЗУ 2, где их запоминают. Кроме этого, Дири(k) и Vсб(k) выдают потребителям информации.
подают на вход седьмого вычислителя 11, где по формулам (50) вычисляют дальность до ИРИ Дири(k) и скорость сближения с ним Vсб(k), которые с его выхода подают на девятый вход ЗУ 2, где их запоминают. Кроме этого, Дири(k) и Vсб(k) выдают потребителям информации.
С первого выхода ЗУ 2 запомненные значения ωв(k) и jв(k) подают на вход восьмого вычислителя 12, где по формуле (35) вычисляют значения компонент вектора состояния Rэири(k+1), которые с его выхода подают на восьмой вход ЗУ 2, где их запоминают.
В ЗУ 2 по запомненным значениям компонент вектора состояния Rэири(k) по формуле (49) присваивают значения соответствующим компонентам матрицы M(k+1) для следующего шага измерений, которые запоминают.
Далее, описанный выше процесс, начиная со второго этапа, повторяют.
Предложенный способ измерения дальности обладает отличием от известных способов, состоящим в возможности определения дальности до интенсивно маневрирующего ИРИ и скорости сближения с ним. Кроме этого, заявляемый способ обладает достаточно высокой точностью определения указанных координат ЛА и ИРИ. Данный вывод основан на результатах моделирования, приведенного в качестве примера реализации измерителя. Графики текущих ошибок Дириист-Дири определения дальности до маневрирующего ИРИ и Vсбист-Vсб скорости сближения с ним приведены на фиг.3 и 4 соответственно.
Таким образом, подтверждено, что предлагаемый способ обеспечивает достижение поставленной цели: высокоточное измерение дальности до маневрирующего ИРИ и скорости сближения с ним по угломерным данным в однопозиционных радиолокационных системах.
Заявляемый способ при его реализации не накладывает никаких ограничений на элементную базу и состав оборудования ЛА и может быть использован на современном ЛА, оборудованном любой современной радиолокационной системой.
Использованная литература
1. Викулов О.В., Добыкин В.Д., Дрогалин В.В. и др. Современное состояние и перспективы развития авиационных средств радиоэлектронной борьбы // Зарубежная радиоэлектроника, 1998, №12, с.3-16.
2. Основы теории радиоэлектронной борьбы / М.П.Бобнев, В.Д.Казаков, Н.Ф.Николенко, под ред. Н.Ф.Николенко. - М.: Воениздат, 1987.
3. Цветнов В.В., Демин В.П., Куприянов А.И. Радиоэлектронная борьба: радиоразведка и радиопротиводействие. - М.: Изд-во МАИ, 1998.
4. Южаков В.В. Современные способы определения местоположения источников электромагнитного излучения // Зарубежная радиоэлектроника, 1987, №8, с.67-79.
5. Соколова Н.С. Возможности наблюдения за маневрами цели с помощью измерения только пеленга или только скорости изменения пеленга // Новости зарубежной науки и техники. Сер. Авиац. системы. - Гос. НИИ авиационных систем, 1993, №4, с.5-15.
6. Макухина Т.П. Оценка текущих координат движущегося объекта по данным его пеленгования // Вопросы радиоэлектроники. Сер. АСУПР, 1992, вып.4.
7. Патент RU 2128848, МКИ 6 G 01 S 15/00. Опубликован 10.4.99.
8. Патент RU 2066458, МКИ 6 G 01 S 5/16. Опубликован 10.9.96.
9. Патент США 5917449, МКИ 6 G 01 S 3/02. Опубликован 29.06.99.
10. Патент США 5479360, МКИ 6 G 01 S 7/00. Опубликован 26.12.95.
11. Патент США 5343212, МКИ 5 G 01 S 5/02. Опубликован 30.08.94.
12. Дрогалин В.В., Дудник П.И., Канащенков А.И. и др. Определение координат и параметров движения источников радиоизлучений по угломерным данным в однопозиционных бортовых радиолокационных системах. // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники, 2002, №3, с.64-94.
13. Булычев Ю.Г., Бурлай И.В., Моторкин В.А. Оценивание параметров движения объектов на базе высокоточных угломерных систем // Радиотехника и электроника, 1992, т. 37, №4, с.618-627.
14. Булычев Ю.Г., Бурлай И.В., Моторкин В.А. Уравнения калмановской фильтрации для псевдотриангуляционных систем локации // Радиотехника, 1992, №3, с.10-13.
15. Белов С.Г., Коданев В.Л. Оптимальная фильтрация текущих координат подвижных радиоэлектронных средств. - Цифровая обработка сигналов: Научно-методические материалы / Под ред. Е.Ф.Толстова. - М.: ВВИА им. проф. Н.Е.Жуковского, 1995, с.332-340.
16. Грооп Д. Способы идентификации систем / Пер с англ. - М.: Мир, 1979.
17. Льюнг Л. Идентификация систем. Теория для пользователей. - М.: Наука, 1991.
18. Меркулов В.И., Лепин В.Н. Авиационные системы радиоуправления, ч.1, ч.2. - М.: Радио и связь, 1997.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ПАРАМЕТРОВ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ С ПОМОЩЬЮ ОДНОПОЗИЦИОННОЙ ПАССИВНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2020 |
|
RU2754349C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ПАРАМЕТРОВ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ ПО ИЗМЕРЕНИЯМ ИХ НЕСУЩЕЙ ЧАСТОТЫ | 2021 |
|
RU2776078C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА ИНТЕНСИВНО МАНЕВРИРУЮЩУЮ ВОЗДУШНУЮ ЦЕЛЬ | 2004 |
|
RU2254542C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА НАЗЕМНЫЕ ОБЪЕКТЫ | 1999 |
|
RU2164654C2 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛОВ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМ АППАРАТОМ ПРИ НАВЕДЕНИИ НА ВОЗДУШНУЮ ЦЕЛЬ | 1999 |
|
RU2189556C2 |
| СПОСОБ ПРОПОРЦИОНАЛЬНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА НАЗЕМНЫЕ ОБЪЕКТЫ | 1999 |
|
RU2148235C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА ОТДЕЛЬНУЮ ВОЗДУШНУЮ ЦЕЛЬ В СОСТАВЕ ПЛОТНОЙ ГРУППЫ ЦЕЛЕЙ | 2003 |
|
RU2253082C1 |
| Способ наведения летательного аппарата на наземные цели с помощью радиолокатора с синтезированием апертуры антенны | 2023 |
|
RU2824690C1 |
| СПОСОБ РАНЖИРОВАНИЯ ЦЕЛЕЙ | 2000 |
|
RU2190863C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ОБЪЕКТА С ИСТОЧНИКОМ ИЗЛУЧЕНИЯ СИГНАЛОВ С РАЗНЫМИ ЧАСТОТАМИ | 2011 |
|
RU2469349C1 |


Заявленный способ определения дальности до источников радиоизлучений (ИРИ) и скорости сближения с ними в однопозиционных радиолокационных системах (РЛС) позволяет определять в РЛС дальность до ИРИ и скорость сближения с ним по измеренным значениям угловых координат ИРИ. Достигаемым техническим результатом является повышение точности определения координат. Процесс определения дальности и скорости разделяют на два этапа. На предварительном этапе по измеренным значениям тангажа, угла рыскания, высоты ЛА, поперечных ускорений ЛА jп, пеленгов ϕ и угловых скоростей линии визирования ИРИ со в горизонтальной и вертикальной плоскостях вычисляют приблизительные значения дальности до ИРИ Дири и скорости сближения с ИРИ Vсб. Осуществляют прогноз ϕ, ω и jп и запоминают их. Запоминают дисперсии ошибок измерений ϕ, ω и jп. По вычисленным значениям Дири и Vсб вычисляют и запоминают значения переменных а1, определяющих степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ. Запоминают априорные и апостериорные дисперсии распределения ϕ, ω и jп. На основном этапе измеряют значения ϕ, ω и jп. Вычисляют и запоминают текущие значения дисперсий распределения ϕ, ω и jп; коэффициенты усиления ошибок прогноза ϕ, ω и jп; оценивают текущие значения переменных a1, по которым вычисляют и запоминают текущие значения компонент fij(k,k-1) фундаментальной матрицы Ф(k,k-1). По полученным значениям компонент fij(k,k-1) матрицы вычисляют Дири(k) и Vсб(k). Делают прогноз значений ϕ, ω и jп на следующий шаг измерений. Далее, описанный выше процесс, начиная со второго этапа, повторяют. 4 ил.

Способ определения дальности до источников радиоизлучений (ИРИ) и скорости сближения с ними в однопозиционных радиолокационных системах, основанный на измерении угловых координат ИРИ, отличающийся тем, что на первом, предварительном, этапе в момент времени k-2 на летательном аппарате (ЛА) измеряют ϑ(k-2) - тангаж, ψ(k-2) - угол рыскания, ула(k-2) - высоту ЛА и принимают радиосигналы от ИРИ, по которым измеряют значения ϕг(k-2), ϕв(k-2) - пеленгов ИРИ в горизонтальной и вертикальной плоскостях, соответственно, измеренные значения ϑ(k-2), ψ(k-2), ула(k-2), ϕг(k-2), ϕв(k-2) запоминают, в следующий момент времени k-1, отстоящего от момента времени k-2 на τ - интервал дискретизации, измеряют значения высоты ула(k-1) ЛА, его тангажа ϑ(k-1) и угла рыскания ψ(k-1), поперечных ускорений jг(k-1), jв(k-1) ЛА в горизонтальной и вертикальной плоскостях, соответственно, принимают радиосигналы от ИРИ, по которым измеряют значения пеленгов ϕг(k-1), ϕв(k-1) ИРИ и угловых скоростей линии визирования ωг(k-1), ωв(k-1) ИРИ в горизонтальной и вертикальной плоскостях, соответственно, измеренные значения ула(k-1), ϑ(k-1) и ψ(k-1) запоминают, измеренные значения ϕг(k-1), ωг(k-1), jг(k-1), ϕв(k-1), ωв(k-1) и jв(k-1) запоминают как значения соответствующих компонент вектора

называемого вектором состояния,
по запомненным в (k-2)-й и (k-1)-й моменты времени значениям высоты yла, пеленга ϕв и тангажа ϑ вычисляют приблизительные значения дальности до ИРИ Дири, имевшей место в моменты времени k-2 и k-1, по формулам
Дири(k-2)=ула(k-2)/sin[ϕв (k-2)-ϑ(k-2)],
Дири(k-1)=ула(k-1)/sin[ϕв(k-1)-ϑ(k-1)],
по вычисленным значениям дальности до ИРИ Дири и запомненным значениям ϕг, ϕв, ϑ и ψ вычисляют приблизительные значения проекций скорости сближения с ИРИ Vусб, Vzсб и Vхсб на оси Y, Z и Х, соответственно, неподвижной земной прямоугольной системы координат OYZX по формулам
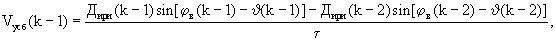


по которым вычисляют приблизительные значения скорости сближения с ИРИ Vсб по формуле

дисперсии ошибок измерений пеленгов ИРИ 
 угловых скоростей линии визирования ИРИ
угловых скоростей линии визирования ИРИ 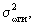
 поперечных ускорений ЛА
поперечных ускорений ЛА 
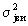 в горизонтальной и вертикальной плоскостях, соответственно, запоминают в виде значений соответствующих компонент матрицы
в горизонтальной и вертикальной плоскостях, соответственно, запоминают в виде значений соответствующих компонент матрицы

называемой матрицей дисперсий шумов измерений, недиагональные компоненты которой равны нулю, по запомненным значениям компонент ϕг(k-1), ωг(k-1), jг(k-1), ϕв(k-1), ωв(k-1), jв(k-1) вектора состояния Rири(k-1) (1) и вычисленным значениям дальности до ИРИ Дири(k-1) и скорости сближения Vсб(k-1) ЛА с ИРИ осуществляют экстраполяцию на k-й момент времени всех значений компонент вектора состояния по формуле

где
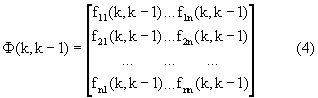
- переходная матрица вектора состояния, компоненты fij(k,k-1), 
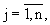 которой представляют собой функции, посредством которых связаны ϕг, ωг, jг, ϕв, ωв, jв с Дири и Vсб, спрогнозированные значения компонент ϕг(k), ωг(k), jг(k), ϕв(k), ωв(k), jв(k) вектора Rэири(k) (3) запоминают, по вычисленным значениям дальности до ИРИ Дири и скорости сближения с ним Vсб вычисляют значения упомянутых функций fij(k,k-1) и по формулам
которой представляют собой функции, посредством которых связаны ϕг, ωг, jг, ϕв, ωв, jв с Дири и Vсб, спрогнозированные значения компонент ϕг(k), ωг(k), jг(k), ϕв(k), ωв(k), jв(k) вектора Rэири(k) (3) запоминают, по вычисленным значениям дальности до ИРИ Дири и скорости сближения с ним Vсб вычисляют значения упомянутых функций fij(k,k-1) и по формулам

присваивают их значения соответствующим компонентам аl(k-1) вектора

называемого вектором параметров модели состояния, которые запоминают, в формуле (6) символ 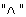 означает, что значения компонент оценены, а значение каждой из компонент
означает, что значения компонент оценены, а значение каждой из компонент 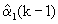 данного вектора, как и значение соответствующей ей функции fij(k,k-1), определяет степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ,
данного вектора, как и значение соответствующей ей функции fij(k,k-1), определяет степень связи между собой различных координат местоположения и параметров взаимного перемещения ЛА и ИРИ,
для учета начальных и впоследствии текущих ошибок оценивания значений компонент вектора  (6) запоминают матрицу
(6) запоминают матрицу
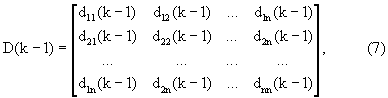
называемую матрицей апостериорных дисперсий и взаимных дисперсий ошибок оценивания вектора параметров модели состояния, значения компонент которой dij(k-1)=0, при i≠j, где 
 n - количество компонент вектора состояния, а диагональные компоненты задают, исходя из априорных сведений о корреляционных функциях распределения значений плотности вероятности соответствующих компонент вектора Rири(1), для учета отсутствия точных данных о движении ИРИ запоминают матрицу
n - количество компонент вектора состояния, а диагональные компоненты задают, исходя из априорных сведений о корреляционных функциях распределения значений плотности вероятности соответствующих компонент вектора Rири(1), для учета отсутствия точных данных о движении ИРИ запоминают матрицу

называемую матрицей дисперсий ошибок вектора состояния, значения компонент которой dij=0, при i≠j, где 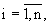
 а диагональные компоненты задают, исходя из конкретной структуры вектора Rири (1) и априорных сведений о корреляционных функциях распределения значений плотности вероятности его компонент,
а диагональные компоненты задают, исходя из конкретной структуры вектора Rири (1) и априорных сведений о корреляционных функциях распределения значений плотности вероятности его компонент,
по запомненным значениям компонент вектор Rэири(k) (3) формируют и запоминают соответствующие значения компонент переходной матрицы вектора параметров модели состояния М(k) для следующего k-го шага вычислений по формуле

где 0 - n-мерные нулевые векторы,
на втором, основном, этапе, начиная с момента времени k, измеряют значения jг, jв, а также принимают радиосигналы от ИРИ, по которым измеряют значения ϕг, ϕв, ωг и ωв, измеренные значения ϕг, ωг, jг, ϕв, ωв и jв запоминают в виде значений соответствующих компонент вектора
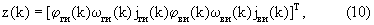
называемого вектором измерений, где ϕги(k)=ϕг(k), ωги(k)=ωг(k), jги(k)=jг(k), ϕви(k)=ϕв(k), ωви(k)=ωв(k), jви(k)=jв(k), по запомненным значениям компонент матриц d(k-1)(7), DR(8) и М(k)(9) по формуле

вычисляют и запоминают текущие значения компонент dij(k) матрицы D(k) (7), по запомненным значениям компонент матриц Dи (2), М(k) (9) и D(k) (11), по формуле

вычисляют и запоминают значения компонент кij(k-1), где 
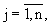 матричного коэффициента усиления К(k), по запомненным значениям компонент векторов
матричного коэффициента усиления К(k), по запомненным значениям компонент векторов  (6), z(k) (10) и матриц М(k) (9), К(k) (12) по формуле
(6), z(k) (10) и матриц М(k) (9), К(k) (12) по формуле

оценивают текущие значения компонент  вектора
вектора  (6), по полученным оцененным значениям компонент
(6), по полученным оцененным значениям компонент  по формулам
по формулам 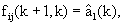

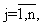
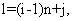 присваивают значения соответствующим компонентам fij(k+1,k) матрицы Ф(k+1,k) (4), по полученным значениям компонент fij(k+1,k) матрицы Ф(k+1,k) вычисляют дальность до ИРИ Дири(k) и скорость сближения с ним Vсб(k) по формулам
присваивают значения соответствующим компонентам fij(k+1,k) матрицы Ф(k+1,k) (4), по полученным значениям компонент fij(k+1,k) матрицы Ф(k+1,k) вычисляют дальность до ИРИ Дири(k) и скорость сближения с ним Vсб(k) по формулам
Дири=η1{fij(k+1,k)},
Vсб=η2{fij(k+1,k)},
где η1{fij(k+1,k)} и η2{fij(k+1,k)} - функции, посредством которых связаны ϕг, ωг, jг, ϕв, ωв, jв с Дири и Vсб, вычисленные значения дальности до ИРИ Дири(k) и скорости сближения с ним Vсб(k) выдают потребителям информации, по запомненным значениям компонент вектора Rири(k) (1) и матрицы Ф(k+1,k) по формуле (3) вычисляют и запоминают значения компонент вектора Rэири(k+1) (3) на следующий (k+1)-й шаг измерений, по запомненным значениям компонент вектора Rэири(k+1) по формуле (9) формируют и запоминают значения компонент матрицы М(k+1) для следующего шага измерений, далее, описанный выше процесс, начиная со второго этапа, повторяют.
| Зарубежная радиоэлектроника, 2002, № 3, с.64-94.RU 2000101254 А, 10.12.2000.RU 2050557 С1, 20.12.1995.US 4633257 А, 30.12.1986.US 4626861 А, 02.12.1986. |
Авторы
Даты
2004-07-10—Публикация
2002-09-16—Подача