Изобретение относится к нейрокибернетике и может использоваться в качестве функциональной единицы различных искусственных нейронных сетей.
Известна техническая и математическая модель искусственного нейрона [1-4]. Первая модель предложена в работе [1]. Позже [2], на основе таких моделей нейронов, реализованы первые искусственные нейронные сети (персептроны) для решения задач распознавания изображений букв. Подобные искусственные нейроны используются в качестве функциональной единицы всех современных искусственных нейронных сетей [3, 4] и представляют собой устройства с несколькими входами и одним выходом. Входные сигналы, поступая на входы, перемножаются с соответствующими весовыми коэффициентами, суммируются и преобразуются функцией передачи, в качестве которой может использоваться пороговая, линейная, сигмоидальная, гиперболическая и др. [3, 4]. Такая модель нейрона позволяет, хотя и достаточно грубо, воспроизводить некоторые из функций естественного нейрона. Объединяя искусственные нейроны в слои и сети, в совокупности с алгоритмами обучения, можно добиться приемлемого решения нейронной сетью сложных задач, не поддающихся адекватной формализации [3, 4].
Наиболее близкой по техническому исполнению к предлагаемой модели нейрона является модель простейшего персептронного нейрона с двумя входами, парой весовых коэффициентов, сумматором и активационным блоком [3, 4]. Достоинством такой модели является возможность реализации ею большинства логических булевых функций. Так, для двух переменных, согласно [5], существует набор из 16 функций алгебры логики. Известная модель нейрона с двумя входами реализует 14 из них [4], т.е. все, за исключением логических булевых функций неравнозначности (или "суммы по модулю 2") и эквивалентности (равнозначности), которые рассмотрены, например, в [6]. Невозможность реализации двух данных логических функций является существенным недостатком такой модели нейрона и носит название проблемы ИСКЛЮЧАЮЩЕГО ИЛИ, которая впервые обнаружена в работе [7]. Данная проблема является фундаментальной в теории искусственных нейронных сетей и наглядно изложена в ряде современных научных изданий [4, 8, 9].
Предлагаемая модель направлена на устранение рассмотренного недостатка (проблемы нереализуемости логической функции неравнозначности) известной модели нейрона.
Проблема нереализуемости нейроном логической функции неравнозначности заключается в следующем [4, 8, 9].
Рассмотрим известную модель нейрона, функциональная схема которой приведена на фиг.1. Входные сигналы х1 и х2 при поступлении в блоки 1 и 2 перемножаются с соответствующими весовыми коэффициентами w1 и w2. Блоки 1 и 2 осуществляют перемножение с учетом знаковых разрядов сигналов [10]. Затем перемноженные сигналы х1w1 и х2w2 поступают на вход сумматора со знаковыми входами/выходом [10], который обозначен блоком 3 на фиг.1. С выхода сумматора сигнал s=(х1w1+х2w2) поступает на активационный блок 4 [10], в котором преобразуется пороговой функцией передачи [4, 8, 9]:
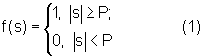
где Р - величина порога. Выход блока 4 является выходом модели нейрона. Требуемые выходные значения модели нейрона для реализации функции неравнозначности, в зависимости от х1 и х2, приведены в таблице 1.
Рассмотрим сумму s как функцию двух переменных (поверхность) от х1 и х2 над плоскостью входных значений Ох1x2, как показано на фиг.2 [4]. Каждая точка этой поверхности находится над соответствующей точкой плоскости Ох1x2 на расстоянии, равном значению s в этой точке. Точки, в которых значение s равно величине порога Р, устанавливаемого в блоке 4, образуют прямую на плоскости Px1х2, параллельную Ох1х2 (на фиг.2 Рх1х2 - полупрозрачным тоном; Р равно 0.5) и проектируются в некоторую разделяющую одномерную гиперплоскость (прямую) на плоскости входных значений Ох1х2. Данная разделяющая прямая на плоскости Ох1х2 приведена на фиг.3, где стрелками к углам (возможным значениям х1 и х2) указаны требуемые значения выхода нейрона для реализации логической функции неравнозначности.
Все точки по одну сторону разделяющей прямой проецируются в значения s, большие порога, а точки по другую сторону дают меньшие значения s, т.е. пороговая прямая разбивает плоскость Ох1x2 на две области. В одной из них активность нейрона равна единице, в другой - нулю. Таким образом, невозможно провести прямую так, чтобы двухвходовым нейроном в соответствии с табл. 1 разделить нули и единицы на плоскости Ох1х2, т.е. реализовать логическую функцию неравнозначности.
Рассмотрим сущность предлагаемой модели нейрона, реализующей логическую функцию неравнозначности.
Функциональная схема устройства приведена на фиг.4.
Предлагаемая модель нейрона, как и известная, содержит два перемножителя (блоки 1 и 2), осуществляющих перемножение входных сигналов с весовыми коэффициентами с учетом их знаков. В модели могут использоваться любые из известных, описанных в [10] перемножителей подобного типа. Как и в известной модели, перемноженные сигналы x1w1 и x2w2 поступают на вход сумматора (блок 3) со знаковыми входами/выходом [10]. В качестве знакового сумматора могут использоваться любые устройства подобного типа, например приведенные в [10]. Предлагаемая модель отличается от модели прототипа тем, что активационный блок состоит из двух последовательно соединенных блоков, как показано на фиг.4. При этом сумма s с выхода сумматора поступает сначала на вход блока 4 (фиг.4), в котором преобразуется модульной функцией активации вида  , а затем с выхода блока 4 поступает на вход блока 5, где преобразуется пороговой функцией (1). В качестве блоков 4 и 5 могут быть использованы описанные в [10] технические устройства, реализующие соответствующие математические функции. Выход блока 5 предлагаемой модели является ее выходом. Таким образом, выход модели нейрона у(х1,х2) является результатом подстановки модуля суммы s в пороговую функцию (1). Полная функция передачи модели будет выглядеть
, а затем с выхода блока 4 поступает на вход блока 5, где преобразуется пороговой функцией (1). В качестве блоков 4 и 5 могут быть использованы описанные в [10] технические устройства, реализующие соответствующие математические функции. Выход блока 5 предлагаемой модели является ее выходом. Таким образом, выход модели нейрона у(х1,х2) является результатом подстановки модуля суммы s в пороговую функцию (1). Полная функция передачи модели будет выглядеть

Математическая модель нейрона в этом случае будет описываться
следующим выражением:

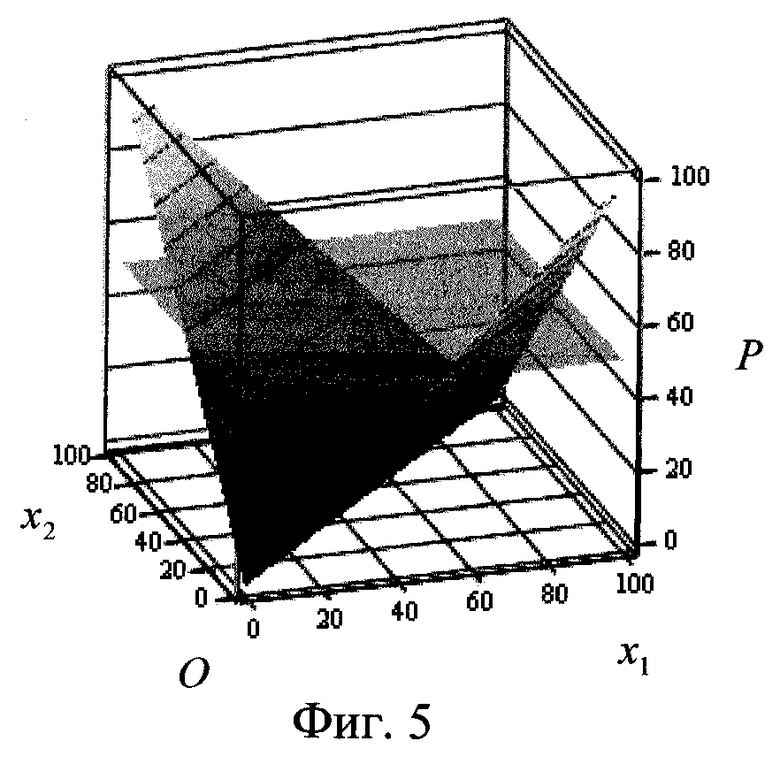
Сумма s=(x1w1+х2w2) должна быть нулевой при равенстве значений х1 и х2, что достижимо при w1=1, w2=-1, как показано на фиг.2. В этом случае, модуль суммы (сигнал на выходе блока 4 фиг.4) как функция от двух переменных х1 и х2 будет иметь вид, в отличие от прототипа, не одной поверхности, а двух подповерхностей под некоторым углом между собой, как показано на фиг.5. Если в этом случае модуль суммы преобразовать пороговой функцией (2) в блоке 5 фиг.4, т.е. ограничить плоскостью Рх1х2, которая на фиг.5 показана полупрозрачным тоном, то пересечение поверхности модуля с плоскостью Рх1x2 образует не одну, как у прототипа, а две разделяющие прямые.
Математически уравнение разделяющей прямой из выражения (3) будет выглядеть 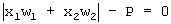 , откуда, в соответствии со свойством модуля, образуются два уравнения разделяющих прямых
, откуда, в соответствии со свойством модуля, образуются два уравнения разделяющих прямых
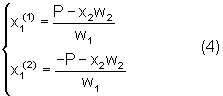
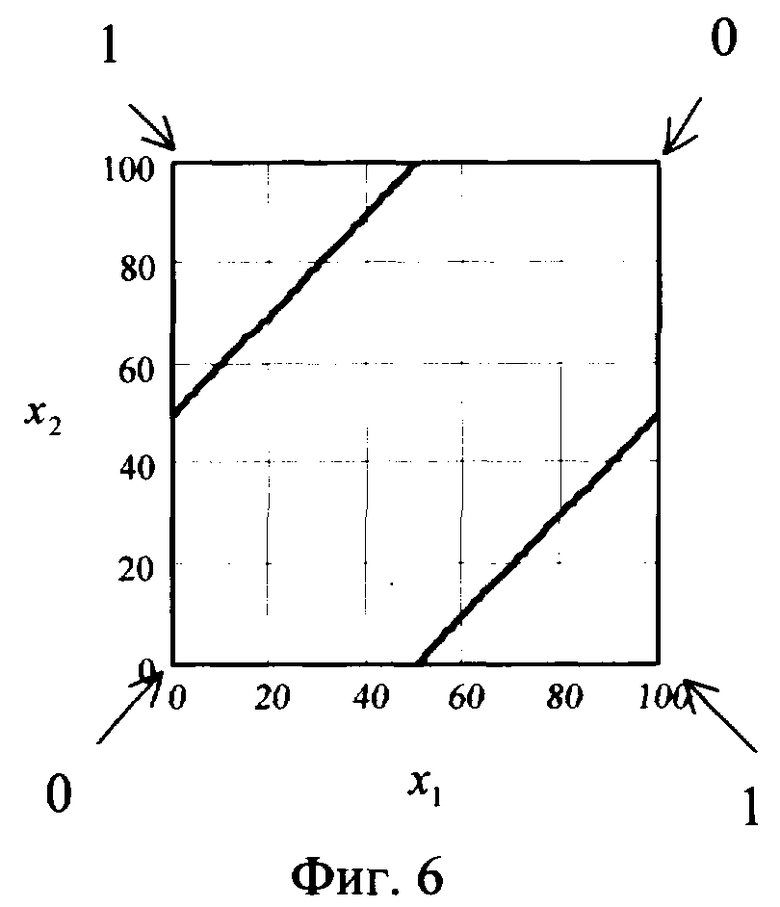
где х1 (1) - первая прямая; х1 (2) - вторая прямая, т.е. две проекции пересечения поверхности s с плоскостью Рх1х2, полученные на плоскости Ох1x2, которые и разделяют ее на три области так, как показано на фиг.6.
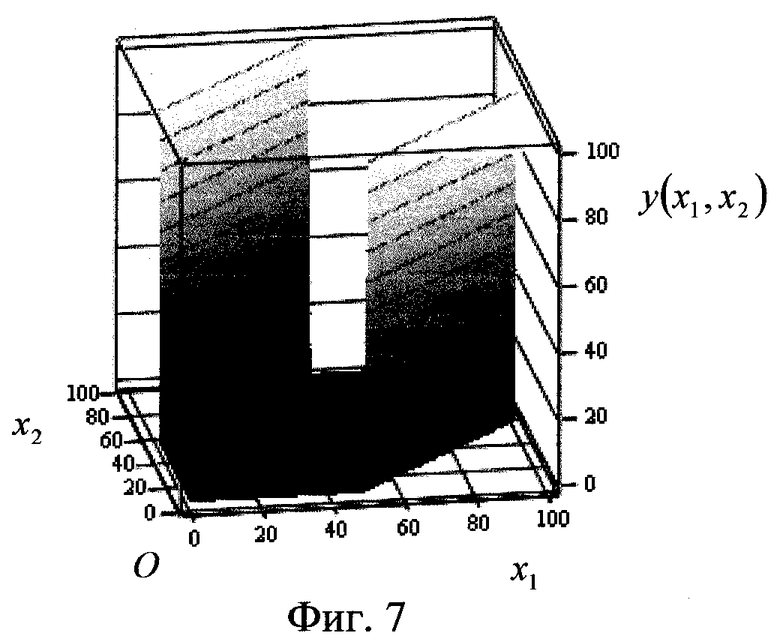
Полный вид зависимости выхода нейрона у(х1,х2) как функции двух переменных от х1 и х2 в рассматриваемом случае, показан на фиг.7.
На фиг.2, 3, 5-7 размерности всех координатных осей приведены в сотых.
Из фиг.5-7 видно, что при x1=х2 (или х1≈x2) нейрон на выходе будет давать нуль, а при х1≠х2 - единицу. Таким образом, отделяя нулевые входные значения от единичных на плоскости Ox1x2 в отличие от прототипа не одной, а двумя прямыми, нейроном реализуется логическая функция неравнозначности.
Для подтверждения возможности осуществления заявленного изобретения рассмотрим работу предлагаемой модели нейрона.
Весовые коэффициенты имеют постоянные значения во всех случаях: w1=1, w2=-1. Величину порога примем равной, например, 0,5. Результат подстановки модульной функции в пороговую будет выглядеть аналогично (2):
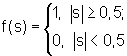
Так как математическая модель нейрона имеет вид
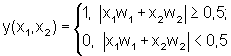
то при подаче на его входы х1 и х2 сигналов, равных нулю, сумма (выход блока 3 фиг.4) будет равна нулю. Преобразуясь модульной функцией активации в блоке 4, сигнал на его выходе будет также нулевым, как и после блока 5 на выходе у(х1, х2) нейрона. При поступлении на входы x1=1, х2=0 сумма будет равна единице; модуль (выход блока 4) - также единице, что превысит порог Р=0.5 в блоке 5 и на выходе нейрона будет единица. При входной комбинации х1=0, х2=1 сумма будет равна минус единице; модуль - единице, что также превысит порог Р=0.5 в блоке 5 и даст единицу на выходе нейрона. В случае х1=1, x2=1, сумма станет нулевой; модуль суммы будет также равен нулю, что даст на выходе нейрона нуль.
Таким образом, предлагаемой моделью нейрона, в соответствии с таблицей 1, реализуется логическая функция неравнозначности.
Входные сигналы нейрона х1 и х2 могут быть не только дискретными, но и непрерывными (от нуля до единицы), так как поверхность модуля суммы s, показанная на фиг.5, существует для всех непрерывных х1 и х2.
Таким образом, предлагаемая модель нейрона, реализуя логическую функцию неравнозначности, преодолевает проблему ИСКЛЮЧАЮЩЕЕ ИЛИ.
Источники информации
1. McCulloch W.S., Pitts W. A logical calculus of the ideas imminent in nervous activity. // Bulletin of Mathematical Biophysics, vol.5, 1943, pp.115-133. (Рус. перевод: Маккаллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной деятельности. Автоматы. / Под ред. К.Э.Шеннона, Дж.Маккарти. - М.: ИЛ, 1956).
2. Rosenblatt F. Principles of neurodinamics. Perceptrons and the theory of brain mechanisms. Spartan Books, Washington, 1962. (Рус. перевод: Розенблатт Ф. Принципы нейродинамики. Перцептроны и теория механизмов мозга. / Под ред. С.М.Осовца. - М: Мир, 1965 - 480 с.).
3. Галушкин А.И. Теория нейронных сетей. Кн.1: Учеб. пособие для вузов / Общая ред. А.И.Галушкина. - М.: ИПРЖР, 2000. - 416 с.
4. Wasserman P. Neurocomputing. Theory and practice, Nostram Reinhold, 1990. (Рус. перевод: Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. / Пер. с англ. Ю.А. уев, В.А.Точенов. - М.: Мир, 1992. - 240 с.).
5. Куринной Г.Ч. Математика: Справочник. - Харьков: Фолио; Ростов н/Д: Феникс, 1997. - 463 с.
6. Залманзон Л.А. Беседы об автоматике и кибернетике. -М.: Наука. Гл. ред. физ.-мат. лит., 1981. - 416 с.
7. Minsky М., Papert S. Perceptrons. An introduction to computational geometry, MIT Press, 1969. (Рус.перевод: Минский М., Пейперт С. Персептроны. / Под ред. В.А.Ковалевского. - М.: Мир, 1971. - 261 с.).
8. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия - Телеком, 2001. - 382 с.
9. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. - СПб.: Питер, 2001. - 480 с.
10. Галушкин А.И. Нейрокомпьютеры. Кн.3: Учеб. пособие для вузов / Общая ред. А.И.Галушкина. - М.: ИПРЖР, 2000. - 528 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РЕАЛИЗАЦИИ НЕЙРОНОМ ЛОГИЧЕСКОЙ ФУНКЦИИ НЕРАВНОЗНАЧНОСТИ | 2006 |
|
RU2308758C1 |
| СПОСОБ МОДЕЛИРОВАНИЯ НЕЙРОНА | 2009 |
|
RU2402813C1 |
| Способ управления реакцией нейропроцессора на входные сигналы | 2018 |
|
RU2724784C2 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО ГРАДИЕНТНОГО ВЫДЕЛЕНИЯ КОНТУРОВ ОБЪЕКТОВ НА ЦИФРОВЫХ ИЗОБРАЖЕНИЯХ | 2008 |
|
RU2360289C1 |
| Многовходовой сумматор по модулю два | 2015 |
|
RU2614370C1 |
| ПОСТРОЕНИЕ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ НЕЙРОНОВ С ФУНКЦИОНАЛЬНЫМ ПРЕОБРАЗОВАНИЕМ ПРОИЗВОЛЬНОГО ВИДА ДЛЯ ВХОДНЫХ СИГНАЛОВ | 2018 |
|
RU2727080C2 |
| СПОСОБ НЕЙРОСЕТЕВОГО ПРОГНОЗИРОВАНИЯ ИЗМЕНЕНИЯ ЗНАЧЕНИЙ ФУНКЦИИ С ЕЁ ПРЕДВАРИТЕЛЬНОЙ ВЕЙВЛЕТ-ОБРАБОТКОЙ И УСТРОЙСТВО ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2600099C1 |
| Способ и устройство автоматического распознавания типа манипуляции радиосигналов | 2017 |
|
RU2665235C1 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО ГРАДИЕНТНОГО ВЫДЕЛЕНИЯ КОНТУРОВ ОБЪЕКТОВ НА ЦИФРОВЫХ ИЗОБРАЖЕНИЯХ | 2015 |
|
RU2589301C1 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |



Изобретение относится к нейрокибернетике и может быть использовано в качестве функциональной единицы различных искусственных нейронных сетей. Техническим результатом является устранение проблемы нереализуемости логической функции неравнозначности известными моделями нейронов. Указанный результат достигается за счет того, что устройство содержит два входа, сигналы с которых перемножаются с соответствующими весовыми коэффициентами и поступают на сумматор, сумма с выхода которого преобразуется в активационном блоке модульной функцией активации, а затем пороговой функцией на выходе нейрона. 7 ил., 1 табл.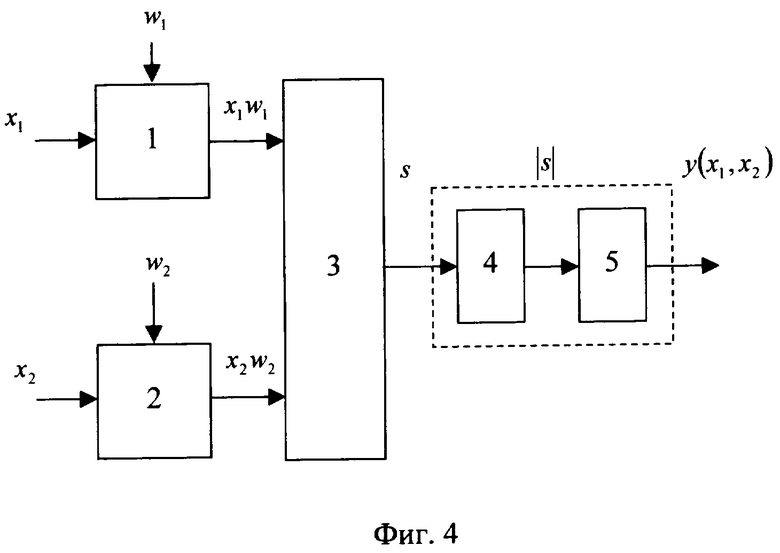
Модель нейрона, реализующая логическую функцию неравнозначности, содержащая два входа, сигналы х1 и х2, принимающие значения 0 или 1, с которых перемножаются с соответствующими весовыми коэффициентами ω1 и ω2, где ω1=1, а ω2=-1,и поступают на сумматор, причем s∈(-1, 0, 1), где s - сумма с выхода сумматора, s=х1ω1+х2ω2, отличающаяся тем, что сумма s преобразуется в активационном блоке модульной функцией активации вида 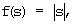 a затем пороговой функцией
a затем пороговой функцией
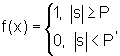
где Р - величина порога, Р=0,5, f(x) - функция на выходе нейрона.
| Нейрокомпьютерная техника: теория и практика / Пер | |||
| с анг | |||
| Ю.А.Зуев и др | |||
| М.: Мир, 1992, 240 с | |||
| RU 94045263 A1, 20.10.1996 | |||
| МОДЕЛЬ НЕЙРОНА | 0 |
|
SU211168A1 |
| Многофункциональный логический модуль | 1979 |
|
SU790329A1 |
| US 6052679 A, 18.04.2000. | |||
Авторы
Даты
2006-01-27—Публикация
2003-08-22—Подача