Искусственные нейронные сети - это эффективный инструмент для решения множества задач интеллектуального анализа данных с очень широким спектром применения в различных производственных отраслях. Основным элементом классических искусственных нейронных сетей является математический нейрон, формулу которого можно выразить как нелинейное преобразование взвешенной суммы входных сигналов с помощью активационной функции, как показано в уравнении 1.

где n - количество входов нейрона, xi - значения входных сигналов нейрона, wi - весовые коэффициенты, f() - нелинейная функция активации, у - выходное значение нейрона.
Активационная функция предназначена для включения (усиления влияния) или выключения (подавления влияния) отдельных входов нейрона, которая обычно имеет вид сглаженной ступенчатой функции, как сигмоидная функция или подобная ей. Если применить ступенчатую функцию (релейную функцию со значениями 0 или 1), то некоторые входы в нейрон будут полностью выключены или включены. Если применить линейную функцию, то нейрон превращается в линейный оператор типа множественная регрессия. В последнем случае есть возможность получить весовые коэффициенты в процессе обучения путем решения системы линейных уравнений на основе массива с известными входами и соответствующими им выходами.
Для обученного нейрона весовые коэффициенты и вид активационной функции являются константами данного нейрона в процессе вычислений, и они должны быть определены в процессе обучения.
В качестве входа нейрона понимается некий набор чисел или вектор, описывающий изучаемый объект. Если подавать последовательно несколько различных векторов на вход нейрона, то каждому из них будет соответствовать уникальный выход. Если эти вектора описывают изменение изучаемого объекта во времени (например, ежедневное изменение курса разных валют в рублях), то в этом случае их можно назвать сигналом, поданного на вход нейрона. Так как мы всегда подразумеваем подачу разных векторов на вход нейрона, то удобно называть такой поток сигналом.
В общем виде нейронную сеть образуют хаотически соединенные нейроны, когда выходы одних нейронов являются входами других нейронов с возможными обратными связями, когда сигнал полученный на выходе некоторого нейрона может быть подан на него как один из возможных входных сигналов, в том числе, когда этот выходной сигнал пройдет через несколько других нейронов. Для таких нейронных сетей общие алгоритмы обучения не разработаны и в настоящее время имеется только несколько частных случаев, для которых имеются теоретические исследования и реализации.
Нейронные сети без обратных связей можно представить в виде многослойной конструкции. Входы иногда называют входным слоем или просто входами. Количество выходных нейронов может быть единичным или больше в соответствии с количеством выходов нейронной сети. Промежуточные слои нейронов между входным слоем и выходными нейронами называют скрытыми слоями. Количество скрытых слоев определяют глубину нейронной сети и, соответственно, ее степень свободы по преобразованию входных сигналов.
Входной вектор подается на входы всех нейронов в первом скрытом слое и все выходы этих нейронов подаются на входы следующего слоя и так далее до выходного слоя.
При использовании нейронных сетей всегда имеется два этапа. Первый этап - это обучение нейронных сетей, когда определяются все ее коэффициенты при заданной ее конфигурации (геометрии связей) - количество входов, количество скрытых слоев, количество нейронов в каждом скрытом слое и количество выходов. Для классических нейронных сетей должен быть определен тип активационной функции, обычно один для всех нейронов. Для обучения используется обучающее множество в виде массива обучающих пар, входной вектор и соответствующим им выходной вектор. В процессе обучения необходимо минимизировать объектную (целевую) функцию, обычно в виде суммы квадратов ошибок - как квадрат разницы вычисленного выхода с текущими весовыми коэффициентами и заданными выходами в обучающих парах.
Чтобы построить классическую нейронную сеть, как правило, используются два основных метода обучения. В первую очередь - это алгоритм обратного распространения ошибки, который является типичным градиентным методом. Второй способ обучения нейронной сети использует стохастические алгоритмы, например, генетические алгоритмы или алгоритм имитации отжига. Все эти способы имеют множество модификаций и могут комбинироваться.
В общем случае, задачу обучения нейронных сетей можно отнести к типичным некорректным задачам - многозначности и неустойчивости решений, а также к возможному отсутствию решения. Например, если количество обучающих пар меньше, чем количество неизвестных весовых коэффициентов, то возникает возможность многозначности такого решения. Если обучающие пары имеют сильную корреляцию и некоторые обучающие пары могут быть вычислены через другие путем линейных операций, то может вообще не
существовать такой нейронной сети для такого обучающего множества. Одним из общепризнанных подходов стабилизации решения для этих методов обучения нейронных сетей является регуляризация по Тихонову (см. [1] Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука. Главная редакция физико-математической литературы, 1979. Изд. 2-е. - 288 с). При использовании регуляризации по Тихонову возникает необходимость применения дополнительного члена для целевой функции, которая, как правило, может быть суммой квадратов для всех коэффициентов в операторе прогнозирования, что не позволяет этому коэффициенту быть большим.
Общеизвестно, что для обеспечения достаточной степени свободы нейронной сети требуется использование большей ее глубины, то есть большего количества скрытых слоев, что повлечет увеличение вычислительных затрат и может существенно влиять на качество обучения. Очевидно, что этот недостаток напрямую зависит от динамической ограниченности математической формулы классического нейрона, который использует нелинейные активационные функции сигмоидальной формы к взвешенным суммам входных сигналов.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Для построения вычислительной системы обработки входных векторных данных для временного или пространственного прогноза выходного вектора параметров или распознавания образов на основе нейронных сетей предлагается использовать новый тип математического нейрона, где постоянные коэффициенты для каждого входа заменяются на произвольные функции, которые выполняют трансформацию входных данных перед суммированием. Собственно трансформацию входных данных для каждого входного сигнала предлагается выполнять в виде таблицы (массива) соответствия входных значений сигнала и выходных значений произвольной функции. Такой нейрон можно назвать как т-нейрон (нейрон на основе функциональной трансформации). Конструкция нейронной сети с включениями т-нейронов предлагается в виде классического многослойного персептрона без обратных связей. Также предлагается применение смешанных нейронных сетей с участием традиционных нейронов и т-нейронов. Для обучения такой нейронной сети предлагается использовать генетический алгоритм или/и градиентный алгоритм на основе гибрида обратного распространения ошибки и метода настройки с возвращениями (backfitting). Применение произвольных функций трансформации на входе т-нейрона значительно увеличивает его степень свободы и тем самым увеличивает возможность нейронных сетей, построенных с использованием таких нейронов, выполнять нелинейные прогнозные построения и обеспечивать уверенное распознавание образов с меньшей глубиной нейронной сети и с меньшим общим количеством используемых нейронов.
Данный раздел сущности изобретения не ставит цель дать полное описание построения системы обработки векторных данных для временного или пространственного прогноза выходного вектора параметров или распознавания образов (классификации) на основе нейронных сетей или дать исчерпывающий перечень признаков и элементов. Ниже дано подробное описание с примерами реализации.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Изобретение поясняется описанием со ссылками на чертежи, на которых:
фиг. 1 изображает схему обработки входных векторов (изображения или набор измеренных параметров процесса во времени или в пространстве) для прогноза параметров или для распознавания образов (классификации);
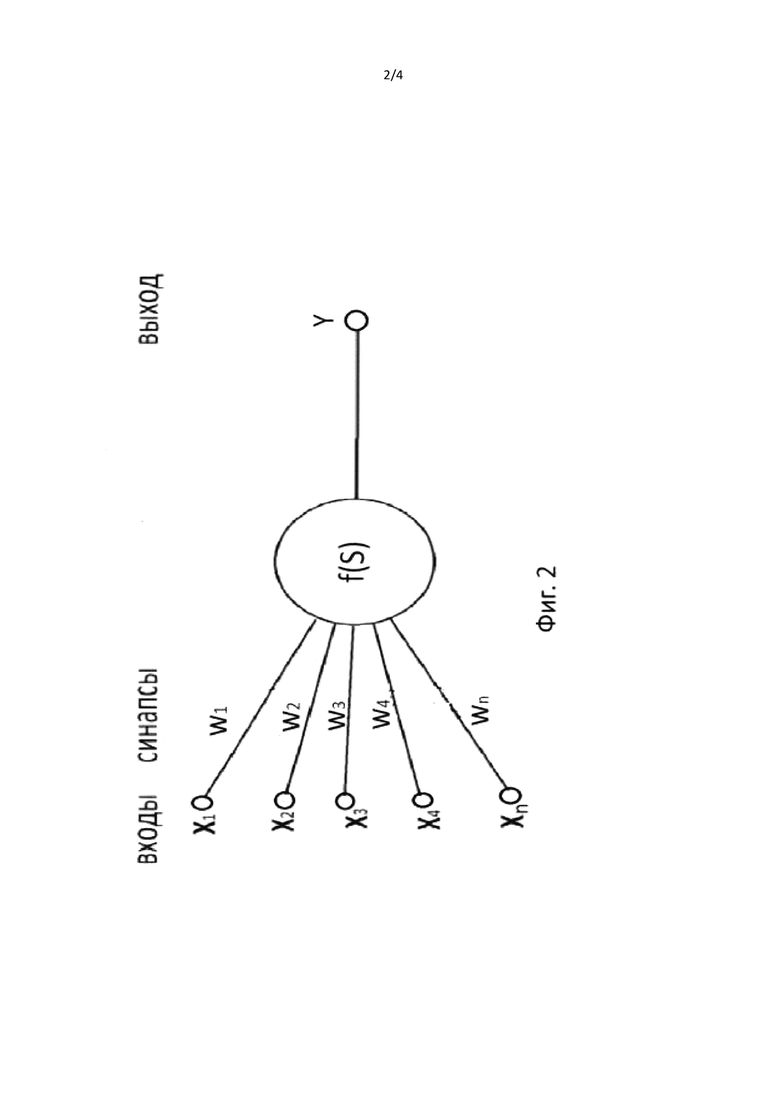
фиг. 2 - схема классического математического нейрона как нелинейный сумматор ƒ(S) с функцией активации ƒ для нескольких входных сигналов;
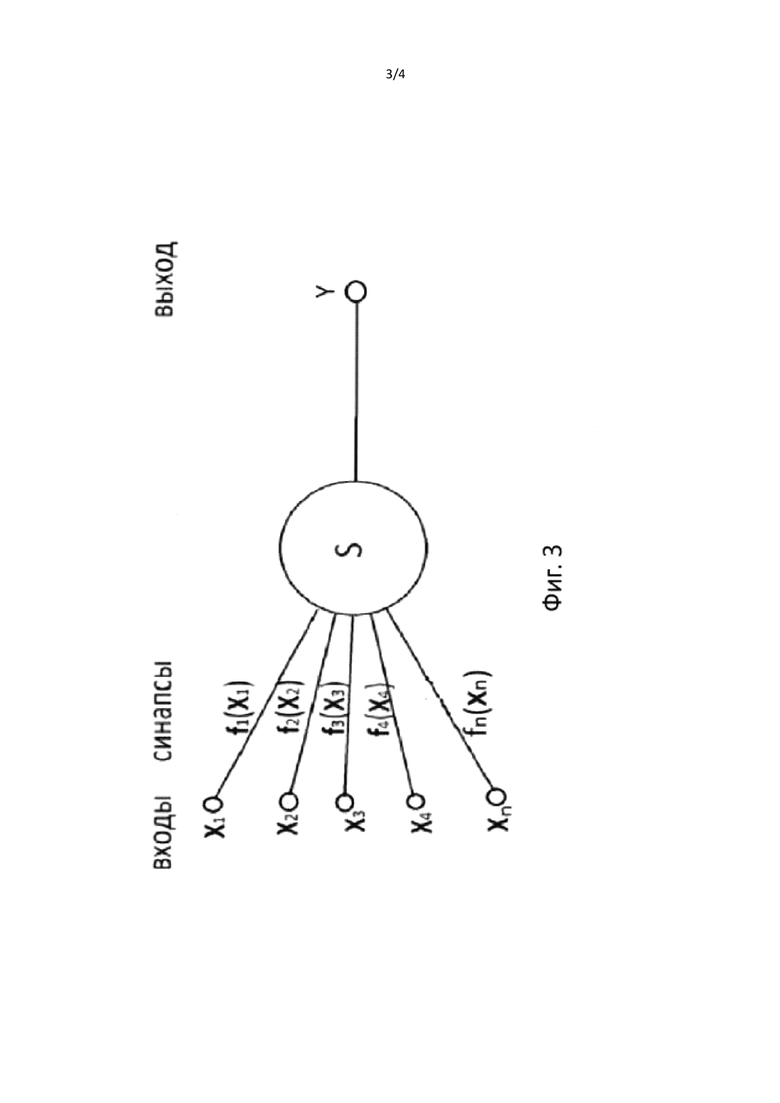
фиг. 3 - схема предлагаемого математического т-нейрона в виде нелинейного сумматора S трансформированных входных сигналов с помощью произвольных функций ƒi(xi);
фиг. 4 - схема табличного задания функции yi=ƒi(xi) в виде таблицы (массива) пар соответствия xi-yi, где xi - входные значения, yi - выходные значения;
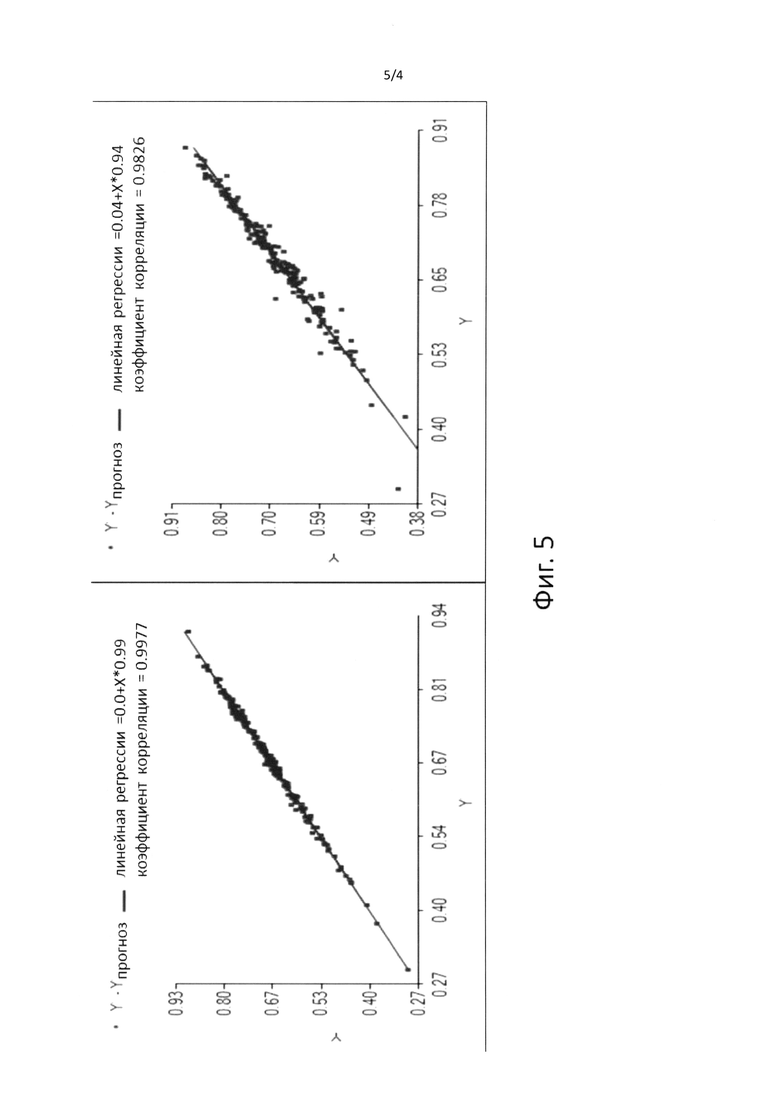
фиг. 5 - графики сравнения точного и прогнозного параметра Y для прогнозного оператора на основе нейронных сетей с использованием предлагаемого математического т-нейрона; слева график по набору данных 1, которые использовались для обучения и справа по набору данных 2, которые не использовались для обучения. Точками обозначены значения точного и прогнозного параметра, обозначенные как Y и Y прогноз, и черная линия показывает линейную регрессию, максимально аппроксимирующую положения точек точного и прогнозного параметра.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
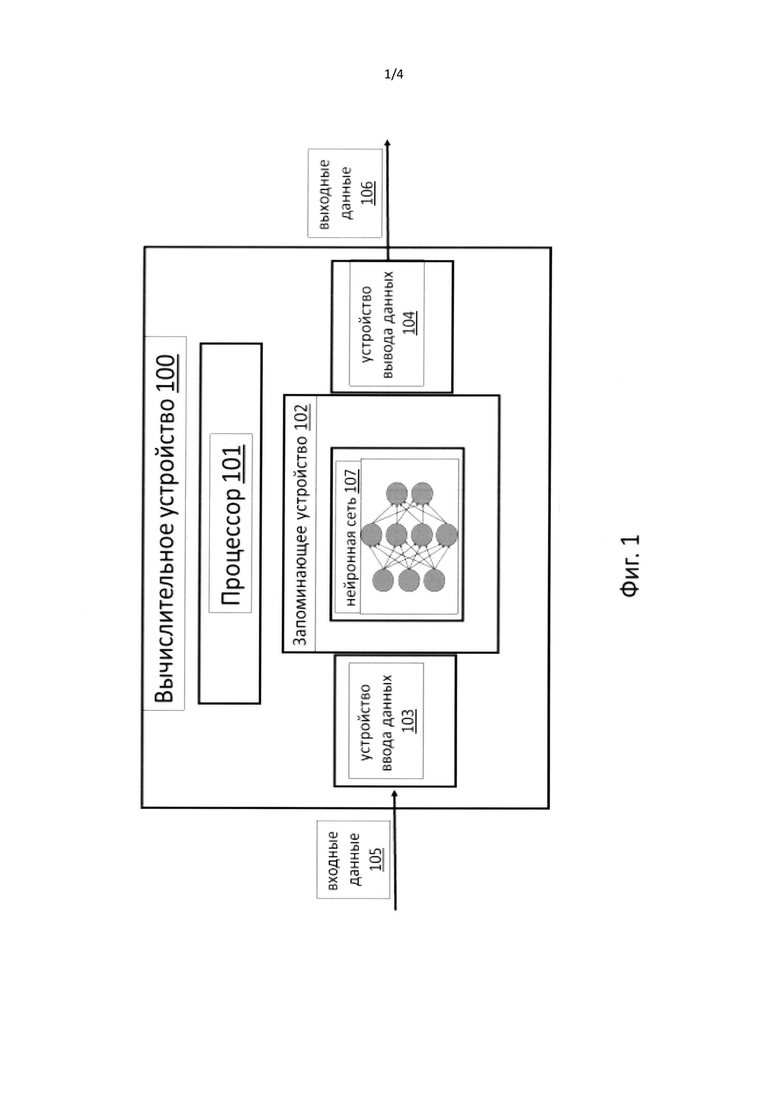
В данном изобретении приводится описание вычислительной системы и способ прогноза параметров во времени или в пространстве, или для распознавания образов (классификации) входных данных на основе нейронных сетей. Пример такой системы показан на фиг. 1. Вычислительная система 100 может быть компьютером, компьютерной сетью или любым устройством, как минимум имеющее процессор 101, запоминающее устройство 102 с загруженным программным кодом нейронных сетей 107, устройство ввода данных 103 и устройство вывода данных 104. На вход вычислительной системы 103 подаются входные данные 105 в виде многомерных векторов параметров описания изучаемых объектов. На выходе системы 104 будут выходные данные 106 в виде вектора прогнозных параметров или номер класса, к которому относится входной объект. Все вычисления выполняются с помощью программного кода нейронных сетей 107, который выполняет преобразование входных данных и формирует выходные данные. Основной целью изобретения является увеличение степени свободы отдельных нейронов и тем самым, уменьшение глубины сети (количества скрытых слоев), а также увеличение скорости вычислений нейронной сети.
Предлагаемая нейронная сеть использует новый тип математического нейрона, где постоянные коэффициенты wi классического нейрона для каждого входа заменяются на произвольные функции вида ƒi(xi). Такой нейрон мы называем т-нейрон (нейрон с функциями трансформации). Сравнение классических нейронов (фиг. 2) с весовым суммированием и применением активационной функцией к этой сумме, а также т-нейронов (фиг. 3), которые выполняют трансформацию входных данных перед суммированием, показано на фиг. 2 и 3. В т-нейронах не применяются активационные функции, так как нет необходимости вносить дополнительную искусственную нелинейность сумматора. Математически предлагаемый т-нейрон можно описать с помощью формулы 2.

Функция трансформации входных сигналов ƒi(xi) задается как численная конструкция в табличном виде соответствия входных значений xi и выходных значений функции (массива пар): значение аргумента - значение функции как показано на фиг. 4. Длина такого массива определяет количеством таких пар. Для однозначного определения функции этот массив должен быть отсортирован по аргументу. С другой стороны, для однозначного определения аргумента по значениям функции массив должен быть отсортирован по значениям функции. Такой вариант сортировки соответствует численному варианту обратной функции ƒ'.
Получение значения функции по заданному аргументу выполняется с помощью линейной интерполяции по формуле 3.
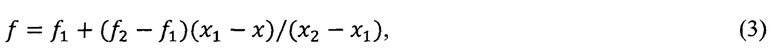
где х - заданное значение аргумента и ƒ вычисленное значение функции
х1, х2 найденные значения аргумента в двух парах, где х>х1 и х<х2.
ƒ1, ƒ2 соответствующие х1, х2 значения функции.
Аналогично формуле 3, можно вычислять значения аргумента по заданным значениям функции, применяя сортировку массива по значения функции. Можно также применять другие схемы интерполяции, например, на основе степенных полиномов или сплайнов.
Размер массива, определяющий функцию трансформации, может быть определен как единый для всей нейронной сети и будет определять степень нелинейности нейронов. Если определить эту функцию двумя парами, то функция трансформации будет линейной. Три пары могут определять функцию трансформации в виде полинома второй степени (при применении соответствующей интерполяции). Также следует ограничить максимальное число таких пар чтобы, с одной стороны, минимизировать количество неизвестных и общего размера используемой памяти и с другой стороны - для построения достаточно гибкой нейронной сети с большой степенью свободы.
Конструкция нейронной сети предлагается в виде классического многослойного персептрона без обратных связей. Единственное отличие предлагаемой нейронной сети от классической заключается в применении т-нейронов. Не исключается применение смешанных нейронных сетей, с участием традиционных нейронов и т-нейронов. Например, такое сочетание может применяться при построении глубоких сверточных (конволюционных) нейронных сетей, когда первые слои используют традиционные нейроны с активационными функциями, а в завершающих слоях применятся т-нейроны.
Для обучения предлагаемых нейронных сетей на основе т-нейронов также можно использовать все классические методы обучения. Кроме этого, нами ранее предложено гибридная комбинация градиентных и генетических алгоритмов при обучении классических нейронных сетей (см. [2] Kobrunov А. and Priezzhev I., 2016, Hybrid combination genetic algorithm and controlled gradient method to train a neural network, GEOPHYSICS, VOL. 81, NO. 4, 1-9). Подобная схема обучения также может быть применена для нейронных сетей на т-нейронах. При использовании алгоритма обратного распространения ошибки необходимо численное вычисление производной функции для всех функций трансформации.
Если рассматривать отдельный т-нейрон, то используемый итерационный метод Ньютона для коррекции функций трансформации на основе известной ошибки может быть описан формулой 4. На начальном этапе все значения функций трансформации для каждого входа инициируются случайными значениями и затем выполняется вычисление т-нейрона и на основе полученной ошибки итерационно вычисляется коррекция функций трансформации.

где 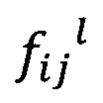 значение функции трансформации для i-гo входа т-нейрона для j-й пары в массиве описание его функции трансформации.
значение функции трансформации для i-гo входа т-нейрона для j-й пары в массиве описание его функции трансформации.
Верхний индекс l обозначает текущий номер итерации и l - 1 и l - 2 обозначают родительские и прародительские значения функции трансформации или выходов т-нейрона.
уl-1 есть текущее значение выхода т-нейрона и в знаменателе (уl-1 - 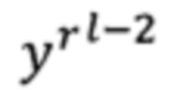 ) есть значение текущей ошибки как разницы родительских и прародительских значений.
) есть значение текущей ошибки как разницы родительских и прародительских значений.
Вычисление значений ошибки для выходного слоя нейронной сети вычисляется как разница вычисленных значений сети и значений в обучающих парах. Для всех остальных слоев значения ошибки вычисляется путем ее пропорционального распределения согласно классического алгоритма обратного распространения ошибки.
При использовании алгоритма на основе генетических алгоритмов или, как вариант, гибридная комбинация генетических и градиентных алгоритмов для обучения предлагаемой нейронной сети должны выполняется следующие шаги.
1. Создать первоначальное поколение нейронных сетей в виде нескольких их вариантов с коэффициентами на основе случайной функции.
2. Сделать выборку небольшого количества лучших вариантов нейронных сетей с наименьшими объектными функциями. (Этап селекции генетического алгоритма.)
3. Создать следующее поколение нейронных сетей на основе выбранных в соответствии со следующими правилами:
• Кросс обмен: обмен коэффициентами между двумя случайно выбранными объектами.
• Мутация: Добавление небольших значений в коэффициенты нейронных сетей.
4. Применение одной итерации градиентного метода для одной нейронной сети в соответствии с значениями коэффициентов на предыдущих итерациях.
Повторение шагов 2, 3 и 4 до тех пор, пока объектная функция не станет достаточно маленькой или не будет достигнуто максимальное количество итераций. Шаг 4 необходим только для гибридной комбинации генетических и градиентных алгоритмов.
Предложенная процедура позволяет избежать многих недостатков классических генетических алгоритмов, особенно их низкой скорости сходимости и наличия случайного фактора для точного попадания в точку минимума объектной функции. Предложенная процедура также позволяет избежать многих недостатков градиентных методов, таких как высокий уровень зависимости от начальных значений и нахождения локального минимума ближайшего к этим значениям.
Кроме классических методов обучения на основе градиентных и генетических алгоритмов для определения функций трансформации может быть использован метод настройки с возвращениями (backfitting), предложенным Breiman and Friedman (см. [3] Breiman, L. and J.H. Friedman, 1985, Estimating optimal transformations for multiple regression and correlation. Journal of the American Statistical Association 80, 580-78). Этот метод может быть применен только в сочетании с методом обратного распространения ошибки для определения входных и выходных массивов обучения для каждого т-нейрона. Метод предполагает следующий алгоритм определения функций трансформации для минимизации ошибки оператора вида описанной в формуле 2. Эта ошибка может быть описана следующим образом (формула 5).

где суммирование по М означает суммирование по всем обучающим парам. Для определения функций ƒi авторами предложен ниже описанный алгоритм. Этот алгоритм упрощен нами и также в оригинале предполагается определение функции трансформации для выходных значений у.
1. Процедура описывает определение функций трансформации только для одного т-нейрона и на входе процедуры задается массив обучения с парами входных векторов X=(х1,х2,х3,…,хn) соответствующих им выходных значений у. Xi означает все значения входа из массива обучения с номером i и Y все значения выходного параметра из массива обучения.
2. Инициализация функций ƒi нулями и нормализация всех выходных значений у в виде Y/||Y|| с E[Y]=0, где ||⋅||=[Е(⋅)2]1/2 и E(⋅) обозначает математическое ожидание.
3. Цикл 1 с проверкой уменьшения ошибки ε2 заканчивается, когда ошибка становится достаточно маленькой.
a. Цикл 2 по всем входам т-нейрона (k=0, 1…, n)
i. 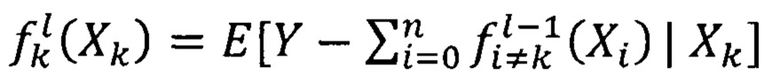
где верхний индекс l обозначает номер итерации.
Е[⋅|⋅] означает условное математическое ожидание.
b. Конец цикла 2.
4. Конец цикла 1.
Вычисление условного математического ожидания можно выполнять, например, по упрощенной процедуре - вычисление 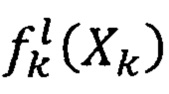 как среднего значения
как среднего значения 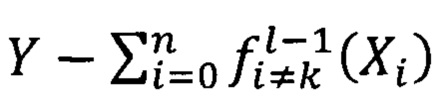 для всех пар из массива обучения, которые попали в интервал по входным значениям Хk±Δх, где заданный интервал.
для всех пар из массива обучения, которые попали в интервал по входным значениям Хk±Δх, где заданный интервал.
Основными отличиями предлагаемого т-нейрона от нейрона в вычислительной системе опубликованной в [4] ([4] US 2014/0379623 А1, опубликованной 25.12.2014, G06N 3/06, на 20-и листах, описание [0019], [0050], [0052], [0054]-[0055], [0089]-[0091]), является то, что:
1. Трансформация входного сигнала в [4] предлагается выполняется только на основе гладких вогнутых аналитически заданных функций [0019], [0050], [0052], [0054]-[0055], [0089]-[0091] и в одном случае [0072] используется табличная форма задания функции трансформации, но также со ссылкой на гладкие аналитические функции, как предварительно вычисленная таблица соответствия.
2. Подбор функции трансформации в [4] предлагается выполнять, включая табличную форму задания функции трансформации, на основе минимума и максимума распределения входной функции и не связан напрямую с требуемым выходом нейрона [0019], [0050], [0052], [0054]-[0055], [0089]-[0091] по сравнению с предлагаемым способом обучения в данной патентной заявке.
3. В предлагаемом методе основная цель трансформации входного сигнала, который не является импульсным как в [4], есть адаптация каждого входа нейрона к сложным много модальным вариациям входного сигнала и выполняется только на основе табличной формы задания функции трансформации.
4. Для определения функции трансформации предлагается использование гибридного способа обучения нейронной сети, на основе совместного использования генетических алгоритмов и градиентных методов обучения, что не используется в [4].
ПРИМЕР ФУНКЦИОНИРОВАНИЯ СИСТЕМЫ
Для проверки работоспособности предлагаемых нейронных сетей с использованием т-нейронов был использован тестовый набор данных, который был сгенерирован на основе вычислений различных функций. В частности, мы использовали следующую функцию для генерации тестового набора данных.
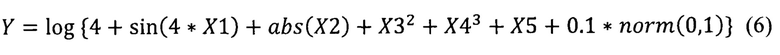
где Y значение для прогноза,
Х1,Х2,Х3,X4,Х5 - случайные числа, вычисленные с помощью генератора случайных чисел с использованием функции random(),
norm(0,1) случайная функция с распределением от 0 до 1.
С помощью формулы 6 были вычислены 100 значений Y и Х1,Х2,Х3,Х4,Х5 (набор данных 1), которые использовались как массив для обучения. Также еще были вычислены дополнительные 100 значений Y и X1,Х2,Х3,Х4,Х5 (набор данных 2), которые использовались как массив для проверки качества полученного в процессе обучения прогнозного оператора. Оба набора данных имеют сугубо нелинейную связь между входными данными X1,Х2,Х3,Х4,X5 и выходными данными Y.
Графики сравнение точного и прогнозного параметра Y для прогнозного оператора на основе алгоритма регрессии на основе нейронных сетей с использованием т-нейронов приведены на фиг. 5; слева график по набору данных 1, которые использовались для обучения и справа по набору данных 2, которые не использовались для обучения. Близкое к линейному соответствие точных и прогнозных функций с коэффициентами корреляции более 0.9 показывает удовлетворительную работоспособность предлагаемых нейронных сетей с использованием т-нейронов.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОДЕЛИРОВАНИЯ НЕЙРОНА | 2009 |
|
RU2402813C1 |
| ИСКУССТВЕННАЯ НЕЙРОННАЯ СЕТЬ | 2014 |
|
RU2573766C1 |
| АНАЛОГОВАЯ АППАРАТНАЯ РЕАЛИЗАЦИЯ НЕЙРОННЫХ СЕТЕЙ | 2020 |
|
RU2796649C2 |
| Способ определения оптической силы интраокулярной линзы с использованием искусственной нейронной сети | 2022 |
|
RU2791204C1 |
| СПОСОБ ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ | 2014 |
|
RU2566979C1 |
| СПОСОБ УПРАВЛЕНИЯ КОМПЬЮТЕРНОЙ СЕТЬЮ | 2014 |
|
RU2542901C1 |
| ЭКСПРЕСС-СПОСОБ ПРОГНОЗИРОВАНИЯ ПОЖАРООПАСНЫХ СВОЙСТВ ПРЕДЕЛЬНЫХ АЛЬДЕГИДОВ С ИСПОЛЬЗОВАНИЕМ МОЛЕКУЛЯРНЫХ ДЕСКРИПТОРОВ И ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ | 2018 |
|
RU2672268C1 |
| СПОСОБ ОБУЧЕНИЯ ИСКУССТВЕННОЙ НЕЙРОННОЙ СЕТИ | 2012 |
|
RU2504006C1 |
| СПОСОБ ОБРАБОТКИ ВЕКТОРНЫХ СИГНАЛОВ ДЛЯ РАСПОЗНАВАНИЯ ОБРАЗОВ НА ОСНОВЕ НЕЙРОННЫХ СЕТЕЙ С ДЕТЕКТИРОВАНИЕМ ВЫБРОСОВ | 2024 |
|
RU2830154C1 |
| Способ обучения искусственной нейронной сети | 2019 |
|
RU2723270C1 |

Изобретение относится к области вычислительных систем и может быть использовано для построения нейронных сетей для временного или пространственного прогноза параметров изучаемых объектов или распознавания образов. Техническим результатом является увеличение степени свободы отдельных нейронов и тем самым уменьшение глубины сети. Вычислительная система реализована на основе нейронной сети, которая включает хотя бы один нейрон, использующий функциональную трансформацию произвольного вида, заданной в виде таблицы (массива) пар соответствия входных данных и выходной функции для каждого входного сигнала с последующим их суммированием, при этом значения табличных функций трансформации подбираются стохастическим образом на основе генетического алгоритма при обучении нейронной сети. 1 з.п. ф-лы, 5 ил.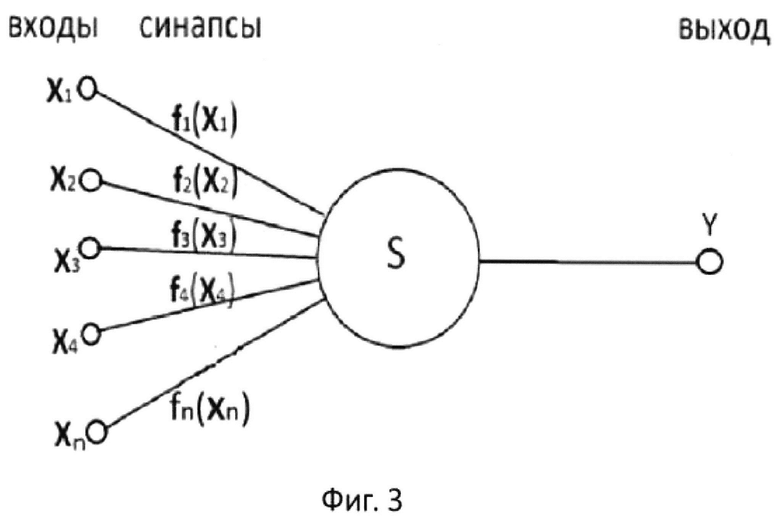
1. Вычислительная система на основе нейронной сети, которая включает хотя бы один нейрон, использующий функциональную трансформацию произвольного вида, заданной в виде таблицы (массива) пар соответствия входных данных и выходной функции для каждого входного сигнала с последующим их суммированием, отличающейся тем, что значения табличных функций трансформации подбирается стохастическим образом на основе генетического алгоритма при обучении нейронной сети.
2. Система по п. 1, отличающаяся тем, что табличные функции трансформации подбираются с помощью сочетания генетического алгоритма и градиентного алгоритма на основе метода настройки с возвращениями (backfitting) и обратного распространения ошибки.
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| US 5748847 A, 05.05.1998 | |||
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Устройство для затылования фрез | 1939 |
|
SU62314A1 |
Авторы
Даты
2020-07-17—Публикация
2018-05-10—Подача