Изобретение относится к нейрокибернетике и может быть использовано в искусственных нейронных сетях при решении различных задач логической обработки данных.
Логическая функция неравнозначности (или «сумма по модулю 2») входит в число двух линейно-неразделимых, т.е. нереализуемых классическими моделями нейронов [1], из полного набора 16 функций алгебры логики для двух переменных [1].
Известен способ реализации булевой функции неравнозначности от двух переменных x1 и x2 двухслойной сетью, содержащей два двухвходовых искусственных нейрона в первом слое и один во втором [1]. При этом при соответствующих настройках весовых коэффициентов и порогов нейроны первого слоя реализуют булевы логические функции «Запрет x1» и «Запрет x2» соответственно, а нейрон второго слоя - булеву функцию «ИЛИ». Возможен и другой вариант - два нейрона первого слоя реализуют функции «Штрих Шеффера» и «ИЛИ» соответственно, а нейрон второго слоя - функцию «И» [1]. Недостатком данного способа является необходимость использования трех нейронов, объединенных в два слоя, большое число и сложность настройки параметров (весовых коэффициентов и порогов), а также большое количество вычислительных операций. Известен другой способ реализации булевой функции неравнозначности одним нейроном высокого (второго) порядка [2]. В этом случае нейрон, кроме входов x1 и x2, имеет третий, дополнительный вход, на который подают произведение x1x2. При этом сумма s на выходе сумматора, описываемая s=(x1w1+x2w2+х1х2w3), где w1, w2, w3 - весовые коэффициенты, представляет собой полиномиальную (седловидную) поверхность как функцию от x1 и x2. Недостатком данного способа является наличие дополнительного входа у нейрона, а также достаточно большое количество вычислительных операций.
Наиболее близким по технической сущности к заявляемому способу является способ реализации логической функции неравнозначности моделью нейрона с двумя входами x1 и x2 [3], заключающийся в том, что входные сигналы x1 и x2, принимающие значения «0» или «1», перемножают с соответствующими весовыми коэффициентами w1 и w2, где w1=1, a w2=-1 (перемножители учитывают знаки сигналов), суммируют в знаковом сумматоре: s=x1w1+х2w2, затем сумму s преобразуют в активационном блоке модульной функцией активации вида
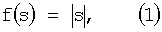
а затем пороговой функцией
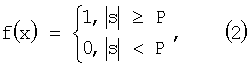
где Р - величина порога, Р=0.5;
f(x) - функция на выходе нейрона.
Последний изложенный способ [3] свободен от недостатков способов [1, 2], т.к. используется один нейрон невысокого (первого) порядка с двумя входами при минимуме вычислительных операций.
Предлагаемый способ направлен на расширение арсенала технических решений, положенных в основу функционирования искусственных нейронов [3], реализующих логическую функцию неравнозначности и свободных от указанных выше недостатков известных способов [1, 2]. Структурная схема устройства, функционирующего по предлагаемому способу, представлена на фиг.1.
Рассмотрим сущность предлагаемого способа. Как и в прототипе, входные сигналы двухвходового нейрона x1 и x2, принимающие непрерывные значения от «0» до «1», перемножают в перемножителях (блоки 1 и 2 фиг.1) с соответствующими весовыми коэффициентами w1 и w2, где w1=1, а w2=-1 и суммируют в сумматоре (блок 3 фиг.1): s=x1w1+x2w2. Перемножители и сумматор учитывают знаки величин.
Однако в отличие от прототипа сумму s преобразуют в активационном блоке сначала квадратичной функцией активации вида
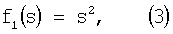
(блок 4 фиг.1), а затем пороговой функцией
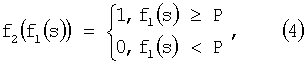
(блок 5 фиг.1) где Р - величина порога, определяемая как 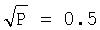 (чтобы положение разделяющих прямых было аналогично [3]), откуда Р=0.25.
(чтобы положение разделяющих прямых было аналогично [3]), откуда Р=0.25.
При этом получают следующую функцию на выходе нейрона: 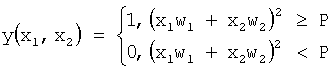 .
.
Проведенный сравнительный анализ заявленного способа и прототипа показывает, что заявленный способ отличается тем, что:
1) изменена операция преобразования сигнала s=x1w1+x2w2 функцией передачи f1(s), поскольку сигнал s преобразуется квадратичной функцией (3);
2) изменено условие преобразования сигнала f1(s) пороговой функцией (4), поскольку величина порога задается Р=0.25.
Рассмотрим предлагаемый способ реализации нейроном логической функции неравнозначности.
Требуемые выходные значения нейрона для реализации логической функции неравнозначности, в зависимости от предельных x1 и x2, приведены в таблице.
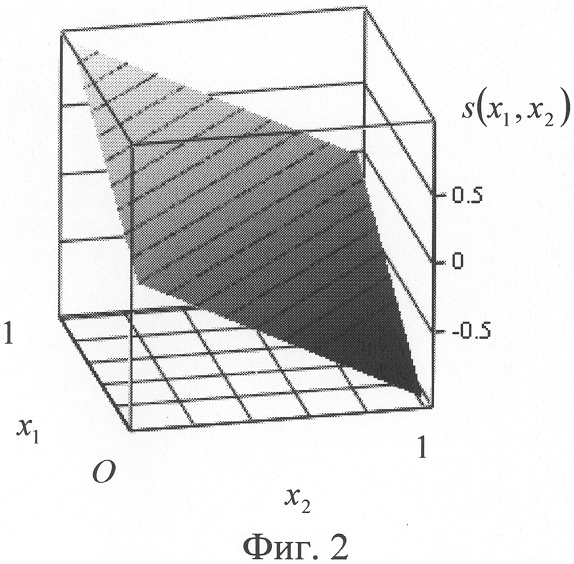
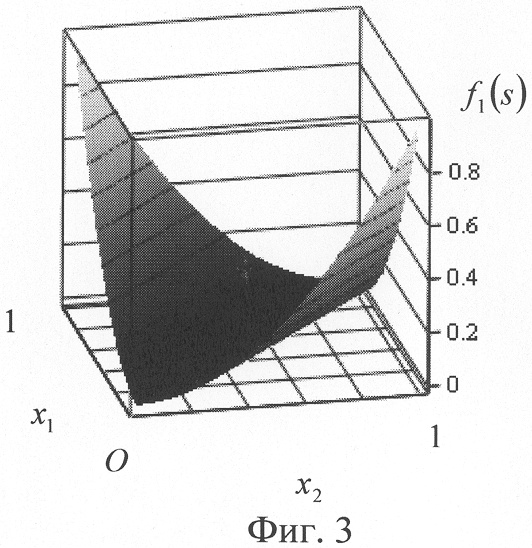
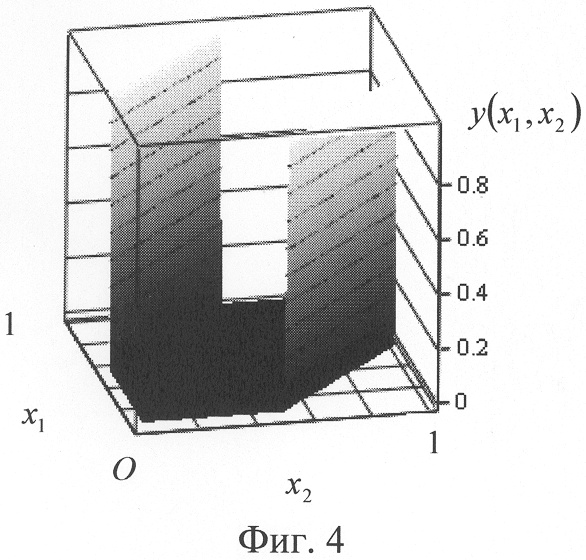
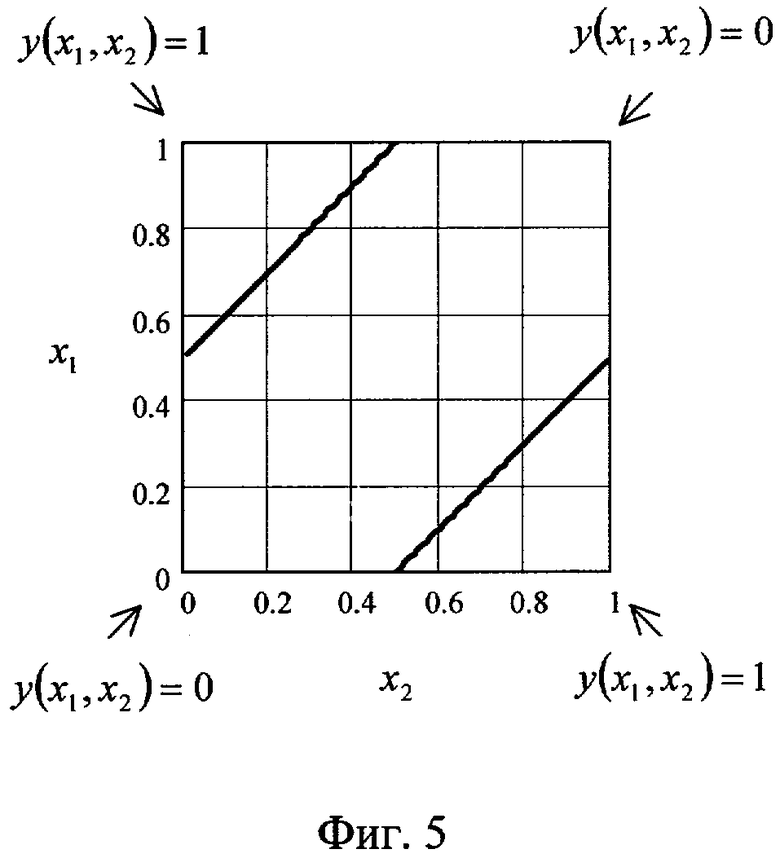
Как и в известном способе [3], входные сигналы двухвходового нейрона x1 и x2, принимающие значения от «0» до «1», перемножают с соответствующими весовыми коэффициентами w1 и w2, причем w1=1, а w2=-1. Перемножение осуществляется также с учетом знаков сигналов. Как и в известном способе [3], перемноженные сигналы x1w1 и x2w2 подают на вход знакового сумматора, где их суммируют: s=x1w1+x2w2. При этом сумма s как функция двух переменных (поверхность) от x1 и x2 над плоскостью входных значений 0x1x2 будет иметь вид, показанный на фиг.2. Предлагаемый способ отличается от прототипа тем, что сумму s с выхода сумматора сначала преобразуют квадратичной функцией активации (3), а затем преобразуют пороговой функцией (4). Результат преобразования s квадратичной функцией (3) показан на фиг.3, а результат ее подстановки в (4) при Р=0.25 - на фиг.4. При этом квадрат суммы как функция двух переменных x1 и x2 будет иметь вид не двух подповерхностей под некоторым углом между собой, как в прототипе [3], а квадратичной поверхности фиг.3. Если в этом случае квадрат суммы преобразовать пороговой функцией (4), т.е. ограничить плоскостью Px1x2, параллельной плоскости Ox1x2 и поднятой на величину порога Р=0.25, то пересечение квадратичной поверхности f1(s) с плоскостью Px1x2 будет образовывать также две разделяющие прямые, показанные на фиг.5. На фиг.5 стрелками к углам показаны получаемые для функции неравнозначности значения выхода нейрона y(x1, x2).
Таким образом, желаемый выход нейрона y(x1, x2), показанный на фиг.4, получают как результат подстановки квадрата суммы s в пороговую функцию (4). Математическая модель нейрона в этом случае будет описываться следующим выражением:
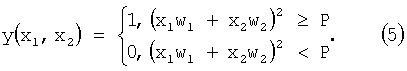
Рассмотрим математически образование двух разделяющих прямых на плоскости 0x1x2. Уравнение разделяющей гиперплоскости из выражения случаях: w1=1, w2=-1. Величина порога Р равна 0.25. Так как математическая модель нейрона имеет вид: 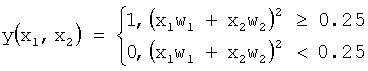 , то при подаче на его входы x1 и x2 сигналов, равных нулю, имеют нулевую сумму s (выход блока 3 фиг.1). Преобразуя сумму квадратичной функцией активации в блоке 4, получают нулевой сигнал на его выходе, как и после блока 5 на выходе y(x1, x2) нейрона. При поступлении на входы: x1=1, x2=0, получают сумму, равную единице; квадрат (выход блока 4) - также единице, что превышает порог Р=0.25 в блоке 5 и на выходе нейрона имеют единицу. При входной комбинации: x1=0, x2=1 сумму получают равной минус единице; квадрат - единице, что превышает порог Р=0.25 в блоке 5. Таким образом, получают единицу на выходе нейрона. В случае x1=1, x2=1 имеют нулевую сумму и соответственно, нуль на выходе нейрона.
, то при подаче на его входы x1 и x2 сигналов, равных нулю, имеют нулевую сумму s (выход блока 3 фиг.1). Преобразуя сумму квадратичной функцией активации в блоке 4, получают нулевой сигнал на его выходе, как и после блока 5 на выходе y(x1, x2) нейрона. При поступлении на входы: x1=1, x2=0, получают сумму, равную единице; квадрат (выход блока 4) - также единице, что превышает порог Р=0.25 в блоке 5 и на выходе нейрона имеют единицу. При входной комбинации: x1=0, x2=1 сумму получают равной минус единице; квадрат - единице, что превышает порог Р=0.25 в блоке 5. Таким образом, получают единицу на выходе нейрона. В случае x1=1, x2=1 имеют нулевую сумму и соответственно, нуль на выходе нейрона.
Таким образом, предлагаемый способ позволяет реализовать одним нейроном невысокого (первого) порядка логическую функцию неравнозначности.
Источники информации
1. Wasserman P. Neurocomputing. Theory and practice, Nostram Reinhold, 1990 (Рус. перевод: Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. / Пер. с англ. Ю.А.Зуев, В.А.Точенов. - М.: Мир, 1992. - 240 с.).
2. Терехов С.А. Нейросетевые информационные модели сложных инженерных систем // Сб. Нейроинформатика / А.Н.Горбань, В.Л.Дунин-Барковский, А.Н.Кирдин и др. - Новосибирск: Наука, Сибирская издательская фирма РАН, 1998. - 296 с.
3. Самойлин Е.А. Модель нейрона, реализующая логическую функцию неравнозначности // Патент РФ №2269155. Б.И. 2006. №3.
4. Галушкин А.И. Нейрокомпьютеры. Кн. 3: Учеб. пособие для вузов / Общая ред. А.И.Галушкина. - М.: ИПРЖР, 2000. - 528 с.
Изобретение относится к нейрокибернетике и может быть использовано в искусственных нейронных сетях при решении различных задач логической обработки двоичных данных. Техническим результатом является реализация одним нейроном первого порядка логической функции неравнозначности от двух переменных. Способ реализации нейроном с двумя входами логической функции неравнозначности основан на том, что входные сигналы перемножают с соответствующими весовыми коэффициентами и суммируют, после чего сумму преобразуют в активационном блоке сначала квадратичной функцией передачи, а затем пороговой функцией на выходе нейрона. 5 ил., 1 табл.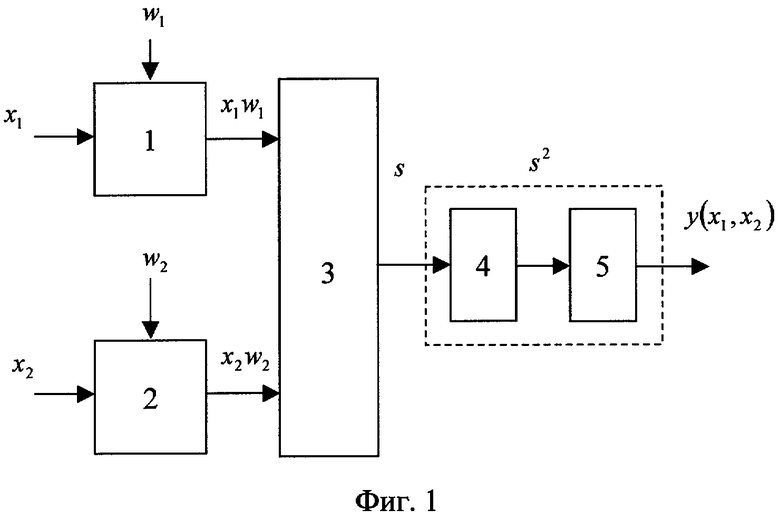
Способ реализации нейроном с двумя входами x1 и x2 логической функции неравнозначности, заключающийся в том, что входные сигналы x1 и x2, принимающие значения от "0" до "1", перемножают с соответствующими весовыми коэффициентами w1 и w2, где w1=1, a w2=-1, и суммируют в сумматоре, причем s∈[-1...1], где s - сумма на выходе сумматора, s=x1w1+x2w2, отличающийся тем, что сумму s преобразуют в активационном блоке сначала квадратичной функцией передачи вида f1(s)=s2, а затем пороговой функцией
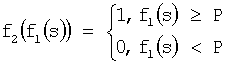 ,
,
где Р - величина порога, Р=0,25, f2(f1(s)) - функция, получаемая на выходе нейрона y(x1, x2), полное выражение которого
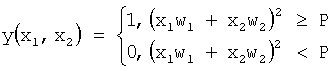 .
.
| Нейрокомпьютерная техника: теория и практика./ Пер | |||
| с анг | |||
| Ю.А.Зуев и др | |||
| - М.: Мир, 1992, с.240 | |||
| RU 94045263 A1, 20.10.1996 | |||
| МОДЕЛЬ НЕЙРОНА | 0 |
|
SU211168A1 |
| Многофункциональный логический модуль | 1979 |
|
SU790329A1 |
| US 6052679 A, 18.04.2000. | |||
Авторы
Даты
2007-10-20—Публикация
2006-04-12—Подача