ПРЕДПОСЫЛКИ ИЗОБРЕТЕНИЯ
Область техники, к которой относится изобретение
Изобретение связано с вычислительной обработкой данных и, более конкретно, относится к методу и устройству для сокращения числа операций с плавающей точкой, необходимых для извлечения целой и дробной компонент.
Уровень техники
Во многих системах обработки данных, существующих в настоящий момент, таких как персональные компьютеры (ПК), математические вычисления играют важную роль. Численные алгоритмы для вычисления значений многих математических функций, таких как операция возведения в степень и тригонометрические операции, требуют разложения чисел с плавающей точкой на соответствующие целые и дробные части. Такие операции могут использоваться для редукции аргументов, указателей к значениям таблицы или для построения результата из некоторого числа составных частей. Разложения чисел с плавающей точкой на целые и дробные части часто встречаются в критических вычислительных путях. В результате время на выполнение вычислений значений математических функций часто ограничено.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Настоящее изобретение иллюстрируется с помощью примера и не ограничивается приведенными поясняющими чертежами, в которых одинаковые ссылки обозначают одинаковые элементы. Необходимо отметить, что ссылки на "одну" или "некоторую" реализацию в данном описании не обязательно относятся к одной и той же реализации и подобные ссылки относятся, по меньшей мере, к одной реализации.
Фиг.1 иллюстрирует стандарт ANSI/IEEE 754-1985, стандарт IEEE для двоичной арифметики с плавающей точкой, IEEE, Нью-Йорк 1985 (IEEE) представление числа с плавающей точкой с одинарной точностью, представление с двойной точностью и представление с расширенной двойной точностью.
Фиг.2 изображает типовой способ вычисления целых чисел и чисел с плавающей точкой для некоторых равенств.
Фиг.3 иллюстрирует одну реализацию настоящего изобретения, в которой уменьшено число операций с плавающей точкой, необходимых для вычисления целой и дробной компонент.
Фиг.4 содержит одну реализацию изобретения, используемую для обобщения выбора константы S.
Фиг.5 иллюстрирует типовой процесс загрузки констант и вычисления необходимых коэффициентов для разложения чисел с плавающей точкой на целую и дробную части.
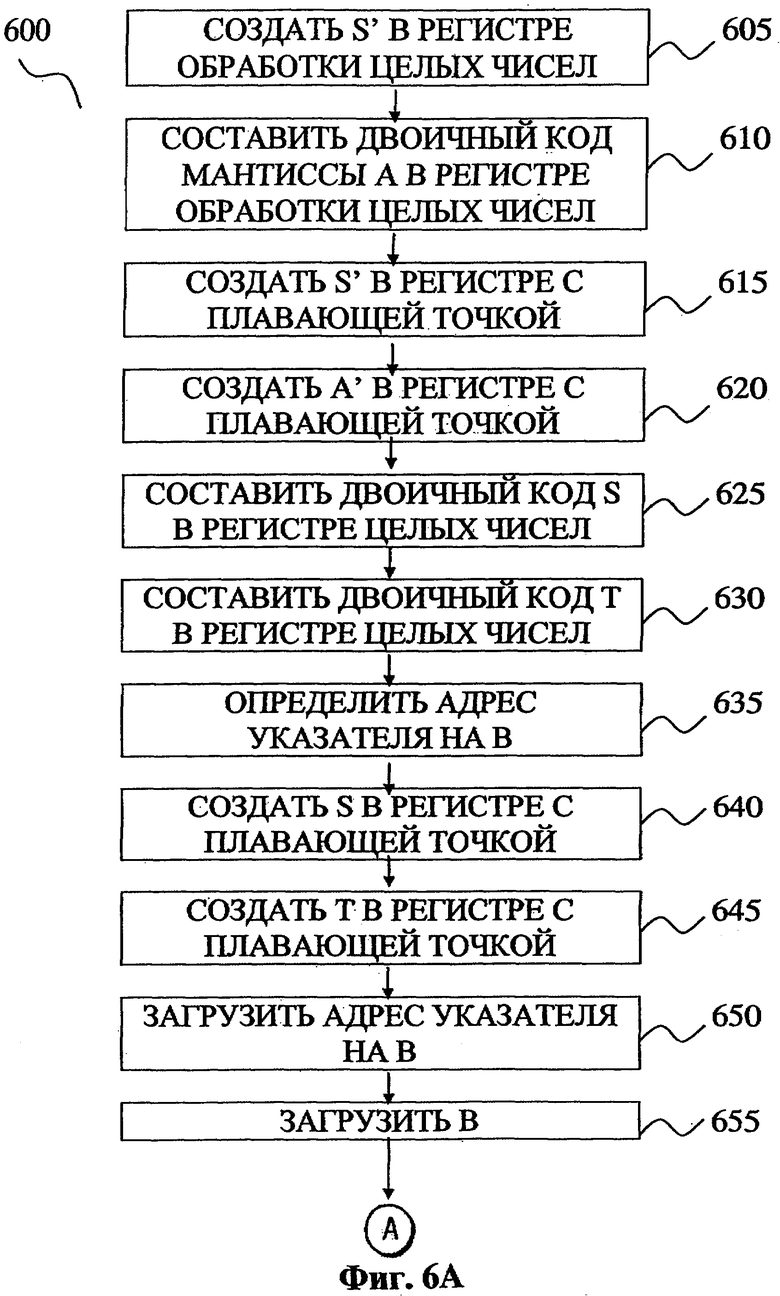
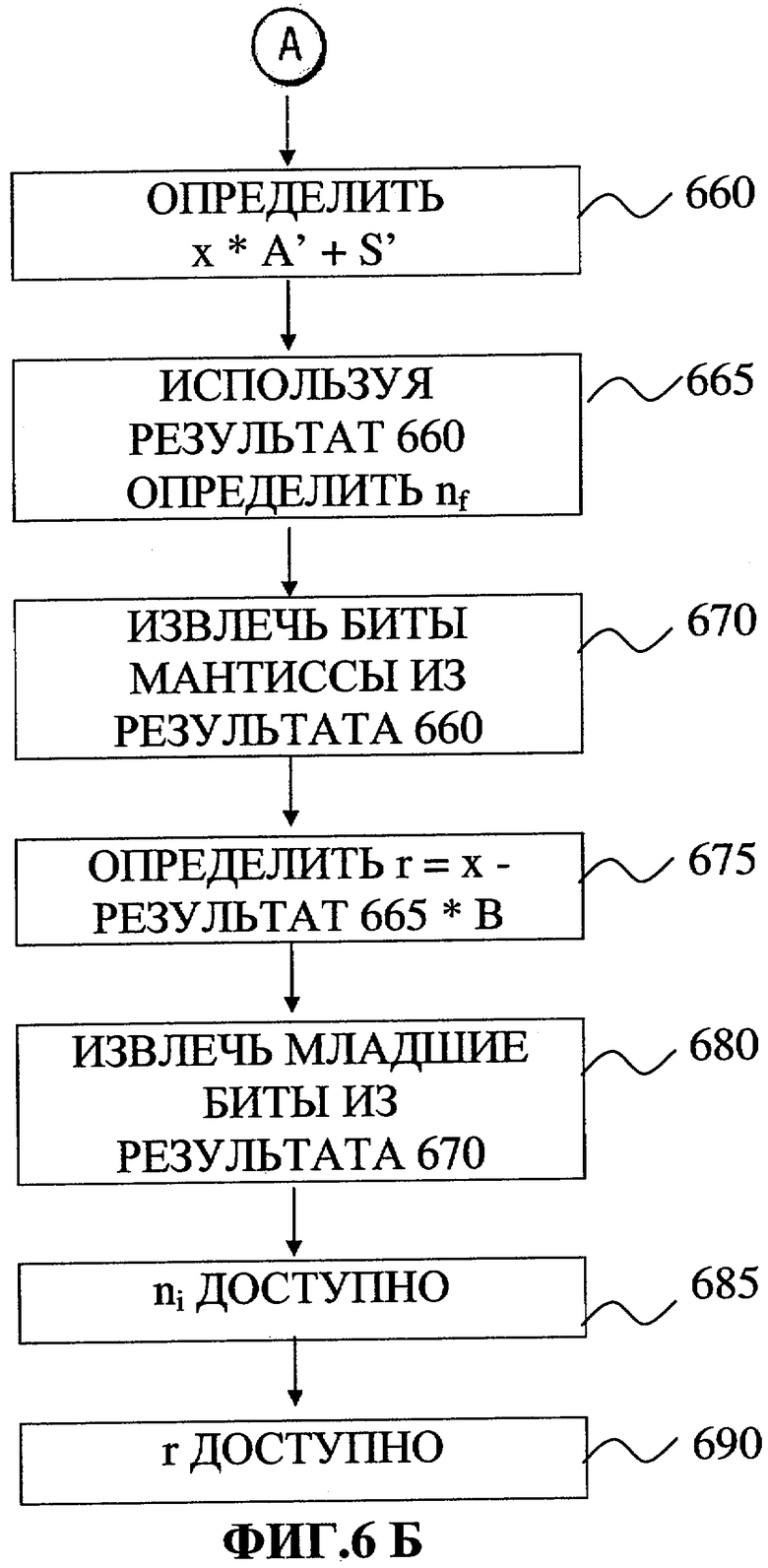
Фиг.6А-Б показывает некоторую реализацию изобретения для загрузки констант и осуществления разложения чисел с плавающей точкой на целую и дробную части.
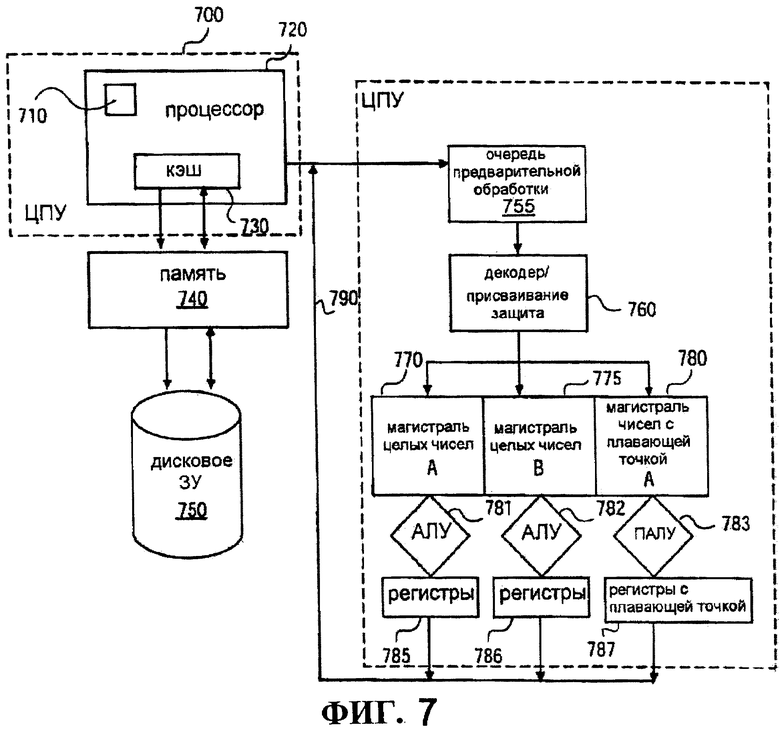
Фиг.7 показывает некоторую реализацию настоящего изобретения, имеющую вычислительную компоненту.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
В целом изобретение касается способа и устройства уменьшения числа операций с плавающей точкой, необходимых для вычисления целой и дробной компонент. Далее со ссылками на фигуры будут описываться типичные реализации настоящего изобретения. Типичные реализации выбраны для того, чтобы проиллюстрировать изобретение и они не должны рассматриваться в качестве какого-либо ограничения рамок изобретения.
Фиг.1 иллюстрирует стандарт ANSI/IEEE 754-1985, стандарт IEEE для двоичной арифметики с плавающей точкой, IEEE, Нью-Йорк 1985 (IEEE) изображения для представления 105 числа с плавающей точкой с одинарной точностью, представления 106 с двойной точностью и представления 107 с расширенной двойной точностью. Для представления 105 IEEE с одинарной точностью необходимо 32-битовое слово. Данное 32-битовое слово может быть представлено битами, пронумерованными слева направо (от 0 до 31). Первый бит, помеченный как S 110, является битом для знака. Следующие восемь бит, помеченные как Е 120, являются битами показателя степени. Последние 23 бита, с 9 по 31 бит, помеченные как F 110, служат для представления значащей части числа (также называемой мантиссой).
Для стандарта IEEE в представлении 106 числа с двойной точностью бит S 110 является битом для знака, биты Е 140 являются битами показателя степени (11 бит), и последние биты представления F 150 являются 52-ми битами представления значащей части числа (также называемой мантиссой).
Для стандарта IEEE в представлении 107 числа с двойной точностью бит S 110 является битом для знака, биты Е 160 являются битами показателя степени (15 бит), и последние биты представления F 170 являются 64-ми битами представления значащей части числа (также называемой мантиссой).
В качестве примера разложения чисел с плавающей точкой на целые и дробные части предлагаются следующие равенства, которые иллюстрируют один подобный пример:
Дано
w=х*А (равенство 1),
где А=1/В (равенство 2).
Найти n и r такие, что х=n*B+r (равенство 3),
где n является целым числом, а А, В, r и w - числа с плавающей точкой. Таким образом задачу можно переформулировать так: для заданных входного числа х и констант А и В надо найти число n такое, что число В ровно n раз "умещается" в числе х и какой при этом получается остаток? Более того, n часто используется в качестве указателя для поиска в таблице или в качестве показателя степени некоторой величины, такой как 2n. Следовательно, необходимо представлять число n и как целое число (ni), и как число с плавающей точкой (nf). Таким образом, после вычислений необходимо получить три величины: ni (n как целое число), nf (n как число с плавающей точкой) и r в виде числа с плавающей точкой.
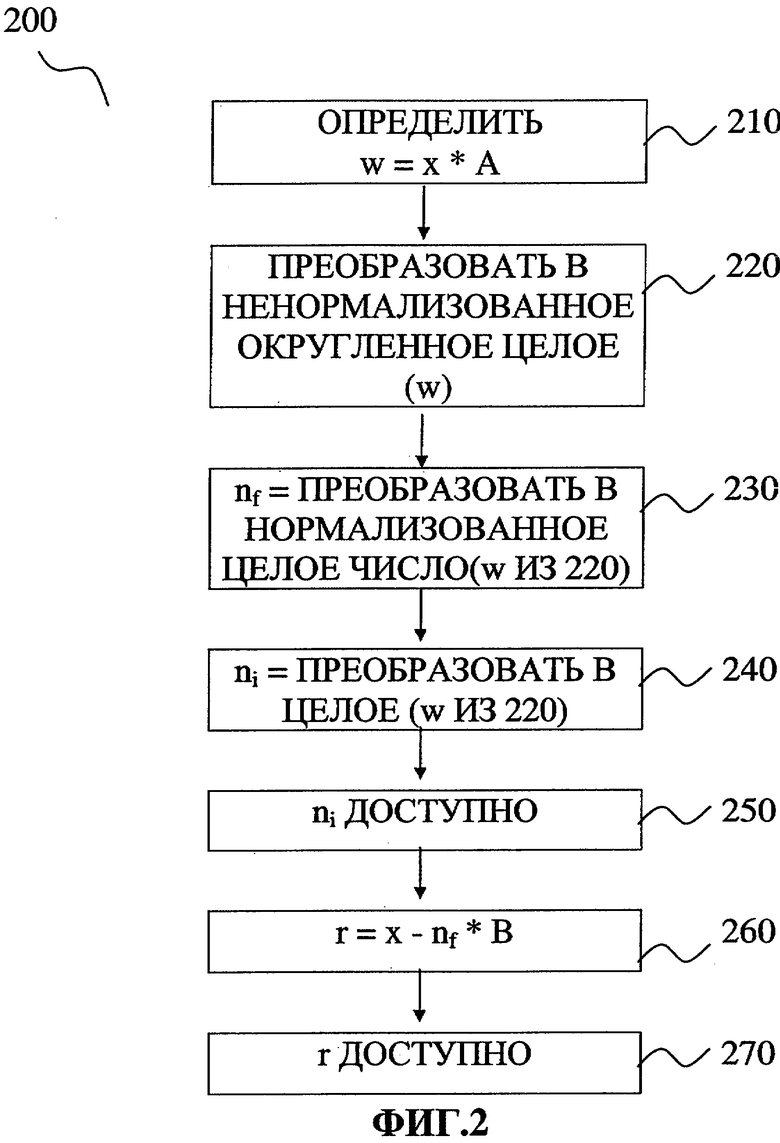
Фиг.2 изображает типовой способ вычисления ni, nf и r. На фиг.2 процесс 200 начинается с блока 210, где w=х*А. В блоке 220 число w преобразуется в ненормализованное целое число, полученное после округления. Значение, вычисленное в блоке 220, затем используется в блоке 230 для вычисления nf посредством его нормализации как целого числа. В блоке 240 также используется значение из блока 220: преобразуя значение из блока 220 в целое число, вычисляется число ni. В блоке 250 полученное значение ni пересылается в арифметико-логическое устройство (АЛУ) или сохраняется в памяти. В блоке 260 вычисляется число r: из числа х вычитается значение nf*В. В блоке 270 значение r можно пересылать в АЛУ или сохранять в памяти.
Таблица I иллюстрирует типовой способ вычисления ni, nf и r в терминах команд псевдокода. Как видно из Таблицы I, существует три операции с плавающей точкой, которые выполняются устройством арифметических и логических операций с плавающей точкой (Палу), и одна операция с целыми числами, выполняемая устройством арифметических и логических операций с целыми числами (Цалу). Заметим, что числа в круглых скобках являются общими количествами тактов работы при выполнении команд (задержка) для процессора, такого как процессор Intel Itanium™.
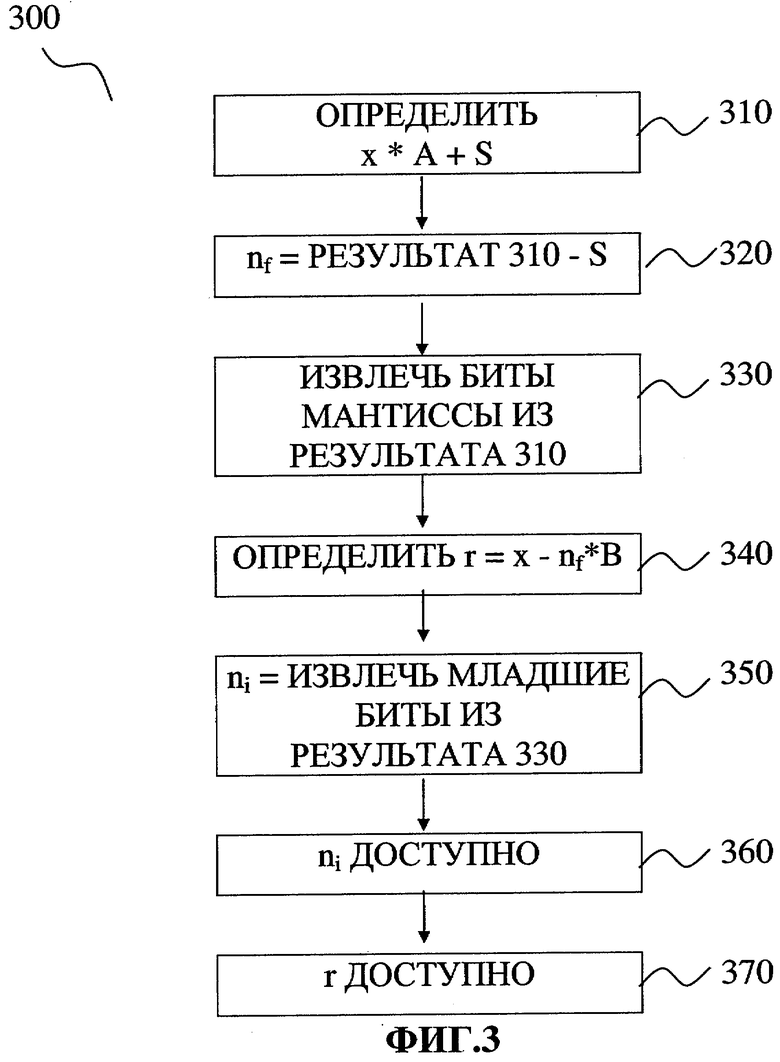
Фиг.3 иллюстрирует одну реализацию настоящего изобретения, в которой уменьшено число операций с плавающей точкой, необходимых для вычисления ni, nf и r. Процесс 300 начинается в блоке 310, в котором вычисляется величина x*A+S, где S и А являются константами, а х - число с плавающей точкой. В одной реализации изобретения константа S выбирается так, чтобы прибавление числа S к числу х*А сдвигает округленную целую часть числа х*А в крайние правые биты мантиссы. Затем в блоке 320 вычисляется nf посредством вычитания S из значения, вычисленного в блоке 310. Таким образом получается целое число. В блоке 330 получается ni+S следующим образом: извлекаются биты мантиссы из результата блока 310. В блоке 340 вычисляется значение r: из х вычитается величина nf*В. В блоке 350 из значения, вычисленного в блоке 330, извлекаются младшие биты и получается значение ni. В блоке 360 значение ni доступно готово для передачи в АЛУ или для сохранения в памяти. В блоке 370 значение r доступно для передачи в АЛУ или для сохранения в памяти.
Таблица II иллюстрирует реализацию настоящего изобретения в виде команд псевдокода, причем в данной реализации уменьшено число операций с плавающей точкой. Заметим, что в качестве примера приведены числа в круглых скобках, которые являются общими количествами тактов работы при выполнении команд (задержка) для процессора, такого как процессор Intel Itanium™. В одной реализации изобретения константа S выбирается так, чтобы прибавление числа S к числу х*А сдвигает округленную целую часть числа х*А в крайние правые биты мантиссы. Таким образом S можно преобразовать в целое число ni после одной операции Палу вместо двух. Более того, представление с плавающей точкой nf может быть непосредственно получено с помощью второй операции Палу: вычитание S из результата первой операции Палу. Таким образом при получении необходимых величин используется на одну команду Палу меньше. Таким образом, реализация изобретения выливается в экономию семи тактов работы процессора, такого как процессор Intel Itanium™.
Выгода в производительности нарастает при использовании данной реализации изобретения в циклах программных продуктов. Многие циклы ограничены количеством команд с плавающей точкой, требуемых для вычислений. Так как данная реализация изобретения предполагает на одну операцию с плавающей точкой меньше, по сравнению с типовым методом, то максимальная производительность цикла увеличивается.
Дальнейшее обсуждение относится к выбору константы S в одном варианте осуществления изобретения. Для простоты предположим, что представление с плавающей точкой содержит b бит мантиссы (например, 64 бита), явный целый бит и b-1 бит дробной части. Поле показателя степени представления числа с плавающей точкой определяет положение двоичной точки внутри или вне значащих цифр. Таким образом целая часть нормализованного числа с плавающей точкой - это крайние справа биты мантиссы после применения операции обратной нормализации, которая сдвигает b-1 бит мантиссы вправо, округляет мантиссу и прибавляет b-1 к показателю степени. Мантисса содержит целые числа как последовательность b бит, являющуюся дополнением до 2. Младшие биты мантиссы, содержащие целую часть первоначального числа с плавающей точкой, могут быть получены с помощью прибавления к числу константы 1.10...000*2b-1. Данная константа является одним из значений S, выбранных в одной из реализации настоящего изобретения.
Результирующая мантисса содержит целое число в виде (b-2) бит, являющихся дополнением до 2. Бит, находящийся сразу левее b-2-x нулей в значащей части, используется для того, чтобы для отрицательных чисел убедиться, что результат не был повторно нормализован, тем самым, сдвигая целое число левее от требуемого положения в самом правом бите мантиссы. Если в последующих операциях с целыми числами используется менее b-2 бит, то команды для вычисления ni, nf и r в Таблице II эквивалентны соответствующим командам из Таблицы I.
В одной реализации изобретения выбор числа S может быть обобщен, если требуемый результат должен быть равен m, где m=n*2k. В этом случае показатель степени константы будет равен (b-k-1). В данной реализации выбор S полезен тогда, когда искомое целое число необходимо разделить на множества индексов для поиска в таблице с несколькими входами. Например, число n может быть разбито следующим образом n=n0*27+n1*24+n2 для того, чтобы вычислить индексы для доступа в таблицы с 16 и 8 входами. Для данной реализации необходимо, чтобы число S было доступно тогда же, когда и константа А. В одной реализации изобретения константу S можно загружать из памяти или для процессоров, таких как Intel Itanium™, S можно легко вычислить с помощью следующих команд: 1) movI для 64-битового IEEE двоичного кода двойной точности, 2) setf.d для загрузки S в регистр для работы с числами с плавающей точкой.
В одной реализации настоящего изобретения константа может иметь следующую форму: "1", за ней десятичная точка, j-1 бит (нули или единицы) сразу справа от десятичной точки, "1" за указанными j-1 битами, а затем b-j-1 бит нулей. Заметим, что реализация, описываемая раньше, содержала константу той же формы c j=1.
Последующее обсуждение относится к реализации данного изобретения, включающего порождение констант, необходимых для вычисления ni, nf и r. Требования алгоритмов математической библиотеки к точности обычно подразумевают, что умножение w=x*A выполняется для представлений с расширенной двойной точностью (64 битовое пространство мантиссы). Таким образом константа А при загрузке должна иметь представление с расширенной двойной точностью. Обычно это достигается следующим образом: константа сохраняется статично в памяти, а затем загружается в регистр для работы с числами с плавающей точкой (например, команда ldfe для процессора Intel Itanium™).
Из-за требования того, что библиотека должна располагаться независимо (то есть быть совместно используемой) загрузка выполняется с помощью косвенной загрузки. При данной косвенной загрузке сначала вычисляется адрес указателя на константу, затем загружается указатель на константу, а затем загружается константа. Для процессора, такого как Intel Itanium™, такая последовательность выполняется как минимум 13 тактов. Эта последовательность действий может потребовать более 13 тактов в случае, если указатель и константы не находятся в кэш-памяти.
Для некоторых процессоров, таких как Intel Itanium™, не существует способа прямой загрузки константы расширенной двойной точности без использования команд памяти. Тем не менее, существует способ прямой загрузки мантиссы константы с плавающей точкой: сначала формируется 64-битная мантисса в регистре для работы с целыми числами, а затем используется команда (например, set.sig для процессора Intel Itanium™) для загрузки мантиссы в регистр с плавающей точкой. Подобная команда устанавливает значение показателя степени в 263. Для процессора, такого как Intel Itanium™, такая последовательность выполняется за 10 тактов. В одной реализации изобретения три такта можно сохранить, используя константу S, имеющую правильную мантиссу, но измененный показатель степени.
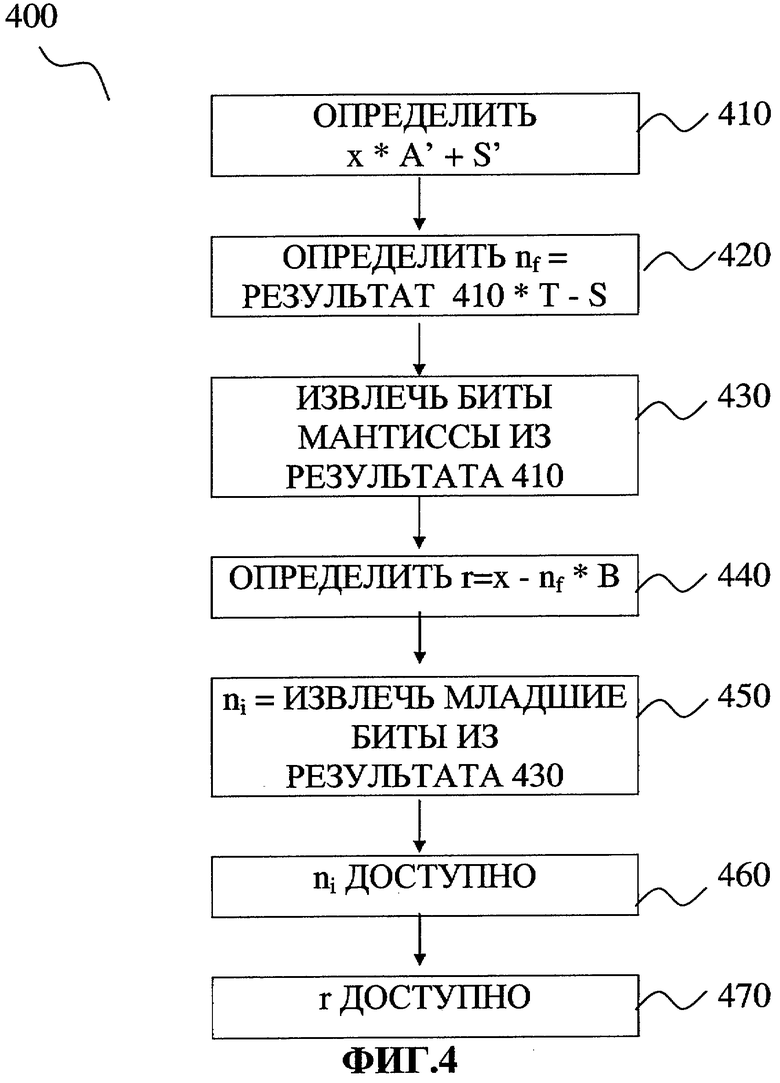
Фиг.4 иллюстрирует одну реализацию изобретения, используемую для обобщения выбора константы S при определении ni, nf и r. В процессе 400 в блоке 410 вычисляется результат х*А'+S' (где S' - это вариант S, который будет обсуждаться ниже). В блоке 420, с использованием результата блока 410, производится умножение результата блока 410 на Т (Т - это множитель, равный 2-(b-1-j)), и из полученного результата вычитается S. В блоке 430 биты мантиссы извлекаются из результата блока 410, таким образом получается целое число. В блоке 440 вычисляется r, а именно вычисляется выражение x-nf*B. В блоке 450 из результата блока 430 извлекаются младшие биты. В блоке 460 значение ni доступно для передачи в АЛУ или для сохранения в памяти. В блоке 470 значение r доступно для передачи в АЛУ или для сохранения в памяти. В процессе 400 величина А равна 2j*F, где F - это мантисса вида 1.xxxxxxxx, 1.0≤|F|<2.0. Также A'=2b-1*F.
Таблица III содержит псевдокоды шагов для процесса 400, показанного на фиг.4.
В одной реализации изобретения для того, чтобы сдвиг происходил корректно, при выполнении команды Палу опер. 1 необходим вариант числа S - число S', где S'=S*2b-1-j. При получении nf во время выполнения Палу опер. 2 число w_плюс_S_сдвинутвправо масштабируют "обратно" с помощью множителя Т, где Т=2-(b-1-j). В данной реализации изобретения генерируются четыре константы: A', S', S и Т. В одной реализации изобретения данные четыре константы задаются параллельно.
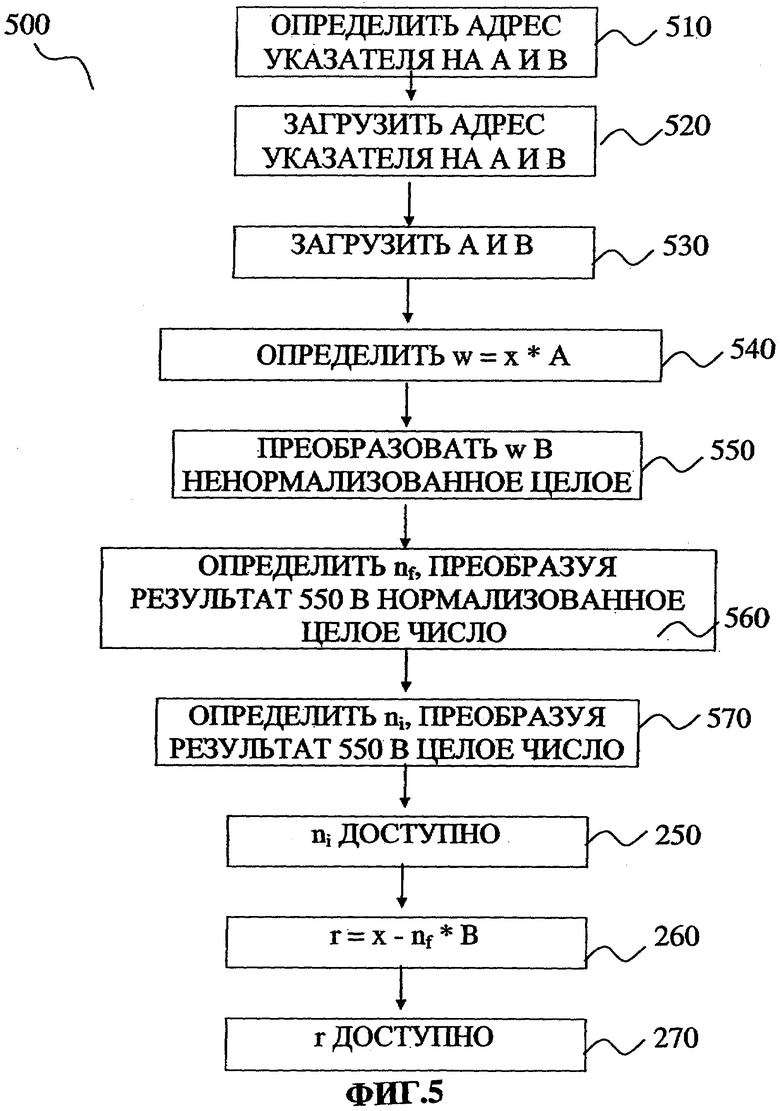
Фиг.5 иллюстрирует типовой процесс 500 загрузки констант и вычисления коэффициентов для разложения чисел с плавающей точкой на целую и дробную части. На обычном процессоре, таком как Intel Itanium™, вся последовательность действий от загрузки констант для вычисления r требует 36 тактов. Процесс 500 начинается в блоке 510, в котором вычисляется адрес указателя на А и В. В блоке 520 загружаются адреса указателя на А и В. В блоке 530 загружаются А и В. В блоке 540 вычисляется значение w=x*A. В блоке 550 результат из блока 540 (число w) преобразуется в ненормализованное целое число. В блоке 560 результат блока 550 нормализуется как целое число и получается nf. В блоке 570, преобразуя значение из блока 550 в целое число, вычисляется число ni. В блоке 580 полученное значение ni доступно для передачи в АЛУ или сохранения в памяти. В блоке 590 вычисляется число r: из числа х вычитается значение nf * В. В блоке 595 значение r доступно для передачи в АЛУ или сохранения в памяти.
Таблица IV иллюстрирует процесс 500 в командах псевдокода. Числа в правой части Таблицы IV представляют собой обычные такты для процессора, такого как Intel Itanium™.

Фиг.6А-Б показывает некоторую реализацию изобретения для загрузки констант и осуществления разложения чисел с плавающей точкой на целую и дробную части. Процесс 600 начинается с блока 605, в котором в регистре для работы с целыми числами формируется двоичный код S'. В блоке 610 в регистре для работы с целыми числами формируется двоичный код мантиссы А. В блоке 615 в регистре с плавающей точкой генерируется S'. В блоке 620 в регистре с плавающей точкой генерируется А'. В блоке 625 в регистре для работы с целыми числами формируется двоичный код для S. В блоке 630 в регистре для работы с целыми числами формируется двоичный код для Т. В блоке 635 вычисляется адрес указателя на В. В блоке 640 в регистре с плавающей точкой генерируется S. В блоке 645 в регистре с плавающей точкой генерируется Т. В блоке 650 загружается адрес указателя на В. В блоке 655 загружается В. В блоке 660 вычисляется x*A'+S'. В блоке 665 производится умножение результата блока 660 на Т и из полученного значения вычитается S. Результатом операций, проводимых в блоке 665, является nf. В блоке 670 биты мантиссы извлекаются из результата блока 660, таким образом получается целое число. В блоке 675 вычисляется r, а именно: вычисляется выражение х-nf*В. В блоке 680 из результата блока 670 извлекаются младшие биты. Результатом операций, проводимых в блоке 680, является ni. В блоке 685 значение ni становится доступным для передачи в АЛУ или для сохранения в памяти. В блоке 690 значение r становится доступным для передачи в АЛУ или для сохранения в памяти.
Таблица V содержит псевдокоды шагов для процесса 600 (смотри фиг.6А-Б). Заметим, что числа в правой части Таблицы V, которые заключены в скобки, представляют такты процессора, такого как Intel Itanium™. В одной реализации настоящего изобретения процесс 300 и процесс 600 загружаются в математические библиотеки, которыми пользуются различные компиляторы. В другой реализации изобретения те же процессы, загруженные в математическую библиотеку, могут использоваться для вычисления функций, таких как скалярный с двойной точностью тангенс, синус, косинус, экспоненциальные функции, гиперболический косинус, гиперболический синус, гиперболический тангенс и так далее. Использование данной реализации позволяет уменьшить число тактов, необходимых для выполнения операций по сравнению с методами, существующими в настоящий момент. Необходимо заметить, что другие реализации данного изобретения могут использоваться для обработки функций, таких как скалярные функции одинарной точности, векторные функции двойной точности и векторные функции одинарной точности.
Фиг.7 показывает некоторую реализацию настоящего изобретения, имеющую вычислительную компоненту 710. Схема 700 также содержит микропроцессор 720, кэш-память 730, память 740, дисковое запоминающее устройство 750, очередь предварительной выборки 755, декодер/присваивание/экстраполятор 760, магистраль для целых чисел А 770, магистраль для целых чисел В 775, магистраль для чисел с плавающей точкой А 780, АЛУ 781-782, АЛУ для плавающей точки 783, наборы регистров для целых чисел 785-786, набор регистров для плавающей точки 787 и шину данных 790. В одной реализации настоящего изобретения вычислительная компонента 710 включает в себя процессы 300, 400 или 600, проиллюстрированные на фиг.3, 4 и 6А-Б соответственно.
Упомянутые выше реализации изобретения могут быть использованы всякий раз, когда целые и дробные компоненты чисел с плавающей точкой необходимы для выполнения редукции аргументов скалярных и векторных функций с двойной точностью, скалярных и векторных функций с одинарной точностью, различных математических функций и предварительной обработки перед вычислением математических функций. При использовании описанных выше вариантов осуществления изобретения уменьшается время вычислений без отрицательного влияния на точность результата.
Указанные выше реализации также могут храниться на устройстве или машинно-считываемом носителе и считываться машиной для выполнения команд. Машинно-считываемые носители включают в себя любые механизмы, которые содержат (то есть хранят и/или передают) информацию, которая может быть считана машиной (например, компьютером). Например, машинно-считываемый носитель может быть постоянным запоминающим устройством (ROM); оперативным запоминающим устройством или памятью с произвольным доступом (RAM); накопителем на магнитных дисках; оптическим диском; флэш-памятью; электрическим, оптическим, звуковым сигналом или любой другой формой распространяемого сигнала (например, несущие волны, инфракрасные сигналы, цифровые сигнала и так далее). Устройство или машинно-считываемый носитель может быть полупроводниковым устройством памяти и/или вращающимся магнитным или оптическим диском. Устройство или машинно-считываемый носитель может быть распределенным, когда части команд разделены между различными машинами, например между соединенными в сеть компьютерами.
Несмотря на то, что некоторые типичные реализации описаны и показаны на сопровождающих чертежах, необходимо понять, что такие реализации являются лишь иллюстрациями и не ограничивают рамки изобретения, и что данное изобретение не ограничивается конкретными структурами и конструкциями, здесь показанными и описанными, так как специалист в соответствующей области может предложить множество других модификаций.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПРЕОБРАЗОВАНИЕ ИЗ ЗОННОГО ФОРМАТА В ДЕСЯТИЧНЫЙ ФОРМАТ С ПЛАВАЮЩЕЙ ТОЧКОЙ | 2012 |
|
RU2565508C2 |
| ПРЕОБРАЗОВАНИЕ В ЗОННЫЙ ФОРМАТ ИЗ ДЕСЯТИЧНОГО ФОРМАТА С ПЛАВАЮЩЕЙ ТОЧКОЙ | 2012 |
|
RU2560796C2 |
| Преобразователь комплексных сигналов | 1983 |
|
SU1104525A1 |
| ЭФФЕКТИВНАЯ ПАРАЛЛЕЛЬНАЯ ОБРАБОТКА ИСКЛЮЧЕНИЯ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ В ПРОЦЕССОРЕ | 2009 |
|
RU2427897C2 |
| УСТРОЙСТВО ДЕЛЕНИЯ И ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ | 2012 |
|
RU2510072C1 |
| СИСТЕМА ПЕРЕДАЧИ, ТЕРМИНАЛЬНЫЙ БЛОК, КОДИРУЮЩЕЕ УСТРОЙСТВО, ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО И АДАПТИВНЫЙ ФИЛЬТР | 1994 |
|
RU2138030C1 |
| СИСТЕМА ПЕРЕДАЧИ, ТЕРМИНАЛЬНЫЙ БЛОК, КОДИРУЮЩЕЕ УСТРОЙСТВО, ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО И АДАПТИВНЫЙ ФИЛЬТР | 1994 |
|
RU2123728C1 |
| ЦЕЛОЧИСЛЕННОЕ УМНОЖЕНИЕ ВЫСОКОГО ПОРЯДКА С ОКРУГЛЕНИЕМ И СДВИГОМ В АРХИТЕКТУРЕ С ОДНИМ ПОТОКОМ КОМАНД И МНОЖЕСТВОМ ПОТОКОВ ДАННЫХ | 2003 |
|
RU2263947C2 |
| ПРОЦЕССОРЫ, СПОСОБЫ, СИСТЕМЫ И КОМАНДЫ ДЛЯ СЛОЖЕНИЯ ТРЕХ ОПЕРАНДОВ-ИСТОЧНИКОВ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ | 2014 |
|
RU2656730C2 |
| Устройство для умножения чисел в модулярной системе счисления | 1986 |
|
SU1352483A1 |
Изобретение относится к обработке данных, более конкретно к методу и устройству для сокращения числа операций с плавающей точкой, необходимых для извлечения целой и дробных компонент. Техническим результатом является уменьшение времени вычислений без отрицательного влияния на точность результата. Указанный результат достигается за счет того, что заявленное устройство содержит вычислительную компоненту, которая генерирует первую константу, второе значение с помощью сдвига округленной целой части значения с плавающей точкой, величину с плавающей точкой путем вычитания первой константы из величины с плавающей точкой, извлекает множество битов мантиссы из второго значения для генерирования целого значения, генерирует остаточное значение из величины с плавающей точкой, извлекает часть бит из целого значения с целью получения целой компоненты, сохраняет остаточное значение, целую компоненту и величину с плавающей точкой в памяти. 7 н. и 18 з.п. ф-лы, 5 табл., 8 ил.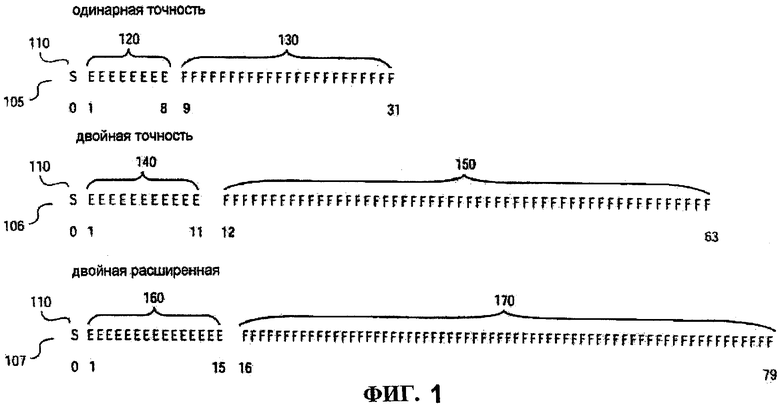
| US 6205460 В1, 20.03.2001 | |||
| SU 1546964 A1, 28.02.1990 | |||
| Арифметическое устройство с плавающей точкой | 1985 |
|
SU1259248A1 |
| Устройство для обработки данных | 1987 |
|
SU1513443A1 |
| Устройство для округления суммы и разности двоично-кодированных чисел с плавающей запятой | 1986 |
|
SU1361542A1 |
| US 6038528 A, 14.03.2000 | |||
| US 5940311 A, 17.08.1999. | |||
Авторы
Даты
2006-05-20—Публикация
2001-07-13—Подача