Изобретение относится к области измерения индукции магнитного поля с помощью феррозондовых трехкомпонентных магнитометров, устанавливаемых в труднодоступных местах.
Примером таких измерений служат измерения магнитного поля корабля с помощью множества (18-30 шт., позднее 2-4 шт.) датчиков, размещаемых на дне моря в линию перпендикулярно курсу корабля на расстоянии 3-6 м друг от друга. Линейка таких датчиков входит в состав магнитоизмерительного стенда. Специфической особенностью стенда является то, что одноименные магниточувствительные оси разных датчиков должны совпадать в пределах заданного углового допуска. Процедура углового выравнивания одного датчика относительно другого представляет собой сложную инженерно-техническую задачу, особенно если датчики располагаются в труднодоступных местах, например на дне моря на глубине 7-50 м. До 1970 г. во всем мире применялись стенды из однокомпонентных датчиков на кардановых подвесах. Их называли стендами первого поколения. Такие стенды применялись только потому, что с ними не возникало проблем ориентации однокомпонентных датчиков по вертикали, но однокомпонентные измерения не обеспечивали достаточной надежности контроля намагниченности кораблей. После 1970 г.в мире стали строиться стенды второго поколения из трехкомпонентных датчиков на кардановых подвесах. В работе [Marshall, B.J., Operational Aspects of Magnetic Measurement Ranges. Сравнительные характеристики магнитоизмерительных стендов. Naval Forces, 1989, v.10 #2, рр.72-78] отмечается, что капитальные затраты на установку линии датчиков оказываются велики из-за сложного и длительного монтажа и геодезической съемки, а стоимость подводных работ, связанная с установкой/ориентацией трехкомпонентных датчиков, составляет значительную часть стоимости затрат за весь срок службы магнитоизмерительного стенда второго поколения. В статье [Matthews, D.C., Contemporary degaussing measuring ranges. Современные магнитоизмерительные стенды для размагничивания. Maritime Defence, 1979, v.4 December #12, pp.499-503] говорится, что наименьшая погрешность, которую можно ожидать при установке водолазами с компасами датчиков транспортируемых стендов, составляет ±5°, тогда как требуемое угловое рассогласование датчика относительно осей опорной системы координат (СК) должно быть не хуже 35'. Вместе с тем, в статье [Improving weapon sensors calls for more care in degaussing. Совершенствование оружия требует большей тщательности дегауссинга (размагничивания кораблей). Maritime Defence, 1989, v.14, #2, рр.44-45] утверждается, что современные феррозонды обладают чувствительностью по углу в две секунды. Из этого следует, что точностные возможности современных трехкомпонентных феррозондов недоиспользуются почти на четыре порядка (5°/2″) из-за сложностей монтажа/согласования подводных датчиков на магнитоизмерительных стендах.
Известен способ согласования трехкомпонентных датчиков магнитоизмерительного стенда, разработанный фирмой Dowty Defence&Air Systems [An improved method of placing harbour ranges. Улучшенный метод монтажа стендов в портах. Maritime Defence 1989, v.14, #2, рр.42-43]. Способ основан на встроенном устройстве ориентации по азимуту, позволяющем водолазу ориентировать датчик без помощи с берега. Кардановый подвес отрабатывает начальные рассогласования по вертикали до ±20°.
Известен также способ углового согласования датчиков трехкомпонентных магнитометров на кардановых подвесах (Патент №2256188, заявка №2003110478/09, приоритет от 07.04.2003). Способ относится к стендам второго поколения. По данному способу магнитометры предварительно настраивают на берегу, затем устанавливают по месту и приближенно ориентируют вдоль геомагнитной СК. В зоне стенда временно устраняют неоднородные магнитные поля сторонних источников, измеряют магнитное поле Земли всеми магнитометрами, а также местное склонение. По результатам измерений строят матрицы углового согласования каждого магнитометра с опорным, опорного магнитометра с геомагнитной СК и геомагнитной СК с географической. Последующие результаты измерения умножают на поправочные матрицы, устраняя установочные угловые рассогласования и приводя результаты к любой из трех СК (геомагнитной, географической или выбранной опорной).
Примерно в 1987 г. началась эпоха стендов третьего поколения, характерным представителем которых является стенд MS90. Особенностью стенда MS90 является то, что он использует только два, в особых случаях четыре, трехкомпонентных датчика. Известен способ согласования датчиков MS90 [Better, cheaper, faster, easier... the MS90 transportable degaussing range. Лучше, дешевле, быстрее, легче... MS90 - транспортируемый стенд для размагничивания кораблей. International Defence Review 1988 v.21, #12, р.1663; A.C. Totterdell. Operational Aspects of a Transportable DG Range // Underwater Measuring Ranges and Techniques. 1990, February, p.391-98. Транспортируемый стенд для размагничивания кораблей (эксплуатационные возможности) // Труды конференции по методам размагничивания кораблей и подводным магнитоизмерительным стендам методы измерения]. Каждый датчик MS90 снабжен глубиномером, системой автоматической компенсации магнитного поля Земли, а также механической системой привязки по вертикали (но не кардановым подвесом), которая отрабатывает начальные углы невертикальности до 30°. Для определения расстояния между датчиками каждый датчик снабжен калиброванной катушкой источника магнитного поля, т.е. однокомпонентной мерой магнитного момента (ММ). Более полных сведений о погрешности определения расстояния или погрешности угловой ориентации датчиков в публикациях не приводится. Лишь при описании стендов третьего поколения упоминается, что на стендах второго поколения иногда требовалась погрешность измерения расстояния между датчиками не более 1 см. Известна также погрешность отечественного глубиномера 0.3 м в диапазоне измерения 0-25 м.
По совокупности существенных признаков в качестве ближайшего аналога заявляемого способа принят способ углового согласования датчиков MS90 [Totterdell 1990, р.393].
Известный способ включает измерение глубины установки датчика, компенсацию магнитного поля Земли, механическую ориентацию одной из компонент датчика вдоль вертикали, измерение каждым датчиком магнитного поля калиброванной катушки источника другого датчика для расчета расстояния между датчиками.
Причиной, препятствующей достижению указанного ниже технического результата при использовании известного способа, является однокомпонентный характер встроенной меры ММ и конструктивное расположение меры ММ внутри датчика.
Задачей, на решение которой направлено заявляемое изобретение, является повышение точности определения местоположения и ориентации трехкомпонентного датчика.
Технический результат, получаемый при осуществлении изобретения, состоит в возможности использования трехкомпонентных датчиков без встроенных механических устройств угловой ориентации.
Указанный технический результат достигается тем, что в заявляемом способе определения местоположения и ориентации трехкомпонентного датчика относительно меры магнитного момента, в отличие от известного способа, в произвольно выбранной точке снаружи от датчика устанавливают трехкомпонентную меру ММ с известными значениями неортогональностей между ее осями 1, 2, 3, по которым строят собственную ортогональную систему координат меры (СОСКМ), в которой поочередно воспроизводят вектор-столбцы ММ положительной и отрицательной полярности 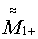 и
и 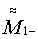 ,
, 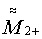 и
и 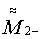 ,
, 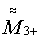 и
и 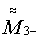 , при этом магнитометром измеряют соответствующие магнитные индукции В1+ и В1-, В2+ и В2-,
, при этом магнитометром измеряют соответствующие магнитные индукции В1+ и В1-, В2+ и В2-, В3+ и В3- и строят их матрицу результатов измерения в собственной ортогональной системе координат магнитометра (СОСКМАГ) по формуле
В3+ и В3- и строят их матрицу результатов измерения в собственной ортогональной системе координат магнитометра (СОСКМАГ) по формуле

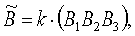
где 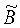 - матрица 3×3 результатов измерений в СОСКМАГ, Тл;
- матрица 3×3 результатов измерений в СОСКМАГ, Тл;
k - заранее определенная корректирующая матрица 3×3 данного магнитометра (см. Патент №2229727 Способ определения корректирующей матрицы трехкомпонентного магнитометра);
B1=(В1+-В1-)/2, В2=(В2+-В2-)/2, В3=(В3+-В3-)/2 - вектор-столбцы показаний магнитометра, Тл,
затем находят произведение матриц 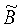 и
и 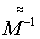 по формуле
по формуле
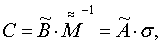
где С=А·σ - известное произведение неизвестных матриц А и σ;
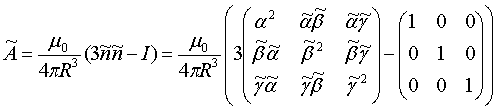 - матрица в СОСКМАГ, м3;
- матрица в СОСКМАГ, м3;
μ0=4π×10-7 Гн/м - магнитная постоянная;
R - расстояние между мерой и датчиком, м;
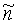 - вектор-столбец единичного направления от меры к датчику в СОСКМАГ;
- вектор-столбец единичного направления от меры к датчику в СОСКМАГ;
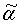 ,
, 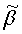 ,
, 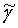 - направляющие косинусы единичного направления
- направляющие косинусы единичного направления 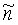 в СОСКМАГ;
в СОСКМАГ;
σ - матрица ортогонального преобразования из СОСКМ в СОСКМАГ;
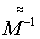 - обратная матрица от
- обратная матрица от 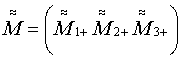 в СОСКМ,
в СОСКМ,
после чего вычисляют произведение матрицы С и ее транспонированной СТ по формуле
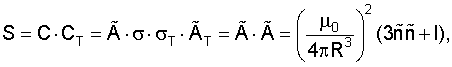
откуда находят искомые расстояние R и направление 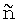 по формулам
по формулам
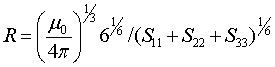
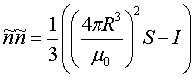
и определяют матрицу 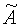 , с помощью которой находят искомую матрицу (по формуле
, с помощью которой находят искомую матрицу (по формуле
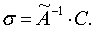
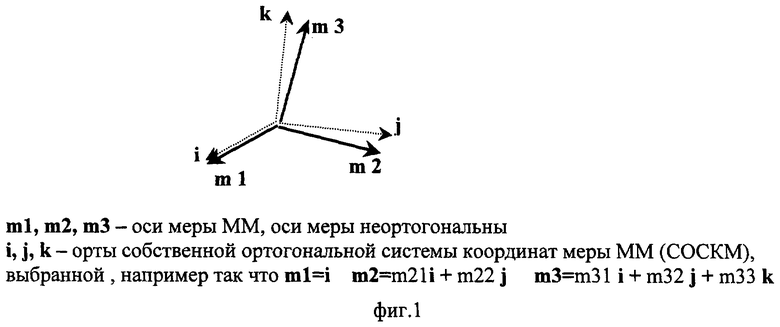
На фиг.1 изображена схема построения собственной ортогональной системы координат меры (СОСКМ) ММ.
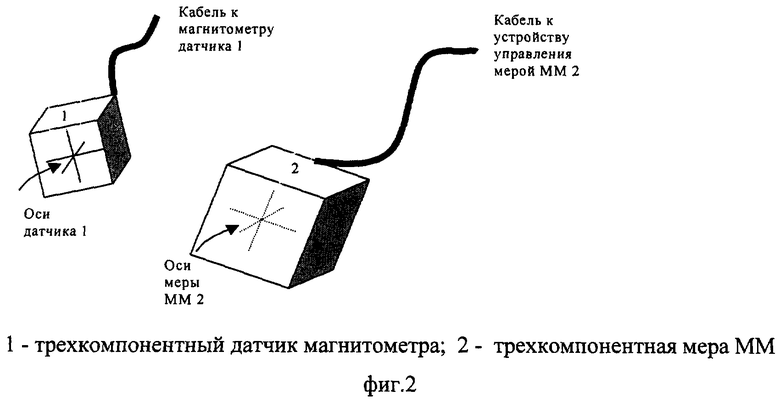
На фиг.2 изображена схема расположения трехкомпонентного датчика магнитометра и трехкомпонентной меры ММ.
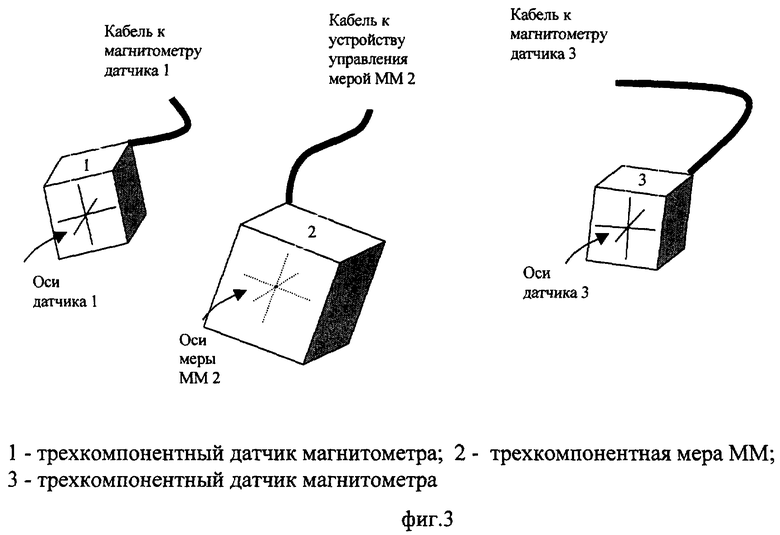
На фиг.3 изображена схема расположения двух трехкомпонентных датчиков магнитометров и трехкомпонентной меры ММ.
Схема на фиг.1 поясняет процедуру построения СОСКМ с ортами i, j, k для трехкомпонентной меры ММ с неортогональными осями m1, m2, m3. Схема на фиг.2 включает трехкомпонентный датчик магнитометра 1 и трехкомпонентную меру ММ 2. Схема на фиг.3 включает трехкомпонентный датчик магнитометра 1, трехкомпонентную меру ММ 2 и трехкомпонентный датчик магнитометра 3.
Заявляемый способ осуществляется следующим образом. Используют трехкомпонентную меру ММ в виде катушек с токами I1, I2, I3, воспроизводящими ММ С1I1, C2I2, C3I3 вдоль единичных осей меры m1, m2, m3. С1, С2, С3 - известные постоянные меры ММ, размерность м2. Известны также неортогональности осей меры ϕ12=m1·m2; ϕ13=m1·m3; ϕ23=m2·m3. Выберем вспомогательную ортогональную систему координат (СК) с ортами i, j, k, связанную следующим образом с осями меры:
m1=i
m2=m21i+m22j,
m3=m31+m32 j+m33k
где mij - направляющие косинусы осей меры относительно ортов выбранной СК.
Т.е. орт i выбирают вдоль оси меры m1, далее вращают СК вокруг орта i так, чтобы орт j попал в плоскость осей m2 и m3, как показано на фиг.1. При таком выборе СК все направляющие косинусы mij могут быть сравнительно просто выражены через известные неортогональности осей меры:
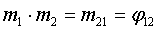 ;
; 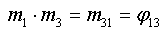 ;
; 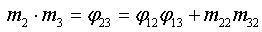 ;
; 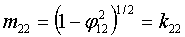 ;
; 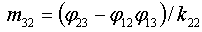 ;
; 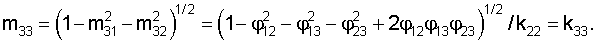
Такую СК называют собственной ортогональной СК меры ММ (СОСКМ). (СОСКМ можно было бы построить еще, по крайней мере, 5-ю похожими способами). Итак, мера ММ может воспроизводить по осям меры 1, 2, 3 величины MM C1I1; C2I2; C3I3 положительной и отрицательной полярности, по которым можно построить матрицу ММ в СОСКМ, используя известную матрицу осей в СОСКМ:
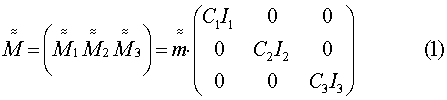
где 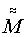 - матрица из вектор-столбцов, воспроизведенных мерой ММ в СОСКМ,
- матрица из вектор-столбцов, воспроизведенных мерой ММ в СОСКМ,
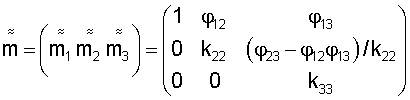 - матрица осей меры в СОСКМ.
- матрица осей меры в СОСКМ.
Как изображено на фиг.2, около трехкомпонентного датчика 1 устанавливают трехкомпонентную меру ММ 2. При обесточенной мере 2 в датчике 1 компенсируют поле Земли. Затем по очереди по каждой оси меры 2 воспроизводят ММ положительной и отрицательной полярности и при каждом ММ измеряют трехкомпонентным датчиком 1 соответствующую индукцию магнитного поля В1+ и В1-, В2+ и В2-, В3+ и В3- и строят их матрицу результатов измерения в собственной ортогональной системе координат магнитометра (СОСКМАГ) по формуле
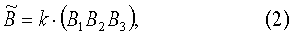
где 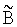 - матрица 3×3 результатов измерений в СОСКМАГ, Тл;
- матрица 3×3 результатов измерений в СОСКМАГ, Тл;
k - заранее определенная корректирующая матрица 3×3 данного магнитометра;
B1=(В1+- B1-)/2, B2=(В2+-В2-)/2, B3=(B3+-B3-)/2 - вектор-столбцы показаний магнитометра, Тл.
Матрицу k берут из паспорта магнитометра. Процедура ее определения известна (Патент №2229727. Способ определения корректирующей матрицы трехкомпонентного магнитометра. Заявка №2002132849. Приоритет изобретения 27 ноября 2002 г.). Эту матрицу определяют заблаговременно с помощью образцовой трехкомпонентной меры магнитной индукции. С помощью этой матрицы корректируют мультипликативные погрешности магнитометра и переводят его показания в СОСКМАГ.
Как известно, дипольный магнитный момент, или просто магнитный момент М=Mm, и индукция его магнитного поля в некоторой точке В связаны следующим векторным соотношением
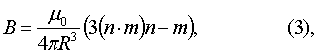
где μ0=4π×10-7 Гн/м - магнитная постоянная;
R=Rn - радиус-вектор между диполем и точкой в которой определяется индукция В, Тл;
n - единичный вектор направления.
В соотношении (3) вектор момента М=Mm можно вынести за скобку.
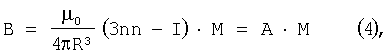
где 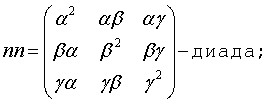
α, β, γ - направляющие косинусы к осям СК, в которой рассматривается (2).
В уравнении (4) все величины должны быть в одной СК. Введем следующим образом матрицу связи между СОСКМ и СОСКМАГ
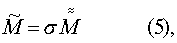
где σ - ортогональная матрица преобразования координат из СОСКМ в СОСКМАГ.
Ортогональной матрицей является матрица, обратная которой равна ее транспонированной

Перепишем (4) в матричном виде в СОСКМАГ, учитывая (1), (2) и (5)
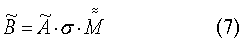
В соотношении (7) матрицы 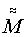 и
и 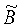 известны, первая как результат воспроизведения ММ мерой 2 в СОСКМ, вторая как соответствующие результаты измерения датчиком 1, скорректированные в СОСКМАГ, а матрицы
известны, первая как результат воспроизведения ММ мерой 2 в СОСКМ, вторая как соответствующие результаты измерения датчиком 1, скорректированные в СОСКМАГ, а матрицы 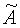 и σ неизвестны. Обратим внимание, что в (4) нельзя делить на вектор ММ, но (7) можно умножить справа на матрицу обратную
и σ неизвестны. Обратим внимание, что в (4) нельзя делить на вектор ММ, но (7) можно умножить справа на матрицу обратную 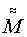 и тем самым найти произведение неизвестных
и тем самым найти произведение неизвестных 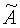 и σ:
и σ:
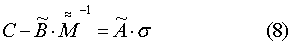
Матрица 3×3 С известна, поскольку известны 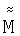 и
и 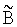 и обратная
и обратная 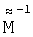 заведомо существует. Рассмотрим произведение С и ее транспонированной СT:
заведомо существует. Рассмотрим произведение С и ее транспонированной СT:
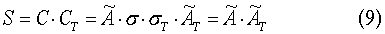
так как по определению ортогональной матрицы σ·σT=I.
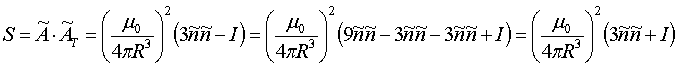
Таким образом, (9) избавлено от неизвестной матрицы σ и содержит только величины, связанные с искомыми расстоянием R и направлением 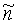 , которые определяются через (9) следующим образом:
, которые определяются через (9) следующим образом:
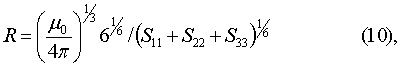
где S11, S22, S33 - диагональные элементы матрицы S,
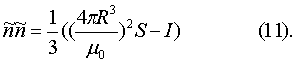
Соотношения (10), (11) определяют местоположения датчика 1 относительно меры ММ 2.
Затем с помощью (10) и (11) вычисляют по (4) 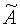 и находят σ с помощью (8):
и находят σ с помощью (8):
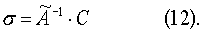
Соотношение (12) определяет ориентацию датчика 1 относительно меры 2.
В качестве дополнительной иллюстрации к решению (10)-(12) рассмотрим схему на фиг.3. Пусть требуется определить радиус-вектор расстояния между трехкомпонентными датчиками 1 и 3 и матрицу ортогонального преобразования между собственными ортогональными СК датчика 1 (СОСКМАГ1) и датчика 3 (СОСКМАГ3) σ13.
Меру ММ 2 устанавливают приблизительно между датчиками 1 и 3. Осуществляют вышеописанные измерительные операции и по (10)-(12) находят расстояние между мерой 2 и датчиком 1, единичное направление от меры 2 к датчику 1 в СОСКМАГ1 и матрицу ортогонального преобразования координат из СОСКМ в СОСКМАГ1. В отличие от ранее принятых обозначений к схеме на фиг.2 (R, 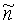 , σ), обозначим к схеме на фиг.3 расстояние R1, направление
, σ), обозначим к схеме на фиг.3 расстояние R1, направление 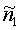 и ортогональное преобразование σ1. По аналогии с (10)-(12) находят расстояние между мерой 2 и датчиком 3 R3, единичное направление от меры 2 к датчику 3 в СОСКМАГ3
и ортогональное преобразование σ1. По аналогии с (10)-(12) находят расстояние между мерой 2 и датчиком 3 R3, единичное направление от меры 2 к датчику 3 в СОСКМАГ3 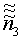 и матрицу ортогонального преобразования координат из СОСКМ в СОСКМАГ3 σ3.
и матрицу ортогонального преобразования координат из СОСКМ в СОСКМАГ3 σ3.
Т.е. 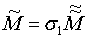 ,
, 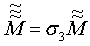 и
и 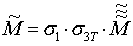 , откуда определяют искомую матрицу ортогонального преобразования координат из СОСКМАГ3 в СОСКМАГ1 как
, откуда определяют искомую матрицу ортогонального преобразования координат из СОСКМАГ3 в СОСКМАГ1 как

При этом искомый радиус-вектор между датчиками, например от датчика 3 к датчику 1, находят как:
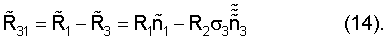
Если датчики 1 и 3 участвуют в совместных измерениях и в качестве опорного выбран датчик 1, то последующие результаты измерения датчиком 3 в СОСКМАГ3 корректируют умножением на σ13:

Заявляемый способ проверен поэтапным моделированием соотношений (4)-(12) на компьютере с помощью системы МатЛаб.
Кроме того, были получены аналитические оценки (СКО) погрешностей определения величин по заявляемому способу при одинаковой величине момента М, воспроизводимого каждой компонентой меры ММ:
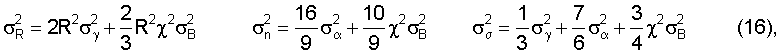
где σR, σn, σσ - СКО погрешностей определения соответственно расстояния R, м, единичного направления n и ориентации (на одну усредненную компоненту матрицы σ);
σγ, σα - СКО мультипликативной погрешности определения соответственно диагональных и боковых элементов корректирующей матрицы 3×3 трехкомпонентного магнитометра (см. Патент №2229727 Способ определения корректирующей матрицы трехкомпонентного магнитометра);
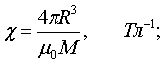
σB - аддитивная погрешность компоненты магнитометра.
Оценки (16), вычисленные при σγ=σα=1,5×10-4, σB=5×10-11 Тл и М=10 Ам2 в функции расстояния R между датчиком и мерой ММ, показаны в таблице.
Для магнитоизмерительных стендов второго поколения, как указывалось в разделе Уровень техники, половина расстояния между парой датчиков стенда лежит в пределах 1.5 м - 3 м. Т.е. заявляемый способ может быть успешно применен для настройки и контроля датчиков трехкомпонентных магнитометров стендов второго поколения, если снизить мультипликативные погрешности магнитометров введением корректирующих матриц (см. Патент №2229727 Способ определения корректирующий матрицы трехкомпонентного магнитометра).
Изобретение относится к области измерения индукции магнитного поля с помощью феррозондовых трехкомпонентных магнитометров, датчики которых устанавливаются в труднодоступных местах, а также к области контроля угловой ориентации датчиков. С помощью воспроизведения магнитных моментов трехкомпонентной мерой магнитного момента и результатов измерения трехкомпонентным датчиком индукции магнитного поля меры определяют координаты радиус-вектора расстояния между датчиком и мерой, а также находят ортогональную матрицу преобразования координат из собственной ортогональной системы координат меры в собственную ортогональную систему координат датчика магнитометра. Технический результат: возможность использования трехкомпонентных датчиков без встроенных механических устройств угловой ориентации. 3 ил., 1 табл.
Способ определения местоположения и ориентации трехкомпонентного датчика магнитометра относительно меры магнитного момента (ММ), включающий компенсацию магнитного поля Земли и измерение магнитного поля меры ММ, отличающийся тем, что в произвольно выбранной точке снаружи от датчика устанавливают трехкомпонентную меру ММ с известными значениями неортогональностей между ее осями 1, 2, 3, по которым строят собственную ортогональную систему координат меры (СОСКМ), в которой поочередно воспроизводят вектор-столбцы ММ положительной и отрицательной полярности 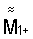 и
и 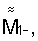
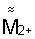 и
и 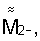
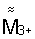 и
и 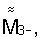 при этом магнитометром измеряют соответствующие магнитные индукции В1+ и B1-, В2+ и В2-, В3+ и В3- и строят их матрицу результатов измерения в собственной ортогональной системе координат магнитометра (СОСКМАГ) по формуле
при этом магнитометром измеряют соответствующие магнитные индукции В1+ и B1-, В2+ и В2-, В3+ и В3- и строят их матрицу результатов измерения в собственной ортогональной системе координат магнитометра (СОСКМАГ) по формуле
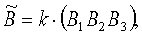
где 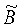 - матрица 3×3 результатов измерений в СОСКМАГ, Тл;
- матрица 3×3 результатов измерений в СОСКМАГ, Тл;
k - заранее определенная корректирующая матрица 3×3 данного магнитометра;
B1=(B1+-B1-)/2, В2=(В2+-В2-)/2, B3=(B3+-B3-)/2 - вектор-столбцы показаний магнитометра, Тл,
затем находят произведение матриц 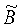 и
и 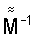 по формуле
по формуле
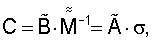
где С=А·σ - известное произведение неизвестных матриц А и σ;
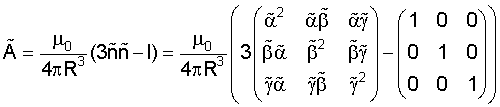 - матрица в СОСКМАГ, м-3;
- матрица в СОСКМАГ, м-3;
μ0=4π·10-7 Гн/м - магнитная постоянная;
R - расстояние между мерой и датчиком, м;
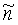 - вектор-столбец единичного направления от меры к датчику в СОСКМАГ;
- вектор-столбец единичного направления от меры к датчику в СОСКМАГ;
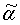 ,
, 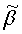 ,
, 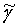 - направляющие косинусы единичного направления
- направляющие косинусы единичного направления 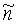 в СОСКМАГ;
в СОСКМАГ;
σ - матрица ортогонального преобразования из СОСКМ в СОСКМАГ;
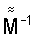 - обратная матрица от
- обратная матрица от 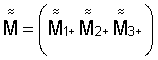 в СОСКМ,
в СОСКМ,
после чего вычисляют произведение матрицы С и ее транспонированной СT, по формуле
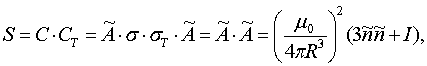
откуда находят искомые расстояние R и направление 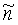 по формулам:
по формулам:
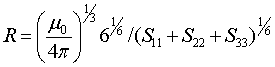
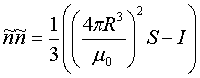
и определяют матрицу 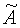 , с помощью которой находят искомую матрицу σ по формуле
, с помощью которой находят искомую матрицу σ по формуле 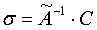 .
.
| А.С.Totterdell | |||
| Operation Aspects of a Transportable DG Range | |||
| Underwater Measuring Ranges and Techniques | |||
| Способ приготовления консистентных мазей | 1919 |
|
SU1990A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩЕЙ МАТРИЦЫ ТРЕХКОМПОНЕНТНОГО МАГНИТОМЕТРА | 2002 |
|
RU2229727C1 |
| Способ поверки ортогональности осей компонентного магнитометра | 1986 |
|
SU1343377A1 |
| US 6130534 A, 10.10.2000 | |||
| УСТРОЙСТВО для БЕЗЫНЕРЦИОННОГО ИЗМЕРЕНИЯ | 0 |
|
SU331262A1 |
Авторы
Даты
2006-12-27—Публикация
2005-08-09—Подача