2420-132239RU/091
Область техники, к которой относится изобретение
Настоящее изобретение относится в общем случае к передаче данных, а более конкретно к методикам получения собственных векторов на основе управляющего опорного сигнала, которые используются для пространственной обработки в системе связи множественного ввода/вывода (MIMO).
Уровень техники
Система MIMO использует множество (NТ) передающих антенн и множество (NR) приемных антенн для передачи данных. Канал MIMO, сформированный с помощью NT передающих и NR приемных антенн, может разбиваться на NS независимых или пространственных каналов, где NS≤min{NT, NR}. Каждый из NS независимых каналов соответствует измерению. Система MIMO может обеспечивать улучшенную производительность (например, увеличенную пропускную способность и/или большую надежность), если дополнительные измерения, созданные с помощью множества передающих и приемных антенн эффективно используются.
В системе радиосвязи данные, которые будут передаваться, обычно обрабатываются (например, кодируются и модулируются) и затем преобразуют с повышением частоты к радиочастоте (РЧ) несущего сигнала для генерации модулированного сигнала РЧ, который больше подходит для передачи по беспроводному каналу. Для беспроводной системы MIMO до NT модулированных сигналов РЧ может генерироваться и передаваться одновременно от NT передающих антенн. Переданные модулированные сигналы РЧ могут достигать NR приемных антенн через множество путей распространения в беспроводном канале. Характеристики путей распространения обычно изменяются во времени из-за различных факторов, таких как, например, затухания, многолучевое распространение и внешние помехи. Следовательно, модулированные РЧ сигналы могут находиться в каналах с различными условиями (например, с различным затуханием и с различным влиянием многолучевого распространения) и могут быть связаны с различными сложными коэффициентами усиления и отношениями сигнал-шум (ОСШ, SNR).
Для достижения высокого качества часто необходимо оценивать ответ (характеристику) беспроводного канала связи между передатчиком и приемником. Для системы MIMO ответ канала может характеризоваться с помощью матрицы H ответа канала, которая включает в себя NTNR значений сложного коэффициента усиления для NTNR различных пар передающая/приемная антенна (т.е. один сложный коэффициент усиления для каждой из NT передающих антенн и для каждой из NR приемных антенн). Оценку канала обычно выполняют с помощью передачи пилот-сигнала (т.е. опорного сигнала) с передатчика на приемник. Пилот-сигнал обычно генерируют на основе известных пилотных символов и обрабатывают известным способом (т.е. известным приемнику априорно). Приемник может затем оценивать коэффициенты усиления каналов как отношение принятых пилотных символов к известным пилотным символам.
Оценка ответа канала может быть необходима передатчику для выполнения пространственной обработки для передачи данных. Оценка ответа канала может также быть необходима приемнику для выполнения пространственной обработки (или согласованной фильтрации) принятых сигналов для восстановления переданных данных. Пространственная обработка должна выполняться приемником и обычно также выполняется передатчиком для использования NS независимых каналов канала MIMO.
Для системы MIMO относительно большое количество системных ресурсов может быть необходимо для передачи пилот-сигнала от NT передающих антенн, так что достаточно точная оценка ответа канала может быть получена приемником в присутствии шума и помех. Кроме того, большие вычисления обычно необходимы для обработки коэффициентов усиления канала для получения собственных векторов, необходимых для пространственной обработки. В частности, приемник обычно должен обрабатывать коэффициенты усиления каналов для получения первого набора собственных векторов, используемых для пространственной обработки для приема данных в одной линии связи, и может дополнительно получать второй набор собственных векторов, используемых для пространственной обработки для передачи данных в другой линии связи. Получение собственных векторов и пространственная обработка для передачи и приема данных описана ниже. Второй набор собственных векторов обычно необходимо посылать назад передатчику для его использования. Как можно заметить, большое количество ресурсов может быть необходимо для поддержания пространственной обработки в передатчике и приемнике.
Поэтому в уровне техники существует потребность в более эффективной методике получения собственных векторов, используемых для пространственной обработки в системах MIMO.
Сущность изобретения
Представлены методики получения собственных векторов на основе управляющего опорного сигнала, которые используются для пространственной обработки для приема и передачи данных. Управляющий опорный сигнал является пилот-сигналом, передаваемым только в одном пространственном канале или в собственной моде канала MIMO в течение заданного периода символа, что достигается с помощью выполнения пространственной обработки с помощью управляющего вектора для этой собственной моды, как описано ниже. Управляющий опорный сигнал используется приемником для получения оценки и диагональной матрицы Σ сингулярных значений и унитарной матрицы U левых собственных векторов матрицы H ответа канала, без необходимости оценки ответа канала MIMO или выполнения разложения по сингулярным числам матрицы H.
Оценки Σ и U могут использоваться для согласованной фильтрации передачи данных, принятой через первую линию связи (например, восходящую линию связи). Для системы дуплексной связи с временным разделением каналов (ДСВРК, TDD), которая характеризуется ответами канала нисходящей линии связи и восходящей линии связи, которые являются обратной величиной друг друга, оценка U может также использоваться для пространственной обработки передачи данных во второй линии связи (например, в нисходящей линии связи).
В другом аспекте матрицу 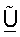 с ортогональными столбцами получают на основе оценок Σ и U. Ортогонализация столбцов
с ортогональными столбцами получают на основе оценок Σ и U. Ортогонализация столбцов 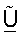 может достигаться с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция, которые все описаны ниже. Ортогональная матрица
может достигаться с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция, которые все описаны ниже. Ортогональная матрица 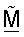 согласованного фильтра может затем быть получена на основе матрицы
согласованного фильтра может затем быть получена на основе матрицы 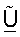 и оценки Σ. Матрица
и оценки Σ. Матрица 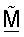 может использоваться для согласованной фильтрации для первой линии связи, и матрица
может использоваться для согласованной фильтрации для первой линии связи, и матрица 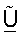 может использоваться для пространственной обработки для второй линии связи.
может использоваться для пространственной обработки для второй линии связи.
Различные аспекты и варианты осуществления изобретения описаны более подробно ниже.
Краткое описание чертежей
Признаки, характер и преимущества настоящего изобретения станут более очевидными из сформулированного ниже подробного описания, которое рассматривают вместе с чертежами, на которых одинаковые обозначения идентифицируют соответственные элементы по всему документу и на которых:
фиг.1 показывает последовательность операций процесса получения ортогональной матрицы согласованного фильтра 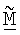 на основе управляющего опорного сигнала;
на основе управляющего опорного сигнала;
фиг.2 показывает систему радиосвязи;
фиг.3 показывает структуру кадра для системы ДСВРК MIMO-OFDM;
фиг.4 показывает передачу управляющего опорного сигнала и данных в нисходящей линии связи и восходящей линии связи для примерной схемы передачи;
фиг.5 показывает структурную схему точки доступа и пользовательского терминала; и
фиг.6 показывает структурную схему пространственной обработки, выполняемой с помощью точки доступа и пользовательского терминала для передачи данных в нисходящей линии связи и восходящей линии связи.
Подробное описание
Используемое в данной работе слово "примерный" означает "служить примером или иллюстрацией". Любой вариант осуществления или образец, описанный как "примерный", не обязательно должен рассматриваться как предпочтительный или преимущественный по сравнению с другими вариантами осуществления или образцами.
Описанные методики для получения собственных векторов могут использоваться для различных систем связи MIMO. Например, эти методики могут использоваться для систем MIMO с одной несущей, а также для систем MIMO с многими несущими. Для ясности эти методики описаны ниже для системы MIMO с одной несущей.
Модель для системы MIMO с одной несущей может быть выражена как:

Где x - "передаваемый" вектор с NT элементами для символов, посланных от NT передающих антенн (т.е. x=[x1 x2 ... xNт]T);
R - "принимаемый" вектор с NR элементами для символов, принятых через NR приемных антенн (т.е. r=[r1 r2 ... rNR]T);
H - матрица ответа канала (NR × NT);
n - вектор аддитивного белого Гауссова шума (AWGN); и
"T" обозначает транспозицию.
Вектор шума n, как предполагают, имеет компоненты с нулевым значением и ковариационной матрицей 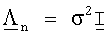 , где I - единичная матрица, и
, где I - единичная матрица, и 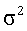 - шумовая дисперсия.
- шумовая дисперсия.
Матрица H ответа канала может быть выражена как:
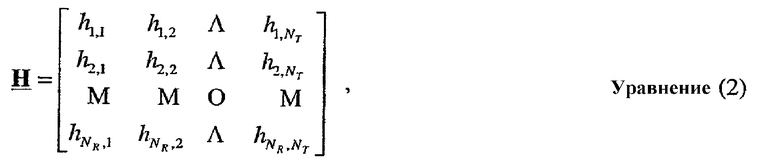
где элемент hi,j, для i ∈ {1... NR} и j ∈ {1... NT}, является связью (т.е. сложным коэффициентом усиления) между j-й передающей антенной и i-й приемной антенной. Для простоты ответ канала, как предполагают, является плоским по всей ширине полосы пропускания системы, и ответ канала для каждой пары антенн передачи/приема может быть представлен единственным сложным значением hi,j. Также для простоты последующее описание предполагает, что NR ≥ NT, матрица H ответа канала имеет полный ранг и NS=NT ≤ NR.
Матрица H ответа канала может "диагонализироваться" для получения NT независимых каналов, которые также упоминаются как пространственные каналы или собственные моды. Эту диагонализацию могут достигать с помощью выполнения или разложения по сингулярным числам матрицы H ответа канала или разложения по собственным значениям корреляционной матрицы H, которая является HHH, где "H" обозначает сопряженную транспозицию. Для ясности в последующем описании используется разложение по сингулярным числам.
Разложение по сингулярным числам матрицы H ответа канала может быть выражено как:

где U - унитарная матрица (NR × NR), столбцами которой являются собственные векторы H;
Σ - диагональная матрица (NR × NT) сингулярных значений H, которая определяется как
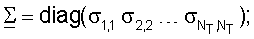 и
и
V - унитарная матрица (NT × NT), столбцы которой - правые собственные векторы H.
Унитарная матрица М характеризуется свойством MHM=I, которое означает, что столбцы унитарной матрицы ортогональны друг другу и строки матрицы также ортогональны друг другу. Столбцы матрицы V также упоминаются как управляющие векторы. Разложение по сингулярным числам описано более подробно Гильбертом Странгом (Gilbert Strang) в книге, озаглавленной "Linear Algebra and Its Applications", второе издание, Academic Press, 1980.
Пространственная обработка может выполняться и передатчиком, и приемником для передачи данных в NT пространственных каналах канала MIMO. Пространственная обработка в передатчике может быть выражена как:

где s - вектор "данных" с количеством ненулевых элементов до NT для символов данных, которые будут передаваться в NT пространственных каналах. Передаваемый вектор x дополнительно обрабатывают и затем передают по каналу MIMO на приемник.
Принятая передача в приемнике может быть выражена как:
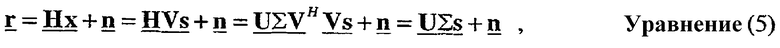
где все термины определены выше.
Пространственная обработка в приемнике для восстановления вектора данных s может быть выражена как:
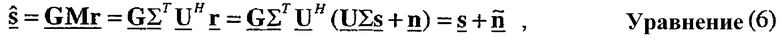
где s - вектор данных;
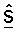 - оценка вектора данных s;
- оценка вектора данных s;
М - (NT × NR) матрица согласованного фильтра, которая определяется как M=ΣTUH;
G - (NT × NT) масштабируемая матрица, которая определяется как
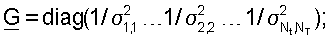 и
и
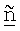 - постобработанный шум, который определяется как
- постобработанный шум, который определяется как  =GΣTUHn.
=GΣTUHn.
Пространственная обработка с помощью приемника часто упоминается как согласованная фильтрация. Поскольку M=ΣTUH и поскольку столбцы U являются собственными векторами H, столбцы МT являются сопряженными левыми собственными векторами H, масштабированными с помощью сингулярных значений в Σ.
Как показано в уравнении (6), приемнику нужны хорошие оценки матриц Σ и U для выполнения согласованной фильтрации для восстановления вектора данных s. Матрицы Σ и U могут быть получены с помощью передачи пилот-сигнала с передатчика на приемник. Приемник может затем оценивать матрицу H ответа канала, основываясь на принятом пилот-сигнале, и выполнять разложение этой оценки по сингулярным числам, как показано в уравнении (3), для получения матриц Σ и U. Однако, как отмечено выше, большое количество ресурсов может быть необходимо для передачи этого пилот-сигнала и выполнения разложения по сингулярным числам.
I. Управляющий опорный сигнал
В одном из аспектов, управляющий опорный сигнал передают с помощью передатчика и используют приемником для получения оценки матриц Σ и U, которые необходимы для согласованной фильтрации. Управляющий опорный сигнал - передача пилот-сигнала только в одном пространственном канале или собственной моде в течение заданного периода символа, что достигается с помощью выполнения пространственной обработки с помощью управляющего вектора для этой собственной моды. Приемник может затем оценивать матрицы Σ и U, основываясь на управляющем опорном сигнале, без необходимости оценивать ответ канала MIMO или выполнения разложения по сингулярным числам.
Управляющий опорный сигнал, посланный передатчиком, может быть выражен как:
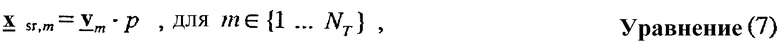
где xsr,m является переданным вектором для управляющего опорного сигнала для m-й собственной моды; vm - правый собственный вектор H для m-й собственной моды; и p - пилотный символ, переданный для управляющего опорного сигнала. Собственный вектор vm является m-м столбцом матрицы V, где V=[v1v2 ... v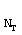 ].
].
Принятый управляющий опорный сигнал в приемнике может быть выражен как:
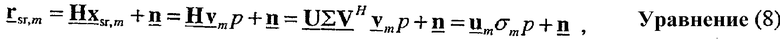
где rsr,m является принимаемым вектором для управляющего опорного сигнала для m-й собственной моды; и σm - сингулярное значение для m-й собственной моды.
Как показано в уравнении (8), в приемнике принятый управляющий опорный сигнал в отсутствие шума равен umσmp, что является известным пилотным символом p, преобразованным с помощью umσm. Собственный вектор um является m-м столбцом матрицы U, и сингулярное значение σm является m-м диагональным элементом матрицы Σ. Приемник может, таким образом, получать оценку umσm, основываясь на управляющем опорном сигнале, посланном передатчиком.
Различные методики могут использоваться для обработки принятого управляющего опорного сигнала для получения оценки um и σm. В одном из вариантов осуществления для получения оценки umσm принимаемый вектор rsr,m для управляющего опорного сигнала, посланного на m-й собственной моде, сначала умножают на комплексное сопряжение пилотного символа p*. Результат может затем интегрироваться по многочисленным символам управляющего опорного сигнала, принятым для каждой собственной моды m для получения оценки umσm. Вектор строки 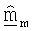 может определяться так, чтобы он был равен сопряженной транспозиции оценки umσm (т.е.
может определяться так, чтобы он был равен сопряженной транспозиции оценки umσm (т.е. 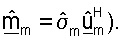 Каждый из NR элементов вектора
Каждый из NR элементов вектора 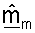 получают, основываясь на соответствующем одном из NR элементов вектора rsr,m.
получают, основываясь на соответствующем одном из NR элементов вектора rsr,m.
Вектор строки 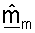 для m-й собственной моды включает в себя оценки и um, и σm и может таким образом упоминаться как масштабируемый вектор. Так как собственные векторы имеют единичную мощность, сингулярное значение σm может оцениваться, основываясь на принятой мощности управляющего опорного сигнала, который может измеряться для каждой собственной моды. В частности, оценка сингулярных значений
для m-й собственной моды включает в себя оценки и um, и σm и может таким образом упоминаться как масштабируемый вектор. Так как собственные векторы имеют единичную мощность, сингулярное значение σm может оцениваться, основываясь на принятой мощности управляющего опорного сигнала, который может измеряться для каждой собственной моды. В частности, оценка сингулярных значений 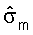 может быть установлена равной квадратному корню мощности для вектора rsr,m, разделенному на величину пилотного символа p. Вектор
может быть установлена равной квадратному корню мощности для вектора rsr,m, разделенному на величину пилотного символа p. Вектор 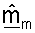 может масштабироваться с помощью
может масштабироваться с помощью 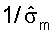 для получения собственного вектора
для получения собственного вектора 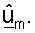
В другом варианте осуществления методика минимальной среднеквадратической ошибки (MMSE) используется для получения оценки um, основываясь на принимаемом векторе rsr,m для управляющего опорного сигнала. Поскольку пилотный символ p известен, приемник может получать оценку um так, что среднеквадратическая ошибка между восстановленным пилотным символом 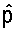 (который получают после выполнения согласованной фильтрации принимаемого вектора rsr,m) и переданным пилотным символом p минимизирована.
(который получают после выполнения согласованной фильтрации принимаемого вектора rsr,m) и переданным пилотным символом p минимизирована.
Управляющий опорный сигнал передают для одной собственной моды каждый момент времени (т.е. одна собственная мода в течение каждого периода символа передачи управляющего опорного сигнала). Управляющий опорный сигнал для всех NT собственных мод может передаваться различными способами. В одном из вариантов осуществления управляющий опорный сигнал передают для одной собственной моды в течение каждого кадра, где кадр - интервал передачи данных для системы, и его определяют так, чтобы он имел определенную продолжительность времени (например, 2 мс). Для данного варианта осуществления управляющий опорный сигнал для многочисленных собственных мод может передаваться в множестве кадров. В другом варианте осуществления управляющий опорный сигнал передают для многочисленных собственных мод в пределах одного кадра. Это может достигаться с помощью циклического повторения NT собственных мод в NT периодах символа. Для обоих вариантов осуществления n-й символ управляющего опорного сигнала может выражаться как:
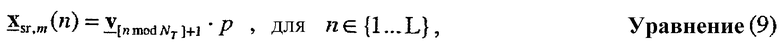
где n - индекс или для периода символа, или для номера кадра, и L - количество символов управляющего опорного сигнала, которые будут передаваться. Многочисленные символы управляющего опорного сигнала могут передаваться для каждой собственной моды m для предоставления возможности приемнику получать более точную оценку umσm.
Приемник может получать вектор строки 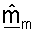 для каждой из NT собственных мод, основываясь на принятом управляющем опорном сигнале для этой собственной моды. Вектор строки
для каждой из NT собственных мод, основываясь на принятом управляющем опорном сигнале для этой собственной моды. Вектор строки 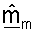 для всех NT собственных мод может использоваться для формирования начальной матрицы согласованного фильтра
для всех NT собственных мод может использоваться для формирования начальной матрицы согласованного фильтра 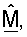 где
где 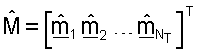 и
и 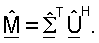 Матрица
Матрица 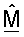 может использоваться для согласованной фильтрации приемником, как показано в уравнении (6), для восстановления переданного вектора данных s.
может использоваться для согласованной фильтрации приемником, как показано в уравнении (6), для восстановления переданного вектора данных s.
Управляющий опорный сигнал посылают для одной собственной моды каждый момент времени, и он может использоваться приемником для получения вектора 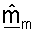 согласованного фильтра для этой собственной моды. Поскольку NT векторов
согласованного фильтра для этой собственной моды. Поскольку NT векторов 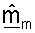 согласованного фильтра матрицы
согласованного фильтра матрицы 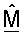 получают индивидуально и за различные периоды символа и из-за шума и других источников ухудшения параметров беспроводного канала, NT векторов
получают индивидуально и за различные периоды символа и из-за шума и других источников ухудшения параметров беспроводного канала, NT векторов 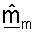 матрицы
матрицы 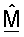 вряд ли будут ортогональны друг другу. Если NT векторов
вряд ли будут ортогональны друг другу. Если NT векторов 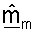 после этого будут использоваться для согласованной фильтрации принятой передачи данных, то любые ошибки в ортогональности между этими векторами приведут к перекрестным помехам (взаимному влиянию) между отдельными потоками символов, посланными на NT собственных модах. Перекрестные помехи могут ухудшать производительность.
после этого будут использоваться для согласованной фильтрации принятой передачи данных, то любые ошибки в ортогональности между этими векторами приведут к перекрестным помехам (взаимному влиянию) между отдельными потоками символов, посланными на NT собственных модах. Перекрестные помехи могут ухудшать производительность.
II. Ортогонализация собственных векторов
В другом аспекте для улучшения производительности усовершенствованную матрицу согласованного фильтра 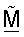 получают, основываясь на управляющем опорном сигнале, и она имеет векторы строки, которые должны быть ортогональными один относительно другого. Ортогонализацию векторов строк
получают, основываясь на управляющем опорном сигнале, и она имеет векторы строки, которые должны быть ортогональными один относительно другого. Ортогонализацию векторов строк 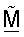 могут выполнять с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция. Все эти методики ортогонализации описаны подробно ниже. Другие методики ортогонализации могут также использоваться, и они находятся в пределах сущности изобретения.
могут выполнять с помощью различных методик, таких как QR-разложение, вычисление минимальной квадратической ошибки и полярная декомпозиция. Все эти методики ортогонализации описаны подробно ниже. Другие методики ортогонализации могут также использоваться, и они находятся в пределах сущности изобретения.
1. QR-разложение
QR-разложение разлагает транспонированную начальную матрицу согласованного фильтра 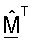 на ортогональную матрицу QF и на верхнюю треугольную матрицу RF. Матрица QF формирует ортогональное основание для столбцов матрицы
на ортогональную матрицу QF и на верхнюю треугольную матрицу RF. Матрица QF формирует ортогональное основание для столбцов матрицы 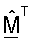 (т.е. строки
(т.е. строки 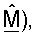 и диагональные элементы матрицы RF задают длину компонентов столбцов
и диагональные элементы матрицы RF задают длину компонентов столбцов 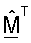 в направлениях соответствующих столбцов QF. Матрицы QF и RF могут использоваться для получения усовершенствованной матрицы согласованного фильтра
в направлениях соответствующих столбцов QF. Матрицы QF и RF могут использоваться для получения усовершенствованной матрицы согласованного фильтра 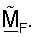
QR-разложение может выполняться различными способами, которые включают в себя процедуру Грама-Шмидта (Gram-Schmidt), преобразование Хаусхолдера (Householder) и т.д. Процедура Грама-Шмидта рекурсивна и может быть в цифровой форме нестабильной. Изобретены различные варианты процедуры Грама-Шмидта, и они известны из предшествующего уровня техники. "Классическая" процедура Грама-Шмидта для ортогонализации матрицы 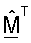 описана ниже.
описана ниже.
Для QR-разложения матрица 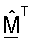 может быть выражена как:
может быть выражена как:

где QF - ортогональная матрица (NR × NR); и RF - верхняя треугольная матрица (NR × NT) с нулями ниже диагонали и возможными ненулевыми значениями по и выше диагонали.
Процедура Грама-Шмидта генерирует матрицы QF и RF столбец за столбцом. Следующие обозначения используются для приведенного ниже описания:
QF=[q1q2 ... qN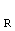 ], где qj является j-м столбцом QF;
], где qj является j-м столбцом QF;
qi,j - элемент в i-й строке и j-м столбце QF;
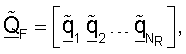 где
где  является j-м столбцом
является j-м столбцом 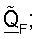
ri,j- элемент в i-й строке и j-м столбце RF;
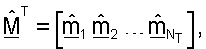 где
где 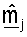 является j-м столбцом
является j-м столбцом 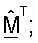 и
и
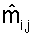 является элементом в i-й строке и j-м столбце
является элементом в i-й строке и j-м столбце 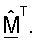
Первый столбец QF и RF может быть получен как:

Первый столбец RF включает в себя одно ненулевое значение r1,1 для первой строки и нули в других местах, где r1,1 - вторая норма 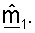 Первый столбец QF является нормализованной версией первого столбца
Первый столбец QF является нормализованной версией первого столбца 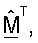 причем нормализацию выполняют с помощью масштабирования каждого элемента
причем нормализацию выполняют с помощью масштабирования каждого элемента 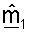 с помощью инвертирования r1,1.
с помощью инвертирования r1,1.
Каждый из оставшихся столбцов QF и RF может быть получен следующим образом:
для j=2, 3, ... NT
для i=1, 2, ... j-1

Процедура Грама-Шмидта генерирует один столбец за один раз для матрицы QF. Каждый новый столбец QF должен быть ортогонален ко всем ранее сгенерированным столбцам слева от нового столбца. Это достигают с помощью уравнений (14) и (16), где j-й столбец QF (или qj) генерируют, основываясь на 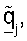 который в свою очередь генерируют, основываясь на j-м столбце
который в свою очередь генерируют, основываясь на j-м столбце 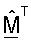 (или
(или 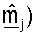 и вычитая любые компоненты в
и вычитая любые компоненты в 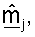 направленные в направлении других (j-1) столбцов слева от
направленные в направлении других (j-1) столбцов слева от 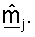 Диагональные элементы RF вычисляют как вторые нормы столбцов
Диагональные элементы RF вычисляют как вторые нормы столбцов 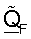 (где
(где 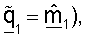 как показано в уравнении (15).
как показано в уравнении (15).
Улучшенная производительность может достигаться с помощью упорядочивания матрицы 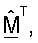 основываясь на оценках сингулярных значений перед выполнением QR-разложения. Начальные оценки сингулярных значений
основываясь на оценках сингулярных значений перед выполнением QR-разложения. Начальные оценки сингулярных значений 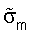 для m ∈ {1 ... NT} для диагональной матрицы
для m ∈ {1 ... NT} для диагональной матрицы 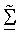 можно вычислять как вторые нормы столбцов
можно вычислять как вторые нормы столбцов 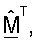 как описано ниже. Начальные оценки сингулярных значений можно затем упорядочить так, что
как описано ниже. Начальные оценки сингулярных значений можно затем упорядочить так, что 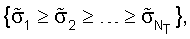 где
где 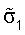 является наибольшей оценкой сингулярных значений и
является наибольшей оценкой сингулярных значений и 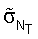 является наименьшей оценкой сингулярных значений. Когда начальные оценки сингулярных значений для диагональной матрицы
является наименьшей оценкой сингулярных значений. Когда начальные оценки сингулярных значений для диагональной матрицы 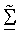 упорядочиваются, столбцы матрицы
упорядочиваются, столбцы матрицы 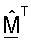 также упорядочиваются соответственно. Первый или крайний левый столбец
также упорядочиваются соответственно. Первый или крайний левый столбец 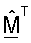 затем связывают с наибольшей оценкой сингулярных значения и самым высоким принятым ОСШ и последний или крайний справа столбец
затем связывают с наибольшей оценкой сингулярных значения и самым высоким принятым ОСШ и последний или крайний справа столбец 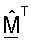 связывают с наименьшей оценкой сингулярных значений и самым низким принятым ОСШ. Для QR-разложения начальные оценки сингулярных значений могут быть получены как вторые нормы столбцов
связывают с наименьшей оценкой сингулярных значений и самым низким принятым ОСШ. Для QR-разложения начальные оценки сингулярных значений могут быть получены как вторые нормы столбцов 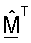 и использоваться для упорядочивания столбцов
и использоваться для упорядочивания столбцов 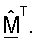 Конечные оценки сингулярных значений получают как вторые нормы столбцов
Конечные оценки сингулярных значений получают как вторые нормы столбцов 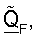 как описано выше. Управляющий опорный сигнал может также передаваться по порядку (например, от наибольшей собственной моды до наименьшей собственной моды), так чтобы оценки сингулярных значений эффективно упорядочивались передатчиком.
как описано выше. Управляющий опорный сигнал может также передаваться по порядку (например, от наибольшей собственной моды до наименьшей собственной моды), так чтобы оценки сингулярных значений эффективно упорядочивались передатчиком.
Если столбцы 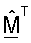 упорядочиваются на основе уменьшения значений соответствующих им оценок сингулярных значений, то столбцы/собственные векторы QF должны быть ортогональны к первому столбцу/собственному вектору с лучшим принятым ОСШ. Это упорядочивание таким образом имеет благоприятное воздействие удаления определенных шумовых компонентов каждого из оставшихся собственных векторов QF. В частности, j-й столбец QF (или qj) генерируют на основе j-го столбца
упорядочиваются на основе уменьшения значений соответствующих им оценок сингулярных значений, то столбцы/собственные векторы QF должны быть ортогональны к первому столбцу/собственному вектору с лучшим принятым ОСШ. Это упорядочивание таким образом имеет благоприятное воздействие удаления определенных шумовых компонентов каждого из оставшихся собственных векторов QF. В частности, j-й столбец QF (или qj) генерируют на основе j-го столбца 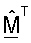 (или
(или 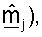 и шумовые компоненты в
и шумовые компоненты в 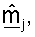 которые указывают в направлении j-1 собственных векторов слева от qj (которые связаны с более высокими принятыми ОСШ), вычитают из
которые указывают в направлении j-1 собственных векторов слева от qj (которые связаны с более высокими принятыми ОСШ), вычитают из 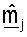 для получения qj. Упорядочивание также имеет благоприятное воздействие улучшения оценок собственных векторов, связанных с меньшими сингулярными значениями. Конечным результатом является улучшенная производительность, особенно если ортогонализированные собственные векторы QF используются для пространственной обработки для передачи данных в другой линии связи, как описано ниже.
для получения qj. Упорядочивание также имеет благоприятное воздействие улучшения оценок собственных векторов, связанных с меньшими сингулярными значениями. Конечным результатом является улучшенная производительность, особенно если ортогонализированные собственные векторы QF используются для пространственной обработки для передачи данных в другой линии связи, как описано ниже.
Усовершенствованная ортогональная матрица согласованного фильтра 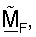 полученная на основе QR-разложения, может затем быть выражена как:
полученная на основе QR-разложения, может затем быть выражена как:

где 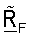 включает в себя только диагональные элементы RF (т.е. элементы выше диагонали установлены в нули). Диагональные элементы
включает в себя только диагональные элементы RF (т.е. элементы выше диагонали установлены в нули). Диагональные элементы 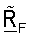 и RF - оценки сингулярных значений H. Поскольку M=ΣTUH и
и RF - оценки сингулярных значений H. Поскольку M=ΣTUH и 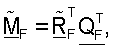 могут быть сделаны следующие замены:
могут быть сделаны следующие замены: 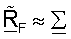 и QF=U*, где "*" обозначает комплексное сопряжение.
и QF=U*, где "*" обозначает комплексное сопряжение.
2. Вычисление среднеквадратической ошибки и полярная декомпозиция
Начальная матрица согласованного фильтра 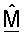 может также ортогонализироваться на основе определенного критерия оптимальности. Одним из возможных критериев является минимизация величины квадратической ошибки между матрицей
может также ортогонализироваться на основе определенного критерия оптимальности. Одним из возможных критериев является минимизация величины квадратической ошибки между матрицей 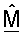 и "оптимальным" согласованным фильтром с требуемыми свойствами ортогональности. Это может быть выражено как:
и "оптимальным" согласованным фильтром с требуемыми свойствами ортогональности. Это может быть выражено как:
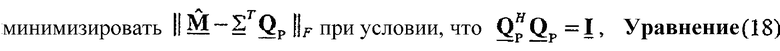
где 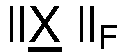 - норма Фробениуса (Frobenius) для X, и задается как:
- норма Фробениуса (Frobenius) для X, и задается как:

Условие 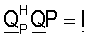 гарантирует, что QP является унитарной матрицей, что означает, что столбцы QP ортогональны друг к другу и строки QP также ортогональны друг к другу. Уравнение (18) приводит к оптимальному согласованному фильтру ΣTQP, который наилучшим образом подходит к измеренным данным, представленным с помощью матрицы
гарантирует, что QP является унитарной матрицей, что означает, что столбцы QP ортогональны друг к другу и строки QP также ортогональны друг к другу. Уравнение (18) приводит к оптимальному согласованному фильтру ΣTQP, который наилучшим образом подходит к измеренным данным, представленным с помощью матрицы 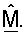
Решение уравнения (18) может быть получено из известного решения ортогональной проблемы Прокруста (Procrustes). Эта проблема задает вопрос: если даны две известные матрицы A и В, может ли быть найдена унитарная матрица QP, которая превращает В в A. Проблема может быть выражена как:
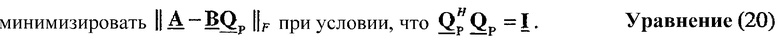
Решение проблемы Прокруста может быть получено следующим образом. Сначала матрицу CP определяют как CP=BHA. Разложение по сингулярным числам CP затем представляют как CP=UpΣP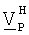 или
или 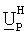 CPVP=ΣP. Унитарную матрицу QP, которая решает проблему минимизации, показанную в уравнении (20), затем представляют как:
CPVP=ΣP. Унитарную матрицу QP, которая решает проблему минимизации, показанную в уравнении (20), затем представляют как:

Получение и доказательство уравнения (21) описаны G. H. Golub и C. F. Van Loan в "Matrix Computation", Third Edition, Johns Hopkins University Press, 1996.
Решение уравнения (20), которое показано в уравнении (21), относится к полярной декомпозиции матрицы C. Эта полярная декомпозиция задается следующим образом:

где ZP - унитарная матрица, которая задается как 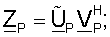
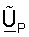 - матрица левых собственных векторов CP, которая охватывает место столбца CP (т.е.
- матрица левых собственных векторов CP, которая охватывает место столбца CP (т.е. 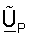 равно UP или субматрице UP в зависимости от размерности CP);
равно UP или субматрице UP в зависимости от размерности CP);
PP - симметрическая положительная полуопределенная Эрмитова (Hermitian) матрица, которая задается как
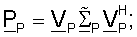 и
и
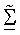 является квадратной матрицей сингулярных значений CP с размерностью, равной количеству столбцов CP.
является квадратной матрицей сингулярных значений CP с размерностью, равной количеству столбцов CP.
Полярная декомпозиция может таким образом выполняться на матрице CP для получения унитарной матрицы ZP, которая может быть равна или QP, или субматрице QP в зависимости от размерности CP. Можно показать, что матрица ZP является оптимальным результатом для проблемы минимизации, показанной в уравнении (20).
Алгоритмы для прямого вычисления полярной декомпозиции описаны P. Zielinski и K. Zietak в "The Polar Decomposition-Properties, Applications and Algorithms," Annals of the Polish Mathematical Society, 38 (1995), и A. A. Dubrulle в "An Optimum Iteration for the Matrix Polar Decomposition," Electronic Transactions on Numerical Analysis, том 8, 1999, стр. 21-25.
Решение для оптимального согласованного фильтра, которое выражено в уравнении (18), может быть получено на основе решения описанной выше ортогональной проблемы Прокруста. Это может выполняться с помощью приравнивания 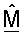 к A и ΣT к В. Для вычисления оценка сингулярных значений
к A и ΣT к В. Для вычисления оценка сингулярных значений 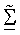 может быть получена как вторая норма столбцов
может быть получена как вторая норма столбцов 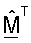 и использоваться вместо Σ. Диагональные элементы
и использоваться вместо Σ. Диагональные элементы 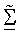 могут быть выражены как:
могут быть выражены как:
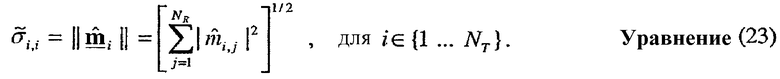
Можно показать, что использование 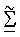 в вычислении для QP приводит почти к неизмеримому ухудшению производительности относительно использования точных сингулярных значений в Σ.
в вычислении для QP приводит почти к неизмеримому ухудшению производительности относительно использования точных сингулярных значений в Σ.
Матрица CM может затем определяться как:

Разложение по сингулярным числам матрицы CM тогда задается следующим образом:
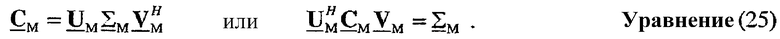
Унитарная матрица QM, которая решает проблему минимизации, показанную в уравнении (18), тогда задается как:

Усовершенствованный ортогональный согласованный фильтр 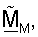 который является решением проблемы минимизации в уравнении (18), может тогда быть выражен как:
который является решением проблемы минимизации в уравнении (18), может тогда быть выражен как:

Альтернативно, полярная декомпозиция CM может выполняться, как описано выше, что может быть выражено как:

Унитарная матрица QM, которая решает проблему минимизации, показанную в уравнении (18), тогда может быть представлена как:

Усовершенствованный ортогональный согласованный фильтр 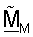 может тогда быть выражен как:
может тогда быть выражен как:

Можно показать, что матрица ZM полярной декомпозиции является оптимальным результатом для матрицы QM для вычисления минимальной квадратической ошибки (т.е. QM=ZM). Таким образом, полярная декомпозиция и вычисление минимальной квадратической ошибки оба приводят к тому же самому ортогональному согласованному фильтру 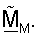
Фиг.1 показывает последовательность операций варианта осуществления процесса 100 для получения ортогональной матрицы 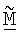 согласованного фильтра, основываясь на управляющем опорном сигнале. Сначала приемник принимает и обрабатывает управляющий опорный сигнал для получения оценки umσm для каждой из множества собственных мод H (этап 112). Эта обработка может выполняться, как описано выше. Затем формируют начальную матрицу
согласованного фильтра, основываясь на управляющем опорном сигнале. Сначала приемник принимает и обрабатывает управляющий опорный сигнал для получения оценки umσm для каждой из множества собственных мод H (этап 112). Эта обработка может выполняться, как описано выше. Затем формируют начальную матрицу 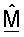 согласованного фильтра, чьи строки
согласованного фильтра, чьи строки 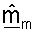 для m ∈ {1...NT} получают, основываясь на оценках umσm. Ортогональная матрица
для m ∈ {1...NT} получают, основываясь на оценках umσm. Ортогональная матрица 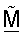 согласованного фильтра может затем быть получена из начальной матрицы
согласованного фильтра может затем быть получена из начальной матрицы 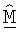 согласованного фильтра, используя любую из описанных выше методик ортогонализации.
согласованного фильтра, используя любую из описанных выше методик ортогонализации.
Для методики QR-разложения матрицу 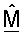 разлагают на множители для получения матриц QF и RF (этап 122). Ортогональную матрицу
разлагают на множители для получения матриц QF и RF (этап 122). Ортогональную матрицу 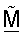 согласованного фильтра затем получают, как показано в уравнении (17) (этап 124), и оценки сингулярных значений
согласованного фильтра затем получают, как показано в уравнении (17) (этап 124), и оценки сингулярных значений 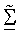 получают как диагональные элементы RF (этап 126).
получают как диагональные элементы RF (этап 126).
Для методики минимальной квадратической ошибки оценки сингулярных значений 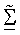 получают как вторые нормы столбцов
получают как вторые нормы столбцов 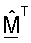 (этап 132). Затем вычисляют матрицу CM, как показано в уравнении (24) (этап 134). Затем вычисляют разложение по сингулярным числам CM, как показано в уравнении (25) (этап 136). Затем получают ортогональную матрицу
(этап 132). Затем вычисляют матрицу CM, как показано в уравнении (24) (этап 134). Затем вычисляют разложение по сингулярным числам CM, как показано в уравнении (25) (этап 136). Затем получают ортогональную матрицу 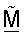 согласованного фильтра, как показано в уравнении (27) (этап 138).
согласованного фильтра, как показано в уравнении (27) (этап 138).
Для методики полярной декомпозиции оценки сингулярных значений 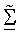 получают как вторые нормы столбцов
получают как вторые нормы столбцов 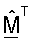 (этап 142). Затем вычисляют матрицу CM, как показано в уравнении (24) (этап 144). Затем вычисляют полярную декомпозицию CM, как показано в уравнении (28) (этап 146). Затем получают ортогональную матрицу согласованного фильтра
(этап 142). Затем вычисляют матрицу CM, как показано в уравнении (24) (этап 144). Затем вычисляют полярную декомпозицию CM, как показано в уравнении (28) (этап 146). Затем получают ортогональную матрицу согласованного фильтра 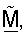 как показано в уравнении (30) (этап 148).
как показано в уравнении (30) (этап 148).
Ортогональная матрица 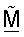 согласованного фильтра может после этого использоваться для выполнения согласованной фильтрации принятой передачи данных (этап 150).
согласованного фильтра может после этого использоваться для выполнения согласованной фильтрации принятой передачи данных (этап 150).
Ортогонализация матрицы согласованного фильтра обеспечивает несколько преимуществ. Во-первых, при использовании ортогональной матрицы 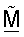 согласованного фильтра избегают перекрестных помех между собственными модами H. Получение начальной матрицы
согласованного фильтра избегают перекрестных помех между собственными модами H. Получение начальной матрицы 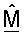 согласованного фильтра по частям, основываясь на управляющем опорном сигнале, не гарантирует, что собственные векторы
согласованного фильтра по частям, основываясь на управляющем опорном сигнале, не гарантирует, что собственные векторы 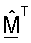 ортогональны. Нехватка ортогональности приводит к ухудшению рабочих характеристик. При ортогонализации матрицы согласованного фильтра избегают этого ухудшения рабочих характеристик.
ортогональны. Нехватка ортогональности приводит к ухудшению рабочих характеристик. При ортогонализации матрицы согласованного фильтра избегают этого ухудшения рабочих характеристик.
Во-вторых, QR-разложение может улучшать качество собственных векторов, связанных с меньшими сингулярными значениями. Без QR-разложения качество оценок собственных векторов не является постоянным, и оценки собственных векторов, связанных с меньшими сингулярными значениями, вероятно, будут ниже по качеству. QR-разложение может улучшать качество собственных векторов, связанных с меньшими сингулярными значениями, удаляя определенные шумовые компоненты, как описано выше. Полярная декомпозиция может иметь подобный эффект, но не прямым способом, как QR-разложение.
В-третьих, ортогонализация может сокращать количество ресурсов, необходимых для передачи управляющего опорного сигнала. Если ортогонализация не выполняется, то высококачественные оценки Σ и U необходимы для того, чтобы гарантировать низкие перекрестные помехи между собственными модами. Более длительный период передачи тогда необходим для управляющего опорного сигнала для собственных векторов, связанных с меньшими сингулярными значениями, чтобы гарантировать получение необходимого качества. Высококачественные оценки Σ и U, таким образом, требуют более длительного периода передачи для управляющего опорного сигнала (что будет потреблять ценные системные ресурсы) и более длительного периода интеграции для управляющего опорного сигнала в приемнике (что может привести к более длительной задержке передачи данных). Ортогонализация может обеспечивать требуемую производительность без необходимости в высококачественных оценках Σ и U.
III. Система MIMO-OFDM
Методики для получения собственных векторов, используемые для пространственной обработки, теперь будут описаны для примерной широкополосной системы связи MIMO, которая использует мультиплексирование с ортогональным частотным разделением (OFDM). OFDM фактически делит полную ширину полосы пропускания системы на множество ортогональных поддиапазонов (NF), которые также упоминаются как сигналы, элементы разрешения по частоте или частотные подканалы. При OFDM каждый поддиапазон связан с соответствующей поднесущей, на которой могут модулироваться данные. Для системы MIMO-OFDM каждый поддиапазон может быть связан с многочисленными собственными модами, и каждая собственная мода каждого поддиапазона может рассматриваться как независимый канал передачи.
Для OFDM данные или пилот-сигнал, которые будут передаваться в каждом пригодном для использования поддиапазоне, сначала модулируют (т.е. отображают на символы модуляции), используя определенные схемы модуляции. Один символ модуляции может передаваться в каждом пригодном для использования поддиапазоне в каждый период символа. Сигнал с нулевым значением могут посылать для каждого неиспользуемого поддиапазона. В течение каждого периода символа OFDM символы модуляции для пригодных для использования поддиапазонов и нулевые значения сигнала для неиспользуемых поддиапазонов (т.е. символы модуляции и нули для всех NF поддиапазонов) преобразовывают к временной области, используя обратное быстрое преобразование Фурье (IFFT) для получения преобразованного символа, который содержит NF выборок временной области. Для борьбы с межсимвольными помехами (ISI), вызванными избирательным затуханием частот, часть каждого преобразованного символа часто повторяется (что часто упоминается как добавление циклического префикса) для формирования соответствующего символа OFDM. Символ OFDM затем обрабатывают и передают по беспроводному каналу. Период символа OFDM, который также упоминается как период символа, соответствует продолжительности одного символа OFDM.
Для данной примерной системы нисходящая линия связи и восходящая линия связи совместно используют один диапазон частот, используя дуплексную связь с временным разделением каналов (ДСВРК). Для системы связи ДСВРК MIMO-OFDM ответы каналов нисходящей линии связи и восходящей линии связи, как можно предположить, являются обратной величиной друг друга. Таким образом, если H(k) представляет матрицу ответа канала от антенной решетки А к антенной решетке В для поддиапазона k, то взаимно-обратный канал подразумевает, что связь от антенной решетки В к антенной решетке A задается с помощью HT(k).
Фиг.2 показывает систему 200 радиосвязи, которая включает в себя множество точек доступа (ТД) 210, которые осуществляют связь с множеством пользовательских терминалов (ПТ) 220. (Для простоты только одна точка доступа показана на фиг.2.) Точка доступа может также упоминаться как базовая станция, или может использоваться некоторая другая терминология. Каждый пользовательский терминал может быть неподвижным или подвижным терминалом, и он может также упоминаться как терминал доступа, подвижная станция, удаленная станция, пользовательское оборудование (ПО), беспроводное устройство, или может использоваться некоторая другая терминология. Каждый пользовательский терминал может осуществлять связь с одной или, возможно, с многими точками доступа в нисходящей линии связи и/или в восходящей линии связи в любой заданный момент. Нисходящая линия связи (т.е. прямая линия связи) относится к передаче от точки доступа к пользовательскому терминалу, и восходящая линия связи (т.е. обратная линия связи) относится к передаче от пользовательского терминала к точке доступа. Ответ канала между каждой точкой доступа и каждым пользовательским терминалом может характеризоваться набором матриц H(k) ответа канала, для k∈K, где K представляет набор всех поддиапазонов, представляющих интерес (например, пригодных для использования поддиапазонов).
В последующем описании для пары осуществляющих связь точки доступа и пользовательского терминала предполагается, что калибровка была выполнена для учета различий между цепями передачи и приема точки доступа и пользовательского терминала. Результатами калибровки являются диагональные матрицы 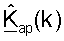 и
и 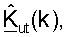 для k∈K, которые используются в точке доступа и в пользовательском терминале, соответственно, в тракте передачи. "Калиброванный" ответ канала нисходящей линии связи, Hcdn(k), наблюдаемый пользовательским терминалом, и "калиброванный" ответ канала восходящей линии связи, Hcup(k), наблюдаемый точкой доступа, могут тогда выражаться как:
для k∈K, которые используются в точке доступа и в пользовательском терминале, соответственно, в тракте передачи. "Калиброванный" ответ канала нисходящей линии связи, Hcdn(k), наблюдаемый пользовательским терминалом, и "калиброванный" ответ канала восходящей линии связи, Hcup(k), наблюдаемый точкой доступа, могут тогда выражаться как:
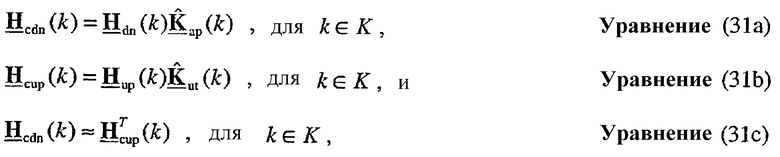
где Hdn(k)=Rut(k)H(k)Tap(k) является "эффективным" ответом канала нисходящей линии связи, который включает в себя ответы цепи передачи Tap(k) в точке доступа и цепи приема Rut(k) в пользовательском терминале;
Hup(k)=Rap(k)HT(k)Tut(k) является "эффективным" ответом канала восходящей линии связи, который включает в себя ответы цепи передачи Tut(k) в пользовательском терминале и цепи приема Rap(k) в точке доступа; и
H(k) является (Nut × Nap) матрицей ответа канала между Nap антеннами в точке доступа и Nut антеннами в пользовательском терминале. Если калибровка не выполнена, то каждую матрицу 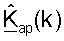 и
и 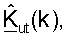 для k∈K, устанавливают в единичную матрицу I.
для k∈K, устанавливают в единичную матрицу I.
Фиг.3 показывает вариант осуществления структуры 300 кадра, который может использоваться для системы ДСВРК MIMO-OFDM. Передача данных происходит в кадрах ДСВРК, причем каждый кадр ДСВРК охватывает определенную продолжительность времени (например, 2 мс). Каждый кадр ДСВРК разделен на фазу нисходящей линии связи и фазу восходящей линии связи. Фаза нисходящей линии связи дополнительно разделена на множество сегментов для множества каналов транспортировки нисходящей линии связи. В варианте осуществления, показанном на фиг.3, каналы транспортировки нисходящей линии связи включают в себя широковещательный канал (BCH), прямой канал управления (FCCH) и прямой канал (FCH). Точно так же фаза восходящей линии связи разделена на множество сегментов для множества транспортных каналов восходящей линии связи. В варианте осуществления, показанном на фиг.3, транспортные каналы восходящей линии связи включают в себя обратный канал (RCH) и канал произвольного доступа (RACH).
В фазе нисходящей линии связи сегмент 310 BCH используют для передачи одного протокольного блока данных (ПБД, PDU) 312 BCH, который включает в себя пилот-сигнал маяка 314, пилот-сигнал 316 MIMO и сообщение 318 BCH. Пилот-сигнал маяка передают от всех антенн точки доступа, и он используется пользовательскими терминалами для синхронизации и получения частоты. Пилот-сигнал MIMO передают от всех антенн точки доступа с различными ортогональными кодами, и он используется пользовательскими терминалами для оценки канала. Сообщение BCH переносит системные параметры для пользовательских терминалов в системе. Сегмент 320 FCCH используют для передачи одного PDU FCCH, который переносит назначение ресурсов для нисходящей линии связи и восходящей линии связи и другой сигнализации для пользовательских терминалов. Сегмент 330 FCH используют для передачи одного или большего количества PDU 332 FCH. Могут определяться различные типы PDU FCH. Например, PDU 332a FCH включает в себя только пакет данных 336a, а PDU 332b FCH включает в себя управляющий опорный сигнал 334b нисходящей линии связи и пакет данных 336b.
В фазе восходящей линии связи сегмент 340 RCH используют для передачи одного или большего количества PDU 342 RCH в восходящей линии связи. Также могут определяться различные типы PDU RCH. Например, PDU 342a RCH включает в себя управляющий опорный сигнал 344a восходящей линии связи и пакет данных 346a. Сегмент 350 RACH используется пользовательскими терминалами для получения доступа к системе и для передачи коротких сообщений в восходящей линии связи. PDU 352 RACH могут посылать в пределах сегмента 350 RACH, и он включает в себя управляющий опорный сигнал 354 восходящей линии связи и сообщение 356.
Для варианта осуществления, показанного на фиг.3, пилот-сигналы маяка и MIMO посылают по нисходящей линии связи в сегменте BCH в каждом кадре ДСВРК. Управляющий опорный сигнал могут посылать, а могут не посылать в любом заданном PDU FCH/RCH. Управляющий опорный сигнал могут также посылать в PDU RACH для предоставления возможности точке доступа оценивать подходящие векторы во время доступа к система.
Для простоты последующее описание приведено для осуществления связи между одной точкой доступа и одним пользовательским терминалом. Пилот-сигнал MIMO передают с помощью точки доступа, и он используется пользовательским терминалом для получения оценки калиброванного ответа канала нисходящей линии связи, 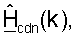 для k∈K. Калиброванный ответ восходящей линии связи могут затем оценивать как
для k∈K. Калиброванный ответ восходящей линии связи могут затем оценивать как 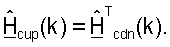 Разложение по сингулярным числам может выполняться для диагонализированной матрицы
Разложение по сингулярным числам может выполняться для диагонализированной матрицы 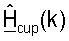 для каждого поддиапазона, что может быть выражено как:
для каждого поддиапазона, что может быть выражено как:
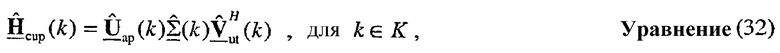
где 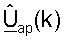 - (Nap × Nap) унитарная матрица левых собственных векторов
- (Nap × Nap) унитарная матрица левых собственных векторов 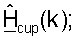
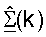 - (Nap × Nut) диагональная матрица сингулярных значений
- (Nap × Nut) диагональная матрица сингулярных значений 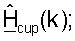 и
и
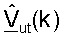 - (Nut × Nut) унитарная матрица правых собственных векторов
- (Nut × Nut) унитарная матрица правых собственных векторов 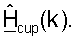
Точно так же разложение по сингулярным числам оценочной калиброванной матрицы ответа канала нисходящей линии связи 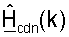 может быть выражено как:
может быть выражено как:
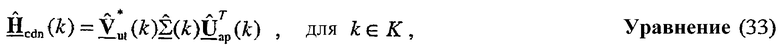
где матрицы 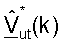 и
и 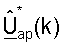 - унитарные матрицы левых и правых собственных векторов, соответственно,
- унитарные матрицы левых и правых собственных векторов, соответственно, 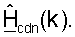
Как показано в уравнениях (32) и (33), матрицы левых и правых собственных векторов для одной линии связи являются комплексным сопряжением матриц правых и левых собственных векторов, соответственно, для другой линии связи. Для простоты ссылка к матрицам 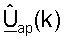 и
и 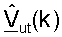 в последующем описании может также относиться к их другим отличающимся формам (например,
в последующем описании может также относиться к их другим отличающимся формам (например, 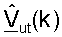 может относиться к
может относиться к 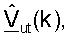
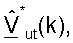 ,
, 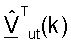 и
и 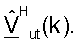 Матрицы
Матрицы 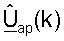 и
и 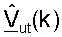 могут использоваться точкой доступа и пользовательским терминалом, соответственно, для пространственной обработки, и они также обозначены соответствующими подстрочными индексами. Матрица
могут использоваться точкой доступа и пользовательским терминалом, соответственно, для пространственной обработки, и они также обозначены соответствующими подстрочными индексами. Матрица 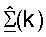 включает в себя оценки сингулярных значений, которые представляют коэффициенты усиления для независимых каналов (или собственных мод) матрицы H(k) ответа канала для k-го поддиапазона.
включает в себя оценки сингулярных значений, которые представляют коэффициенты усиления для независимых каналов (или собственных мод) матрицы H(k) ответа канала для k-го поддиапазона.
Разложение по сингулярным числам может выполняться независимо для матрицы 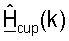 ответа канала для каждого из пригодных для использования поддиапазонов для определения Ns собственных мод для поддиапазона. Оценки сингулярных значений для каждой диагональной матрицы
ответа канала для каждого из пригодных для использования поддиапазонов для определения Ns собственных мод для поддиапазона. Оценки сингулярных значений для каждой диагональной матрицы 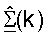 можно упорядочить так, что
можно упорядочить так, что 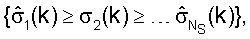 где
где 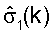 - наибольшая оценка сингулярных значении и
- наибольшая оценка сингулярных значении и 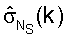 - наименьшая оценка сингулярных значений для поддиапазона k. Когда оценки сингулярных значений для каждой диагональной матрицы
- наименьшая оценка сингулярных значений для поддиапазона k. Когда оценки сингулярных значений для каждой диагональной матрицы 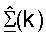 упорядочиваются, собственные векторы (или столбцы) связанных матриц
упорядочиваются, собственные векторы (или столбцы) связанных матриц 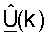 и
и 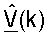 также упорядочиваются, соответственно. После упорядочивания
также упорядочиваются, соответственно. После упорядочивания 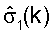 представляет оценку сингулярных значений для лучшей собственной моды для поддиапазона k, которая также часто упоминается как "основная" собственная мода.
представляет оценку сингулярных значений для лучшей собственной моды для поддиапазона k, которая также часто упоминается как "основная" собственная мода.
"Широкополосная" собственная мода может определяться как набор собственных мод того же самого порядка всех поддиапазонов после упорядочивания. Таким образом, m-я широкополосная собственная мода включает в себя m-е собственные моды всех поддиапазонов. Каждая широкополосная собственная мода связана с соответствующим набором собственных векторов для всех поддиапазонов. "Основная" широкополосная собственная мода - та, которая связана с наибольшей оценкой сингулярных значений в матрице 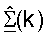 для каждого из поддиапазонов.
для каждого из поддиапазонов.
Пользовательский терминал может передавать управляющий опорный сигнал в восходящей линии связи. Управляющий опорный сигнал восходящей линии связи для m-й широкополосной собственной моды может быть выражен как:
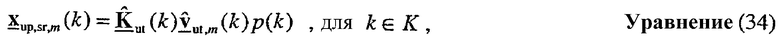
где 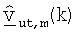 является m-м столбцом матрицы
является m-м столбцом матрицы 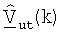 для k-го поддиапазона, причем
для k-го поддиапазона, причем
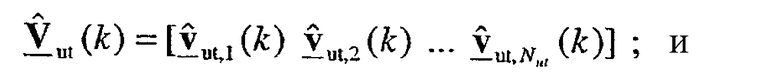
p(k) является пилотным символом для k-го поддиапазона.
Принятый управляющий опорный сигнал восходящей линии связи в точке доступа может быть выражен как:
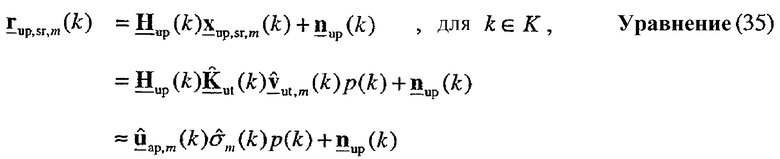
где 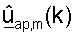 является m-м столбцом матрицы
является m-м столбцом матрицы 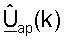 для k-го поддиапазона, причем
для k-го поддиапазона, причем
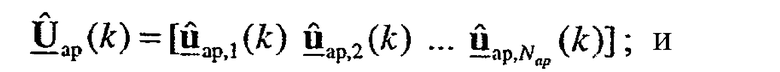
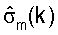 является оценкой сингулярных значений для k-го поддиапазона m-й широкополосной собственной моды.
является оценкой сингулярных значений для k-го поддиапазона m-й широкополосной собственной моды.
Точка доступа может получать начальную матрицу 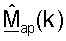 согласованного фильтра, для k∈K, на основе управляющего опорного сигнала восходящей линии связи, как описано выше. Точка доступа может после этого получать усовершенствованную ортогональную матрицу
согласованного фильтра, для k∈K, на основе управляющего опорного сигнала восходящей линии связи, как описано выше. Точка доступа может после этого получать усовершенствованную ортогональную матрицу 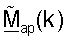 согласованного фильтра, для k∈K, основываясь на
согласованного фильтра, для k∈K, основываясь на 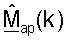 и используя любую из описанных выше методик ортогонализации.
и используя любую из описанных выше методик ортогонализации.
Используя QR-разложение, матрица 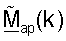 может быть получена как:
может быть получена как:
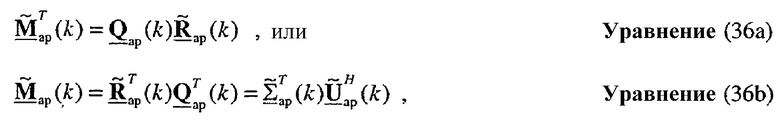
где Qap(k) - унитарная матрица, которая является орто-нормальным основанием для 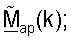
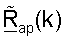 - диагональная матрица, полученная на основе
- диагональная матрица, полученная на основе 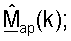 и
и
Используя вычисление среднеквадратической ошибки, матрица  может быть получена как:
может быть получена как:
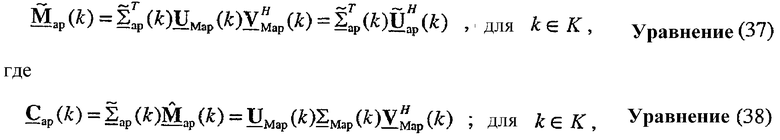
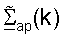 - диагональная матрица, элементы которой являются вторыми нормами столбцов
- диагональная матрица, элементы которой являются вторыми нормами столбцов 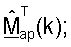 и
и
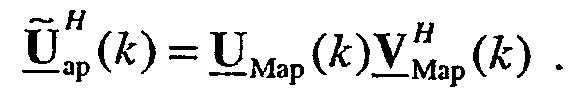
Используя полярную декомпозицию, матрица 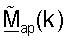 может быть получена как:
может быть получена как:
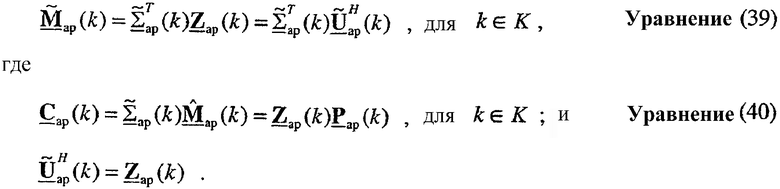
Матрица 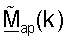 может использоваться точкой доступа для согласованной фильтрации передачи данных восходящей линии связи от пользовательского терминала, как описано ниже.
может использоваться точкой доступа для согласованной фильтрации передачи данных восходящей линии связи от пользовательского терминала, как описано ниже.
Пространственная обработка, выполняемая пользовательским терминалом для передачи данных по множеству собственных мод в восходящей линии связи, может быть выражена как:
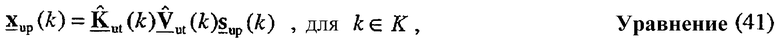
где sup(k) является вектором данных и xup(k) является вектором передачи для k-го поддиапазона для восходящей линии связи. Передача данных восходящей линии связи может происходить на любом количестве широкополосных собственных мод от 1 до NS.
Принятая передача данных восходящей линии связи в точке доступа может быть выражена как:
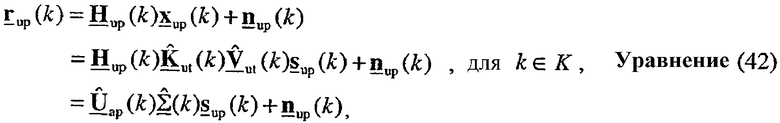
где rup(k) - принимаемый вектор для передачи данных восходящей линии связи для k-го поддиапазона.
Согласованная фильтрация с помощью точки доступа может выражаться как:
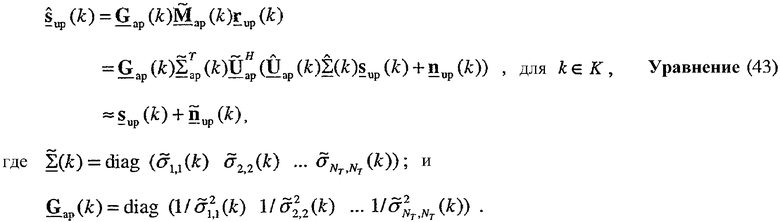
Для системы ДСВРК MIMO точка доступа может также использовать матрицы 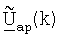 , для k∈K, для пространственной обработки для передачи данных в нисходящей линии связи на пользовательский терминал. Пространственная обработка, выполненная точкой доступа для передачи данных по множеству собственных мод в нисходящей линии связи, может быть выражена как:
, для k∈K, для пространственной обработки для передачи данных в нисходящей линии связи на пользовательский терминал. Пространственная обработка, выполненная точкой доступа для передачи данных по множеству собственных мод в нисходящей линии связи, может быть выражена как:
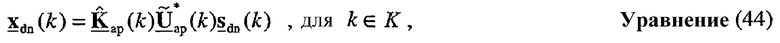
где sdn(k) - вектор данных, и xdn(k) - вектор передачи для k-го поддиапазона для нисходящей линии связи. Передача данных нисходящей линии связи может таким же образом происходить по любому количеству широкополосных собственных мод от 1 до NS.
Принятая передача данных нисходящей линии связи в пользовательском терминале может быть выражена как:
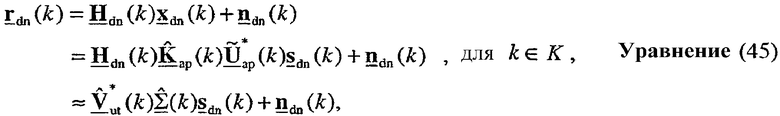
где rdn(k) - принимаемый вектор для передачи данных нисходящей линии связи для k-го поддиапазона.
Согласованная фильтрация с помощью пользовательского терминала может быть выражена как:
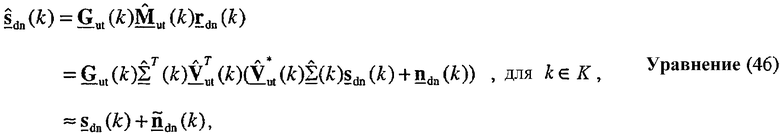
где 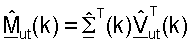 - согласованный фильтр для пользовательского терминала;
- согласованный фильтр для пользовательского терминала;
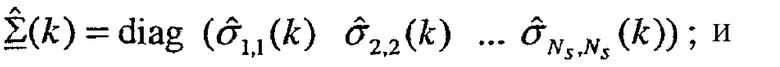
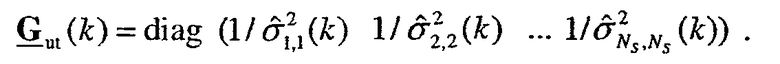
Диагональную матрицу 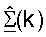 получают из разложения по сингулярным числам, показанного в уравнении (32).
получают из разложения по сингулярным числам, показанного в уравнении (32).
Таблица суммирует пространственную обработку в точке доступа и пользовательском терминале и для передачи данных, и для приема по множеству широкополосных собственных мод.
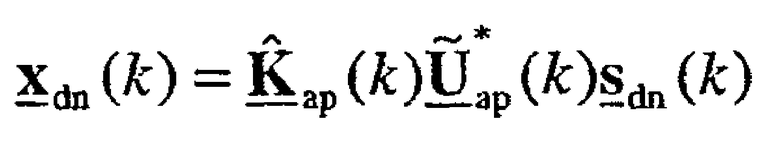
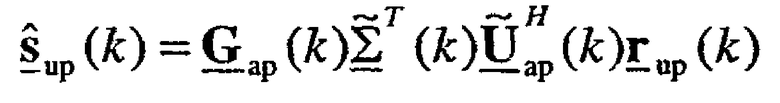
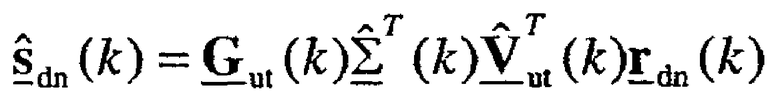
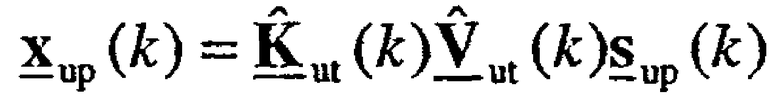
В таблице s(k) - вектор данных, x(k) - передаваемый вектор, r(k) - принимаемый вектор и 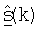 - оценка вектора данных s(k), где все векторы принадлежат поддиапазону k. Нижние индексы "dn" и "up" для этих векторов обозначают передачи нисходящей линии связи и восходящей линии связи соответственно.
- оценка вектора данных s(k), где все векторы принадлежат поддиапазону k. Нижние индексы "dn" и "up" для этих векторов обозначают передачи нисходящей линии связи и восходящей линии связи соответственно.
Можно показать, что использование матриц 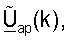 для k∈K (с ортоганизированными столбцами) для пространственной обработки для передачи данных нисходящей линии связи может обеспечивать существенное улучшение относительно использования матриц
для k∈K (с ортоганизированными столбцами) для пространственной обработки для передачи данных нисходящей линии связи может обеспечивать существенное улучшение относительно использования матриц 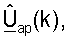 для k∈K (с неортоганизированными столбцами), полученных из начальной матрицы
для k∈K (с неортоганизированными столбцами), полученных из начальной матрицы 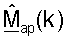 согласованного фильтра, для k∈K.
согласованного фильтра, для k∈K.
Фиг.4 показывает передачу управляющего опорного сигнала и данных по нисходящей линии связи и восходящей линии связи для примерной схемы передачи. Пилот-сигнал MIMO передают в нисходящей линии связи с помощью точки доступа в каждом кадре ДСВРК (этап 412). Пользовательский терминал принимает и обрабатывает пилот-сигнал нисходящей линии связи MIMO для получения оценки ответа канала нисходящей линии связи 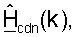 для k∈K. Пользовательский терминал затем оценивает ответ канала восходящей линии связи как
для k∈K. Пользовательский терминал затем оценивает ответ канала восходящей линии связи как 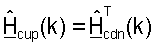 и выполняет разложение по сингулярным числам
и выполняет разложение по сингулярным числам 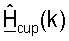 для получения матрицы
для получения матрицы 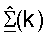 и
и 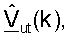 для k∈K, как показано в уравнении (32) (этап 414).
для k∈K, как показано в уравнении (32) (этап 414).
Пользовательский терминал затем передает управляющий опорный сигнал восходящей линии связи в RACH или RCH, используя матрицы 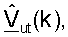 для k∈K, как показано в уравнении (34) и на фиг.3, во время доступа к системе (этап 422). Столбцы
для k∈K, как показано в уравнении (34) и на фиг.3, во время доступа к системе (этап 422). Столбцы 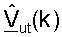 также упоминаются как управляющие векторы, когда они используется для передачи данных. Точка доступа принимает и обрабатывает управляющий опорный сигнал восходящей линии связи в RACH или RCH для получения матрицы
также упоминаются как управляющие векторы, когда они используется для передачи данных. Точка доступа принимает и обрабатывает управляющий опорный сигнал восходящей линии связи в RACH или RCH для получения матрицы 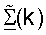 и
и 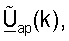 для k∈K, как описано выше (этап 424). Столбцы
для k∈K, как описано выше (этап 424). Столбцы 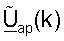 - собственные векторы, которые могут использоваться и для приема данных, и для передачи данных. Пользовательский терминал может после этого передавать управляющий опорный сигнал восходящей линии связи и данные по RCH, используя матрицы
- собственные векторы, которые могут использоваться и для приема данных, и для передачи данных. Пользовательский терминал может после этого передавать управляющий опорный сигнал восходящей линии связи и данные по RCH, используя матрицы 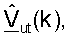 для k∈K, как показано в уравнении (41) и на фиг.3 (этап 432). Точка доступа принимает и обрабатывает управляющий опорный сигнал восходящей линии связи в RCH для обновления матриц
для k∈K, как показано в уравнении (41) и на фиг.3 (этап 432). Точка доступа принимает и обрабатывает управляющий опорный сигнал восходящей линии связи в RCH для обновления матриц 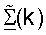 и
и 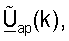 для k∈K (этап 434). Точка доступа также выполняет согласованную фильтрацию для принятой передачи данных восходящей линии связи, используя матрицы
для k∈K (этап 434). Точка доступа также выполняет согласованную фильтрацию для принятой передачи данных восходящей линии связи, используя матрицы 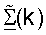 и
и 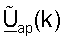 (также этап 434).
(также этап 434).
Точка доступа может после этого передавать дополнительный управляющий опорный сигнал нисходящей линии и данные по FCH, используя матрицы 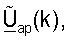 для k∈K, как показано в уравнении (44) и на фиг.3 (этап 442). Если передают управляющий опорный сигнал нисходящей линии связи, то пользовательский терминал может обрабатывать управляющий опорный сигнал нисходящей линии связи для обновления матриц
для k∈K, как показано в уравнении (44) и на фиг.3 (этап 442). Если передают управляющий опорный сигнал нисходящей линии связи, то пользовательский терминал может обрабатывать управляющий опорный сигнал нисходящей линии связи для обновления матриц 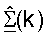 и
и 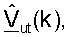 для k∈K (этап 444) и может также выполнить ортогонализацию для того, чтобы гарантировать, что столбцы
для k∈K (этап 444) и может также выполнить ортогонализацию для того, чтобы гарантировать, что столбцы 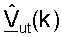 ортогональны. Пользовательский терминал также выполняет согласованную фильтрацию для принятой передачи данных нисходящей линии связи, используя матрицы
ортогональны. Пользовательский терминал также выполняет согласованную фильтрацию для принятой передачи данных нисходящей линии связи, используя матрицы 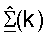 и
и 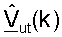 (также этап 444).
(также этап 444).
Схема передачи пилот-сигнала и данных, показанная на фиг.4, обеспечивает несколько преимуществ. Во-первых, пилот-сигнал MIMO, передаваемый точкой доступа, может использоваться многими пользовательскими терминалами в системе для оценки ответа их соответствующих каналов MIMO. Во-вторых, вычисление для разложения по сингулярным числам 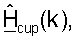 для k∈K, распределяют между пользовательскими терминалами (т.е. каждый пользовательский терминал выполняет разложение по сингулярным числам своего собственного набора оценочных матриц ответа канала для пригодных для использования поддиапазонов). В-третьих, точка доступа может получать матрицы
для k∈K, распределяют между пользовательскими терминалами (т.е. каждый пользовательский терминал выполняет разложение по сингулярным числам своего собственного набора оценочных матриц ответа канала для пригодных для использования поддиапазонов). В-третьих, точка доступа может получать матрицы 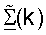 и
и 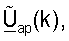 для k∈K, которые используются для пространственной обработки восходящей линии связи и нисходящей линии связи на основе управляющего опорного сигнала, без необходимости оценки ответа канала MIMO.
для k∈K, которые используются для пространственной обработки восходящей линии связи и нисходящей линии связи на основе управляющего опорного сигнала, без необходимости оценки ответа канала MIMO.
Различные другие схемы передачи могут также воплощаться для систем MIMO и MIMO-OFDM, и это находится в пределах сущности изобретения. Например, пилот-сигнал MIMO может передаваться пользовательским терминалом, и управляющий опорный сигнал может передаваться точкой доступа.
Фиг.5 показывает структурную схему варианта осуществления точки доступа 210x и пользовательского терминала 220x в системе 200 MIMO-OFDM. Для ясности в этом варианте осуществления точка доступа 210x оборудована четырьмя антеннами, которые могут использоваться для передачи и приема данных, и пользовательский терминал 220x также оборудован четырьмя антеннами для передачи/приема данных. В общем случае точка доступа и пользовательский терминал могут каждый быть оборудованы любым количеством передающих антенн и любым количеством приемных антенн.
В нисходящей линии связи в точке доступа 210x процессор 514 обработки данных передачи (ПД) принимает данные трафика из источника 512 данных и сигнализацию и другие данные от контроллера 530. Процессор 514 обработки данных ПД форматирует, кодирует, перемежает и модулирует данные для обеспечения символов модуляции, которые также упоминаются как символы данных. Пространственный процессор 520 передачи затем принимает и мультиплексирует символы данных с пилотными символами, выполняет необходимую пространственную обработку с помощью матриц 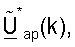 для k∈K, и обеспечивает четыре потока передаваемых символов для этих четырех передающих антенн. Каждый модулятор (МОД) 522 принимает и обрабатывает соответствующий поток передаваемых символов для обеспечения соответствующего модулированного сигнала нисходящей линии связи. Четыре модулированных сигнала нисходящей линии связи от модуляторов с 522a по 522d затем передают от антенн с 524a по 524d соответственно.
для k∈K, и обеспечивает четыре потока передаваемых символов для этих четырех передающих антенн. Каждый модулятор (МОД) 522 принимает и обрабатывает соответствующий поток передаваемых символов для обеспечения соответствующего модулированного сигнала нисходящей линии связи. Четыре модулированных сигнала нисходящей линии связи от модуляторов с 522a по 522d затем передают от антенн с 524a по 524d соответственно.
В пользовательском терминале 220x четыре антенны с 552a по 552d принимают передаваемые модулированные сигналы нисходящей линии связи, и каждая антенна обеспечивает передачу принятого сигнала к соответствующему демодулятору (ДЕМОД) 554. Каждый демодулятор 554 выполняет обработку, обратную к обработке, выполняемой модулятором 522, и обеспечивает принятые символы. Пространственный процессор 560 приема (ПР) затем выполняет согласованную фильтрацию принятых символов от всех демодуляторов с 554a по 554d для обеспечения восстановленных символов данных, которые являются оценками символов данных, передаваемых точкой доступа. Процессор 570 приема дополнительно обрабатывает (например, выполняет обратное отображение символов, деперемежает и декодирует) символы данных, которые восстанавливают для обеспечения декодированных данных, которые могут обеспечиваться к приемнику 572 данных для хранения и/или контроллеру 580 для дальнейшей обработки.
Пространственный процессор 560 ПР также обрабатывает принятые пилотные символы для получения оценки ответа канала нисходящей линии связи, 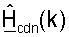 для k∈K. Контроллер 580 может затем разлагать каждую матрицу
для k∈K. Контроллер 580 может затем разлагать каждую матрицу 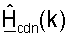 для получения
для получения 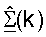 и
и 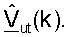 Контроллер 580 может далее получать (1) матрицы согласованного фильтра нисходящей линии связи
Контроллер 580 может далее получать (1) матрицы согласованного фильтра нисходящей линии связи 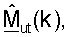 для k∈K, на основе
для k∈K, на основе 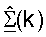 и
и 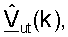 и (2) матрицы масштабирования Gut(k), для k∈K, на основе
и (2) матрицы масштабирования Gut(k), для k∈K, на основе 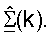 Контроллер 580 может затем обеспечивать передачу
Контроллер 580 может затем обеспечивать передачу 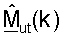 к процессору 560 обработки данных приема для согласованной фильтрации нисходящей линии связи и
к процессору 560 обработки данных приема для согласованной фильтрации нисходящей линии связи и 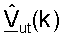 к пространственному процессору 590 ПД.
к пространственному процессору 590 ПД.
Обработка для восходящей линии связи может быть той же самой или отличаться от обработки для нисходящей линии связи. Данные и сигнализацию обрабатывают (например, кодируют, перемежают и модулируют) с помощью процессора 588 обработки данных ПД, мультиплексируют с пилотными символами и дополнительно пространственно обрабатывают с помощью пространственного процессора 590 ПД с матрицами 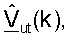 для k∈K. Переданные символы от пространственного процессора 590 ПД далее обрабатывают с помощью модуляторов с 554a по 554d для генерации четырех модулированных сигналов восходящей линии связи, которые затем передают через антенны с 552a по 552d.
для k∈K. Переданные символы от пространственного процессора 590 ПД далее обрабатывают с помощью модуляторов с 554a по 554d для генерации четырех модулированных сигналов восходящей линии связи, которые затем передают через антенны с 552a по 552d.
В точке доступа 510 модулированные сигналы восходящей линии связи принимают с помощью антенн с 524a по 524d и демодулируют с помощью демодуляторов с 522a по 522d для обеспечения принятых символов для управляющего опорного сигнала восходящей линии связи и передачи данных. Пространственный процессор 540 ПР затем обрабатывает принятый управляющий опорный сигнал восходящей линии связи для получения оценки umσm, для k∈K и m∈{1 ... NS}, которые обеспечивают на контроллер 530. Контроллер затем получает 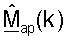 и
и 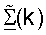 на основе оценок umσm, выполняет ортогонализацию
на основе оценок umσm, выполняет ортогонализацию 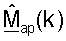 для получения
для получения 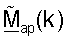 и
и 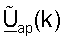 и получает Gap(k) на основе
и получает Gap(k) на основе 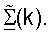 Контроллер 580 затем обеспечивает
Контроллер 580 затем обеспечивает 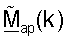 и Gap(k) к пространственному процессору 540 ПР для согласованной фильтрации восходящей линии связи и
и Gap(k) к пространственному процессору 540 ПР для согласованной фильтрации восходящей линии связи и 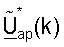 к пространственному процессору 520 ПД для пространственной обработки нисходящей линии связи.
к пространственному процессору 520 ПД для пространственной обработки нисходящей линии связи.
Пространственный процессор 540 ПР выполняет согласованную фильтрацию принятой передачи данных восходящей линии связи с 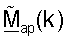 и Gap(k) для обеспечения восстановленных символов данных, которые дополнительно обрабатывают с помощью процессора 542 обработки данных ПР для обеспечения декодированных данных. Декодированные данные могут обеспечиваться к приемнику 544 данных для хранения и/или к контроллеру 530 для дальнейшей обработки.
и Gap(k) для обеспечения восстановленных символов данных, которые дополнительно обрабатывают с помощью процессора 542 обработки данных ПР для обеспечения декодированных данных. Декодированные данные могут обеспечиваться к приемнику 544 данных для хранения и/или к контроллеру 530 для дальнейшей обработки.
Контроллер 530 выполняет обработку для получения матрицы 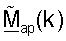 согласованного фильтра и матрицы Gap(k) масштабирования, для k∈K, для передачи данных восходящей линии связи и матрицы
согласованного фильтра и матрицы Gap(k) масштабирования, для k∈K, для передачи данных восходящей линии связи и матрицы 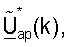 для k∈K, для передачи данных нисходящей линии связи. Контроллер 580 выполняет обработку для получения матрицы
для k∈K, для передачи данных нисходящей линии связи. Контроллер 580 выполняет обработку для получения матрицы 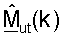 согласованного фильтра и матрицы Gut(k) масштабирования, для k∈K, для передачи данных нисходящей линии связи и матрицы
согласованного фильтра и матрицы Gut(k) масштабирования, для k∈K, для передачи данных нисходящей линии связи и матрицы 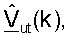 для k∈K, для передачи данных восходящей линии связи. Контроллеры 530 и 580 дополнительно управляют операциями различных процессоров в точке доступа и пользовательском терминале соответственно. Блоки памяти 532 и 582 хранят данные и коды программ, используемые контроллерами 530 и 580 соответственно.
для k∈K, для передачи данных восходящей линии связи. Контроллеры 530 и 580 дополнительно управляют операциями различных процессоров в точке доступа и пользовательском терминале соответственно. Блоки памяти 532 и 582 хранят данные и коды программ, используемые контроллерами 530 и 580 соответственно.
Фиг.6 показывает структурную схему пространственной обработки, выполняемой точкой доступа 210x и пользовательским терминалом 220x для передачи данных по многочисленным собственным модам в нисходящей линии связи и восходящей линии связи.
В нисходящей линии связи в пределах пространственного процессора 520 ПД в точке доступа 210x сначала умножают вектор данных sdn(k) для каждого поддиапазона k на матрицу 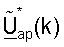 с помощью модуля 610 и дополнительно умножают на матрицу
с помощью модуля 610 и дополнительно умножают на матрицу 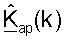 коррекции с помощью модуля 612 для получения вектора передачи xdn(k) для поддиапазона k. Столбцы матрицы
коррекции с помощью модуля 612 для получения вектора передачи xdn(k) для поддиапазона k. Столбцы матрицы 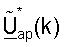 ортогонализируют, как описано выше. Векторы передачи xdn(k), для k∈K, затем обрабатывают с помощью цепи 614 передачи в пределах модулятора 522 и передают по каналу MIMO на пользовательский терминал 220x. Модуль 610 выполняет пространственную обработку для передачи данных нисходящей линии связи.
ортогонализируют, как описано выше. Векторы передачи xdn(k), для k∈K, затем обрабатывают с помощью цепи 614 передачи в пределах модулятора 522 и передают по каналу MIMO на пользовательский терминал 220x. Модуль 610 выполняет пространственную обработку для передачи данных нисходящей линии связи.
В пользовательском терминале 220x модулированные сигналы нисходящей линии связи обрабатывают с помощью цепи 654 приема в пределах демодулятора 554 для получения принимаемых векторов rdn(k), для k∈K. В пределах пространственного процессора 560 ПР сначала умножают принимаемый вектор rdn(k) для каждого поддиапазона k на матрицу 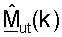 согласованного фильтра с помощью модуля 656 и дополнительно умножают на матрицу Gut(k) масштабирования с помощью модуля 658 для получения вектора
согласованного фильтра с помощью модуля 656 и дополнительно умножают на матрицу Gut(k) масштабирования с помощью модуля 658 для получения вектора 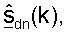 который является оценкой вектора данных sdn(k), переданного для поддиапазона k. Модули 656 и 658 выполняют согласованную фильтрацию нисходящей линии связи.
который является оценкой вектора данных sdn(k), переданного для поддиапазона k. Модули 656 и 658 выполняют согласованную фильтрацию нисходящей линии связи.
В восходящей линии связи в пределах пространственного процессора 590 ПД в пользовательском терминале 220x сначала умножают вектор данных sup(k) для каждого поддиапазона k на матрицу  с помощью модуля 660 и затем дополнительно умножают на матрицу коррекции
с помощью модуля 660 и затем дополнительно умножают на матрицу коррекции 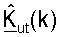 с помощью модуля 662 для получения передаваемого вектора xup(k) для поддиапазона k. Передаваемые векторы xup(k), для k∈K затем обрабатывают с помощью цепи 664 передачи в пределах модулятора 554 и передают по каналу MIMO к точке доступа 210x. Модуль 660 выполняет пространственную обработку для передачи данных восходящей линии связи.
с помощью модуля 662 для получения передаваемого вектора xup(k) для поддиапазона k. Передаваемые векторы xup(k), для k∈K затем обрабатывают с помощью цепи 664 передачи в пределах модулятора 554 и передают по каналу MIMO к точке доступа 210x. Модуль 660 выполняет пространственную обработку для передачи данных восходящей линии связи.
В точке доступа 210x модулированные сигналы восходящей линии связи обрабатывают с помощью цепи 624 приема в пределах демодулятора 522 для получения принимаемого вектора rup(k), для k∈K. В пределах пространственного процессора 540 ПР сначала умножают принимаемый вектор rup(k) для каждого поддиапазона k на матрицу согласованного фильтра 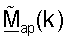 с помощью модуля 626 и дополнительно умножают масштабируемую матрицу Gap(k) с помощью модуля 628 для получения вектора
с помощью модуля 626 и дополнительно умножают масштабируемую матрицу Gap(k) с помощью модуля 628 для получения вектора 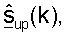 который является оценкой вектора данных sup(k), переданного для поддиапазона k. Модули 626 и 628 выполняют согласованную фильтрацию восходящей линии связи.
который является оценкой вектора данных sup(k), переданного для поддиапазона k. Модули 626 и 628 выполняют согласованную фильтрацию восходящей линии связи.
Описанные методики для получения собственных векторов для пространственной обработки можно реализовать с помощью различных средств. Например, эти методики можно реализовать в оборудовании, программном обеспечении или в их комбинации. При реализации в оборудовании элементы, используемые для этих методик, можно реализовать в пределах одной или большего количества специализированных интегральных схем (СПИС, ASIS), процессоров цифровой обработки сигналов (ПЦОС, DSP), устройств цифровой обработки сигналов (УЦОС, DSPD), программируемых логических устройств (ПЛУ, PLD), программируемых пользователем вентильных матриц (ППВМ, FPGA), процессоров, контроллеров, микроконтроллеров, микропроцессоров, других электронных модулей, предназначенных для выполнения описанных функций, или в их комбинации.
При программной реализации методики можно реализовать с помощью модулей (например, процедур, функций и т.д.), которые выполняют описанные функции. Программные коды могут храниться в блоке памяти (например, в блоках памяти 532 и 582 на фиг. 5) и выполняться процессором (например, контроллерами 530 и 580). Блок памяти можно реализовать в пределах процессора или вне процессора, в этом случае он может быть связан с возможностью обмена данными с процессором через различные средства, которые известны из предшествующего уровня техники.
Данное описание включает в себя заголовки для ссылки и помощи в определении расположения определенных разделов. Эти заголовки не предназначены для ограничения формы концепций, описанных под этими заголовками, и эти концепции могут применяться в других разделах по всему описанию.
Предыдущее описание раскрытых вариантов осуществления обеспечено для предоставления возможности любому специалисту изготавливать или использовать настоящее изобретение. Различные модификации этих вариантов осуществления будут вполне очевидны специалистам, и определенные общие принципы могут применяться к другим вариантам осуществления, не отступая от объема или сущности изобретения. Таким образом, настоящее изобретение не ограничивается показанными вариантами осуществления, но должно соответствовать самому широкому объему, совместимому с раскрытыми принципами и новыми признаками.
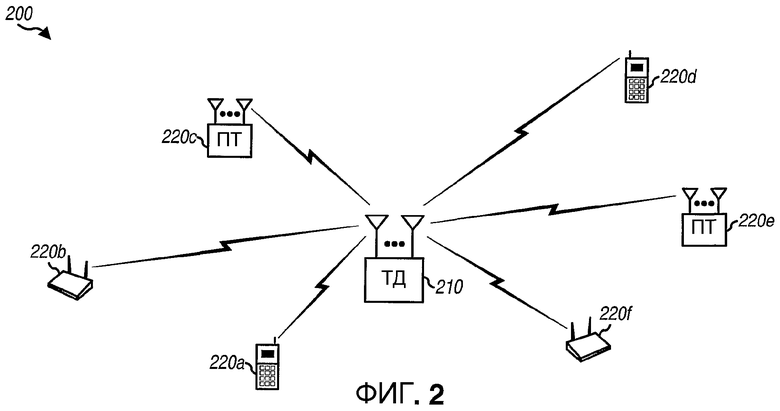
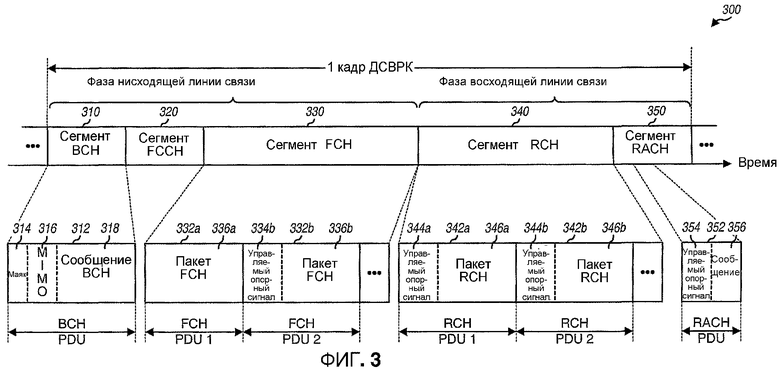
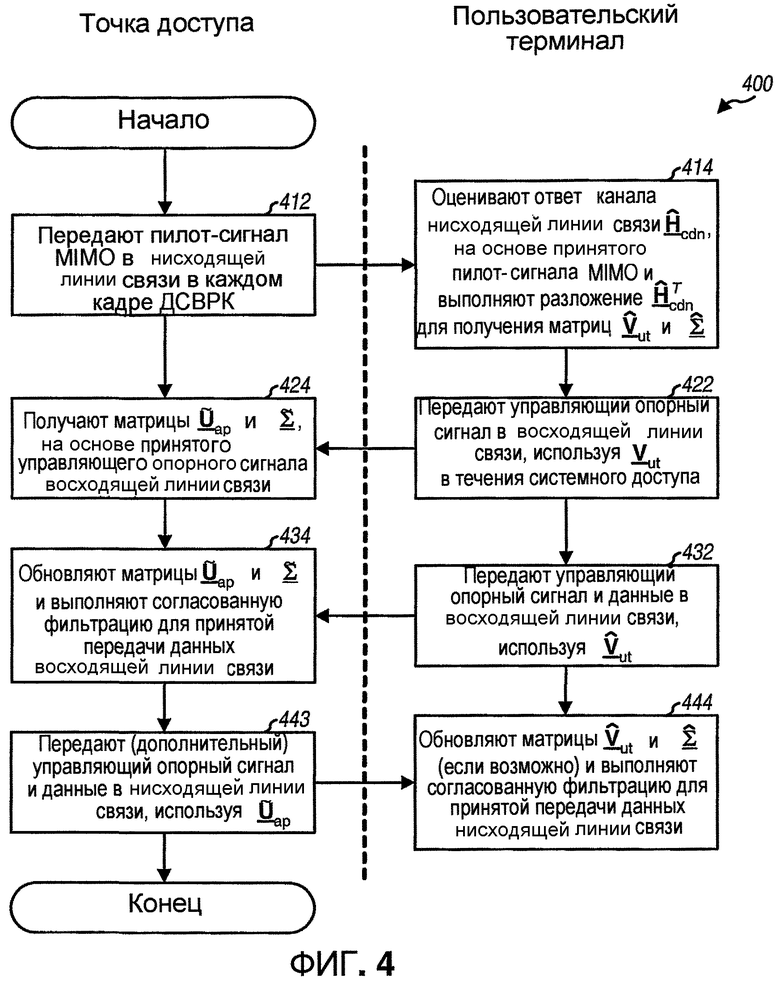
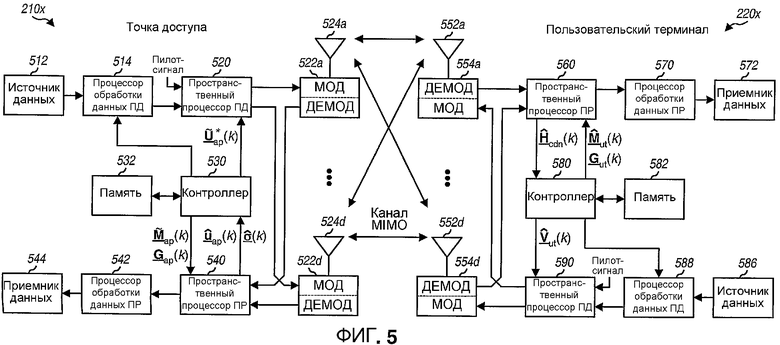
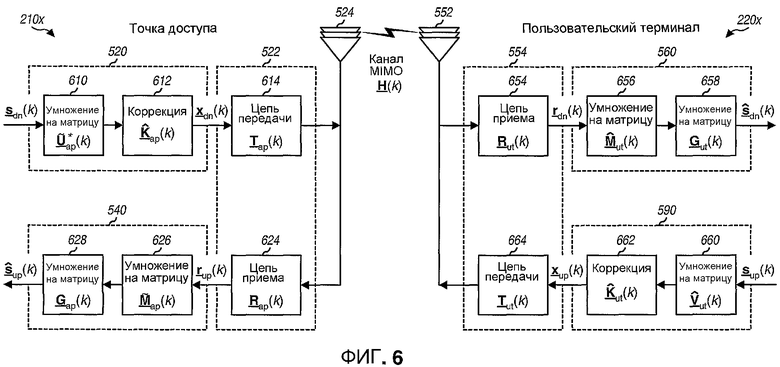
Изобретение относится к технике связи. Технический результат состоит в получении собственных векторов на основе управляющего опорного сигнала. Для этого предложены способы получения собственных векторов на основе управляющего опорного сигнала, которые используются для пространственной обработки. Управляющий опорный сигнал является передачей пилот-сигнала на одной собственной моде канала MIMO в период символа с использованием управляющего вектора для этой собственной моды. Управляющий опорный сигнал используют для оценки и матрицы сингулярных значений, и матрицы левых собственных векторов матрицы ответа канала. Матрица с ортогонализированными столбцами может быть получена с использованием QR-разложения, вычисления минимальной квадратической ошибки или полярной декомпозиции. Оценки матриц могут использоваться для согласованной фильтрации передачи данных, принятой через первую линию связи, а также использоваться для пространственной обработки передачи данных по второй линии связи (для обратных первой и второй линий связи). 3 н. и 20 з.п. ф-лы, 6 ил, 1 табл.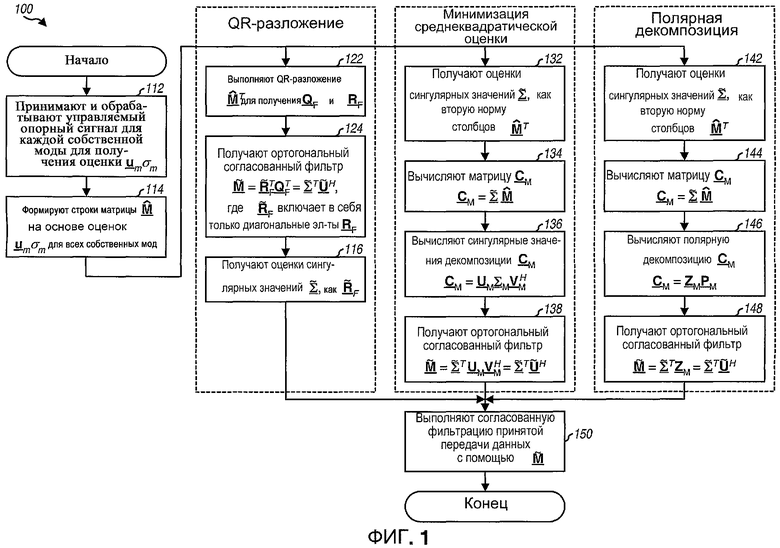
получают множество собственных векторов на основе множества наборов принятых символов, причем множество собственных векторов пригодно для использования для пространственной обработки.
оценивают коэффициенты усиления, связанные с множеством
управляющих векторов, на основе множестве наборов принятых символов;
и упорядочивают множество собственных векторов на основе оцененных коэффициентов усиления.
выполняют согласованную фильтрацию передачи данных, принятой через первую линию связи MIMO, используя множество собственных векторов.
пространственный процессор передачи (ПД), предназначенный для выполнения пространственной обработки для второй передачи данных по второй линии связи MIMO, с использованием множества собственных векторов.
средство для определения множества масштабируемых векторов на основе множества наборов принятых символов для управляющего опорного сигнала, принятого через первую линию связи MIMO и сгенерированного на основе множества управляющих векторов, причем каждый из множества масштабируемых векторов соответствует соответствующему вектору из множества управляющих векторов; и
средство для получения множества собственных векторов на основе множестве масштабируемых векторов, причем множество собственных векторов пригодно для использования для пространственной обработки.
| СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ СВЯЗИ ПО ИЗМЕНЯЮЩЕМУСЯ ВО ВРЕМЕНИ КАНАЛУ СВЯЗИ, ПЕРЕДАЮЩЕЕ УСТРОЙСТВО, ПРИЕМНОЕ УСТРОЙСТВО | 1995 |
|
RU2158479C2 |
| Способ изготовления волноводного спирально-конического ребристого рупора | 1980 |
|
SU905920A1 |
| US 5490165 А, 06.02.1996. | |||
Авторы
Даты
2008-10-27—Публикация
2003-12-09—Подача