Изобретение относится к области техники связи, и в частности к системам передачи информации, в которых для ее защиты от искажений в канале связи применяют несистематические сверточные коды, и может быть использовано в кодеках (кодер-декодерах) систем передачи данных, а также в устройствах помехоустойчивого кодирования при передаче и хранении дискретной информации.
Известен способ синдромного декодирования несистематических сверточных кодов [1], который основан на последовательном вычислении для кодовой последовательности {bi} синдромной последовательности {si}, которая поступает в τ-разрядный сдвиговый регистр (τ=2×max{deg[fi(x)]}+1, где fi(x) - порождающие многочлены несистематического сверточного кода). При появлении в старшем разряде сдвигового регистра ненулевого элемента считается, что в регистре сформирован синдром sj, по которому из заранее построенной таблицы лидеров смежных классов векторов ошибок выбирается вектор коррекции еj. Затем вектор коррекции ej поразрядно складывается по mod2 с соответствующим фрагментом искаженной кодовой последовательности {bj}. После чего откорректированная кодовая последовательность преобразуется в информационную последовательность.
К недостаткам данного способа декодирования следует отнести необходимость хранить таблицу лидеров смежных классов векторов ошибок, объем которой равен 2τ-1×(max{deg[fi(x)]}+1)-разрядных векторов, что при больших значениях τ технически невыполнимо. Кроме того, данный способ декодирования обладает существенно более низким качеством (достоверностью) декодирования по сравнению с известными способами последовательного декодирования или декодирования по алгоритму Витерби [1÷5].
Целью предлагаемого изобретения является повышение достоверности (качества) декодирования, понижение аппаратной и вычислительной сложности декодирования, уменьшение времени задержки и, в частности, реализация оптимальной процедуры декодирования как с «мягким», так и с «жестким» решениями.
Для достижения цели предложен способ синдромного декодирования несистематических сверточных кодов, в которых вектор коррекции е выбирается не из таблицы лидеров смежных классов векторов ошибок, а формируется в результате поиска в синдромной последовательности {si} локализованных синдромов sj, представления каждого из них в виде линейных комбинации синдромов однократных ошибок s(m) подпотоков {bi (m)} кодовой последовательности {bi} (m=1÷n; n - количество порождающих многочленов несистематического сверточного кода), причем каждой линейной комбинации однозначно соответствует вектор ошибки, вычисления для каждого вектора ошибки метрики и выбора в качестве наиболее вероятного вектора коррекции того вектора ошибки, который при декодировании с «жестким» решением имеет наименьшую метрику (вес вектора ошибки), а при декодировании с «мягким» решением обладает наибольшей модифицированной метрикой.
Как известно [1], синдромная последовательность {si} несистематического сверточного кода - это последовательность, элементами которой являются коэффициенты при неизвестном многочлена s(x):
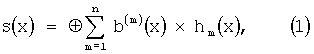
где: b(m)(x) - многочлен, коэффициентами при неизвестном которого являются элементы m-того подпотока кодовой последовательности сверточного кода b(x)=|b(1)(x), ... b(n)(x)|;
hm(x) - m-ный многочлен проверочного многочлена Н(х)=|h1(x), ... hm(x), ... hn(x)| несистематического сверточного кода.
Отметим также то, что конфигурация синдрома s(m) однократной ошибки в m-ном подпотоке {bi (m)} кодовой последовательности {bi} соответствует последовательности коэффициентов при неизвестном многочлена hm(x) несистематического сверточного кода, начиная с младшей степени.
Проверочный многочлен Н(х)=|h1(x), ... hm(x), ... hn(x)| несистематического сверточного кода представляет собой вектор, элементами которого являются многочлены hm(x), которые формируют нулевые коэффициенты при неизвестном многочлена s(x) при вычислении по формуле (1) для неискаженной кодовой последовательности b(х). Тогда с учетом искажений выражение (1) можно представить в виде:
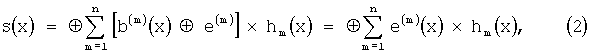
где: е(m)(x) - многочлен, коэффициентами при неизвестном которого являются элементы вектора ошибки m-ного подпотока кодовой последовательности сверточного кода е(x)=|е(1)(x), ... е(n)(х)|.
Из выражения (2) следует, что синдромная последовательность s(x) есть сумма по модулю два синдромов однократных ошибок соответствующих подпотоков.
Локализованный синдром - это фрагмент синдромной последовательности, который начинается с ненулевого элемента. Помимо этого внутри фрагмента отсутствуют серии нулевых элементов длиной более τ-1, а перед фрагментом и за ним следует серия нулевых элементов длиной не менее τ.
Для декодирования несистематического сверточного кода предлагается способ, заключающийся в следующем.
Для принятой возможно искаженной кодовой последовательности несистематического сверточного кода вычисляют синдромную последовательность {si} (1), в которой выделяют локализованные синдромы sj. Каждый локализованный синдром sj можно рассматривать независимо от других локализованных синдромов. Поэтому его можно с помощью итеративной процедуры представить в виде линейных комбинаций синдромов s(m) однократных ошибок в подпотоках {bi (m)} кодовой последовательности {bi}. Для этого перед декодированием кодовой последовательности несистематического сверточного кода формируют два вспомогательных множества комбинаций синдромов однократных ошибок: множество S1={s1 (i)} мощности s1 (множество, каждый синдром которого начинается с ненулевого элемента) и множество S0={s0 (i)} мощности s0 (множество, каждый синдром которого начинается с нулевого элемента). Во множество S1 включают все n синдромов однократных ошибок s(m) и, если n>2, все нечетные линейные комбинации синдромов s(m) однократных ошибок. Во множество S0 включают все четные линейные комбинации синдромов s(m) однократных ошибок. Далее анализируют элементы локализованного синдрома sq. Первый ненулевой элемент локализованного синдрома порождает s1 возможных вариантов линейных комбинаций блоков ошибок. Каждому варианту ставят в соответствие текущий синдром s1=s⊕s1 (i) (i=1÷s1) и текущую локализованную ошибку, которая имеет ненулевые элементы в тех позициях n-разрядного блока, которые соответствуют номерам синдромов однократных ошибок s(m), принимавших участие в формировании текущего синдрома si. В результате вычисления текущего синдрома первый его элемент становится нулевым. Далее просматривают вторые элементы текущего синдрома. Для каждого текущего синдрома sj, у которого на второй позиции расположен ненулевой элемент, вычисляют s1 новых модификаций данного текущего синдрома sr=sj⊕s1 (i) (i=1÷s1, j=1÷s1). Если у синдрома sj на второй позиции расположен нулевой элемент, то вычисляют s0 новых модификаций данного текущего синдрома sr=sj⊕s0 (i) (i=1÷s0, j=1÷s0). Затем для каждого модифицированного текущего синдрома sr формируют вектор ошибки путем добавления к j-той локализованной ошибке очередного n-разрядного блока, который имеет ненулевые элементы в тех позициях, которые соответствуют номерам синдромов s(m) однократных ошибок, принимавших участие в формировании текущего синдрома sr. В результате вычисления модифицированного текущего синдрома и второй его элемент становится нулевым. Далее просматривают третьи и т.д. элементы текущего синдрома до тех пор, пока не будут сформированы всевозможные линейные комбинации рассматриваемого локализованного синдрома и векторы ошибок, им соответствующие.
Следует отметить, что локализованный синдром имеет конечную длину. Поэтому текущие синдромы также должны локализоваться на этой длине. Данное условие приведет к резкому сокращению рассматриваемых линейных комбинаций локализованного синдрома и векторов ошибок, им соответствующих.
При декодировании с «жестким» решением для определения оптимального вектора коррекции необходимо выбрать тот вектор ошибки, который имеет наименьший вес (метрику).
В том случае когда декодирование несистематического сверточного кода выполняется с «мягким» решением, предлагается вариант способа, описанного выше, в котором для каждого вектора ошибки вычисляют модифицированную метрику:
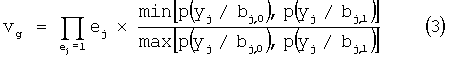
или
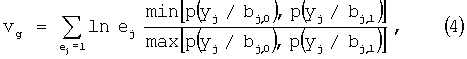
где: p(yj/bj,c) - условная вероятность того, что на выходе демодулятора получена величина yj при передаче по каналу связи на j-той позиции кодовой последовательности элемента с, который для двоичного кода может принимать значение 0 или 1;
ej - элемент локализованной ошибки, исказивший j-тый элемент кодовой последовательности;
и выбирают тот вектор ошибки, у которого метрика vg имеет максимальное значение. Модифицированная метрика является отношением общепринятой метрики [3] фрагмента кодовой последовательности к метрике принятого из канала связи с «жестким» решением искаженного фрагмента кодовой последовательности.
Предлагаемое техническое решение позволяет решить задачу оптимального синдромного декодирования несистематических сверточных кодов как с «жестким», так и с «мягким» решениями с меньшей вычислительной и аппаратной сложностью, а также с меньшим временем задержки декодирования, чем у известных декодеров [1÷5].
Изобретение поясняется чертежом, на котором изображена структурная схема оптимального синдромного декодера несистематического сверточного кода.
Синдромный декодер несистематического сверточного кода содержит: блок вычисления синдромной последовательности 20, блок поиска локализованного синдрома 40, блок разложения локализованного синдрома 60, блок хранения и обновления текущей информации 80, блок выбора решения и коррекции 100 и блок формирования информационной последовательности 120.
Блок вычисления синдромной последовательности 20 предназначен для вычисления синдромной последовательности {si} в соответствии с выражением (1).
Блок поиска локализованного синдрома 40 предназначен для выделения в синдромной последовательности {si} очередного локализованного синдрома sj. Он может быть реализован в виде сдвигового регистра, у которого анализируется старший разряд на наличие нуля и подсчитывается длина нулевой серии. В этом случае в сдвиговый регистр последовательно поступает синдромная последовательность {si} и выполняются ее сдвиги в сторону старшего разряда. При появлении ненулевого элемента номер его позиции фиксируется и фрагмент синдромной последовательности запоминается вплоть до момента прихода серии нулевых элементов длиной не менее τ.
Блок разложения локализованного синдрома 60 предназначен для представления локализованного синдрома sj в виде линейных комбинации синдромов однократных ошибок и формирования соответствующих им фрагментов векторов ошибок, а при декодировании с «мягким» решением для каждой группы вычисляет метрику vr по формуле (2) или (3).
Блок хранения и обновления текущей информации 80 предназначен для хранения текущих синдромов и фрагментов векторов ошибок при разложении локализованного синдрома. Он представляет собой оперативное запоминающее устройство, у которого каждая строка состоит из двух (трех) полей для хранения текущего синдрома, его фрагмента вектора ошибки, а при декодировании с «мягким» решением соответствующей метрики.
Блок выбора решения и коррекции 100 предназначен для сложения по mod 2 фрагмента кодовой последовательности с тем вектором ошибки, который при декодировании с «жестким» решением имеет наименьший вес (метрику), а при декодировании с «мягким» решением обладает наибольшей метрикой.
Блок формирования информационной последовательности 120 предназначен для преобразования откорректированной кодовой последовательности несистематического сверточного кода в информационную последовательность. Блок 120 может быть выполнен в виде кодопреобразователя, использующего либо решетку Форни, либо кодовое дерево.
Предлагаемое устройство работает следующим образом.
Принятая, возможно искаженная в канале связи кодовая последовательность n-разрядными блоками поступает по шине 10 в блок вычисления синдромной последовательности 20, а по шине 11 в блок выбора решения и коррекции 100.
В блоке вычисления синдромной последовательности 20 поэлементно формируется синдромная последовательность кода в соответствии с выражением (1) и по шине 30 передается в блок поиска локализованного синдрома 40.
Блок поиска локализованного синдрома 40 анализирует протяженность нулевых серий в синдромной последовательности, выделяет локализованный синдром и передает его по шине 50 в блок разложения локализованного синдрома 60.
Получив локализованный синдром, блок разложения локализованного синдрома 60 в соответствии с итеративной процедурой, описанной в предлагаемом выше способе, приступает к его разложению. В результате формируются всевозможные линейные комбинации синдромов однократных ошибок на интервале локализации анализируемого синдрома. Параллельно формируются соответствующие им векторы ошибок. Промежуточные результаты: текущие синдромы со своими фрагментами векторов ошибок, а при декодировании с «мягким» решением и их метрики - передаются по шине 70 для хранения в блок хранения и обновлении текущей информации 80.
После завершения процедуры разложения локализованного синдрома блок выбора решения и коррекции 100 по шине 91 последовательно считывает из блока хранения и обновления текущей информации 80 сформированные векторы ошибок. При декодировании с «жестким» решением выбирается тот, который имеет наименьший вес (метрику), а при декодировании с «мягким» решением - тот, который обладает наибольшей модифицированной метрикой. Затем во фрагменте кодовой последовательности, которая соответствует локализованному синдрому, инвертируются те элементы, которые отмечены ненулевыми элементами выбранного вектора ошибки.
Откорректированная кодовая последовательность несистематического сверточного кода, поступающая по шине 110 с выхода блока выбора решения и коррекции 100 на вход блока примитивного декодирования 120, преобразуется в нем в информационную последовательность. После чего она по шине 130 передается на выход декодера.
Для декодирования каскадного кода с «мягким» решением другим конструктивным вариантом является модификация блока вычисления синдромной последовательности 20, который перед вычислением синдромной последовательности формирует кодовую последовательность с «жестким» решением. В блоке разложения локализованного синдрома 60 для каждой формируемой группы локализованных ошибок вычисляется метрика по формулам (2) или (3), а в блоке выбора решения и коррекции 100 выбирается та из них, которая имеет наибольшую метрику vg.
Реализация описанного способа может быть аппаратной, программной или аппаратно-программной.
Достигаемым техническим результатом предлагаемого способа синдромного декодирования несистематического сверточного кода является построение оптимального декодера с «жестким» и «мягким» решениями, а также повышение достоверности (качества) декодирования, повышение его быстродействия и уменьшения аппаратной сложности по сравнению с известными декодерами [1÷5]. Предлагаемый способ может быть использован для декодирования систематических сверточных кодов, а также перфорированных несистематических сверточных кодов.
Список литературы
1. Кларк Дж., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. - М.: Радио и связь. 1987.
2. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение: Пер. с англ. В.Б.Афанасьева. - М.: Техносфера, 2005. - 320 с.
3. Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования: Пер. с англ. - М.: Радио и связь, 1982.
4. Карташевский В.Г., Мишин Д.В. Прием кодированных сигналов в каналах с памятью. - М.: Радио и связь, 2004.
5. Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование. Методы и алгоритмы: Справочник / Под ред. чл. кор. РАН Ю.Б.Зубарева. - М.: Горячая линия - Телеком, 2004.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДЕКОДИРОВАНИЯ ТУРБОКОДА (ВАРИАНТЫ) | 2006 |
|
RU2340090C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ ПОСЛЕДОВАТЕЛЬНОГО КАСКАДНОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340091C2 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340088C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКИХ КОДОВ С "ЖЕСТКИМ" РЕШЕНИЕМ ПО ВЕКТОРУ-УКАЗАТЕЛЮ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2575394C1 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ | 2004 |
|
RU2282307C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ КОДА-ПРОИЗВЕДЕНИЯ С ИСПОЛЬЗОВАНИЕМ УПОРЯДОЧЕННОГО ПО ВЕСУ СМЕЖНОГО КЛАССА ВЕКТОРОВ ОШИБОК И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541844C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ LDPC-КОДОВ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2575399C1 |
| Кодек несистематического сверточного кода | 1990 |
|
SU1714812A1 |
| Кодер несистематического сверточного кода | 1990 |
|
SU1695516A1 |
| Декодер сверточного кода | 1985 |
|
SU1320904A1 |
Изобретение относится к области техники связи, в частности к системам передачи данных, в которых для защиты информации от искажений в канале связи применяются несистематические сверточные коды, и может быть использовано в кодеках систем передачи данных, а также в устройствах помехоустойчивого кодирования. Сущность заявленного изобретения состоит в том, что для принятой искаженной кодовой реализации вычисляют синдромную последовательность, в которой определяют локализованные синдромы и, используя итеративную процедуру представления локализованного синдрома в виде линейных комбинаций синдромов однократных ошибок, определяют группу локализованных блоков ошибок минимального веса при декодировании с «жестким» решением, а при декодировании с «мягким» решением выбирают группу локализованных блоков ошибок, которая имеет наибольшую метрику. Техническим результатом является повышение достоверности (качества) декодирования, снижение аппаратной и вычислительной сложности, а также повышения быстродействия декодера при реализации оптимальной процедуры декодирования как с «мягким», так и с «жестким» решениями. 2 н.п. ф-лы, 1 ил.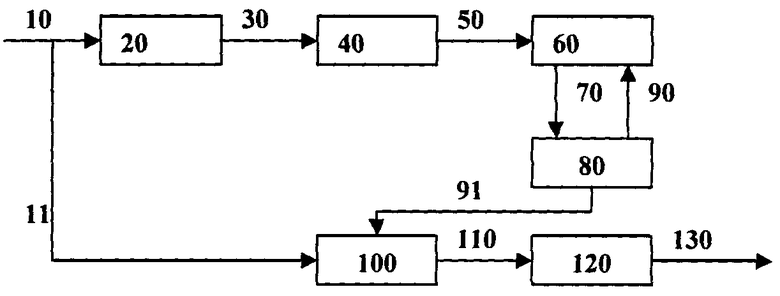
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ | 2004 |
|
RU2282307C2 |
| ПАРАЛЛЕЛЬНЫЙ КАСКАДНЫЙ СВЕРТОЧНЫЙ КОД С КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ БИТОВ И ДЕКОДЕР ДЛЯ ТАКОГО КОДА | 1997 |
|
RU2187196C2 |
| Бесколесный шариковый ход для железнодорожных вагонов | 1917 |
|
SU97A1 |
| US 5577053 A, 19.11.1996 | |||
| Теплообменный аппарат | 1975 |
|
SU611098A2 |
Авторы
Даты
2008-11-27—Публикация
2006-11-23—Подача