Изобретение относится к области техники связи, в частности к системам передачи информации, в которых для ее защиты от искажений в канале связи применяются циклические линейные блочные коды, и может быть использовано в кодеках (кодер-декодерах) систем передачи данных, а также в устройствах помехоустойчивого кодирования при передаче и хранении дискретной информации.
Известен способ декодирования линейных блочных (n,k)-кодов [1-3] (n - длина кодового слова, k - количество кодируемых бит или систематическая часть кодового слова), который включает в себя вычисление (n-k)-разрядного синдрома s кодового слова, искаженного в канале связи, выбор вектора коррекции, который соответствует синдрому s, из заранее сформированной таблицы лидеров смежных классов векторов ошибок, поразрядное сложение по mod 2 вектора коррекции с искаженным кодовым словом и выделение откорректированной систематической части кодового слова.
К недостаткам данного способа декодирования следует отнести необходимость хранить таблицу лидеров смежных классов векторов ошибок, объем которой равен 2n-k×n-разрядных (или k-разрядных) векторов, что при больших значениях n-k технически невыполнимо.
Целью предлагаемого изобретения является повышение достоверности (качества) декодирования, а также уменьшение аппаратной и вычислительной сложности и, в частности, реализация оптимальной процедуры декодирования как с «жестким», так и с «мягким» решением.
Для достижения цели предложен способ декодирования циклического линейного блочного (n,k)-кода, в котором вектор коррекции е выбирается не из таблицы лидеров смежных классов векторов ошибок, а формируется в результате представления n-разрядного расширенного синдрома s в виде линейных комбинаций строк расширенной проверочной матрицы Нn,n. Номера строк расширенной проверочной матрицы однозначно указывают на номера искаженных позиций в принятом искаженном кодовом слове. Расширенная проверочная матрица Нn,n является транспонированной проверочной матрицей [1], у которой j-ая строка состоит из коэффициентов при неизвестном полинома:
hj(x)=xjh(x)mod(xn+1),
где h(x)=(xn+1)/p(x) - проверочный многочлен циклического (n,k)-кода,
p(x) - порождающий многочлен кода,
j=0, 1, ... n-1.
Транспонированная расширенная проверочная матрица Нn,n отличается от проверочной матрицы Hn,n-k [1, 2] только тем, что в ней добавлено еще k строк, каждая из которых также является циклическим сдвигом предшествующей строки на один разряд направо.
Для декодирования циклического линейного блочного (n,k)-кода предлагается способ, заключающийся в следующем.
Для принятой искаженной кодовой реализации (b⊕eкс) вычисляют расширенный синдром s=(b⊕eкс)×Нn,n, в котором определяют позицию j любого ненулевого элемента. После чего в расширенной проверочной матрице Нn,n находят те строки, которые содержат в j-ой позиции также ненулевой элемент. Далее вычисляют текущие синдромы s1,i первого шага итерации (первый шаг итерационной процедуры представления расширенного синдрома в виде линейных комбинаций строк расширенной проверочной матрицы Нn,n). Для этого каждую из найденных строк складывают по mod 2 с расширенным синдромом s. Каждому текущему синдрому s1,i ставят в соответствие вектор N1,i, в который заносят номер строки расширенной проверочной матрицы Нn,n, участвовавший в формировании текущего синдрома s1,i. Таких пар векторов s1,i, N1,i на первом шаге итерации будет сформировано 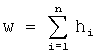 (hi - коэффициенты при неизвестном проверочного многочлена h(x) циклического линейного блочного (n,k)-кода).
(hi - коэффициенты при неизвестном проверочного многочлена h(x) циклического линейного блочного (n,k)-кода).
Если один из текущих синдромов s1,i - нулевой вектор, то вектор ошибки минимального веса найден, а искаженный в канале связи элемент кодового слова указан в N1,i. После коррекции (инверсии) искаженного элемента в качестве декодированной информации выбирают откорректированную систематическую часть кодового слова. На этом декодирование заканчивается.
Если ни один из w текущих синдромов s1,i не является нулевым вектором, то выполняют переход к очередному шагу итерации. Для каждого текущего синдрома предыдущего m-того шага итерации sm,i вычисляют w пар векторов sm+1,i, Nm+1,i, также как и на первом шаге итерации. Общее количество пар векторов sm+1,i и Nm+1,i на m+1-ом шаге равно wm+1=wm+1.
Если хотя бы один из текущих синдромов sm+1,i - нулевой вектор, то вектор ошибки минимального веса найден, а искаженные в канале связи элементы кодового слова указаны в Nm+1,i. После коррекции (инверсии) искаженных элементов в качестве декодированной информации выбирают откорректированную систематическую часть кодового слова. На этом декодирование заканчивается.
Если ни один из wm+1 текущих синдромов sm+1,i не является нулевым вектором, то выполняют переход к следующему шагу итерации и т.д., до тех пор, пока не будет сформирован текущий синдром, являющийся нулевым вектором. Тогда после коррекции (инверсии) искаженных элементов в качестве декодированной информации выбирают откорректированную систематическую часть кодового слова.
При декодировании совершенных кодов с «жестким» решением для поиска оптимального вектора коррекции (вектора минимального веса) потребуется не более t итераций (где t - кратность исправляемых ошибок (n,k)-кода).
В том случае, когда декодируются несовершенные коды с «жестким» решением, предлагается вариант способа, описанного выше, для которого также необходимо выполнить не более t итераций. Если на t-том шаге итерации не найден синдром, являющийся нулевым вектором, то необходимо отказаться от коррекции данного искаженного кодового слова, так как вес вектора коррекции превышает кратность исправляемых ошибок (n,k)-кода и равен t+1. Если все же необходимо корректировать и исправляемые t+1-кратные ошибки несовершенного кода, то необходимо выполнить t+1 итерацию. Причем, если на t+1-ой итерации среди вычисленных синдромов только один является нулевым вектором, то найдена исправляемая t+1-кратная ошибка, искаженные элементы которой заданы вектором Nt+1,i. Если на t+1-ой итерации среди вычисленных синдромов несколько синдромов являются нулевыми векторами, то найдена неисправляемая t+1-кратная ошибка и от коррекции следует отказаться.
В том случае, когда декодируется «расширенный» код [1-3] с «жестким» решением, предлагаются варианты способов, описанные выше, в которых перед декодированием из полученного по каналу связи возможно искаженного кодового слова удаляют элемент расширения.
В том случае, когда декодируется «укороченный» код [1-3] с «жестким» решением, предлагаются варианты способов, описанные выше, в которых перед декодированием в начало полученного по каналу связи возможно искаженного кодового слова добавляют нулевые элементы, количество которых равно величине укорочения. Очевидно, что добавленные в начало нулевые позиции не могут быть искажены в канале связи, так как они по нему не передавались. Этот факт позволяет сократить количество текущих синдромов Sm,i на m-той итерации, что приведет к уменьшению вычислительной сложности декодирования.
В том случае, когда декодирование выполняется с «мягким» решением совершенных, несовершенных и расширенных кодов, предлагаются варианты способов, описанных выше, в которых для каждой пары векторов sm,i и Nm,i вычисляют модифицированную метрику:
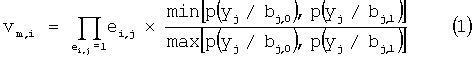
или
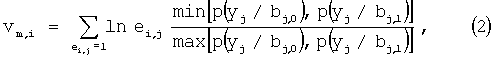
где p(yj/bj,c) - условная вероятность того, что на выходе демодулятора получена величина уj при передаче по каналу связи на j-ой позиции кодового слова c-ого символа, который для двоичного кода может принимать два значения: bj,0=0 и bj,1=1,
ei,j - j-тый элемент i-того вектора ошибки еi, принадлежащего смежному классу ошибок синдрома sm,i,
Модифицированная метрика (1) и (2) является отношением общепринятой метрики [1-3] i-того кодового слова к метрике принятого из канала связи с «жестким» решением искаженного кодового слова. Корректируют те элементы приятого с «жестким» решением искаженного кодового слова, которые заданы вектором Nm,i, и для которого sm,i=0, а метрика mm,i максимальна.
В том случае, когда декодируется «укороченный» код с «мягким» решением, предлагается вариант способа, описанный выше, в котором перед декодированием в начало полученного по каналу связи возможно искаженного кодового слова добавляют нулевые элементы с условными вероятностями p(yj/bj,0)=1 и p(yj/bj,1)=0.
Для уменьшения вычислительной сложности предлагаются варианты способов, описанных выше, в которых из рассмотрения исключаются текущие синдромы sm,i, у которых в векторе Nm,i появляются повторы позиций искаженных элементов.
Для уменьшения вычислительной сложности предлагаются варианты способов, описанных выше, в которых из рассмотрения, исключаются повторяющиеся текущие синдромы sm,i.
Предлагаемые технические решения позволяют решить задачу оптимального декодирования циклических линейных блочных кодов как с «жестким», так и с «мягким» решениями с меньшей вычислительной и аппаратной сложностью, чем известные декодеры [1-3].
Изобретение поясняется чертежом, на котором изображена структурная схема оптимального синдромного декодера циклического линейного блочного кода.
Синдромный декодер циклического линейного блочного кода содержит: блок вычисления синдрома 20, блок хранения и обновления текущей информации 40, блок считывания 60, блок поиска ненулевого элемента 80, блок поиска строк расширенной проверочной матрицы 100, блок вычисления текущей информации 120, блок коррекции искаженного кодового слова 140, блок формирования декодированной информации 160.
Блок вычисления синдрома 20 предназначен для вычисления расширенного синдрома s по формуле s=(b⊕eкс)×Hn,n.
Блок хранения и обновления текущей информации 40 предназначен для хранения текущих значений синдромов sm,i и соответствующих им векторов Nm,i, а также при декодировании с «мягким» решением метрик vm,i. Блок хранения и обновления текущей информации 40 представляет собой оперативное запоминающее устройство, которое может быть реализовано в виде стека («первый пришел, первый на обслуживание»), у которого каждая строка состоит из двух (трех) полей для хранения текущих векторов sm,i, Nm,i, а при декодировании с «мягким» решением метрики vm,i.
Блок считывания 60 предназначен для последовательного считывания хранящихся в блоке хранения и обновления текущей информации 40 текущих векторов sm,i, Nm,i, а при декодировании с «мягким» решением и метрики vm,i. После считывания строки sm,i передается в блок поиска ненулевого элемента 80, a sm,i, Nm,i и vm,i в блок вычисления текущей информации 120. Блок считывания 60 может быть реализован в виде демультиплексора на два направления.
Блок поиска ненулевого элемента 80 предназначен для определения позиции j любого ненулевого элемента расширенного синдрома sm,i. Он может быть реализован в виде сдвигового регистра, у которого анализируется старший разряд на наличие 0. В этом случае в сдвиговый регистр заносится текущий синдром sm,i и выполняются его сдвиги в сторону старшего разряда до тех пор, пока в старшем разряде не появится ненулевой элемент. Количество сдвигов j, которое является номером позиции одного из ненулевых элементов, фиксируется счетчиком.
Блок поиска строк расширенной проверочной матрицы 100 предназначен для определения номеров строк расширенной проверочной матрицы Нn,n, у которых на позиции j расположены ненулевые элементы. Блок 100 может быть выполнен в виде сдвигового регистра, у которого анализируется старший разряд на наличие 0, и счетчиков номеров строк, количество которых равно w (количество ненулевых коэффициентов проверочного многочлена h(x)). В сдвиговый регистр заносится j-тый столбец расширенной проверочной матрицы Нn,n, который сдвигается в сторону старшего разряда до тех пор, пока он не обнулится. Счетчики номеров строк подсчитывают количество сдвигов и при появлении ненулевого элемента в старшем разряде регистра сдвига последовательно отключаются. При обнулении регистра сдвига номера искомых строк расширенной проверочной матрицы находятся в счетчиках.
Блок вычисления текущей информации 120 предназначен для вычисления текущих синдромов sm+1,j=sm,i⊕hj (где hj - одна из w строк расширенной проверочной матрицы Нn,n, номера которых поступают по шине 110). Затем он формирует для каждого текущего синдрома sm+1,j вектор Nm+1,j путем добавления в вектор Nm,i номера строки hj расширенной проверочной матрицы Нn,n. При декодировании с «мягким» решением по формулам 1 или 2 вычисляются метрики vm+1,j, соответствующие синдромам sm+1,j.
Блок коррекции 140 выполняет инверсию тех элементов принятого искаженного кодового слова, которые указаны в поступившем по шине 131 векторе Nm,i.
Блок формирования декодированной информации 160 предназначен для выделения систематической части в откорректированном кодовом слове, которая и является декодированной информацией.
Предлагаемое устройство работает следующим образом.
Принятое, возможно искаженное в канале связи, кодовое слово (b⊕eкс) поступает с выхода канала связи (демодулятора) по шине 11 на блок коррекции искаженного кодового слова 140, а по шине 10 - на блок вычисления синдрома 20.
Если вычисленный в блоке вычисления синдрома 20 синдром s=0 (нулевой вектор), то кодовое слово не искажено и информация об этом передается по шине 31 блоку коррекции искаженного кодового слова 140. После чего кодовое слово по шине 150 поступает в блок формирования декодированной информации 160, в котором выделяется систематическая часть кодового слова, и по шине 170 поступает на выход декодера. На этом процесс декодирования кодового слова завершается.
Если же вычисленный синдром s≠0, то по шине 30 он поступает в блок хранения и обновления текущей информации 40. Поля вектора Nm,i, а при декодировании с «мягким» решением и поле метрики vm,i обнуляются.
Как только в блок 40 поступает первый синдром s, сразу запускается блок считывания 60, который по шине 50 принимает очередной синдром sm,i вместе с вектором Nm,i а при декодировании с «мягким» решением и с метрикой vm,i. Далее по шине 70 синдром sm,i, передается на блок поиска ненулевого элемента 80, а по шине 71 синдром sm,i, вектор Nm,i, а при декодировании с «мягким» решением метрика vm,i, передаются на блок вычисления текущей информации 120.
Затем блок поиска ненулевого элемента 80 определяет позицию любого ненулевого элемента j расширенного синдрома и передает значение этой позиции по шине 90 в блок поиска строк расширенной проверочной матрицы 100.
Далее блок поиска строк расширенной проверочной матрицы 100 по полученному числу j определяет номера строк расширенной проверочной матрицы Нn,n, у которых на позиции j расположен ненулевой элемент и передает их по шине 110 в блок вычисления текущей информации 120.
После этого в блоке вычисления текущей информации 120 формируются текущие синдромы Sm+1,j и соответствующие им векторы Nm+1,j, а при декодировании с «мягким» решением вычисляются по формулам 1 или 2 соответствующие метрики vm+1,j.
Если один из текущих синдромов sm+1,j=0, то при декодировании с «жестким» решением по шине 131 в блок коррекции 140 передается вектор Nm+1,j. Искаженное кодовое слово, поступившее в блок 140 по шине 11, корректируется (инвертируются те элементы искаженного кодового слова, которые указаны в векторе Nm+1,j) и передается по шине 150 в блок формирования декодированной информации 160, в котором выделяется декодированная информация и по шине 170 поступает на выход декодера. Процесс декодирования закончен. При декодировании с «мягким» решением вектор Nm+1,j передается по шине 131 в блок коррекции 140 только в том случае, когда метрика vm+1,j максимальна. В противном случае sm+1,j=0, Nm+1,j и vm+1,j по шине 130 поступают в блок хранения и обновления текущей информации 40, а блок вычисления текущей информации 120 переходит к вычислению очередного синдрома.
Если же все вычисленные синдромы sm+1,j≠0, то по шине 130 они поступают на хранение вместе со своими векторами Nm+1,j и метриками vm+1,j при декодировании с «мягким» решением в блок хранения и обновления текущей информации 40.
Затем, как уже рассматривалось ранее, блок считывания 60 по шине 50 вновь считывает очередной расширенный синдром sm,i вместе с вектором Nm,i и метрикой vm,j при декодировании с «мягким» решением и т.д. до тех пор, пока не будет вычислен текущий синдром, являющийся нулевым вектором. Тогда после коррекции (инверсии) искаженных элементов кодового слова в качестве декодированной информации выбирается его откорректированная систематическая часть, и процесс декодирования заканчивается.
При декодировании «укороченных» кодов другим конструктивным вариантом является модификация блока вычисления синдрома 20, который перед вычислением расширенного синдрома s в начало принятого из канала связи возможно искаженного кодового слова добавляет нулевые элементы, количество которых равно величине укорочения кода. Кроме того, блок выделения строк расширенной проверочной матрицы 100 удаляет те строки, номера которых меньше величины укорочения. Данное конструктивное решение позволяет не только декодировать «укороченные» линейные циклические блочные коды, но и повысить быстродействие декодера.
Для декодирования «расширенных» кодов другим конструктивным вариантом является модификация блока вычисления синдрома 20, который перед вычислением расширенного синдрома s удаляет последний элемент (элемент расширения или элемент четности кодового слова) принятого из канала связи возможно искаженного кодового слова. При декодировании с «жестким» решением данный элемент более ни в одном из блоков не учитывается. При декодировании с «мягким» решение условные вероятности элемента расширения используется при вычислении метрик в блоке вычисления текущей информации 120. Данное конструктивное решение позволяет декодировать «расширенные» линейные циклические блочные коды.
Другим конструктивным вариантом является модификация блока вычисления текущей информации 120, в котором перед вычислением текущего синдрома sm+1,j сравнивается номер j-той строки с номерами строк вектора Nm,i. Если обнаруживается совпадение строк, то текущий синдром не вычисляется. Данное конструктивное решение позволяет повысить быстродействие декодера.
Другим конструктивным вариантом является модификация блока вычисления текущей информации 120, в котором вновь вычисленный текущий синдром sm+1,j сравнивается со всеми текущими синдромами. Если обнаруживается совпадение текущих синдромов, то данный синдром из дальнейшей обработки исключается. Данное конструктивное решение позволяет повысить быстродействие декодера.
Реализация описанного способа может быть аппаратной, программной или аппаратно-программной и использоваться как для двоичных, так и q-ичных кодов.
Достигаемым техническим результатом предлагаемого способа декодирования циклического линейного блочного кода является повышение достоверности (качества) декодирования как с «жестким», так и с «мягким» решениями, а также повышение быстродействия и уменьшения аппаратной сложности по сравнению с известными способами декодирования [1-3].
Список литературы
1. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение: Пер. с англ. В.Б.Афанасьева. - М.: Техносфера, 2005.
2. Галлагер Р. Теория информации и надежная связь: Пер. с англ., под ред. М.С Пинскера и Б.С.Цыбакова, М., «Советское радио», 1974.
3. Витерби А.Д., Омура Дж.К. Принципы цифровой связи и кодирования: Пер. с англ. - М.: Радио и связь, 1982.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ДЕКОДИРОВАНИЯ ПОСЛЕДОВАТЕЛЬНОГО КАСКАДНОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340091C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ ТУРБОКОДА (ВАРИАНТЫ) | 2006 |
|
RU2340090C2 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ НЕСИСТЕМАТИЧЕСКОГО СВЕРТОЧНОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340089C2 |
| СПОСОБ ДЕКОДИРОВАНИЯ LDPC-КОДОВ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2575399C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКИХ КОДОВ С "ЖЕСТКИМ" РЕШЕНИЕМ ПО ВЕКТОРУ-УКАЗАТЕЛЮ И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2014 |
|
RU2575394C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ КОДА-ПРОИЗВЕДЕНИЯ С ИСПОЛЬЗОВАНИЕМ УПОРЯДОЧЕННОГО ПО ВЕСУ СМЕЖНОГО КЛАССА ВЕКТОРОВ ОШИБОК И УСТРОЙСТВО ЕГО РЕАЛИЗУЮЩЕЕ | 2013 |
|
RU2541844C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ВЫБОРА ИСХОДНОГО ПОМЕХОУСТОЙЧИВОГО КОДА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2271604C2 |
| Способ декодирования блочных помехоустойчивых кодов по критерию минимального среднего риска | 2019 |
|
RU2706171C1 |
| УСТРОЙСТВО ПАРАЛЛЕЛЬНОГО ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКИХ КОДОВ НА ПРОГРАММИРУЕМЫХ ЛОГИЧЕСКИХ ИНТЕГРАЛЬНЫХ СХЕМАХ | 2015 |
|
RU2612593C1 |
| Декодер циклического кода | 1988 |
|
SU1599996A1 |
Изобретение относится к области техники связи, в частности к системам передачи информации, в которых для ее защиты от искажений в канале связи применяются циклические линейные блочные коды, и может быть использовано в кодеках систем передачи данных, а также в устройствах помехоустойчивого кодирования. Сущность способа состоит в том, что для принятой искаженной кодовой реализации вычисляют расширенный синдром и, используя расширенную проверочную матрицу, определяют те наборы строк, которые являются линейными комбинациями вычисленного синдрома, причем каждой линейной комбинации однозначно соответствует вектор ошибки и для каждого вектора ошибки вычисляют метрику, а для исправления наиболее вероятных ошибок в качестве вектора коррекции при декодировании с «жестким» решением выбирают вектор ошибки, который имеет минимальную метрику (вектор ошибки минимального веса), и при декодировании с «мягким» решением выбирают вектор ошибки, который имеет максимальную модифицированную метрику. Затем инвертируют элементы в систематической части кодового слова, номера которых соответствуют позициям ненулевых элементов вектора коррекции. Техническим результатом является повышение достоверности (качества) декодирования, а также понижение аппаратной и вычислительной сложности, что позволяет реализовать оптимальную процедуру декодирования как с "жестким" решением, так и с «мягким» решением. 2 н. и 2 з.п. ф-лы, 1 ил.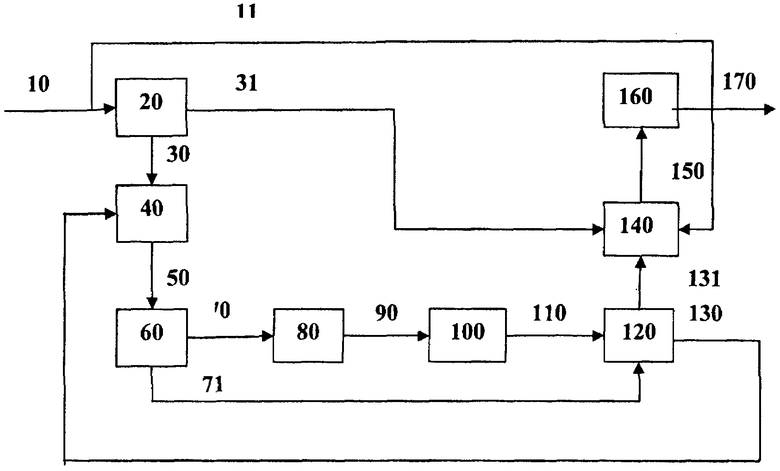
| КОДЕК ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2212101C1 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2003 |
|
RU2214678C1 |
| Бесколесный шариковый ход для железнодорожных вагонов | 1917 |
|
SU97A1 |
| US 5577053 A, 19.11.1996 | |||
| Теплообменный аппарат | 1975 |
|
SU611098A2 |
Авторы
Даты
2008-11-27—Публикация
2006-11-23—Подача