ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Настоящее изобретение в целом относится к кодированию и декодированию данных, а в частности к способу и устройству для кодирования данных, использующему коды с контролем по четности низкой плотности (LDPC).
УРОВЕНЬ ТЕХНИКИ
Код с контролем по четности низкой плотности (LDPC) является кодом линейных блоков, заданным проверочной матрицей H. В общем случае LDPС-код определен на поле Галуа GF(q), q≥2. Если q=2, код является бинарным кодом. Все коды линейных блоков могут быть описаны как произведение k-битного информационного вектора
s 1×k на кодогенерирующую матрицу Gk×n для порождения n-битовой кодовой комбинации x 1×n, где кодовая скорость равна r=k/n. Кодовая комбинация x передается через канал с помехами, и принятый вектор y сигнала передается на декодер для оценки вектора s 1×k информации.
При заданном n-мерном пространстве строки G охватывают k-мерное подпространство C кодовых комбинаций, а строки проверочной матрицы H m×n , охватывают m-мерное дуальное пространство C┴, где m=n-k. Поскольку x=sG и GH T =0, следует, что xH T =0 для всех кодовых комбинаций в подпространстве С, где “T” (или "T") обозначает транспонирование матрицы. При обсуждении LDPС-кодов в общем написано, что
Hx T =0 T (1),
где 0 - вектор-строка из нулей, и кодовая комбинация
x =[s р]=[s 0 , s 1 ,...s k-1 ,p 0 ,p 1 ,...,p m-1], где p 0 ,...,p m-1 являются контрольными битами; а s 0 ,..,s k-1 являются систематическими битами, равными информационным битам в информационном векторе.
Для LDPС-кода плотность ненулевых позиций в H низкая, т.е. существует только маленькая доля 1 в H, позволяющая лучшую эффективность корректировки ошибок и более простое декодирование, чем использование плотного H. Проверочная матрица может быть также описана двудольным графом. Двудольный граф является не только графическим описанием кода, но также моделью декодера. В двудольном графе бит кодовой комбинации (следовательно, каждой колонки H) представлен переменной вершиной слева, и каждое проверочное уравнение (следовательно, каждая строка H) представлено проверочной вершиной справа. Каждая переменная вершина соответствует колонке H, и каждая проверочная вершина соответствует строке H, здесь “переменная вершина” и “колонка” H упоминаются взаимозаменяемо, как и “проверочная вершина” и “строка” H. Переменные вершины являются присоединенными только к проверочным вершинам, и проверочные вершины являются присоединенными только к переменным вершинам. Для кода с n битами кодовой комбинации и m битами четности переменная вершина v i присоединена к проверочной вершине d посредством ребра, если бит i кодовой комбинации участвует в проверочном уравнении j, i=0,1...,n-1, j=0,1,...,m-l. Другими словами, переменная вершина i присоединена к проверочной вершине j, если позиция h ji проверочной матрицы H равна 1. Отображающее уравнение (1), переменная вершина представляет допустимую кодовую комбинацию, если все проверочные вершины имеют равную четность. Ниже показан пример для иллюстрирования отношения между проверочной матрицей, проверочными уравнениями и двудольным графом. Пусть n=12, код Ѕ скорости будет определен посредством
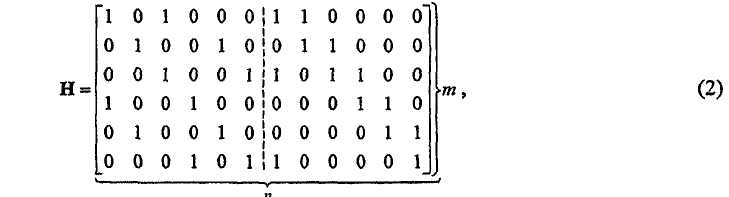
с левой частью, соответствующей k (=6) информационным битам s , левой частью соответствующей m (=6) битами p четности. Применяя (1), H в (2) определяет 6 проверочных уравнений следующим образом:
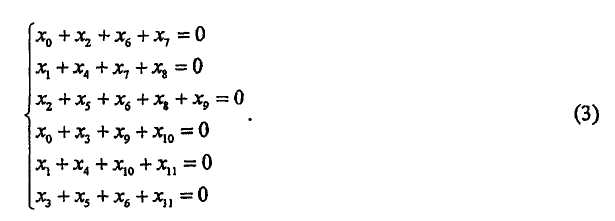
H также имеет соответствующий двудольный граф, показанный на фиг. 1.
Двудольный граф LDPC кода подходящей конечной длины неизбежно имеет циклы. Цикл длины 2d (обозначенный как цикл-2d) является путем 2d ребер, который проходит через d переменных вершин и d проверочных вершин и соединяет каждую вершину с собой без повторения каждого ребра. Короткие циклы, особенно циклы 4, ухудшают производительность итеративного декодера и обычно избегаются в модели кода.
Когда размер кода становится большим, трудно закодировать и декодировать беспорядочно составленный LDPС-код. Вместо прямого построения большой m×n псевдослучайной матрицы H структурированная модель LDPC начинается с маленькой m b ×n b базовой матрицы Нb, делает z копий Нb и соединяет z копий для формирования большой m×n матрицы H, где m=m b ×z, n=n b ×z. Используя матричное представление, для построения H из Нb каждая 1 в Нb заменяется z×z подматрицей перестановок, и каждый 0 в Нb заменяется z×z подматрицей, состоящей из нулей. Показано, что перестановка может быть очень простой без риска для производительности. Например, простой циклический сдвиг вправо, где подматрица перестановок получается сдвигом циклически вправо колонок единичной матрицы на заданную величину, может быть использован без ухудшения производительности декодирования. Так как циклический сдвиг (x mod z) раз эквивалентен циклическому правому сдвигу ((z-х) mod z) раз, этот текст обсуждает только циклический сдвиг вправо и упоминает его как циклический сдвиг для краткости. С этим ограничением каждая матрица H может быть уникально представлена m b ×n b модельной матрицей
Нbm, которая получается заменой каждой h ij =0 в H b на p(i,j)=-1 для обозначения z×z матрицы из нулей и заменой каждой h ij=1 в Нb на циклический сдвиг величины p(i,j)≥0.
Следовательно, вместо использования расширенной матрицы H код уникально определяется модельной матрицей Нbm. Кодирование и декодирование может быть выполнено на основе много меньшей m b ×n b Нbm и векторов битов, с каждым вектором, имеющим размер z.
Эта процедура по существу отображает каждое ребро H bm в векторное ребро размера z в H (представленное p(i,j) H bm), каждую переменную вершину H bm в векторную переменную вершину длины z в H (соответствующую колонке Н bm) и каждую проверочную вершину Н bm в векторную вершину длины z в H (соответствующую строке H bm). В структурированной модели произвольность встроена в H вследствие двух этапов: (a) псевдослучайной базовой матрице H bm; (b) псевдослучайного сдвига ребер в каждом векторном ребре. Сложность хранения и обработки структурированной модели ниже, поскольку обе стадии рандомизации очень простые.
Часто требуются системы, такие как определенные в стандарте IEEE 802.16, для предоставления корректирующих ошибки кодов для семейства кодов размера (n f, k f ), где все коды в семействе имеют одинаковую кодовую скорость R=k f /n f и размер кода, увеличенный от базовой величины, n f = z f ×n b , k f =z f ×k b , f=0, 1,...,f max, где (f max+1) является общим количеством членов в семействе кодов, и zf является коэффициентом расширения для f-го кода в семействе. Для этих систем возможно получить коды для всех (nf, k f ) из одной базовой матрицы H b и набора подходящих z f. Пусть p(f,i,j) будет величиной сдвига векторного ребра, расположенного в позиции (i,j) в f-й модельной матрице H bm(f) коэффициента z f расширения. Соответственно, набор {p(f,i,j)} величин сдвигов и модельная матрица H bm (f) могут быть упоминаемы взаимозаменяемо.
Тем не менее не понятно, как определять величины p(f,i,j) сдвигов для каждой H bm(f). Одним способом определения семейства кодов является поиск базовой матрицы H b и/или p(f,i,j), 0≤i≤m-1, 0≤j≤n-1 независимо для всех заданных f. Тем не менее этот подход требует, чтобы H b и/или p(f,i,j), 0≤i≤m-1, 0≤j≤n-1 были заданы и сохранены для всех f.
Поскольку H b определяет базовую структуру и взаимную связь сообщений LDPC декодера, будет предпочтительным повторно использовать H b для всех кодов семейства. Когда один и тот же H b совместно используется всеми кодами в семействе,
- Величина сдвига p(f,i,j)=-1, когда позиция (i,j) H b равна 0. Величина сдвига p(f,i,j)=-1 используется для обозначения z f ×z f полностью нулевой подматрицы, которая используется для замены позиции (i,j) модельной матрицы H bm(f), в расширении до двоичной проверочной матрицы H(f). Если позиция (i,j) H b равна 0, p(f,i,j) одинаково для любого f, т.е. p(f,i,j)≡-1. Заметим, что "-1" является только меткой для подматрицы из нулей, и может быть равнозначно использована любая другая метка, которая не является неотрицательным целым, например "-2" или "∞".
- Величина сдвига p(f,i,j)≥0, когда позиция (i,j) H b равна 1. Величина сдвига p(f,i,j)≥0 используется для отметки z j ×z f единичной подматрицы, циклически сдвинутой вправо на p(f,i,j) колонок. Подматрица используется для замены позиции (i,j) модельной матрицы H bm(f) в расширении до двоичной проверочной матрицы H(f). Значение p(f,i,j) может быть различным для разных f, например, позиция (i,j) H bm(f) может быть различной для разных f.
В отношении значения неотрицательного p(f,i,j) предложено использовать для любого p(f,i,j)-p(i,j) mod z f для любого z f, где набор {p(i,j)} величин сдвигов является одинаковым для всех z f . Следовательно, только один набор {p(i,j)} требует определения, и это потенциально уменьшает сложность осуществления кодов различных z f . Тем не менее вследствие действия операции взятия модуля набор {p(i,j)}, предназначенный для того, чтобы избежать плохих моделей циклов для определенного z f, может служить причиной большого количества циклов и кодовых комбинаций с низким весом для другого z f, имеющих следствием ухудшение эффективности корректировки ошибок для некоторых (n f, k f).
Таким образом, существует потребность в способе получения величин сдвигов
{p(f, i,j)} из определенного набора {p(i,j)}, в то же время поддерживая требуемые параметры кода для всех размеров кодов (n f, k j ).
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг. 1 иллюстрирует двудольный граф матрицы H (12, 6).
Фиг. 2 - блок-схема кодера.
Фиг. 3 - блок-схема декодера.
Фиг. 4 - схема последовательности операций кодера на фиг. 2.
Фиг. 5 - схема последовательности операций декодера на фиг. 3.
Описание чертежей
Чтобы направить усилия на вышеупомянутые потребности, базовая модельная матрица определена для наибольшей длины кода для каждой кодовой скорости. Набор сдвигов {p(i,j)} в базовой модельной матрице используется для определения величин сдвигов для всех остальных длин кодов той же кодовой скорости. Величины сдвигов {p(f,i,j)} для размера кода, соответствующего коэффициенту расширения z f выводятся из {p(i,j)} пропорциональным масштабированием p(i,j), и модельная матрица, определенная посредством {p(f,i,j)}, используется для определения битов контроля по четности для f-го кода.
Настоящее изобретение предлагает способ управления передатчиком, который генерирует биты контроля по четности на основе блока информации. Способ содержит этапы, на которых определяют базовую модельную матрицу, имеющую набор величин сдвигов p(i,j) для наибольшей длины кода, и определяют величины сдвигов p(f,i,j) для всех остальных длин кодов на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j)=F(p(i,j),z 0 /z f ), z 0 - коэффициент расширения наибольшей длины кода, z f - коэффициент расширения f-й длины кода. Блок информации принимают и модельную матрицу используют для определения битов контроля по четности. Модельную матрицу определяют посредством p(f,i,j).
Настоящее изобретение дополнительно предлагает устройство, содержащее средства хранения для хранения базовой модельной матрицы, имеющей набор величин сдвигов p(i,j) для наибольшей длины кода. Устройство дополнительно содержит микропроцессор, принимающий блок информации s=(s 0,...,s kf-1 ) и базовую модельную матрицу. Микропроцессор определяет величины сдвигов p(f,i,j) для всех других длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов,
p(f,i,j)=F(p(i,j),z 0 /z f ), z 0 - коэффициент расширения наибольшей длины кода, z f - коэффициент расширения f-й длины кода. Микропроцессор выводит биты контроля по четности на основе модельной матрицы, определенной посредством p(f,i,j) и блока информации
s=(s 0,..., s kf-1).
Настоящее изобретение дополнительно предлагает способ управления приемником, который оценивает блок информации s=(s 0 ,...,s k-1). Способ содержит этапы, на которых принимают вектор сигнала, определяют базовую модельную матрицу, имеющую набор величин сдвигов p(i,j) для наибольшей длины кода, и определяют величины сдвигов p(f,i,j) для всех остальных длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j) = F(p(i, j),z 0 /z f ), z 0 - коэффициент расширения наибольшей длины кода, z f - коэффициент расширения f-й длины кода. Блок информации s=(s 0,..., s kf-1) затем оценивают на основе модельной матрицы, определенной посредством p(f,i,j) и принятого вектора сигнала.
В заключение, настоящее изобретение предлагает устройство, содержащее средства хранения для хранения базовой модельной матрицы, имеющей набор величин сдвигов p(i,j) для наибольшей длины кода. Устройство дополнительно содержит декодер, принимающий вектор сигнала и определяющий величины сдвигов p(f,i,j) для всех других длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j)=F(p(i,j),z 0 /z f), z 0 - коэффициент расширения наибольшей длины кода, z f - коэффициент расширения f-й длины кода. Декодер выводит оценку для блока информации s=(s 0 ,..., s kf-1 ) на основе модельной матрицы, определенной p(f,i,j) и принятым вектором сигнала.
Показано, что свойства расширенной матрицы H тесно связаны со свойствами базовой матрицы Нb и величинами сдвигов p(i,j). Определенные нежелательные шаблоны величин сдвигов p(i,j) будут сохранять циклы и шаблоны Нb кодовых комбинаций и повторять их многократно в расширенной матрице H вследствие квазициклической природы модели кода, приводя к неприемлемой эффективности корректировки ошибок.
Так как кодовые комбинации с низким весом содержат короткие циклы, если Нb не имеет ни одной колонки с весом 1, достаточно убедиться, что короткие циклы разорваны для всех интересующих размеров кодов (n f , k j ) для того, чтобы получить хорошую эффективность декодирования.
Обнаружено, что цикл Нb дублируется в расширенной матрице, если удовлетворяется следующее условие.
Если в базовой матрице H b 2c ребер из цикла длины 2c, тогда в расширенной матрице H соответствующие 2c векторных ребер из z циклов длины 2c тогда и только тогда, если
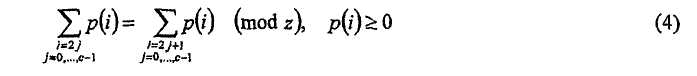
где z - коэффициент расширения, p(i) - величина циклического сдвига ребра i в модельной матрице H bm , и ребра 0, 1, 2,..., 2c-l (в этом порядке) формируют цикл в H b .
Тогда как фиксированный набор величин {p(i,j)} сдвигов, который не удовлетворяет уравнению (4) для одного значения z f может фактически удовлетворять уравнению (4) для другого значения z f, линейность уравнения (4) показывает, что уравнение может не удовлетворять ему для всех z f, если {p(i,j)} масштабируется пропорционально z f.
Допустим, что один набор величин {p(i,f)} сдвигов должен использоваться для расширения данной базовой матрицы Нb для двух коэффициентов расширения z 0 и z 1, α=Z 0 /Z 1>1. Допустим, что набор величин сдвигов {p(i,j)} = {р(0,i,j)} освобожден от циклов длины 2c для коэффициента Z0 расширения,
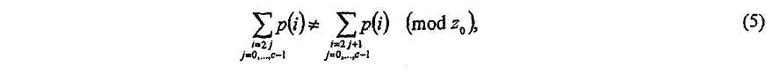
тогда
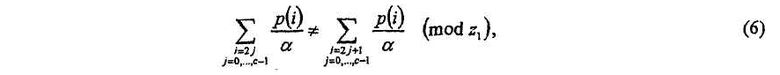
где p(i) - величина циклического сдвига ребра i в модельной матрице H bm(0), и ребра 0, 1, 2,..., 2c-l (в этом порядке) формируют цикл в H b. Уравнение (6) показывает, что если набор масштабированных величин {p(i,j)/α} сдвигов используется для коэффициента расширения z 1, тогда матрица H, расширенная от z 1, будет также освобождена от циклов длины 2с. Так как 2c может быть любой длиной цикла, использование отмасштабированных величин {p(i,j)/α} будет аннулировать все типы циклов для z 1, которые аннулированы набором {p(i,j)} для z0.
Обсуждение выше пренебрегает ограничением, таким что величины сдвигов после масштабирования по-прежнему должны быть целыми. Например, должна быть выполнена функция пола └x┘ (которая является наибольшим целым числом, меньшим или равным x), функция потолка ┌x┐ (которая является наименьшим целым числом, большим или равным x) или функция округления [x](которая является целым числом, которое менее всего отличается от x) над всеми p(i,j)/α для получения целого числа. В общем, при заданных величинах сдвигов p(i,j)=p(0,i,j) для Z 0 величины сдвигов для z 1 могут быть получены как функция F(.) от p(i,f) и α.
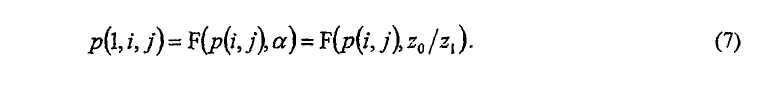
Например, если функция округления используется на верхнем уровне (6) и величинами сдвигов, предназначенных для z 0, являются p(i,j), тогда набором величин сдвигов, применяемых к z 1, является
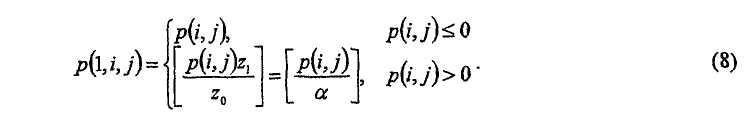
Хотя обычно все положительные p(i,j) будут отмасштабированы, масштабирование, такое как (8), может быть применено к единственному поднабору {p(i,j)}. Например, те, которые не затронуты никакими циклами, не должны быть отмасштабированы, например ребра колонок Нb веса 1, если они существуют. В зависимости от определения функции F(.) и если масштабирование применяется только всем неотрицательным p(i,j), базовые матрицы H bm(0) и H bm(1) могут быть или не быть одинаковыми.
Вышеприведенный анализ без труда применен для нахождения p(f,i,j), если система требует более двух коэффициентов расширения. В этом случае определяется материнская модельная матрица (также называемая базовой модельной матрицей) H bm(0), имеющая набор величин сдвигов p(0,i,j) для наибольшей длины кода, из которой получается модельная матрица H bm(f), имеющая величины сдвигов p(f,i,j) для f-го семейства кодов, f=1,...,f max. При условии z 0=max(z f) и p(0,i,j)=p(i,f), α f =z 0 /z f должно быть использовано в выражениях, аналогичных (8) в получении p(f,i,j) из p(i,j), так что одинаковые циклы базовой матрицы исключаются для всего диапазона z f. В частности, при условии того, что все p(i,j) найдены,
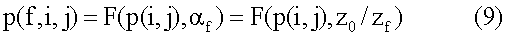
в общем используется для получения p(f,i,j) из p(i,j). Более того, в качестве примера, функция F(.) может быть определена как
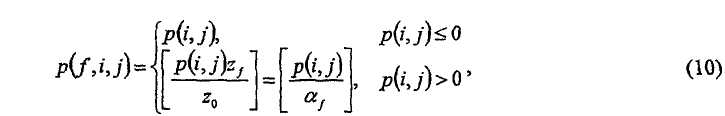
при условии z 0 = max(z f) и используя функцию округления, соответствующую (8). Сходным образом, может быть использована функция пола └x┘ или функция потолка ┌x┐ вместо функции округления [x].
Заметим, что вышеупомянутая методика расчета применяется к любой базовой матрице Н b. Например, она может применяться к Н b, состоящим из двух частей,
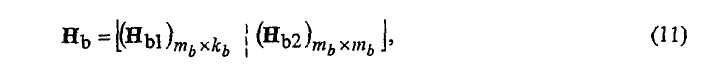
чья детерминированная часть Н b2 может быть дополнительно разделена на две части, где hb имеет нечетный вес w h>2 и H'b2 имеет детерминированную ступенчатую структуру:

Другими словами, Н'b2 содержат матричные элементы для строки i, столбца j, равные:
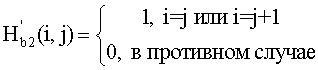
Реализация кодера для семейства кодов
Поскольку все члены семейства, соответствующего вышеприведенному плану, получаются из материнской модельной матрицы H bm=H bm(0), таким образом все имеющие одинаковую структуру, процесс кодировки для каждого члена семейства является аналогичным. Часть или целая модельная матрица может быть сохранена и интерпретироваться в качестве инструкций для многорегистровой схемы циклического сдвига для выполнения циклических сдвигов сгруппированной информационной последовательности.
Так как все члены семейства получаются из материнской модельной матрицы H bm=H bm(0), реализация кодера для семейства требует только, что материнская матрица была сохранена. При условии, что используется функция [x] округления, для f-го члена семейства циклические сдвиги p(i,j) материнской модельной матрицы заменяются циклическими сдвигами [p(i,j)/(z 0 /z f )] для p(i,j)>0, где z f обозначает коэффициент расширения f-го члена семейства, которое кодируется. Непосредственной реализацией этого является хранение значений α f -1=(z 0 /z f ) -1 (или α f=z 0 /z f ) для каждого члена семейства в постоянной памяти и вычисление значений [p(i,j)/(z 0 /z f )], p(i,j)>0 "на лету" с использованием умножителя. В качестве альтернативы наборы {p(f,i,f)}, f=0, 1,...,f max величин сдвигов для каждого члена семейства могут быть заранее рассчитаны, используя (8) (или в более общем смысле, (7)), и сохранены в постоянной памяти.
Многорегистровая схема циклического сдвига может быть модифицирована для обеспечения циклических сдвигов для всех длин слов z f, соответствующих членам семейства. Несмотря на то, что модификация многорегистровой схемы циклического сдвига будет усложнять логику многорегистровой схемы циклического сдвига и неизбежно влечь за собой более медленные тактовые частоты, альтернативой, требующей дополнительных логических ресурсов, является осуществление различных многорегистровых схем циклического сдвига для каждого размера z f слова.
Фиг. 2 - блок-схема кодера 200. Как показано, кодер 200 содержит микропроцессор 201, таблицу 203 поиска и логическую схему 205 для определения коэффициента z f расширения. Хотя и показаны существующие внешне по отношению друг к другу, рядовой специалист в данной области техники будет давать себе отчет, что функциональные возможности логической схемы 205 могут быть осуществлены в микропроцессоре 201.
Микропроцессор 201 предпочтительно содержит цифровой процессор сигналов (DSP), такой как, но не ограниченный DSP MSC8300 и DSP56300. Дополнительно таблица 203 поиска служит в качестве средств хранения для хранения матрицы и содержит постоянную память; тем не менее рядовой специалист в данной области техники будет отдавать себе отчет, что другие виды памяти (например, память с произвольной выборкой, магнитная запоминающая память и т.д.) могут быть также использованы. Во втором варианте осуществления функциональные возможности микропроцессора 201 и таблицы 203 поиска и логической схемы 205 могут быть включены в специализированную интегральную схему (ASIC) или программируемую вентильную матрицу (FPGA). В частности, таблица 203 поиска может быть реализована в виде памяти, соответствующей наличию или отсутствию путей сигнала в схеме.
Как обсуждалось выше, закодированные данные обычно принимают вид множества битов контроля по четности в дополнение к систематическим битам, где вместе биты контроля по четности и систематические биты формируют кодовую комбинацию x. В первом варианте осуществления настоящего изобретения базовая модельная матрица H bm хранится в таблице 203 поиска и выбирается микропроцессором 201 для нахождения битов контроля по четности. В частности, микропроцессор 201 определяет соответствующие значения для битов p=(p 0 ,...,p mf-1) контроля по четности на основе блока информации s=(s 0,...,s kf-1 ), коэффициента z f расширения и базовой модельной матрицы Нbm. Коэффициент z f расширения определяется логикой 205, использующей z f =k f /k b =n f /n b , и использованием групповых битов в векторы длины z f так же, как нахождение α f =z 0 /z f. После того как биты контроля по четности найдены, они и набор систематических битов затем переправляется передатчику и передается в приемник.
Фиг. 3 - блок-схема декодера 300 согласно одному варианту осуществления настоящего изобретения. Как показано, декодер 300 содержит микропроцессор 301, таблицу 303 поиска и логическую схему 305 для определения коэффициента расширения z f . В первом варианте осуществления настоящего изобретения микропроцессор 301 содержит цифровой процессор сигналов (DSP), такой как, но не ограниченный DSP MSC8300 и DSP56300. Дополнительно таблица 303 поиска действует как средства хранения для хранения базовой модельной матрицы H bm и содержит постоянную память. Тем не менее рядовой специалист в данной области техники будет отдавать себе отчет, что другие виды памяти (например, память с произвольной выборкой, магнитная запоминающая память и т.д.) могут быть также использованы. Во втором варианте осуществления функциональность микропроцессора 301 и таблицы 303 поиска может быть включена в специализированную интегральную схему (ASIC) или программируемую вентильную матрицу (FPGA). В частности, таблица 303 поиска может быть реализована в виде памяти, соответствующей наличию или отсутствию путей сигнала в схеме.
Принятый вектор y =(y 0 ,...,y n-1) сигнала (принятый посредством приемника) соответствует кодовой комбинации x, переданной через канал с шумом, где закодированные данные x, как обсуждалось выше, являются вектором f-го члена семейства кодов. В первом варианте осуществления настоящего изобретения базовая модельная матрица Нbm хранится в таблице 303 поиска и выбирается микропроцессором 301 для декодирования y и оценки блока информации S=(s 0,...,s kf-1). В частности, микропроцессор 301 оценивает блок информации (s 0 ,...,s kf-1 ) на основе принятого вектора y=(у 0 ,...,y kf-1 ) сигнала и базовой модельной матрицы Нbm. Коэффициент z f расширения определяется логикой 305, использующей z f =k f /k b =n f /n b , и используется для группировки принятых сигналов и битов в векторы длины z f так же, как нахождения α f =z 0 /z f.
Фиг. 4 - схема последовательности операций кодера 200 и, в частности, микропроцессора 201. Поток начинается на этапе 401, где текущий блок (s 0 ,...,s k-1 ) информации принимается микропроцессором 201. На этапе 403 значения битов контроля по четности определяются на основе блока информации и H bm(f), где H bm(f) уникально определяется {p(f,i,j)}. В частности, набор {p(i,j)} величин сдвигов базовой модельной матрицы H bm считывается из памяти. Микропроцессор использует {p(i,j)} и α f для определения {p(f,i,j)}. Биты (p 0 ,...,p mf-1 ) контроля по четности определяются посредством решения уравнения (1). На этапе 405 информационный блок и биты контроля по четности передаются по каналу.
Фиг. 5 - схема последовательности операций кодера 300 и, в частности, микропроцессора 301. Поток логики начинается на этапе 501, где принятый вектор
y=(y 0,...,y n-1) сигнала принимается. На этапе 503 оценки блока информации s=(s 0 ,...,s kf-1 ) определяются на основе H bm(f), где H bm(f) уникально определена посредством {p(f,i,j)}. В частности, набор {p(i,j)} величин сдвигов базовой модельной матрицы H bm считывается из памяти. Микропроцессор использует {p(i,j)} и α f для определения {p(f,i,j)}. Как обсуждалось, микропроцессор обрабатывает принятый вектор сигнала в соответствии с величинами сдвигов {p(f,i,j)} (или эквивалентно, Нbm(f)) для получения оценок блока информации. В предпочтительном варианте осуществления микропроцессор выполняет обработку согласно алгоритму пересылки сообщений, используя двудольный граф кода.
Примеры
В качестве примера описывается модель кода для 19 размеров кода n f в диапазоне от 576 до 2304 битов. Каждая базовая модельная матрица предназначена для величины сдвига Z0 =96. Набор величин сдвигов {p(i,j)} определен для базовой модельной матрицы и используется для других размеров кодов той же скорости. Для других размеров кодов величины сдвигов получаются из базовой модельной матрицы следующим образом.
Для размера кода, соответствующего коэффициенту расширения z f, его величины {p(f,i,j)} сдвига получаются из {p(i,j)} пропорциональным масштабированием p(i,j)
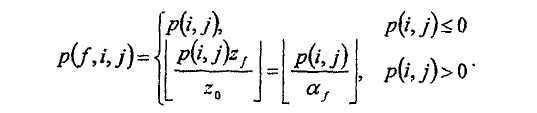
Заметим, что α f=z 0 /z f и └x┘ обозначает функцию пола, которая дает ближайшее целое число в направлении -∞.
Базовые модельные матрицы сведены в таблицы внизу для трех кодовых скоростей 1/2, 2/2 и 3/4. Здесь f является индексом длин кодов для данной кодовой скорости, f = 0,1,2,... 18.
Скорость 1/2:
Базовая модельная матрица имеет размер nb=24, m b =12 и коэффициент расширения
z 0=96 (т.е., n0=24*96=2304). Для получения других размеров кодов n f коэффициент расширения z f равен nf/24.

Скорость 2/3:
Базовая модельная матрица имеет размер nb=24, m b =8 и коэффициент расширения z 0=96 (т.е. n0=24*96=2304). Для получения других размеров кодов n f коэффициент расширения z f равен nf/24.


Скорость 3/4:
Базовая модельная матрица имеет размер nb=24, m b =6 и коэффициент расширения z 0=96 (т.е. n0=24*96=2304).
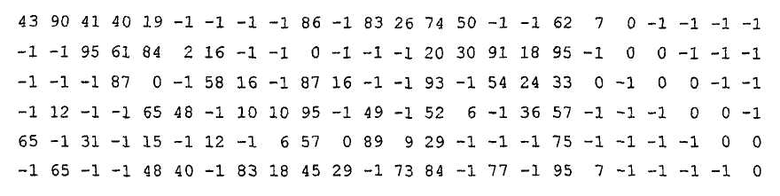
Для получения других размеров кодов n f коэффициент расширения z f равен nf/24.
Несмотря на то, что изобретение было подробно показано и описано со ссылкой на определенный предпочтительный вариант осуществления, специалистами в данной области техники будет понято, что в нем могут быть сделаны различные изменения по форме и содержанию, не выходя из сущности и объема изобретения. Например, когда диапазон размеров кодов очень большой, например α приближается к z/2, становится очень трудно найти подходящий набор {p(i,j)} величин сдвигов. Следовательно, если диапазон размеров кодов очень велик, т.е. α велико, могут использовать различные наборы {p{i,f)}, каждый из которых покрывает диапазон z f для семейства кодов. В другом примере, хотя обсуждение допускало, что используются материнская модельная матрица Нbm(0), z0=max(z f), и p(0,i,j)=p(i,j) используются для 0-го члена семейства кодов, специалисты в данной области техники будут понимать, что Нbm(0),
z 0 и p(i,j) могут быть определены для размера кода не в семействе кодов, но использоваться для получения величин p(f,i,j) сдвигов интересующего семейства кодов. В другом примере, хотя обсуждение допускало, что z 0 = max(z f), специалисты в данной области техники будут понимать, что значение z 0, не равное max(z f), может быть использовано в выводе величины сдвига. Подразумевается, что такие изменения появляются в объеме последующей формулы изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 2005 |
|
RU2370886C2 |
| СПОСОБЫ СОГЛАСОВАНИЯ СКОРОСТИ ДЛЯ LDPC-КОДОВ | 2017 |
|
RU2730434C1 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740154C1 |
| АППАРАТУРА, СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И АППАРАТУРА СВЯЗИ | 2018 |
|
RU2758968C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ И УСТРОЙСТВО СВЯЗИ | 2017 |
|
RU2740151C1 |
| КОЭФФИЦИЕНТЫ LDPC-СДВИГА ДЛЯ НОВОГО СТАНДАРТА РАДИОСВЯЗИ | 2018 |
|
RU2731883C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ИНФОРМАЦИИ, УСТРОЙСТВО СВЯЗИ И СИСТЕМА СВЯЗИ | 2018 |
|
RU2752420C2 |
| Способ кодирования канала в системе связи, использующей LDPC-код | 2020 |
|
RU2769945C2 |
| СПОСОБЫ И СИСТЕМЫ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ LDPC КОДОВ | 2016 |
|
RU2716044C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ, УСТРОЙСТВО ХРАНЕНИЯ ДАННЫХ, СИСТЕМА ОБМЕНА ДАННЫМИ И СПОСОБ ДЕКОДИРОВАНИЯ | 2008 |
|
RU2440669C1 |
Изобретение относится к кодированию и декодированию данных, в частности к способу и устройству для кодирования данных, использующему коды с контролем по четности низкой плотности (LDPC). Технический результат - повышение точности кодирования и декодирования данных. Для этого биты контроля по четности рассчитывают для принятой информации. Базовую модельную матрицу определяют для самой большой длины кода каждой кодовой скорости. Набор {p(i,j)} сдвигов в базовой модельной матрице используют для определения величин сдвигов для всех остальных длин кодов той же кодовой скорости. Величины {p(f,i,j)} сдвигов для размера кода, соответствующего коэффициенту расширения zf, выводят из {p(i,j)} пропорциональным масштабированием p(i,j) и модельную матрицу посредством {p(f,i,j)} используют для определения битов контроля по четности для f-го кода. 3 н. и 7 з.п. ф-лы, 5 ил.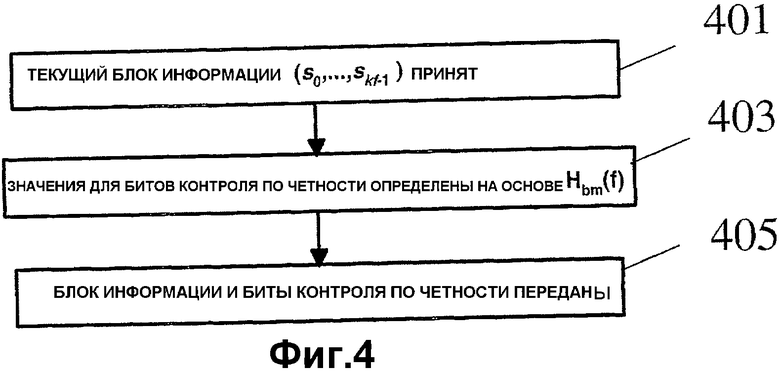
1. Способ управления передатчиком, который генерирует биты контроля по четности на основе блока информации, заключающийся в том, что
определяют базовую модельную матрицу, имеющую набор величин сдвигов p(i,j) для наибольшей длины кода;
определяют величины сдвигов p(f,i,j) для всех других длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j)=F(p(i,j),z0/zf), z0 - коэффициент расширения наибольшей длины кода, zf - коэффициент расширения f-й длины кода;
принимают блок информации s=(s0, …, skf-1);
используют модельную матрицу, определенную посредством p(f,i,j) для определения битов контроля по четности; и
передают биты контроля по четности вместе с блоком информации, где {p{i,j)}=
2. Способ по п.1, в котором
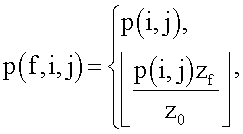
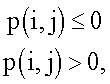
a 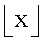 обозначает функцию пола.
обозначает функцию пола.
3. Способ по п.1, в котором
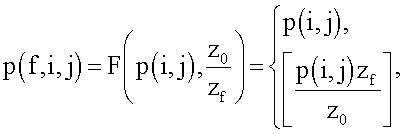
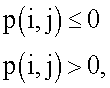
а [x] обозначает функцию округления.
4. Способ по п.1, в котором
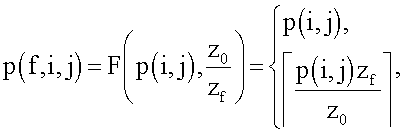
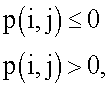
а 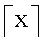 обозначает функцию потолка.
обозначает функцию потолка.
5. Способ по п.1, в котором биты контроля по четности находят на основе проверочной матрицы H(f), которую расширяют из модельной матрицы Нbm(f), определенной посредством p(f,i,j) с коэффициентом Zf расширения.
6. Устройство связи, включающее в себя передатчик, который генерирует биты контроля по четности на основе блока информации, и содержащее
средство хранения для хранения базовой модельной матрицы, имеющей набор величин сдвигов p(i,j) для наибольшей длины кода;
и
микропроцессор, принимающий блок информации s=(s0, …, skf-1) и базовую модельную матрицу и определяющий величины сдвигов p(f,i,j) для всех других длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j)=F(p(i,j,z0/zf), z0 - коэффициент расширения наибольшей длины кода, zf - коэффициент расширения f-й длины кода; причем микропроцессор выводит биты контроля по четности на основе модельной матрицы, определенной посредством p(f,i,j) и блока информации s=(s0, …, skf-1); где {p(i,j)}=
7. Устройство по п.6, в котором
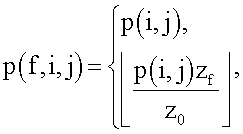
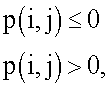
где 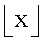 обозначает функцию пола.
обозначает функцию пола.
8. Устройство по п.6, дополнительно содержащее постоянную память, имеющую значения для p(f,i,j)=F(p(i,j),z0/zf).
9. Устройство по п.6 дополнительно содержащее постоянную память, имеющую значения для z0/zf.
10. Способ управления приемником, который оценивает блок информации
s=(s0, …, skf-1), заключающийся в том, что
принимают вектор сигнала;
определяют базовую модельную матрицу, имеющую набор величин сдвигов p(i,j) для наибольшей длины кода;
определяют величины сдвигов p(f,i,j) для всех других длин кода на основе набора величин сдвигов p(i,j), где f - индекс длин кодов, p(f,i,j)=F(p(i,j,z0/zf), z0 - коэффициент расширения наибольшей длины кода, zf - коэффициент расширения f-й длины кода;
оценивают блок информации s=(s0, …, skf-1) на основе модельной матрицы, определенной посредством p(f,i,j) и принятого вектора сигнала, где {p(i,j)=
| US 5140596 A, 18.08.1992 | |||
| УСТРОЙСТВО И СПОСОБ ВСТАВКИ ЗАРАНЕЕ ИЗВЕСТНЫХ БИТОВ НА ВХОДНОМ КАСКАДЕ КАНАЛЬНОГО КОДЕРА | 1999 |
|
RU2190296C2 |
| ПАРАЛЛЕЛЬНЫЙ КАСКАДНЫЙ СВЕРТОЧНЫЙ КОД С КОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ БИТОВ И ДЕКОДЕР ДЛЯ ТАКОГО КОДА | 1997 |
|
RU2187196C2 |
| US 6578171 B1, 10.10.2003 | |||
| Подмости | 1979 |
|
SU806839A1 |
Авторы
Даты
2009-08-20—Публикация
2005-08-03—Подача