СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ, ПРИСПОСОБЛЕНИЕ И УСТРОЙСТВО СВЯЗИ Российский патент 2022 года по МПК H03M13/11 

Область техники, к которой относится изобретение

Варианты осуществления настоящего изобретения относятся к области связи и, в частности, к способу обработки информации и устройству связи.

Уровень техники

Код с низкой плотностью проверок на четность (low density parity check, LDPC) представляет собой тип линейного блочного кода с разреженной матрицей проверки на четность и характеризуется гибкой структурой и низкой сложностью декодирования. Поскольку при декодировании LDPC кода используют частично параллельный алгоритм итеративного декодирования, LDPC код имеет более высокую производительность, чем обычный турбокод. Для повышения надежности передачи канала и эффективного использования мощности в системе связи LDPC код может быть использован в качестве кода с исправлением ошибок в системе связи. LDPC код может также широко применяться для космической связи, волоконно-оптической связи, систем персональной связи, ADSL, устройств магнитной записи и тому подобного. В настоящее время LDPC схема кода рассматривается как одна из схем канального кодирования в мобильной связи 5-го поколения.

В практических применениях могут быть использованы LDPC матрицы, характеризующиеся различными специальными структурами. LDPC матрица Н, имеющая специальную структуру, может быть получена путем расширения LDPC базовой матрицы, имеющей квазициклическую (quasi cycle, QC) структуру. Схема кодирования с использованием QC-LDPC матриц подходит для аппаратных средств с высокой степенью параллелизма и обеспечивает более высокую производительность.

QC-LDPC подходит для аппаратных средств с высокой степенью параллелизма и обеспечивает более высокую производительность. LDPC матрица может быть разработана для применения в канальном кодировании.

Сущность изобретения

Варианты осуществления настоящего изобретения предоставляют способ обработки информации и устройство и систему связи для поддержки кодирования и декодирования последовательностей информационных бит множества длин.

Согласно первому аспекту предоставлены способ кодирования и кодер. Кодер кодирует входную последовательность, используя матрицу кода с низкой плотностью проверок на четность, LDPC.

Согласно второму аспекту предоставлены способ декодирования и декодер. Декодер декодирует входную последовательность, используя матрицу кода с низкой плотностью проверок на четность, LDPC.

В первой реализации первого аспекта или второго аспекта LDPC матрицу получают на основании коэффициента Z поднятия и базовой матрицы.

На основании вышеизложенной реализации базовая матрица базового графа 30a может включать в себя от строки 0 до строки 4 и от столбца 0 до столбца 26 в одной из матриц 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 и 30b-80, или базовая матрица включает в себя от строки 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в одной из матриц 30b-10 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 и 30b-80 или базовая матрица может быть матрицей, полученной путем выполнения перестановки строка/столбец в матрице, включающей в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в одной из матриц с 30b-10 по 30b-80, или базовая матрица может быть матрицей, полученной путем выполнения перестановки строка/столбец для матрицы, включающей в себя от строки 0 до строки 4 и некоторые их столбцов от 0 до столбца 26 в одной из матриц 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 и 30b-80.

Кроме того, базовая матрица базового графа 30a может дополнительно включать в себя строку 0 до строки (m-1) и столбец 0 до столбца (n-1) в одной из матриц 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 и 30b-80 или базовая матрица может быть матрицей, полученной путем выполнения перестановки строка/столбец на матрице включающей в себя строки от 0 до строки (m-1) и от 0 до столбца (n-1) в одной из матриц 30b-10, 30b-11, 30b-20, 30b-21, 30b-30, 30b-40, 30b-50, 30b-60, 30b-70 и 30b-80, где 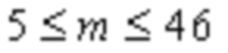и .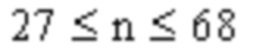

Чтобы поддерживать разные длины кодовых блоков, для LDPC кода требуются разные коэффициенты Z поднятия. На основании вышеизложенной реализации в возможной реализации, основанной на различных коэффициентах Z поднятия, используются базовые матрицы, соответствующие различным коэффициентам Z поднятия. Например, 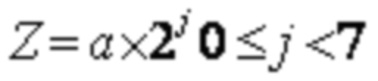и .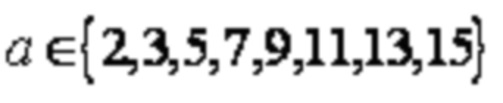

Если a = 2, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-10 или 30b-11, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбца 0 до столбца 26 в матрице 30b-10 или 30b-11. Кроме того, базовая матрица дополнительно включает в себя строки от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в матрице 30b-10 или 30b-11.

Если a = 3, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-20 или 30b-21, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбца 0 до столбца 26 в матрице 30b-20 или 30b-21. Кроме того, базовая матрица дополнительно включает в себя строки от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в матрице 30b-20 или 30b-21.

Если a = 5, базовая матрица может включать в себя строки от 0 до строки 4 и столбцы от 0 до столбца 26 в матрице 30b-30, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в матрица 30b-30. Кроме того, базовая матрица дополнительно включает в себя строку от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в матрице 30b-30.

Если a = 7, базовая матрица может включать в себя строку 0 до строки 4 и столбец 0 до столбца 26 в матрице 30b-40, или базовая матрица включает строку 0 по строку 4 и некоторые столбцы 0 по столбец 26 в матрице 30b-40. Кроме того, базовая матрица дополнительно включает в себя строку 0 по строку (m-1) и столбец от 0 до столбца (n-1) в матрице 30b-40.

Если a = 9, базовая матрица может включать в себя строку от 0 по строку 4 и столбец 0 по столбец 26 в матрице 30b-50, или базовая матрица включает в себя строку 0 - строку 4 и некоторые столбцы 0 - столбец 26 в матрица 30b-50. Кроме того, базовая матрица дополнительно включает в себя строку от 0 по строки (m-1) и столбец от 0 до столбца (n-1) в матрице 30b-50.

Если a = 11, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-60, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в матрица 30b-60. Кроме того, базовая матрица дополнительно включает в себя строку от 0 до строки (m-1) и столбец от 0 до столбца (n-1) в матрице 30b-60.

Если a = 13, базовая матрица может включать в себя строки от 0 до строки 4 и столбцы от 0 до столбца 26 в матрице 30b-70, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в матрица 30b-70. Кроме того, базовая матрица дополнительно включает в себя строку от 0 до строки (m-1) и столбец от 0 до столбца (n-1) в матрице 30b-70.

Если a = 15, базовая матрица может включать в себя строку от 0 до строки 4 и столбец 0 до столбца 26 в матрице 30b-80, или базовая матрица включает строку от 0 до строки 4 и некоторые столбцы от 0 до столбца 26 в матрице 30b-80. Кроме того, базовая матрица дополнительно включает в себя строку от 0 до строки (m-1) и столбец от 0 до столбца (n-1) в матрице 30b-80.

Базовая матрица может быть матрицей, полученной путем выполнения перестановки строка/столбец над вышеупомянутыми базовыми матрицами.

Кроме того, альтернативно, на основании вышеупомянутых реализаций, LDPC матрица может быть получена на основании коэффициента Z поднятия и матрицы Hs, полученной посредством смещения каждой из вышеупомянутых базовых матриц, или может быть получена на основании коэффициента Z поднятия и матрица, полученная путем выполнения перестановки строка/столбец для матрицы Hs, полученной путем смещения каждой из вышеупомянутых базовых матриц. Смещение каждой из вышеупомянутых базовых матриц может содержать: увеличение или уменьшение значений сдвига, больших или равных 0, в одном или нескольких столбцах на величину смещения.

Базовый граф и базовые матрицы LDPC матрицы в вышеприведенных реализациях могут удовлетворять требованиям к производительности кодовых блоков множества длин блоков.

На основании любого из вышеупомянутых аспектов или возможных реализаций аспектов, в другой возможной реализации, способ дополнительно включает в себя: определение коэффициента Z поднятия. Например, значение коэффициента Z поднятия определяют на основании длины K входной последовательности. Минимальное значение Z₀, которое удовлетворяет 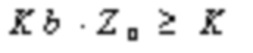, может быть определено из поддерживаемого коэффициента поднятия, установленного в качестве значения коэффициента Z поднятия. В возможной реализации Kb может быть количеством столбцов, соответствующих информационным битам в базовой матрице LDPC кода. Например, для базового графа 30a, Kb = 22. В другой возможной реализации значение Kb может варьироваться в зависимости от значения K, но не превышает количество столбцов, соответствующих информационным битам в базовой матрице LDPC кода. Например, когда K больше первого порогового значения, Kb = 22; когда K меньше или равно первому пороговому значению, Kb = 21. В качестве альтернативы, когда K превышает первое пороговое значение, Kb = 22; когда K меньше или равен первому пороговому значению и больше второго порогового значения, Kb = 21; когда K меньше или равен второму пороговому значению, Kb = 20.

Коэффициент Z поднятия может быть определен кодером или декодером на основании длины K входной последовательности или может быть определен другим компонентом и предоставлен кодеру или декодеру в качестве входного параметра.

Возможно, LDPC матрица может быть получена на основании полученного коэффициента Z поднятия и базовой матрицы, соответствующей коэффициенту Z поднятия.

Во второй реализации первого аспекта или второго аспекта LDPC матрицу получают на основании коэффициента Z поднятия и параметров LDPC матрицы.

Параметры LDPC матрицы могут включать в себя индекс строки, позицию столбца, в котором расположен ненулевой элемент, и значение сдвига ненулевого элемента, и хранят в соответствии с таблицей 3- 10, таблицей 3-11, таблицей 3-20, таблицей 3-21, таблицей 3-30, таблицей 3-40, таблицей 3-50, таблицей 3-60, таблицей 3-70 и таблицей 3-80. Параметры могут дополнительно включать в себя вес строки. Позиции столбцов, в которых расположен ненулевой элемент, находятся во взаимно однозначном соответствии со значениями сдвига ненулевого элемента.

Следовательно, кодер кодирует входную последовательность на основании коэффициента Z поднятия и параметров LDPC матрицы. Параметры, сохраненные на основании таблицы 3-10, соответствуют матрице 30b-10, параметры, сохраненные на основании таблицы 3-11, соответствуют матрице 30b-11, параметры, сохраненные на основании таблицы 3-20, соответствуют матрице 30b-20, параметры, сохраненные на основании таблицы 3-21, соответствуют матрице 30b-21, параметры, сохраненные на основании таблицы 3-30, соответствуют матрице 30b-30, параметры, сохраненные на основании таблицы 3-40, соответствуют матрице 30b-40, параметры, сохраненные на основании таблицы 3-50, соответствуют матрице 30b-50, параметры, сохраненные на основании таблицы 3-60, соответствуют матрице 30b-60, параметры, сохраненные на основе таблицы 3-70, соответствуют матрице 30b-70, и параметры, сохраненные на основании таблицы 3-80, соответствуют матрице 30b-80.

Для устройства связи на передающей стороне кодирование входной последовательности с использованием LDPC матрицы может включать в себя:

кодирование входной последовательности с использованием LDPC матрицы, соответствующей коэффициенту Z поднятия; или кодирование входной последовательности с использованием матрицы, причем матрицу получают путем выполнения перестановки строк/столбцов на LDPC матрице, соответствующей коэффициенту Z поднятия. В настоящем изобретении перестановка строк/столбцов относится к перестановке строк, перестановок столбцов или перестановке строк и перестановок столбцов.

Для устройства связи на принимающей стороне декодирование входной последовательности с использованием LDPC матрицы включает в себя:

декодирование входной последовательности с использованием LDPC матрицы, соответствующей коэффициенту Z поднятия; или декодирование входной последовательности с использованием матрицы, в котором матрицу получают путем выполнения перестановки строк/столбцов на LDPC матрице, соответствующей коэффициенту Z поднятия. В настоящем изобретении перестановка строк/столбцов относится к перестановке строк, перестановок столбцов или перестановке строк и перестановок столбцов.

В возможной реализации LDPC матрица может быть сохранена в памяти, и входную последовательность кодируют с использованием LDPC матрицы, или перестановку (перестановка строк/столбцов) или поднятие выполняют на основании LDPC матрицы, чтобы получить LDPC матрицу, которую можно использовать для кодирования.

В другой возможной реализации может быть сохранен один или несколько параметров, LDPC матрица, используемая для кодирования или декодирования, может быть получена на основании одного или нескольких параметров, и поэтому входная последовательность может быть кодирована или декодирована на основании LDPC матрицы. Один или несколько параметров включают в себя, по меньшей мере, одно из следующего: базовый граф, базовую матрицу, переставленную матрицу, полученную путем выполнения перестановки строк/столбцов на основании базового графа или базовой матрицы, поднятую матрицу на основании базового графа или базовой матрицы, значение сдвига ненулевого элемента в базовой матрице или любой параметр, относящийся к получению LDPC матрицы.

В еще одном возможном варианте осуществления базовая матрица LDPC матрицы может храниться в памяти.

В еще одной возможной реализации базовый граф LDPC матрицы может быть сохранен в памяти, и значения смещения ненулевых элементов в базовой матрице LDPC матрицы могут быть сохранены в памяти.

В еще одной возможной реализации параметры LDPC матрицы сохраняют в памяти в соответствии с таблицами с 3-10 по 3-80.

На основании вышеизложенных возможных реализаций, в возможной реализации, по меньшей мере, один из базовый граф и базовая матрица, которые используют для LDPC кодирования или декодирования, получают путем выполнения перестановки строк, или перестановки столбцов, или перестановки строк и столбцов, перестановкой, по меньшей мере, на одном из базовом графе и базовой матрицы вышеупомянутой LDPC матрицы.

Согласно третьему аспекту предоставлено устройство связи. Устройство связи может включать в себя соответствующий модуль, выполненный с возможностью выполнять вышеизложенные способы реализаций. Модуль может быть программным и/или аппаратным.

В возможной реализации устройство связи, предусмотренное в третьем аспекте, включает в себя процессор и компонент приемопередатчика. Процессор и компонент приемопередатчика могут быть выполнены с возможностью реализации функций описанного выше способа кодирования или декодирования. В реализации, если устройство связи является терминалом, базовой станцией или другим сетевым устройством, компонент приемопередатчика устройства связи может быть приемопередатчиком; если устройство связи представляет собой микросхему основной полосы частот или схему обработки основной полосы частот, компонент приемопередатчика устройства связи может быть схемой ввода/вывода микросхемы основной полосы частот или схемы обработки основной полосы частот и выполнена с возможностью принимать/отправлять входной/выходной сигнал. Возможно, устройство связи может дополнительно включать в себя память, выполненную с возможностью хранить данные и/или инструкции.

В реализации процессор может включать в себя кодер согласно первому аспекту и блок определения. Блок определения выполнен с возможностью определять коэффициент Z поднятия, необходимого для кодирования входной последовательности. Кодер выполнен с возможностью кодировать входную последовательность с использованием LDPC матрицы, соответствующей коэффициенту Z поднятия.

В другой реализации процессор может включать в себя декодер согласно второму аспекту и модуль получения. Модуль получения выполнен с возможностью получения мягких значений кода LDPC и коэффициента подъема Z. Декодер выполнен с возможностью декодировать мягкие значения кода LDPC на основе базовой матрицы HB, соответствующей коэффициенту подъема Z, для получения информационного бита. последовательность.

В соответствии с четвертым аспектом предоставлено устройство связи, включающее в себя один или несколько процессоров.

В возможной реализации один или более процессоров могут реализовывать функции кодера в первом аспекте. В другом возможном варианте кодер в первом аспекте может быть частью процессора. Процессор может реализовывать другие функции в дополнение к функциям кодера в первом аспекте.

В возможной реализации один или несколько процессоров могут реализовывать функции декодера, описанные во втором аспекте. В другой возможной реализации декодер во втором аспекте может быть частью процессора.

Возможно, устройство связи может дополнительно включать в себя приемопередатчик и антенну.

Возможно, устройство связи может дополнительно включать в себя компонент, выполненный с возможностью генерировать CRC транспортный блок, компонент, выполненный с возможностью выполнять сегментацию кодового блока и CRC присоединение, перемежитель, выполненный с возможностью выполнять перемежение, модулятор, выполненный с возможностью выполнять обработку модуляции, или т.п..

Возможно, устройство связи может дополнительно включать в себя демодулятор, выполненный с возможностью выполнять демодуляцию, обращенный перемежитель, выполненный с возможностью выполнять обратное перемежение, компонент, выполненный с возможностью выполнять согласования с пониженной скоростью, или тому подобное. Функции этих компонентов могут быть реализованы с использованием одного или нескольких процессоров.

В возможной реализации функции этих компонентов могут быть реализованы с использованием одного или нескольких процессоров.

Согласно пятому аспекту вариант осуществления настоящего изобретения предоставляет систему связи. Система включает в себя устройство связи, описанное в третьем аспекте.

Согласно шестому аспекту вариант осуществления настоящего изобретения предоставляет систему связи. Система включает в себя одно или несколько устройств связи, описанных в четвертом аспекте.

Согласно другому аспекту вариант осуществления настоящего изобретения предоставляет компьютерный носитель данных. Компьютерный носитель данных хранит программу, и когда программа выполняется на компьютере, компьютер выполняет способ в соответствии с любым из вышеупомянутых аспектов.

Согласно еще одному аспекту настоящего изобретения предоставлен компьютерный программный продукт, включающий в себя инструкции. Когда компьютерный программный продукт выполняют на компьютере, компьютер выполняет способ в соответствии с любым из вышеупомянутых аспектов.

Согласно способу обработки информации, приспособлению, устройству связи и системе связи в вариантах осуществления настоящего изобретения могут быть удовлетворены требования гибкой длины кода и скорости кодирования системы с точки зрения производительности кодирования и минимального уровня ошибок.

Краткое описание чертежей

Фиг. 1 является схемой базового графа, базовой матрицы и матриц круговой перестановки базовой матрицы в схеме LDPC кода;

Фиг. 2 является схемой базового графа LDPC кода;

Фиг. 3a является схемой базового графа LDPC кода согласно варианту осуществления настоящего изобретения;

Фиг. 3b-1 является схемой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-2 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-3 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-4 является схемой другой базовой матрицы согласно варианту осуществления настоящего изобретения;

Фиг. 3b-5 является схемой другой базовой матрицы согласно варианту осуществления настоящего изобретения;

Фиг. 3b-6 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-7 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-8 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-9 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 3b-10 является схемой другой базовой матрицы в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 4 является схемой производительности в соответствии с вариантом осуществления настоящего изобретения;

Фиг. 5 является блок-схемой последовательности операций способа обработки информации в соответствии с другим вариантом осуществления настоящего изобретения;

Фиг. 6 является блок-схемой последовательности операций способа обработки информации в соответствии с другим вариантом осуществления настоящего изобретения;

Фиг. 7 является схемой устройства обработки информации в соответствии с другим вариантом осуществления настоящего изобретения;

Фиг. 8 является схемой системы связи в соответствии с другим вариантом осуществления настоящего изобретения; и

Фиг. 9 является схемой значений сдвига базовой матрицы в соответствии с другим вариантом осуществления настоящего изобретения.

Описание вариантов осуществления

С целью облегчения понимания, ниже приведены некоторые термины, используемые в настоящем изобретении.

В настоящем изобретении термины «сеть» и «система» обычно используют взаимозаменяемо, и термины «приспособление» и «устройство» также обычно используют взаимозаменяемо. Специалист в данной области может понять значения терминов. «Устройство связи» может быть микросхемой (такой как микросхема основной полосы частот, микросхема цифровой обработки сигналов или микросхема общего назначения), терминалом, базовой станцией или другим сетевым устройством. Терминал представляет собой устройство, имеющее функцию связи, и может включать в себя портативное устройство, автомобильное устройство, носимое устройство, вычислительное устройство, другое устройство обработки, подключенное к беспроводному модему, или тому подобное, которое имеет функцию беспроводной связи. Терминал может иметь разные названия в разных сетях, например, устройство пользователя, мобильная станция, абонентское устройство, станция, сотовый телефон, персональный цифровой помощник, беспроводной модем, устройство беспроводной связи, портативное устройство, портативный компьютер, беспроводной телефон и станция беспроводной локальной сети. Для простоты описания в настоящем изобретении эти устройства кратко упоминаются как терминал. Базовая станция (base station, BS) также может называться устройством базовой станции и представляет собой устройство, развернутое в сети радиодоступа для обеспечения функции беспроводной связи. Базовая станция может иметь разные названия в разных системах беспроводного доступа. Например, базовая станция в сети универсальной системы мобильной связи (Universal Mobile Telecommunications System, UMTS) упоминается как NodeB (NodeB), базовая станция в LTE сети упоминается как развитый NodeB (evolved NodeB, eNB или eNodeB), базовая станция в сети «Новое радио» (new radio, NR) упоминается как точка приема передачи (transmission reception point, TRP) или NodeB следующего поколения (generation nodeB, gNB) или базовая станция в другой усовершенствованной сети может иметь другое название. Данный аспект не ограничен в настоящем изобретении.

Далее приведено описание технических решений в вариантах осуществления настоящего изобретения со ссылкой на прилагаемые чертежи в вариантах осуществления настоящего изобретения.

LDPC код может быть определен с использованием матрицы H проверки на четность. Матрица H проверки на четность для LDPC кода может быть получена с использованием базового графа (base graph) и значений сдвига. Базовый граф обычно может включать в себя m × n записей матрицы (entry) и может быть представлен с использованием матрицы из m строк и n столбцов. Значением матричного элемента является либо 0, либо 1. Элемент, значение которого равно 0, иногда называют нулевым элементом, который может быть заменен на нулевую матрицу (zero matrix) размера Z × Z. Элемент, значение которого равно 1, иногда называют ненулевым элементом, который может быть заменен матрицей круговой перестановки размера Z × Z. Другими словами, каждый элемент матрицы представляет собой одну нулевую матрицу или одну матрицу круговой перестановки. Фиг. 1 показывает пример 10a базового графа LDPC кода, в котором m = 5 и n = 27 и который имеет QC структуру. Следует отметить, что в этой спецификации просто для простоты описания индексы строк и индексов столбцов базового графа и матрицы нумеруются, начиная с 0. Например, столбец 0 представляет первый столбец базового графа и матрицы, и первый столбец представляет второй столбец базового графа и матрицы, строка 0 представляет первую строку базового графа и матрицы, строка 1 представляет вторую строку базового графа и матрицы и так далее. Следует понимать, что строки и столбцы базового графа или базовой матрицы нумеруют различными способами и настоящее изобретение не ограничено конкретным способом нумерации.

Следует понимать, что индексы строк и индексы столбцов могут альтернативно быть пронумерованы, начиная с 1, и в этом случае, индексы строк и индексов столбцов, показанные в этой спецификации, увеличиваются на 1, чтобы получить соответствующие индексы строк и индексов столбцов. Например, если номера строк или индексы столбцов нумеруют начиная с 1, то столбец 1 представляет первый столбец базового графа и матрицы, столбец 2 представляет второй столбец базового графа и матрицы, строка 1 представляет первую строку базовый граф и матрицы, строка 2 представляет вторую строку базового графа и матрицы и так далее.

Если значение элемента в строке i и столбце j в базовом графе равно 1, и значение сдвига элемента равно P_i,j, где P_i,j, является целым числом, большим или равным 0, то указывает, что элемент может быть заменен матрицей круговой перестановки размером Z × Z, соответствующей P_i,j,. Матрица круговой перестановки может быть получена путем кругового сдвига единичной матрицы размера Z × Z вправо P_i,j, раз. Можно узнать, что каждый элемент, значение которого в базовом графе равно 0, заменяют нулевой матрицей размером Z × Z, и каждый элемент, значение которого равно 1, заменяют матрицей круговой перестановки размером Z × Z, соответствующей значению сдвига элемента, для получения матрицы проверки на четность LDPC кода. Базовый граф может использоваться для указания позиций значений сдвига, и каждый ненулевой элемент в базовом графе соответствует значению сдвига. Z является положительным целым числом и может также упоминаться как коэффициент поднятия, или иногда может упоминаться как размер поднятия, фактор поднятия или тому подобное. Z может быть определен на основании размера кодового блока, поддерживаемого системой, и размера информационных данных. Можно узнать, что матрица Н проверки на четность имеет размер (m × Z) * (n × Z). Например, если коэффициент Z поднятия равен 4, то каждый нулевой элемент заменяют нулевой матрицей размером 4 × 4 11a. Если P_2,3 равно 2, ненулевой элемент в строке 2 и столбце 3 заменяют матрицей 11d круговой перестановки размером 4 × 4, и матрицу 11d получают путем кругового сдвига единичной матрицы 11b 4 × 4 вправо дважды. Если P_2,4 равно 0, то ненулевой элемент в строке 2 и столбце 4 заменяют единичной матрицей 11b. Следует отметить, что в настоящем документе описаны только примеры, и примеры не являются ограничением.

Значение P_i,j может зависеть от коэффициента Z поднятия, для элемента 1 (ненулевого элемента) в строке i и столбце j базового графа, P_i,j может быть различным для разных коэффициентов Z поднятия. Для простоты реализации, базовая матрица (base matrix) m строк и n столбцов, которые иногда называют матрицей проверки на четность (PCM), могут быть определены в системе. Элементы в базовой матрице взаимно однозначно соответствуют элементам в базовом графе. Нулевой элемент в базовом графе имеет такую же позицию в базовой матрице. В матрице нулевой элемент представлен значением -1 или нулевым значением. Ненулевой элемент в строке i и столбце j, значение которого равно 1 в базовом графе, соответствует ненулевому элементу в той же позиции в базовой матрице. Ненулевой элемент представлен значением P_i,j, где P_i,j может быть значением сдвига, определенным относительно предустановки или конкретного коэффициента Z поднятия. В вариантах осуществления настоящего изобретения базовая матрица иногда также упоминается как матрица сдвига базового графа.

Как показано на фиг. 1, 10b является базовой матрице, соответствующей базовому графу 10a.

Как правило, базовый граф или базовая матрица LDPC кода могут дополнительно включать в себя p столбцов, соответствующие предопределенным выколотым битам (built-in puncture), и p может быть целым числом в диапазоне от 0 до 2. Эти столбцы могут использоваться при кодировании, но системные биты, соответствующие кодированию с использованием столбцов, соответствующих предопределенным выколотым битам, не отправляют. Кодовая скорость базовой матрицы LDPC кода удовлетворяет R=(n-m)/(n-p). Используя базовый граф 10a в качестве примера, если есть два столбца, соответствующих предопределенным выколотым битам, кодовая скорость составляет (27-5) / (27-2) = 0,88, что приблизительно равно 8/9.

LDPC код, используемый в системе беспроводной связи, представляет собой QC-LDPC код, и часть матрицы, которая соответствует битам четности QC-LDPC кода, имеет двухдиагональную структуру или структуру, похожую на структуру захвата. Это может упростить кодирование и поддерживать гибридное повторение с возрастающей избыточностью. В декодере для QC-LDPC кода QC-LDPC сдвига (QC-LDPC shift network, QSN), Баньян-сети или Бенеша-сети обычно используют для реализации циклического сдвига информации.

Базовый граф QC-LDPC кода с хищной структурой представляет собой матрицу из m строк и n столбцов. Базовый граф может включать в себя пять подматриц: A, B, C, D и E, где вес матрицы определяется количеством ненулевых элементов, вес строки (row weight) относится к количеству из ненулевых элементов в строке вес столбца (вес столбца) относится к количеству ненулевых элементов в столбце. Как показано в 200 на фиг. 2:

Подматрица A является матрицей, включающей в себя строки m_A и столбцы n_A, и размер подматрицы A равен m_A × n_A. Каждый столбец соответствует Z систематических битов в LDPC коде, и систематический бит иногда упоминается как информационный бит.

Подматрица B является матрицей, включающей в себя строки m_A и столбцы m_A, и размер подматрицы B равен m_A × m_A. Каждый столбец соответствует Z битам четности в LDPC коде. Подматрица B включает в себя подматрицу B' с двухдиагональной структурой и столбец матрицы, вес столбца которого равен 3 (для короткого столбца с весом 3), столбец веса 3 может быть расположен с левой стороны подматрицы B', как показано на 20а на фиг. 2. Подматрица B может дополнительно включать в себя один или несколько столбцов матрицы, вес столбца которых равен 1 (для короткого столбца веса 1). Например, возможная реализация показана на 20b или 20c на фиг. 2.

Обычно матрица, сгенерированная на основании подматрицы A и подматрицы B, может упоминаться как базовая матрица и может использоваться для поддержки кодирования с высокой скоростью кодирования.

Подматрица C является полностью нулевой матрицей и имеет размер m_A × m_D.

Подматрица E является единичной матрицей и имеет размер m_D × m_D.

Подматрица D имеет размер m_D (n_A + m_A) и может обычно использоваться для генерирования битов четности для низкой кодовой скорости.

Понятно, что базовый граф описан выше с точки зрения математического определения. Поскольку подматрица C является нулевой матрицей и E является единичной матрицей, в возможной реализации может использоваться матрица, включающая в себя подматрицу A и подматрицу B, или матрица, включающая в себя подматрицу A, подматрицу B и подматрицу D просто представлять базовый граф матрицы при кодировании или декодировании.

Поскольку подматрица C и подматрица E имеют относительно определенные структуры, структуры подматрицы A, подматрицы B и подматрицы D являются одним из факторов, влияющих на производительность кодирования и декодирования LDPC кода.

Когда для кодирования используют LDPC матрицу с хищной структурой, в возможной реализации матрица, включающая в себя подматрицу A и подматрицу B, другими словами, базовую матрицу, могут сначала использовать для кодирования для получения одного или более битов четности, соответствующих подматрице B, и затем используют всю матрицу для кодирования для получения одного или нескольких битов четности, соответствующих подматрице E. Поскольку подматрица B может включать в себя подматрицу B' с двухдиагональной структурой и один или более столбцов веса 1, во время кодирования сначала могут быть получены биты четности, соответствующие двухдиагональной структуре, а затем могут быть получены биты четности, соответствующие столбцам веса 1.

Нижеследующее обеспечивает примерную реализацию кодирования. Предполагают, что основной матрицей, включающей в себя подматрицу A и подматрицу B, является H_core. Последняя строка и последний столбец в H_core удаляют из H_core, другими словами, столбец весом 1 и строка, в которой ненулевой элемент в столбце веса 1 расположен в H_core, удалены из H_core для получения матрицы H_core-dual. Часть битов четности H_core-dual представлена H_e = [H_e1 H_e2]. H_e1 является столбцом с весом 3, и H_e2 имеет двухдиагональную структуру. Согласно определению LDPC матрицы, H_core-dual⋅[S P_e]^T = 0, где S является входной последовательностью и представлена вектором информационных битов, P_e является вектором, включающим в себя биты четности, и [SP_e]^T представляет собой транспонированную матрицу, образованную входной последовательностью S и P_e. Следовательно, биты четности, соответствующие H_core-dual, могут быть сначала вычислены на основании входной последовательности S и H_core-dual, где входная последовательность S включает в себя все информационные биты. Затем биты четности, соответствующие одному или нескольким столбцам веса 1 в подматрице B, вычисляют на основании полученных битов четности, соответствующих H_core-dual и входной последовательности S. В этом случае, могут быть получены все биты четности, соответствующие подматрице B, Затем, биты четности, соответствующие подматрице E, получают путем кодирования подматрицы D и на основании входной последовательности S и битов четности, соответствующих подматрице B. Таким образом, получают все информационные биты и все биты четности. Эти биты образуют кодированную последовательность, другими словами, LDPC кодовое слово (слова).

Возможно, кодирование LDPC кода может дополнительно включать в себя операцию укорочения (shortening) и операцию выкалывания (puncturing). Укороченные биты и выколотые биты не отправляют.

Укорочение обычно выполняется, начиная с последнего бита информационных битов, и может выполняться различными способами. Например, для количества укороченных битов, равного s₀, последние s₀ битов во входной последовательности S могут быть установлены как известные биты, например, установить на 0 или ноль, или другое значение, чтобы получить входную последовательность S', и затем кодируют входную последовательность S' с использованием LDPC матрицы. В другом примере, последние (s₀ mod Z) биты во входной последовательности S могут быть установлены как известные биты, например, равны 0 или нулю, или другому значению для получения входной последовательности S', и последние 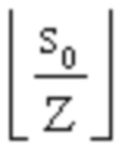столбцы в подматрица A удаляют для получения LDPC матрицы H', и кодируют входную последовательность S' с использованием LDPC матрицы H', или последние столбцы в подматрице A не участвуют в кодировании входной последовательности S'. После кодирования укороченные биты не отправляют.

Выкалывание может быть выполнено на предопределенном выколотом бите (битах) или бите (битах) четности во входной последовательности. Выкалывание бита (битов) четности обычно выполняют, начиная с последнего бита в битах четности. Альтернативно, выкалывание бита (битов) четности может выполняться в соответствии с предварительно установленным порядком выкалывания системы. В возможной реализации сначала кодируют входную последовательность, а затем, на основании количества p битов, которые должны быть выколоты, выбирают последний бит (биты) в битах четности, или p бит (биты) выбирают на основании предустановленной последовательности выкалывания в системе, где p бит (биты) не отправляют. В другой возможной реализации могут быть определены p столбцов, соответствующих выколотым битам в матрице, и p строк, в которых расположены ненулевые элементы в этих столбцах, и строки и столбцы не участвуют в кодировании и, следовательно, не генерируют соответствующие биты четности.

Следует отметить, что реализации кодирования просто используется в качестве примера в данном документе, и другая реализация кодирования, известная специалисту в данной области техники, может быть использована на основании базового графа и/или базовых матриц, предоставленных в настоящем изобретении без ограничений. В настоящем изобретении выполняют декодирование с использованием множества способов декодирования, например, способа декодирования с минимальной суммой (MS) или способа декодирования с распространением степени уверенности. Способ декодирования MS иногда также упоминается как способ лавинного декодирования MS. Например, инициализируют входную последовательность и выполняют итерацию для инициализированной входной последовательности. После итерации выполняют жесткое обнаружение, и проверяют результат жесткого решения. Если результат декодирования соответствует уравнению проверки на четность, декодирование завершается успешно, итерационная обработка заканчивается, и выводят результат решения. Если результат декодирования не соответствует уравнению проверки на четность, итерация выполняется снова с максимальным количеством итераций. Если проверка по-прежнему не проходит, при достижении максимального количества итераций, декодирование завершается неудачно. Очевидно, что специалисту в данной области техники понятно, что принцип декодирования MS общеизвестен, и подробности в данном документе не описаны.

Следует отметить, что способ декодирования просто используется в качестве примера в данном документе, и другой известный способ декодирования для специалиста в данной области техники может использоваться на основании базового графа и/или базовой матрицы, предоставленной в настоящем изобретении без ограничений.

LDPC код обычно может быть получен на основании схемы базового графа или базовой матрицы. Например, верхний предел производительности LDPC кода может быть определен путем выполнения эволюции плотности на базовом графе или базовой матрице, и определяют минимальный уровень ошибки LDPC кода на основании значений сдвига в базовой матрице. Повышение производительности кодирования или декодирования и снижение минимального уровня ошибок являются одними из целей разработки базового графа и базовой матрицы. Длина кода широко варьируется в системе беспроводной связи. Например, длина кода может составлять 2560 бит, 38400 бит или тому подобное. На фиг.3а показан пример базового графа 30а LDPC кода. Фиг. с 3b-1 по фиг. 3b-10 являются примерами базовых матриц базового графа 30a, и могут быть удовлетворены требования к производительности для различных длин блоков. Для простоты описания и понимания индексы строк и столбцов отдельно показаны на самой верхней стороне и самой левой стороне на фиг. 3а и фиг. 3b-1 - 3b-10.

На фиг. 3а показан пример базового графа 30а LDPC кода. На чертеже от 0 до 67 (то есть, от столбца 0 до столбца 67) в самой верхней строке указывают индексы столбца, и от 0 до 45 (то есть, от строки 0 до строки 45) в крайнем левом столбце указывают индексы строки. То есть, базовый граф имеет размер 46 строк и 68 столбцов.

В реализации подматрица A и подматрица B могут рассматриваться как базовая матрица базового графа LDPC кода и могут использоваться для кодирования с высокой скоростью кодирования. Матрица, включающая в себя 5 строк и 27 столбцов, как показано на базовом графе 10a, может быть основной матрицей базового графа, которая представляет собой матрицу, включающую 5 строк и 27 столбцов.

В реализации подматрица A может включать в себя один или несколько столбцов, соответствующих встроенным выколотым битам, например, может включать в себя два столбца, соответствующих встроенным выколотым битам. После выкалывания кодовая скорость, которая может поддерживаться базовой матрицей, составляет 0,88.

Подматрица B может включать в себя столбец веса 3, то есть, вес столбца 0 подматрицы B (столбец 22 основной матрицы) равен 3. Подматрица B имеет двухдиагональную структуру, которая включает в себя столбец 1 - столбец 3 (столбец 23 - столбец 25 основной матрицы) и строки 0 - строка 3 подматрицы, и подматрица B дополнительно содержит столбец веса 1 (столбец 26 основной матрицы).

В реализации подматрица А может соответствовать систематическим битам. Систематические биты иногда называют информационными битами. Подматрица A имеет размер m_A строк и 22 столбцов, если m_A = 5, и подматрица A включает в себя элементы от строки 0 до строки 4 и от столбца 0 до столбца 21 в базовом графе 30a.

В реализации подматрица B может соответствовать битам четности, подматрица B имеет размер m_A строк и столбцов m_A и включает в себя элементы от строки 0 до строки 4 и от столбца 22 до столбца 26 в базовом графе 30a.

Для получения гибких кодовых скоростей, подматрица C, подматрица D и подматрица E соответствующих размеров могут быть добавлены на основании основной матрицы, чтобы получить разные кодовые скорости. Подматрица C является полностью нулевой матрицей. Подматрица Е является единичной матрицей, размеры матриц определяют в соответствии с кодовой скоростью, и структуры матриц являются относительно фиксированными. Следовательно, производительность кодирования и производительность декодирования, в основном, зависят от основной матрицы и подматрицы D. Строки и столбцы добавляют на основании основной матрицы для формирования соответствующих C, D и E, так что могут быть получены разные скорости кодирования.

Число столбцов подматрицы D является суммой количества столбцов подматрицы A и количества столбцов подматрицы B, и количество строк подматрицы D, главным образом, связано с кодовой скоростью. Базовый граф 30a используется в качестве примера. Количество столбцов подматрицы D составляет 27 столбцов. Если кодовая скорость, поддерживаемая LDPC кодом, равна R_m, базовый граф или базовая матрица LDPC кода имеет размер m строк и n столбцов, где 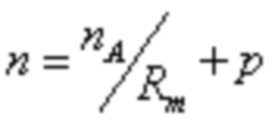и 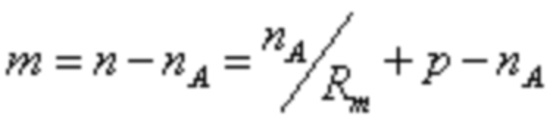. Если минимальная кодовая скорость R_m равна 1/3, и количество p столбцов, соответствующих встроенным выколотым битам, равно 2, в примере базового графа 30a, n = 68, m = 46, количество строк m_D подматрицы D может составлять до m-m_A = 46-5 = 41 и 0≤m_D≤41.

Базовый граф 30a используется в качестве примера. Подматрица D может включать в себя m_D строки в строке от 5 до 41 в базовом графе 30a.

В настоящем изобретении, при наличии не более одного ненулевого элемента в одном столбце для двух смежных строк в базовом графе, эти две строки взаимно ортогональны. В других столбцах, отличающихся от некоторых столбцов для двух смежных строк в базовом графе, если в одном и том же столбце других столбцов для двух смежных строк содержится не более одного ненулевого элемента, эти две строки являются квазиортогональными. Например, для двух смежных строк, если в столбце есть только один ненулевой элемент, отличный от столбцов, соответствующих встроенным выколотым битам, две соседние строки являются квазиортогональными.

Строка 5 - строка 41 в базовом графе 30a может включать в себя множество строк с квазиортогональной структурой и, по меньшей мере, две строки с ортогональной структурой. Например, строки от 5 до 41 в базовом графе 30a включают в себя, по меньшей мере, 15 строк, которые соответствуют квазиортогональной структуре. Существует не более одного ненулевого элемента в одном и том же столбце в столбцах, отличных от столбцов, соответствующих встроенным выколотым битам в любых двух смежных строках из 15 строк. Строка от 5 до строки 41 в базовом графе 30a может дополнительно включать в себя от 10 до 26 строк, которые соответствуют ортогональной структуре. Другими словами, в этих строках имеется не более одного ненулевого элемента в одном и том же столбце для любых двух соседних строк. Другими словами, в столбце также содержится не более одного ненулевого элемента, соответствующего встроенным выколотым битам.

Если m_D = 15, подматрица D в базовом графе LDPC кода имеет размер 15 строк и 27 столбцов. Подматрица D может быть матрицей, состоящей из строки 5 - строки 19 и столбца 0 - столбца 26 в базовом графе 30a. Соответствующая кодовая скорость, поддерживаемая LDPC кодом, составляет 22/40 = 0,55. При этой кодовой скорости базовый граф LDPC кода соответствует матрице, состоящей из строки 0 - строки 19 и столбца 0 - столбца 41 в базовом графе 30a. Подматрица E является единичной матрицей из 15 строк и 15 столбцов, и подматрица C является полностью нулевой матрицей из 5 строк и 15 столбцов.

Если m_D = 19, подматрица D в базовом графе LDPC кода имеет размер 19 строк и 27 столбцов. Подматрица D может быть матрицей, состоящей из строки 5 - строки 23 и столбца 0 - столбца 26 в базовом графе 30a. Соответствующая кодовая скорость, поддерживаемая LDPC кодом, составляет 22/44 = 1/2. При этой кодовой скорости базовый граф LDPC кода соответствует матрице, образованной строкой 0 - строкой 23 и столбцом 0 - столбцом 45 в базовом графе 30a. Подматрица E является единичной матрицей из 19 строк и 19 столбцов, и подматрица C является полностью нулевой матрицей из 5 строк и 19 столбцов.

То же самое верно, если m_D является другим значением, и подробности не описаны.

В реализации перестановка строк/столбцов может выполняться на базовом графе и/или базовой матрице. Другими словами, может быть выполнена перестановка строк, или перестановка столбцов, или перестановка строк и перестановок столбцов. Операция перестановки строк/столбцов не изменяет вес строки или вес столбца, а также не меняет количество ненулевых элементов. Следовательно, базовый граф и/или базовая матрица, полученные с помощью перестановки строк/столбцов, оказывают ограниченное влияние на производительность системы. В целом, влияние на производительность системы из-за перестановки строк/столбцов является приемлемым и находится в допустимом диапазоне. Например, в некоторых сценариях или в некоторых диапазонах производительность снижается в допустимом диапазоне, в то время, как в некоторых сценариях или в некоторых диапазонах производительность улучшается. В целом, и на общую производительность это никак не сказывается.

Например, строка 34 и строка 36 в базовом графе 30a могут быть взаимозаменяемыми, и столбец 44 и столбец 45 могут быть взаимозаменяемыми. В другом примере подматрица D включает в себя строки m_D в матрице F, перестановка строк может не выполняться в строках m_D, или перестановка строк может выполняться в одной или нескольких строках строк m_D; и подматрица E все еще имеет диагональную структуру, и перестановка строк или перестановка столбцов не выполняется на подматрице E. Например, строки 27 и строка 29 в матрице F взаимозаменяемы, подматрица D включает в себя строки m_D в подматрице F, и подматрица E все еще имеет диагональную структуру. Понятно, что если базовый граф или базовая матрица включает в себя подматрицу D, то, когда обмен столбцами выполняется для столбцов в основной матрице, обмен столбцами должен выполняться соответственно на подматрице D.

Матрицы с 30b-10 по 30b-80, показанные на фиг. 3b-1 по фиг. 3b-10 являются соответственно структурами множества базовых матриц базового графа 30a. Положение ненулевого элемента в строке i и столбце j на базовом графе 30a в каждой из матриц с 30b-10 по 30b-80 не изменяется, и значение ненулевого элемента в строке i и столбец j в каждой из матриц являются значениями V_i,j смещения, и нулевой элемент представлен -1 или нулем в базовой матрице. Соответствующая часть подматрицы D в базовых матрицах может включать в себя строки m_D в строках с 5 по 45 любой из базовых матриц, и значение m_D может быть выбрано на основании разных кодовых скоростей. Понятно, что, если базовый граф является матрицей, полученной путем выполнения преобразования строки/столбца на базовом графе 30a, базовая матрица также является матрицей, полученной путем выполнения преобразования строки/столбца в любой из матриц 30b-10 - 30b-80.

В возможной реализации базовая матрица LDPC кода может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в любой из матриц с 30b-10 по 30b-80, показанных на фиг. 3b-1 по фиг. 3б-10. В этом случае, матрица, включающая в себя строки от 0 до строки 4 и от 0 до столбца 26 матрицы, показанной на фиг. 3b-1 по фиг. 3b-10, может использоваться в качестве части основной матрицы базовой матрицы. В этой реализации структура другой части базовой матрицы LDPC кода, например, матрицы C, матрицы D или матрицы E, не ограничена. Например, любая структура, показанная на фиг. 3b-1 по фиг. 3b-10, или могут использоваться другие структуры матрицы.

В другом возможном варианте базовая матрица LDPC кода может включать в себя: матрицу, включающую в себя строки от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в любой из матриц с 30b-10 по 30b-80 как показано на фиг. 3b-1 по фиг. 3b-10, где 5≤m≤46, m - целое число, 27≤n≤68, и n - целое число.

В этой реализации структура другой части базовой матрицы LDPC кода не ограничена. Например, могут использовать любую структуру, показанную на фиг. 3b-1 по фиг. 3b-10, могут использоваться и другие структуры матрицы.

В другой возможной реализации базовая матрица LDPC кода может включать в себя: строки от 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в любой из матриц с 30b-10 по 30b-80, показанных на фиг. 3b-1 по фиг. 3b-10. Например, укорочение (shortening) и/или выкалывание (puncturing) может выполняться на части основной матрицы (строка 0 - строка 4 и столбец 0 - колонка 26), показанной на фиг. 3b-1 по фиг. 3b-10. В реализации базовая матрица LDPC кода может не включать в себя столбец, соответствующий укороченным и/или выколотым битам.

В этой реализации другая часть базовой матрицы LDPC кода не ограничена. Например, могут быть сделаны ссылки на структуры, показанные на фиг. 3b-1 по фиг. 3b-10, или могут использоваться другие структуры.

В другой возможной реализации базовая матрица LDPC кода может включать в себя: матрицу, включающую в себя строки от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в любой из матриц с 30b-10 по 30b-80, показанные на фиг. 3b-1 по фиг. 3b-10, где 5≤m≤46, m - целое число, 27≤n≤68, и n - целое число. Например, могут выполнять укорочение (shortening) и/или выкалывание(puncturing) в строке от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в любой из матриц с 30b-10 по 30b-80, как показано на фиг. 3b-1 по фиг. 3b-10. В реализации базовая матрица LDPC кода может не включать в себя столбец (столбцы), соответствующий укороченному и/или выколотому биту (битам). В этой реализации другая часть базовой матрицы LDPC кода не ограничена. Например, могут быть сделаны ссылки на структуры, показанные на фиг. 3b-1 по фиг. 3b-10, или использовать другую структуру.

В реализации операция укорочения может выполняться над информационными битами. Например, любая матрица, показанная на фиг. 3b-1 по фиг. 3b-10 используется в качестве примера. Если один или несколько столбцов от столбца 0 до столбца 21 укорочены, то базовая матрица LDPC кода может не включать в себя один или несколько укороченных столбцов матриц, показанных на фиг. 3b-1 по фиг. 3b-10. Например, если столбец 21 укорочен, базовая матрица LDPC кода может включать в себя: от столбца 0 до столбца 20 и от столбца 22 до столбца 26 в любой из матриц с 30b-10 по 30b-80. Для матрицы, включающей в себя строки от 0 до строки 4, от столбца 0 до столбца 20 и от столбца 22 до столбца 26 в любой из матриц с 30b-10 по 30b-80, кодовая скорость, поддерживаемая матрицей в этом случае, составляет 7/8,

В другой реализации выкалывание может выполняться над битами четности. Например, любая матрица, показанная на фиг. 3b-1 по фиг. 3b-10 используется в качестве примера, и один или несколько столбцов от столбца 22 до столбца 26 выколоты. Базовая матрица LDPC кода может не включать в себя выколотый один или несколько столбцов в матрицах, показанных на фиг. 3b-1 по фиг. 3b-10. Например, если столбец 26 выколот, то базовая матрица LDPC кода может включать в себя: от столбца 0 до столбца 25 в любой из матриц с 30b-10 по 30b-80.

Для LDPC кода предназначены различные коэффициенты Z поднятия для поддержки последовательностей информационных битов различной длины. В возможной реализации могут использоваться разные базовые матрицы для разных коэффициентов поднятия для получения относительно высокой производительности. Например, коэффициенты Z = a × 2^j поднятия, где 0 ≤ j <7, и 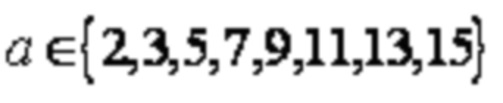. Таблица 1 представляет собой возможно поддерживаемый набор коэффициентов поднятия {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18, 20, 22, 24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}. Каждая из ячеек, за исключением самой верхней строки и самого левого столбца, представляет значение Z, соответствующее значениям соответствующих a и j. Например, для столбца, в котором a = 2, и строки, в которой j = 1, Z = 4. Для другого примера, для a = 11 и j = 3, Z = 88. По аналогии подробности не описаны.

Таблица 1

Z a=2 a=3 a=5 a=7 a=9 a=11 a=13 a=15 j=0 2 3 5 7 9 11 13 15 j=1 4 6 10 14 18 22 26 30 j=2 8 12 20 28 36 44 52 60 j=3 16 24 40 56 72 88 104 120 j=4 32 48 80 112 144 176 208 240 j=5 64 96 160 224 288 352 j=6 128 192 320 j=7 256 384

Набор коэффициентов подъема, поддерживаемый базовым графом, может быть всеми или некоторыми из коэффициентов поднятия в таблице 1, например, может быть {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}, в которых Z больше чем или равно 24. Для другого примера, набор коэффициентов поднятия может быть набором объединения одного или нескольких из {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 , 15, 16, 18, 20, 22} и {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}. Следует отметить, что здесь приведены только примеры. Набор коэффициентов поднятия, поддерживаемый базовым графом, может быть разделен на различные поднаборы на основе значения a. Например, если a = 2, подмножество коэффициента Z поднятия может включать в себя один или несколько из {2, 4, 8, 16, 32, 64, 128, 256}. В другом примере, если a = 3, подмножество коэффициента Z поднятия может включать в себя один или несколько из {3, 6, 12, 24, 48, 96, 192, 384} и так далее.

Набор коэффициентов поднятия, поддерживаемый базовым графом, может быть разделен на основании различных значений, и определена соответствующая базовая матрица.

Если a = 2 или значение коэффициента Z поднятия равно одному из {2, 4, 8, 16, 32, 64, 128, 256}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-10 или 30b-11; или базовая матрица включает в себя строки от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-10 или 30b-11, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строки от 0 до строки (m-1) и некоторые из столбцов от 0 до столбца (n-1) в матрице 30b-10 или 30b-11, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 3 или значение коэффициента Z поднятия равно одному из {3, 6, 12, 24, 48, 96, 192, 384}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-20 или 30b-21; или базовая матрица включает в себя строки от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-20 или 30b-21, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строки от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в матрице 30b-20 или 30b-21, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 5 или значение коэффициента Z поднятия равно одному из {5, 10, 20, 40, 80, 160, 320}, базовая матрица может включать в себя строки от 0 до 4 и от 0 до 26 в матрица 30b-30; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-30, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в матрице 30b-30, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 7 или значение коэффициента Z поднятия равно одному из {7, 14, 28, 56, 112, 224}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-40; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-40, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в матрице 30b-40, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 9 или значение коэффициента Z поднятия равно одному из {9, 18, 36, 72, 144, 288}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-50; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-50, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в матрице 30b-50, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 11 или значение коэффициента Z поднятия равно одному из {11, 22, 44, 88, 176, 352}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-60; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-60, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые столбцы от 0 до столбца (n-1) в матрице 30b-60, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 13 или значение коэффициента Z поднятия равно одному из {13, 26, 52, 104, 208}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-70; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-70, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые из столбца от 0 до столбца (n-1) в матрице 30b-70, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом.

Если a = 15 или значение коэффициента Z поднятия равно одному из {15, 30, 60, 120, 240}, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-80; или базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в матрице 30b-80, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом; или базовая матрица включает в себя строку от 0 до строки (m-1) и некоторые столбцы от 0 до столбца (n-1) в матрице 30b-80, где 5≤m≤46 m является целым числом, 27≤n≤68 и n является целым числом.

Возможно, для базовой матрицы для LDPC кода значения смещения ненулевых элементов в одном или нескольких столбцах в матрице могут быть увеличены или уменьшены посредством смещений Offset_s без существенного влияния на производительность системы. Смещения ненулевых элементов в разных столбцах могут быть одинаковыми или могут быть разными. Например, чтобы компенсировать один или несколько столбцов в матрице, значения компенсации для разных столбцов могут быть одинаковыми или могут отличаться. Это не ограничено в настоящем изобретении.

Незначительное влияние на производительность системы означает, что влияние на производительность системы является приемлемым и находится в допустимом диапазоне в целом. Например, производительность снижается в пределах допустимого диапазона в некоторых сценариях или в некоторых диапазонах. Однако в некоторых сценариях или в некоторых диапазонах производительность улучшается до некоторой степени. Влияние на общую производительность является не существенным.

Например, каждое значение смещения, большее или равное 0 в столбце s в любой из матриц с 30b-10 по 30b-80, увеличивается или уменьшается посредством смещений Offset_s так что может быть получена матрица Hs смещения матрицы, где Offset_s является целым числом, большее или равное 0, и . Смещения Offset_s одного или нескольких столбцов могут быть одинаковыми или разными.

На схеме производительности, показанной на фиг. 4, проиллюстрированы кривые производительности LDPC кодов, закодированных на основании матриц с 30b-10 по 30b-80. Горизонтальная координата представляет длину последовательности информационных битов, и единицей длины является бит. Вертикальная координата представляет отношение сигнал/шум символа (Es/N₀), необходимое для достижения соответствующего значения BLER. Две строки каждой кодовой скорости соответственно соответствуют двум случаям, когда значения BLER равны 0,01 и 0,0001. При той же кодовой скорости случай, когда BLER равен 0,01, соответствует верхней кривой, а случай, когда BLER равен 0,0001, соответствует нижней кривой. Если каждая кривая является плавной, это указывает на то, что матрица имеет относительно хорошую производительность в случаях различной длины кода.

На фиг. 1 по фиг. 3а и фиг. 3b-1 по фиг. 3b-10 показывают структуры базового графа и базовой матрицы LDPC кода. Для описания структуры базового графа и/или базовых матриц в реализациях настоящего изобретения, структуры могут быть дополнительно описаны в таблице 2-10 и таблице 2-11.

В реализации базовый граф 10a на фиг. 1 представляет собой матрицу из 5 строк и 27 столбцов, и соответствующие параметры могут быть выражены в таблице 2-10.

Таблица 2-10

Индекс строки
(row index) Вес строки
(row degree/row weight) Индекс столбца ненулевого элемента (позиция столбца ненулевого элемента в строке) 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 4 3 0, 1, 26

В реализации базовая матрица, показанная на фиг. 10b на фиг. 1, представляет собой матрицу из 5 строк и 27 столбцов, и соответствующие параметры могут быть выражены в таблице 2-11.

Таблица 2-11

Индекс строки
(row index) Вес строки
(row degree/row weight) Индекс столбца ненулевого элемента
(позиция столбца ненулевого элемента в строке) Значение смещения ненулевого элемента
(значение смещения ненулевого элемента в строке) 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 172, 143, 247, 249, 15, 169, 234, 136, 138, 70, 6, 207, 120, 164, 7, 218, 128, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 213, 67, 0, 145, 144, 21, 135, 153, 151, 88, 185, 151, 189, 13, 193, 196, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 141, 0, 199, 140, 3, 0, 19, 1, 224, 224, 226, 156, 157, 18, 1, 0, 195, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 69, 27, 157, 128, 144, 0, 211, 218, 200, 128, 101, 155, 11, 55, 39, 95, 173, 1, 0 4 3 0, 1, 26 166, 244, 0

В реализации матрица 30b-10 на фиг. 3b-1 может быть выражена в таблице 3-10.

Таблица 3-10

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 172, 143, 247, 249, 15, 169, 234, 136, 138, 70, 6, 207, 120, 164, 7, 218, 128, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 213, 67, 0, 145, 144, 21, 135, 153, 151, 88, 185, 151, 189, 13, 193, 196, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 141, 0, 199, 140, 3, 0, 19, 1, 224, 224, 226, 156, 157, 18, 1, 0, 195, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 69, 27, 157, 128, 144, 0, 211, 218, 200, 128, 101, 155, 11, 55, 39, 95, 173, 1, 0 4 3 0, 1, 26 166, 244, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 2, 123, 119, 84, 49, 87, 163, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 211, 201, 184, 180, 127, 31, 150, 30, 0 7 7 0, 1, 4, 7, 8, 14, 29 236, 83, 251, 241, 137, 42, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 210, 18, 239, 8, 85, 219, 104, 6, 127, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 247, 64, 71, 188, 16, 72, 80, 84, 0 10 7 1, 2, 4, 7, 8, 14, 32 46, 11, 229, 191, 97, 176, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 87, 3, 190, 20, 168, 128, 93, 0 12 7 0, 1, 10, 11, 13, 18, 34 149, 64, 243, 135, 52, 132, 0 13 6 0, 3, 7, 20, 23, 35 208, 161, 27, 5, 212, 0 14 7 0, 12, 15, 16, 17, 21, 36 96, 120, 210, 203, 195, 224, 0 15 7 0, 1, 10, 13, 18, 25, 37 93, 26, 214, 30, 130, 238, 0 16 6 1, 3, 11, 20, 22, 38 14, 225, 159, 213, 90, 0 17 6 0, 14, 16, 17, 21, 39 159, 239, 149, 19, 249, 0 18 6 1, 12, 13, 18, 19, 40 243, 200, 242, 60, 134, 0 19 6 0, 1, 7, 8, 10, 41 23, 38, 41, 104, 247, 0 20 6 0, 3, 9, 11, 22, 42 139, 141, 199, 66, 106, 0 21 6 1, 5, 16, 20, 21, 43 197, 21, 204, 31, 152, 0 22 5 0, 12, 13, 17, 44 17, 136, 0, 205, 0 23 5 1, 2, 10, 18, 45 18, 119, 188, 67, 0 24 6 0, 3, 4, 11, 22, 46 215, 109, 128, 224, 90, 0 25 5 1, 6, 7, 14, 47 232, 191, 128, 70, 0 26 5 0, 2, 4, 15, 48 92, 0, 249, 135, 0 27 4 1, 6, 8, 49 24, 33, 116, 0 28 5 0, 4, 19, 21, 50 227, 246, 203, 64, 0 29 5 1, 14, 18, 25, 51 7, 79, 142, 85, 0 30 5 0, 10, 13, 24, 52 65, 149, 105, 144, 0 31 5 1, 7, 22, 25, 53 0, 204, 75, 150, 0 32 5 0, 12, 14, 24, 54 67, 80, 85, 168, 0 33 5 1, 2, 11, 21, 55 26, 128, 138, 74, 0 34 5 0, 7, 15, 17, 56 196, 44, 34, 2, 0 35 5 1, 6, 12, 22, 57 34, 128, 131, 48, 0 36 5 0, 14, 15, 18, 58 179, 136, 216, 160, 0 37 4 1, 13, 23, 59 134, 51, 39, 0 38 5 0, 9, 10, 12, 60 33, 209, 28, 93, 0 39 5 1, 3, 7, 19, 61 204, 64, 252, 56, 0 40 4 0, 8, 17, 62 39, 62, 107, 0 41 5 1, 3, 9, 18, 63 89, 154, 189, 244, 0 42 4 0, 4, 24, 64 159, 216, 61, 0 43 5 1, 16, 18, 25, 65 149, 74, 238, 228, 0 44 5 0, 7, 9, 22, 66 129, 30, 117, 49, 0 45 4 1, 6, 10, 67 0, 45, 212, 0

В реализации матрица 30b-11 на фиг. 3b-2 может быть выражена в таблице 3-11.

Таблица 3-11

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 252, 38, 0, 190, 197, 128, 233, 3, 91, 100, 16, 103, 8, 180, 182, 65, 64, 96, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 184, 85, 140, 32, 111, 119, 194, 16, 36, 40, 32, 152, 32, 64, 33, 134, 127, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 218, 170, 22, 234, 130, 48, 160, 232, 236, 5, 107, 37, 32, 87, 136, 176, 128, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 93, 249, 98, 148, 114, 241, 16, 12, 17, 64, 135, 11, 131, 44, 163, 105, 5, 96, 0 4 3 0, 1, 26 208, 209, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 235, 2, 57, 186, 160, 45, 131, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 167, 134, 20, 136, 32, 178, 64, 132, 0 7 7 0, 1, 4, 7, 8, 14, 29 127, 21, 123, 204, 90, 108, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 13, 160, 11, 166, 39, 137, 64, 28, 4, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 195, 129, 233, 24, 65, 241, 70, 61, 0 10 7 1, 2, 4, 7, 8, 14, 32 79, 10, 48, 152, 101, 196, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 83, 128, 229, 229, 52, 9, 200, 0 12 7 0, 1, 10, 11, 13, 18, 34 158, 130, 246, 112, 173, 187, 0 13 6 0, 3, 7, 20, 23, 35 239, 234, 160, 94, 194, 0 14 7 0, 12, 15, 16, 17, 21, 36 128, 165, 169, 128, 34, 69, 0 15 7 0, 1, 10, 13, 18, 25, 37 203, 16, 119, 200, 207, 26, 0 16 6 1, 3, 11, 20, 22, 38 172, 192, 71, 198, 7, 0 17 6 0, 14, 16, 17, 21, 39 103, 13, 98, 96, 206, 0 18 6 1, 12, 13, 18, 19, 40 121, 34, 64, 97, 104, 0 19 6 0, 1, 7, 8, 10, 41 168, 0, 212, 176, 74, 0 20 6 0, 3, 9, 11, 22, 42 151, 164, 218, 106, 40, 0 21 6 1, 5, 16, 20, 21, 43 235, 248, 92, 8, 32, 0 22 5 0, 12, 13, 17, 44 116, 216, 0, 43, 0 23 5 1, 2, 10, 18, 45 193, 46, 82, 156, 0 24 6 0, 3, 4, 11, 22, 46 242, 251, 144, 96, 240, 0 25 5 1, 6, 7, 14, 47 212, 112, 193, 116, 0 26 5 0, 2, 4, 15, 48 243, 193, 96, 245, 0 27 4 1, 6, 8, 49 208, 80, 209, 0 28 5 0, 4, 19, 21, 50 243, 180, 240, 192, 0 29 5 1, 14, 18, 25, 51 224, 244, 209, 112, 0 30 5 0, 10, 13, 24, 52 230, 118, 248, 80, 0 31 5 1, 7, 22, 25, 53 225, 116, 241, 226, 0 32 5 0, 12, 14, 24, 54 192, 246, 228, 177, 0 33 5 1, 2, 11, 21, 55 247, 80, 224, 246, 0 34 5 0, 7, 15, 17, 56 176, 250, 244, 250, 0 35 5 1, 6, 12, 22, 57 181, 208, 224, 179, 0 36 5 0, 14, 15, 18, 58 225, 162, 192, 144, 0 37 4 1, 13, 23, 59 176, 245, 243, 0 38 5 0, 9, 10, 12, 60 183, 208, 96, 194, 0 39 5 1, 3, 7, 19, 61 226, 160, 180, 247, 0 40 4 0, 8, 17, 62 244, 117, 240, 0 41 5 1, 3, 9, 18, 63 113, 224, 225, 248, 0 42 4 0, 4, 24, 64 245, 48, 241, 0 43 5 1, 16, 18, 25, 65 228, 177, 160, 240, 0 44 5 0, 7, 9, 22, 66 192, 226, 84, 224, 0 45 4 1, 6, 10, 67 212, 177, 210, 0

В реализации матрица 30b-20 на фиг. 3b-3 может быть выражена в таблице 3-20.

Таблица 3-20

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 280, 211, 253, 383, 266, 14, 279, 227, 30, 195, 288, 273, 202, 206, 234, 192, 245, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 235, 367, 204, 308, 261, 253, 296, 192, 290, 312, 377, 241, 212, 240, 323, 223, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 357, 231, 192, 366, 24, 334, 310, 192, 283, 276, 343, 251, 288, 236, 251, 192, 254, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 268, 296, 355, 257, 263, 213, 308, 285, 216, 197, 335, 213, 218, 158, 201, 195, 334, 1, 0 4 3 0, 1, 26 318, 380, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 218, 287, 241, 191, 245, 43, 206, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 207, 333, 233, 0, 118, 280, 210, 284, 0 7 7 0, 1, 4, 7, 8, 14, 29 230, 0, 288, 155, 55, 225, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 74, 144, 27, 366, 215, 112, 192, 24, 236, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 61, 48, 95, 39, 246, 272, 37, 41, 0 10 7 1, 2, 4, 7, 8, 14, 32 315, 20, 188, 135, 238, 285, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 320, 10, 251, 205, 304, 263, 192, 0 12 7 0, 1, 10, 11, 13, 18, 34 252, 5, 164, 35, 296, 278, 0 13 6 0, 3, 7, 20, 23, 35 309, 199, 209, 108, 23, 0 14 7 0, 12, 15, 16, 17, 21, 36 52, 331, 208, 195, 0, 250, 0 15 7 0, 1, 10, 13, 18, 25, 37 288, 96, 267, 192, 306, 365, 0 16 6 1, 3, 11, 20, 22, 38 327, 0, 330, 347, 192, 0 17 6 0, 14, 16, 17, 21, 39 216, 297, 312, 89, 255, 0 18 6 1, 12, 13, 18, 19, 40 293, 166, 48, 56, 336, 0 19 6 0, 1, 7, 8, 10, 41 323, 48, 378, 146, 34, 0 20 6 0, 3, 9, 11, 22, 42 174, 145, 211, 210, 236, 0 21 6 1, 5, 16, 20, 21, 43 104, 88, 308, 33, 209, 0 22 5 0, 12, 13, 17, 44 46, 127, 0, 316, 0 23 5 1, 2, 10, 18, 45 243, 246, 213, 317, 0 24 6 0, 3, 4, 11, 22, 46 348, 236, 192, 328, 103, 0 25 5 1, 6, 7, 14, 47 128, 248, 96, 359, 0 26 5 0, 2, 4, 15, 48 102, 268, 72, 141, 0 27 4 1, 6, 8, 49 24, 322, 241, 0 28 5 0, 4, 19, 21, 50 334, 38, 74, 51, 0 29 5 1, 14, 18, 25, 51 256, 291, 0, 356, 0 30 5 0, 10, 13, 24, 52 257, 239, 26, 281, 0 31 5 1, 7, 22, 25, 53 230, 154, 325, 168, 0 32 5 0, 12, 14, 24, 54 117, 3, 297, 361, 0 33 5 1, 2, 11, 21, 55 299, 96, 144, 90, 0 34 5 0, 7, 15, 17, 56 20, 135, 351, 5, 0 35 5 1, 6, 12, 22, 57 316, 140, 192, 6, 0 36 5 0, 14, 15, 18, 58 51, 296, 151, 133, 0 37 4 1, 13, 23, 59 230, 97, 227, 0 38 5 0, 9, 10, 12, 60 87, 327, 0, 239, 0 39 5 1, 3, 7, 19, 61 99, 96, 114, 264, 0 40 4 0, 8, 17, 62 60, 139, 64, 0 41 5 1, 3, 9, 18, 63 96, 336, 192, 270, 0 42 4 0, 4, 24, 64 306, 203, 274, 0 43 5 1, 16, 18, 25, 65 120, 117, 262, 190, 0 44 5 0, 7, 9, 22, 66 20, 240, 136, 79, 0 45 4 1, 6, 10, 67 214, 342, 23, 0

В реализации матрица 30b-21 на фиг. 3b-4 может быть выражена в таблице 3-21.

Таблица 3-21

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 286, 12, 27, 10, 51, 25, 21, 0, 7, 19, 6, 60, 1, 42, 7, 0, 5, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 6, 31, 144, 0, 102, 8, 8, 3, 40, 96, 29, 37, 0, 6, 95, 0, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 32, 206, 0, 39, 10, 96, 24, 3, 48, 1, 100, 43, 0, 36, 12, 108, 68, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 185, 27, 20, 197, 15, 83, 0, 8, 18, 36, 0, 12, 142, 30, 31, 150, 81, 1, 0 4 3 0, 1, 26 10, 13, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 124, 5, 54, 173, 1, 69, 8, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 6, 8, 246, 5, 123, 99, 31, 26, 0 7 7 0, 1, 4, 7, 8, 14, 29 373, 6, 218, 186, 29, 4, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 2, 246, 102, 19, 16, 26, 50, 216, 113, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 54, 26, 227, 12, 84, 157, 201, 22, 0 10 7 1, 2, 4, 7, 8, 14, 32 174, 60, 112, 9, 122, 74, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 355, 2, 214, 14, 369, 102, 192, 0 12 7 0, 1, 10, 11, 13, 18, 34 132, 0, 202, 96, 49, 228, 0 13 6 0, 3, 7, 20, 23, 35 111, 170, 291, 32, 354, 0 14 7 0, 12, 15, 16, 17, 21, 36 222, 203, 315, 30, 4, 101, 0 15 7 0, 1, 10, 13, 18, 25, 37 1, 0, 218, 108, 323, 43, 0 16 6 1, 3, 11, 20, 22, 38 151, 328, 100, 143, 194, 0 17 6 0, 14, 16, 17, 21, 39 96, 134, 10, 101, 13, 0 18 6 1, 12, 13, 18, 19, 40 265, 219, 12, 63, 138, 0 19 6 0, 1, 7, 8, 10, 41 99, 0, 76, 36, 48, 0 20 6 0, 3, 9, 11, 22, 42 312, 48, 176, 38, 301, 0 21 6 1, 5, 16, 20, 21, 43 61, 168, 123, 6, 4, 0 22 5 0, 12, 13, 17, 44 26, 110, 12, 166, 0 23 5 1, 2, 10, 18, 45 82, 11, 185, 1, 0 24 6 0, 3, 4, 11, 22, 46 379, 350, 360, 305, 370, 0 25 5 1, 6, 7, 14, 47 375, 371, 72, 87, 0 26 5 0, 2, 4, 15, 48 94, 324, 270, 382, 0 27 4 1, 6, 8, 49 191, 310, 233, 0 28 5 0, 4, 19, 21, 50 381, 180, 358, 258, 0 29 5 1, 14, 18, 25, 51 376, 383, 362, 282, 0 30 5 0, 10, 13, 24, 52 84, 284, 184, 332, 0 31 5 1, 7, 22, 25, 53 329, 306, 373, 364, 0 32 5 0, 12, 14, 24, 54 252, 274, 330, 276, 0 33 5 1, 2, 11, 21, 55 363, 365, 380, 375, 0 34 5 0, 7, 15, 17, 56 378, 285, 353, 252, 0 35 5 1, 6, 12, 22, 57 182, 335, 354, 376, 0 36 5 0, 14, 15, 18, 58 352, 374, 348, 327, 0 37 4 1, 13, 23, 59 281, 357, 262, 0 38 5 0, 9, 10, 12, 60 348, 378, 66, 236, 0 39 5 1, 3, 7, 19, 61 382, 366, 276, 358, 0 40 4 0, 8, 17, 62 372, 162, 287, 0 41 5 1, 3, 9, 18, 63 189, 351, 334, 282, 0 42 4 0, 4, 24, 64 356, 306, 377, 0 43 5 1, 16, 18, 25, 65 275, 286, 160, 287, 0 44 5 0, 7, 9, 22, 66 372, 380, 277, 278, 0 45 4 1, 6, 10, 67 254, 381, 279, 0

В реализации матрица 30b-30 на фиг. 3b-5 может быть выражена в таблице 3-30.

Таблица 3-30

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 293, 215, 0, 0, 4, 36, 40, 20, 97, 1, 0, 162, 48, 160, 0, 17, 0, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 104, 18, 29, 232, 160, 74, 56, 4, 202, 183, 187, 237, 0, 173, 8, 30, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 46, 271, 27, 2, 185, 16, 80, 180, 277, 178, 11, 241, 196, 161, 252, 163, 203, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 10, 160, 13, 208, 71, 165, 10, 106, 40, 80, 4, 259, 22, 0, 48, 86, 210, 1, 0 4 3 0, 1, 26 132, 235, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 156, 84, 255, 153, 301, 315, 112, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 186, 125, 303, 198, 10, 59, 117, 314, 0 7 7 0, 1, 4, 7, 8, 14, 29 203, 240, 181, 261, 234, 122, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 174, 265, 306, 248, 85, 75, 120, 113, 275, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 183, 159, 245, 250, 162, 196, 232, 13, 0 10 7 1, 2, 4, 7, 8, 14, 32 288, 39, 91, 233, 200, 313, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 112, 35, 108, 62, 309, 80, 191, 0 12 7 0, 1, 10, 11, 13, 18, 34 292, 78, 216, 189, 175, 227, 0 13 6 0, 3, 7, 20, 23, 35 122, 65, 39, 60, 179, 0 14 7 0, 12, 15, 16, 17, 21, 36 201, 293, 63, 95, 136, 116, 0 15 7 0, 1, 10, 13, 18, 25, 37 200, 31, 86, 250, 189, 182, 0 16 6 1, 3, 11, 20, 22, 38 83, 298, 317, 147, 200, 0 17 6 0, 14, 16, 17, 21, 39 240, 306, 215, 51, 218, 0 18 6 1, 12, 13, 18, 19, 40 316, 304, 81, 270, 197, 0 19 6 0, 1, 7, 8, 10, 41 221, 0, 212, 255, 234, 0 20 6 0, 3, 9, 11, 22, 42 160, 207, 305, 289, 246, 0 21 6 1, 5, 16, 20, 21, 43 128, 94, 286, 86, 5, 0 22 5 0, 12, 13, 17, 44 57, 239, 80, 111, 0 23 5 1, 2, 10, 18, 45 247, 279, 112, 89, 0 24 6 0, 3, 4, 11, 22, 46 214, 129, 0, 0, 40, 0 25 5 1, 6, 7, 14, 47 262, 310, 92, 280, 0 26 5 0, 2, 4, 15, 48 292, 0, 277, 204, 0 27 4 1, 6, 8, 49 56, 80, 116, 0 28 5 0, 4, 19, 21, 50 95, 115, 137, 0, 0 29 5 1, 14, 18, 25, 51 93, 119, 0, 175, 0 30 5 0, 10, 13, 24, 52 0, 91, 98, 307, 0 31 5 1, 7, 22, 25, 53 98, 231, 311, 282, 0 32 5 0, 12, 14, 24, 54 0, 240, 60, 40, 0 33 5 1, 2, 11, 21, 55 0, 0, 63, 293, 0 34 5 0, 7, 15, 17, 56 144, 69, 123, 0, 0 35 5 1, 6, 12, 22, 57 166, 120, 0, 15, 0 36 5 0, 14, 15, 18, 58 14, 317, 88, 30, 0 37 4 1, 13, 23, 59 222, 160, 265, 0 38 5 0, 9, 10, 12, 60 0, 186, 209, 6, 0 39 5 1, 3, 7, 19, 61 290, 0, 181, 273, 0 40 4 0, 8, 17, 62 205, 185, 226, 0 41 5 1, 3, 9, 18, 63 246, 0, 232, 34, 0 42 4 0, 4, 24, 64 199, 242, 299, 0 43 5 1, 16, 18, 25, 65 26, 87, 0, 304, 0 44 5 0, 7, 9, 22, 66 0, 94, 16, 41, 0 45 4 1, 6, 10, 67 160, 285, 164, 0

В реализации матрица 30b-40 на фиг. 3b-6 может быть выражена в таблице 3-40.

Таблица 3-40

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 198, 143, 153, 155, 32, 71, 219, 140, 77, 10, 28, 33, 44, 1, 42, 117, 56, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 94, 147, 171, 35, 0, 69, 4, 98, 84, 28, 88, 0, 14, 0, 137, 216, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 33, 30, 112, 132, 85, 213, 119, 28, 33, 117, 36, 16, 149, 186, 7, 0, 0, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 50, 11, 120, 151, 33, 20, 43, 166, 2, 90, 44, 126, 129, 42, 32, 46, 103, 1, 0 4 3 0, 1, 26 217, 175, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 110, 56, 156, 208, 94, 126, 0, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 14, 186, 140, 48, 91, 14, 187, 35, 0 7 7 0, 1, 4, 7, 8, 14, 29 86, 70, 30, 188, 28, 116, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 44, 150, 192, 177, 73, 103, 129, 138, 195, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 81, 15, 59, 42, 179, 132, 196, 5, 0 10 7 1, 2, 4, 7, 8, 14, 32 188, 112, 65, 199, 128, 7, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 61, 0, 58, 123, 82, 73, 35, 0 12 7 0, 1, 10, 11, 13, 18, 34 162, 0, 149, 117, 168, 191, 0 13 6 0, 3, 7, 20, 23, 35 151, 16, 172, 162, 105, 0 14 7 0, 12, 15, 16, 17, 21, 36 149, 171, 102, 118, 7, 182, 0 15 7 0, 1, 10, 13, 18, 25, 37 173, 29, 203, 37, 215, 220, 0 16 6 1, 3, 11, 20, 22, 38 0, 174, 175, 168, 145, 0 17 6 0, 14, 16, 17, 21, 39 21, 222, 56, 94, 111, 0 18 6 1, 12, 13, 18, 19, 40 70, 120, 17, 148, 125, 0 19 6 0, 1, 7, 8, 10, 41 57, 118, 189, 25, 11, 0 20 6 0, 3, 9, 11, 22, 42 96, 77, 195, 0, 143, 0 21 6 1, 5, 16, 20, 21, 43 122, 0, 179, 142, 28, 0 22 5 0, 12, 13, 17, 44 188, 212, 35, 148, 0 23 5 1, 2, 10, 18, 45 60, 147, 137, 49, 0 24 6 0, 3, 4, 11, 22, 46 102, 112, 0, 0, 6, 0 25 5 1, 6, 7, 14, 47 93, 0, 0, 105, 0 26 5 0, 2, 4, 15, 48 84, 14, 0, 194, 0 27 4 1, 6, 8, 49 28, 70, 112, 0 28 5 0, 4, 19, 21, 50 37, 0, 59, 0, 0 29 5 1, 14, 18, 25, 51 42, 0, 112, 0, 0 30 5 0, 10, 13, 24, 52 0, 115, 28, 0, 0 31 5 1, 7, 22, 25, 53 0, 0, 38, 109, 0 32 5 0, 12, 14, 24, 54 0, 119, 0, 57, 0 33 5 1, 2, 11, 21, 55 0, 0, 110, 0, 0 34 5 0, 7, 15, 17, 56 0, 0, 189, 0, 0 35 5 1, 6, 12, 22, 57 168, 0, 56, 91, 0 36 5 0, 14, 15, 18, 58 181, 70, 0, 17, 0 37 4 1, 13, 23, 59 80, 42, 7, 0 38 5 0, 9, 10, 12, 60 0, 2, 0, 0, 0 39 5 1, 3, 7, 19, 61 55, 0, 1, 84, 0 40 4 0, 8, 17, 62 0, 0, 112, 0 41 5 1, 3, 9, 18, 63 0, 0, 107, 168, 0 42 4 0, 4, 24, 64 130, 124, 56, 0 43 5 1, 16, 18, 25, 65 76, 0, 0, 140, 0 44 5 0, 7, 9, 22, 66 0, 112, 56, 36, 0 45 4 1, 6, 10, 67 0, 120, 0, 0

В реализации матрица 30b-50 на фиг. 3b-7 может быть выражена в таблице 3-50.

Таблица 3-50

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0 4 3 0, 1, 26 246, 235, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 261, 181, 72, 283, 254, 79, 144, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 80, 144, 169, 90, 59, 177, 151, 108, 0 7 7 0, 1, 4, 7, 8, 14, 29 169, 189, 154, 184, 104, 164, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 54, 0, 252, 41, 98, 46, 15, 230, 54, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 162, 159, 93, 134, 45, 132, 76, 209, 0 10 7 1, 2, 4, 7, 8, 14, 32 178, 1, 28, 267, 234, 201, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 55, 23, 274, 181, 273, 39, 26, 0 12 7 0, 1, 10, 11, 13, 18, 34 225, 162, 244, 151, 238, 243, 0 13 6 0, 3, 7, 20, 23, 35 231, 0, 216, 47, 36, 0 14 7 0, 12, 15, 16, 17, 21, 36 0, 186, 253, 16, 0, 79, 0 15 7 0, 1, 10, 13, 18, 25, 37 170, 0, 183, 108, 68, 64, 0 16 6 1, 3, 11, 20, 22, 38 270, 13, 99, 54, 0, 0 17 6 0, 14, 16, 17, 21, 39 153, 137, 0, 0, 162, 0 18 6 1, 12, 13, 18, 19, 40 161, 151, 0, 241, 144, 0 19 6 0, 1, 7, 8, 10, 41 0, 0, 118, 144, 0, 0 20 6 0, 3, 9, 11, 22, 42 265, 81, 90, 144, 228, 0 21 6 1, 5, 16, 20, 21, 43 64, 46, 266, 9, 18, 0 22 5 0, 12, 13, 17, 44 72, 189, 72, 257, 0 23 5 1, 2, 10, 18, 45 180, 0, 0, 165, 0 24 6 0, 3, 4, 11, 22, 46 236, 199, 0, 266, 0, 0 25 5 1, 6, 7, 14, 47 205, 0, 0, 183, 0 26 5 0, 2, 4, 15, 48 0, 0, 0, 277, 0 27 4 1, 6, 8, 49 45, 36, 72, 0 28 5 0, 4, 19, 21, 50 275, 0, 155, 62, 0 29 5 1, 14, 18, 25, 51 0, 180, 0, 42, 0 30 5 0, 10, 13, 24, 52 0, 90, 252, 173, 0 31 5 1, 7, 22, 25, 53 144, 144, 166, 19, 0 32 5 0, 12, 14, 24, 54 0, 211, 36, 162, 0 33 5 1, 2, 11, 21, 55 0, 0, 76, 18, 0 34 5 0, 7, 15, 17, 56 197, 0, 108, 0, 0 35 5 1, 6, 12, 22, 57 199, 278, 0, 205, 0 36 5 0, 14, 15, 18, 58 216, 16, 0, 0, 0 37 4 1, 13, 23, 59 72, 144, 0, 0 38 5 0, 9, 10, 12, 60 190, 0, 0, 0, 0 39 5 1, 3, 7, 19, 61 153, 0, 165, 117, 0 40 4 0, 8, 17, 62 216, 144, 2, 0 41 5 1, 3, 9, 18, 63 0, 0, 0, 183, 0 42 4 0, 4, 24, 64 27, 0, 35, 0 43 5 1, 16, 18, 25, 65 52, 243, 0, 270, 0 44 5 0, 7, 9, 22, 66 18, 0, 0, 57, 0 45 4 1, 6, 10, 67 168, 0, 144, 0

В реализации матрица 30b-60 на фиг. 3b-8 может быть выражена в таблице 3-60.

Таблица 3-60

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 330, 183, 178, 311, 222, 287, 301, 258, 207, 228, 213, 296, 216, 267, 200, 343, 36, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 211, 314, 319, 268, 256, 246, 327, 204, 323, 264, 177, 254, 189, 338, 249, 206, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 237, 218, 339, 285, 209, 280, 204, 203, 193, 328, 180, 215, 264, 212, 289, 176, 258, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 273, 208, 209, 264, 278, 45, 250, 187, 196, 188, 299, 154, 345, 194, 318, 203, 220, 1, 0 4 3 0, 1, 26 340, 351, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 331, 21, 170, 42, 50, 271, 216, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 202, 351, 307, 86, 254, 240, 31, 124, 0 7 7 0, 1, 4, 7, 8, 14, 29 160, 28, 347, 183, 190, 275, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 9, 182, 264, 350, 69, 257, 173, 28, 200, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 172, 308, 304, 27, 67, 133, 106, 294, 0 10 7 1, 2, 4, 7, 8, 14, 32 316, 270, 183, 252, 217, 291, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 251, 132, 160, 43, 304, 81, 25, 0 12 7 0, 1, 10, 11, 13, 18, 34 268, 44, 131, 41, 289, 126, 0 13 6 0, 3, 7, 20, 23, 35 140, 14, 261, 289, 124, 0 14 7 0, 12, 15, 16, 17, 21, 36 312, 158, 254, 219, 88, 110, 0 15 7 0, 1, 10, 13, 18, 25, 37 129, 0, 336, 308, 255, 231, 0 16 6 1, 3, 11, 20, 22, 38 39, 241, 331, 346, 202, 0 17 6 0, 14, 16, 17, 21, 39 294, 51, 121, 305, 219, 0 18 6 1, 12, 13, 18, 19, 40 191, 54, 186, 195, 22, 0 19 6 0, 1, 7, 8, 10, 41 319, 202, 218, 26, 152, 0 20 6 0, 3, 9, 11, 22, 42 45, 40, 209, 330, 147, 0 21 6 1, 5, 16, 20, 21, 43 233, 329, 317, 61, 31, 0 22 5 0, 12, 13, 17, 44 199, 298, 167, 177, 0 23 5 1, 2, 10, 18, 45 247, 138, 283, 299, 0 24 6 0, 3, 4, 11, 22, 46 180, 80, 43, 264, 292, 0 25 5 1, 6, 7, 14, 47 41, 320, 0, 90, 0 26 5 0, 2, 4, 15, 48 309, 176, 351, 105, 0 27 4 1, 6, 8, 49 336, 187, 88, 0 28 5 0, 4, 19, 21, 50 91, 182, 176, 107, 0 29 5 1, 14, 18, 25, 51 253, 245, 35, 323, 0 30 5 0, 10, 13, 24, 52 177, 207, 212, 198, 0 31 5 1, 7, 22, 25, 53 0, 249, 322, 220, 0 32 5 0, 12, 14, 24, 54 194, 319, 20, 244, 0 33 5 1, 2, 11, 21, 55 177, 41, 181, 208, 0 34 5 0, 7, 15, 17, 56 10, 276, 264, 211, 0 35 5 1, 6, 12, 22, 57 227, 19, 214, 130, 0 36 5 0, 14, 15, 18, 58 224, 144, 41, 122, 0 37 4 1, 13, 23, 59 37, 98, 190, 0 38 5 0, 9, 10, 12, 60 32, 335, 94, 158, 0 39 5 1, 3, 7, 19, 61 10, 88, 8, 107, 0 40 4 0, 8, 17, 62 248, 135, 324, 0 41 5 1, 3, 9, 18, 63 11, 212, 15, 260, 0 42 4 0, 4, 24, 64 319, 73, 265, 0 43 5 1, 16, 18, 25, 65 134, 308, 8, 259, 0 44 5 0, 7, 9, 22, 66 41, 251, 43, 230, 0 45 4 1, 6, 10, 67 264, 68, 88, 0

В реализации матрица 30b-70 на фиг. 3b-9 может быть выражена в таблице 3-70.

Таблица 3-70

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 171, 13, 22, 68, 133, 132, 173, 41, 11, 126, 0, 151, 52, 197, 64, 86, 58, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 135, 82, 7, 122, 9, 115, 0, 0, 44, 15, 116, 26, 12, 19, 79, 10, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 125, 22, 9, 158, 104, 104, 0, 34, 72, 89, 141, 59, 87, 23, 7, 65, 102, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 96, 105, 5, 114, 192, 95, 2, 98, 99, 156, 51, 149, 35, 142, 32, 20, 78, 1, 0 4 3 0, 1, 26 196, 172, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 105, 104, 24, 104, 77, 116, 128, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 156, 205, 123, 104, 204, 38, 207, 76, 0 7 7 0, 1, 4, 7, 8, 14, 29 58, 52, 163, 53, 49, 20, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 74, 52, 111, 70, 47, 104, 3, 99, 18, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 67, 10, 108, 13, 72, 195, 57, 120, 0 10 7 1, 2, 4, 7, 8, 14, 32 15, 107, 165, 50, 45, 149, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 198, 30, 120, 177, 200, 52, 10, 0 12 7 0, 1, 10, 11, 13, 18, 34 107, 99, 206, 117, 148, 86, 0 13 6 0, 3, 7, 20, 23, 35 69, 156, 182, 207, 7, 0 14 7 0, 12, 15, 16, 17, 21, 36 127, 162, 38, 136, 24, 176, 0 15 7 0, 1, 10, 13, 18, 25, 37 117, 19, 207, 135, 153, 90, 0 16 6 1, 3, 11, 20, 22, 38 104, 72, 21, 190, 192, 0 17 6 0, 14, 16, 17, 21, 39 26, 177, 122, 104, 64, 0 18 6 1, 12, 13, 18, 19, 40 48, 54, 66, 135, 30, 0 19 6 0, 1, 7, 8, 10, 41 23, 143, 191, 0, 166, 0 20 6 0, 3, 9, 11, 22, 42 120, 112, 198, 6, 33, 0 21 6 1, 5, 16, 20, 21, 43 171, 205, 175, 180, 11, 0 22 5 0, 12, 13, 17, 44 74, 129, 156, 136, 0 23 5 1, 2, 10, 18, 45 189, 18, 163, 30, 0 24 6 0, 3, 4, 11, 22, 46 188, 124, 0, 179, 66, 0 25 5 1, 6, 7, 14, 47 0, 0, 182, 185, 0 26 5 0, 2, 4, 15, 48 86, 52, 3, 67, 0 27 4 1, 6, 8, 49 102, 25, 0, 0 28 5 0, 4, 19, 21, 50 194, 156, 130, 0, 0 29 5 1, 14, 18, 25, 51 18, 53, 0, 0, 0 30 5 0, 10, 13, 24, 52 104, 141, 0, 106, 0 31 5 1, 7, 22, 25, 53 2, 40, 202, 120, 0 32 5 0, 12, 14, 24, 54 13, 192, 0, 207, 0 33 5 1, 2, 11, 21, 55 128, 109, 168, 68, 0 34 5 0, 7, 15, 17, 56 0, 199, 164, 113, 0 35 5 1, 6, 12, 22, 57 166, 26, 0, 9, 0 36 5 0, 14, 15, 18, 58 80, 4, 0, 0, 0 37 4 1, 13, 23, 59 163, 166, 111, 0 38 5 0, 9, 10, 12, 60 135, 2, 0, 0, 0 39 5 1, 3, 7, 19, 61 169, 83, 0, 127, 0 40 4 0, 8, 17, 62 0, 156, 112, 0 41 5 1, 3, 9, 18, 63 119, 69, 116, 191, 0 42 4 0, 4, 24, 64 104, 30, 201, 0 43 5 1, 16, 18, 25, 65 0, 159, 76, 204, 0 44 5 0, 7, 9, 22, 66 125, 8, 0, 48, 0 45 4 1, 6, 10, 67 144, 121, 44, 0

В реализации матрица 30b-80 на фиг. 3b-10 может быть выражена в таблице 3-80.

Таблица 3-80

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 226, 113, 180, 11, 85, 65, 183, 15, 47, 35, 103, 92, 45, 223, 147, 30, 234, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 24, 197, 0, 21, 181, 83, 99, 44, 71, 17, 102, 142, 1, 195, 145, 91, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 107, 222, 112, 100, 199, 15, 30, 0, 90, 131, 196, 149, 64, 221, 177, 125, 105, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 120, 90, 188, 135, 70, 157, 71, 94, 123, 150, 0, 105, 13, 0, 6, 36, 95, 1, 0 4 3 0, 1, 26 228, 119, 0 5 8 0, 1, 3, 12, 16, 21, 22, 27 235, 30, 122, 88, 79, 51, 64, 0 6 9 0, 6, 10, 11, 13, 17, 18, 20, 28 7, 59, 222, 0, 80, 33, 132, 38, 0 7 7 0, 1, 4, 7, 8, 14, 29 196, 125, 37, 187, 216, 152, 0 8 10 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 4, 6, 60, 75, 82, 99, 160, 123, 222, 0 9 9 0, 1, 10, 11, 13, 17, 18, 20, 31 183, 60, 206, 0, 143, 130, 97, 65, 0 10 7 1, 2, 4, 7, 8, 14, 32 206, 150, 0, 130, 2, 77, 0 11 8 0, 1, 12, 16, 21, 22, 23, 33 194, 30, 1, 24, 212, 96, 93, 0 12 7 0, 1, 10, 11, 13, 18, 34 231, 14, 38, 30, 40, 88, 0 13 6 0, 3, 7, 20, 23, 35 213, 34, 208, 228, 180, 0 14 7 0, 12, 15, 16, 17, 21, 36 120, 51, 195, 0, 149, 229, 0 15 7 0, 1, 10, 13, 18, 25, 37 147, 0, 169, 95, 73, 22, 0 16 6 1, 3, 11, 20, 22, 38 61, 71, 73, 227, 120, 0 17 6 0, 14, 16, 17, 21, 39 60, 36, 35, 1, 0, 0 18 6 1, 12, 13, 18, 19, 40 17, 145, 15, 184, 0, 0 19 6 0, 1, 7, 8, 10, 41 204, 0, 99, 0, 0, 0 20 6 0, 3, 9, 11, 22, 42 221, 23, 146, 0, 90, 0 21 6 1, 5, 16, 20, 21, 43 222, 174, 152, 116, 0, 0 22 5 0, 12, 13, 17, 44 67, 211, 2, 30, 0 23 5 1, 2, 10, 18, 45 58, 15, 3, 205, 0 24 6 0, 3, 4, 11, 22, 46 227, 120, 0, 0, 25, 0 25 5 1, 6, 7, 14, 47 174, 0, 0, 0, 0 26 5 0, 2, 4, 15, 48 180, 0, 0, 26, 0 27 4 1, 6, 8, 49 92, 22, 0, 0 28 5 0, 4, 19, 21, 50 128, 0, 226, 0, 0 29 5 1, 14, 18, 25, 51 65, 186, 0, 239, 0 30 5 0, 10, 13, 24, 52 3, 0, 78, 103, 0 31 5 1, 7, 22, 25, 53 163, 0, 105, 15, 0 32 5 0, 12, 14, 24, 54 0, 50, 51, 116, 0 33 5 1, 2, 11, 21, 55 60, 0, 21, 142, 0 34 5 0, 7, 15, 17, 56 90, 155, 179, 0, 0 35 5 1, 6, 12, 22, 57 144, 168, 220, 20, 0 36 5 0, 14, 15, 18, 58 126, 135, 0, 120, 0 37 4 1, 13, 23, 59 0, 199, 135, 0 38 5 0, 9, 10, 12, 60 124, 0, 60, 0, 0 39 5 1, 3, 7, 19, 61 167, 75, 0, 87, 0 40 4 0, 8, 17, 62 24, 93, 150, 0 41 5 1, 3, 9, 18, 63 90, 0, 102, 120, 0 42 4 0, 4, 24, 64 122, 28, 65, 0 43 5 1, 16, 18, 25, 65 224, 231, 0, 78, 0 44 5 0, 7, 9, 22, 66 0, 150, 120, 150, 0 45 4 1, 6, 10, 67 0, 143, 98, 0

Очевидно, что фиг. 1 по фиг. 3а, фиг. 3b-1 по фиг. 3b-10, таблица 2-10, таблица 2-11 и таблицы с 3-10 по таблицу 3-80 должны помочь понять схемы базового графа и матрицы, и формы выражений структур не ограничиваются формами выражений в фиг. 1 по фиг. 3а, фиг. 3b-1 по фиг. 3b-10 или таблице 2-10, таблице 2-11 и таблице 3-10 по таблицу 3-80. Может быть использован другой возможный вариант.

В реализации параметр «вес строки» в таблице 2-10, таблице 2-11 и таблице 3-10 по таблицу 3-80 альтернативно может быть опущен. Количество ненулевых элементов в строке может быть получено в соответствии с позициями столбцов ненулевых элементов в строке. Следовательно, информация о весе строки также получена.

В реализации значения параметров в «индексе столбца ненулевого элемента» в таблице 2-10, таблице 2-11 и таблице 3-10 по таблицу 3-80 не могут быть отсортированы в порядке возрастания при условии, что положение столбца ненулевого элемента может быть получено с использованием значений параметров. Дополнительно, значения параметров в «значении смещения ненулевого элемента» в таблице 2-10, таблице 2-11 и таблице 3-10 по таблицу 3-80 не могут быть отсортированы на основании порядка столбцов, при условии, что значения параметров в «значении смещения ненулевого элемента» находятся в однозначном соответствии со значениями параметров в «индексе столбца ненулевого элемента».

В реализации для экономии объема хранения положение ненулевого элемента в части с относительно определенной структурой в базовом графе или базовой матрице может быть вычислено на основе позиции строки или позиции столбца, и могут быть не сохранены.

Например, подматрица E является диагональной матрицей и включает в себя ненулевые элементы только по диагонали матрицы. Значения смещения этих ненулевых элементов на диагонали равны 0. Индекс столбца ненулевого элемента в подматрице E может быть вычислен на основании индекса строки, или индекс строки ненулевого элемента может быть рассчитан на основании индекса столбца. Используя матрицу 30b-50 на фиг. 3b-7 в качестве примера, индекс столбца ненулевого элемента в строке m_e является столбец (m_e + K_b), где m_e≥4 и K_b = 22. Например, индекс столбца ненулевого элемента в строке 7 является столбцом 29, и значение смещения ненулевого элемента равно 0.

Для другого примера, двухдиагональная структура B' в подматрице B расположена в строке от 0 до строки 3 и от столбца 23 до столбца 25 в матрице 30b-50. Индекс столбца ненулевого элемента в двухдиагональной структуре B' может быть вычислен на основании индекса строки, или позиция строки ненулевого элемента может быть вычислена на основе индекса столбца. Индексы столбцов ненулевых элементов в строке m_B включают столбец (m_B + K_b) и столбец (m_B + K_b + 1), где 0 <m_B <3. Индексы столбца ненулевого элемента в строке m_B включают в себя столбец (m_B + K_b), где m_B = 0 или m_B = 3. Значение смещения ненулевого элемента в двухдиагональной структуре подматрицы B также равно 0. Можно также узнать, что часть матрицы, включающая в себя столбцы 23 и 25, которые принадлежат подматрице D, индексы столбцов ненулевые элементы в строке 5 - строке 47 не являются фиксированными, значения смещения ненулевых элементов не равны 0, и положения и значения смещения ненулевых элементов все еще должны быть сохранены.

Для другого примера, для столбца с весом 1 в подматрице B, другими словами, для столбца 26 в матрице 30b-50, индекс столбца ненулевого элемента в строке m_B включает в себя столбец (m_B + K_b), где m_B = 4, и значение сдвига ненулевого элемента также равно 0.

Таблица 3-90 показывает параметры, относящиеся к строкам в матрице 30b-50. Индексы столбцов ненулевых элементов в столбцах с 0 по 25 могут быть сохранены, тогда как индексы столбцов ненулевых элементов в столбцах с 26 по 68 не сохранены. Другими словами, индексы столбцов ненулевых элементов в столбцах веса 1 в подматрице E и подматрице B не сохраняются.

Таблица 3-90

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещения ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0 4 2 0, 1 246, 235 5 7 0, 1, 3, 12, 16, 21, 22 261, 181, 72, 283, 254, 79, 144 6 8 0, 6, 10, 11, 13, 17, 18, 20 80, 144, 169, 90, 59, 177, 151, 108 7 6 0, 1, 4, 7, 8, 14 169, 189, 154, 184, 104, 164 8 9 0, 1, 3, 12, 16, 19, 21, 22, 24 54, 0, 252, 41, 98, 46, 15, 230, 54 9 8 0, 1, 10, 11, 13, 17, 18, 20 162, 159, 93, 134, 45, 132, 76, 209 10 6 1, 2, 4, 7, 8, 14 178, 1, 28, 267, 234, 201 11 7 0, 1, 12, 16, 21, 22 55, 23, 274, 181, 273, 39, 26 12 6 0, 1, 10, 11, 13, 18 225, 162, 244, 151, 238, 243 13 5 0, 3, 7, 20, 23 231, 0, 216, 47, 36 14 6 0, 12, 15, 16, 17, 21 0, 186, 253, 16, 0, 79 15 6 0, 1, 10, 13, 18, 25 170, 0, 183, 108, 68, 64 16 5 1, 3, 11, 20, 22 270, 13, 99, 54, 0 17 5 0, 14, 16, 17, 21 153, 137, 0, 0, 162 18 5 1, 12, 13, 18, 19 161, 151, 0, 241, 144 19 5 0, 1, 7, 8, 10 0, 0, 118, 144, 0 20 5 0, 3, 9, 11, 22 265, 81, 90, 144, 228 21 5 1, 5, 16, 20, 21 64, 46, 266, 9, 18 22 4 0, 12, 13, 17 72, 189, 72, 257 23 4 1, 2, 10, 18 180, 0, 0, 165 24 5 0, 3, 4, 11, 22 236, 199, 0, 266, 0 25 4 1, 6, 7, 14 205, 0, 0, 183 26 4 0, 2, 4, 15 0, 0, 0, 277 27 3 1, 6, 8 45, 36, 72 28 4 0, 4, 19, 21 275, 0, 155, 62 29 4 1, 14, 18, 25 0, 180, 0, 42 30 4 0, 10, 13, 24 0, 90, 252, 173 31 4 1, 7, 22, 25 144, 144, 166, 19 32 4 0, 12, 14, 24 0, 211, 36, 162 33 4 1, 2, 11, 21 0, 0, 76, 18 34 4 0, 7, 15, 17 197, 0, 108, 0 35 4 1, 6, 12, 22 199, 278, 0, 205 36 4 0, 14, 15, 18 216, 16, 0, 0 37 3 1, 13, 23 72, 144, 0 38 4 0, 9, 10, 12 190, 0, 0, 0 39 4 1, 3, 7, 19 153, 0, 165, 117 40 3 0, 8, 17 216, 144, 2 41 4 1, 3, 9, 18 0, 0, 0, 183 42 3 0, 4, 24 27, 0, 35 43 4 1, 16, 18, 25 52, 243, 0, 270 44 4 0, 7, 9, 22 18, 0, 0, 57 45 3 1, 6, 10 168, 0, 144

Таблица 3-91 показывает параметры, относящиеся к строкам в матрице 30b-50. Позиции столбцов ненулевых элементов в столбцах с 0 по 26 могут быть сохранены, тогда как позиции столбцов ненулевых элементов в столбцах с 27 по 68 не сохранены. Другими словами, позиции столбцов ненулевых элементов в подматрице E не сохраняют.

Таблица 3-91

Индекс строки Вес строки Индекс столбца ненулевого элемента Значение смещение ненулевого элемента 0 19 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0 1 19 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0 2 19 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0 3 19 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0 4 2 0, 1, 26 246, 235, 0 5 7 0, 1, 3, 12, 16, 21, 22 261, 181, 72, 283, 254, 79, 144 6 8 0, 6, 10, 11, 13, 17, 18, 20 80, 144, 169, 90, 59, 177, 151, 108 7 6 0, 1, 4, 7, 8, 14 169, 189, 154, 184, 104, 164 8 9 0, 1, 3, 12, 16, 19, 21, 22, 24 54, 0, 252, 41, 98, 46, 15, 230, 54 9 8 0, 1, 10, 11, 13, 17, 18, 20 162, 159, 93, 134, 45, 132, 76, 209 10 6 1, 2, 4, 7, 8, 14 178, 1, 28, 267, 234, 201 11 7 0, 1, 12, 16, 21, 22 55, 23, 274, 181, 273, 39, 26 12 6 0, 1, 10, 11, 13, 18 225, 162, 244, 151, 238, 243 13 5 0, 3, 7, 20, 23 231, 0, 216, 47, 36 14 6 0, 12, 15, 16, 17, 21 0, 186, 253, 16, 0, 79 15 6 0, 1, 10, 13, 18, 25 170, 0, 183, 108, 68, 64 16 5 1, 3, 11, 20, 22 270, 13, 99, 54, 0 17 5 0, 14, 16, 17, 21 153, 137, 0, 0, 162 18 5 1, 12, 13, 18, 19 161, 151, 0, 241, 144 19 5 0, 1, 7, 8, 10 0, 0, 118, 144, 0 20 5 0, 3, 9, 11, 22 265, 81, 90, 144, 228 21 5 1, 5, 16, 20, 21 64, 46, 266, 9, 18 22 4 0, 12, 13, 17 72, 189, 72, 257 23 4 1, 2, 10, 18 180, 0, 0, 165 24 5 0, 3, 4, 11, 22 236, 199, 0, 266, 0 25 4 1, 6, 7, 14 205, 0, 0, 183 26 4 0, 2, 4, 15 0, 0, 0, 277 27 3 1, 6, 8 45, 36, 72 28 4 0, 4, 19, 21 275, 0, 155, 62 29 4 1, 14, 18, 25 0, 180, 0, 42 30 4 0, 10, 13, 24 0, 90, 252, 173 31 4 1, 7, 22, 25 144, 144, 166, 19 32 4 0, 12, 14, 24 0, 211, 36, 162 33 4 1, 2, 11, 21 0, 0, 76, 18 34 4 0, 7, 15, 17 197, 0, 108, 0 35 4 1, 6, 12, 22 199, 278, 0, 205 36 4 0, 14, 15, 18 216, 16, 0, 0 37 3 1, 13, 23 72, 144, 0 38 4 0, 9, 10, 12 190, 0, 0, 0 39 4 1, 3, 7, 19 153, 0, 165, 117 40 3 0, 8, 17 216, 144, 2 41 4 1, 3, 9, 18 0, 0, 0, 183 42 3 0, 4, 24 27, 0, 35 43 4 1, 16, 18, 25 52, 243, 0, 270 44 4 0, 7, 9, 22 18, 0, 0, 57 45 3 1, 6, 10 168, 0, 144

В таблицах с 3-10 по 3-91 вес строки является возможным и индекс строки и индексы столбца ненулевых элементов указывают положения столбцов ненулевых элементов в каждой строке, что также упоминается и информация о базовом графе LDPC матрицы. В реализации информация о базовом графе и значениях смещения LDPC матрицы может быть хранена на основании способов, приведенных в таблицах с 3-10 по 3-91.

В другом исполнении базовый граф LDPC матрицы и значения смещения LDPC матрицы могут храниться отдельно. Информация о значениях смещения LDPC матрицы может храниться с использованием индексов строк и значений сдвига ненулевых элементов в таблицах с 3-10 по 3-91. Базовый граф LDPC матрицы может быть сохранен множеством способов, например, может быть сохранен в виде матрицы базового графа 30a, показанного на фиг. 3a, или могут быть сохранены на основании индексов строк и позиций ненулевых элементов в таблицах с 3-10 по 3-91, или могут быть сохранены таким образом, что 1 и 0 в каждой строке или каждом столбце в базовый граф может рассматриваться как двоичные числа, и базовый граф хранится в форме десятичных чисел или шестнадцатеричных чисел для экономии объема хранения. Базовый граф 30a используют в качестве примера. В каждой строке позиции ненулевых элементов в первых 26 столбцах или первых 27 столбцах могут храниться в четырех шестнадцатеричных числах. Например, если первые 26 столбцов в строке 0 являются 11110110 01111101 10111111 00, позиции ненулевых элементов в строке 0 могут быть обозначены как 0xF6, 0x7D, 0xBF и 0x00. Чтобы быть точным, каждые восемь столбцов образуют одну шестнадцатеричную цифру 0 может быть добавлен в последние два или три столбца для получения восьми цифр, так что получается соответствующая шестнадцатеричная цифра. То же самое верно для другой строки, и подробности здесь не описывают снова.

Возможно, в вышеупомянутых различных вариантах значения смещения LDPC могут быть сохранены в другом преобразовании. Например, чтобы облегчить обработку циклического сдвига, может быть сохранена разница между значением смещения и предшествующим значением смещения в столбце, в котором находится значение смещения. Фиг. 9 показывает значения смещения строки 0 в строку 4 и столбца 0 в столбец 26 в матрице 3b-50 после преобразования. В примере, показанном на фиг. 9, строка 0 является начальной строкой, и значение смещения в строке 0 не изменяются. Нулевые элементы в каждой строке не изменяются, и значение смещения ненулевого элемента в каждой строке представляет собой разницу между значением смещения в той же позиции в матрице 30b-50 и предшествующим ненулевым элементом в матрице 30b-50 в столбце, в котором находится значение смещения. При отсутствии ненулевого элемента перед строкой, в которой находится значение смещения и в столбце, в котором находится значение смещения, значение смещения не изменяется. Например, значение смещения в строке 1 и столбце 0 матрицы 30b-50 составляет 179, и значение смещения в строке 1 и столбце 0 на фиг. 9 является разностью -32 между 179 и предшествующим значением 211 смещения в столбце 0. Поскольку элемент в строке 0 и столбце 4 на фиг. 9 представляет собой нулевой элемент, значение смещения в строке 1 и столбце 4 на фиг. 9 соответствует значению смещения в строке 1 и столбце 4 в матрице 30b-50. Элемент в строке 2 и столбце 3 на фиг. 9 является нулевым элементом, и элемент в строке 1 и столбце 3 является ненулевым элементом, и поэтому значение смещения в строке 3 и столбце 3 представляет собой разницу -57 между значением 166 смещения в строке 3 и столбце 3 в матрице 30b-50, и значение 223 смещения в строке 1 и столбце 3 и так далее. Из-за ограниченного пространства другие строки матрицы 30b-50 не показаны на фиг. 9. То же самое относится и к другим строкам, и подробности здесь не описываются снова. Когда разность значений смещения в данном случае является положительным числом, циклическое смещение вправо выполняется на единичной матрице; когда разность является отрицательным числом, выполняют круговое смещение влево на единичной матрице. Соответственно, значение смещения, полученное после перестановки, другими словами, разность значения смещения, может быть сохранено в «значениях смещения ненулевых элементов» в таблице 3-10 - таблице 3-91. Выше приведены только примеры, и примеры не являются ограничением.

Фиг. 5 представляет собой схему процесса обработки данных. Процесс обработки данных может быть реализован с использованием устройства связи. Устройство связи может быть базовой станцией, терминалом или другим объектом, таким как микросхема связи или кодер/декодер.

Часть 501. Получают входную последовательность.

В реализации входная последовательность для кодирования может быть последовательностью информационных битов. Последовательность информационных битов иногда упоминается как кодовый блок (code block), например, может быть выходной последовательностью, полученной после того, как сегментация кодового блока выполнена на транспортном блоке. Возможно, входная последовательность может включать в себя, по меньшей мере, одно из следующего: биты заполнители или биты циклического избыточного кода (CRC). В возможной реализации последовательность информационных битов может быть вставлена в биты заполнители для получения входной последовательности, так что длина входной последовательности составляет K = K_b⋅Z и Z = K/K_b. Последовательность информационных битов может быть вставлена в биты заполнители во время сегментации кодового блока или может быть вставлена после сегментации кодового блока.

В возможной реализации значения битов заполнителей могут быть нулевыми, 0 или другими значениями, согласованными в системе. Таким образом, после кодирования эти биты заполнители могут быть идентифицированы и не отправлены. Настоящее изобретение не ограничивается этим.

В реализации входная последовательность для декодирования может быть последовательностью мягких значений LDPC кода.

Часть 502. Кодирование/декодирование входной последовательности на основании LDPC матрицы, где базовой матрицей LDPC матрицы может быть любая базовая матрица в вышеприведенных примерах.

В реализации LDPC матрица Н может быть получена на основании коэффициента Z поднятия и базовой матрицы.

В реализации параметры, относящиеся к LDPC матрице Н, могут быть сохранены, и параметры включают в себя одно или несколько из следующего:

(a) параметр, используемый для получения любой базовой матрицы, описанной в предшествующих реализациях. Базовая матрица может быть получена на основании параметров и, например, параметры могут быть одним или несколькими из следующих: индекс строки, вес строки, индекс столбца, вес столбца, позиции ненулевого элемента (такого как индексы строки ненулевых элементов или индексы столбца ненулевых элементов), значения смещения базовой матрицы, значения смещения ненулевых элементов и соответствующих позиций, смещения, коэффициента поднятия, базовый граф, кодовая скорость и т.п;

(b) базовая матрица, которая является одной из любых базовых матриц, описанных в предшествующих реализациях;

(c) матрица Hs смещения, полученная смещением, по меньшей мере, одного столбца любой базовой матрицы, перечисленной в предшествующих реализациях;

(d) матрицу, полученную поднятием базовой матрицы или поднятием матрицы Hs смещения базовой матрицы;

(e) базовая матрица, полученная путем выполнения преобразования строки/столбца в любой базовой матрице, перечисленной в предшествующих реализациях или в матрице Hs смещения;

(f) матрицу, полученную поднятием строки/столбца преобразованной базовой матрицы или строки/столбца преобразованной матрицы Hs смещения базовой матрицы; и

(g) матрица, полученную путем укорочения или выкалывания любой базовой матрицы или матрицы Hs смещения базовой матрицы, описанной в предшествующих реализациях.

В возможной реализации входная последовательность может быть кодирована/декодирована на основании LDPC матрицы с низкой плотностью проверки на четность в процессе кодирования/декодирования одним или несколькими из следующих способов:

i) получают базовую матрицу на основании (а): и выполнить кодирование/декодирование на основании полученной базовой матрицы, или выполнить перестановку строк/столбцов на основании полученной базовой матрицы, и выполнить кодирование/декодирование на основании базовой матрицы, полученной путем выполнения перестановки строк/столбцов, или выполнить кодирование/декодирование на основании матрицы смещения, полученной базовой матрицы или выполнить кодирование/декодирование на матрице, полученной путем выполнения перестановки строки/столбца на основании матрицы Hs смещения, полученной базовой матрицы. Возможно, выполнение кодирования/декодирования на основании базовой матрицы или матрицы Hs смещения в данном документе может дополнительно включать в себя: выполнение кодирования/декодирования на основании поднятой матрицы базовой матрицы или поднятой матрицы Hs смещения или выполнение на основании кодирования/декодирования на матрице, полученной путем укорочения или выкалывания базовой матрицы или матрицы смещения.

ii) выполнение кодирования/декодирования на основании базовой матрицы (сохраненной базовой матрицы H или Hs или сохраненной базовой матрицы, полученной путем выполнения перестановки строк/столбцов на базовой матрице H или Hs), сохраненной в (b), (c), (d) или (е); или выполнить перестановку строк/столбцов на основании сохраненной базовой матрицы и выполнить кодирование/декодирование на основании базовой матрицы, полученной путем выполнения перестановок строк/столбцов. Возможно, выполнение кодирования/декодирования на основании базовой матрицы или матрицы Hs смещения в данном документе может дополнительно включать в себя: выполнение кодирования/декодирования на основании поднятой матрицы базовой матрицы или поднятой матрицы Hs смещения или выполнение на основании кодирования/декодирования на матрице, полученной путем укорочения или выкалывания базовой матрицы или матрицы смещения.

iii) выполните кодирования/декодирования на основании (d), (f) или (g).

Часть 503. Выводят битовую последовательность, полученную после кодирования/декодирования.

На фиг. 6 проиллюстрирована схема процесса обработки данных, и схема может быть применена к части 502 на фиг. 5.

Часть 601. Получают коэффициент Z поднятия.

В реализации, коэффициент Z поднятия может быть определен на основании длины K входной последовательности. Например, минимальное значение Z₀ может быть определено в поддерживаемом наборе коэффициентов поднятия и используют в качестве значения коэффициента Z поднятия, где выполняется 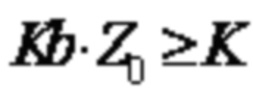. В возможной схеме K_b может быть количеством столбцов информационных битов в базовой матрице LDPC кода. Для базового графа 30a количество столбцов информационных битов равно K_bmax = 22, и предполагают, что набор коэффициентов поднятия, поддерживаемый базовым графом 30a, равен {24, 26, 28, 30, 32, 36, 40, 44, 48, 52, 56, 60, 64, 72, 80, 88, 96, 104, 112, 120, 128, 144, 160, 176, 192, 208, 224, 240, 256, 288, 320, 352, 384}.

Если длина K входной последовательности составляет 529 битов, то Z равно 26; если длина K входной последовательности составляет 5000 битов, то Z составляет 240. Следует отметить, что в данном документе представлены только примеры, и примеры не составляют ограничение.

В другом примере значение K_b может варьироваться в зависимости от значения K, но не превышает количество столбцов информационных битов в базовой матрице LDPC кода. Например, когда K больше первого порогового значения, K_b = 22; когда K меньше или равно первому пороговому значению, K_b = 21. В качестве альтернативы, когда K больше, чем первое пороговое значение, K_b = 22; когда K меньше или равен первому пороговому значению и больше второго порогового значения, K_b = 21; когда K меньше или равен второму пороговому значению, K_b = 20. Следует отметить, что в настоящем документе приведены только примеры, и примеры не являются ограничением.

Кроме того, на основании любой из вышеприведенных реализаций для заданной длины К информации, например, когда 104≤K≤512, Z может быть выбран на основании определенного системой правила. Когда K имеет длину, отличную от 104≤K≤512, Z по-прежнему выбирают на основании любой из вышеприведенных реализаций, например, выбирают минимальное значение Z₀, которое удовлетворяет 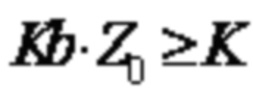, где значение K_b равно 22 или определяют на основании порогового значения.

В реализации, когда 104≤K≤512, значение Z показано в таблице 4-1. Для другой длины Z выбирается на основании любой из вышеприведенных реализаций.

Таблица 4-1

Диапазон значений K Коэффициент Z поднятия 104-111 7 112-127 8 128-135 6 136-143 9 144-183 8 184-223 10 224-247 11 248-287 13 288-335 15 336-359 16 360-399 18 400-447 20 448-487 22 488-512 24

В другой возможной реализации выбрано минимальное значение Z₀, которое удовлетворяет 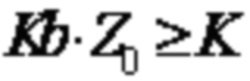. Когда 104≤K≤512, значение K_b может варьироваться в зависимости от значения K, например, как показано в таблице 4-2. Когда K является длиной, отличной от 104≤K≤512, K_b выбирают на основании любой из вышеприведенных реализаций, например, K_b = 22 или K_b определяют на основании порогового значения.

Таблица 4-2

Значение K Kb 112 14 104,120 15 136 16 144 18 152,184 19 160, 192, 200, 248, 256, 288, 296, 360, 400 20 168, 208, 224, 264, 272, 304, 312, 336, 368, 376, 408, 416, 448, 456, 488, 496, 504 21 128, 176, 216, 232, 240, 280, 320, 328, 344, 352, 384, 392, 424, 432, 440, 464, 472, 480 22

Коэффициент Z поднятия может быть определен устройством связи на основании длины K входной последовательности или может быть получен устройством связи от другого объекта (например, процессора).

Часть 602. Получают LDPC матрицу на основании коэффициента поднятия и базовой матрицы.

Базовая матрица является любой базовой матрицей, описанной в предшествующих реализациях, или матрицей смещения, полученной смещением, по меньшей мере, одного столбца в любой базовой матрице, описанной выше, или базовой матрицей, полученной путем выполнения перестановки строк, или перестановки столбцов, или перестановки строк и столбцов, перестановки на любой базовой матрице или матрице смещения, описанной выше. Базовый граф базовой матрицы включает в себя, по меньшей мере, подматрицу A и подматрицу B. Возможно, базовый граф базовой матрицы может дополнительно включать в себя подматрицу C, подматрицу D и подматрицу E. Для подматриц может быть сделана ссылка на вышеприведенные варианты осуществления и подробности не описываются здесь снова.

В возможной реализации соответствующая базовая матрица определяется на основании коэффициента Z поднятия, и базовая матрица переставляется на основании коэффициента Z поднятия для получения LDPC матрицы.

В реализации может сохраняться соответствие между коэффициентом поднятия и базовой матрицей, и соответствующая базовая матрица определяется на основе коэффициента Z поднятия, полученного в части 601.

Например, когда Z равно 26 и a = 13, базовая матрица может включать в себя строки от 0 до строки 4 и от столбца 0 до столбца 26 в матрице 30b-70; или базовая матрица включает в себя строки от 0 до 4 и некоторые из столбцов от 0 до 26 в матрице 30b-70. Альтернативно, базовая матрица может включать в себя строку 0 для строки (m-1) и столбец 0 для столбца (n-1) в матрице 30b-70, где 5≤m≤46, m представляет собой целое число, 27≤n≤68 и n представляет собой целое число; или базовая матрица включает в себя строку от 0 до строки (m-1) и от столбца 0 до столбца (n-1) в матрице 30b-70, где 5≤m≤46, m является целым числом, 27≤n≤68 и n является целым числом. Кроме того, базовая матрица может включать в себя одну или несколько строк от строки 5 до строки 45 и один или несколько столбцов от столбца 27 до столбца 67 в матрице 30b-70. LDPC матрицу получают путем перестановки базовой матрицы на основании коэффициента Z поднятия.

Следует отметить, что Z = 26, a = 13, и матрица, показанная на фиг. 3b-7, просто используют в качестве примера в данном документе. Здесь приведены только примеры, и настоящее изобретение не ограничивается ими. Можно понять, что, если коэффициенты поднятия различны, базовые матрицы также различны.

В возможной реализации соответствие между коэффициентом поднятия и базовой матрицей может быть показано в таблице 5. Индекс базовой матрицы, соответствующий коэффициенту поднятия, определяют на основании таблицы 5. В возможной реализации PCM1 может быть матрицей 30b-10, показанной на фиг. 3b-1, или представляет собой матрицу 30b-11, показанную на фиг. 3b-2; PCM2 может быть матрицей 30b-20, показанной на фиг. 3b-3, или представляет собой матрицу 30b-21, показанную на фиг. 3b-4; PCM3 может представлять собой матрицу 30b-30, показанную на фиг. 3b-5; PCM4 может представлять собой матрицу 30b-40, показанную на фиг. 3b-6; PCM5 может представлять собой матрицу 30b-50, показанную на фиг. 3b-7; PCM6 может представлять собой матрицу 30b-60, показанную на фиг. 3б-8; PCM7 может представлять собой матрицу 30b-70, показанную на фиг. 3b-9; и PCM8 может быть матрицей 30b-80, показанной на фиг. 3b-80. Здесь приведены только примеры, и примеры не являются ограничением.

Таблица 5

Индекс базовой матрицы Коэффициент Z поднятия PCM1 2 4 8 16 32 64 128 256 PCM2 3 6 12 24 48 96 192 384 PCM3 5 10 20 40 80 160 320 PCM4 7 14 28 56 112 224 PCM5 9 18 36 72 144 288 PCM6 11 22 44 88 176 352 PCM7 13 26 52 104 208 PCM8 15 30 60 120 240

В возможной реализации, как показано в таблице 6, устанавливают наборы индексов для восьми наборов коэффициентов поднятия в таблице 5.

Таблица 6

Индекс 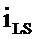набора
(Индекс () набора) Набор коэффициентов поднятия
Набор размеров поднятия 1 {2, 4, 8, 16, 32, 64, 128, 256} 2 {3, 6, 12, 24, 48, 96, 192, 384} 3 {5, 10, 20, 40, 80, 160, 320} 4 {7, 14, 28, 56, 112, 224} 5 {9, 18, 36, 72, 144, 288} 6 {11, 22, 44, 88, 176, 352} 7 {13, 26, 52, 104, 208} 8 {15, 30, 60, 120, 240}

Каждый индекс набора соответствует одному РСМ. Например, 1 соответствует PCM1, 2 соответствует PCM2, 3 соответствует PCM3,…, и 8 соответствует PCM8 и так далее.

Возможно, в возможной реализации для коэффициента Z поднятия элемент 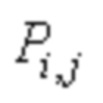в строке i и столбце j в базовой матрице может соответствовать следующему соотношению:

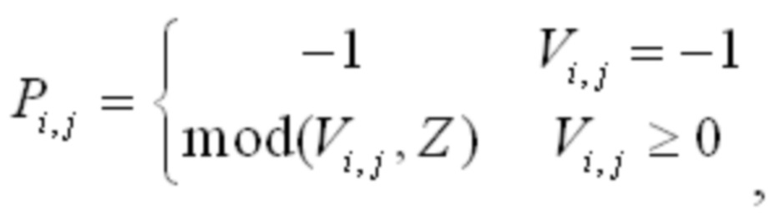
где V_ij является значением смещения элемента в строке i и столбце j в базовой матрице набора, которому принадлежит коэффициент Z поднятия, или значение смещения ненулевого элемента в строке i и столбце j в базовой матрице максимального коэффициента поднятия в наборе, к которому принадлежит коэффициент Z поднятия.

Например, для Z равен 13, и элемент V_i,j в строке i и столбце j в базовой матрице Z соответствует следующему соотношению:

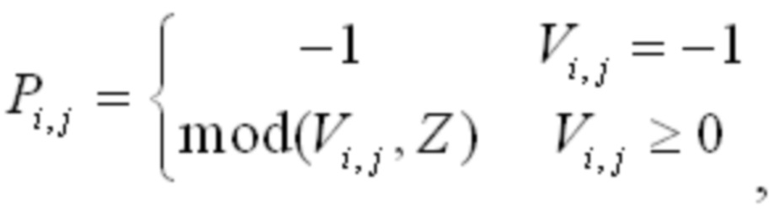
где V_ij является значением смещения ненулевого элемента в строке i и столбце j в PCM7, другими словами, в матрице 30b-70, где, когда Z = 13, необходимо выполнить операцию по модулю, используя значение V_ij смещения ненулевого элемента в строке i и столбце j в матрице 30b-70 по модулю Z, где Z = 13.

Следует отметить, что в настоящем документе представлены только примеры, и настоящее изобретение не ограничивается этим.

Часть 603. Кодируют/декодируют входной последовательности на основании LDPC матрицы.

В реализации входная последовательность для кодирования может быть последовательностью информационных битов. В другой реализации входная последовательность для декодирования может быть последовательностью мягких значений LDPC кода. Изложение подробного описания очевидно из описания на фиг. 5.

В возможной реализации входная последовательность для кодирования представляет собой 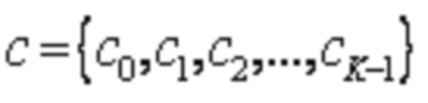, длина входной последовательности с равна K, и выходной последовательности, полученной после того, как входная последовательность с закодирована, является . K является целым числом больше 0, и K может быть целым кратным коэффициенту Z поднятия.

Выходная последовательность d включает в себя биты K₀ во входной последовательности c и биты четности в последовательности битов четности w, где K₀ - целое число, большее 0 и меньшее или равное K, длина последовательности w проверки на четность равна N - K₀, и .

Последовательность w битов четности и входная последовательность c удовлетворяют формуле (1):

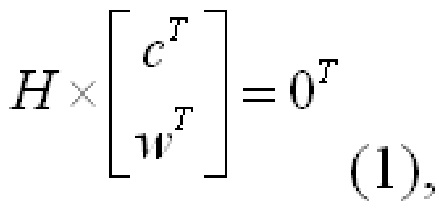
где 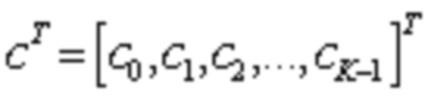, c^T является транспонированный вектор вектора, включающего в себя биты во входной последовательности, 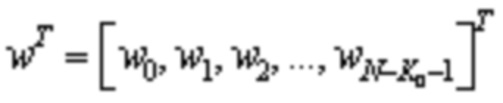, w^T является транспонированным вектором вектора, включающего в себя биты в последовательности битов четности, 0^T является вектором столбца, и значения всех элементов 0^T равны 0.

H представляет собой LDPC матрицу, полученную на основании любого базового графа или базовой матрицы, описанной в предшествующих вариантах осуществления. Базовый граф H имеет m строк и n столбцов и может быть любым графом, описанным в предшествующих вариантах осуществления, например, базовый граф 30a.

В реализации базовый граф H включает в себя p столбцов, соответствующих встроенным выколотым битам, p представляет собой целое число, большее или равное 0, информационные биты, соответствующие p столбцам, соответствующим встроенным выколотым битам, не выводят, и выходная последовательность не включает в себя информационные биты, соответствующие столбцам p, соответствующим встроенным выколотым битам. В этом случае, K₀ = K-p⋅Z. Например, если p = 2, K₀ = K-2⋅Z и длина последовательности w битов четности равна N+2⋅Z-K. Если p столбцы, соответствующие встроенным выколотым битам, используют в кодировании, K₀=K и длина последовательности w битов четности равна N - K.

Соответственно, H может иметь M строк и (N + p⋅Z) столбцов или M строк и N столбцов, и размер базового графа H составляет: m = M / Z и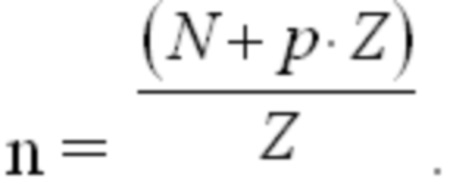

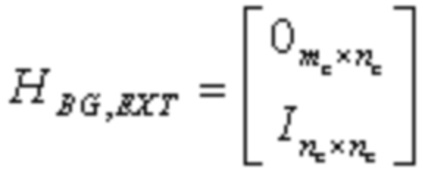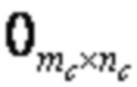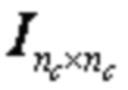Базовый граф LDPC матрицы H может быть представлен [H_BG H_BG,EXT], где , представляет полностью нулевую матрицу размером и представляет единичную матрицу размера .

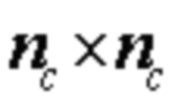В возможном варианте осуществления, если 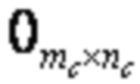является подматрицей C в базовом графе в предшествующих вариантах осуществления, и 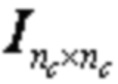является подматрицей E в вышеупомянутых вариантах осуществления, 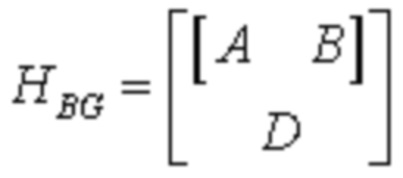, где A, B и D являются соответственно подматрицей A, подматрицей B, и подматрица D в базовом графе в вышеприведенных вариантах осуществления m_c = 5, 0≤n_c≤41, число строк H_BG меньше или равно 46 и больше или равно 5 и число столбцов H_BG равно 27.

В другой возможной реализации, поскольку столбец 26 является столбцом с весом 1, и ненулевой элемент в столбце 26 расположен в строке 5, также может включать в себя первые четыре строки в столбце 26 в базовом графе в вышеупомянутых вариантах осуществления и первые четыре строки в подматрице C в вышеупомянутых вариантах осуществления, и также могут включать в себя подматрицу E в базовом графе в предшествующих вариантах осуществления, от строки 5 до строки 46 в столбце 26 и последнюю строку в подматрице C, где m_c = 4, 0≤n_c≤42, H_BG является матрицей, полученной после удаления последнего столбца из части, включающей в себя подматрицу A, подматрицу B и подматрицу D в базовом графе в вышеприведенных вариантах осуществления, количество строк H_BG меньше или равно 46 и больше или равно 5 и количество столбцов H_BG равно 26. Возможно, если требуется увеличить кодовую скорость, H_BG может иметь четыре строки: от строки 0 до строки 3.

Соответственно, LDPC матрица H может быть представлена как H = [H1 H2].

H1 может быть получена путем замены каждого нулевого элемента в H_BG на полностью нулевую матрицу размером Z × Z и замены каждого ненулевого элемента матрицей h_i,j круговой перестановки размера Z × Z. Матрицу h_i,j круговой перестановки получают путем кругового смещения единичной матрицы размера Z × Z вправо P_ij раз, и иногда она представлена I (P_ij), где i является индексом строки, и j является индексом столбца. В возможной реализации P_i,j = mod (V_i,j, Z) и V_i,j является ненулевым элементом в строке i и столбце в базовой матрице, соответствующей индексу i_LS набора коэффициентов поднятия, соответствующему Z.

Н2 может быть получена путем замены каждого нулевого элемента в H_BGEXT полностью нулевой матрицей размером Z × Z и замены каждого ненулевого элемента на единичную матрицу размера Z × Z.

Кодер может выполнять кодирование и вывод множеством способов. Базовый граф 30a и базовая матрица 30b-50, описанные в предшествующем варианте осуществления, используют в качестве примера для описания ниже. Базовый граф и базовая матрица имеют максимум 46 строк и максимум 68 столбцов, каждый из которых включает в себя два столбца, соответствующих встроенным выколотым битам. Для простоты описания в настоящем изобретении базовый граф, который имеет максимальное количество строк и максимальное количество столбцов, иногда называют полным базовым графом, и базовая матрица имеет максимальное количество строк и максимальное количество столбцов иногда называют полной базовой матрицей.

Способ 1

Выполняют кодирование на основании полного базового графа или полной базовой матрицы, чтобы можно было получить как можно больше битов четности. В этом случае, m = 46 и n = 68, которые соответствуют строке 0 строке 45 и столбцу 0 столбцу 67 на базовом графике 30a, или значения смещения строки 0 строки 45 и столбца 0 столбца 67 в базовой матрице 30b-50.

Соответственно, M=46⋅Z для LDPC матрицы H. Если выходная последовательность включает в себя информационные биты, соответствующие столбцам, соответствующим встроенным выколотым битам, N=68⋅Z; или, если выходная последовательность не включает в себя 2⋅Z информационных битов, которые являются встроенными выколотыми битами, N=66⋅Z.

Во время последующей обработки информационные биты и биты четности, которые должны быть отправлены, могут быть определены из выходной последовательности, сгенерированной кодером.

Способ 2

Выполняют кодирование на основании некоторых строк и некоторых столбцов в полном базовом графе или полной базовой матрице. Строки и столбцы могут быть выбраны на основании скорости кодирования для передачи или количества информационных битов и количества битов четности или тому подобного из полного базового графа или полной базовой матрицы для кодирования.

Например, кодовая скорость составляет 8/9, m = 5 и n = 27. Другими словами, выполняют кодирование на основании строки 0 - строки 4 и столбца 0 - столбца 26 в базовом графе 30a, или выполняют кодирование на основании значений смещения строки 0 - строки 4 и столбца 0 - столбца 26 в базовой матрице 30b-50.

Соответственно, M=5⋅Z для LDPC матрицы H. Если выходная последовательность включает в себя информационные биты, соответствующие столбцам, соответствующим встроенным выколотым битам, N=27⋅Z; или, если выходная последовательность не включает в себя информационные биты, соответствующие столбцам, соответствующим встроенным выколотым битам, N=25⋅Z.

Для другого примера, кодовая скорость составляет 1/3, m = 46 и n = 68.

Можно выяснить, что таким образом размеры базового графа H или базовой матрицы удовлетворяют 5≤m≤46 и 27≤n≤68 и, соответственно, для LDPC матрицы H, 5⋅Z≤M≤46⋅Z и 27⋅Z≤N≤68⋅Z.

В возможной реализации столбец 26 на базовом графе 30a является столбцом с весом 1, и выкалывание может быть выполнено для столбца с весом 1 в основной матрице, так что один ряд и один столбец удаляют из основной матрицы соответственно и m = 4 и n = 26. Другими словами, выполняют кодирование на основании строки 0 - строки 3 и столбца 0 - столбца 25 в базовом графе 30a или базовой матрице 30b-50. Таким образом можно получить более высокую кодовую скорость. Следовательно, размеры базового графа или базовой матрицы соответствуют 4≤m≤46 и 26≤n≤68 и, соответственно, для LDPC матрицы H 4⋅Z≤M≤46⋅Z и 26⋅Z≤N≤68⋅Z.

Поскольку декодирование является обратным процессом кодирования, для описания LDPC матрицы H и базового графа, и базовой LDPC матрицы H может быть сделана ссылка на вышеупомянутый способ кодирования. Декодирование может быть выполнено на основании полного базового графа или полной базовой матрицы, или декодирование может быть выполнено на основании некоторых строк или некоторых столбцов в полном базовом графе или полной базовой матрице.

Когда входная последовательность должна быть закодирована/декодирована, базовая матрица может быть поднята на основе Z, чтобы получить LDPC матрицу H. Матрицу h_ij круговой перестановки размера Z × Z определяют для каждого ненулевого элемент P_i,j в базовой матрице, где h_i,j является матрицей круговой перестановки, полученной путем кругового смещения единичной матрицы P_i,j раз. Ненулевой элемент P_ij заменяют на h_i,j, и нулевой элемент в базовой матрице H_B заменяют на полностью нулевую матрицу размером Z × Z для получения матрицы Н проверки на четность.

В возможной реализации базовая матрица LDPC кода может быть сохранена в памяти, и устройство связи получает LDPC матрицу, соответствующую коэффициенту Z поднятия для кодирования/декодирования входной последовательности.

В возможной реализации, поскольку существует множество базовых матриц LDPC кода, и относительно большой объем хранения занят, если базовые матрицы хранят на основании структуры матрицы, базовый граф LDPC кода может быть сохранен в памяти значения смещения ненулевых элементов в каждой базовой матрице могут быть сохранены по строке или по столбцу, и затем LDPC матрица может быть получена на основании базового графа и значений смещения базовой матрицы, соответствующих коэффициенту Z поднятия.

Базовый граф может указывать позиции ненулевых элементов каждой базовой матрицы. Получение LDPC матрицы на основании базового графа и значений смещения базовой матрицы, соответствующих коэффициенту Z поднятия, может дополнительно включать в себя: получение LDPC матрицы на основании положений ненулевого элемента и значений смещения базовой матрицы, соответствующих коэффициенту Z поднятия.

В другой возможной реализации сохранение базового графа может сохранять позиции ненулевых элементов в базовом графе. Положение ненулевого элемента может быть указано индексом строки и индексом столбца, в котором расположен ненулевой элемент. Например, позиции ненулевых элементов могут быть позициями столбцов ненулевых элементов в каждой строке или позициями ненулевых элементов в каждом столбце. В другой возможной реализации сохранение базового графа может быть сохранением позиций нулевых элементов в базовом графе. Аналогично, позиция нулевого элемента может также быть указана индексом строки и индексом столбца, в котором расположен нулевой элемент. Например, позиции нулевых элементов могут быть позициями столбцов нулевых элементов в каждой строке, или позиции строк нулевых элементов в каждом столбце, и соответствующие позиции ненулевых элементов могут быть получены путем исключения позиций нулевых элементов. Следует отметить, что в данном документе представлены только примеры, и настоящее изобретение этим не ограничивается.

В возможной реализации значения смещения ненулевых элементов каждой базовой матрицы могут быть сохранены способами таблицы 2-10, таблицы 2-11, таблицы 3-10 и таблицы 3-80, таблицы 3-90 и таблицы 3-91, и используют в качестве параметров LDPC матрицы. Столбец «вес строки» в таблице 2-10, таблице 2-11, таблице 3-10 - таблице 3-80, таблице 3-90 и таблице 3-91 является Возможным. Другими словами, возможно, столбец «вес строки» может быть сохранен или не сохранен. Количество ненулевых элементов в строке определяют с помощью позиций столбцов ненулевых элементов в строке. Следовательно, вес строки известен. В возможной реализации значения параметров в «индексе столбца ненулевого элемента» в таблице 2-10, таблице 2-11, таблице с 3-10 - таблице 3-80, таблице 3-90 и таблице 3-91 могут не сортировать в порядке возрастания при условии, что позиции столбцов ненулевых элементов могут быть получены с использованием значений параметров. Кроме того, значения параметров в «значениях смещения ненулевых элементов» в таблице 2-10, таблице 2-11, таблице 3-10 в таблице 3-80, таблице 3-90 и таблице 3-91 возможно сортируют на основании порядка столбцов либо при условии, что значения параметров в «значениях смещения ненулевых элементов» находятся во взаимно однозначном соответствии со значениями параметров в «положениях столбцов ненулевых элементов», и при условии, что устройство связи может узнать, в какой строке и в каком столбце находится ненулевой элемент, на основании значения смещения ненулевого элемента. Например:

В возможной реализации, соответствующие параметры LDPC матрицы могут быть сохранены со ссылкой на соответствующее описание на фиг. 5.

В возможной реализации, в случае сохранения соответствующих параметров LDPC матрицы, сохраненные параметры могут не содержать все строки матриц, показанных на фиг. 1 по фиг. 3а, фиг. 3b-1 по фиг. 3b-10, или таблице 2-10, таблице 2-11, таблице 3-10 - таблице 3-80, таблице 3-90 и таблице 3-91, и параметр, обозначенный соответствующей строкой в таблице, может быть сохранен на основании строк, содержащиеся в базовой матрице. Например, может быть сохранена матрица, включающая в себя строки и столбцы, содержащиеся в базовой матрице LDPC матрицы, описанной в предшествующем варианте осуществления, или сохранены параметры, относящиеся к матрице, включающей в себя строки и столбцы.

Например, если базовая матрица включает в себя строки от 0 до 4 и от 0 до 26 в любой из матриц с 30b-10 по 30b-80 и матрицы, показанные в таблицах 3-90 и 3-91, матрица, включающая в себя: строки от 0 до строки 4 и от столбца 0 до столбца 26 могут быть сохранены, и/или параметры, относящиеся к матрице, включающей в себя строки от 0 до строки 4 и от столбца 0 до столбца 26. Подробное описание может быть выполнено со ссылкой на параметры, показанные в таблицах с 3-10 по 3-80, таблице 3-90 и таблице 3-91, и описания в предшествующей части.

Если базовая матрица включает в себя строку от 0 до строки (m-1) и от 0 до столбца (n-1) в любой из матриц с 30b-10 по 30b-80 и матрицы, показанные в таблицах 3-90 и таблице 3- 91, где 5≤m≤46, m представляет собой целое число, 27≤n≤68, n представляет собой целое число, может быть сохранена матрица, включающая в себя строки от 0 до строки (m-1) и от столбца 0 до столбца (n-1) и/или параметры, относящиеся к матрице, включая строки от 0 до строки (m-1) и от столбца 0 до столбца (n-1), сохраняются. Подробное описание понятно со ссылкой на параметры, показанные в таблицах с 3-10 по 3-80, таблице 3-90 и таблице 3-91, и описаниями в предшествующей части.

В возможной реализации каждое значение смещения больше или равно 0 и обозначено, по меньшей мере, одной позицией s «индекса столбца ненулевого элемента» в любой из таблиц с 3-10 по таблицу 3-80, таблица 3- 90, и таблица 3-91 может быть увеличена или уменьшена смещением Offset_s.

В возможной реализации одно или более преобразованных значений смещения, описанных в предшествующем варианте осуществления, могут быть сохранены в «значении сдвига ненулевого элемента» в любой из таблиц с 3-10 по таблицу 3-80, таблицу 3-90 и таблица 3-91, например, одно или более значений смещения, показанных на фиг. 9.

В другом исполнении базовый граф LDPC матрицы и значения смещения LDPC матрицы могут храниться отдельно. Информация о значениях смещения LDPC матрицы может храниться с использованием индексов строк и значений смещений ненулевых элементов в таблицах с 3-10 по 3-91. Базовый граф LDPC может быть сохранен множеством способов, например, может быть сохранен в виде матрицы базового графа 30a, показанного на фиг. 3a, или могут быть сохранены на основе индексов строк и позиций ненулевых элементов в таблицах с 3-10 по 3-91, или могут быть сохранены таким образом, что 1 и 0 в каждой строке или каждом столбце в базовый граф может рассматриваться как двоичные цифры, и базовый граф хранят в форме десятичных чисел или шестнадцатеричных чисел для экономии объема хранения. Базовый граф 30a используют в качестве примера. Позиции ненулевых элементов в первых 26 столбцах или первых 27 столбцах могут храниться в четырех шестнадцатеричных числах в каждой строке. Например, если первые 26 столбцов в строке 0 являются 11110110 01111101 10111111 00, позиции ненулевых элементов в строке 0 могут быть обозначены как 0xF6, 0x7D, 0xBF и 0x00. Чтобы быть точным, каждые восемь столбцов образуют один шестнадцатеричный номер. 0 может быть добавлен в последние два или три столбца для получения восьми цифр, так что получается соответствующий шестнадцатеричный номер. То же самое верно для другой строки, и подробности здесь не описываются снова. Следует отметить, что здесь приведены только примеры, и примеры не являются ограничением.

Фиг. 1 используют в качестве примера. После того, как определяют базовую матрицу H_B, биты четности, соответствующие столбцу 22 - столбцу 25, могут быть сначала получены с использованием входной последовательности и строки 0 - строки 3 и столбца 0 - столбца 25 в базовой матрице, другими словами, Hcore-dual, затем биты четности, соответствующие столбцу 26, другими словами, столбцу веса 1, могут быть получены на основании входной последовательности и битов четности, соответствующих Hcore-dual, и затем кодирование может быть выполнено на основании входной последовательности, четности биты, соответствующие столбцам 22 - 26 и подматрице D, для получения битов четности, соответствующих подматрице E. Таким образом, кодирование завершено. Что касается процесса кодирования LDPC кода, обратитесь к описаниям в вышеприведенных реализациях, и подробности здесь не описываются снова.

В возможной реализации LDPC матрица H может быть поднята относительно коэффициента поднятия на основании коэффициента Z поднятия перед кодированием, другими словами, каждое значение смещения заменяют соответствующей матрицей круговой перестановки на основании каждого значения смещения.

В другой возможной реализации значение смещения, соответствующее ненулевому элементу, получают на основании позиции ненулевого элемента, соответствующего битам, которые должны быть закодированы во время кодирования, и ненулевой элемент заменяют соответствующей круговой матрицей перестановок и выполняется обработка.

В другой возможной реализации LDPC матрица H не поднимается напрямую во время использования, и биты во входной последовательности обрабатываются на основании отношения соединения, которое находится между строками и столбцами эквивалентной матрицы, и которое вычисляется на основании значений смещения.

В другой возможной реализации кодирование может выполняться с использованием QSN способа. Для каждого ненулевого элемента, который должен быть обработан, на основании значения смещения ненулевого элемента выполняется операция смещения в битовом сегменте, который должен быть закодирован, соответствующем ненулевому элементу; и затем выполняют операцию кодирования на всех битовых сегментах, на которых выполняют операцию смещения.

В другой возможной реализации порождающая матрица G LDPC матрицы Н также может быть сохранена, и входная последовательность c и выходная последовательность d удовлетворяют формуле (2):

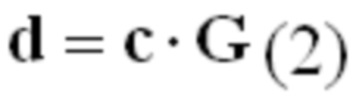
Если перестановка строк/столбцов выполняется на LDPC матрице H для получения H', где правая сторона H' является единичной матрицей I и левая сторона матрицы равна P, H '= [PI], и порождающая матрица G удовлетворяет следующей формуле (3):

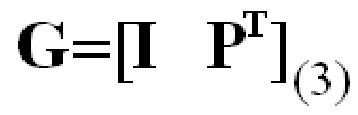
Следует отметить, что вышеприведенное описание является примером, и настоящее изобретение этим не ограничивается.

Возможно, в системе связи LDPC код может быть получен после того, как выполнено кодирование с использованием вышеизложенного способа. После получения LDPC кода устройство связи может дополнительно выполнить одну или несколько из следующих операций: выполнение согласования скорости для LDPC кода; выполнение, на основании схемы перемежения, перемежения на LDPC коде с согласованной скоростью; модулирование, на основании схемы модуляции, чередованного LDPC кода для получения битовой последовательности X; и отправку битовой последовательности X.

Декодирование является обратным процессом кодирования, и базовая матрица, используемая во время декодирования и базовая матрица во время кодирования, имеют одинаковую характеристику. Изложение процесса кодирования LDPC кода понятно из описаний в вышеизложенных реализациях, и подробности не описываются здесь снова. В реализации перед декодированием устройство связи может дополнительно выполнять одну или несколько из следующих операций: прием сигнала, полученного после кодирования LDPC кода; и выполнение демодуляции, обратного перемежения и десогласования скорости на сигнале для получения последовательности мягких значений LDPC кода; и декодирование последовательности мягких значений LDPC кода.

Сохранение в настоящем изобретении может быть сохранением в одной или нескольких памяти. Одно или несколько памяти могут быть расположены отдельно или могут быть интегрированы в кодер, декодер, процессор, микросхему, устройство связи или терминал. Некоторые из одного или нескольких памяти могут быть расположены отдельно, а другие могут быть интегрированы в декодер, процессор, микросхему, устройство связи или терминал. Типом памяти может быть любая форма носителя данных, и настоящее изобретение этим не ограничено.

В соответствии со схемами процессов обработки данных на фиг. 5 и фиг. 6, вариант осуществления настоящего изобретения дополнительно предоставляет соответствующее устройство связи. Устройство связи включает в себя модули, выполненные с возможностью выполнять каждую часть на фиг. 5 или фиг. 6. Модуль может быть программным или аппаратным, или может быть комбинацией программного и аппаратного обеспечения. Например, модули могут включать в себя память, электронное устройство, электронный компонент, логическую схему или тому подобное, или любую их комбинацию. Фиг. 7 является структурной схемой устройства 700 связи. Устройство 700 может быть выполнено с возможностью реализации способа, описанного в вышеупомянутом варианте осуществления способа. Подробное описание понятно из описания в вышеупомянутом варианте осуществления способа. Устройство 700 связи может быть микросхемой, базовой станцией, терминалом или другим сетевым устройством.

Устройство 700 связи включает в себя один или несколько процессоров 701. Процессор 701 может быть процессором общего назначения, процессором специального назначения или тому подобным. Например, процессор 701 может быть процессором основной полосы частот или центральным процессором. Процессор основной полосы частот может быть выполнен с возможностью обрабатывать протокол связи и данных связи. Центральный процессор может быть выполнен с возможностью управлять устройством связи (таким как базовая станция, терминал или микросхема), выполнять программу программного обеспечения и обрабатывать данные программы.

В возможной реализации один или несколько модулей на фиг. 5 и фиг. 6, может быть реализован с использованием одного или нескольких процессоров или может быть реализован с использованием одного или нескольких процессоров и одного или нескольких памяти.

В возможной реализации устройство 700 связи включает в себя один или несколько процессоров 701. Один или несколько процессоров 701 могут реализовывать функции кодирования/декодирования. Например, устройство связи может быть кодером или декодером. В другой возможной реализации процессор 701 может реализовывать другие функции в дополнение к функциям кодирования/декодирования.

Устройство 700 связи кодирует/декодирует входную последовательность на основании LDPC матрицы. Базовая матрица LDPC матрицы может быть любой базовой матрицей в вышеприведенных примерах или базовой матрицей, полученной путем выполнения перестановки строк, или перестановки столбцов, или перестановки строк и перестановок столбцов на любой базовой матрице в вышеприведенных примерах, или базовой матрицей. полученной путем выполнения укорочения или выкалывания на любой базовой матрице в предшествующих примерах или матрицей, полученной путем поднятия любой базовой матрицы в предшествующих примерах. Описание процесса обработки кодирования/декодирования может быть выполнено со ссылкой на описания соответствующих частей на фиг. 5 и фиг. 6, и подробности не описываются здесь снова.

Возможно, в реализации процессор 701 может включать в себя инструкцию 703 (иногда также называемую кодом или программой). Инструкция может выполняться на процессоре, так что устройство 700 связи выполняет способ, описанный в вышеупомянутом варианте осуществления способа. В другом возможном варианте устройство 700 связи также может включать в себя схему, и схема может реализовывать функции кодирования/декодирования в вышеизложенном варианте осуществления.

Возможно, в реализации устройство 700 связи может включать в себя одно или несколько памяти 702. Память хранит инструкцию 704, и инструкция может выполняться на процессоре, так что устройство 700 связи выполняет способ, описанный в вышеизложенном способе воплощения.

Возможно, память может дополнительно хранить данные. Возможно, процессор может дополнительно хранить инструкцию и/или данные. Процессор и память могут быть расположены отдельно или могут быть объединены вместе.

Возможно, «хранилище» в вышеприведенном варианте осуществления может хранить данные в памяти 702 или может хранить данные в другой периферийной памяти или устройстве хранения.

Например, одно или несколько памяти 702 могут хранить один или несколько параметров, относящихся к LDPC матрице в вышеприведенном примере, например, один или несколько параметров, относящихся к базовой матрицей, таких как значения смещения, базовый граф, поднятая матрица, основанная на базовом графе, строки в базовой матрице, коэффициент поднятия, базовая матрица или поднятая матрица, основанная на базовой матрице. Подробное описание понятно из соответствующих описаний на фиг. 5.

Возможно, устройство 700 связи может дополнительно включать в себя приемопередатчик 705 и антенну 706. Процессор 701 может называться блоком обработки и управлять устройством связи (терминалом или базовой станцией). Приемопередатчик 705 может упоминаться как приемопередающий блок или схема приемопередатчика и выполнены с возможностью реализации функции приемопередачи устройства связи с использованием антенны 706.

Возможно, устройство 700 связи может дополнительно включать в себя компонент, выполненный с возможностью генерировать CRC транспортного блока, компонент, выполненный с возможностью выполнять сегментацию кодового блока и проверки CRC, перемежитель, выполненный с возможностью выполнять перемежение, компонент, выполненный с возможностью выполнять согласование скорости, модулятор, выполненный с возможностью выполнять обработку модуляции или тому подобное. Функции этих компонентов могут быть реализованы одним или несколькими процессорами 701.

[0259] Возможно, устройство 700 связи может дополнительно включать в себя демодулятор, выполненный с возможностью выполнять демодуляцию, деперемежитель, выполненный с возможностью выполнять обратное перемежение, компонент, выполненный с возможностью выполнять десогласование скорости, компонент, выполненный с возможностью выполнять конкатенацию кодовых блоков и проверку CRC или т.п. Функции этих компонентов могут быть реализованы одним или несколькими процессорами 701.

Фиг. 8 является схемой системы 800 связи. Система 800 связи включает в себя устройство 80 связи и устройство 81 связи. Устройство 80 связи и устройство 81 связи принимают информационные данные друг от друга и отправляют информационные данные друг другу. Устройство 80 связи и устройство 81 связи могут быть устройством 700 связи, или каждое из устройств 80 связи и устройства 81 связи включает в себя устройство 700 связи и может принимать и/или отправлять информационные данные. Например, устройство 80 связи может быть терминалом и, соответственно, устройство 81 связи может быть базовой станцией. В другом примере, устройство 80 связи является базовой станцией, и, соответственно, устройство 81 связи может быть терминалом.

Специалист в данной области техники может также понимать, что различные иллюстративные логические блоки (иллюстративный логический блок) и этапы (этап), которые перечислены в вариантах осуществления настоящего изобретения, могут быть реализованы с использованием электронного аппаратного обеспечения, компьютерного программного обеспечения или их комбинация. Реализация функций с использованием аппаратного или программного обеспечения зависит от конкретных приложений и требований к проектированию всей системы. Специалист в данной области техники может использовать различные способы для реализации описанных функций для каждого конкретного приложения, но не следует считать, что реализация выходит за рамки вариантов осуществления настоящего изобретения.

Технологии, описанные в настоящем изобретении, могут быть реализованы различными способами. Например, эти технологии могут быть реализованы с использованием аппаратного обеспечения, программного обеспечения или их комбинации. Для реализации с помощью аппаратного обеспечения блок обработки, выполненный с возможностью выполнять эти технологии в устройстве связи (например, базовой станции, терминале, сетевом объекте или микросхеме), может быть реализован в одном или нескольких процессорах общего назначения, цифровом сигнальном процессоре (DSP), устройстве цифровой обработки сигналов (DSPD), специализированной интегральной схемы (ASIC), программируемом логическом устройстве (PLD), программируемом пользователем логической матрицы (FPGA) или другие программируемые логические устройства, дискретные логические элементы или транзисторная логика, дискретное оборудование компоненты или любая их комбинация. Процессор общего назначения может быть микропроцессором. Возможно, универсальный процессор может быть любым обычным процессором, контроллером, микроконтроллером или машиной состояния. Процессор может быть реализован с помощью комбинации вычислительных устройств, таких как процессор цифровых сигналов и микропроцессор, множества микропроцессоров, одного или нескольких микропроцессоров с ядром процессора цифровых сигналов или любой другой подобной конфигурации.

Этапы способов или алгоритмов, описанных в вариантах осуществления настоящего изобретения, могут быть непосредственно встроены в аппаратные средства, команду, выполняемую процессором, или их комбинацию. Память может быть памятью RAM, флэш-памятью, памятью ROM, памятью EPROM, памятью EEPROM, регистром, жестким диском, съемным магнитным диском, CD-ROM или носителем данных любой другой формы в искусство. Например, память может быть подключена к процессору, так что процессор может считывать информацию из памяти и записывать информацию в память. Возможно, память может быть интегрирована в процессор. Процессор и память могут быть установлены в ASIC, и ASIC может быть расположена в UE. Возможно, процессор и память могут быть расположены в разных компонентах UE.

На основании описаний вышеупомянутых реализаций специалист в данной области техники может четко понимать, что технологии могут быть реализованы посредством аппаратного обеспечения, встроенного программного обеспечения или их комбинации. Для реализации программным обеспечением реализация может быть полностью или частично выполнена в форме компьютерного программного продукта. Компьютерный программный продукт включает в себя одну или несколько компьютерных инструкций. Когда компьютерные инструкции загружают и выполняют на компьютере, полностью или частично генерируют процедуру или функцию согласно вариантам осуществления настоящего изобретения. При реализации настоящего изобретения с помощью программного обеспечения, вышеупомянутые функции могут быть сохранены на машиночитаемом носителе или переданы в виде одной или нескольких инструкций или кода на машиночитаемом носителе. Компьютер может быть компьютером общего назначения, выделенным компьютером, компьютерной сетью или другим программируемым устройством. Компьютерная инструкция может храниться на машиночитаемом носителе данных или может передаваться с одного машиночитаемого носителя на другой. Машиночитаемый носитель включает в себя компьютерный носитель данных и среду связи. Среда связи включает в себя любую среду, которая обеспечивает передачу компьютерной программы из одного места в другое. Носитель данных может быть любым доступным носителем, доступным для компьютера. Ниже приведен пример, но не накладывает ограничение: машиночитаемый носитель может включать в себя RAM, ROM, EEPROM, CD-ROM или другое хранилище на оптических дисках, дисковый носитель или другое магнитное запоминающее устройство, или любой другой носитель, который может нести или хранить ожидаемый программный код в форме инструкции или структуры данных и может быть доступен с помощью компьютера. Кроме того, любое соединение может быть соответствующим образом определено как машиночитаемый носитель. Например, если программное обеспечение передается с веб-сайта, сервера или другого удаленного источника с использованием коаксиального кабеля, оптоволокна/кабеля, витой пары, цифровой абонентской линии (DSL) или беспроводных технологий, таких как инфракрасное излучение, радио и сигнал микроволнового диапазона, коаксиальный кабель, оптоволокно/кабель, витая пара, DSL или беспроводные технологии, такие как инфракрасное излучение, радио и сигнал микроволнового диапазона, содержаться в среде, к которой они принадлежат. Например, диск (Disk) и диск (disk), используемые в настоящем изобретении, включают в себя компакт-диск (CD), лазерный диск, оптический диск, цифровой универсальный диск (DVD), дискету и диск Blu-ray., на котором обычно копируют данные магнитным способом, и диск оптически копирует данные лазерным способом. Вышеуказанная комбинация также должна быть включена в объем защиты машиночитаемого носителя.

Следует отметить, что в данном изобретении «/» обозначает «и/или». Например, «кодирование/декодирование (кодирование и/или декодирование)» указывает кодирование или декодирование, или кодирование и декодирование.

В заключение, необходимо отметить, что приведенное выше описание, является просто предпочтительными вариантами осуществления технических решений настоящего изобретения, но не предназначено для ограничения объема защиты настоящего изобретения. Любая модификация, эквивалентная замена или улучшение, выполненные без отклонения от сущности и принципа настоящего изобретения, должны находиться в рамках объема защиты настоящего изобретения.

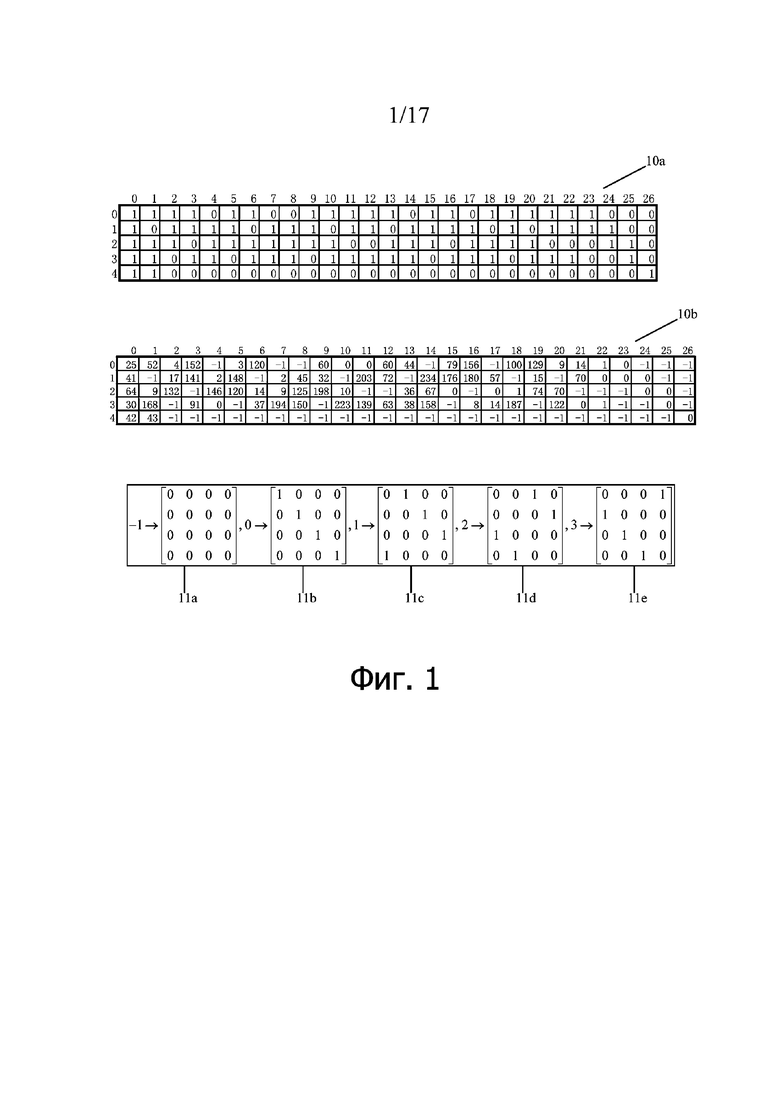
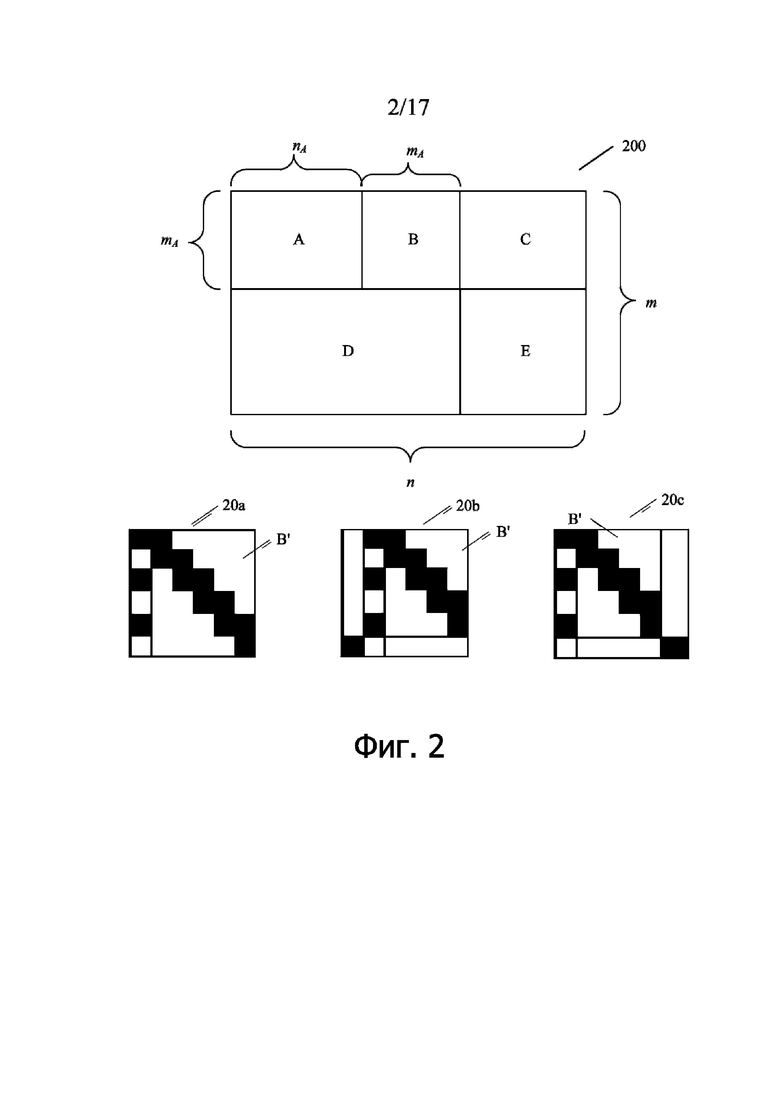
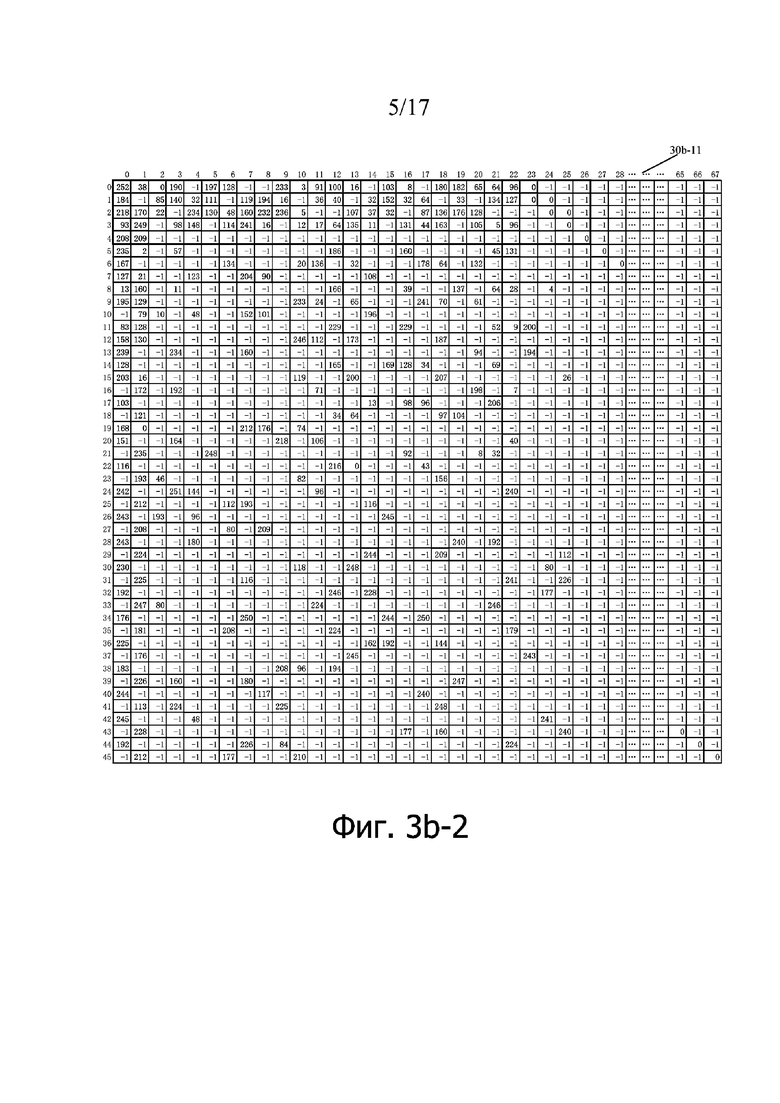
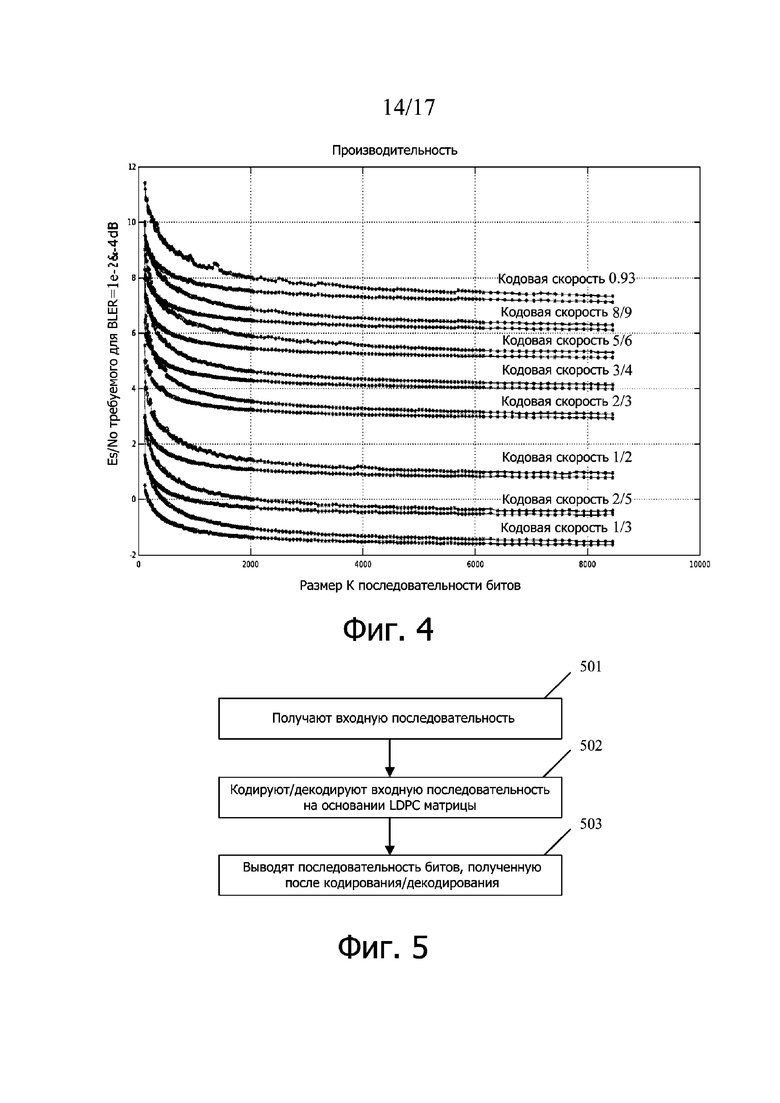
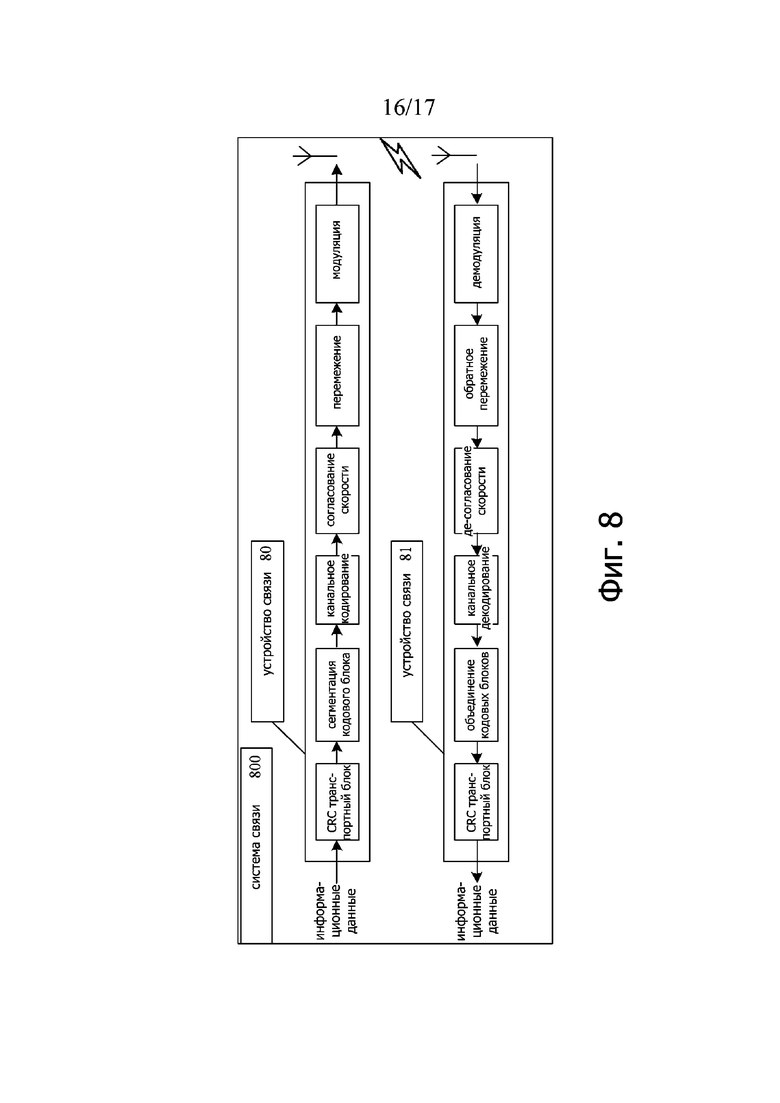
Изобретение относится к области связи. Технический результат заключается в повышении надежности передачи канала и эффективного использования мощности в системе связи LDPC (low density parity check, LDPC). Такой результат достигается тем, что способ включает в себя кодирование входной битовой последовательности с использованием LDPC матрицы кода с низкой плотностью проверок на четность, где LDPC матрицу получают на основании коэффициента Z поднятия и базовой матрицы, базовая матрица включает в себя строки от 0 до строки 4 и столбец 0 в столбец 26 в одной из матриц, или базовая матрица включает в себя строки от 0 до строки 4 и некоторые из столбцов от 0 до столбца 26 в одной из матриц. 8 н. и 27 з.п. ф-лы, 6 табл., 19 ил.

1. Способ кодирования, содержащий:

кодирование входной последовательности c на основании LDPC матрицы H кода с низкой плотностью проверок на четность для получения кодированной последовательности, в котором входная последовательность содержит К битов, в котором

базовая матрица LDPC матрицы H содержит m строк и n столбцов и m и n являются целыми числами и 5≤m≤46 и n является целым числом 27≤ n≤68, и базовая матрица содержит множество ненулевых элементов (i, j), в котором i является индексом строки, j является индексом столбца, 0≤i<m, 0≤j<n, каждый ненулевой элемент (i, j) соответствует матрицей круговой перестановки размера Z × Z, и матрица круговой перестановки равна матрице, полученной путем кругового смещения единичной матрицы размера Z × Z вправо P_i,j раз, в котором P_i,j = mod (V_{i j}, Z), Z является коэффициентом поднятия, и каждый из ненулевых элементов (i, j) и соответствующий V_i,j имеет следующий вид:

i = 0, j = 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 и V_i,j равен соответственно 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0;

i = 1, j = 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 и V_i,j равен соответственно 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0;

i = 2, j = 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 и V_i,j равен соответственно 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0;

i = 3, j = 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 и V_i,j равен соответственно 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; и

i = 4, j = 0, 1, 26, V_i,j равен и составляет соответственно 246, 235, 0.

2. Способ по п.1, в котором

входная последовательность является c = {c₀, c₁, c₂,…c_K-1}, кодированная

последовательность является d = {d₀, d₁, d₂,…, d_N-1}, в котором K и N оба являются положительными целыми числами, и N=66∙Z.

3. Способ по п.2, в котором кодированная последовательность d содержит биты K₀ из

входной последовательности c и N – K₀ биты четности в последовательности w = {w₀ , w₁, w₂,…, w_N-K0-1} четности, в котором K₀ представляет собой целое число больше 0 и меньше или равно K,

в котором последовательность w четности и входная последовательность c удовлетворяют:

,

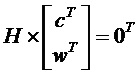
в котором c^T = [c0, c1, c2,…, c_K-1]^T, w^T = [w0, w1, w2,…, w_N-K0-1]^Т , 0^T является вектором столбца и значения всех элементов 0^T равны 0.

4. Способ по п.3, в котором K₀= K- 2∙Z.

5. Способ по п.1, в котором базовая матрица Н дополнительно содержит следующие

ненулевые элементы (i, j), и соответствующие значения V_i,j ненулевых элементов (i, j) имеют следующий вид:

i = 5, j = 0, 1, 3, 12, 16, 21, 22, 27 и V_i,j составляет соответственно 261, 181, 72, 283,

254, 79, 144, 0;

i = 6, j = 0, 6, 10, 11, 13, 17, 18, 20, 28 и V_i,j составляет соответственно 80, 144, 169, 90, 59, 177, 151, 108, 0;

i = 7, j = 0, 1, 4, 7, 8, 14, 29 и V_i,j составляет соответственно 169, 189, 154, 184, 104,

164, 0;

i = 8, j = 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 и V_i,j составляет соответственно 54, 0, 252,

41, 98, 46, 15, 230, 54, 0;

i = 9, j = 0, 1, 10, 11, 13, 17, 18, 20, 31 и V_i,j составляет соответственно 162, 159, 93,

134, 45, 132, 76, 209, 0;

i = 10, j = 1, 2, 4, 7, 8, 14, 32 и V_i,j составляет соответственно 178, 1, 28, 267, 234,

201, 0;

i = 11, j = 0, 1, 12, 16, 21, 22, 23, 33 и V_i,j составляет соответственно 55, 23, 274, 181,

273, 39, 26, 0;

i = 12, j = 0, 1, 10, 11, 13, 18, 34 и V_i,j составляет соответственно 225, 162, 244, 151,

238, 243, 0;

i = 13, j = 0, 3, 7, 20, 23, 35 и V_i,j составляет соответственно 231, 0, 216, 47, 36, 0;

i = 14, j = 0, 12, 15, 16, 17, 21, 36 и V_i,j составляет 0, 186, 253, 16, 0, 79, 0;

i = 15, j = 0, 1, 10, 13, 18, 25, 37 и V_i,j составляет соответственно 170, 0, 183, 108, 68,

64, 0;

i = 16, j = 1, 3, 11, 20, 22, 38 и V_i,j составляет соответственно 270, 13, 99, 54, 0, 0;

i = 17, j = 0, 14, 16, 17, 21, 39 и V_i,j составляет соответственно 153, 137, 0, 0, 162, 0;

i = 18, j = 1, 12, 13, 18, 19, 40 и V_i,j составляет соответственно 161, 151, 0, 241, 144,

0;

i = 19, j = 0, 1, 7, 8, 10, 41 и V_i,j составляет 0, 0, 118, 144, 0, 0;

i = 20, j = 0, 3, 9, 11, 22, 42 и V_i,j составляет соответственно 265, 81, 90, 144, 228, 0;

i = 21, j = 1, 5, 16, 20, 21, 43 и V_i,j составляет соответственно 64, 46, 266, 9, 18, 0;

i = 22, j = 0, 12, 13, 17, 44 и V_i,j составляет соответственно 72, 189, 72, 257, 0;

i = 23, j = 1, 2, 10, 18, 45 и V_i,j составляет соответственно 180, 0, 0, 165, 0;

i = 24, j = 0, 3, 4, 11, 22, 46 и V_i,j составляет соответственно 236, 199, 0, 266, 0, 0;

i = 25, j = 1, 6, 7, 14, 47 и V_i,j составляет соответственно 205, 0, 0, 183, 0;

i = 26, j = 0, 2, 4, 15, 48 и V_i,j составляет 0, 0, 0, 277, 0;

i = 27, j = 1, 6, 8, 49 и V_i,j составляет соответственно 45, 36, 72, 0;

i = 28, j = 0, 4, 19, 21, 50 и V_i,j составляет соответственно 275, 0, 155, 62, 0;

i = 29, j = 1, 14, 18, 25, 51 и V_i,j составляет 0, 180, 0, 42, 0;

i = 30, j = 0, 10, 13, 24, 52 и V_i,j составляет 0, 90, 252, 173, 0;

i = 31, j = 1, 7, 22, 25, 53 и V_i,j составляет соответственно 144, 144, 166, 19, 0;

i = 32, j = 0, 12, 14, 24, 54 и V_i,j составляет 0, 211, 36, 162, 0;

i = 33, j = 1, 2, 11, 21, 55 и V_i,j составляет 0, 0, 76, 18, 0;

i = 34, j = 0, 7, 15, 17, 56 и V_i,j составляет соответственно 197, 0, 108, 0, 0;

i = 35, j = 1, 6, 12, 22, 57 и V_i,j составляет соответственно 199, 278, 0, 205, 0;

i = 36, j = 0, 14, 15, 18, 58 и V_i,j составляет соответственно 216, 16, 0, 0, 0;

i = 37, j = 1, 13, 23, 59 и V_i,j составляет соответственно 72, 144, 0, 0;

i = 38, j = 0, 9, 10, 12, 60 и V_i,j составляет соответственно 190, 0, 0, 0, 0;

i = 39, j = 1, 3, 7, 19, 61 и V_i,j составляет соответственно 153, 0, 165, 117, 0;

i = 40, j = 0, 8, 17, 62 и V_i,j составляет соответственно 216, 144, 2, 0;

i = 41, j = 1, 3, 9, 18, 63 и V_i,j составляет 0, 0, 0, 183, 0;

i = 42, j = 0, 4, 24, 64 и V_i,j составляет соответственно 27, 0, 35, 0;

i = 43, j = 1, 16, 18, 25, 65 и V_i,j составляет соответственно 52, 243, 0, 270, 0;

i = 44, j = 0, 7, 9, 22, 66 и V_i,j составляет соответственно 18, 0, 0, 57, 0; и

i = 45, j = 1, 6, 10, 67 и V_i,j составляет соответственно 168, 0, 144, 0.

6. Способ по п.1, в котором Z является одним из 9, 18, 36, 72, 144 и 288.

7. Способ по п.1, в котором в базовой матрице элементы, которые не являются

ненулевыми элементами, являются нулевыми элементами;

в котором каждый нулевой элемент соответствует полностью нулевой матрице размером Z * Z в LDPC матрице Н,

8. Способ по п.1, в котором кодирование входной последовательности c на основании

LDPC матрицы H содержит:

кодирование входной последовательности c на основании преобразованной матрицы;

в котором базовую матрицу преобразованной матрицы получают путем выполнения преобразования строки, или преобразования столбца, или преобразования строки и преобразования столбца в базовой матрице LDPC матрицы H.

9. Способ декодирования, содержащий:

декодирование входной последовательности на основании LDPC матрицы H кода с низкой плотностью проверок на четность для получения информационной последовательности, в котором

базовая матрица H содержит m строк и n столбцов и m и n являются целыми числами и 5≤m≤46 и n является целым числом 27≤ n≤68, и базовая матрица содержит множество ненулевых элементов (i, j), в котором i является индексом строки, j является индексом столбца, 0≤i<m, 0≤j<n, каждый ненулевой элемент (i, j) соответствует матрицей круговой перестановки размера Z × Z, и матрица круговой перестановки равна матрице, полученной путем кругового смещения единичной матрицы размера Z × Z вправо P_i,j раз, в котором P_i,j = mod (V_{i j}, Z), Z является коэффициентом поднятия, и каждый из ненулевых элементов (i, j) и соответствующий V_i,j имеет следующий вид:

i = 0, j = 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 и V_i,j, равно соответственно 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0;

i = 1, j = 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 и V_i,j, равно соответственно 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0;

i = 2, j = 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 и V_i,j, равно соответственно 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0;

i = 3, j = 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 и V_i,j, равно соответственно 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; и

i = 4, j = 0, 1, 26 и V_i,j, равно соответственно 246, 235, 0.

10. Способ по п.9, в котором базовая матрица Н дополнительно содержит следующие

ненулевые элементы (i, j), и соответствующие значения V_i,j, ненулевых элементов (i, j) имеют следующий вид:

i = 5, j = 0, 1, 3, 12, 16, 21, 22, 27 и V_i,j, равно соответственно 261, 181, 72, 283, 254, 79, 144, 0;

i = 6, j = 0, 6, 10, 11, 13, 17, 18, 20, 28 и V_i,j, равно соответственно 80, 144, 169, 90, 59, 177, 151, 108, 0;

i = 7, j = 0, 1, 4, 7, 8, 14, 29 и V_i,j, равно соответственно 169, 189, 154, 184, 104, 164, 0;

i = 8, j = 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 и V_i,j, равно соответственно 54, 0, 252, 41, 98, 46, 15, 230, 54, 0;

i = 9, j = 0, 1, 10, 11, 13, 17, 18, 20, 31 и V_i,j, равно соответственно 162, 159, 93, 134, 45, 132, 76, 209, 0;

i = 10, j = 1, 2, 4, 7, 8, 14, 32 и V_i,j, равно соответственно 178, 1, 28, 267, 234, 201, 0;

i = 11, j = 0, 1, 12, 16, 21, 22, 23, 33 и V_i,j, равно соответственно 55, 23, 274, 181, 273, 39, 26, 0;

i = 12, j = 0, 1, 10, 11, 13, 18, 34 и V_i,j, равно соответственно 225, 162, 244, 151, 238, 243, 0;

i = 13, j = 0, 3, 7, 20, 23, 35 и V_i,j, равно соответственно 231, 0, 216, 47, 36, 0;

i = 14, j = 0, 12, 15, 16, 17, 21, 36 и V_i,j, равно 0, 186, 253, 16, 0, 79, 0;

i = 15, j = 0, 1, 10, 13, 18, 25, 37 и V_i,j, равно соответственно 170, 0, 183, 108, 68, 64, 0;

i = 16, j = 1, 3, 11, 20, 22, 38 и V_i,j, равно соответственно 270, 13, 99, 54, 0, 0;

i = 17, j = 0, 14, 16, 17, 21, 39 и V_i,j, равно соответственно 153, 137, 0, 0, 162, 0;

i = 18, j = 1, 12, 13, 18, 19, 40 и V_i,j, равно соответственно 161, 151, 0, 241, 144, 0;

i = 19, j = 0, 1, 7, 8, 10, 41 и V_i,j, равно 0, 0, 118, 144, 0, 0;

i = 20, j = 0, 3, 9, 11, 22, 42 и V_i,j, равно соответственно 265, 81, 90, 144, 228, 0;

i = 21, j = 1, 5, 16, 20, 21, 43 и V_i,j, равно соответственно 64, 46, 266, 9, 18, 0;

i = 22, j = 0, 12, 13, 17, 44 и V_i,j, равно соответственно 72, 189, 72, 257, 0;

i = 23, j = 1, 2, 10, 18, 45 и V_i,j, равно соответственно 180, 0, 0, 165, 0;

i = 24, j = 0, 3, 4, 11, 22, 46 и V_i,j, равно соответственно 236, 199, 0, 266, 0, 0;

i = 25, j = 1, 6, 7, 14, 47 и V_i,j, равно соответственно 205, 0, 0, 183, 0;

i = 26, j = 0, 2, 4, 15, 48 и V_i,j, равно 0, 0, 0, 277, 0;

i = 27, j = 1, 6, 8, 49 и V_i,j, равно соответственно 45, 36, 72, 0;

i = 28, j = 0, 4, 19, 21, 50 и V_i,j, равно соответственно 275, 0, 155, 62, 0;

i = 29, j = 1, 14, 18, 25, 51 и V_i,j, равно 0, 180, 0, 42, 0;

i = 30, j = 0, 10, 13, 24, 52 и V_i,j, равно 0, 90, 252, 173, 0;

i = 31, j = 1, 7, 22, 25, 53 и V_i,j, равно соответственно 144, 144, 166, 19, 0;

i = 32, j = 0, 12, 14, 24, 54 и V_i,j, равно 0, 211, 36, 162, 0;

i = 33, j = 1, 2, 11, 21, 55 и V_i,j, равно 0, 0, 76, 18, 0;

i = 34, j = 0, 7, 15, 17, 56 и V_i,j, равно соответственно 197, 0, 108, 0, 0;

i = 35, j = 1, 6, 12, 22, 57 и V_i,j, равно соответственно 199, 278, 0, 205, 0;

i = 36, j = 0, 14, 15, 18, 58 и V_i,j, равно соответственно 216, 16, 0, 0, 0;

i = 37, j = 1, 13, 23, 59 и V_i,j, равно соответственно 72, 144, 0, 0;

i = 38, j = 0, 9, 10, 12, 60 и V_i,j, равно соответственно 190, 0, 0, 0, 0;

i = 39, j = 1, 3, 7, 19, 61 и V_i,j, равно соответственно 153, 0, 165, 117, 0;

i = 40, j = 0, 8, 17, 62 и V_i,j, равно соответственно 216, 144, 2, 0;

i = 41, j = 1, 3, 9, 18, 63 и V_i,j, равно 0, 0, 0, 183, 0;

i = 42, j = 0, 4, 24, 64 и V_i,j, равно соответственно 27, 0, 35, 0;

i = 43, j = 1, 16, 18, 25, 65 и V_i,j, равно соответственно 52, 243, 0, 270, 0;

i = 44, j = 0, 7, 9, 22, 66 и V_i,j, равно соответственно 18, 0, 0, 57, 0; а также

i = 45, j = 1, 6, 10, 67 и V_i,j, равно соответственно 168, 0, 144, 0.

11. Способ по п.9, в котором Z является одним из 9, 18, 36, 72, 144 и 288.

12. Способ по п.9, в котором в базовой матрице элементы, которые не являются

ненулевыми элементами, являются нулевыми элементами;

в котором каждый нулевой элемент соответствует полностью нулевой матрице размером Z * Z в LDPC матрице Н.

13. Способ по п.9, в котором декодирование входной последовательности на основе LDPC матрицы H содержит:

декодирование входной последовательности на основании преобразованной матрицы;

в котором базовую матрицу преобразованной матрицы получают путем выполнения преобразования строки, или преобразования столбца, или преобразования строки и преобразования столбца в базовой матрице LDPC матрицы H.

14. Устройство связи, содержащее кодер и блок определения, в котором

блок определения выполнен с возможностью определять коэффициент Z поднятия; и

кодер выполнен с возможностью кодировать входную последовательность на основании LDPC матрицы H кода с низкой плотностью проверок на четность для получения LDPC кодового слова, в котором базовая матрица H содержит m строк и n столбцов и m и n являются целыми числами и 5≤m≤46 и n является целым числом 27≤ n≤68, и базовая матрица содержит множество ненулевых элементов (i, j), в котором i является индексом строки, j является индексом столбца, 0≤i<m, 0≤j<n, каждый ненулевой элемент (i, j) соответствует матрицей круговой перестановки размера Z × Z, и матрица круговой перестановки равна матрице, полученной путем кругового смещения единичной матрицы размера Z × Z вправо P_i,j раз, в котором P_i,j = mod (V_{i j}, Z), Z является коэффициентом поднятия, и каждый из ненулевых элементов (i, j) и соответствующий V_i,j имеет следующий вид:

i = 0, j = 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 и V_i,j равно соответственно 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0;

i = 1, j = 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 и V_i,j равно соответственно 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0, 0;

i = 2, j = 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 и V_i,j равно соответственно 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0;

i = 3, j = 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 и V_i,j равно соответственно 187, 145 , 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; и

i = 4, j = 0, 1, 26 и V_i,j равно соответственно 246, 235, 0.

15. Устройство по п.14, в котором

входная последовательность является c = {c₀, c₁, c₂,…c_K-1}, кодированная

последовательность является d = {d₀, d₁, d₂,…, d_N-1}, в котором K и N оба являются положительными целыми числами, и N=66∙Z.

16. Устройство по п.14, в котором кодированная последовательность d содержит K₀ биты во входной последовательности c и N – K₀ биты четности в последовательности w = {w₀ , w₁, w₂,…, w_N-K0-1} четности, в котором K₀ представляет собой целое число биты четности в последовательности w четности, в котором K₀ представляет собой целое число, и 0 <K₀≤K; и

последовательность w четности и входная последовательность c удовлетворяют: ,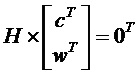

в котором c^T= [c₀, c₁, c₂,…, _cK-1]^T , w^T = [w₀ , w₁, w₂,…, w_N-K0-1]^T , 0^T является вектором столбца, и значения всех элементов 0^T равны 0.

17. Устройство по п.16, в котором K₀= K- 2∙Z.

18. Устройство по п.14, в котором базовая матрица Н дополнительно содержит

следующие ненулевые элементы (i, j), и соответствующие значения V_i,j ненулевых элементов (i, j) представляют собой следующее:

i = 5, j = 0, 1, 3, 12, 16, 21, 22, 27 и V_i,j составляет соответственно 261, 181, 72, 283, 254, 79, 144, 0;

i = 6, j = 0, 6, 10, 11, 13, 17, 18, 20, 28 и V_i,j составляет соответственно 80, 144, 169, 90, 59, 177, 151, 108, 0;

i = 7, j = 0, 1, 4, 7, 8, 14, 29 и V_i,j составляет соответственно 169, 189, 154, 184, 104, 164, 0;

i = 8, j = 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 и V_i,j составляет соответственно 54, 0, 252, 41, 98, 46, 15, 230, 54, 0;

i = 9, j = 0, 1, 10, 11, 13, 17, 18, 20, 31 и V_i,j составляет соответственно 162, 159, 93, 134, 45, 132, 76, 209, 0;

i = 10, j = 1, 2, 4, 7, 8, 14, 32 и V_i,j составляет соответственно 178, 1, 28, 267, 234, 201, 0;

i = 11, j = 0, 1, 12, 16, 21, 22, 23, 33 и V_i,j составляет соответственно 55, 23, 274, 181, 273, 39, 26, 0;

i = 12, j = 0, 1, 10, 11, 13, 18, 34 и V_i,j составляет соответственно 225, 162, 244, 151, 238, 243, 0;

i = 13, j = 0, 3, 7, 20, 23, 35 и V_i,j составляет соответственно 231, 0, 216, 47, 36, 0;

i = 14, j = 0, 12, 15, 16, 17, 21, 36 и V_i,j составляет 0, 186, 253, 16, 0, 79, 0;

i = 15, j = 0, 1, 10, 13, 18, 25, 37 и V_i,j составляет соответственно 170, 0, 183, 108, 68, 64, 0;

i = 16, j = 1, 3, 11, 20, 22, 38 и V_i,j составляет соответственно 270, 13, 99, 54, 0, 0;

i = 17, j = 0, 14, 16, 17, 21, 39 и V_i,j составляет соответственно 153, 137, 0, 0, 162, 0;

i = 18, j = 1, 12, 13, 18, 19, 40 и V_i,j составляет соответственно 161, 151, 0, 241, 144, 0;

i = 19, j = 0, 1, 7, 8, 10, 41 и V_i,j составляет 0, 0, 118, 144, 0, 0;

i = 20, j = 0, 3, 9, 11, 22, 42 и V_i,j составляет соответственно 265, 81, 90, 144, 228, 0;

i = 21, j = 1, 5, 16, 20, 21, 43 и V_i,j составляет соответственно 64, 46, 266, 9, 18, 0;

i = 22, j = 0, 12, 13, 17, 44 и V_i,j составляет соответственно 72, 189, 72, 257, 0;

i = 23, j = 1, 2, 10, 18, 45 и V_i,j составляет соответственно 180, 0, 0, 165, 0;

i = 24, j = 0, 3, 4, 11, 22, 46 и V_i,j составляет соответственно 236, 199, 0, 266, 0, 0;

i = 25, j = 1, 6, 7, 14, 47 и V_i,j составляет соответственно 205, 0, 0, 183, 0;

i = 26, j = 0, 2, 4, 15, 48 и V_i,j составляет 0, 0, 0, 277, 0;

i = 27, j = 1, 6, 8, 49 и V_i,j составляет соответственно 45, 36, 72, 0;

i = 28, j = 0, 4, 19, 21, 50 и V_i,j составляет соответственно 275, 0, 155, 62, 0;

i = 29, j = 1, 14, 18, 25, 51 и V_i,j составляет 0, 180, 0, 42, 0;

i = 30, j = 0, 10, 13, 24, 52 и V_i,j составляет 0, 90, 252, 173, 0;

i = 31, j = 1, 7, 22, 25, 53 и V_i,j составляет соответственно 144, 144, 166, 19, 0;

i = 32, j = 0, 12, 14, 24, 54 и V_i,j составляет 0, 211, 36, 162, 0;

i = 33, j = 1, 2, 11, 21, 55 и V_i,j составляет 0, 0, 76, 18, 0;

i = 34, j = 0, 7, 15, 17, 56 и V_i,j составляет соответственно 197, 0, 108, 0, 0;

i = 35, j = 1, 6, 12, 22, 57 и V_i,j составляет соответственно 199, 278, 0, 205, 0;

i = 36, j = 0, 14, 15, 18, 58 и V_i,j составляет соответственно 216, 16, 0, 0, 0;

i = 37, j = 1, 13, 23, 59 и V_i,j составляет соответственно 72, 144, 0, 0;

i = 38, j = 0, 9, 10, 12, 60 и V_i,j составляет соответственно 190, 0, 0, 0, 0;

i = 39, j = 1, 3, 7, 19, 61 и V_i,j составляет соответственно 153, 0, 165, 117, 0;

i = 40, j = 0, 8, 17, 62 и V_i,j составляет соответственно 216, 144, 2, 0;

i = 41, j = 1, 3, 9, 18, 63 и V_i,j составляет 0, 0, 0, 183, 0;

i = 42, j = 0, 4, 24, 64 и V_i,j составляет соответственно 27, 0, 35, 0;

i = 43, j = 1, 16, 18, 25, 65 и V_i,j составляет соответственно 52, 243, 0, 270, 0;

i = 44, j = 0, 7, 9, 22, 66 и V_i,j составляет соответственно 18, 0, 0, 57, 0; и

i = 45, j = 1, 6, 10, 67 и V_i,j составляет соответственно 168, 0, 144, 0.

19. Устройство по п.14, в котором Z является одним из 9, 18, 36, 72, 144 и 288.

20. Устройство по п.14, в котором в базовой матрице элементы, которые не являются ненулевыми элементами, являются нулевыми элементами;

в котором каждый нулевой элемент соответствует полностью нулевой матрице размером Z * Z в LDPC матрице Н,

21. Устройство по п.14, в котором кодирование входной последовательности c на

основе LDPC матрицы H содержит:

кодирование входной последовательности c на основе преобразованной матрицы;

в котором базовую матрицу преобразованной матрицы получают путем выполнения преобразования строки, или преобразования столбца, или преобразования строки и преобразования столбца в базовой матрице LDPC матрицы H.

22. Устройство по п.21, в котором базовую матрицу или коэффициент Z поднятия, или

преобразованную матрицу получают из одной или более памяти.

23. Устройство по п. 18, дополнительно содержащее:

компонент, выполненный с возможностью выполнять согласование скорости в кодированной последовательности для получения последовательности согласованной скорости;

компонент, выполненный с возможностью выполнять перемежение в последовательности согласованной скорости для получения перемеженной последовательности; и

компонент, выполненный с возможностью модулировать перемеженную последовательность.

24. Устройство связи, содержащее декодер и блок получения, в котором

блок получения выполнен с возможностью получать входную последовательность и коэффициент Z поднятия; и

декодер выполнен с возможностью декодировать входную последовательность на основании LDPC матрицы H для получения последовательности информационных битов, в котором базовая матрица H содержит m строк и n столбцов и m и n являются целыми числами и 5≤m≤46 и n является целым числом 27≤ n≤68, и базовая матрица содержит множество ненулевых элементов (i, j), в котором i является индексом строки, j является индексом столбца, 0≤i<m, 0≤j<n, каждый ненулевой элемент (i, j) соответствует матрицей круговой перестановки размера Z × Z, и матрица круговой перестановки равна матрице, полученной путем кругового смещения единичной матрицы размера Z × Z вправо P_i,j раз, в котором P_i,j = mod (V_{i j}, Z), Z является коэффициентом поднятия, и каждый из ненулевых элементов (i, j) и соответствующий V_i,j имеет следующий вид:

i = 0, j = 0, 1, 2, 3, 5, 6, 9, 10, 11, 12, 13, 15, 16, 18, 19, 20, 21, 22, 23 и V_i,j равно соответственно 211, 198, 188, 186, 219, 4, 29, 144, 116, 216, 115, 233, 144, 95, 216, 73, 261, 1, 0;

i = 1, j = 0, 2, 3, 4, 5, 7, 8, 9, 11, 12, 14, 15, 16, 17, 19, 21, 22, 23, 24 и V_i,j равно соответственно 179, 162, 223, 256, 160, 76, 202, 117, 109, 15, 72, 152, 158, 147, 156, 119, 0, 0;

i = 2, j = 0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 20, 24, 25 и V_i,j равно соответственно 258, 167, 220, 133, 243, 202, 218, 63, 0, 3, 74, 229, 0, 216, 269, 200, 234, 0, 0, 0;

i = 3, j = 0, 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 20, 21, 22, 25 и V_i,j равно соответственно 187, 145, 166, 108, 82, 132, 197, 41, 162, 57, 36, 115, 242, 165, 0, 113, 108, 1, 0; и

i = 4, j = 0, 1, 26 и V_i,j равно соответственно 246, 235, 0.

25. Устройство по п.24, в котором базовая матрица Н дополнительно содержит

следующие ненулевые элементы (i, j), и соответствующие значения V_i,j ненулевых элементов (i, j) представляют собой следующее:

i = 5, j = 0, 1, 3, 12, 16, 21, 22, 27 и V_i,j равно соответственно 261, 181, 72, 283, 254, 79, 144, 0;

i = 6, j = 0, 6, 10, 11, 13, 17, 18, 20, 28 и V_i,j равно соответственно 80, 144, 169, 90, 59, 177, 151, 108, 0;

i = 7, j = 0, 1, 4, 7, 8, 14, 29 и V_i,j равно соответственно 169, 189, 154, 184, 104, 164, 0;

i = 8, j = 0, 1, 3, 12, 16, 19, 21, 22, 24, 30 и V_i,j равно соответственно 54, 0, 252, 41, 98, 46, 15, 230, 54, 0;

i = 9, j = 0, 1, 10, 11, 13, 17, 18, 20, 31 и V_i,j равно соответственно 162, 159, 93, 134, 45, 132, 76, 209, 0;

i = 10, j = 1, 2, 4, 7, 8, 14, 32 и V_i,j равно соответственно 178, 1, 28, 267, 234, 201, 0;

i = 11, j = 0, 1, 12, 16, 21, 22, 23, 33 и V_i,j равно соответственно 55, 23, 274, 181, 273, 39, 26, 0;

i = 12, j = 0, 1, 10, 11, 13, 18, 34 и V_i,j равно соответственно 225, 162, 244, 151, 238, 243, 0;

i = 13, j = 0, 3, 7, 20, 23, 35 и V_i,j равно соответственно 231, 0, 216, 47, 36, 0;

i = 14, j = 0, 12, 15, 16, 17, 21, 36 и V_i,j равно 0, 186, 253, 16, 0, 79, 0;

i = 15, j = 0, 1, 10, 13, 18, 25, 37 и V_i,j равно соответственно 170, 0, 183, 108, 68, 64, 0;

i = 16, j = 1, 3, 11, 20, 22, 38 и V_i,j равно соответственно 270, 13, 99, 54, 0, 0;

i = 17, j = 0, 14, 16, 17, 21, 39 и V_i,j равно соответственно 153, 137, 0, 0, 162, 0;

i = 18, j = 1, 12, 13, 18, 19, 40 и V_i,j равно соответственно 161, 151, 0, 241, 144, 0;

i = 19, j = 0, 1, 7, 8, 10, 41 и V_i,j равно 0, 0, 118, 144, 0, 0;

i = 20, j = 0, 3, 9, 11, 22, 42 и V_i,j равно соответственно 265, 81, 90, 144, 228, 0;

i = 21, j = 1, 5, 16, 20, 21, 43 и V_i,j равно соответственно 64, 46, 266, 9, 18, 0;

i = 22, j = 0, 12, 13, 17, 44 и V_i,j равно соответственно 72, 189, 72, 257, 0;

i = 23, j = 1, 2, 10, 18, 45 и V_i,j равно соответственно 180, 0, 0, 165, 0;

i = 24, j = 0, 3, 4, 11, 22, 46 и V_i,j равно соответственно 236, 199, 0, 266, 0, 0;

i = 25, j = 1, 6, 7, 14, 47 и V_i,j равно соответственно 205, 0, 0, 183, 0;

i = 26, j = 0, 2, 4, 15, 48 и V_i,j равно 0, 0, 0, 277, 0;

i = 27, j = 1, 6, 8, 49 и V_i,j равно соответственно 45, 36, 72, 0;

i = 28, j = 0, 4, 19, 21, 50 и V_i,j равно соответственно 275, 0, 155, 62, 0;

i = 29, j = 1, 14, 18, 25, 51 и V_i,j равно 0, 180, 0, 42, 0;

i = 30, j = 0, 10, 13, 24, 52 и V_i,j равно 0, 90, 252, 173, 0;

i = 31, j = 1, 7, 22, 25, 53 и V_i,j равно соответственно 144, 144, 166, 19, 0;

i = 32, j = 0, 12, 14, 24, 54 и V_i,j равно 0, 211, 36, 162, 0;

i = 33, j = 1, 2, 11, 21, 55 и V_i,j равно 0, 0, 76, 18, 0;

i = 34, j = 0, 7, 15, 17, 56 и V_i,j равно соответственно 197, 0, 108, 0, 0;

i = 35, j = 1, 6, 12, 22, 57 и V_i,j равно соответственно 199, 278, 0, 205, 0;

i = 36, j = 0, 14, 15, 18, 58 и V_i,j равно соответственно 216, 16, 0, 0, 0;

i = 37, j = 1, 13, 23, 59 и V_i,j равно соответственно 72, 144, 0, 0;

i = 38, j = 0, 9, 10, 12, 60 и V_i,j равно соответственно 190, 0, 0, 0, 0;

i = 39, j = 1, 3, 7, 19, 61 и V_i,j равно соответственно 153, 0, 165, 117, 0;

i = 40, j = 0, 8, 17, 62 и V_i,j равно соответственно 216, 144, 2, 0;

i = 41, j = 1, 3, 9, 18, 63 и V_i,j равно 0, 0, 0, 183, 0;

i = 42, j = 0, 4, 24, 64 и V_i,j равно соответственно 27, 0, 35, 0;

i = 43, j = 1, 16, 18, 25, 65 и V_i,j равно соответственно 52, 243, 0, 270, 0;

i = 44, j = 0, 7, 9, 22, 66 и V_i,j равно соответственно 18, 0, 0, 57, 0; и

i = 45, j = 1, 6, 10, 67 и V_i,j равно соответственно 168, 0, 144, 0.

26. Устройство по п.24, в котором Z составляет одно из 9, 18, 36, 72, 144 и 288.

27. Устройство по п.24, в котором в базовой матрице элементы, которые не являются

ненулевыми элементами, являются нулевыми элементами;

в котором каждый нулевой элемент соответствует полностью нулевой матрице с размером Z * Z в LDPC матрице Н.

28. Устройство по п.24, в котором декодирование входной последовательности на основе LDPC матрицы Н содержит:

декодирование входной последовательности на основании преобразованной матрицы;

в котором базовую матрицу преобразованной матрицы получают путем выполнения преобразования строки, или преобразования столбца, или преобразования строки и преобразования столбца в базовой матрице LDPC матрицы H.

29. Устройство по п.28, в котором базовую матрицу или коэффициент Z поднятия, или

преобразованную матрицу получают из одной или более памяти.

30. Устройство по п.25, дополнительно содержащее:

демодулятор, выполненный с возможностью демодулировать сигнал для получения демодулированной последовательности;

обращенный перемежитель, выполненный с возможностью выполнять обратное перемежение демодулированной последовательности для получения обратно перемеженной последовательности; и

компонент десогласования скорости, выполненный с возможностью выполнять десогласование скорости в демодулированной последовательности для получения входной последовательности.

31. Терминал, содержащий устройство по любому из пп.14-30 и приемопередатчик.

32. Базовая станция, содержащая устройство по любому из пп.14-30 и

приемопередатчик.

33. Система связи, содержащая терминал по п.31 и базовую станцию.

34. Система связи, содержащая терминал и базовую станцию по п.32.

35. Машиночитаемый носитель данных, содержащий одну или несколько инструкций,

в котором, при запуске на компьютере, одна или несколько инструкций побуждают компьютер выполнять способ по любому из пп.1-13.