Изобретение относится к радиолокации и может использоваться в спутниковых радионавигационных системах и комплексах радиоэлектронного подавления для повышения качества решаемых ими задач.
В настоящее время для некоторых измерительных комплексов (например, систем радионавигации и комплексов радиоэлектронного подавления) актуальна задача оперативного приближенного определения наклонной дальности до цели по минимальному количеству измерений пеленгов, получаемых автономной угломерной системой. Известен ряд способов, используемых для определения наклонной дальности до подвижной цели по минимальному количеству пеленгов, текущих координат подвижных целей [1-8]. Такая задача возникает, например, на этапе ранжирования потока целей по ориентировочной дальности, под которой понимается значение дальности, определяемое с точностью, пригодной для решения задачи ранжирования целей при проведении РЭП. При этом рассматриваются цели с частично известными параметрами [9], когда заданы тип траектории, величины скорости, ускорения и т.д., а также некоторые тактико-технические характеристики сопровождаемых целей.
Для указанных комплексов не предъявляется повышенных требований к точности определения дальности до цели, а, в первую очередь, важна оперативность формируемых оценок данного параметра движения. Это позволяет отказаться от высокоточных статистических методов оценивания (метода наименьших квадратов, максимума правдоподобия, максимума апостериорной плотности вероятности и др. [10]) и использовать методы косвенного оценивания на базе несложных конечных формул.
Так, в прототипе [2-4, 6, 9] проблема оперативного определения дальности решается на базе автономной угломерной системы по трем и более измерениям пеленга на цель, движущуюся прямолинейно и равномерно с известной величиной скорости. Однако к недостаткам прототипа следует отнести условие равномерности движения цели, что зачастую является жестким ограничением. Кроме того, использование более двух измерений пеленга снижает оперативность решения целевых задач измерительных комплексов, функционирующих в реальном времени.
Целью предлагаемого изобретения является устранение недостатков прототипа, заключающееся в разработке способа оперативного определения наклонной дальности до движущейся цели по двум последовательным во времени измерениям пеленгов с учетом того, что цель движется прямолинейно, но при этом полагаются известными величины скорости, ускорения и т.д., а также мощности принимаемых автономной угломерной системой сигналов для рассматриваемых моментов измерений.
Геометрия задачи представлена на фиг.1, где точка О соответствует геометрическому центру автономной угломерной системы, ЛБ - линия перемещения цели, точки Ц1 и Ц2 соответствуют измерениям пеленгов на цель в моменты времени t1 и t2 соответственно. Кроме того, на фиг.1 указаны расстояния 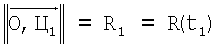 ,
,  и углы β и Δα12.
и углы β и Δα12.
Предполагается, что цель движется прямолинейно, при этом проходимое расстояние описывается моделью:
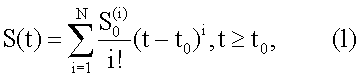
где  .
.
Величины 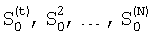 в модели (1) полагаются известными.
в модели (1) полагаются известными.
Известны также время Δt12 пролета цели между точками Ц1 и Ц2, угол Δα12 и величины  и
и  (где P1=P(t1) и Р2=P(t2) - мощности сигналов, принимаемых автономной угломерной системой, в моменты времени t1 и t2 соответственно).
(где P1=P(t1) и Р2=P(t2) - мощности сигналов, принимаемых автономной угломерной системой, в моменты времени t1 и t2 соответственно).
Из фиг.1 видно, что


С учетом (2) и (3) имеем

С другой стороны

Из (4) и (5) вытекает
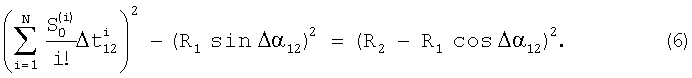
Известно [11], что мощность P=P(t) сигнала на входе автономной угломерной системы обратно пропорциональна квадрату дальности R=R(t) до цели:
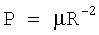 ,
,
где µ=µ(t) - коэффициент пропорциональности, сложным образом зависящий от условий наблюдения цели.
За промежуток времени Δt12 мощность принимаемых сигналов на входе автономной угломерной системы меняется от величины P1=P(t1) до величины P2=P(t2), поэтому справедливы соотношения
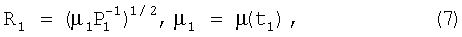
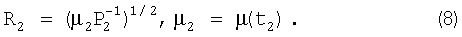
Поскольку на практике для малых временных интервалов Δt12 принимается ограничение µ1=µ2=µ, получим следующую формулу для отношения дальностей
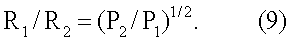
С учетом (6) и (9) имеем

Преобразовывая выражение в фигурных скобках и вводя обозначения  и
и 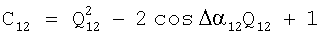 , с учетом (10) получаем искомую формулу для наклонной дальности в момент времени t1
, с учетом (10) получаем искомую формулу для наклонной дальности в момент времени t1

По аналогии с (11) с учетом того, что Δα12=Δα21, можно получить формулу для наклонной дальности в момент времени t2
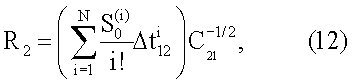
где
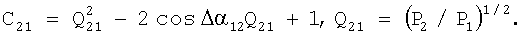
Выражения (11) и (12) позволяют определить наклонную дальность до цели по двум последовательным во времени измерениям пеленга и относительной мощности измеряемого сигнала.
Анализ выражений (11), (12) показывает, что метод неработоспособен в двух случаях, когда  и когда С12<0. Ситуация, когда
и когда С12<0. Ситуация, когда 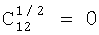 , возможна при одновременном выполнении двух условий: Q21=0 и Δα12=0. Выполнение этих условий на практике может означать цель, находящуюся на большом удалении от автономной угломерной системы и движущуюся на очень малой скорости, так что угол между пеленгами на цель Δα12≈0, а значения мощности сигнала на входе системы при первом и втором измерении пеленга одинаковы (Q21≈1). Но такой случай, скорее, является исключением для практики, поэтому перейдем к анализу второго случая, когда С12<0. Решая квадратное неравенство
, возможна при одновременном выполнении двух условий: Q21=0 и Δα12=0. Выполнение этих условий на практике может означать цель, находящуюся на большом удалении от автономной угломерной системы и движущуюся на очень малой скорости, так что угол между пеленгами на цель Δα12≈0, а значения мощности сигнала на входе системы при первом и втором измерении пеленга одинаковы (Q21≈1). Но такой случай, скорее, является исключением для практики, поэтому перейдем к анализу второго случая, когда С12<0. Решая квадратное неравенство 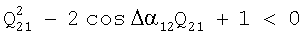 относительно параметра Ql2, приходим к выводу, что данное неравенство не имеет решений на множестве действительных чисел. Следовательно, выражения (11), (12) пригодны для определения наклонной дальности в рамках рассматриваемой задачи.
относительно параметра Ql2, приходим к выводу, что данное неравенство не имеет решений на множестве действительных чисел. Следовательно, выражения (11), (12) пригодны для определения наклонной дальности в рамках рассматриваемой задачи.
Учтем случайный характер основных параметров, входящих в формулы для наклонной дальности, полагая их нормально распределенными некоррелированными случайными величинами. Для нахождения дисперсии ошибки определения дальности воспользуемся широко распространенным на практике принципом линеаризации (первым приближением [6-10]). Кроме того, по аналогии с [9] ограничимся случаем прямолинейного равномерного движения цели.
Рассматривая R1 и R2 (далее R1(2)) как функции R1(2)=φ(V, Δα12, Q12, Q21)=φ1(2) случайных некоррелированных аргументов V, Δαl2, Q12 и Q21 (далее Q12(21)), в условиях высокоточных измерений с учетом метода линеаризации искомые дисперсии ошибок определения наклонной дальности находятся по формуле
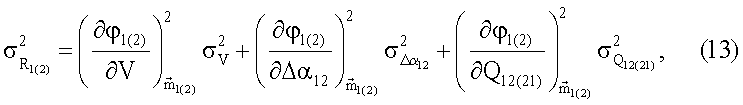
где 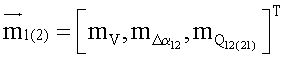 - вектор математических ожиданий,
- вектор математических ожиданий, 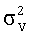 - дисперсия ошибки определения скорости V,
- дисперсия ошибки определения скорости V, 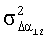 - дисперсия ошибки определения угла Δα12,
- дисперсия ошибки определения угла Δα12, 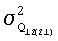 - дисперсия ошибки определения величины Q12(21).
- дисперсия ошибки определения величины Q12(21).
Частные производные в (13) с учетом (11), (12) находятся по формулам

Подставляя (14) в (13), окончательно получаем формулу для дисперсий ошибок определения наклонной дальности в моменты времени t1 и t2 соответственно
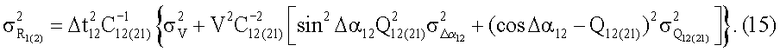
Формула (15) позволяет исследовать потенциальные возможности развитого метода для различных условий пеленгационно-мощностных измерений. Используемое при выводе формулы (15) условие некоррелированности случайных величин V, Δα12, Ql2 и Q21 не является принципиальным. В случае их коррелированности достаточно в правую часть формулы (15) добавить слагаемое, учитывающее соответствующие коэффициенты корреляции между случайными величинами.
Более жестким, но принципиально необходимым является требование высокоточных измерений, при которых развитый метод является работоспособным. Об этом убедительно свидетельствуют результаты расчетов в соответствии с формулой (15) и статистического моделирования.
Для анализа эффективности развитого метода применим два подхода: первый основан на расчетах согласно формуле (15), второй основан на статистическом моделировании с использованием датчиков случайных чисел.
Зададимся следующей моделью движения цели: x(t)=х1+Vxt, y(t)=у1+Vyt, 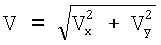 , V=2·102 [м/с], σV=3 [м/с], t≥0, t1=0 [с], х1=103 [м], H=5·104 [м],
, V=2·102 [м/с], σV=3 [м/с], t≥0, t1=0 [с], х1=103 [м], H=5·104 [м],  ,
, 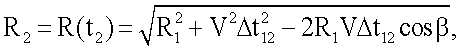
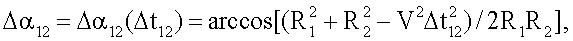 t2=Δt12, Q12=R2/R1, Q21=R1/R2.
t2=Δt12, Q12=R2/R1, Q21=R1/R2.
На фиг.2 представлен график зависимости 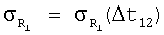 и
и 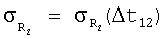 для первого варианта (y1=6·104 [м]), причем
для первого варианта (y1=6·104 [м]), причем 
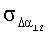 =5 [угл. с].
=5 [угл. с].
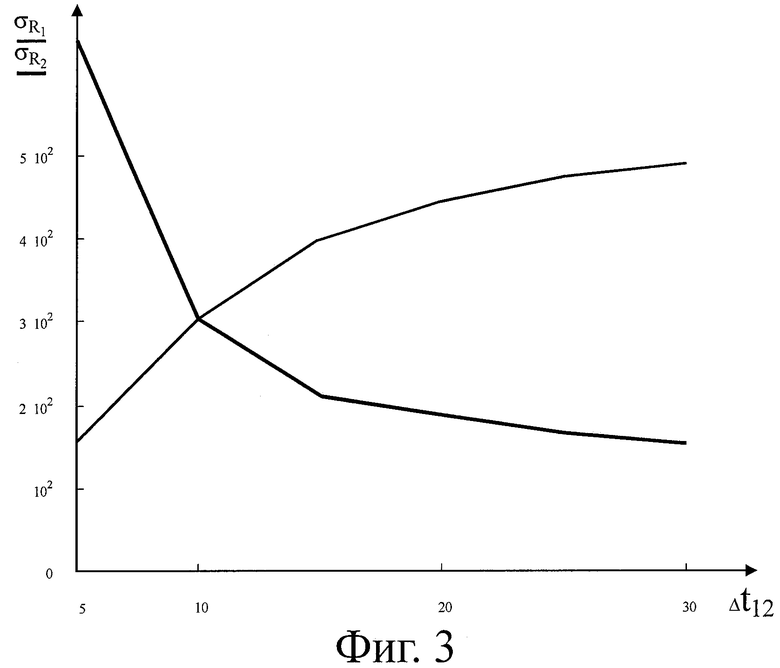
На фиг.3 представлен график зависимости 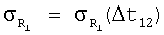 и
и 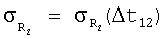 для второго варианта (y1=5·104 [м]), причем
для второго варианта (y1=5·104 [м]), причем  ,
,  =15 [угл. с].
=15 [угл. с].
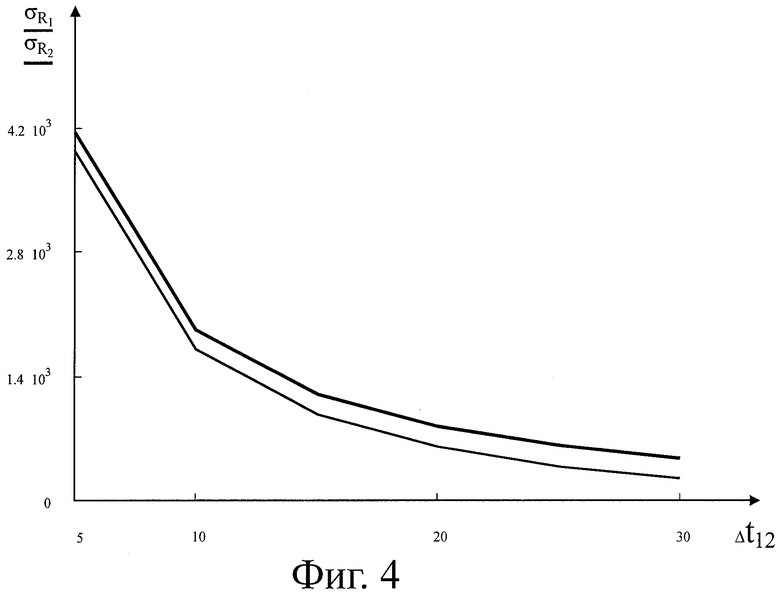
На фиг.4 представлен график зависимости 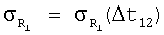 и
и 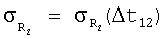 для третьего варианта (y1=4·104 [м]), причем
для третьего варианта (y1=4·104 [м]), причем  ,
, 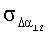 =30 [угл. с].
=30 [угл. с].
Введем расстояние  , где
, где 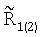 - результирующая оценка наклонной дальности, полученная на основе развитого метода по результатам усреднения по 100 реализациям
- результирующая оценка наклонной дальности, полученная на основе развитого метода по результатам усреднения по 100 реализациям
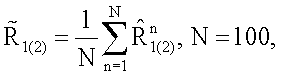
где 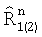 - единичная оценка, соответствующая n-му эксперименту, получаемая с использованием формул (11), (12),
- единичная оценка, соответствующая n-му эксперименту, получаемая с использованием формул (11), (12), 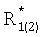 - истинные значения наклонной дальности, вычисленные по формулам
- истинные значения наклонной дальности, вычисленные по формулам

При построении единичных и результирующих оценок с помощью датчиков случайных чисел формировались ошибки измерений  с соответствующими среднеквадратическими отклонениями
с соответствующими среднеквадратическими отклонениями 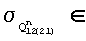 {0.009, 0.045, 0.09},
{0.009, 0.045, 0.09},  ,
, 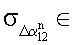 {5, 15, 30} [угл. с].
{5, 15, 30} [угл. с].
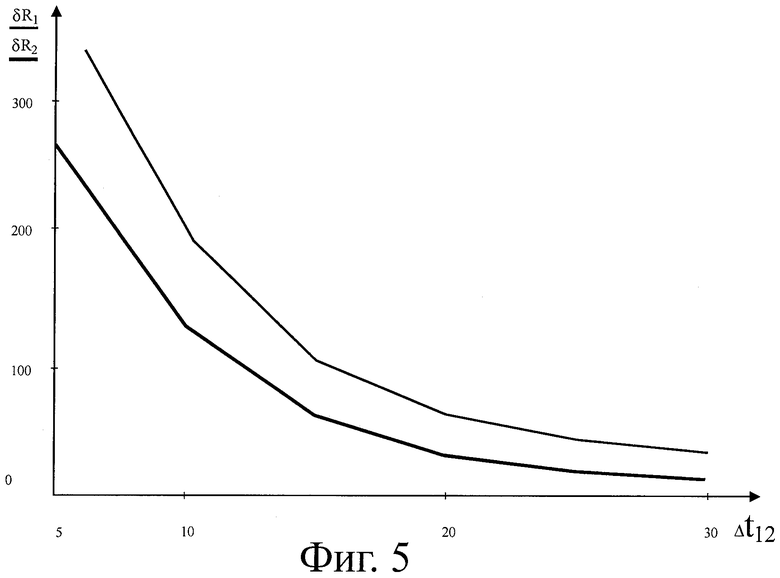
На фиг.5, 6, 7 представлены зависимости δR1(Δt12) и δR2(Δt12), построенные с учетом исходных данных рассмотренных ранее вариантов 1, 2 и 3.
Анализ результатов расчетов (фиг.2, 3, 4) и моделирования (фиг.5, 6, 7) показывает, что расчетные и модельные оценки подтверждают работоспособность метода для различных условий наблюдения цели.
Отличительной особенностью предлагаемого способа от традиционных подходов к решению задачи определения наклонной дальности является его оперативность при удовлетворительных точностных значениях оценки, а также снятие ограничения равномерного движения цели.
Технический результат заключается в определении наклонной дальности до прямолинейно движущейся цели по двум измерениям пеленгов, получаемых автономной угломерной системой. При этом рассматриваются цели с частично известными параметрами, когда заданы тип траектории, величины скорости и ускорения, а также мощности принимаемых автономной угломерной системой сигналов.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Палий А.И. Радиоэлектронная борьба. М.: Воениздат, 1981.
2. Основы маневрирования кораблей. Под ред. М.И.Скворцова. М.: Воениздат, 1996.
3. Хвощ В.А. Тактика подводных лодок. М.: Воениздат, 1989.
4. Мельников Ю.П., Попов С.В. Методы оценки погрешностей определения параметров движения объекта при локации в условиях радиоэлектронного подавления. // Радиотехника, 1998, №3, стр.34.
5. Макухина Т.П., Миленький А.В., Натальченко О.С., Попов С.В. Оценка текущих координат движущегося объекта по данным пеленгования. // Вопросы радиоэлектроники, сер. АСУПР, 1992, вып.2, стр.52.
6. Булычев Ю.Г., Коротун А.А., Манин А.П. Идентификация параметров траекторий по измерениям подвижного пеленгатора. // Радиотехника, 1990, №1, стр.16.
7. Булычев Ю.Г., Коротун А.А., Манин А.П., Моторкин В.А. Определение координат цели по угломерным данным подвижного приемного пункта. // Радиотехника, 1992, №4, стр.14.
8. Булычев Ю.Г., Шухардин А.Н. Идентификация параметров траекторий цели на базе одноканального подвижного пеленгатора. // Радиотехника, 2004, №8, стр.3.
9. Мельников Ю.П., Попов С.В. Определение дальности при пеленговании объекта с частично известными параметрами движения. // Радиотехника, 2003, №4, стр.71.
10. Жданюк Б.Ф. Основы статистической обработки траекторных измерений. М.: Сов. радио, 1978.
11. Справочник по радиолокации: перевод с английского. Под ред. К.Н.Трофимова. Том №4. М.: Сов. радио, 1976.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ НАКЛОННОЙ ДАЛЬНОСТИ ДО ДВИЖУЩЕЙСЯ ЦЕЛИ ПАССИВНЫМ МОНОСТАТИЧЕСКИМ ПЕЛЕНГАТОРОМ | 2014 |
|
RU2557808C1 |
| СПОСОБ ПАССИВНОЙ РАДИОЛОКАЦИИ ДВИЖУЩЕГОСЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2016 |
|
RU2645712C1 |
| Способ пассивной однопозиционной угломерно-разностно-доплеровской локации перемещающегося в пространстве радиоизлучающего объекта и радиолокационная система для реализации этого способа | 2016 |
|
RU2617830C1 |
| ПАССИВНАЯ ПЕЛЕНГАЦИОННАЯ СИСТЕМА | 2005 |
|
RU2298803C2 |
| АДАПТИВНЫЙ СПОСОБ ПАССИВНОЙ РАДИОЛОКАЦИИ | 2015 |
|
RU2593149C1 |
| ВРЕМЕННОЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ СКАНИРУЮЩЕГО ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2020 |
|
RU2742581C1 |
| Способ обзорной пассивной однопозиционной моноимпульсной трёхкоординатной угломерно-разностно-доплеровской локации перемещающихся в пространстве радиоизлучающих объектов | 2017 |
|
RU2661357C1 |
| ПОДВИЖНЫЙ ПЕЛЕНГАТОР | 2005 |
|
RU2298804C2 |
| Способ пассивной однопозиционной угломерно-доплеровской локации перемещающихся в пространстве радиоизлучающих объектов | 2019 |
|
RU2699552C1 |
| ПОДВИЖНЫЙ ПЕЛЕНГАТОР | 1997 |
|
RU2124222C1 |



Изобретение относится к радиолокации и может использоваться в спутниковых радионавигационных системах и комплексах радиоэлектронного подавления для повышения качества решаемых задач. Технический результат заключается в определении наклонной дальности до прямолинейно движущейся цели по двум измерениям пеленгов, получаемых автономной угломерной системой. При этом рассматриваются цели с частично известными параметрами, когда заданы тип траектории, величины скорости и ускорения, а также мощности принимаемых автономной угломерной системой сигналов. 7 ил.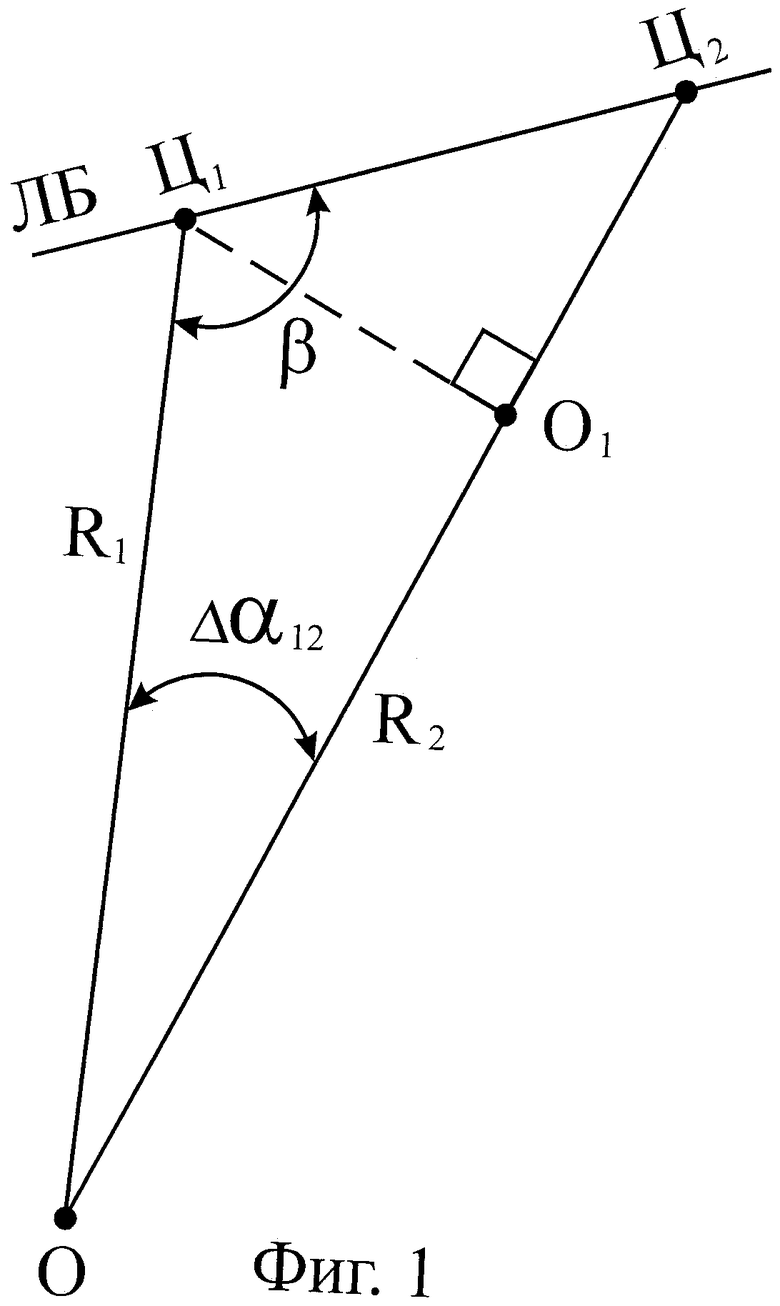
Способ определения наклонной дальности до движущейся цели по минимальному числу пеленгов, заключающийся в совместной обработке измерений пеленгов автономной угломерной системы, и отличающийся тем, что по двум последовательным во времени измерениям пеленгов определяют наклонную дальность до цели, полагая известными величины скорости, ускорения, мощности принимаемых автономной угломерной системой сигналов для рассматриваемых моментов измерений и других технических характеристик, учитывая, что базовая точка измерения соответствует геометрическому центру автономной угломерной системы, а линия ЛБ - траектория движения цели - соответствует точкам Ц1 и Ц2 измерения пеленга на цель в конкретные моменты времени t1 и t2, предполагая, что цель движется прямолинейно, при этом проходимое расстояние описывают моделью:
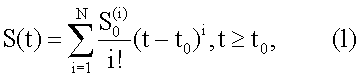
где  а величины
а величины  в модели (1) полагаются известными, кроме того, известными полагают также время Δt12 пролета цели между точками Ц1 и Ц2, угол Δα12 и величины
в модели (1) полагаются известными, кроме того, известными полагают также время Δt12 пролета цели между точками Ц1 и Ц2, угол Δα12 и величины  и
и 
(где P1
=P(t1) и Р2=P(t2) - мощности сигналов, принимаемых автономной угломерной системой, в моменты времени t1 и t2 соответственно), определяя из геометрии задачи соотношения


получая с учетом (2) и (3)
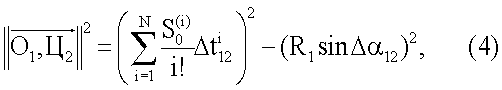
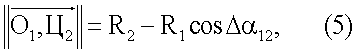
а из (4) и (5) получая
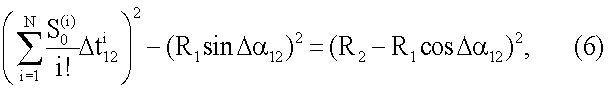
используя то, что мощность P=P(t) сигнала на входе автономной угломерной системы обратно пропорциональна квадрату дальности R=R(t) до цели:
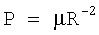 ,
,
где µ=µ(t) - коэффициент пропорциональности, зависящий от условий наблюдения цели; учитывая, что за промежуток времени Δt12 мощность принимаемых сигналов на входе автономной угломерной системы меняется от величины P1=P(t1) до величины P2=P(t2), справедливы соотношения
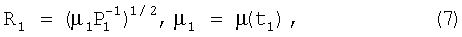
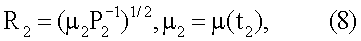
принимая на практике для малых временных интервалов Δt12 ограничение µ1=µ2=µ, получают следующую формулу для отношения дальностей:
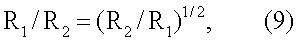
которая с учетом (6) и (9) принимает вид

преобразовывая выражение в фигурных скобках и вводя обозначения Q12=(P1/P2)1/2 и  с учетом (10) получают искомую формулу для наклонной дальности в момент времени t1:
с учетом (10) получают искомую формулу для наклонной дальности в момент времени t1:

учитывая, что ΔαI2=Δα21, по аналогии с (11) получают формулу для наклонной дальности в момент времени t2:
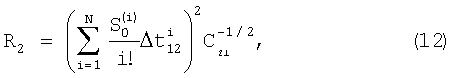
где 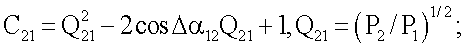 выражения (11) и (12) позволяют получить оперативную оценку наклонной дальности до прямолинейно движущейся цели по двум последовательным во времени измерениям пеленга и относительной мощности измеряемого сигнала.
выражения (11) и (12) позволяют получить оперативную оценку наклонной дальности до прямолинейно движущейся цели по двум последовательным во времени измерениям пеленга и относительной мощности измеряемого сигнала.
| СПОСОБ РАДИОКОНТРОЛЯ | 1999 |
|
RU2158002C1 |
| СПОСОБ ОБНАРУЖЕНИЯ И ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ | 2002 |
|
RU2240576C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО АЭРОЛОГИЧЕСКОГО РАДИОЗОНДА | 2004 |
|
RU2304290C2 |
| JP 2008051523 A, 06.03.2008 | |||
| Коммутационное устройство | 1989 |
|
SU1635190A1 |
Авторы
Даты
2010-12-10—Публикация
2009-07-06—Подача