Изобретение относится к пассивной радиолокации и может быть использовано в двух- и многопозиционных измерительных комплексах для определения координат местоположения источников радиоизлучения (ИРИ).
В настоящее время не ослабевает интерес к разработке адаптивных многопозиционных измерительных комплексов, реализующих классические методы пассивной радиолокации ИРИ, к которым относятся триангуляционный метод (ТМ), разностно-дальномерный метод (РДМ) и угломерно-разностно-дальномерный метод (УРДМ) ([1], с. 494-497).
Однако реализация указанных методов, предполагающих совместную обработку принимаемых сигналов всех позиций, весьма проблематична в условиях возможной «деградации» структуры многопозиционного измерительного комплекса. «Деградация» зачастую связана с причинами естественного и искусственного происхождения, которые могут приводить к кратковременным и длительным сбоям в работе аппаратуры, выходу из строя отдельных позиций и линий связи, нарушению условий синхронизации, необходимых для совместной обработки сигналов и т.д.
Ввиду указанного, а также с технико-экономической точки зрения весьма привлекательным является двухпозиционный измерительный комплекс (ДИК). Необходимо отметить, что ДИК также можно образовать в многопозиционном измерительном комплексе путем выделения из него двухпозиционных измерительных структур, получаемых неповторяющимися парами позиций комплекса.
Определение плоскостных координат местоположения ИРИ на базе ДИК возможно путем реализации ТМ или УРДМ.
В соответствии с ТМ ([1], с. 494-495; [2]) координаты местоположения ИРИ определяются как точка (без учета ошибок пеленгования) пересечения пеленгов ИРИ, измеренных с разнесенных в пространстве позиций (пеленгаторов) ДИК. Для определения плоскостных координат местоположения ИРИ на основе ТМ достаточно ограничиться измерением только углов азимута на ИРИ с каждой позиции ДИК. Основными недостатками ТМ, ограничивающими его применение, являются низкая точность определения координат местоположения ИРИ при его нахождении в окрестности линии базы и (или) при больших дальностях до ИРИ.
УРДМ ([1], с. 497) основан на измерении угловых координат ИРИ и определении разности расстояний от него до позиций ДИК. Для определения плоскостных координат местоположения ИРИ на основе УРДМ достаточно измерить только один азимут и определить разность расстояний от ИРИ до позиций ДИК. Основным недостатком УРДМ являются ошибки, вызванные неодновременностью измерений.
Помимо классических методов пассивной радиолокации используются альтернативные методы определения координат местоположения ИРИ, основанные, в том числе, на других физических принципах.
В [3] показана возможность определения координат местоположения ИРИ на основе использования измерений лишь энергетических параметров излучения ИРИ. Однако для реализации метода [3] необходимо не менее четырех измерителей, распределенных в пространстве определенным образом.
В патенте [4] представлен способ определения наклонной дальности до движущегося ИРИ на базе однопозиционной измерительной системы. Для реализации указанного способа используются угловые и энергетические измерения. Существенным недостатком способа [4] является необходимость априорного знания скорости движения ИРИ.
Известны также энергетические методы [5-6], реализуя которые удается сформировать раздельные оценки дальности до ИРИ относительно каждой позиции ДИК (эти оценки используются далее для построения результирующей оценки координат местоположения ИРИ). Однако методы [5-6] имеют жесткие ограничения на точность пеленгования и ориентированы, в первую очередь, на узконаправленные и, как следствие, дорогостоящие антенные системы.
Проведенный краткий анализ классических и альтернативных методов пассивной радиолокации показал их недостатки и, как следствие, указал на целесообразность одновременной параллельной реализации нескольких классических методов и последующего выбора из них одного метода, реализация которого способствует достижению наибольшей точности определения координат местоположения ИРИ. Кроме того, очевидна необходимость одновременного использования наряду с классическими методами пассивной радиолокации ИРИ и альтернативных методов для повышения точности определения координат местоположения ИРИ.
Наиболее близким к предлагаемому изобретению (прототипом) является триангуляционно-гиперболический способ определения координат радиоизлучающих воздушных объектов в пространстве [7], поскольку для его реализации используется комбинация двух классических методов пассивной радиолокации - ТМ и РДМ. Триангуляционные оценки координат местоположения ИРИ уточняются путем использования РДМ.
Недостатком прототипа является то, что система, предполагаемая для реализации способа, должна содержать как минимум три измерительные (приемные) позиции для определения плоскостных координат местоположения ИРИ. А также то, что точность определения координат местоположения ИРИ будет недостаточно высокой.
Известно ([1], с. 505), что погрешности определения координат местоположения ИРИ с помощью ТМ характеризуются погрешностями пеленгования и существенно зависят от того, под каким углом пересекаются линии положения (для ТМ - пеленги), измеренные с различных приемных позиций многопозиционного измерительного комплекса. При этом погрешности максимальны, когда ИРИ находится в окрестности линии базы и (или) на больших дальностях. Поскольку ТМ является одним из этапов реализации способа [7], то следует ожидать невысокой точности определения координат местоположения ИРИ способом [7] при нахождении ИРИ в окрестности линии базы и (или) на больших дальностях.
Вид и размеры рабочей зоны ТМ характеризуются точностью определения координат местоположения ИРИ, требуемой для конкретной решаемой задачи. Ввиду указанной ограниченной точности способа [7] следует ожидать его ограниченную рабочую зону.
Задачей изобретения является повышение точности определения координат местоположения ИРИ и расширение рабочей зоны измерительного комплекса при адаптивном способе пассивной радиолокации на базе ДИК.
Для решения задачи в предлагаемом способе, включающем измерение с приемных позиций измерительного комплекса угловых координат ИРИ и определение временной задержки прихода волнового фронта излучения ИРИ на позиции комплекса, а также применение ТМ для определения координат местоположения ИРИ, в качестве измерительного комплекса используют ДИК. На приемных позициях дополнительно измеряют мощности излучения ИРИ, а координаты местоположения ИРИ определяют на плоскости, причем параллельно с ТМ применяют УРДМ и угломерно-мощностной метод (УММ). Для каждого из методов определяют значение дисперсии дальности до ИРИ, затем сравнивают эти значения и выбирают те значения координат местоположения ИРИ, которые соответствуют наименьшему значению дисперсии. При равных значениях дисперсии используют правило нахождения среднего арифметического для значений одноименных координат, получаемых двумя или тремя методами. При этом УММ определения значений плоскостных координат местоположения ИРИ осуществляют следующим образом:
вычисляют коэффициенты
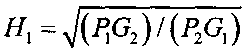 и
и 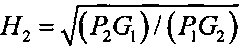 ,
,
где P1 и P2 - измеренные мощности излучения ИРИ на первой и второй позициях ДИК соответственно,
G, и G2 - коэффициенты усиления приемных антенн первой и второй позиций ДИК соответственно;
вычисляют угол θ=α2-α1,
где αi (i=1, 2) - измеренные угловые координаты ИРИ;
вычисляют значения параметров
 и
и 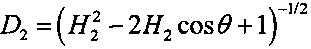 ;
;
вычисляют дальность от ИРИ до первой позиции комплекса R1=bD1 и дальность от ИРИ до второй позиции комплекса R2=bD2,
где b - величина базы (расстояние между позициями ДИК);
определяют плоскостные координаты местоположения ИРИ
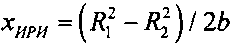 ,
,
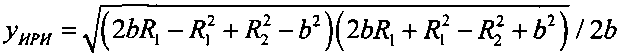 .
.
Повышение точности определения плоскостных координат местоположения ИРИ на базе ДИК достигается за счет адаптивного характера способа, заключающегося в том, что сначала несколькими методами определяют значения плоскостных координат местоположения ИРИ, а затем из них выбирают значения, которые получены на основе метода (методов), имеющего (имеющих) для данных условий наблюдения ИРИ наибольшую точность. Ввиду указанного повышения точности происходит расширение рабочей зоны ДИК.
В многопозиционном измерительном комплексе координаты местоположения ИРИ определяют путем построения в нем ДИК, получаемых неповторяющимися парами приемных позиций многопозиционного комплекса. Затем получают значения плоскостных координат местоположения ИРИ на основе каждого такого ДИК, формируют за счет этого избыточность оценок местоположения ИРИ и далее совместно обрабатывают эти оценки.
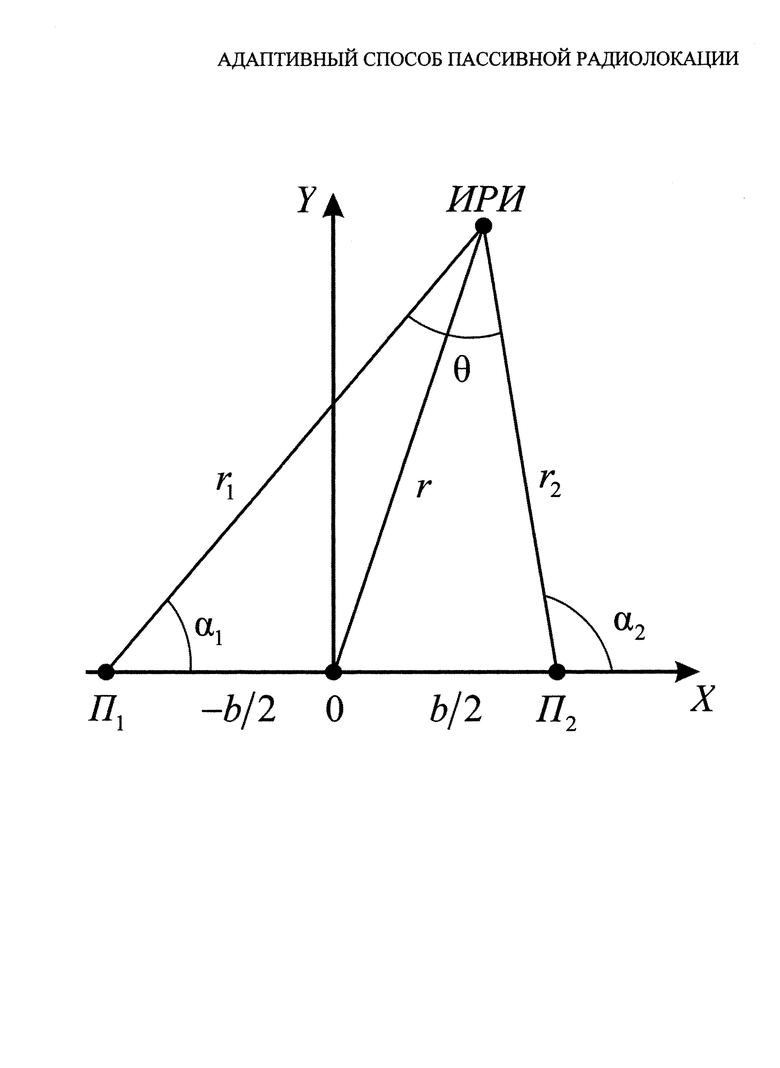
Предлагаемый способ поясняется чертежом, на котором изображена схема определения на плоскости координат ИРИ на базе ДИК.
На схеме изображен один ИРИ и две приемные позиции ДИК (П1 и П2), отстоящие друг от друга на величину базы b. Под r, r1 и r2 понимаются соответствующие радиус-векторы ИРИ (||r||=R, ||r1||=R1 и ||r2||=R2), под R - дальность до ИРИ от середины базы. Начало координат совмещено с серединой базы.
Измерители Пi (i=1, 2) измеряют угловые координаты ИРИ αi (i=1, 2) с ошибками, распределенными по нормальному закону с нулевыми математическими ожиданиями и дисперсиями 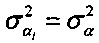 (i=1, 2).
(i=1, 2).
Также измерители Пi (i=1, 2) имеют в своем составе антенны с известными с дисперсией  (i=1, 2) коэффициентами усиления Gi (i=1, 2) и измеряют мощности Pi (i=1, 2) принимаемых сигналов. При этом ошибки измерения мощности характеризуются дисперсиями
(i=1, 2) коэффициентами усиления Gi (i=1, 2) и измеряют мощности Pi (i=1, 2) принимаемых сигналов. При этом ошибки измерения мощности характеризуются дисперсиями 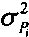 (i=1, 2) при нулевых математических ожиданиях. Измерения угловых координат ИРИ и мощности его излучения проводятся на приемных позициях ДИК П1 и П2 синхронно.
(i=1, 2) при нулевых математических ожиданиях. Измерения угловых координат ИРИ и мощности его излучения проводятся на приемных позициях ДИК П1 и П2 синхронно.
Кроме того с дисперсией 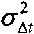 определяется временная задержка Δt прихода волнового фронта излучения ИРИ на две разнесенные на расстояние базы b приемные позиции ДИК П1 и П2. Для этого по аналогии с РДМ может использоваться, например, базово-корреляционный метод ([1], с. 498-501).
определяется временная задержка Δt прихода волнового фронта излучения ИРИ на две разнесенные на расстояние базы b приемные позиции ДИК П1 и П2. Для этого по аналогии с РДМ может использоваться, например, базово-корреляционный метод ([1], с. 498-501).
В изобретении параллельно реализуются следующие три метода определения плоскостных координат местоположения ИРИ:
1. Триангуляционный метод.
Из геометрии задачи по теореме синусов вычисляют


где

С учетом геометрии задачи координаты местоположения ИРИ определяют как точку пересечения двух окружностей: одна - радиусом R1 с центром в точке П1, другая - радиусом R2 с центром в точке П2. Для определения используют следующие аналитические выражения:


Для получения одной числовой характеристики точности ТМ, учитывающей погрешности определения обеих плоскостных координат xИРИ и yИРИ, запишем
 .
.
С другой стороны, дальность R является медианой треугольника П1 ИРИ П2 и может быть вычислена по формуле
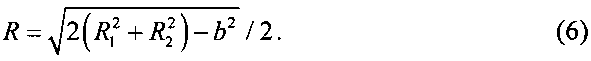
Применительно к формуле (6) воспользуемся широко известным в теории вероятностей методом линейных приближений ([8], с. 252-259):

где
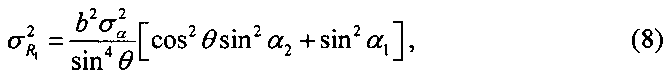
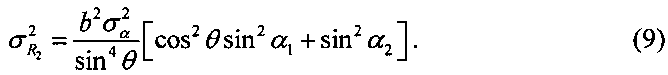
Таким образом, выражения (7)-(9) позволяют определить дисперсию 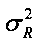 дальности R, учитывающую дисперсии определения дальностей R1 и R2 с помощью ТМ.
дальности R, учитывающую дисперсии определения дальностей R1 и R2 с помощью ТМ.
2. Угломерно-мощностной метод.
Из геометрии задачи следует, что


где
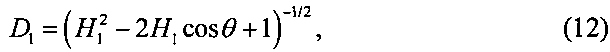
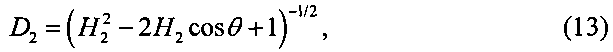
H1=R2/R1,
H2=R1/R2,
H1, H2 - относительные энергетические коэффициенты.
Если учесть, что
 , i=1, 2,
, i=1, 2,
где µi - неизвестные обобщенные коэффициенты радиолокации, то, полагая µ1=µ2 (по аналогии с [3, 4, 9, 10]), величины H1 и H2 вычисляют:


Искомые плоскостные координаты местоположения ИРИ определяются по общим формулам (4), (5) путем подстановки значений дальностей R1 и R2, полученных с помощью УММ.
Для оценки точностных характеристик УММ также воспользуемся методом линейных приближений ([8], с. 252-259). При этом будем учитывать случайные ошибки измерений не только угловых координат, но и принимаемой мощности излучения ИРИ.
С учетом случайного характера ошибок пеленгования и измерения мощности, дисперсии ошибок определения дальностей Ri (i=1, 2) на основе формул (10), (11) вычисляют так:
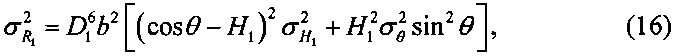
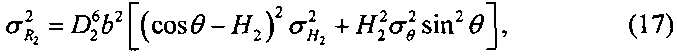
где ,
, 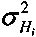 - дисперсии ошибок измерения случайных величин θ и Hi соответственно.
- дисперсии ошибок измерения случайных величин θ и Hi соответственно.
Так как θ=α2-α1, то при условии 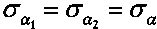 имеем
имеем

При этом дисперсии ошибок расчета коэффициентов Hi (i=1, 2) равны


где
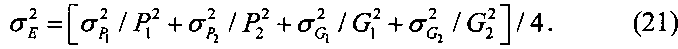
Дисперсия 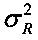 дальности R, учитывающая дисперсии определения дальностей R1 и R2 с помощью УММ, вычисляется по общей формуле (7).
дальности R, учитывающая дисперсии определения дальностей R1 и R2 с помощью УММ, вычисляется по общей формуле (7).
3. Угломерно-разностно-дальномерный метод.
Из геометрии задачи вычисляют:


где
разность дальностей от ИРИ до позиций комплекса

c - скорость света,
Δt - временная задержка прихода волнового фронта излучения ИРИ на две разнесенные на расстояние базы приемные позиции ДИК П1 и П2, определяемая известным способом (например, базово-корреляционным методом ([1], с. 498-501).
Искомые плоскостные координаты местоположения ИРИ определяются по общим формулам (4), (5) путем подстановки значений дальностей R1 и R2, полученных с помощью УРДМ.
Дисперсия 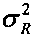 дальности R, учитывающая дисперсии определения дальностей R1 и R2 с помощью УРДМ, вычисляется по общей формуле (7).
дальности R, учитывающая дисперсии определения дальностей R1 и R2 с помощью УРДМ, вычисляется по общей формуле (7).
При этом
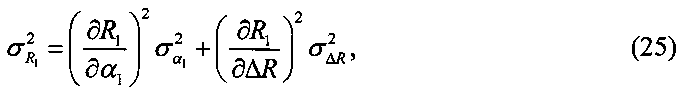
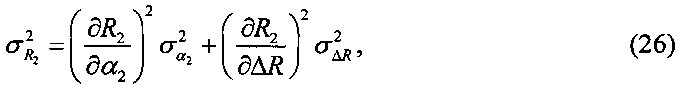
где

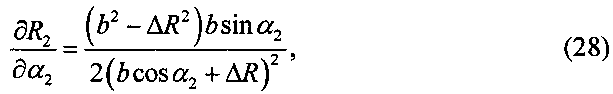
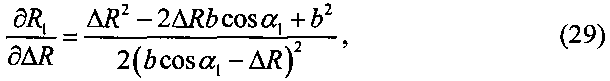
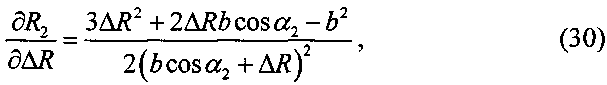

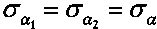 .
.
Правило выбора значений плоскостных координат местоположения ИРИ из значений, полученных параллельно тремя рассмотренными методами (ТМ, УММ и УРДМ), основано на точности метода, с помощью которого получены выбранные значения: выбираются значения плоскостных координат местоположения ИРИ, соответствующие наибольшей точности метода (методов) для данных условий наблюдения ИРИ. Наибольшая точность определяется наименьшим значением дисперсии дальности 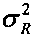 . Если с наименьшим значением дисперсии
. Если с наименьшим значением дисперсии 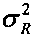 оказалось несколько методов, то для определения значений искомых координат местоположения ИРИ реализуется известное правило вычисления среднего арифметического значения одноименных координат. В этом и состоит сущность адаптивного характера заявляемого способа.
оказалось несколько методов, то для определения значений искомых координат местоположения ИРИ реализуется известное правило вычисления среднего арифметического значения одноименных координат. В этом и состоит сущность адаптивного характера заявляемого способа.
Для осуществления изобретения и достижения заявленного технического результата выполняют следующие действия:
1 одновременно на двух приемных позициях ДИК принимают излучение ИРИ и измеряют угловые координаты ИРИ αi (i=1, 2) и мощности Pi (i=1, 2) принимаемого излучения. Для этого используют пассивные пеленгаторы, снабженные каналом измерения мощности принимаемого излучения ИРИ.
2 Используя базово-корреляционный метод, вычисляют временную задержку Δt прихода волнового фронта излучения ИРИ на две разнесенные на расстояние базы b приемные позиции ДИК П1 и П2.
Далее параллельно проводят вычисления по пунктам 3, 4 и 5. Для этого используется высокопроизводительная ЭВМ.
3 Определяют координаты xИРИ, yИРИ и дисперсию 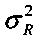 для ТМ. Для этого:
для ТМ. Для этого:
3.1 вычисляют угол θ=α2-α1;
3.2 вычисляют дальность R1=bsinα2/sinθ;
3.3 вычисляют дальность R2=bsinα1/sinθ;
3.4 вычисляют дальность 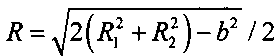 ;
;
3.5 вычисляют дисперсию 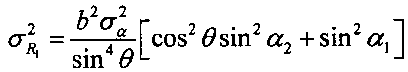 ;
;
3.6 вычисляют дисперсию 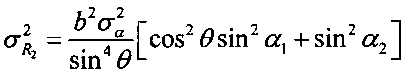 ;
;
3.7 вычисляют дисперсию ТМ  ;
;
3.8 определяют плоскостные координаты местоположения ИРИ
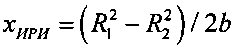 ;
;
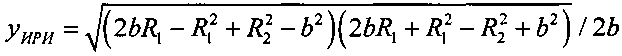 ;
;
4 определяют координаты xИРИ, yИРИ и дисперсию  для УММ. Для этого:
для УММ. Для этого:
4.1 вычисляют дисперсию  ;
;
4.2 вычисляют коэффициент 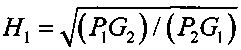 ;
;
4.3 вычисляют коэффициент  ;
;
4.4 вычисляют дисперсию  ;
;
4.5 вычисляют дисперсию 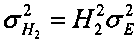 ;
;
4.6 вычисляют дисперсию 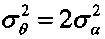 ;
;
4.7 вычисляют 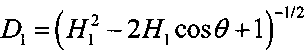 ;
;
4.8 вычисляют 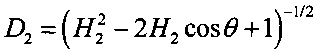 ;
;
4.9 вычисляют дисперсию 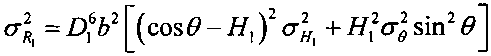 ;
;
4.10 вычисляют дисперсию  ;
;
4.11 вычисляют дальность R1=bD1;
4.12 вычисляют дальность R2=bD2;
4.13 вычисляют дальность 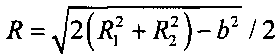 ;
;
4.14 вычисляют дисперсию УММ 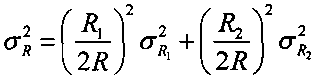 ;
;
4.15 определяют плоскостные координаты местоположения ИРИ
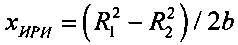 ;
;
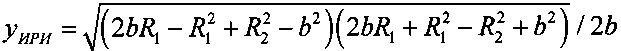 ;
;
5 определяют координаты xИРИ, YИРИ и дисперсию 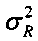 для УРДМ. Для этого:
для УРДМ. Для этого:
5.1 вычисляют параметр ΔR=Δtc;
5.2 вычисляют частную производную 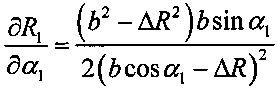 ;
;
5.3 вычисляют частную производную 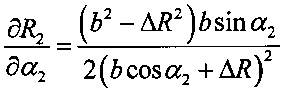 ;
;
5.4 вычисляют частную производную 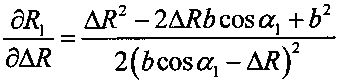 ;
;
5.5 вычисляют частную производную 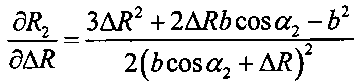 ;
;
5.6 вычисляют дисперсию 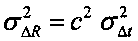 ;
;
5.7 вычисляют дисперсию 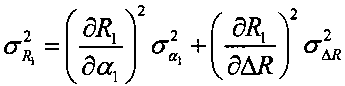 ;
;
5.8 вычисляют дисперсию  ;
;
5.9 вычисляют дальность 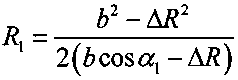 ;
;
5.10 вычисляют дальность 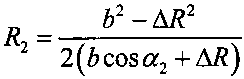 ;
;
5.11 вычисляют дальность 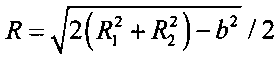 ;
;
5.12 вычисляют дисперсию УРДМ  ;
;
5.13 определяют плоскостные координаты местоположения ИРИ
 ;
;
 ;
;
6 сравнивают полученные по пунктам 3.7, 4.14 и 5.12 значения дисперсии  и выбирают наименьшее из трех значений;
и выбирают наименьшее из трех значений;
6.1 если наименьшим оказалось значение, полученное по пункту 3.7, то значения плоскостных координат местоположения ИРИ принимают равными значениям, полученным по пункту 3.8;
6.2 если наименьшим оказалось значение, полученное по пункту 4.14, то значения плоскостных координат местоположения ИРИ принимают равными значениям, полученным по пункту 4.15;
6.3 если наименьшим оказалось значение, полученное по пункту 5.12, то значения плоскостных координат местоположения ИРИ принимают равными значениям, полученным по пункту 5.13;
6.4 если наименьшими и равными между собой оказались два любых значения дисперсии из трех, рассчитанных по пунктам 3.7, 4.14 и 5.12, то значения плоскостных координат местоположения ИРИ вычисляют как средние арифметические значений соответствующих координат, полученных методами, дисперсии которых равны между собой;
6.5 если значения дисперсии, рассчитанные по пунктам 3.7, 4.14 и 5.12, равны между собой, то значения плоскостных координат местоположения ИРИ вычисляют как средние арифметические значений соответствующих координат, полученных по пунктам 3.8, 4.15 и 5.13.
Предлагаемый способ реализуют в пассивных ДИК, а также в многопозиционных пассивных измерительных комплексах в случае возникновения нештатных ситуаций, сопровождающихся деградацией измерительных структур комплекса.
Кроме того, изобретение можно применять в нормальных условиях функционирования многопозиционного измерительного комплекса для повышения точности решения задачи пассивной радиолокации за счет формирования информационной избыточности ([1], с. 501-506; [11-13]) на различных измерительных структурах, получаемых неповторяющимися парами приемных позиций комплекса. Например, в многопозиционном комплексе, состоящем из трех позиций, выделяют три независимых ДИК, на которых получают три разные по точности оценки координат местоположения ИРИ. Затем их совместно обрабатывают и получают более точную оценку координат местоположения ИРИ.
При этом реализация изобретения в пассивных измерительных комплексах не требует существенных финансово-экономических затрат, поскольку изобретение ориентировано на совершенствование программной составляющей измерительных комплексов, осуществляющей обработку входных измерительных данных (угловых координат и мощности принимаемого излучения ИРИ).
Источники информации
1. Теоретические основы радиолокации / под ред. Я. Ширмана. М: Сов. радио. 1970. 561 с.
2. Булычев Ю.Г., Головской В.А. Обработка измерений угломерных систем в условиях априорной неопределенности // Радиотехника и электроника. 2010. Т. 55. №1. С. 71-77.
3. Сытенький В.Д. Пассивная локация на основе амплитудных измерений // Известия ВУЗов России. Радиоэлектроника. 2011. №1. С. 69-75.
4. Патент РФ №2406098, МПК G01S 3/00, опубл. 10.12.2010. Способ определения наклонной дальности до движущейся цели по минимальному числу пеленгов.
5. Евдокимов Ю.Ф., Медведев В.П. Амплитудная система определения местоположения источников излучения с использованием метода наименьших квадратов и исследование ее точности // Телекоммуникации. 2003. №11. С. 34-37.
6. Уфаев В.А., Афанасьев В.И., Разиньков С.П. Оценка координат источника радиоизлучения на основе измерений амплитуды электромагнитного поля // Радиотехника. 2003. №10. С. 71-73.
7. Патент РФ №2503969, МПК G01S 3/02, G01S 3/46, опубл. 10.01.2014. Триангуляционно-гиперболический способ определения координат радиоизлучающих воздушных объектов в пространстве.
8. Вентцель Е.С. Теория вероятностей. М.: Высшая школа. 1969. 576 с.
9. Булычев Ю.Г., Вернигора В.Н., Мозоль А.А. Пеленгационно-мощностной метод определения дальности до цели по двум измерениям автономной угломерной системы // Изв. вузов. Радиоэлектроника. 2009. Т. 52. №11. С. 51-60.
10. Евдокимов Ю.Ф., Медведев В.П. Расчет погрешностей амплитудного метода определения местоположения излучающих объектов с использованием регрессионного анализа // Современные проблемы теории радиотехнических сигналов, цепей и систем. Сборник научных статей. - Таганрог: Изд-во ТРТУ. 2004. С. 133-139.
11. Рекомендации по межгосударственной стандартизации / РМГ 64 - 2003 / Обеспечение эффективности измерений при управлении технологическими процессами / Методы и способы повышения точности измерений. - Москва. ИПК Издательство стандартов. 2004.
12. Обеспечение эффективности измерений при управлении технологическими процессами / Методы и способы повышения точности измерений / МИ 2301-2000. - Москва. ВНИИМС. 2000.
13. Брюханов В.А. Методы повышения точности измерений в промышленности. - М.: Изд-во стандартов, 1991. - 108 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПАССИВНОЙ РАДИОЛОКАЦИИ ДВИЖУЩЕГОСЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2016 |
|
RU2645712C1 |
| ВРЕМЕННОЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО СКАНИРУЮЩЕГО ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ БЕЗ ИЗМЕРЕНИЯ ПЕЛЕНГА | 2018 |
|
RU2704029C1 |
| ВРЕМЕННОЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ СКАНИРУЮЩЕГО ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2020 |
|
RU2742581C1 |
| ТРИАНГУЛЯЦИОННО-ГИПЕРБОЛИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ РАДИОИЗЛУЧАЮЩИХ ВОЗДУШНЫХ ОБЪЕКТОВ В ПРОСТРАНСТВЕ | 2012 |
|
RU2503969C1 |
| Способ одноэтапного адаптивного определения координат источников радиоизлучений | 2021 |
|
RU2768011C1 |
| СПОСОБ ОТОЖДЕСТВЛЕНИЯ ПЕЛЕНГОВ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ В УГЛОМЕРНЫХ ДВУХПОЗИЦИОННЫХ ПАССИВНЫХ РАДИОЛОКАЦИОННЫХ СИСТЕМАХ | 2004 |
|
RU2253126C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ИЗЛУЧАЮЩЕЙ ОБЗОРНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2010 |
|
RU2444748C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАКЛОННОЙ ДАЛЬНОСТИ ДО ДВИЖУЩЕЙСЯ ЦЕЛИ ПО МИНИМАЛЬНОМУ ЧИСЛУ ПЕЛЕНГОВ | 2009 |
|
RU2406098C1 |
| СПОСОБ ОЦЕНИВАНИЯ ПАРАМЕТРОВ ТРАЕКТОРИИ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ В ДВУХПОЗИЦИОННОЙ УГЛОМЕРНОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2003 |
|
RU2246121C9 |
| СПОСОБ ПОЛУЧЕНИЯ РАДИОТЕХНИЧЕСКОЙ ИНФОРМАЦИИ И РАДИОТЕХНИЧЕСКИЙ КОМПЛЕКС ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2562616C1 |
Изобретение относится к пассивной радиолокации и может быть использовано в двух- и многопозиционных измерительных комплексах для определения координат местоположения источников радиоизлучения (ИРИ). Достигаемый технический результат - повышение точности определения местоположения ИРИ и расширение рабочей зоны измерительного комплекса при адаптивном способе пассивной радиолокации на базе двухпозиционного измерительного комплекса (ДИК). Способ заключается в измерении с приемных позиций ДИК угловых координат и мощности излучения ИРИ, определении временной задержки прихода волнового фронта излучения ИРИ на позиции комплекса. Далее применяют параллельно триангуляционный, угломерно-разностно-дальномерный и угломерно-мощностной методы для определения координат местоположения ИРИ. Для каждого из методов определяют значение дисперсии дальности до ИРИ, затем сравнивают эти значения и выбирают те значения координат местоположения ИРИ, которые соответствуют наименьшему значению дисперсии. При равных значениях дисперсии используют правило нахождения среднего арифметического для значений одноименных координат, получаемых двумя или тремя методами. 1 з.п. ф-лы, 1 ил.
1. Адаптивный способ пассивной радиолокации, включающий измерение с приемных позиций измерительного комплекса угловых координат источника радиоизлучения (ИРИ), определение временной задержки прихода волнового фронта излучения ИРИ на позиции комплекса, применение триангуляционного метода для определения координат местоположения ИРИ, отличающийся тем, что в качестве измерительного комплекса используют двухпозиционный измерительный комплекс (ДИК), на приемных позициях дополнительно измеряют мощности излучения ИРИ, а координаты местоположения ИРИ определяют на плоскости, причем параллельно с триангуляционным методом применяют угломерно-разностно-дальномерный и угломерно-мощностной методы, для каждого из методов определяют значение дисперсии дальности до ИРИ, затем сравнивают эти значения и выбирают те значения координат местоположения ИРИ, которые соответствуют наименьшему значению дисперсии, а при равных значениях дисперсии используют правило нахождения среднего арифметического для значений одноименных координат, получаемых двумя или тремя методами, при этом угломерно-мощностной метод определения значений плоскостных координат местоположения ИРИ осуществляют следующим образом:
вычисляют коэффициенты
 и
и 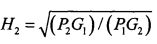 ,
,
где P1 и P2 - измеренные мощности излучения ИРИ на первой и второй позициях ДИК соответственно,
G1 и G2 - коэффициенты усиления приемных антенн первой и второй позиций ДИК соответственно;
вычисляют угол θ=α2-α1,
где αi (i=1,2) - измеренные угловые координаты ИРИ;
вычисляют значения параметров
 и
и  ;
;
вычисляют дальность от ИРИ до первой позиции комплекса 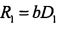 и дальность от ИРИ до второй позиции комплекса
и дальность от ИРИ до второй позиции комплекса 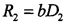 ,
,
где b - величина базы (расстояние между позициями ДИК);
определяют плоскостные координаты местоположения ИРИ
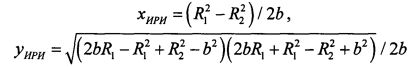 .
.
2. Способ по п. 1, отличающийся тем, что плоскостные координаты местоположения ИРИ определяют с помощью многопозиционного измерительного комплекса путем построения в нем ДИК, получаемых неповторяющимися парами приемных позиций комплекса, получения значений плоскостных координат местоположения ИРИ на основе каждого такого ДИК, формирования за счет этого избыточности оценок координат местоположения ИРИ и последующей совместной обработки этих оценок.
| ТРИАНГУЛЯЦИОННО-ГИПЕРБОЛИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ РАДИОИЗЛУЧАЮЩИХ ВОЗДУШНЫХ ОБЪЕКТОВ В ПРОСТРАНСТВЕ | 2012 |
|
RU2503969C1 |
| СПОСОБ МЕСТООПРЕДЕЛЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ И ПАССИВНАЯ РАДИОЛОКАЦИОННАЯ СТАНЦИЯ, ИСПОЛЬЗУЕМАЯ ПРИ РЕАЛИЗАЦИИ ЭТОГО СПОСОБА | 2004 |
|
RU2275649C2 |
| ДАЛЬНОМЕРНЫЙ СПОСОБ И УСТРОЙСТВО ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2011 |
|
RU2506605C2 |
| СПОСОБ КОНТРОЛЯ ВОЗДУШНОГО ПРОСТРАНСТВА, ОБЛУЧАЕМОГО ВНЕШНИМИ ИСТОЧНИКАМИ ИЗЛУЧЕНИЯ, И РАДИОЛОКАЦИОННАЯ СТАНЦИЯ ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2285939C1 |
| US 6275189 B1, 14.08.2001 | |||
| US 20060158375 A1, 20.07.2006 | |||
| JP 4460171 B2, 12.05.2010 | |||
| US 20090243933 A1, 01.10.2009. | |||
Авторы
Даты
2016-07-27—Публикация
2015-07-29—Подача