Область техники, к которой относится изобретение
Настоящее изобретение относится к способу кодирования сигнала изображения, позволяющему легко и эффективно кодировать сигнал изображения, который представляет гауссов целочисленный сигнал; способу декодирования сигнала изображения, предназначенному для декодирования кодированных данных, сгенерированных способом кодирования сигнала изображения; способу кодирования источника информации, предназначенному для простого и эффективного кодирования гауссова целочисленного сигнала, и к соответствующему устройству; способу декодирования источника информации для декодирования кодированных данных, сгенерированных способом кодирования источника информации, и к соответствующему устройству; программе кодирования источника информации, предназначенной для воплощения способа кодирования источника информации, и к считываемому компьютером носителю информации, на котором содержится программа; и программе декодирования источника информации, предназначенной для воплощения способа декодирования источника информации, и к считываемому компьютером носителю информации, на котором содержится эта программа.
Испрашивается приоритет по заявке № 2006-307512 на патент Японии, поданной 14 ноября 2006 г., содержание которой приведено здесь в качестве ссылочного материала.
Уровень техники
Гауссов сигнал представляет собой сигнал, вероятность генерирования которого соответствует нормальному распределению (также называемому "гауссовым распределением"), где нормальное распределение возникает в различных сценах в области математики и техники, и, таким образом, представляет собой чрезвычайно важное распределение.
Предполагается, что гауссов сигнал как цель кодирования здесь имеет целочисленные значения сигнала. Кроме того, в общем, предполагается, что среднее значение сигнала равно нулю, и значения сигнала являются "iid" ("нир", независимыми и идентично распределенными).
Известно множество способов кодирования целочисленного сигнала. Например, широко используют коды Голомба, с помощью которых сигнал, который соответствует экспоненциальному распределению (который можно назвать "распределением Лапласа" или "геометрическим распределением" и который представляет собой двустороннее экспоненциальное распределение, если только не будет указано другое), можно эффективно кодировать без использования таблицы для кодирования или декодирования, где коды могут быть очень легко обработаны и мгновенно декодированы. Кроме того, любое большое целочисленное входное значение может быть кодировано с использованием кодов Голомба.
Представление кода для кодов Голомба изменяется в зависимости от параметра кода Голомба (здесь обозначается как "g"), который имеет целочисленное значение, большее или равное 1.
В таблице на фиг.20 показаны коды Голомба (параметр кода Голомба g=1, …, 6), что соответствует целому числу z=0, …, 10. Коды Голомба имеют такую взаимозависимость для каждого параметра g кода, что когда значение целого числа z (предназначенного для кодирования) увеличивается на величину g, длина кода увеличивается на 1.
Поскольку увеличение длины кода сдерживают в соответствии с увеличением параметра g кода Голомба, относительно большое значение параметра g кода Голомба пригодно для кодирования пологого распределения. В отличие от этого, когда увеличение длины кода становится быстрым в соответствии с уменьшением параметра g кода Голомба, относительно малое значение параметра g кода Голомба пригодно для кодирования круто изменяющегося распределения, которое сходится к нулю.
В сигнале изображения различие яркости между пикселями, которые расположены рядом друг с другом в области времени или в пространстве, или коэффициент ортогонального преобразования значения яркости каждого пикселя представляют собой пример сигнала, который соответствует экспоненциальному распределению, и коды Голомба можно использовать для кодирования такого сигнала.
С другой стороны, в кодах Хаффмана используется кодовая таблица, они могут быть моментально декодированы, и среднее значение этих кодов является наименьшим (то есть компактные коды) среди всех кодов с переменной длиной. Кроме того, арифметические коды могут сжимать статический источник сигнала до логического предела (который может быть превосходящим по сравнению с компактными кодами) при использовании способа, отличающегося от используемого в кодах с переменной длиной.
В патентном документе 1, как описано ниже, раскрыто изобретение, направленное на векторное квантование величины свойства изображения в соответствии с двоичным деревом поиска с использованием нейронной сети, и данное изобретение относится к технологии кодирования изображения с использованием динамических кодов Хаффмана.
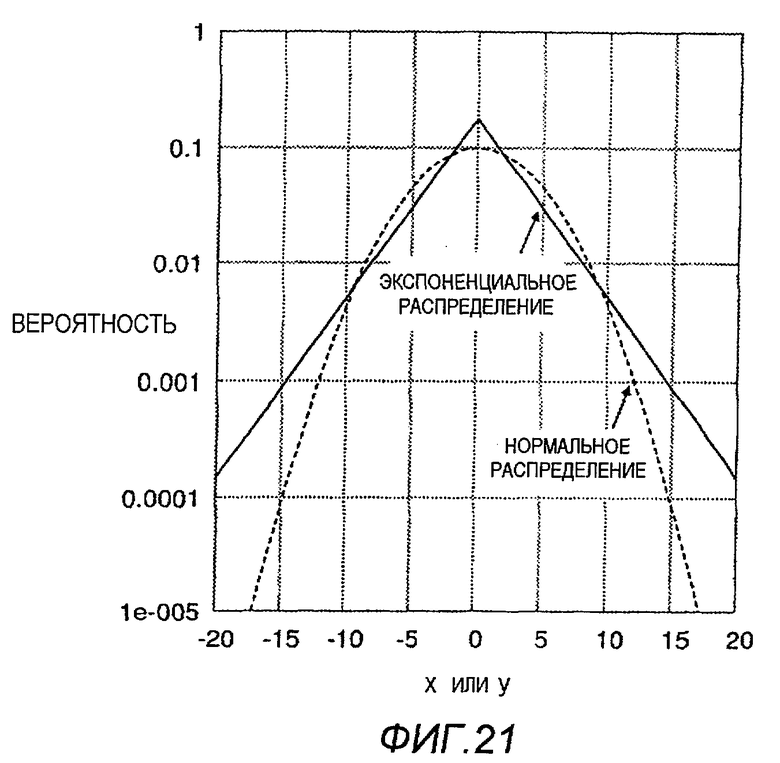
На фиг.21 показано распределение частоты для нормального распределения и экспоненциального распределения, где среднее значение равно 0, и дисперсия равна 16. По вертикальной оси показана вероятность частоты, и для представления обеих хвостовых частей каждого распределения в легко понятном представлении используется логарифм. Как показано на фиг.21, по вертикальной логарифмической шкале нормальное распределение имеет параболическую форму, и экспоненциальное распределение имеет треугольную форму.
Для того чтобы кодировать такое двустороннее симметричное целочисленное распределение, каждое значение должно быть преобразовано в целое число, большее или равное нулю, путем применения, в основном, способа представления каждого значения с использованием информации знака (положительный/отрицательный) и информации абсолютного значения по отдельности, или относительно простого преобразования, как показано ниже.
Когда значения до и после описанного выше превращения соответствующим образом будут обозначены как a и b, преобразование может быть представлено следующим образом:
b=2a-1, когда a>0
когда a>0
b=-2a,  когда а≤0.
когда а≤0.
В соответствии с этим преобразованием, а=-3, -2, -1, 0, 1, 2, 3 преобразуют соответственно в значения b=6, 4, 2, 0, 1, 3, 5.
Когда коды Голомба используют для кодирования гауссова сигнала, эффективность кодирования значительно ухудшается по сравнению с кодами Хаффмана и арифметическими кодами. Это представляет собой существенную проблему, возникающую из-за того, что вероятность сгенерированного сигнала, предназначенного для кодов Голомба, не соответствует нормальному распределению, но соответствует экспоненциальному распределению.
Аналогично кодам Голомба, имеется множество видов кодов, для которых нет необходимости использовать кодовую таблицу и которые могут представлять собой коды Фибоначчи, коды Элиаса или экспоненциальные коды Голомба. Однако отсутствуют коды, в которых применяется предположение, что вероятность генерирования сигнала соответствует нормальному распределению.
В непатентном документе 1 (описан ниже) на странице 8 указано, что "в отличие от того, что происходит для геометрического и двустороннего геометрического распределения, отсутствует простой, мгновенный код для нормального распределения". То есть, отсутствуют коды, для которых применяют предположение, что вероятность генерирования сигнала соответствует нормальному распределению.
Поэтому, если будет задан приоритет эффективности кодирования при кодировании гауссова сигнала, обычно используют коды Хаффмана или арифметические коды.
Однако при этом также возникают следующие проблемы:
(i) Для арифметических кодов требуются таблицы частот, которые не требуются для кодов Голомба, как в кодере, так и в декодере.
(ii) Для кодов Хаффмана требуется кодовая таблица или таблицы частот, которые не требуются для кодов Голомба, как в кодере, так и в декодере.
(iii) Для обоих видов кодов требуется заранее определять диапазон, в котором кодирование каждого входного значения не может быть выполнено без обработки исключения, то есть требуется детектировать диапазон входного значения.
(iv) Для обоих видов кодов объем обработки больше, чем для кодов Голомба, причем объем обработки для арифметических кодов особенно велик.
Кроме того, в непатентном документе 2, описанном ниже, представлены гибридные коды Голомба, с помощью которых можно моментально декодировать обобщенный источник гауссова сигнала. Хотя возможно кодировать и декодировать любое большое целочисленное входное значение, в данном случае требуется сложная структура, которая нацелена на распределение, еще более крутое, чем экспоненциальное распределение, которое круче, чем нормальное распределение.
Кроме того, если во время кодирования гауссова сигнала будет задан приоритет простоте кодирования, обычно, как показано в непатентном документе 1, используют коды Голомба из-за эффективности кодирования. Однако в данном случае возникает проблема, состоящая в том, что необходима оптимизация параметра кода Голомба.
Патентный документ 1: находящаяся на экспертизе заявка на японский патент, первая публикация № 2001-5967;
Непатентный документ 1: P. Boldi, S. Vigna: "Compressed perfect embedded skip lists for quick inverted-index lookups", Proceedings of String Processing and Information Retrieval, 12th International Conference, pp.1-15, 2005;
Непатентный документ 2: S. Xue, Y. Xu, B. Oelmann: "Hybrid Golomb codes for a group of quantised GG sources", IEE Proceedings, Vision Image and Signal Processing, Vol.150, No.4, pp.256-260, 2003.
Сущность изобретения
Задачи, решаемые изобретением
Хотя существуют универсальные коды для эффективного кодирования различных видов обобщенных источников сигнала, таких как сигналы изображения и голосовые сигналы, которые следуют нормальному распределению, отсутствуют коды, в которых используется предположение, что вероятность генерирования сигнала следует нормальному распределению, как показано в непатентном документе 1.
Поэтому можно ожидать кодирование гауссова сигнала с использованием кодов Голомба.
Как описано выше, сигнал, который соответствует экспоненциальному распределению, можно эффективно кодировать, используя коды; при этом при использовании кодов Голомба не требуются таблицы для кодирования и декодирования; коды Голомба могут быть очень просто обработаны и мгновенно декодированы; и, кроме того, любое крупное целочисленное входное значение может быть кодировано с помощью кодов Голомба.
Однако вероятность генерирования сигнала при экспоненциальном распределении назначается как допущение для кодов Голомба. Поэтому, если гауссов сигнал кодируется с использованием кодов Голомба, эффективность кодирования существенно ухудшается по сравнению с эффективностью кодов Хаффмана или арифметических кодов.
Поэтому обычно, когда кодируют гауссов сигнал, используют коды Хаффмана или арифметические коды.
Однако, когда используют коды Хаффмана или арифметические коды, возникает проблема, состоящая в том, что необходимо использовать таблицу частот, которая не требуется для кодов Голомба; диапазон входного значения требуется определять заранее; и объем обработки больше, чем при использовании кодов Голомба.
Учитывая описанные выше проблемы, в непатентном документе 2 предложены гибридные коды Голомба. Однако в данном случае требуется сложная конструкция, и она направлена на распределение, которое дополнительно круче, чем экспоненциальное распределение, которое круче, чем нормальное распределение.
Кроме того, в непатентном документе 1 установлен приоритет простоте обработки кодирования, и коды Голомба используются путем оптимизации параметра кода Голомба без учета эффективности кодирования. Однако в этом случае эффективность кодирования ухудшается по сравнению с кодами Хаффмана или арифметическими кодами, и при этом необходимо оптимизировать параметр кода Голомба.
Учитывая описанные выше обстоятельства, цель настоящего изобретения состоит в том, чтобы обеспечить новые технологии кодирования и декодирования источника информации для простого и эффективного кодирования и декодирования целочисленного гауссова сигнала.
Средство решения задачи
(1) Устройство кодирования источника информации в соответствии с настоящим изобретением
Для того чтобы легко и эффективно кодировать гауссов целочисленный сигнал, устройство кодирования источника информации в соответствии с настоящим изобретением включает в себя (i) блок ввода, предназначенный для ввода последовательности значений сигнала гауссова целочисленного сигнала, как цель кодирования; (ii) блок преобразования пары целых чисел, предназначенный для преобразования значений сигнала, включенных в последовательность значений сигналов (вводимых входным устройством), в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода; (iii) блок рассмотрения, предназначенный для рассмотрения каждой из пар целых чисел (полученных в результате преобразования в устройстве преобразования пары целых чисел) в виде точек решетки в двумерных координатах и получения целочисленных значений, больших или равных нулю, в результате выполнения двумерного на одномерное отображение, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают точке решетки в результате отображения; и (iv) блок кодирования, предназначенный для кодирования целочисленных значений (полученных устройством отображения) с использованием кодов, которые использовали для кодирования источника информации, который соответствует экспоненциальному распределению.
В описанной выше конструкции блок кодирования может кодировать целочисленные значения (полученные устройством отображения) с использованием кодов Голомба, которые пригодны для кодирования источника информации, который соответствует экспоненциальному распределению. В таком случае, для того чтобы автоматически установить параметры кода Голомба, устройство может дополнительно включать в себя (i) устройство расчета дисперсии, предназначенное для расчета дисперсии значений сигнала, вводимых входным устройством; и (ii) устройство определения параметра кода, предназначенное для определения параметра кода для кодов Голомба, который имеет значение, пропорциональное дисперсии, рассчитанной устройством расчета дисперсии.
Устройство кодирования источника информации, в соответствии с настоящим изобретением, может иметь цель кодирования, которая представляет собой сигнал изображения, обозначающий гауссов целочисленный сигнал, в таком случае устройство кодирования источника информации в соответствии с настоящим изобретением работает как устройство кодирования сигнала изображения.
Способ кодирования источника информации в соответствии с настоящим изобретением, который воплощается при работе описанных выше устройств, также может быть воплощен в виде компьютерной программы. Такая компьютерная программа может быть предоставлена в результате сохранения ее на соответствующем считываемом компьютером носителе информации или путем передачи по сети, и она может быть установлена и может работать в устройстве управления, таком как ЦПУ, для воплощения настоящего изобретения.
(2) Устройство декодирования источника информации в соответствии с настоящим изобретением
Для того чтобы декодировать кодированные данные, генерируемые устройством кодирования источника информации в соответствии с настоящим изобретением, устройство декодирования источника информации в соответствии с настоящим изобретением включает в себя (i) блок декодирования, предназначенный для декодирования целочисленных значений путем декодирования их кодированных данных, которые генерируют устройством кодирования источника информации в соответствии с настоящим изобретением; (ii) блок восстановления, предназначенный для восстановления пар целых чисел (которые были отображены для получения значений целых чисел) путем выполнения для значений целых чисел (декодированных устройством декодирования) одномерного-двумерного отображения, которое представляет собой обратное отображение для двумерного-одномерного отображения, используемого устройством кодирования источника информации в соответствии с настоящим изобретением; и (iii) блок вывода, предназначенный для вывода целых чисел, которые формируют каждую пару целых чисел (восстановленных устройством восстановления) от первого его элемента до второго элемента.
Для описанной выше структуры, если устройство кодирования источника информации в соответствии с настоящим изобретением генерирует кодированные данные в виде значений целых чисел, используя коды Голомба, устройство декодирования декодирует кодированные данные значений этих целых чисел путем декодирования соответствующих кодов Голомба.
Также для описанной выше структуры, если устройство кодирования источника информации в соответствии с настоящим изобретением определяет параметр кода для кодов Голомба, который имеет значение, пропорциональное дисперсии значений сигнала - цели кодирования, тогда устройство декодирования дополнительно включает в себя устройство ввода параметра кода Голомба для ввода параметра кода Голомба, как определено выше, как параметра кода Голомба, используемого для декодирования.
Если устройство кодирования источника информации в соответствии с настоящим изобретением генерирует кодированные данные цели кодирования, которые представляют собой сигнал изображения, обозначающий гауссов целочисленный сигнал, тогда устройство декодирования источника информации в соответствии с настоящим изобретением выполняет функцию устройства декодирования сигнала изображения.
Способ декодирования источника информации в соответствии с настоящим изобретением, который воплощают при работе описанного выше устройства, также может быть воплощен с помощью компьютерной программы. Такая компьютерная программа может быть предоставлена в результате сохранения ее на соответствующем считываемом компьютером носителе информации или путем передачи по сети, и она может быть установлена и может работать в устройстве управления, таком как ЦПУ, для воплощения настоящего изобретения.
Эффект изобретения
Как описано выше, в соответствии с настоящим изобретением, становится возможным просто и эффективно кодировать и декодировать гауссов целочисленный сигнал, который нельзя было эффективно кодировать с использованием известных кодов Голомба или тому подобного, хотя гауссов целочисленный сигнал появляется в различных сценах в области математики и техники.
Кроме того, обычно, по мере того, как источник информации расширяется, эффективность кодирования соответствующего кодирования с переменной длиной улучшается. Преобразование между парами целых чисел и целыми числами, используемыми в настоящем изобретении, представляет собой всего лишь двумерные расширения источника информации, и, таким образом, эффективность кодирования может быть улучшена в соответствии с настоящим изобретением.
Краткое описание чертежей
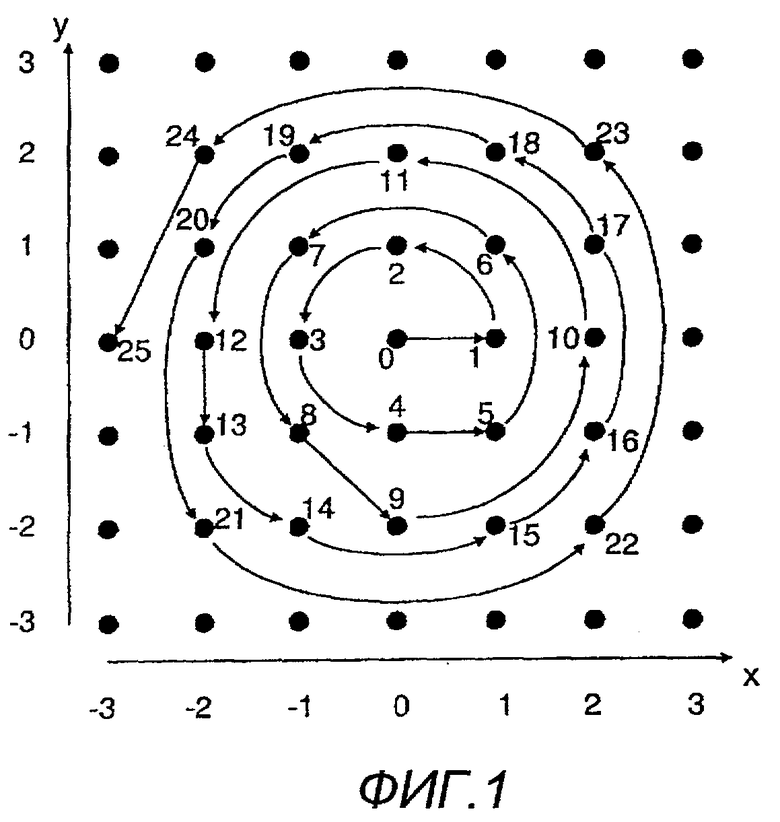
На фиг.1 показана схема, представляющая пример двумерного-одномерного отображения, выполняемого в настоящем изобретении.
На фиг.2 показана схема, поясняющая таблицу, в которой сохраняются соответствующие взаимозависимости между парами целых чисел и целыми числами.
На фиг.3 показана конструкция устройства кодирования источника информации и устройства декодирования источника информации, как вариант воплощения настоящего изобретения.
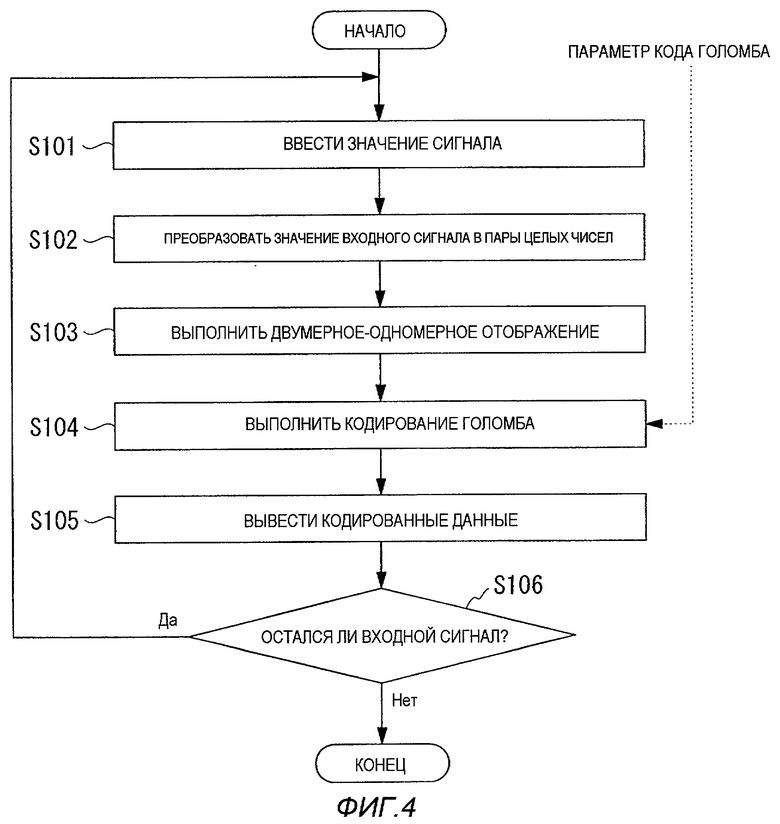
На фиг.4 показана блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантами воплощения.
На фиг.5 показана схема, поясняющая алгоритм для воплощения двумерного-одномерного отображения, выполняемого в настоящем изобретении.
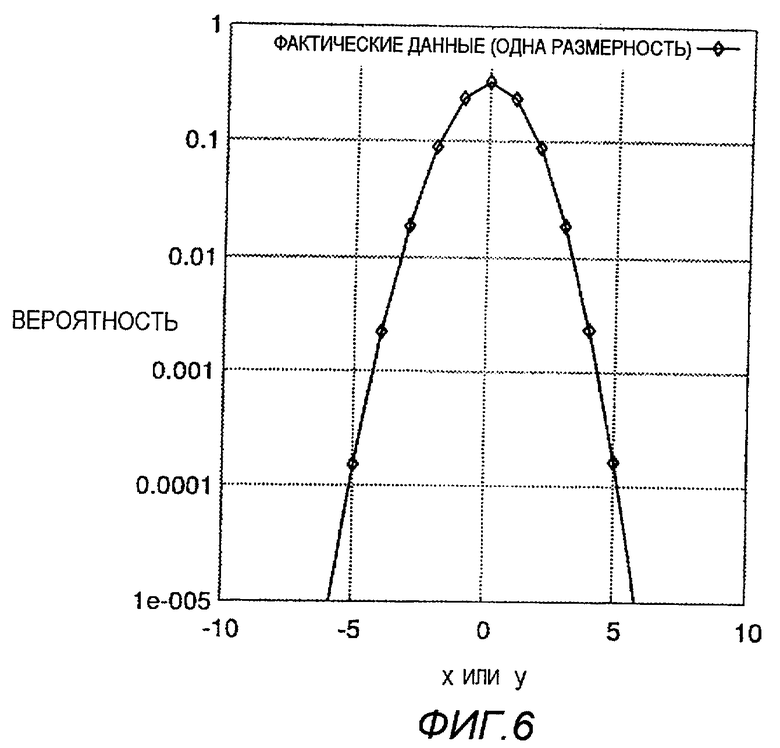
На фиг.6 показана схема, представляющая результаты эксперимента, выполняемого для проверки эффективности настоящего изобретения.
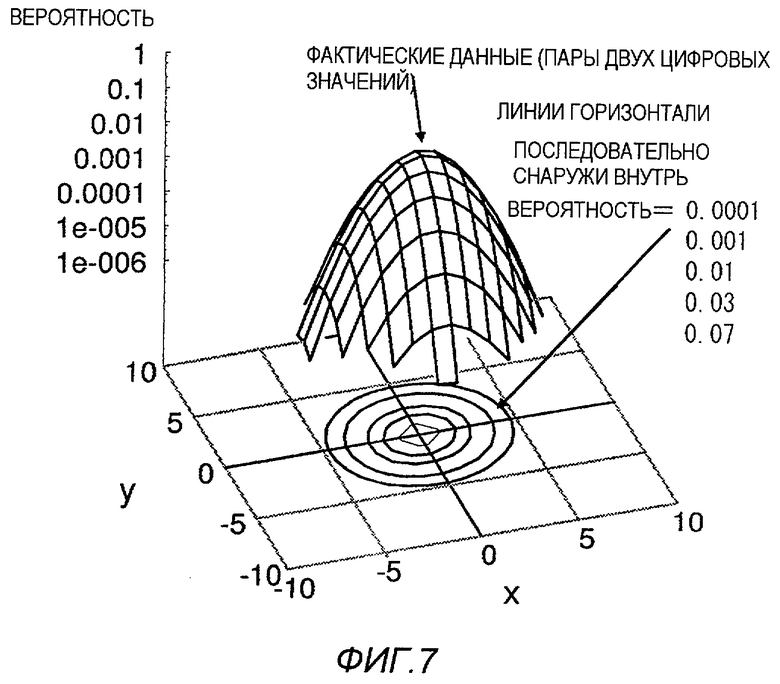
На фиг.7 также показана схема, представляющая результаты эксперимента, выполняемого для проверки эффективности настоящего изобретения.
На фиг.8 также показана схема, представляющая результаты эксперимента, выполняемого для проверки эффективности настоящего изобретения.
На фиг.9 также показана схема, представляющая результаты эксперимента, выполняемого для проверки эффективности настоящего изобретения.
На фиг.10 также показана схема, представляющая результаты эксперимента, выполняемого для проверки эффективности настоящего изобретения.
На фиг.11 показана блок-схема последовательности операций, выполняемая устройством декодирования источника информации в соответствии с вариантом воплощения.
На фиг.12 показана подробная блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантом воплощения.
На фиг.13 также представлена подробная блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантом воплощения.
На фиг.14 также представлена подробная блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантом воплощения.
На фиг.15 также представлена подробная блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантом воплощения.
На фиг.16 также представлена подробная блок-схема последовательности операций, выполняемая устройством кодирования источника информации в соответствии с вариантом воплощения.
На фиг.17 показана подробная блок-схема последовательности операций, выполняемая устройством декодирования источника информации в соответствии с вариантом воплощения.
На фиг.18 показана подробная блок-схема последовательности операций, выполняемая устройством декодирования источника информации в соответствии с вариантом воплощения.
На фиг.19 также показана подробная блок-схема последовательности операций, выполняемая устройством декодирования источника информации в соответствии с вариантом воплощения.
На фиг.20 показана схема, поясняющая коды Голомба.
На фиг.21 показана схема, поясняющая нормальное распределение и экспоненциальное распределение.
Номера ссылочных позиций
1 - устройство кодирования источника информации
2 - устройство декодирования источника информации
10 - модуль ввода сигнала
11 - модуль преобразования пар целых чисел
12 - модуль двумерного-одномерного отображения
13 - кодер Голомба
20 - модуль ввода кодированных данных
21 - декодер Голомба
22 - модуль одномерного-двумерного обратного отображения
23 - модуль последовательного вывода
Подробное описание изобретения
В способе кодирования источника информации в соответствии с настоящим изобретением гауссов целочисленный сигнал, который вводят в порядке a1, a2, a3, а4, …, преобразуют в пары целых чисел, каждая из которых имеет два элемента, такие как (а1, a2), (a3, a4),..., в соответствии с порядком ввода. Каждая пара целых чисел представлена как (x, y).
Затем пару (x, y) целых чисел подвергают двумерному-одномерному отображению, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают для точки решетки во время отображения, таким образом, что получают соответствующее целое число (значение) z (больше или равное 0).
В соответствии с таким двумерным-одномерным отображением, при котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают для этой точки решетки, каждую пару (x, y) целых чисел преобразуют в целое число z, как показано на фиг.1.
Описанная выше обработка отображения может быть выполнена путем подготовки таблицы (см. фиг.2), в которой заранее сохраняют соответствующие взаимозависимости между парами целых чисел и значениями целых чисел, и путем ссылки к таблице, с использованием пары (x, y) целых чисел в качестве ключа, получают, таким образом, целое число z как результат отображения для этой пары (x, y) целых чисел.
В отличие от таблицы частот, требуемой при использовании кодов Хаффмана или арифметических кодов, описанная выше подготовленная таблица не зависит от источника информации как цели кодирования и может использоваться обобщенно.
Кроме того, описанный выше процесс отображения можно выполнять путем повторения (i) расчета минимального расстояния от точки решетки в начале координат, используемой как начальная точка для несжатых точек решетки (то есть еще не скомпонованных), и (ii) компоновки каждой точки решетки, имеющей минимальное расстояние от начала координат, в определенном порядке с назначением индивидуального целого значения для каждой скомпонованной точки решетки, получая, таким образом, целое число z как результат отображения для каждой пары (x, y) целых чисел.
Путем использования описанного выше способа можно установить соответствие между каждой парой (x, y) целых чисел и каждым целым числом (z) без назначения верхнего и нижнего пределов для значения сигнала.
В способе кодирования источника информации в соответствии с настоящим изобретением используется двумерное-одномерное отображение, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки по следующей причине.
Значение z точки, которая расположена далеко от начала координат на расстоянии L, приблизительно равно количеству точек решетки в пределах круга, радиус которого равен L, и также приблизительно равно площади этого круга, то есть "z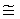 πL2". Это общее приближение (фактическое количество точек решетки очень велико) и "приблизительное равенство" эффективны, когда, например, величина z составляет несколько сотен.
πL2". Это общее приближение (фактическое количество точек решетки очень велико) и "приблизительное равенство" эффективны, когда, например, величина z составляет несколько сотен.
Вероятность для точек решетки первоначально может быть представлена с использованием нормального распределения, то есть "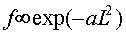 ", где a представляет собой константу. Поэтому, используя описанную выше взаимозависимость "z
", где a представляет собой константу. Поэтому, используя описанную выше взаимозависимость "z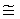 πL2", для z получают экспоненциальное распределение
πL2", для z получают экспоненциальное распределение
"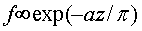 ".
".
В соответствии с этим, обратимое отображение для преобразования источника гауссова сигнала в источник сигнала с экспоненциальным распределением реализуют с применением двумерного-одномерного отображения (используемого в способе кодирования источника информации в соответствии с настоящим изобретением), в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки.
Поэтому в способе кодирования источника информации в соответствии с настоящим изобретением целое число z получают путем применения двумерного-одномерного отображения для пары (x, y) целых чисел и затем кодируют, используя коды (например, коды Голомба), которые используют для кодирования источника информации, который следует экспоненциальному распределению.
Как описано выше, сигнал, который следует экспоненциальному распределению, может быть эффективно кодирован с использованием кодов Голомба, при этом не требуется таблица кодов для соответствующего кодирования и декодирования, коды Голомба могут быть очень просто обработаны и мгновенно декодированы, и можно кодировать любое большое целочисленное входное значение.
Поэтому, в соответствии со способом кодирования источника информации, в соответствии с настоящим изобретением, гауссов целочисленный сигнал может быть легко и эффективно кодирован.
Кроме того, в способе декодирования источника информации в соответствии с настоящим изобретением кодированные данные для целых чисел, которые вводят как "z1, z2, z3, z4, …", декодируют таким образом, что каждое целочисленное значение z, которое было кодировано с использованием способа кодирования источника информации в соответствии с настоящим изобретением, декодируют в порядке ввода кодированных данных.
При описанной выше обработке, если кодированные данные для целых чисел генерируют с помощью способа кодирования источника информации в соответствии с изобретением, в котором используются коды Голомба, тогда кодированные данные подвергают декодированию Голомба для получения декодированного целочисленного значения.
Затем декодированное целое число z подвергают одномерному-двумерному отображению, которое представляет собой обратное отображение для двумерного-одномерного отображения, использовавшегося в способе кодирования источника информации в соответствии с настоящим изобретением, таким образом, что восстанавливают пару (x, y) целых чисел (то есть в том виде, как они были введены в первое отображение).
Когда выполняют двумерное-одномерное отображение, используемое в способе кодирования источника информации в соответствии с настоящим изобретением, и затем получают декодированное целое число z, описанное выше одномерное-двумерное отображение выполняют путем определения пары (x, y) целых чисел, назначенной для z.
Поэтому, аналогично обработке кодирования, выполняемой в способе кодирования источника информации в соответствии с настоящим изобретением, одномерное-двумерное отображение может быть выполнено путем подготовки таблицы (см. фиг.2), в которой заранее сохраняют соответствующие взаимозависимости между парами целых чисел и значениями целых чисел, и путем ссылки к таблице с использованием целого числа z в качестве ключа, получая, таким образом, пару (x, y) целых чисел как результат отображения для целого числа z.
Кроме того, описанный выше процесс отображения может выполняться путем повторения следующего: (i) рассчитывают минимальное расстояние от точки решетки в начале координат, которую используют как начальную точку для точек решетки, которые еще не были скомпонованы, и (ii) компонуют каждую точку решетки, имеющую минимальное расстояние от начала координат, в определенном порядке и назначают индивидуальное целое значение каждой точке решетки, получая, таким образом, пару (x, y) целых чисел как результат отображения для каждого целого числа z.
На следующем этапе способа декодирования источника информации в соответствии с настоящим изобретением целые значения x и y, которые формируют пару (x, y) целых чисел, последовательно выводят (x и затем y).
Как описано выше, в соответствии со способом декодирования источника информации, в соответствии с настоящим изобретением, кодированные данные, которые получают путем кодирования, применяя коды, используемые для кодирования источника информации, который соответствует экспоненциальному распределению, декодируют так, что можно просто и эффективно декодировать гауссов целочисленный сигнал.
Ниже настоящее изобретение поясняется подробно в соответствии с вариантом воплощения, в котором источник гауссова сигнала преобразуют в источник экспоненциального сигнала, используя двумерное расширение и формирование одномерной последовательности источника гауссова сигнала, и преобразованный результат кодируют, используя коды Голомба, пригодные для источника экспоненциального сигнала.
На фиг.3 показана структура устройства 1 кодирования источника информации и устройства 2 декодирования источника информации в качестве вариантов воплощения настоящего изобретения.
Как показано на фиг.3, устройство 1 кодирования источника информации в соответствии с настоящим изобретением включает в себя модуль 10 ввода сигнала, в который вводят последовательность значений сигнала гауссова целочисленного сигнала (в качестве цели кодирования); модуль 11 преобразования пары целых чисел, предназначенный для преобразования значений сигнала (вводимых через модуль 10 ввода сигнала) в пары целых чисел (каждая из которых имеет два элемента) в порядке вывода; модуль 12 двумерного-одномерного отображения, предназначенный для применения двумерного-одномерного отображения к парам целых чисел, полученным в результате преобразования выполняемого модулем 11 преобразования пары целых чисел, в котором, при отображении, чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают для этой точки решетки, в результате чего получают целочисленные значения, большие или равные нулю; и кодер 13 Голомба, предназначенный для кодирования значений целых чисел, полученных модулем 12 двумерного-одномерного отображения, используя коды Голомба.
С другой стороны, устройство 2 декодирования источника информации в соответствии с настоящим изобретением включает в себя модуль 20 ввода кодированных данных, в который вводят кодированные данные для целочисленных значений; декодер 21 Голомба, предназначенный для обработки кодированных данных, которые были введены через модуль 20 ввода кодированных данных, с декодированием Голомба для восстановления целочисленных значений; модуль 22 одномерного-двумерного обратного отображения, предназначенный для восстановления пар целых чисел, когда процесс отображения был выполнен модулем 12 одномерного-двумерного отображения в устройстве 1 кодирования источника информации, в соответствии с настоящим изобретением, и были получены целочисленные значения, декодированные декодером 21 Голомба, где пары целых чисел, восстановленные модулем 22, соответствуют входным данным двумерно-одномерного отображения для генерирования значений целых чисел, декодированных декодером 21 Голомба и восстановленных путем указания пар целых чисел, соответствующих декодированным значениям целых чисел; и модуль 23 последовательного вывода, предназначенный для вывода целых чисел, которые формируют пары целых чисел, восстановленные модулем 22 одномерного-двумерного обратного отображения, в порядке от первого элемента до второго элемента в каждой паре.
На фиг.4 показан пример блок-схемы последовательности операций, выполняемых устройством 1 кодирования источника информации, имеющего описанную выше структуру, в соответствии с настоящим изобретением.
Ниже подробно поясняется обработка, выполняемая устройством 1 кодирования источника информации на основе настоящего изобретения, со ссылкой на блок-схему последовательности операций.
В устройстве 1 кодирования источника информации на основе настоящего изобретения на первом этапе S101 значения сигнала для гауссова целочисленного сигнала вводят в виде каждой пары из двух элементов, начиная с начала сигнала.
На следующем этапе S102 гауссов целочисленный сигнал, который вводят в порядке от а1, a2 → a3, a4 →,..., преобразуют в пары целых чисел, каждая из которых имеет два элемента, такие как (а1, a2), (a3, a4),..., в соответствии с порядком ввода. Каждая пара целых чисел представлена как (x, y).
На следующем этапе S103 пару (x, y) целых чисел подвергают двумерному-одномерному отображению, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают точке решетки в результате отображения, таким образом, что получают соответствующее целое число (значение) z (большее или равное 0).
На следующем этапе S104 целое число z подвергают кодированию Голомба, используя параметр g кода Голомба, который предоставляют отдельно, и на следующем этапе S105 выводят полученные кодированные данные.
На следующем этапе S106 определяют, был ли закончен ввод гауссова целочисленного сигнала. Если он еще не был закончен, обработка снова возвращается на этап S101, в то время как, если ввод был закончен, операция заканчивается.
Как указано выше, параметр g кода Голомба предоставляется отдельно. Однако статистические характеристики входного сигнала можно исследовать заранее, и параметр g может быть соответствующим образом определен на основе результата исследования.
Например, если входной сигнал имеет дисперсию σ2, тогда параметр g кода Голомба может быть определен следующим образом:
g=2∙loge2∙π∙σ2,
где значение g соответствующим образом округляют.
В приведенном выше пояснении со ссылкой на фиг.20, когда выполняют кодирование, используя коды Голомба, большое значение параметра g кода Голомба пригодно для кодирования плавного распределения, в то время как малое значение параметра g кода Голомба пригодно для кодирования крутого распределения, которое сходится к нулю. Поэтому, когда параметр g кода Голомба определяют в соответствии с таким правилом, соответствующее значение параметра g кода Голомба может быть автоматически определено.
Ниже поясняется двумерное-одномерное отображение, выполняемое на этапе S103.
При двумерном-одномерном отображении (см., например, фиг.1), чем короче расстояние от каждой точки решетки до начала координат, тем меньшее целочисленное значение z назначают этой точке решетки. Поэтому одномерное-двумерное отображение для первых девяти z значений показано на фиг.2.
Обычно существует множество точек решетки, имеющих одинаковое расстояние от начала координат. Однако можно применять любой способ нумерации для таких точек решетки. Как показано на фиг.1, может быть выполнена нумерация против часовой стрелки от начала до конца. Однако можно использовать любой способ нумерации на основе однородного правила таким образом, чтобы сторона кодера могла выполнять соответствующее обратное преобразование.
Кроме того, хотя необходимо принять верхние и нижние пределы входных значений x и y, соответствующая таблица, такая как показана на фиг.2, может быть заранее подготовлена так, что двумерное расширение, формирование одномерной последовательности и процессы, обратные для них, могут быть легко выполнены только путем обращения к таблице.
Для практического использования в большинстве случаев могут быть приняты верхние и нижние пределы входных значений. Например, если будет установлен как цель дифференциальный сигнал для 8-битного изображения, тогда возможно установить -255≤x и y≤255. В этом случае будет предусмотрена таблица, имеющая 261121 элемент, где:
(255-(-255)+1)2=5112=261121.
Даже когда верхний и нижний пределы входных значений не могут быть установлены, можно установить бесконечное соответствие между (x, y) и z путем компоновки точек решетки в порядке степени близости к началу координат, без ограничений, используя псевдокоды, генерируемые с помощью такого алгоритма, как показано на фиг.5. Этот алгоритм будет подробно описан ниже.
На фиг.5 l(x, y) обозначает расстояние между началом координат и точкой (x, y), где в качестве расстояния обычно используют евклидово расстояние:
l(x, y)=(x2+y2)1/2.
Вместо этого можно использовать квадратное евклидово расстояние, которое проще обрабатывать и с помощью которого получают тот же результат нумерации:
l(x, y)=x2+y2.
Кроме того, функция l(x, y) расстояния может не быть изотропной. Если элементы входного источника гауссовой информации не строго соответствует iid (независимый и идентично распределенный) и существует корреляция между ними, тогда можно использовать следующую формулу, применяя соответствующую константу α:
l(x, y)=x2+y2+αxy,
где α<0, когда существует положительная корреляция между x и y, и α>0, когда существует отрицательная корреляция между x и y.
Кроме того, в соответствии с формой двумерного распределения пар входного сигнала можно использовать норму L1, такую как:
l(x, y)=|x|+|y|,
или в более общем случае можно использовать следующую норму Lγ (γ представляет собой степень каждого элемента сигнала):
[Формула 1]
l(x, y)=|x|γ+|y|γ.
Ниже будут представлены результаты эксперимента, выполненного для проверки эффективности настоящего изобретения.
На фиг.6 показано распределение частоты источника сигнала, который очень близок к гауссову сигналу, полученного в результате обработки фактического изображения. По вертикальной оси представлен логарифм соответствующей вероятности. Очевидно, что распределение частоты текущего источника сигнала имеет параболическую форму, то есть он соответствует нормальному распределению.
На фиг.7 показан график, полученный путем последовательного выделения элементов описанного выше источника сигнала в виде пар двух числовых значений (x, y) с представлением его распределения частоты в трехмерной форме. Аналогично, по вертикальной оси представлен логарифм соответствующей вероятности. На графике показан параболоид вращения, формируемый в результате вращения параболы.
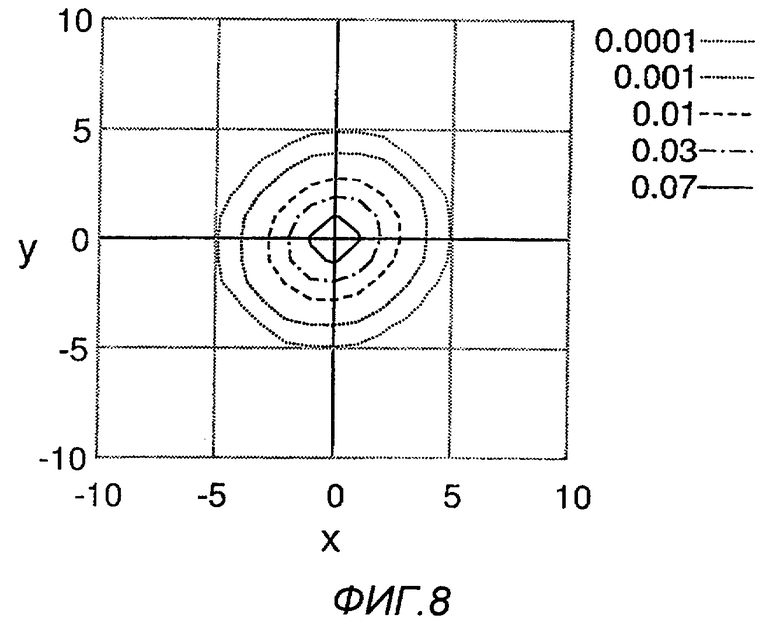
На фиг.8 показаны линии горизонтали параболоида вращения. Эти линии горизонтали практически концентричны, хотя между ними наблюдается слабая положительная корреляция.
На графике, имеющем вертикальную логарифмическую шкалу, экспоненциальное распределение проявляет треугольную форму, как представлено на фиг.21. Однако после того как сигнал будет преобразован так, что он имеет одностороннее распределение, с помощью описанных выше формул:
b=2a-1, когда a>0
b=-2a, когда a≤0,
получают прямую линию, снижающуюся вправо.
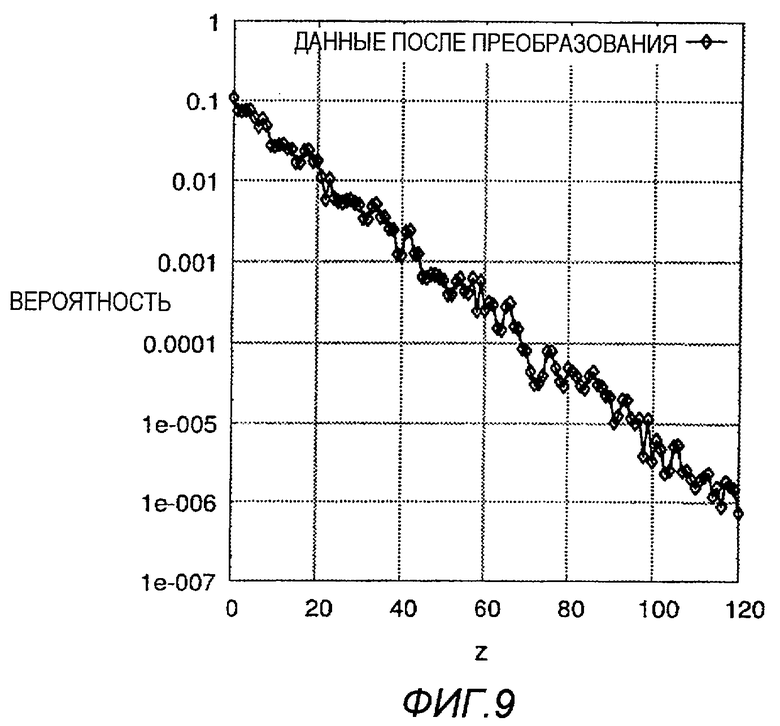
На фиг.9 показано распределение частоты одномерного значения z, которое получают путем выполнения для пары (x, y) значений двумерного-одномерного отображения в соответствии с настоящим изобретением по вертикальной логарифмической шкале, аналогично фиг.6.
На графике показана практически прямая линия, продолжающаяся вправо, что означает, что распределение практически совпадает с экспоненциальным распределением. Поэтому можно ожидать эффективное кодирование с использованием кодов Голомба.
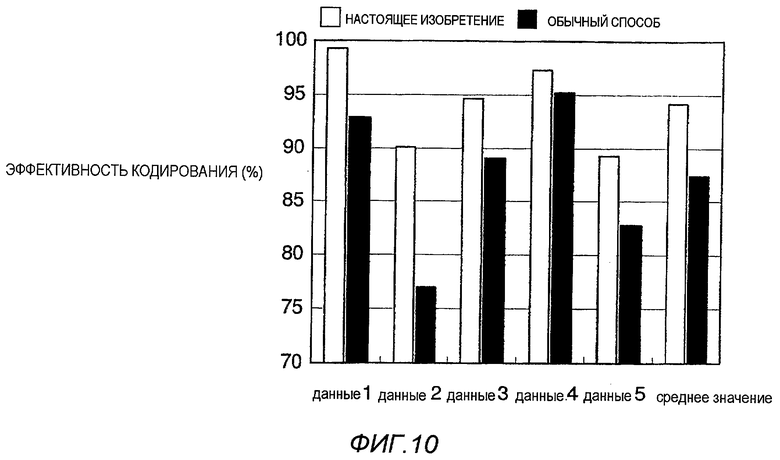
Фактические результаты кодирования будут представлены ниже. Используемый источник информации включает в себя 13509440 выборок, и объем информации, рассчитанный с использованием энтропии, составляет 64035731 (битов). Это значение является теоретическим, и величина кода, генерируемого при фактическом кодировании, всегда превышает это значение.
Описанный выше источник информации подвергали двумерному-одномерному отображению в соответствии с настоящим изобретением, и результат, представленный с помощью параметра g=7 кода Голомба, составил 64503706 (битов) таким образом, что кодирование можно было выполнить с увеличением количества кода на 0,73% (то есть эффективность кодирования составила 0,9927).
В обычном способе, выполняемом как сравнительный пример, тот же источник информации подвергали кодированию Голомба без какого-либо определенного отображения, где коды Голомба при g=1 позволяют получить минимальный результат, который составил 68898893 (бита) (то есть эффективность кодирования составила 0,9294).
Другие четыре типа данных подвергали аналогичным экспериментам.
На фиг.10 представлены результаты сравнения эффективности кодирования, полученные в ходе экспериментов. Среди данных 1-5 на фиг.10 данные 1 соответствуют описанному выше результату. Эффективность кодирования настоящего изобретения всегда составляла 90% или выше. Что касается среднего значения эффективности кодирования, настоящее изобретение имеет среднее значение 94,1%, в то время как обычный способ имеет среднее значение 87,4%, таким образом наблюдали разность между ними приблизительно на 7 пунктов.
В соответствии с этим, эффективность процесса кодирования, выполняемого устройством 1 кодирования источника информации в соответствии с настоящим изобретением, может быть проверена в случае, когда устройство 1 кодирования источника информации кодирует гауссов целочисленный сигнал на основе блок-схемы последовательности операций, показанной на фиг.4.
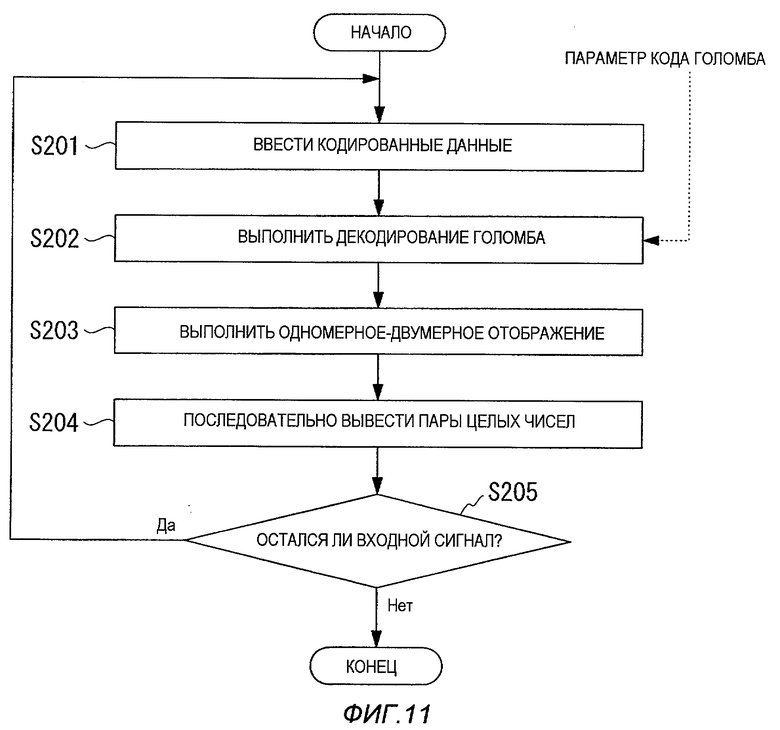
На фиг.11 показан пример блок-схемы последовательности операций, выполняемых устройством 2 декодирования источника информации, имеющим структуру, показанную на фиг.3, в соответствии с настоящим изобретением.
Процесс, выполняемый устройством 2 декодирования источника информации на основе настоящего изобретения, подробно поясняется ниже со ссылкой на блок-схему последовательности операций.
В устройстве 2 декодирования источника информации на основе настоящего изобретения на первом этапе S201 элементы кодированных данных (коды Голомба целочисленных значений z), генерируемые устройством 1 кодирования источника информации на основе настоящего изобретения, вводят один за другим, начиная с начала кодированных данных.
На следующем этапе S202 входные коды Голомба декодируют, используя параметр g кода Голомба, для получения целочисленных значений z, больше или равных нулю.
На следующем этапе S203 целочисленные значения z подвергают одномерному-двумерному отображению для отображения целочисленных значений z в пары (x, y) целых чисел. На следующем этапе S204 каждую пару (x, y) целых чисел выводят в порядке от x до y.
Когда выполняют двумерное-одномерное отображение, используемое в устройстве 1 кодирования источника информации на основе настоящего изобретении, и затем получают декодированное целое число z, выполняют одномерное-двумерное отображение на этапе S203 путем указания пары (x, y) целых чисел, назначенных для z.
На следующем этапе S205 определяют, был или нет закончен ввод кодов Голомба. Если он еще не был закончен, операция снова возвращается на этап S201, в то время как, если ввод был закончен, операция заканчивается.
Конкретные варианты воплощения
Ниже будут представлены конкретные варианты воплощения процессов, выполняемых на этапах S102 и S103 в блок-схеме последовательности операций на фиг.4, и процессов, выполняемых на этапах S203 и S204 в блок-схеме фиг.11.
(1) Конкретный вариант воплощения процесса, выполняемого на этапе S102 в блок-схеме последовательности операций, показанной на фиг.4
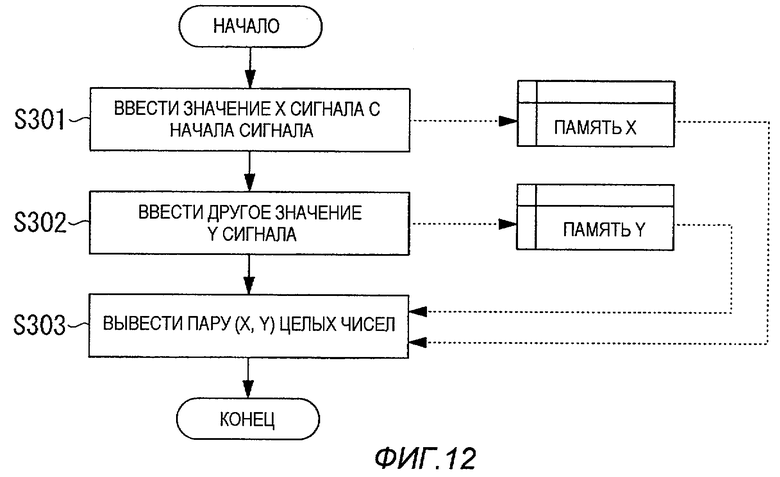
На фиг.12 представлена подробная блок-схема последовательности операций процесса, выполняемого на этапе S102 в блок-схеме последовательности операций, показанной на фиг.4.
На соответствующем этапе S102, когда принимают два значения сигнала гауссова целочисленного сигнала, которые вводят через этап S101, на первом этапе S301 блок-схемы последовательности операций на фиг.12 значение x сигнала вначале принимаемых данных сохраняют в памяти x, и на следующем этапе S302 другое значение y сигнала принятых данных сохраняют в памяти y.
На следующем этапе S303 значения x и y сигнала соответствующим образом получают из памяти x и y и выводят как пару (x, y) целых чисел.
В соответствии с этим, на этапе S102 выполняют блок-схему последовательности операций по фиг.12 таким образом, что значения в последовательности сигнала гауссова целочисленного сигнала выводят по два как пары.
(2) Конкретный вариант воплощения процесса, выполняемого на этапе S103 в блок-схеме последовательности операций по фиг.4
На фиг.13-16 показаны подробные блок-схемы последовательности операций процесса, выполняемого на этапе S102 в блок-схеме последовательности операций по фиг.4.
На соответствующем этапе S103 выполняют двумерное-одномерное отображение с помощью алгоритма, показанного на фиг.5, таким образом, чтобы отобразить пару (x, y) целых чисел на целое число z, и затем выводят это целое число z.
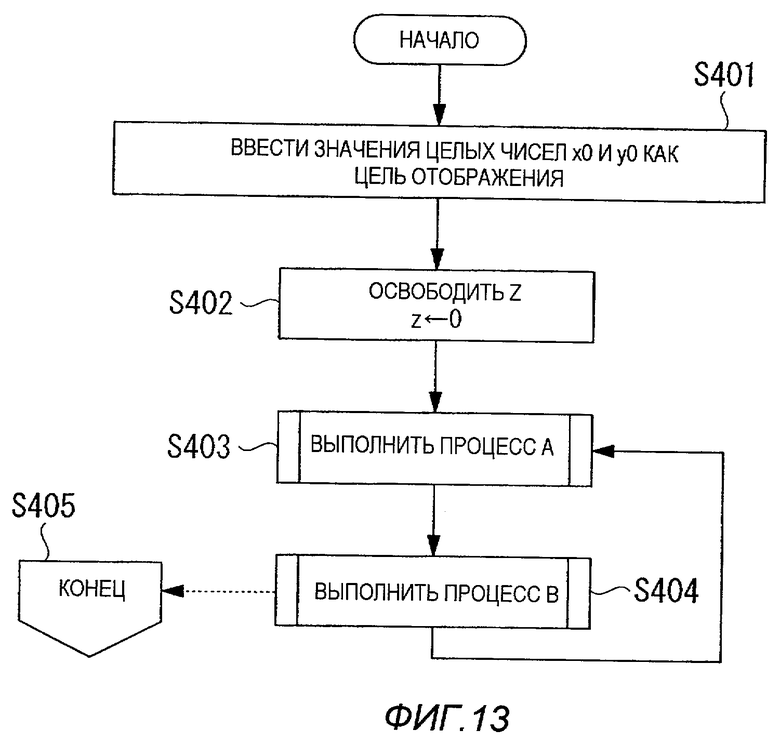
Таким образом, как показано в блок-схеме последовательности операций на фиг.13, на первом этапе S401 вводят целое значение x0 и y0 как цель отображения, и на следующем этапе S402 освобождают память Z накопителя точки решетки и переменную z инициируют, задавая для нее значение 0.
На следующем этапе S403 выполняют процесс А, определенный по блок-схеме последовательности операций на фиг.14, и на следующем этапе S404 выполняют процесс B, определенный в блок-схеме последовательности операций по фиг.15.
В процессе B выполняют процесс X, определенный по блок-схеме последовательности операций на фиг.16. В процессе X, если условие удовлетворяется, определяют, что было получено целое число z как результат отображения пары (x0, y0) целых чисел, и выводят это число z. Операция затем переходит на этап S405 и заканчивается.
В отличие от этого, если условие не удовлетворяется, данные не выводят, и операция возвращается на этап S403, то есть в процесс A.
Хотя процессы A, B и X поясняются подробно ниже, их краткое пояснение состоит в том, что в процессе A для точек (x, y) решетки, которые еще не были скомпонованы и уже имеют назначенное им целое число, рассчитывают минимальное значение dmin расстояния между началом координат и каждой точкой решетки, где "-dmin≤x≤dmin" и "-dmin≤y≤dmin", которые установлены в процессе B. Обычно множество точек решетки обеспечивают минимальное значение dmin.
Поэтому в процессе B каждую из таких точек решетки выделяют в соответствии с конкретным порядком выделения и целое значение назначают для каждой выделенной точки решетки, в то время как назначенное целое значение последовательно увеличивают на единицу для каждого назначения.
Для описанного выше назначения в процессе X определяют, появилось или нет входное значение (x0, y0) как точка (x, y) решетки. Если определяют, что значение (x0, y0) появилось, целое число z, назначенное для соответствующей точки (x, y) решетки, определяют как результат отображения. Если определяют, что значение (x0, y0) еще не появилось, dmin последовательно увеличивают на единицу в процессе B таким образом, что аналогичную операцию повторяют до тех пор, пока не появится входное значение (x0, y0).
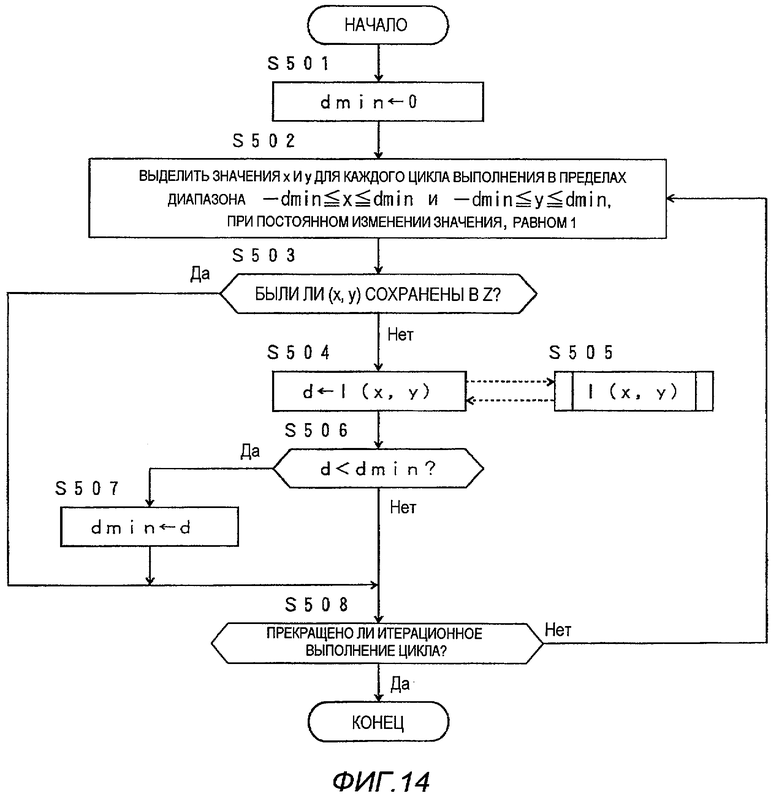
Ниже со ссылкой на блок-схему последовательности операций по фиг.14 поясняется процесс A.
В процессе A среди точек (x, y) решетки в двумерном диапазоне, где каждое из значений x и y больше или равно -dmin, и также все они меньше или равны dmin (dmin представляет собой целое число, последовательно увеличиваемое на единицу в процессе B), те точки, которые еще не были скомпонованы, устанавливают цели обработки, и минимальное значение расстояния от начала координат рассчитывают для этих целей.
На первом этапе S501 целочисленное значение dmin инициируют с установкой в 0. На следующем этапе S502 один набор из значений x и y генерируют для каждого цикла выполнения (с этапа S502 до этапа S508) в пределах диапазона "-dmin≤x≤dmin" и
"-dmin≤y≤dmin" в соответствии с конкретным порядком выбора значения, где изменение значения всегда равно 1.
На следующем этапе S503 определяют, был ли сохранен сгенерированный набор (x, y) в памяти Z сохранения точки решетки. Если он уже был сохранен, операция переходит на этап S508, и если он еще не был сохранен, операция переходит на этап S504. На этапе S504 переменную d устанавливают на расстояние l(x, y) между точкой (x, y) решетки и началом координат, которое рассчитывают с помощью процесса, выполняемого на этапе S505.
Расстояние l(x, y) может быть рассчитано с использованием следующей функции:
l(x, y)=x2+y2.
На следующем этапе S506 значения d и dmin сравнивают друг с другом. Если d больше или равно dmin, операция сразу переходит на этап S508. Если d меньше, чем dmin, операция переходит на этап S507, где dmin устанавливают равным d, и затем переходит на этап S508.
На этапе S508 определяют, появились ли все возможные комбинации между x и y в пределах диапазона "-dmin≤x≤dmin" и "-dmin≤y≤dmin". Если они еще не все появились, операция возвращается на этап S502, и если они уже все появились, процесс A заканчивают.
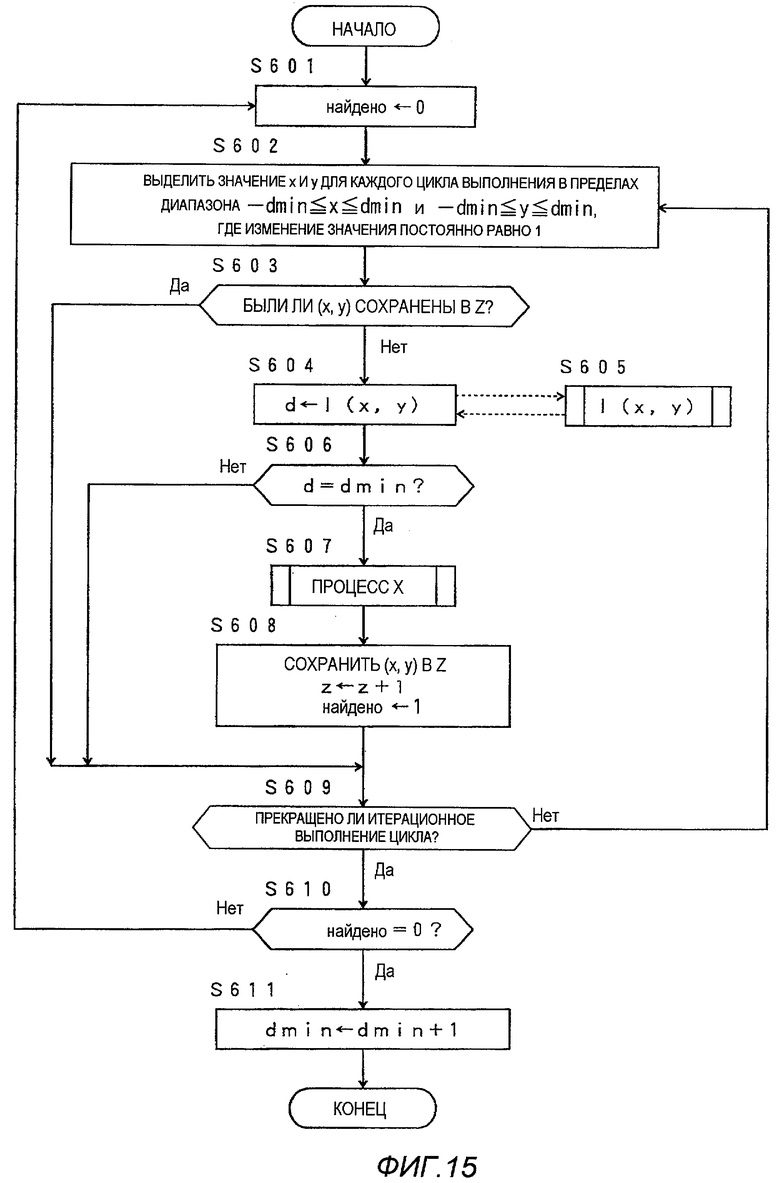
Ниже процесс B поясняется со ссылкой на блок-схему последовательности операций по фиг.15.
В процессе B среди точек (x, y) решетки в двумерной области, где каждое из значений x и y больше или равно -dmin и также меньше или равно dmin (dmin представляет собой целое число, последовательно увеличиваемое на единицу), те точки, которые еще не были скомпонованы и удовлетворяют условию "l(x, y)=dmin" (dmin получают в процессе A), подвергают процессу X в блок-схеме последовательности операций, показанной на фиг.16.
На первом этапе S601 для флага "найдено" (found) устанавливают значение 0. На следующем этапе S602 один набор значений x и y генерируют для каждого цикла выполнения (с S602 по S609) в пределах диапазона "-dmin≤x≤dmin" и "-dmin≤y≤dmin" в соответствии с определенным порядком выбора значения, в котором изменение значения всегда равно 1.
На следующем этапе S603 определяют, был ли сгенерированный набор (x, y) сохранен в памяти Z накопителя точек решетки. Если он был уже сохранен, операция переходит на этап S609, и если он еще не был сохранен, операция переходит на этап S604. На этапе S604 переменную d устанавливают равной расстоянию l(x, y) между точкой (x, y) решетки и началом координат, которое рассчитывают с помощью процесса, выполняемого на этапе S605.
Расстояние l(x, y) можно рассчитывать с использованием следующей функции:
l(x, y)=x2+y2.
На следующем этапе S606 значения d и dmin сравнивают друг с другом. Если d не совпадает с dmin, операция сразу переходит на этап S609. Если d совпадает с dmin, операция переходит на этап S607, где выполняют процесс X.
На этапе S608 пару (x, y) целых чисел сохраняют в памяти Z сохранения точки решетки; целочисленное значение z (которое определяют отдельно) последовательно увеличивают на единицу; и значение флага "найдено" устанавливают равным 1. Операция затем переходит на этап S609.
На этапе S609 определяют, появились или нет все возможные комбинации между x и y в пределах диапазона "-dmin≤x≤dmin" и "-dmin≤y≤dmin". Если они еще не появились, операция возвращается на этап S602, и если они уже все появились, операция переходит на этап S610. На этапе S610 определяют, равно или нет 0 значение флага "найдено".
В соответствии с определением на этапе S610, когда определяют, что значение флага "найдено" не равно 0, операция возвращается на этап S601, и когда определяют, что значение флага "найдено" равно 0, операция переходит на этап S611. На этапе S611 значение dmin последовательно увеличивают на единицу, и процесс B заканчивается.
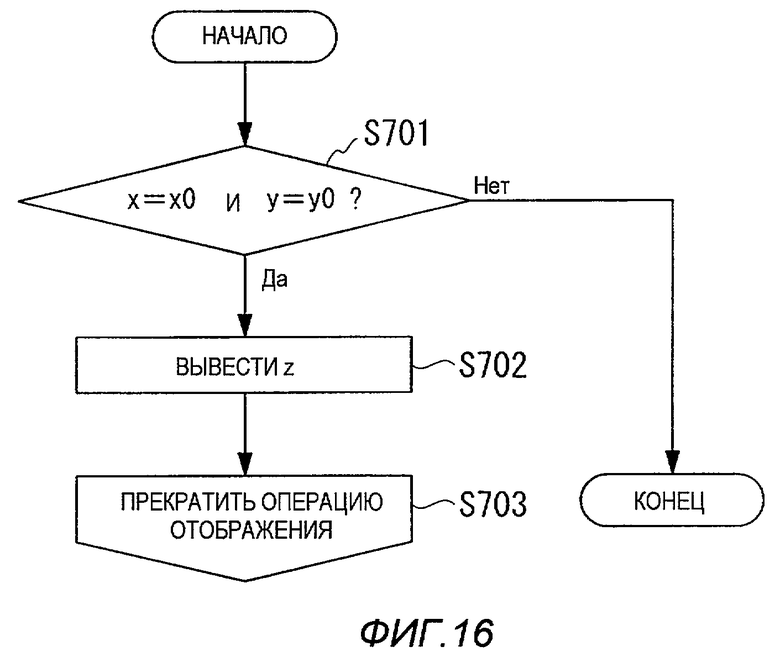
Ниже со ссылкой на блок-схему последовательности операций, показанную на фиг.16 поясняется обработка X.
В процессе X, когда значения x0 и y0, которые были введены как цель отображения, становятся равными значениям x и y, которые теперь обрабатывают в соответствующем цикле, выводят соответствующее им одномерное отображенное значение z.
На первом этапе S701 определяют, выполняется ли условие x=x0 и y=y0. Если определяют, что x=x0 и y=y0, операция переходит на этап S702, где целочисленное значение z, назначенное для (x, y), выводят как результат отображения. Операция затем переходит на этап S703, на котором прекращают операцию двумерного-одномерного отображения. В отличие от этого, если определяют, что условие "x=x0 и y=y0" не удовлетворяется, обработка X заканчивается (то есть операция возвращается на этап S608 в процессе B).
В соответствии с этим, путем выполнения блок-схемы последовательности операций по фиг.13-16, на этапе S103 на фиг.4, двумерное-одномерное отображение, воплощенное в виде алгоритма, показанного на фиг.5, выполняют для отображения пары (x, y) целых чисел на целое число z, и это целое число z затем выводят.
(3) Конкретный вариант воплощения процесса, выполняемого на этапе S203 в блок-схеме последовательности операций, показанной на фиг.11
На фиг.17 и 18 показаны подробные блок-схемы последовательности операций процесса, выполняемого на этапе S203 по блок-схеме последовательности операций, показанной на фиг.11.
На этапе S203 одномерное-двумерное отображение, воплощенное с помощью алгоритма, показанного на фиг.5, выполняют для отображения целого числа z (декодированного, используя процесс этапа S202) в пару (x, y) целых чисел и эту пару (x, y) целых чисел затем выводят.
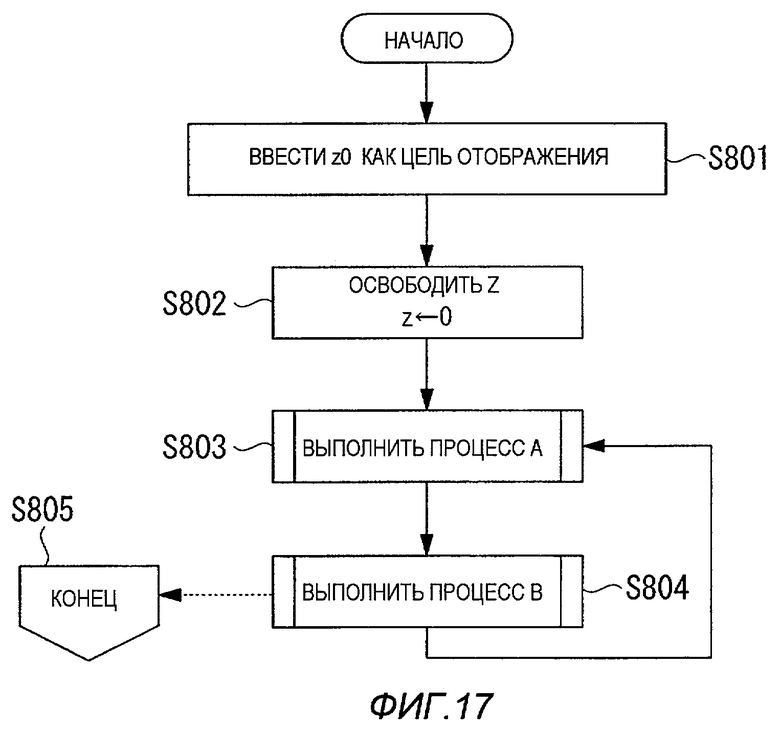
В частности, как показано на блок-схеме последовательности операций по фиг.17, на первом этапе S801 целочисленное значение z0 вводят как цель отображения. На следующем этапе S802 освобождают память Z накопителя точки решетки и переменную z инициируют с установкой в 0.
На следующем этапе S803 выполняют процесс А, определенный с помощью блок-схемы последовательности операций, показанной на фиг.14, и на следующем этапе S804 выполняют процесс B, определенный по блок-схеме последовательности операций по фиг.15 (однако при этом процесс X модифицирован в процесс X', как поясняется ниже).
Таким образом, в процессе B выполняют процесс X', определенный по блок-схеме последовательности операций на фиг.18. В процессе X', если условие удовлетворяется, определяют, что была получена пара (x, y) целых чисел как результат отображения целого числа z0, и выводят эту пару (x, y) целых чисел. Операция затем переходит на этап S805 и заканчивается.
В отличие от этого, если условие не удовлетворяется, данные не выводят, и обработка возвращается на этап S803, то есть в процесс A.
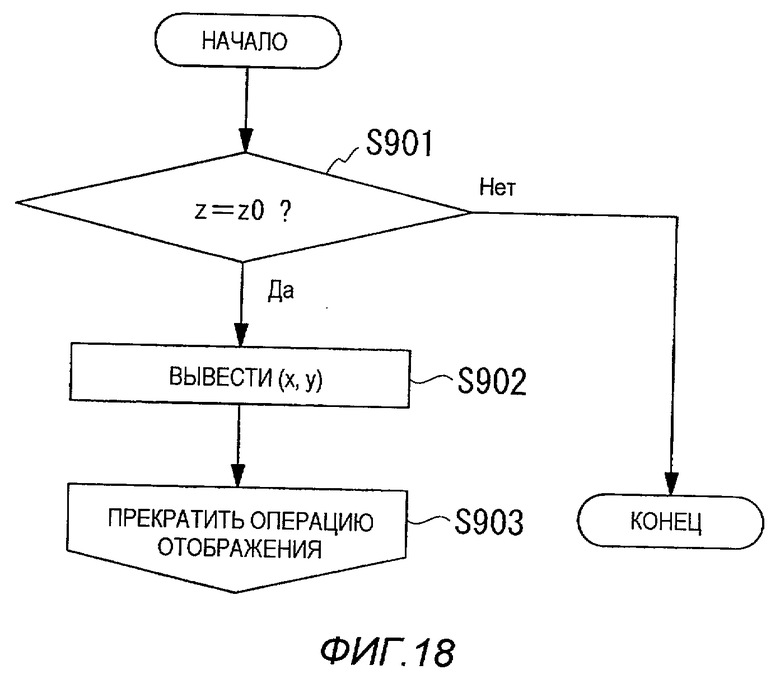
Ниже процесс X' поясняется со ссылкой на блок-схему последовательности операций по фиг.18.
В процессе X', когда значение z0, которое вводят как цель отображения, становится равным значению z, которое обрабатывают в данный момент в соответствующем цикле, выводят двумерные отображенные значения (x, y), соответствующие ему.
На первом этапе S901 определяют, выполняется или нет условие z=z0. Если определяют, что z=z0, операция переходит на этап S902, где целые числа (x и y), назначенные целому числу z, выводят как результат отображения. Обработка затем переходит на этап S903, и операцию одномерного-двумерного отображения прекращают. В отличие от этого, если определяют, что z≠z0, процесс X' заканчивается (то есть операция возвращается на этап S608 в процессе B).
В соответствии с этим, в ходе выполнения блок-схемы последовательности операций по фиг.17-18, на этапе S203 по фиг.11 одномерное-двумерное отображение, воплощенное с помощью алгоритма, показанного на фиг.5, выполняют для отображения целого числа z на пару (x, y) целых чисел и пару (x, y) целых чисел затем выводят.
(4) Конкретный вариант воплощения процесса, выполняемого на этапе S204 в блок-схеме последовательности операций по фиг.11
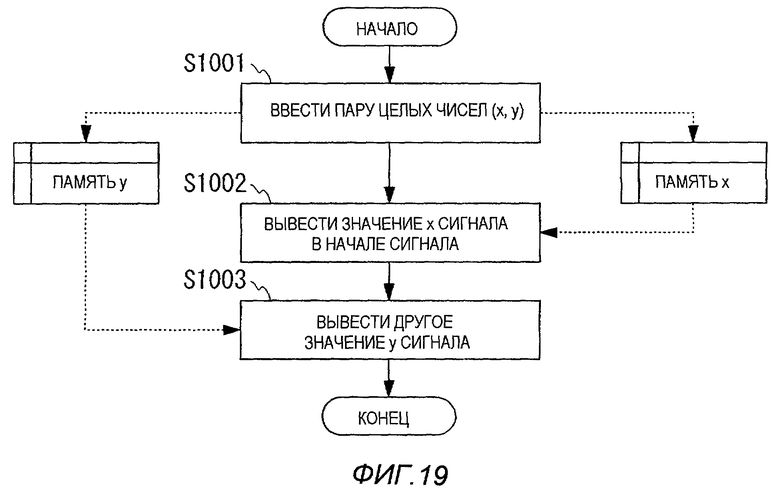
На фиг.19 показана подробная блок-схема последовательности операций процесса, выполняемого на этапе S204 в блок-схеме по фиг.11.
На соответствующем этапе S204, когда принимают пару (x, y) целых чисел, полученную в результате процесса на этапе S203, на первом этапе S1001 блок-схемы по фиг.19 значение x сигнала в начале принимаемых данных сохраняют в памяти x, и другое значение y сигнала принимаемых данных сохраняют в памяти y.
На следующем этапе S1002 значение x сигнала в начале данных получают из памяти x и выводят, и на следующем этапе S1003 другое значение y сигнала получают из памяти y и выводят.
В соответствии с этим, на этапе S204 путем выполнения блок-схемы последовательности операций, показанной на фиг.19, целые значения x и y, которые формируют пару (x, y) целых чисел как результат отображения, выводят в порядке от x до y.
Промышленная применимость
В настоящем изобретении гауссов целочисленный сигнал представляет собой цель кодирования и декодирования, и при этом используют структуру, которая воплощает реверсивное отображение для преобразования гауссова источника сигнала в источник сигнала с экспоненциальным распределением. В соответствии с этим становится возможным легко и эффективно кодировать и декодировать гауссов целочисленный сигнал, который нельзя было эффективно кодировать, используя известные коды Голомба или тому подобное, хотя гауссов целочисленный сигнал появляется при различных обстоятельствах в области математики и техники.



Изобретение относится к системам кодирования/декодирования сигнала изображения. Техническим результатом является эффективное кодирование различных видов обобщенных источников сигнала, таких как сигналы изображения и голосовые сигналы с использованием кодов Голомба. Указанный технический результат достигается тем, что вводят последовательность значений сигнала гауссова целочисленного сигнала как цели кодирования; преобразуют эти значения сигнала, включенные в последовательность значений входного сигнала, в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода; рассматривают каждую из пар целых чисел как точку решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, в результате выполнения двумерного-одномерного отображения, при котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают точке решетки в результате отображения; и кодируют значения целых чисел, используя коды, которые используются для кодирования источника информации, который соответствует экспоненциальному распределению. 8 н. и 10 з.п ф-лы, 21 ил.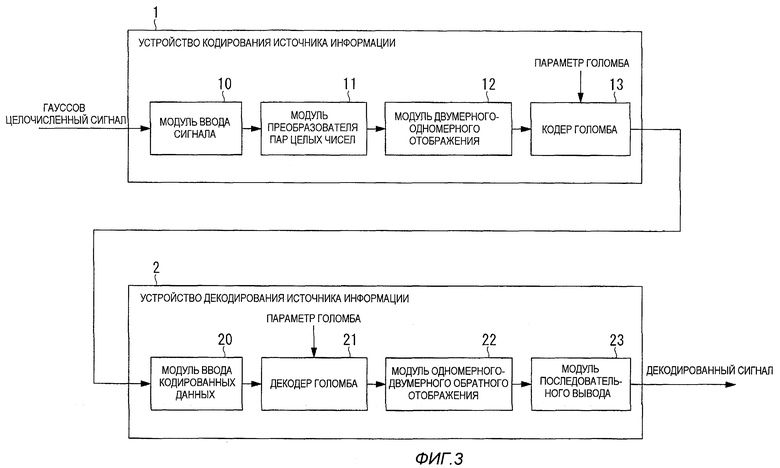
1. Способ кодирования сигнала изображения, предназначенный для кодирования сигнала изображения, который обозначает гауссов целочисленный сигнал, причем способ содержит этапы, на которых:
вводят последовательность значений сигнала для сигнала изображения в качестве цели кодирования;
преобразуют значения сигнала, включенные в последовательность значений входного сигнала, в пары целых чисел, каждое из которых имеет два целых числа, расположенных в порядке ввода;
рассматривают каждую из пар целых чисел в качестве точки решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, в результате выполнения двумерного-одномерного отображения, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают точке решетки в результате отображения; и
кодируют значения целых чисел, используя коды Голомба.
2. Способ декодирования сигнала изображения, предназначенный для декодирования кодированных данных, которые генерируют путем преобразования последовательности значений сигнала для сигнала изображения, который представляет собой цель кодирования и обозначает гауссов целочисленный сигнал, в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода последовательности значений сигнала; рассматривают каждую из пар целых чисел в качестве точки решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, в результате выполнения двумерного-одномерного отображения, при котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают для точки решетки в результате отображения; и кодируют значения целых чисел, используя коды Голомба, причем способ содержит этапы, на которых:
декодируют значения целых чисел, подвергая их кодированные данные декодированию Голомба;
восстанавливают пары целых чисел, подвергая декодированные значения целых чисел одномерному-двумерному отображению, которое представляет собой обратное отображение для двумерного-одномерного отображения; и
выводят целые числа, которые формируют восстановленную пару целых чисел, от первого элемента до второго ее элемента.
3. Способ кодирования источника информации, предназначенный для кодирования гауссова целочисленного сигнала, причем способ содержит этапы, на которых:
вводят последовательность значений сигнала гауссова целочисленного сигнала в качестве цели кодирования;
преобразуют значения сигнала, включенные в последовательность значений входного сигнала, в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода;
рассматривают каждую из пар целых чисел в качестве точки решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, в результате выполнения двумерного-одномерного отображения, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки в результате отображения; и
кодируют значения целых чисел, используя коды, которые используются для кодирования источника информации, который соответствует экспоненциальному распределению.
4. Способ кодирования источника информации по п.3, в котором на этапе кодирования значения целых чисел кодируют, используя коды Голомба.
5. Способ кодирования источника информации по п.4, дополнительно содержащий этапы, на которых: рассчитывают дисперсию значений входного сигнала; и определяют параметр кода для кодов Голомба, который имеет значение, пропорциональное рассчитанной дисперсии.
6. Способ кодирования источника информации по п.3, в котором на этапе получения значений целых чисел эти значения целых чисел получают как результат отображения для пар целых чисел путем обращения к таблице, которая была приготовлена заранее, и в которой содержатся соответствующие взаимозависимости между парами целых чисел и значениями целых чисел.
7. Способ кодирования источника информации по п.3, в котором на этапе получения значений целых чисел эти значения целых чисел получают как результат отображения для пар целых чисел путем повторения этапов, на которых: рассчитывают минимальное значение расстояния от точки решетки в начале координат для каждой точки решетки, которая еще не была скомпонована; и компонуют точки решетки, которые имеют минимальное расстояние, в заданном порядке, и назначают индивидуальное значение целого числа для каждой скомпонованной точки решетки.
8. Способ декодирования источника информации, предназначенный для декодирования кодированных данных, сгенерированных путем преобразования последовательности значений сигнала для гауссова целочисленного сигнала, представляющего собой цель кодирования, в пары целых чисел, каждое из которых имеет два целых числа, скомпонованных в порядке ввода последовательности значений сигнала; рассматривают каждую из пар целых чисел в качестве точки решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, в результате выполнения двумерного-одномерного отображения, при котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки в результате отображения; и кодируют эти значения целых чисел, используя коды, которые используют для кодирования источника информации, который соответствует экспоненциальному распределению, причем способ содержит этапы, на которых:
декодируют значения целых чисел путем декодирования их кодированных данных;
восстанавливают пары целых чисел, подвергая декодированные значения целых чисел одномерному-двумерному отображению, которое представляет собой обратное отображение для двумерного-одномерного отображения; и
выводят целые числа, которые формируют каждую восстановленную пару целых чисел, от первого элемента до второго ее элемента.
9. Способ декодирования источника информации по п.8, в котором коды Голомба используют как коды, использовавшиеся для кодирования источника информации, который соответствует экспоненциальному распределению.
10. Способ декодирования источника информации по п.9, в котором: параметр кода Голомба для кодов Голомба используют для декодирования кодированных данных в виде значений целых чисел; и способ дополнительно содержит этап, на котором: вводят параметр кода Голомба, установленный так, что он имеет значение, пропорциональное дисперсии значений сигналов, включенных в последовательность значений сигнала.
11. Способ декодирования источника информации по п.8, в котором на этапе восстановления пар целых чисел эти пары целых чисел восстанавливают как результат обратного отображения для значений целых чисел путем обращения к таблице, которая была подготовлена заранее, и в которой содержатся соответствующие взаимозависимости между парами целых чисел и значениями целых чисел.
12. Способ декодирования источника информации по п.8, в котором, если при двумерном-одномерном отображении значения целых чисел получают как результат отображения для пар целых чисел путем повторения этапов, на которых: рассчитывают минимальное значение расстояния от точки решетки в начале координат до каждой точки решетки, которая еще не была скомпонована; и компонуют точки решетки, которые имеют минимальное расстояние, в заданном порядке и назначают индивидуальное значение целого числа для каждой скомпонованной точки решетки, тогда на этапе восстановления пар целых чисел, на основе описанного выше результата отображения, пары целых чисел восстанавливают как результат обратного отображения для значений целых чисел.
13. Устройство кодирования источника информации, предназначенное для кодирования гауссова целочисленного сигнала, причем устройство содержит:
блок ввода последовательности значений сигнала для гауссова целочисленного сигнала как цели кодирования;
блок преобразования значений сигнала, включенных в последовательность значений входного сигнала, в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода;
блок рассмотрения каждой из пар целых чисел в качестве точки решетки в двумерных координатах и получения значений целых чисел, больших или равных нулю, в результате выполнения двумерного-одномерного отображения, при котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки в результате отображения; и
блок кодирования значений целых чисел, использующий коды, которые используют для кодирования источника информации, который соответствует экспоненциальному распределению.
14. Устройство кодирования источника информации по п.13, в котором блок кодирования кодирует значения целых чисел, используя коды Голомба.
15. Устройство декодирования источника информации, предназначенное для декодирования кодированных данных, которые генерируют путем преобразования последовательности значений сигнала гауссова целочисленного сигнала как цели кодирования, в пары целых чисел, каждая из которых имеет два целых числа, расположенных в порядке ввода последовательности значений сигнала; каждую из пар целых чисел рассматривают в качестве точки решетки в двумерных координатах и получают значения целых чисел, большие или равные нулю, путем выполнения двумерного-одномерного отображения, в котором чем короче расстояние от каждой точки решетки до начала координат, тем меньшее значение назначают этой точке решетки путем отображения; и кодируют значения целых чисел, используя коды, которые используются для кодирования источника информации, который соответствует экспоненциальному распределению, причем устройство содержит:
блок декодирования значений целых чисел путем декодирования его кодированных данных;
блок восстановления пар целых чисел в результате обработки декодированных значений целых чисел с одномерным-двумерным отображением, которое представляет собой обратное отображение для двумерного-одномерного отображения; и
блок вывода целых чисел, каждое из которых формирует восстановленную пару целых чисел от ее первого элемента до второго элемента.
16. Устройство декодирования источника информации по п.15, в котором коды Голомба используют как коды, используемые для декодирования источника информации, который соответствует экспоненциальному распределению.
17. Считываемый компьютером носитель информации, на котором сохранена программа кодирования источника информации, с помощью которой компьютер выполняет этапы в способе кодирования источника информации по п.3.
18. Считываемый компьютером носитель информации, на котором записана программа декодирования источника информации, с помощью которой компьютер выполняет этапы в способе декодирования источника информации по п.8.
| JP 10243395 А, 11.09.1998 | |||
| АДАПТИВНЫЙ СПОСОБ И СИСТЕМА ДЛЯ ОТОБРАЖЕНИЯ ЗНАЧЕНИЙ ПАРАМЕТРОВ В ИНДЕКСЫ КОДОВЫХ СЛОВ | 2003 |
|
RU2313174C2 |
| US 2003118242 A1, 26.06.2003 | |||
| US 5764374 A, 09.06.1998 | |||
| US 6628717 B1, 30.09.2003 | |||
| US 2006273937 A1, 07.12.2006 | |||
| Устройство для измельчения растительных материалов | 1989 |
|
SU1653628A1 |
| US 2002163965 A1, 07.11.2002 | |||
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ | 1995 |
|
RU2117388C1 |
| A.KIELY AND M.KLIMESH, Generalized Golomb Codes and Adaptive Coding of Wavelet-Transformed Image | |||
Авторы
Даты
2010-12-10—Публикация
2007-11-08—Подача