Изобретение относится к измерительной технике и может быть использовано для дистанционного контроля геометрической формы и скорости проскальзывания колеса движущегося железнодорожного состава.
Известны способы измерения параметров колес движущегося железнодорожного состава.
В способе (Патент США №5808906. МКИ G01V 9/04. Installation and process for measuring rolling parameters by means of artificial vision on railway vehicles. 1998) осуществляется контроль геометрической формы колеса методом фотографирования с короткой экспозицией и с последующей обработкой полученных изображений. Скорость проскальзывания колес относительно рельс не измеряется.
Недостатком этого способа является высокая чувствительность к помехам в виде пыли, грязи, снега, дождя, при работе в натурных условиях, а также ограничение на допустимую скорость движения состава длительностью экспозиции. Поэтому измерения должны выполняться в специальных депо в статическом режиме либо при малых скоростях движения. Вследствие этого измерение параметров колес на штатных режимах движения железнодорожного состава оказывается невозможной.
Прототипом предлагаемого изобретения является способ измерения параметров колес движущегося железнодорожного состава, описанный в работе (Байбаков А.Н., Гуренко В.М., Патерикин В.И., Плотников С.В., Сотников В.В., Чугуй Ю.В., Юношев С.П. Автоматический контроль геометрических параметров колесных пар во время движения поезда // Автометрия. - 2004. - Т. 40, №5. - С.94-103). В этом способе определяется геометрия (радиус и профиль) колеса в движении с помощью лазерных триангуляторов. Используется принцип самосканирования. На пути движения колеса формируются лазерные лучи. Движущееся колесо пересекает лазерные лучи. Точки пересечения каждого лазерного луча с поверхностью колеса проектируется на позиционно-чувствительный фотоприемник. Траектория перемещения проекций этих точек, регистрируемых позиционно-чувствительными фотоприемниками, однозначно определяет профиль колеса при заданной ориентации зондирующих лучей. Радиус колеса вычисляется по длине хорды, которая находится как произведение поступательной скорости колеса на временной интервал между последовательными пересечениями зондирующих лучей внешним контуром колеса.
Полученное значение радиуса является усредненным по малому углу поворота. Отсутствует контроль текущего радиуса как функции полярного угла по всему периметру колеса, поскольку измеряется лишь средний радиус ограниченного малым углом фрагмента колеса. Скорость проскальзывания колеса относительно железнодорожного полотна не измеряется, поскольку триангуляционный способ в лабораторной системе отсчета такой возможности не дает. Отсутствие информации о скорости проскальзывания дает дополнительную погрешность измерения радиуса и профиля колеса.
Задачей является разработка способа измерения параметров колес движущегося железнодорожного состава, улучшающего качество измерения.
Задача решается тем, что в способе измерения параметров колес движущегося железнодорожного состава, заключающемся в том, что освещают поверхность колеса лазерными лучами и измеряют параметры рассеянного света, однозначно отображающие динамические параметры колеса, и отличающемся тем, что одновременно измеряют локальные линейные скорости в двух точках на разных известных расстояниях от рельса, мгновенную угловую скорость находят как отношение разности измеренных локальных скоростей к расстоянию, равному разности расстояний от этих точек до поверхности рельса, мгновенный радиус вращения находят как отношение локальной скорости движения оси колеса в направлении, параллельном рельсу, к мгновенной угловой скорости, текущий геометрический радиус колеса определяют как сумму известного расстояния от поверхности рельса до нижней точки, в которой измеряют локальную скорость, и отношения разности линейных скоростей движения оси колеса и его поверхности в нижней из двух точек к мгновенной угловой скорости, а линейную скорость проскальзывания находят как произведение разности текущих значений радиуса вращения и геометрического радиуса колеса на мгновенную угловую скорость.
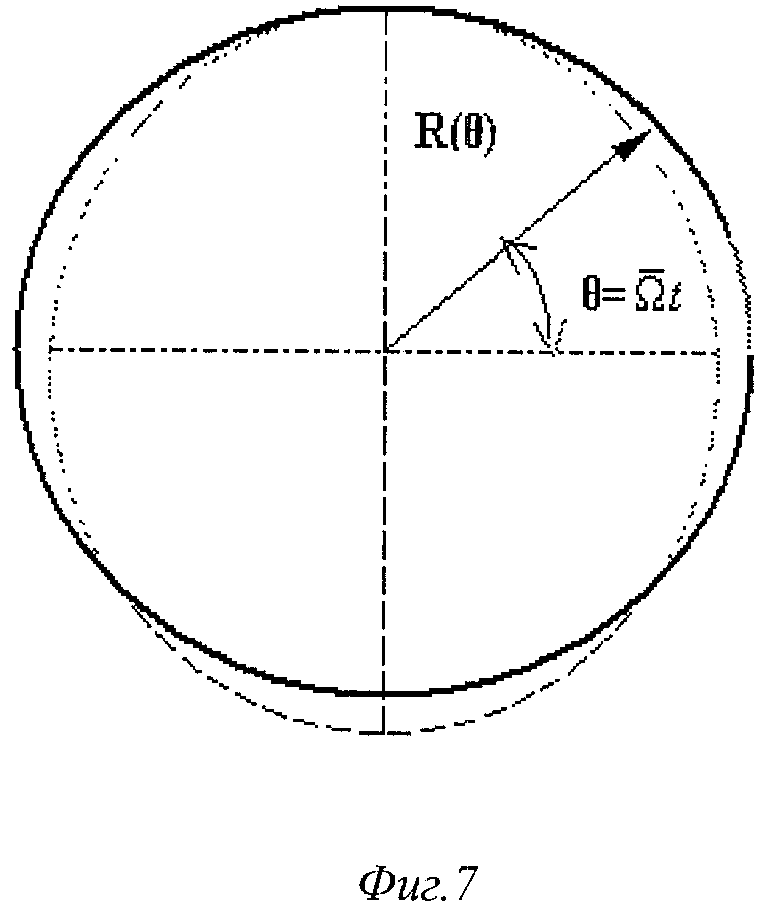
Структура устройства, реализующего предлагаемый способ, показана на фиг.1, на фиг.2 приведена схема распределения скоростей в различных точках катящегося колеса, на фиг.3 приведена схема, поясняющая предлагаемый способ диагностики колеса, на фиг.4 отображена ситуация, когда в лабораторной системе отсчета определяется радиус и скорость проскальзывания колеса действующего локомотива, на фиг.5 показана схема, поясняющая предлагаемый способ измерения формы колеса и скорости проскальзывания в системе отсчета, движущейся относительно железнодорожного полотна со скоростью поезда V, на фиг.6 показана одна из форм представления зависимости геометрического радиуса R(θ) и скорости проскальзывания Vп(θ) от угла поворота θ колеса, на фиг.7 показана форма представления измеренного геометрического радиуса колеса как функции полярного угла θ.
Устройство (Фиг.1) содержит: 1 - колесо; 2 - опора оси колеса; 3 - рельс; 4 - измеритель скорости движения вагона (локомотива) V, 5 - измеритель скоростей V1х и V2х. Выходы измерителей подключены к компьютеру 6.
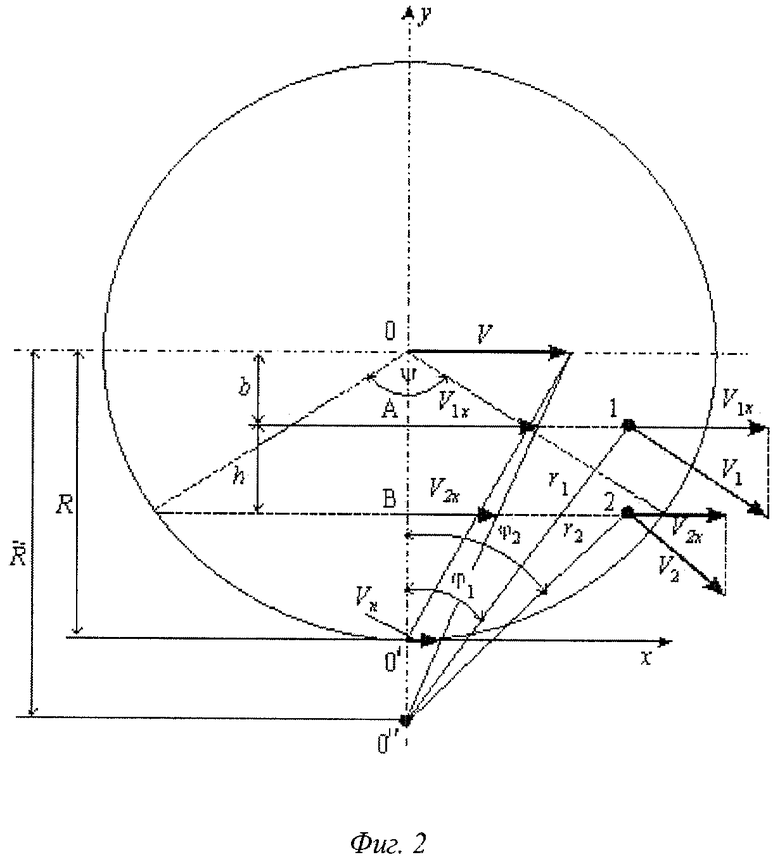
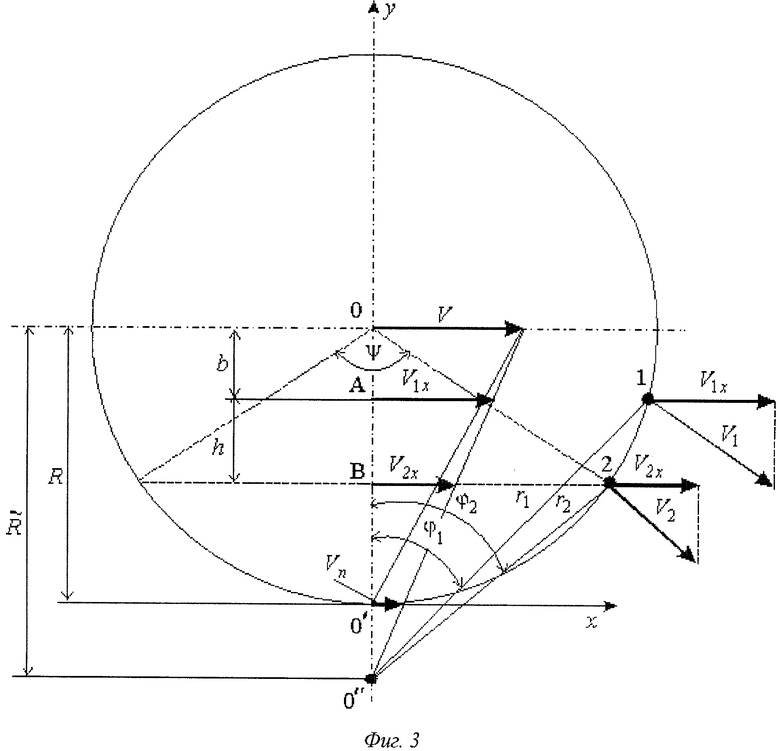
Способ осуществляется следующим образом. На Фиг.2 приведена схема распределения скоростей в различных точках катящегося колеса, поясняющая предлагаемый способ. Контур колеса изображен окружностью с центром 0. 0' - точка касания колеса с поверхностью рельса. В ситуации, когда проскальзывание отсутствует, 0' отображает в лабораторной системе отсчета мгновенный центр (ось), относительно которого вращается колесо при качении по рельсу. Если же колесо катится с проскальзыванием, угловая скорость его уменьшается и мгновенная ось вращения смещается в положение 0''. На фигуре введена ортогональная система координат: ось х направлена вдоль поверхности рельса, ось у проходит через точки 0 и 0'.
Пусть в точках 1 и 2 одновременно измеряются локальные линейные скорости V1х и V2х, параллельные оси х. Измерения могут выполняться дистанционно оптическими методами с помощью, например, лазерных доплеровских измерителей скорости (Дубнищев Ю.Н., Арбузов В.А., Белоусов П.П., Белоусов П.Я. Оптические методы исследования потоков. Новосибирск: Сибирское университетское издательство. 2003, 418 с). Проекция расстояния между точками 1 и 2 на ось у равна h. Для измеряемых скоростей V1х и V2х, согласно фигуре, имеем:


где 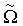 - мгновенная угловая скорость относительно мгновенной оси вращения 0"; r1 и r2 - мгновенные радиусы вращения точек 1 и 2 относительно центра вращения 0"; φ1 - угол между радиусом вращения r1 и осью у; φ2 - угол между радиусом вращения r2 и осью у. Вычитая из выражения (1) выражение (2), находим разность линейных скоростей в точках 1 и 2:
- мгновенная угловая скорость относительно мгновенной оси вращения 0"; r1 и r2 - мгновенные радиусы вращения точек 1 и 2 относительно центра вращения 0"; φ1 - угол между радиусом вращения r1 и осью у; φ2 - угол между радиусом вращения r2 и осью у. Вычитая из выражения (1) выражение (2), находим разность линейных скоростей в точках 1 и 2:
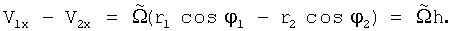
Следовательно,
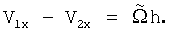
Отсюда находим мгновенную угловую скорость 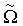 как отношение разности линейных скоростей V1x-V2x и h:
как отношение разности линейных скоростей V1x-V2x и h:
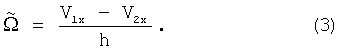
Линейная скорость движения центра вращения колеса V параллельна оси х и совпадает со скоростью движения буксы колеса или вагона. Измерение этой скорости также выполняется, например, лазерным доплеровским измерителем. Скорость V равна произведению угловой скорости 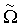 на мгновенный радиус
на мгновенный радиус 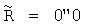 . При наличии проскальзывания
. При наличии проскальзывания

Если же проскальзывание отсутствует, скорость V определяется произведением угловой скорости Ω на реальный геометрический радиус колеса R:

Угловые скорости 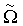 и Ω связаны соотношением
и Ω связаны соотношением

где Ωn - изменение угловой скорости вращения колеса, вызванное проскальзыванием. Знак «-» в (6) выбирается для колеса вагона, знак «+» для колеса действующего локомотива, когда на оси колеса действует активный вращающийся момент. Если проскальзывание отсутствует, Ωn=0 и 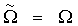 . Радиус колеса R, как видно из фигуры, равен
. Радиус колеса R, как видно из фигуры, равен
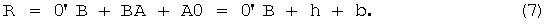
Расстояние 0'В равно расстоянию от точки 2 до поверхности рельса. Оно является известным и определяется при позиционировании зондирующего светового поля лазерного доплеровского измерителя скорости V2x на поверхности колеса. Величина отрезка b=0А находится из соотношения, следующего из подобия треугольников, ограниченных сторонами 0''0 и V, 0''А и V1x:
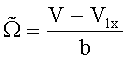
откуда
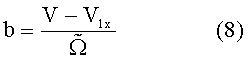
Подставляя в (8) выражение для мгновенной угловой скорости из (3), получаем
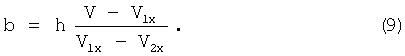
Из (7) с учетом (9) находим текущий радиус колеса R:
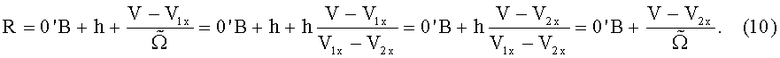
Выражение (10) описывает геометрическую форму колеса,  в пределах поворота колеса на угол ψ, определяемого временным интервалом τ, в течение которого зондирующее поле лазерного измерителя скоростей V1x и V2x и их разность V1x-V2x, находится в пределах поверхности катящегося колеса:
в пределах поворота колеса на угол ψ, определяемого временным интервалом τ, в течение которого зондирующее поле лазерного измерителя скоростей V1x и V2x и их разность V1x-V2x, находится в пределах поверхности катящегося колеса:

Скорость проскальзывания Vn в пределах этого интервала находится как произведение угловой скорости  на разность текущих значений мгновенного радиуса вращения R и геометрического радиуса
на разность текущих значений мгновенного радиуса вращения R и геометрического радиуса 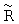 :
:

На Фиг.3 приведена схема, поясняющая предлагаемый способ диагностики колеса в случае, когда локальные скорости V1x и V2x измеряются на ободе колеса. Обозначения и пояснения полностью совпадают с описанием схемы, показанной на Фиг.2.
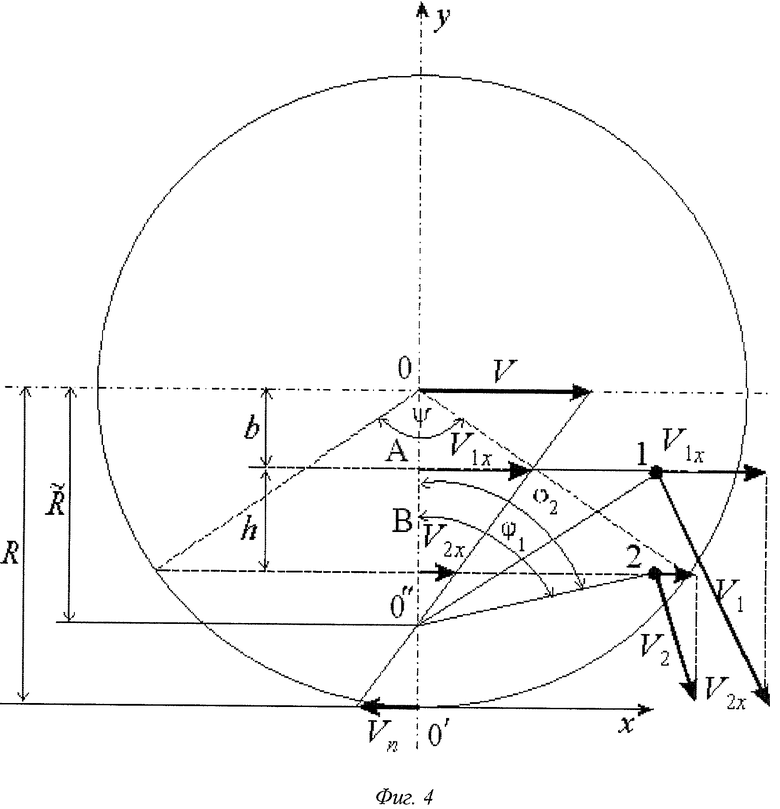
Ситуация, когда в лабораторной системе отсчета определяются радиус и скорость проскальзывания колеса действующего локомотива, отображена на Фиг.4. В этом случае, как видно из фигуры, текущее значение измеряемого геометрического радиуса колеса больше или равно значению мгновенного радиуса вращения,  , и скорость проскальзывания меняет знак. При этом мгновенный центр вращения оказывается смещенным по оси у внутрь круга, ограниченного контуром колеса. Обозначения и пояснения способа те же, что и для Фиг.2.
, и скорость проскальзывания меняет знак. При этом мгновенный центр вращения оказывается смещенным по оси у внутрь круга, ограниченного контуром колеса. Обозначения и пояснения способа те же, что и для Фиг.2.
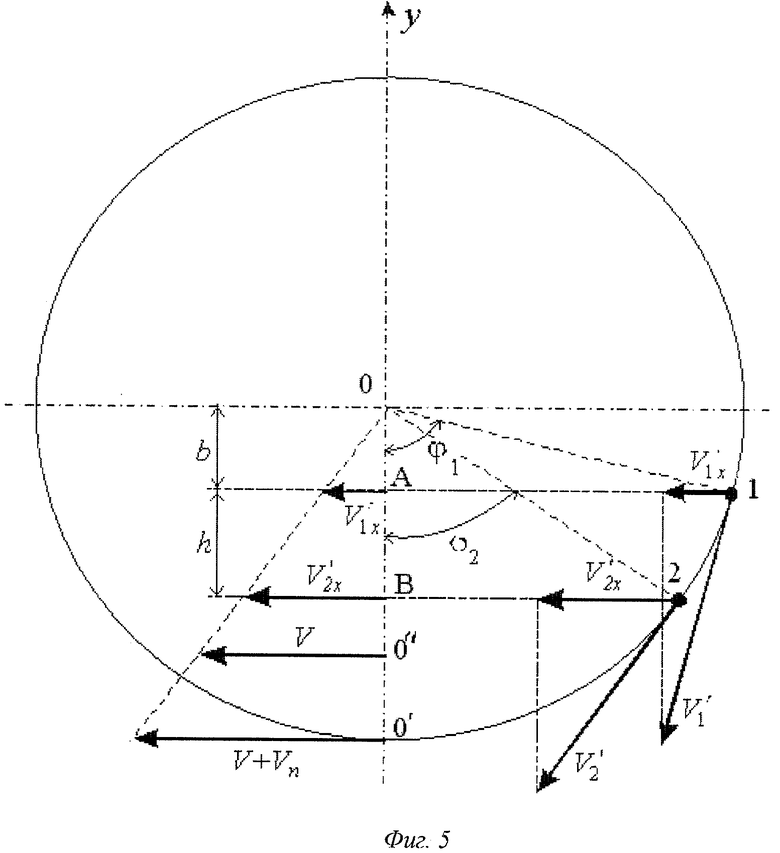
На Фиг.5 показана схема, поясняющая предлагаемый способ измерения формы колеса и скорости проскальзывания в системе отсчета, движущейся относительно железнодорожного полотна со скоростью поезда V. В такой системе отсчета удобно контролировать скорость проскальзывания и геометрический радиус ведущих колес действующего локомотива с целью оптимизации управления крутящим моментом.
Фиг.5 получается из Фиг.4 путем галилеевых преобразований системы отсчета:
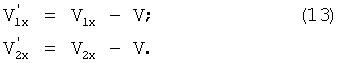
Измеряются горизонтальные компоненты 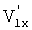 и
и 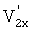 мгновенных скоростей поверхности обода V1 и V2 в точках 1 и 2. Геометрический радиус колеса в этой системе отсчета определяется выражением (10), в котором в соответствии с преобразованиями (13) делается подстановка:
мгновенных скоростей поверхности обода V1 и V2 в точках 1 и 2. Геометрический радиус колеса в этой системе отсчета определяется выражением (10), в котором в соответствии с преобразованиями (13) делается подстановка:
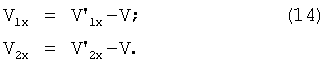
В результате выражение (10) для текущего значения геометрического радиуса после подстановки V1x и V2x из (14) принимает вид:
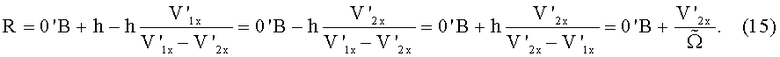
Для скорости проскальзывания остается справедливой формула (12), где
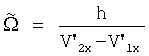 ;
; 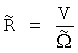 .
.
Как видно из Фиг.1, Фиг.2 и Фиг.3, мгновенный радиус вращения 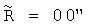 для колеса вагона в случае проскальзывания больше геометрического радиуса колеса
для колеса вагона в случае проскальзывания больше геометрического радиуса колеса 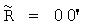 :
:
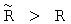 ,
,
Для ведущего колеса действующего локомотива мгновенный радиус вращения меньше геометрического радиуса
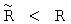 .
.
Это следует из фигур 4 и 5. При отсутствии проскальзывания (Vn=0) радиус вращения и геометрический радиус колеса одинаковы, 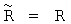 .
.
Для измерения геометрического радиуса и скорости проскальзывания колеса в пределах полного его оборота в устройстве, показанном на Фиг.1, используют несколько измерителей 5, позиционированных вдоль рельса на известных расстояниях друг от друга. Расстояние между соседними измерителями и их число выбираются из необходимости измерения локальных скоростей V1x и V2x на пространственном интервале, соответствующем полному обороту колеса. Расстояние L между соседними измерителями оценивается согласно Фиг.2 и Фиг.4 как L≤RΨ, а число измерителей должно удовлетворять условию
NRΨ≥2πR
Выполнение этого условия обеспечивает измерение 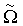 и
и 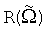 при движении колеса на пространственном интервале, не меньшем длины окружности, ограничивающей контур колеса.
при движении колеса на пространственном интервале, не меньшем длины окружности, ограничивающей контур колеса.
В ситуации, когда измеряются локальные скорости V1x и V2x на поверхности обода
колеса в лабораторной системе отсчета (Фиг.3) или в системе отсчета локомотива (Фиг.5), достаточно одного измерителя разности скоростей V1x и V2x, ориентированного вдоль рельсового полотна (Фиг.5) или под небольшим известным углом к его направлению (Фиг.3).
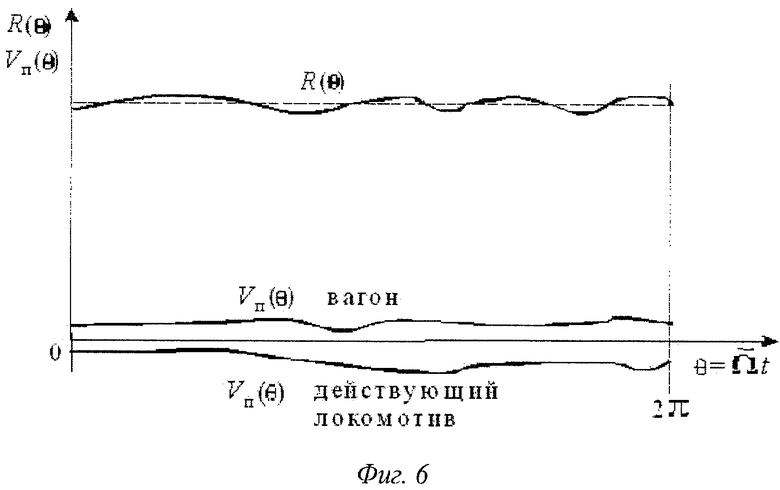
На Фиг.6 показана одна из форм представления зависимости геометрического радиуса R(θ) и скорости проскальзывания Vп(θ) от угла поворота θ колеса в случае, когда скорость проскальзывания существует.
Как видно из Фиг.6, скорость проскальзывания колес вагона и действующего локомотива имеют разные знаки. Это следует из схем на фигурах 2-5, поясняющих действие предложенного способа.
На Фиг.7 показана форма представления измеренного геометрического радиуса колеса как функции полярного угла θ.
Таким образом, предлагаемое изобретение, по сравнению с прототипом, обеспечивает возможность измерения в реальном времени геометрического радиуса колеса и скорости проскальзывания колес вагонов и локомотива, движущегося железнодорожного состава, что улучшает качество измерения. Кроме того, измерения могут выполняться как в лабораторной системе отсчета, так и в движущейся системе отсчета, связанной с подвеской колес. Реализация предложенного способа позволит оперативно выявлять дефектные колеса, тем самым повышая безопасность железнодорожного транспорта. Измерение скорости проскальзывания и радиуса ведущих колес локомотива дает возможность оптимально управлять крутящим моментом, приложенным к оси колеса, что повышает энергосбережение при эксплуатации железнодорожного транспорта.
Изобретение относится к измерительной технике и может быть использовано для дистанционного контроля геометрической формы и скорости проскальзывания колеса движущегося железнодорожного состава. Технический результат - повышение точности измерения в режиме реального времени геометрического радиуса колеса и скорости проскальзывания колес вагонов. Способ измерения параметров колес движущегося железнодорожного состава заключается в том, что освещают поверхность колеса лазерными лучами и измеряют параметры рассеянного света, однозначно отображающие динамические параметры колеса, одновременно измеряют локальные линейные скорости в двух точках на разных известных расстояниях от рельса, мгновенную угловую скорость находят как отношение разности измеренных локальных скоростей к расстоянию, равному разности расстояний от этих точек до поверхности рельса, мгновенный радиус вращения находят как отношение локальной скорости движения оси колеса в направлении, параллельном рельсу, к мгновенной угловой скорости, текущий геометрический радиус колеса определяют как сумму известного расстояния от поверхности рельса до нижней точки, в которой измеряют локальную скорость, и отношения разности линейных скоростей движения оси колеса и его поверхности в нижней из двух точек к мгновенной угловой скорости, а линейную скорость проскальзывания находят как произведение разности текущих значений радиуса вращения и геометрического радиуса колеса на мгновенную угловую скорость. 7 ил.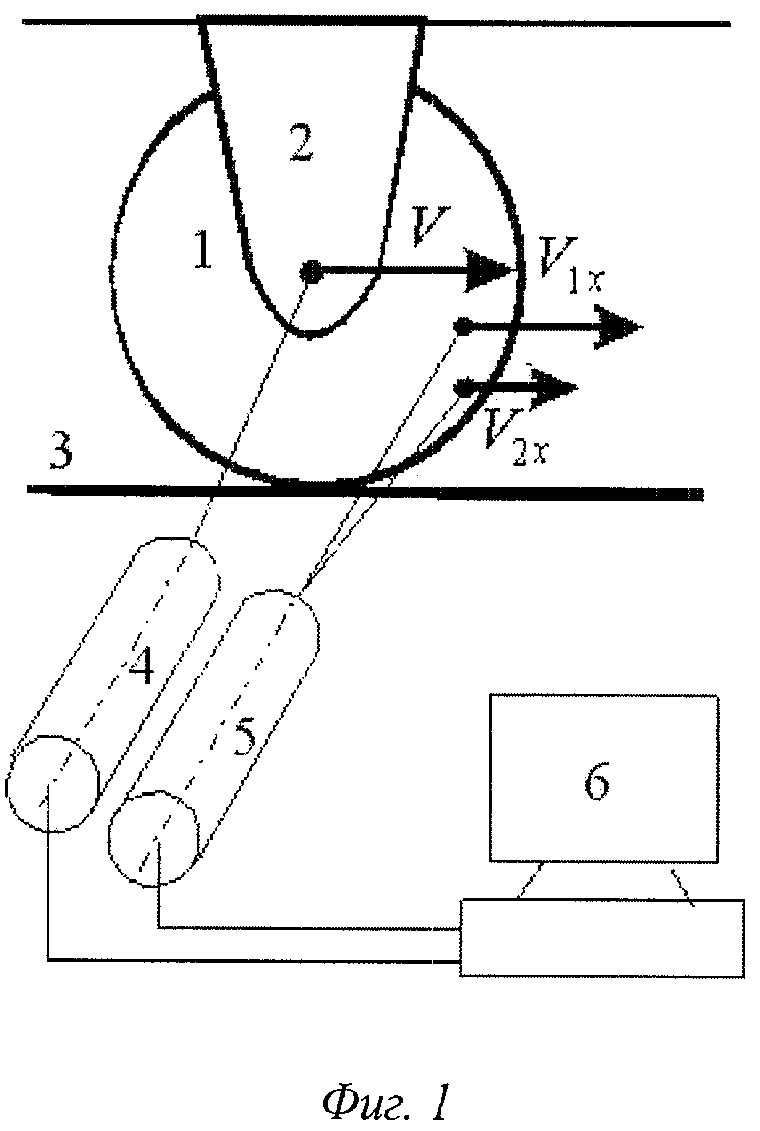
Способ измерения параметров колес движущегося железнодорожного состава, заключающийся в том, что освещают поверхность колеса лазерными лучами и измеряют параметры рассеянного света, однозначно отображающие динамические параметры колеса, отличающийся тем, что одновременно измеряют локальные линейные скорости в двух точках на разных известных расстояниях от рельса, мгновенную угловую скорость находят как отношение разности измеренных локальных скоростей к расстоянию, равному разности расстояний от этих точек до поверхности рельса, мгновенный радиус вращения находят как отношение локальной скорости движения оси колеса в направлении, параллельном рельсу, к мгновенной угловой скорости, текущий геометрический радиус колеса определяют как сумму известного расстояния от поверхности рельса до нижней точки, в которой измеряют локальную скорость, и отношения разности линейных скоростей движения оси колеса и его поверхности в нижней из двух точек к мгновенной угловой скорости, а линейную скорость проскальзывания находят как произведение разности текущих значений радиуса вращения и геометрического радиуса колеса на мгновенную угловую скорость.
| Байбаков А.Н., Гуренко В.М., В.И.Патерикин В.И., Плотников С.В., Сотников В.В., Чугуй Ю.В., Юношев С.П | |||
| Автоматический контроль геометрических параметров колесных пар во время движения поезда | |||
| Автометрия, 2004, т.40, №5, с.94-103 | |||
| US 5808906 A, 15.09.1998 | |||
| ВЕРТИКАЛЬНАЯ ЦЕПНАЯ СУШИЛКА | 1926 |
|
SU30970A1 |
| СПОСОБ БЕСКОНТАКТНОГО ДИНАМИЧЕСКОГО КОНТРОЛЯ ПАРАМЕТРОВ КОЛЕС ПОДВИЖНОГО СОСТАВА | 2004 |
|
RU2268183C1 |
Авторы
Даты
2011-05-10—Публикация
2009-12-23—Подача