Текст описания приведен в факсимильном виде.
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических процедур суммирования позиционных аргументов [ni]f(2n) и [mi]f(2n). Техническим результатом является повышение быстродействия. В одном из вариантов функциональная структура выполнена с использованием элементов, реализующих логические функции И, ИЛИ, И-НЕ, НЕ. 5 н.п. ф-лы.
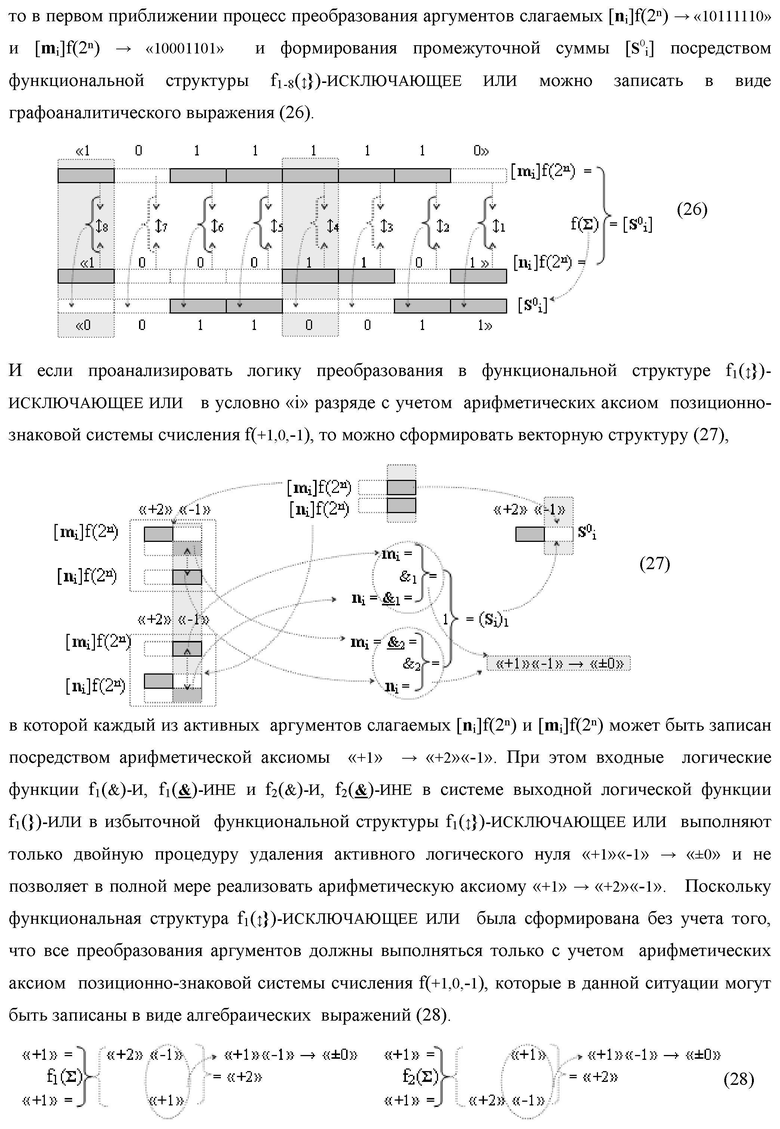
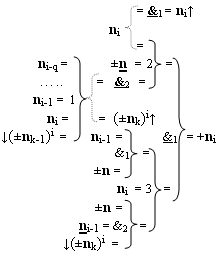
1. Функциональная структура процедуры преобразования позиционных условно отрицательных аргументов «-»[ni]f(2n) в структуру аргументов «дополнительный код» позиционно-знакового формата с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логическую функцию f2(})-ИЛИ и логические функции f1(})-ИЛИ и f1(&)-HE, функциональные выходные связи которых являются функциональными входными связями логических функций f1(&)-И, a функциональная выходная связь логической функции f1(&)-И-HE является функциональной входной связью логической функции f2(&)-И, отличающаяся тем, что введена дополнительная логическая функция f2(&)-И-НЕ, а функциональные связи логических функций в структуре преобразователя выполнены в соответствии с математической моделью вида
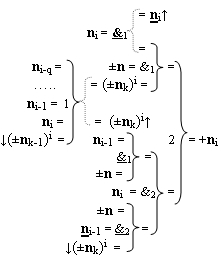
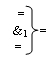- логическая функция f1(&)-И; 
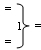- логическая функция f1(})-
ИЛИ;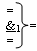 
- логическая функция f1(&)-И-HE;
«=&1=» - логическая функция f1(&)-HE изменения активности входных аналоговых сигналов.
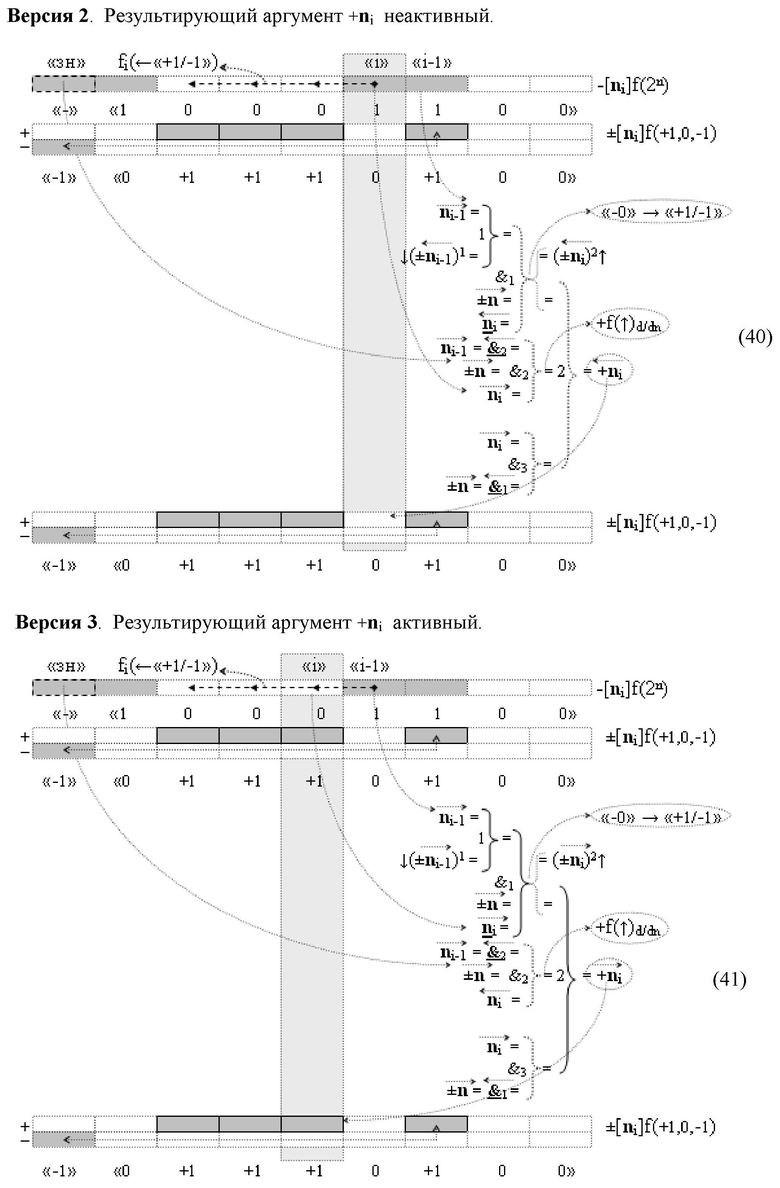
2. Функциональная структура процедуры преобразования позиционных условно отрицательных аргументов «-»[ni]f(2n) в структуру аргументов «дополнительный код» позиционно-знакового формата с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f2(})-ИЛИ, f2(&)-И и f1(}&)-ИЛИ-НЕ и логические функции f1(})-ИЛИ и f1(&)-HE, функциональные выходные связи которых являются функциональными входными связями логических f1(}&)-И, отличающаяся тем, что введена дополнительная логическая функция f3(&)-И, а функциональные связи логических функций в структуре преобразователя выполнены в соответствии с математической моделью вида
где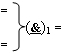 
- логическая функция f1(}&)-ИЛИ-НЕ.
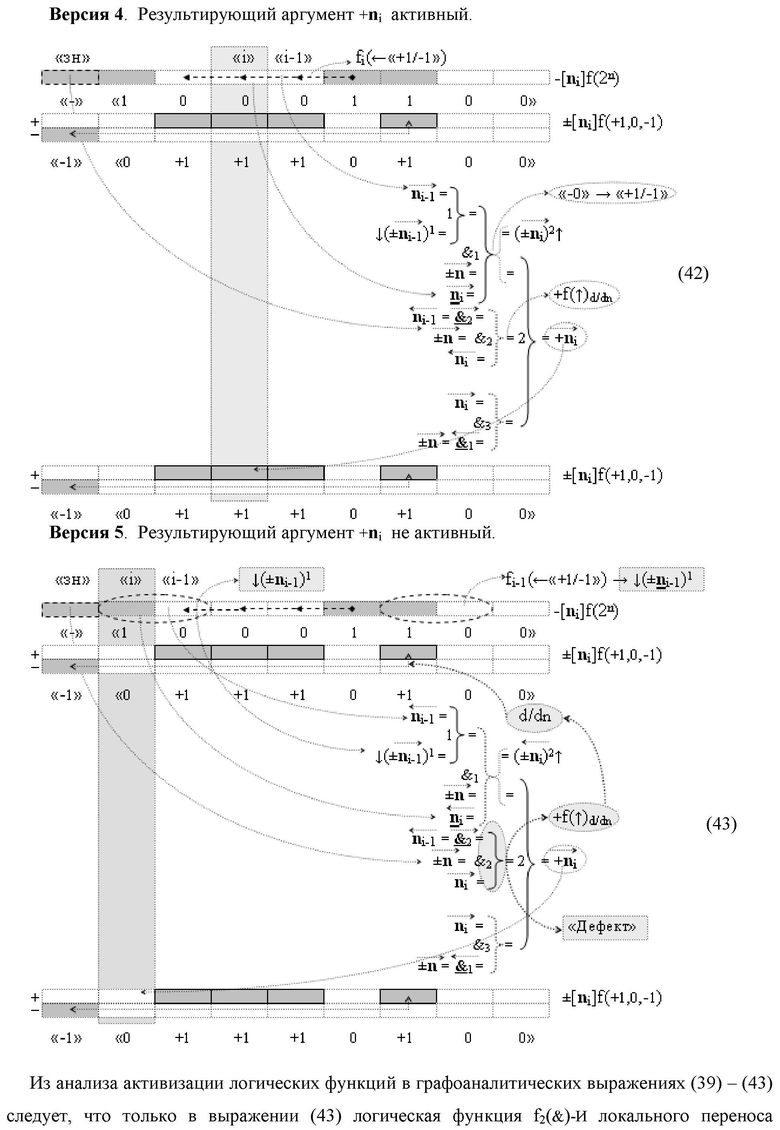
3. Функциональная структура процедуры преобразования позиционных условно отрицательных аргументов «-»[ni]f(2n) в структуру аргументов «дополнительный код» позиционно-знакового формата с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f1(})-ИЛИ, f2(})-ИЛИ, f1(&)-И, f2(&)-И, f1(&)-HE и f1(&)-И-HE, отличающаяся тем, что введена дополнительная логическая функция f2(&)-И-НЕ, а функциональные связи логических функций в структуре преобразователя выполнены в соответствии с математической моделью вида
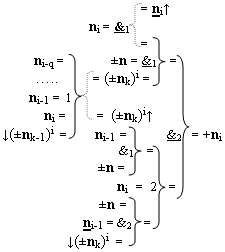
4. Функциональная структура процедуры преобразования позиционных условно отрицательных аргументов «-»[ni]f(2n) в структуру аргументов «дополнительный код» позиционно-знакового формата с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f1(})-ИЛИ, f1(&)-HE и f3(&)-И-НЕ, отличающаяся тем, что введены дополнительные логические функции f1(&)-И-HE, f2(&)-И-НЕ, f4(&)-И-НЕ и f5(&)-И-НЕ, а функциональные связи логических функций в структуре преобразователя выполнены в соответствии с математической моделью вида
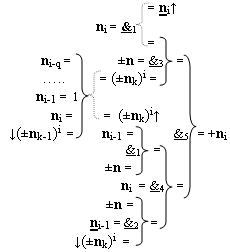
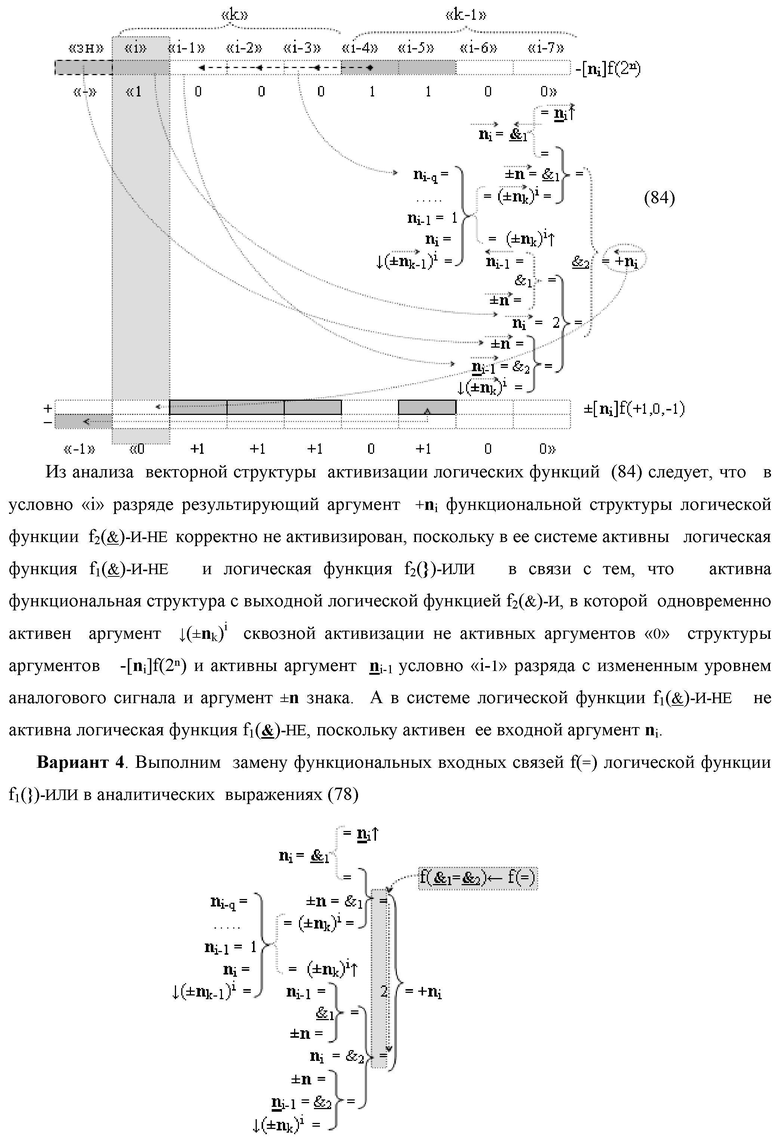
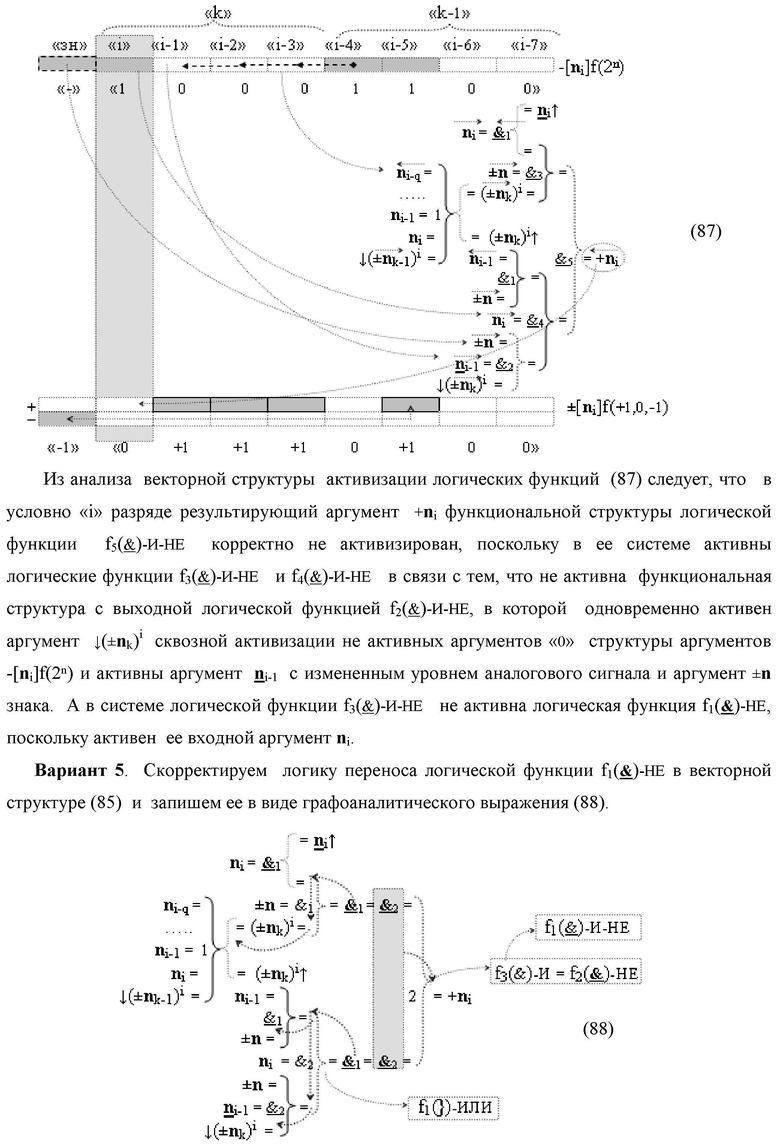
5. Функциональная структура процедуры преобразования позиционных условно отрицательных аргументов «-»[ni]f(2n) в структуру аргументов «дополнительный код» позиционно-знакового формата с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f1(})-ИЛИ, f2(})-ИЛИ, f3(})-ИЛИ, f1(&)-HE, f1(&)-И и f2(&)-И и f1(&)-И-НЕ, отличающаяся тем, что функциональные связи логических функций в структуре преобразователя выполнены в соответствии с математической моделью вида
| ЦИЛЬКЕР Б.Я | |||
| и др | |||
| Организация ЭВМ и систем | |||
| - С.-Пб.: ПИТЕР, 2004, с.339, рис.7.13 | |||
| ПРЕОБРАЗОВАТЕЛЬ ПАРАЛЛЕЛЬНОГО ЗНАКОРАЗРЯДНОГО КОДА В ДОПОЛНИТЕЛЬНЫЙ ДВОИЧНЫЙ КОД | 1990 |
|
RU2022337C1 |
| Устройство для преобразования знакоразрядного кода в дополнительный двоичный код | 1990 |
|
SU1753599A1 |
| DE 4308112 A1, 13.10.1994 | |||
| US 4623872 A, 18.11.1986. | |||
