Текст описания приведен в факсимильном виде.
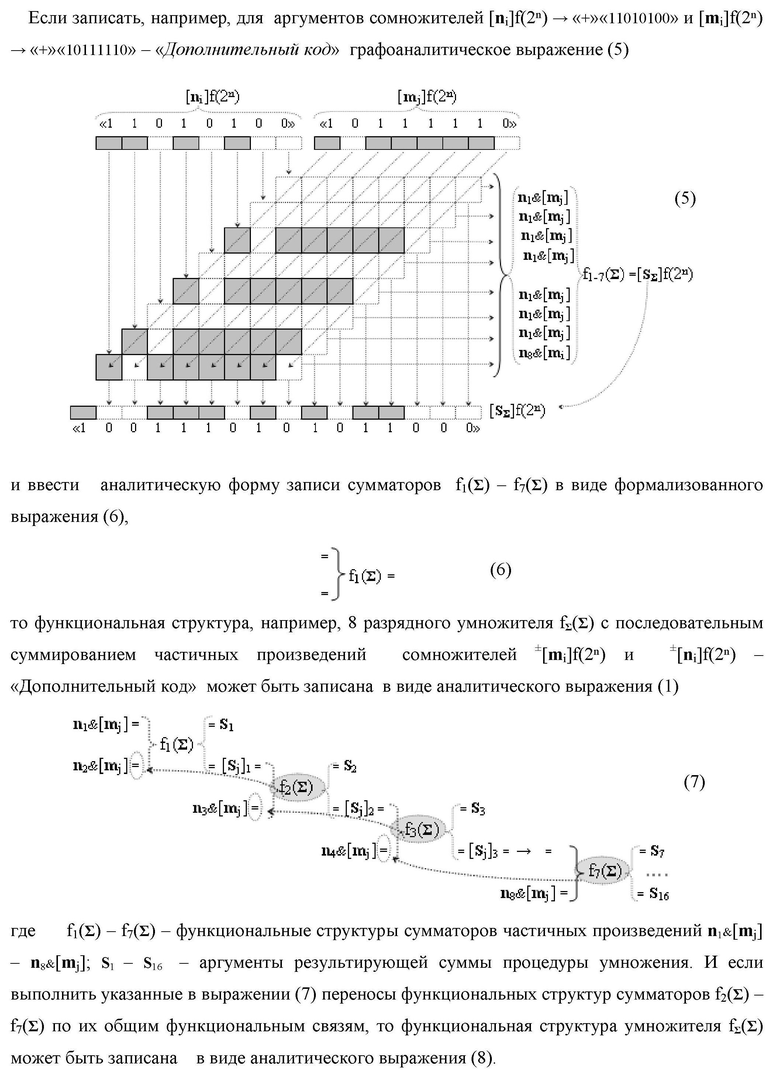
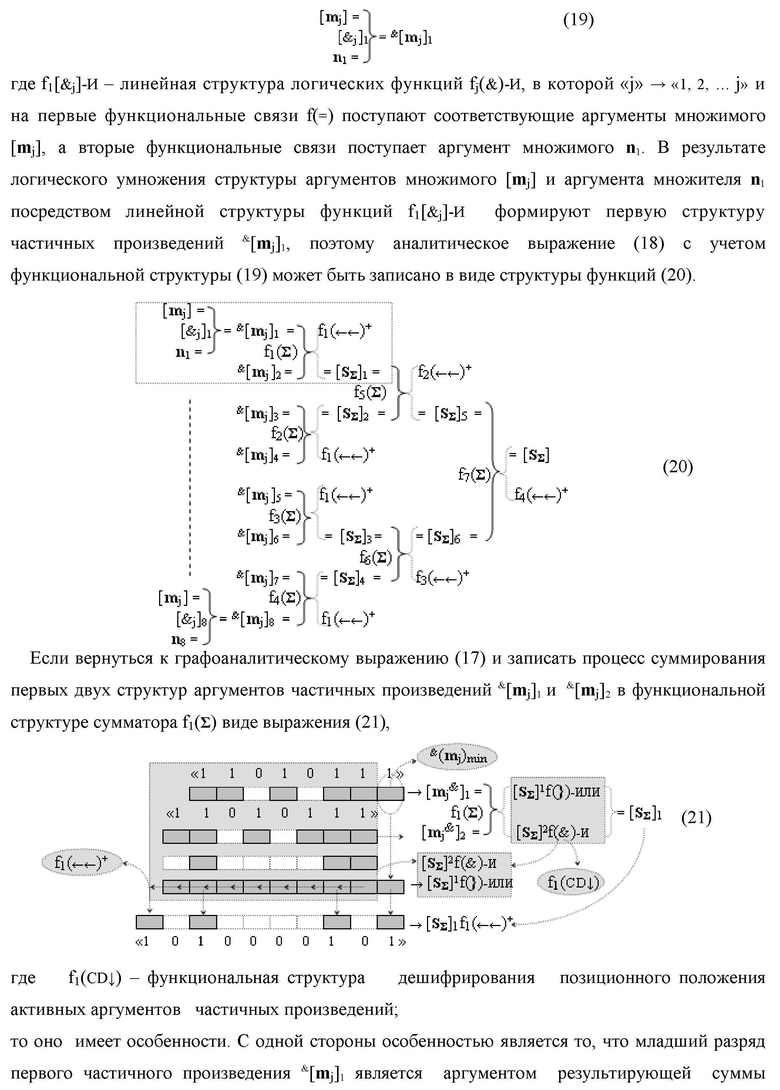
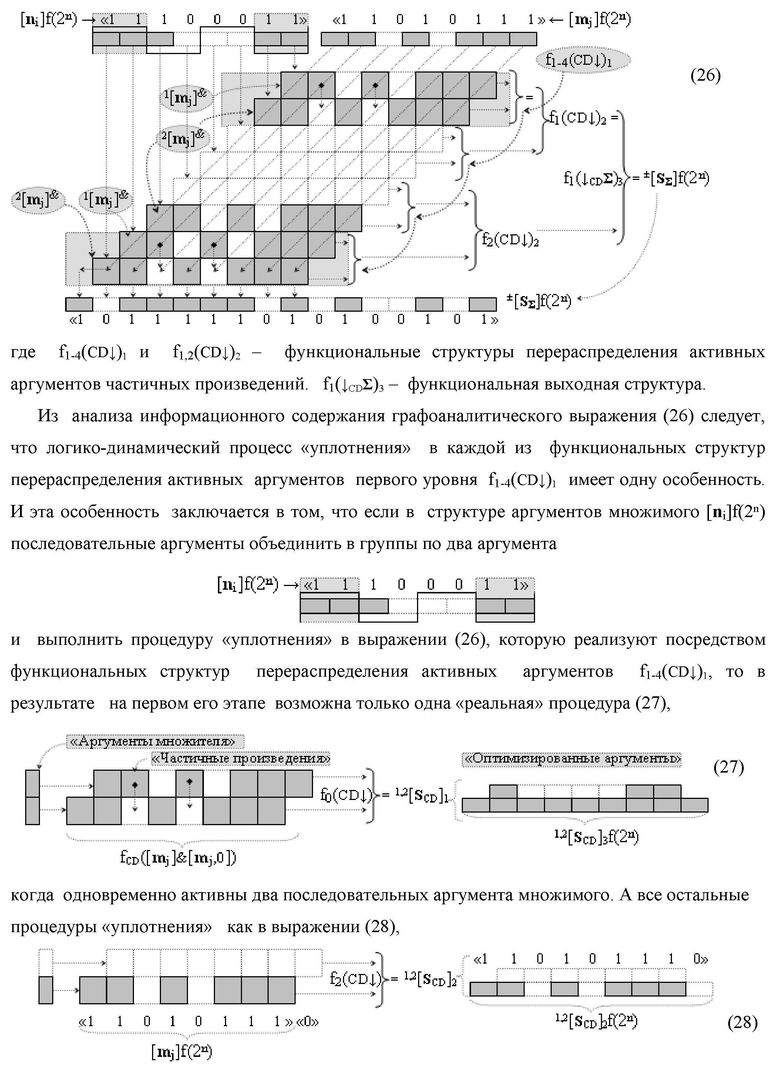
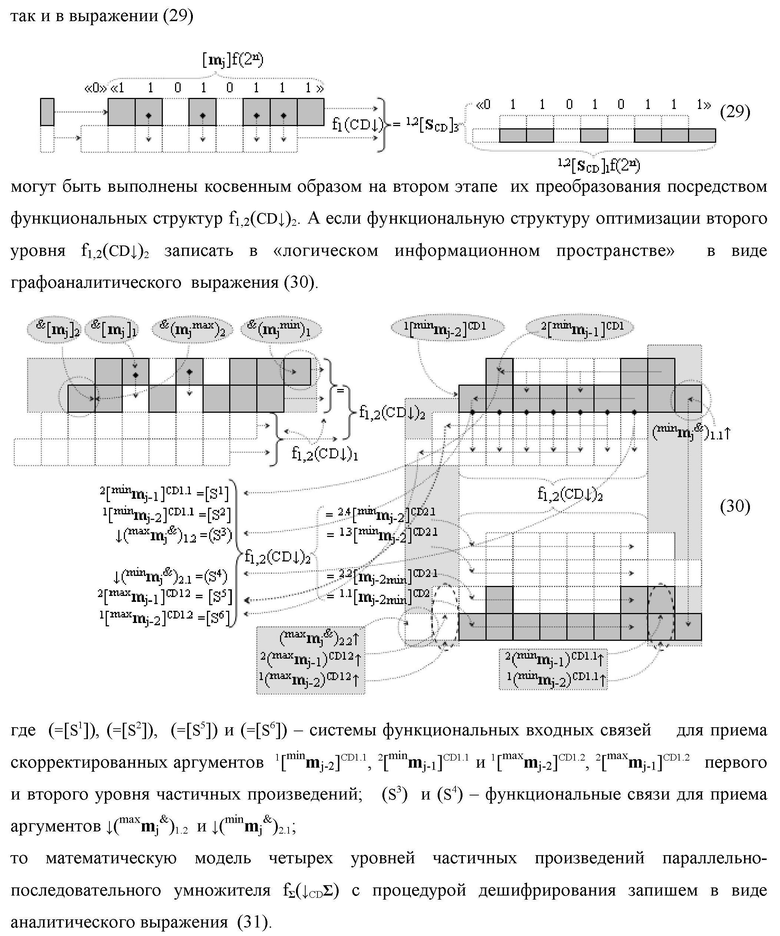
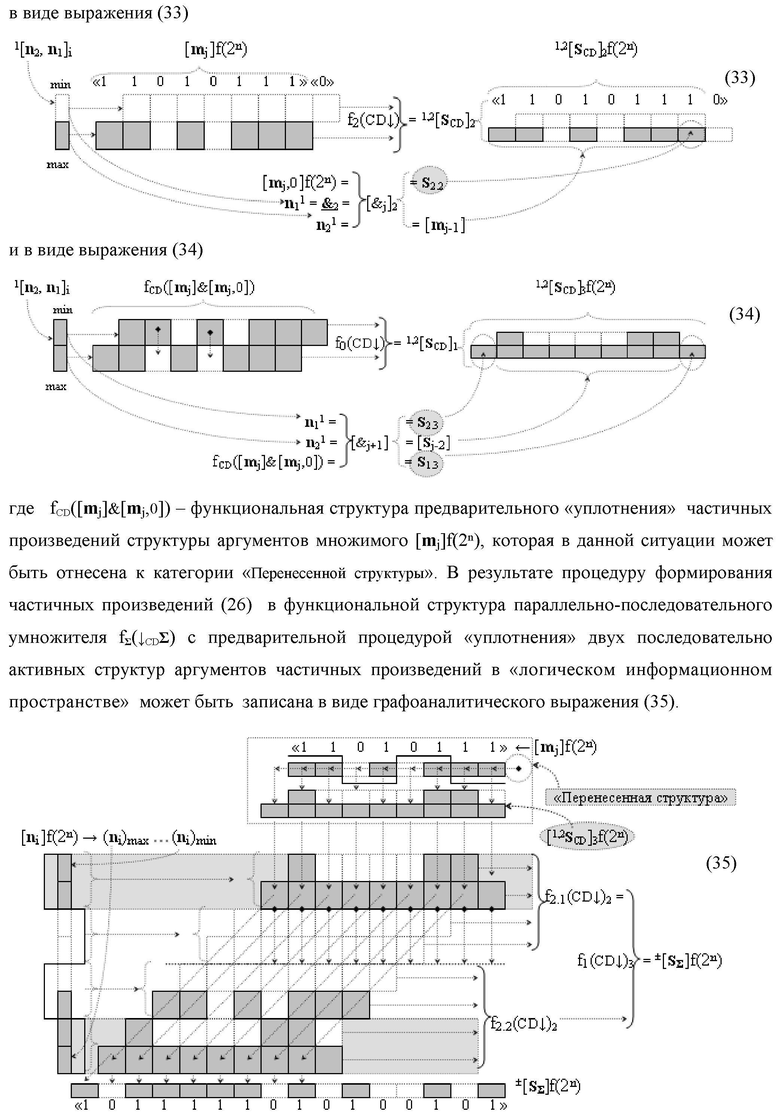
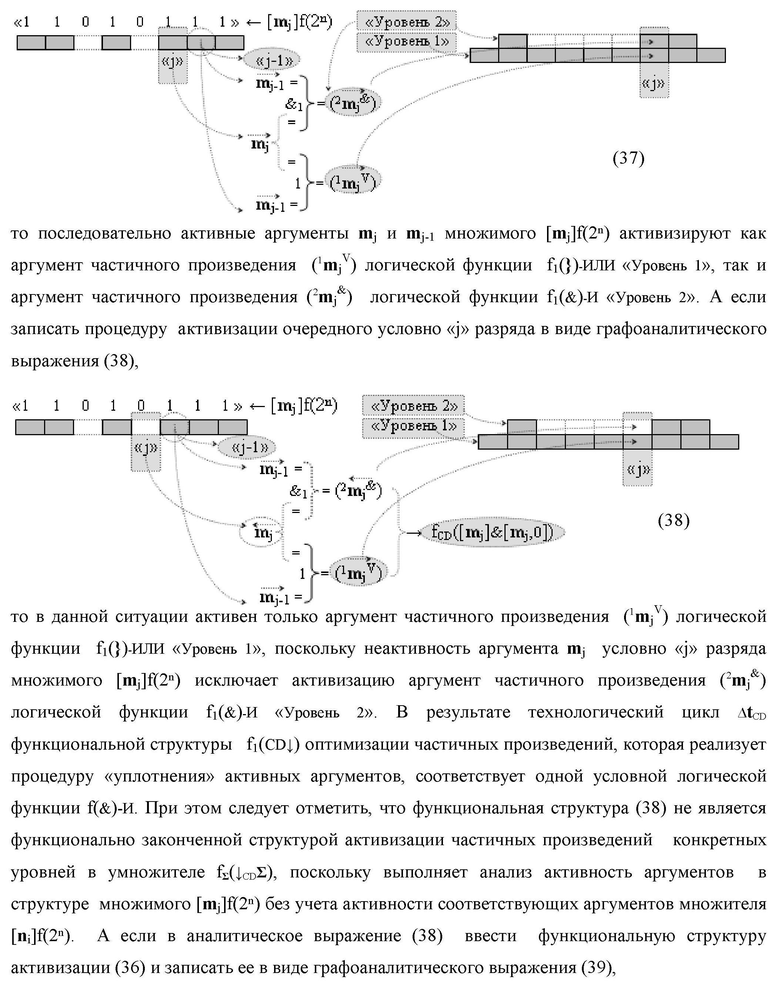
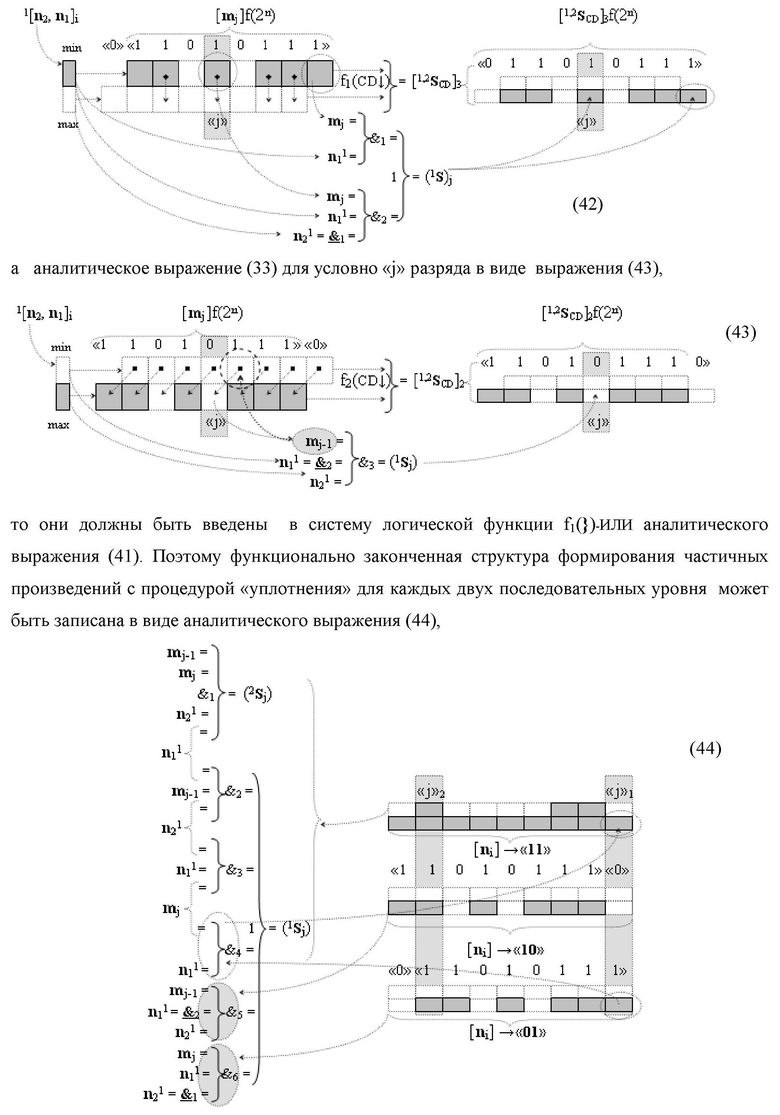
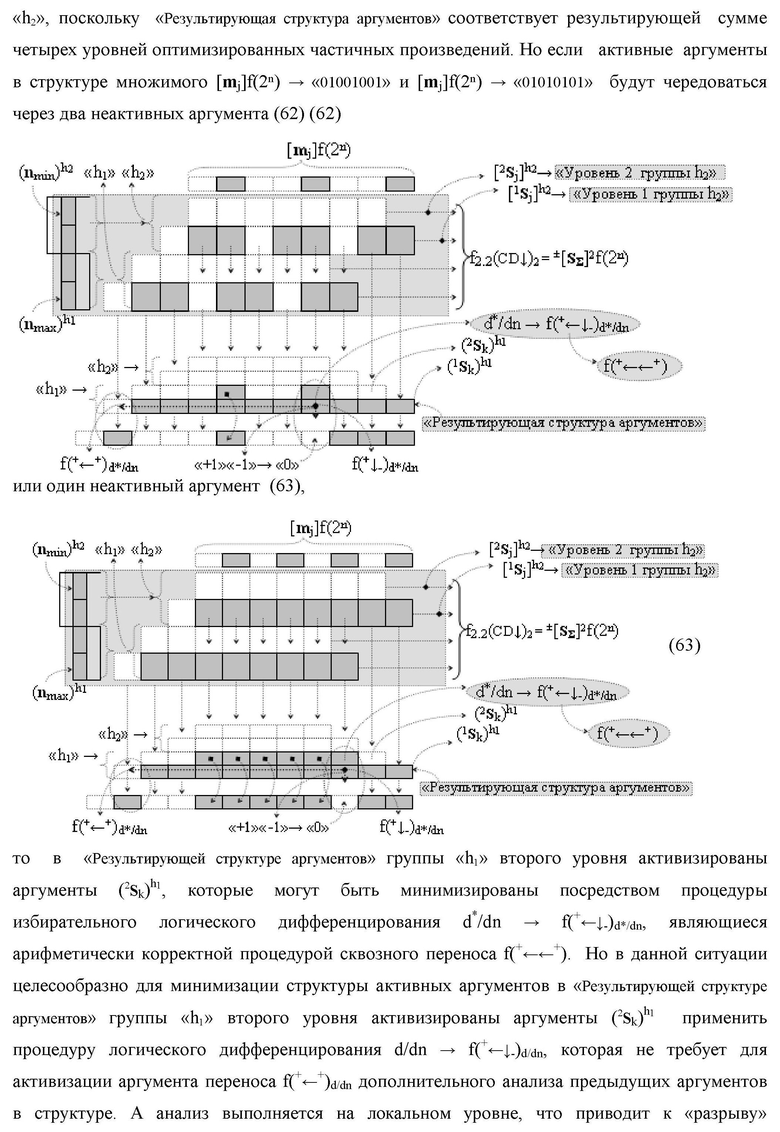
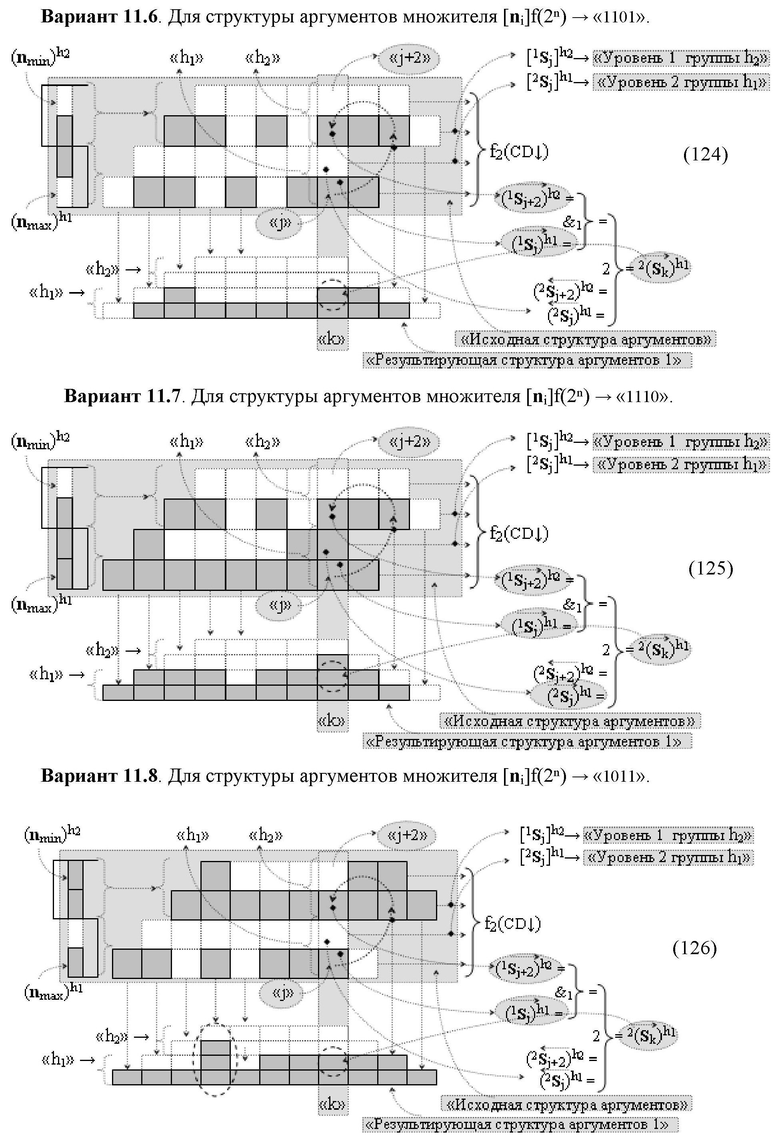
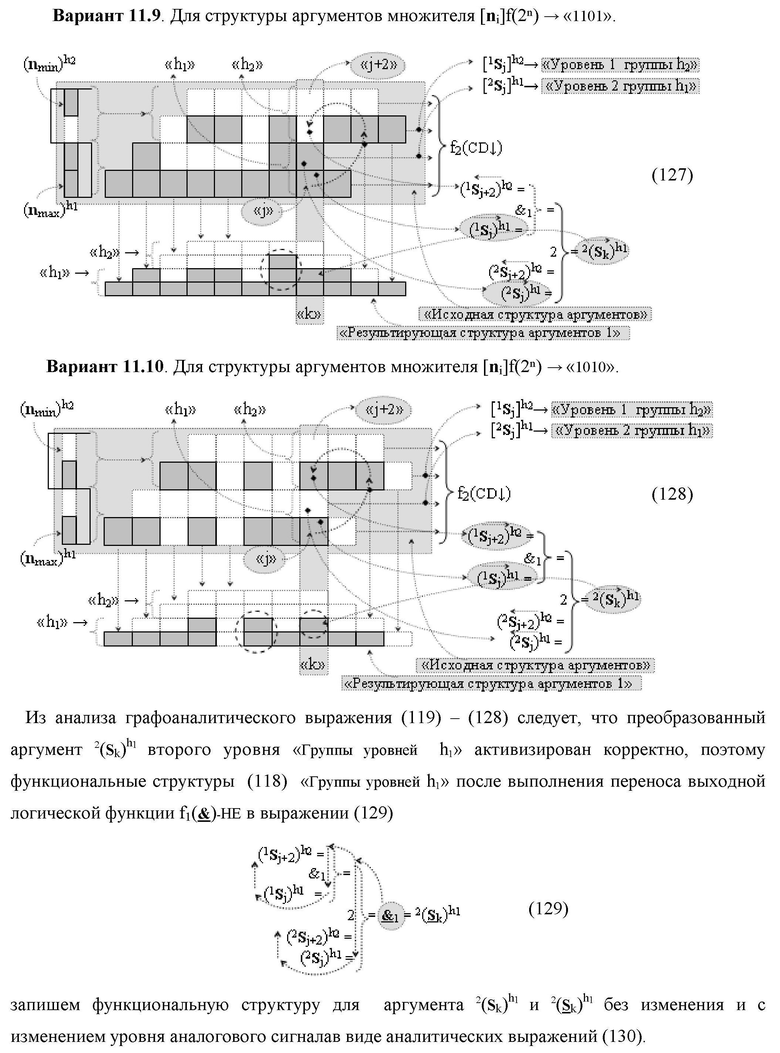
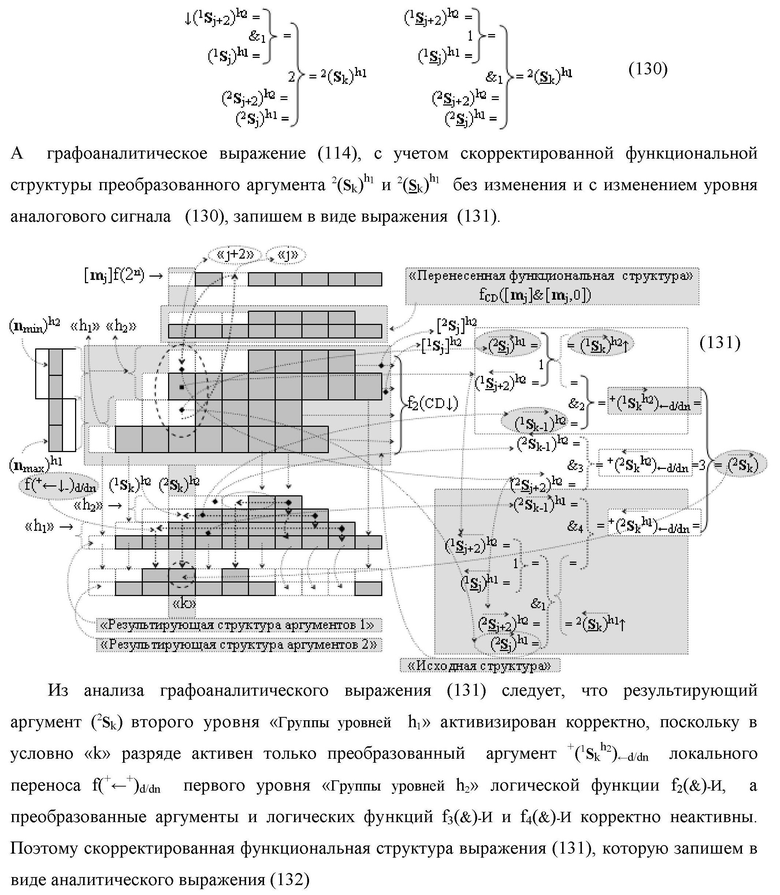
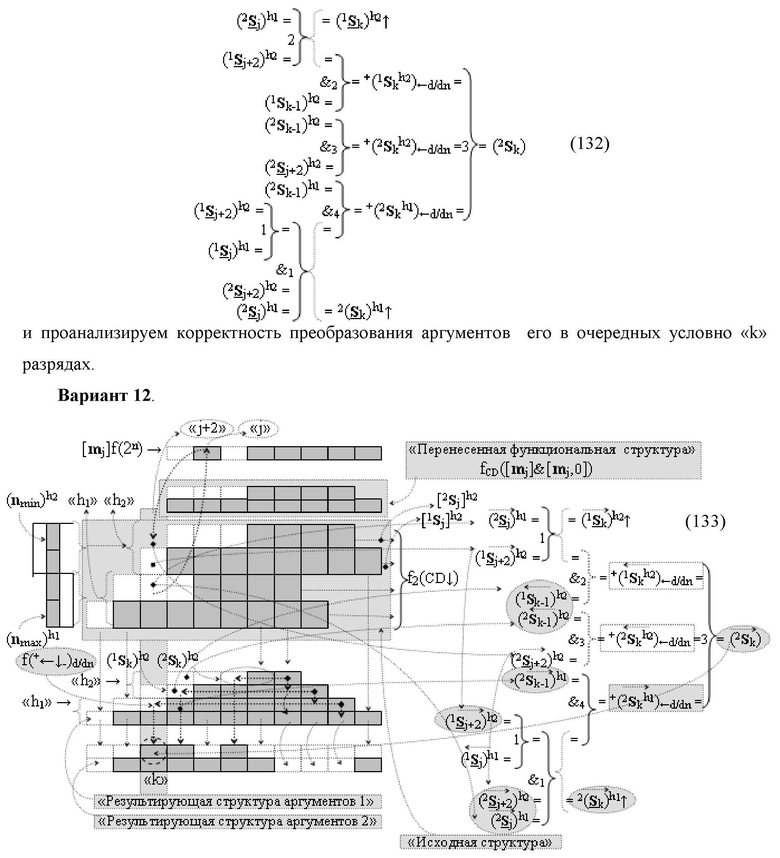
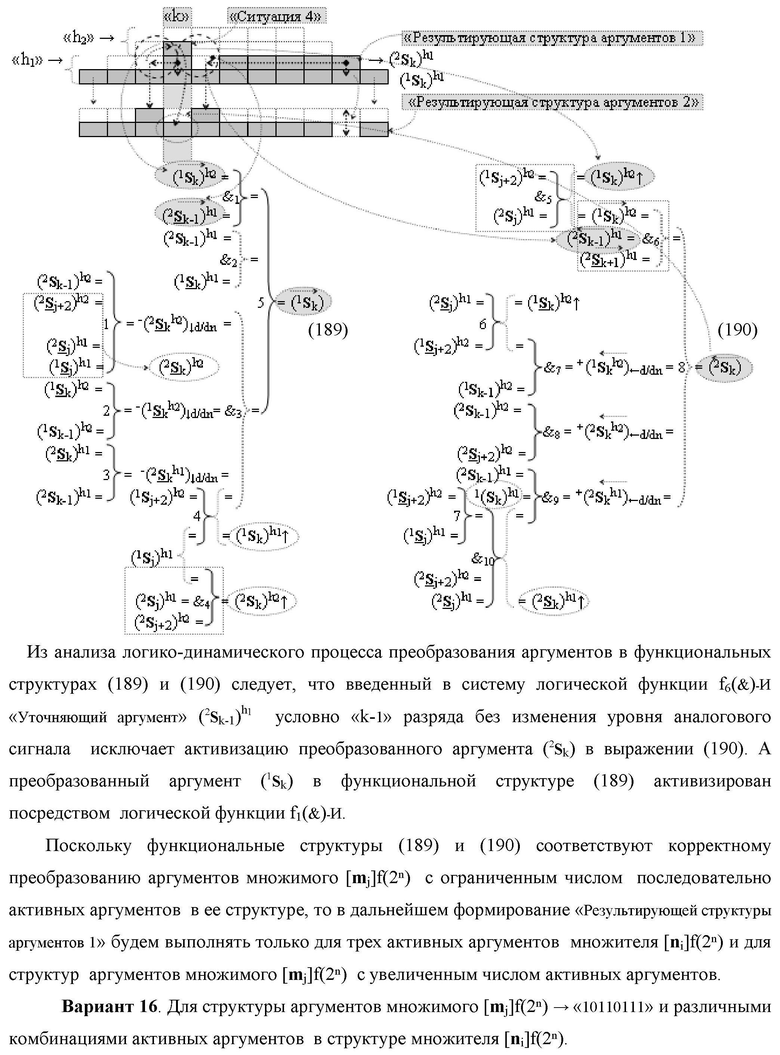
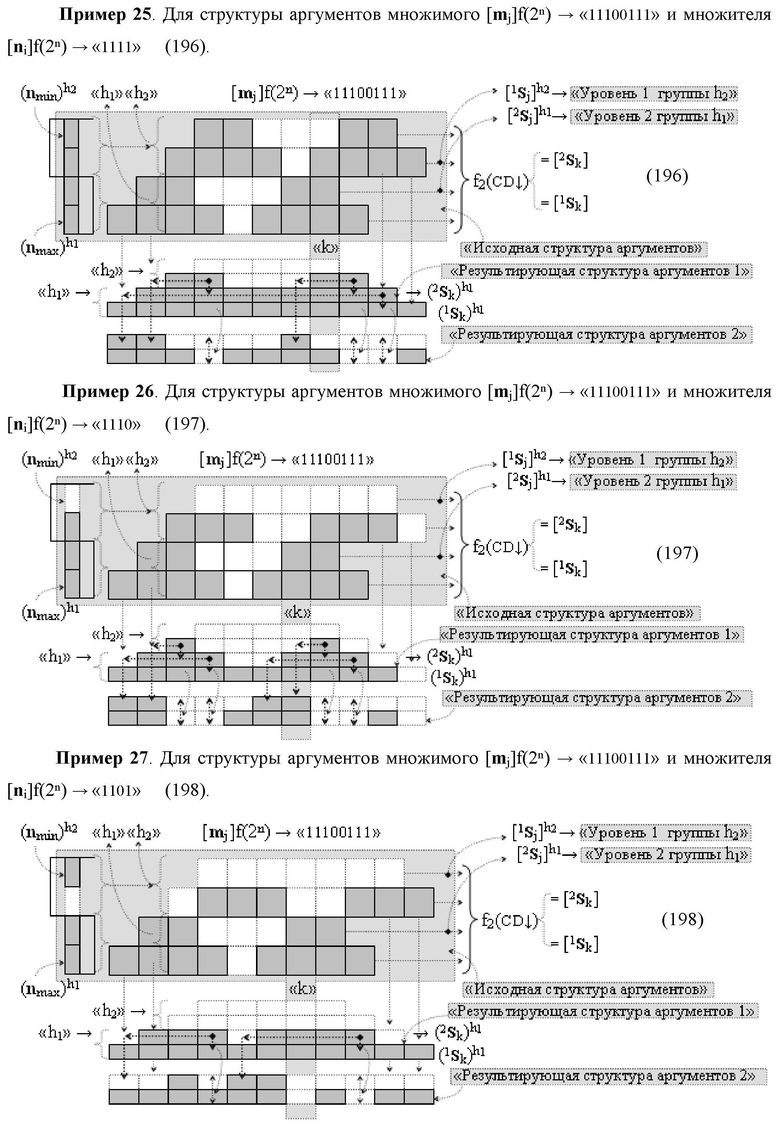
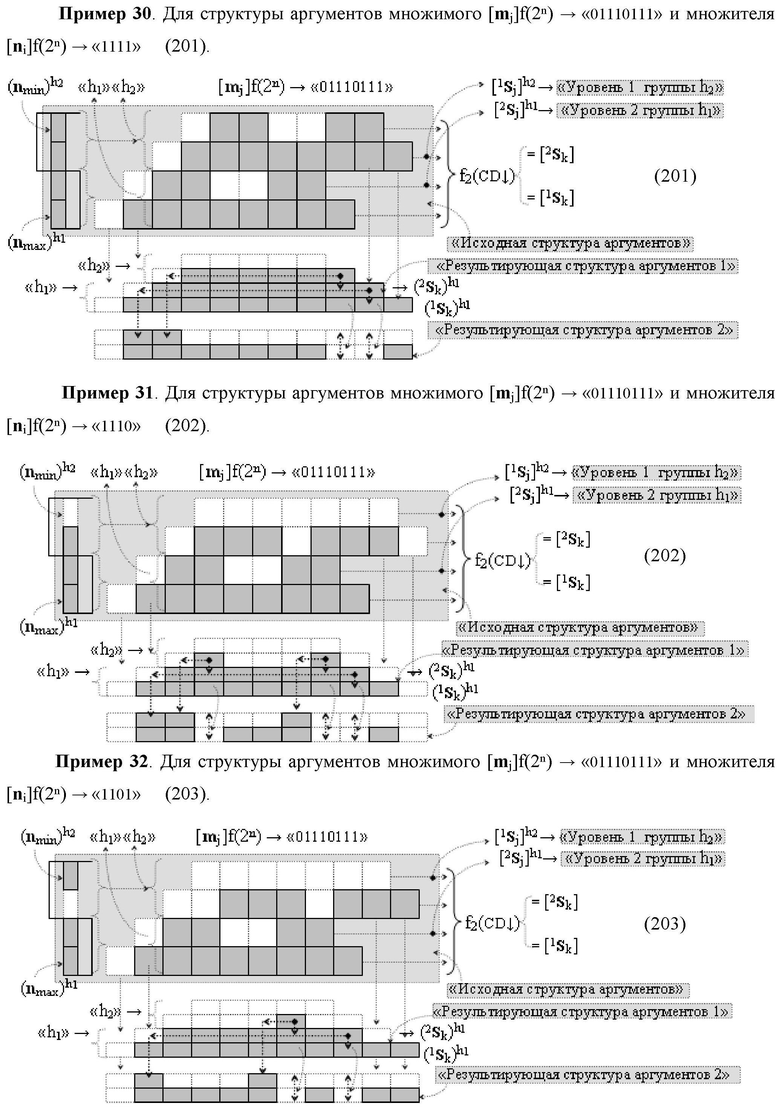
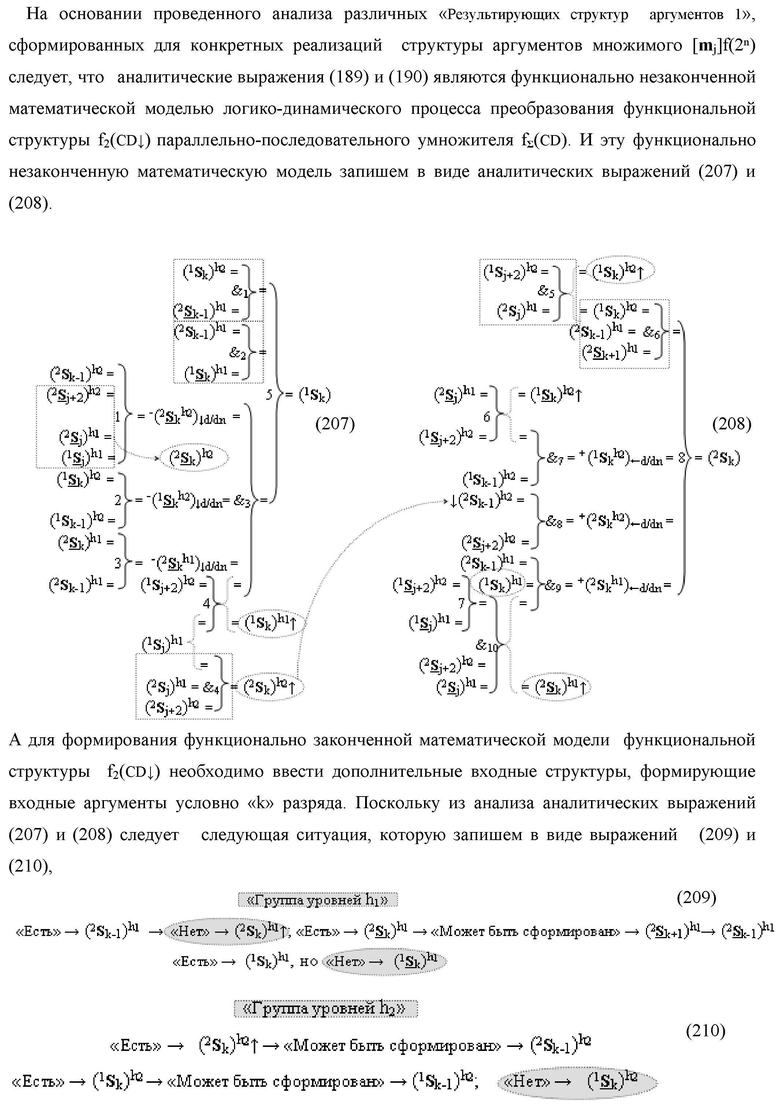
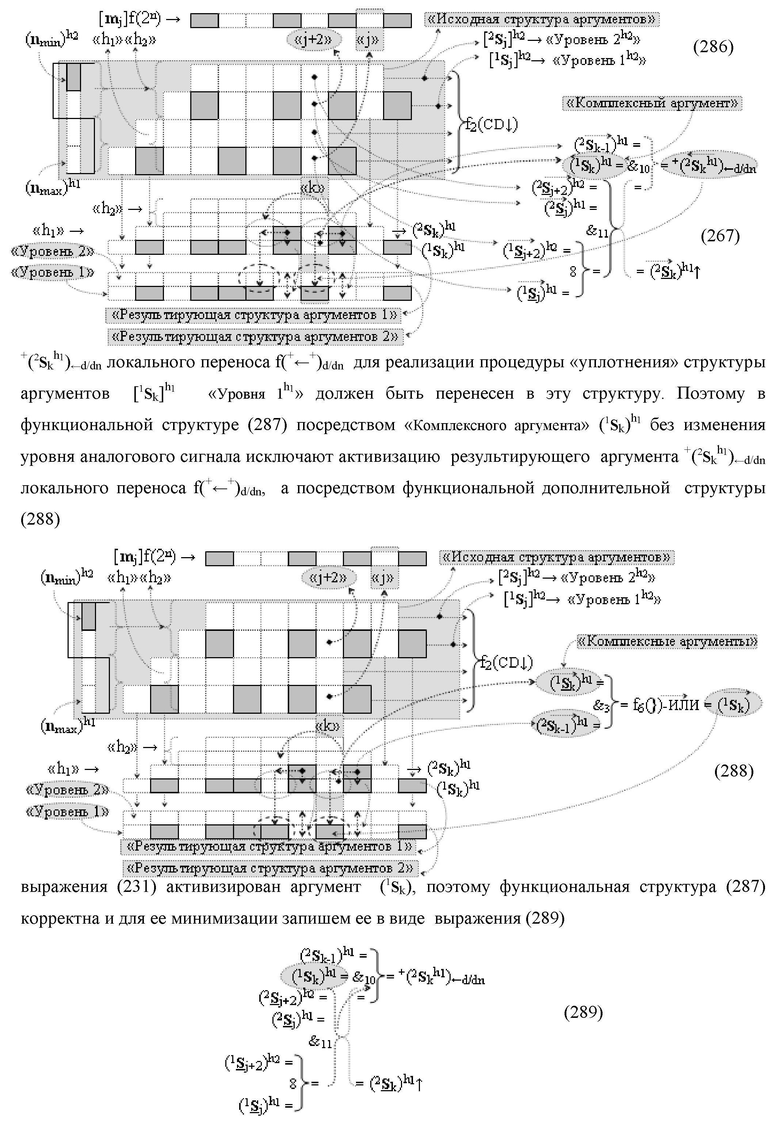
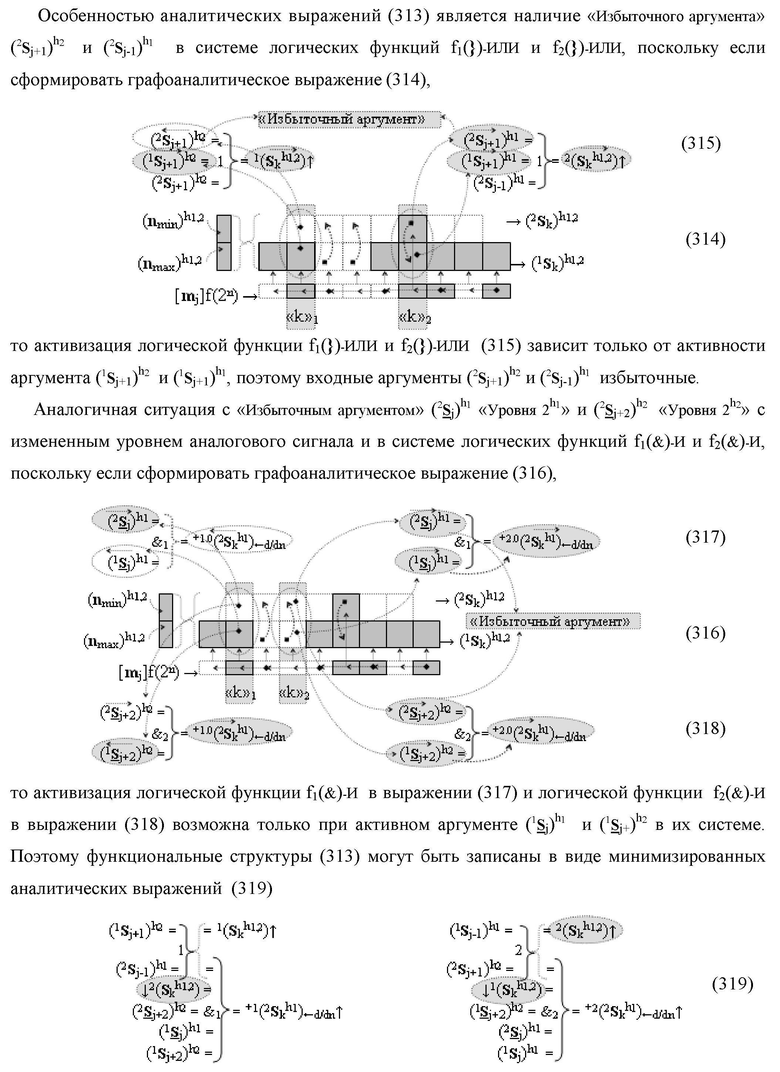
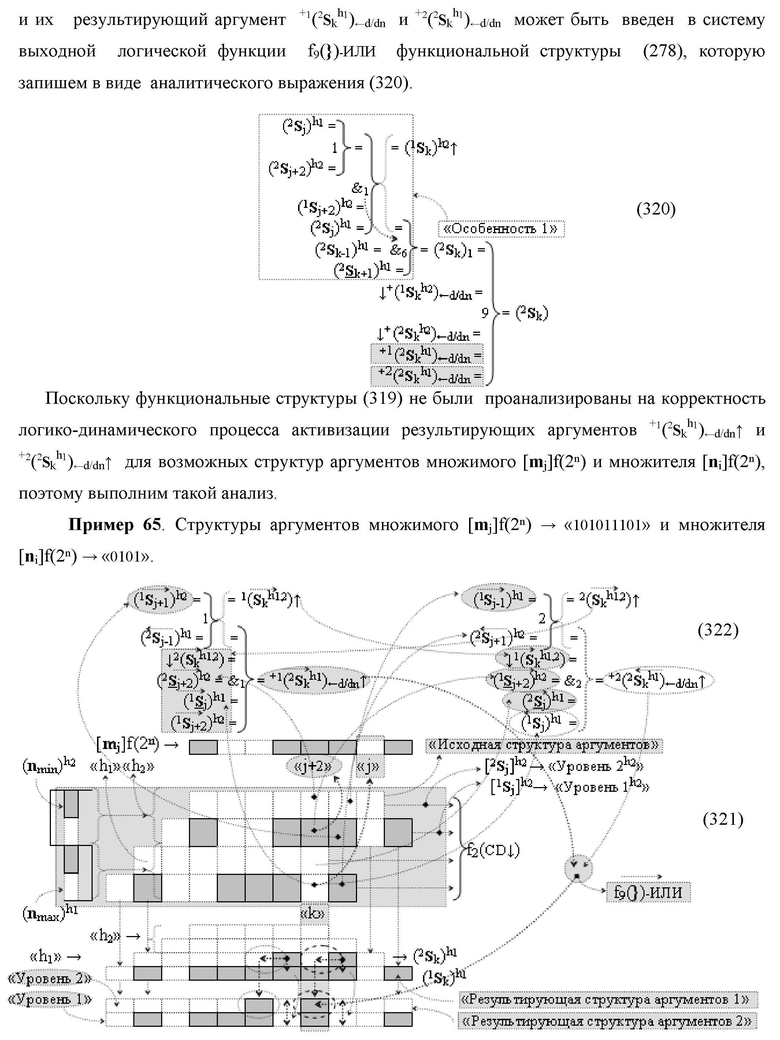
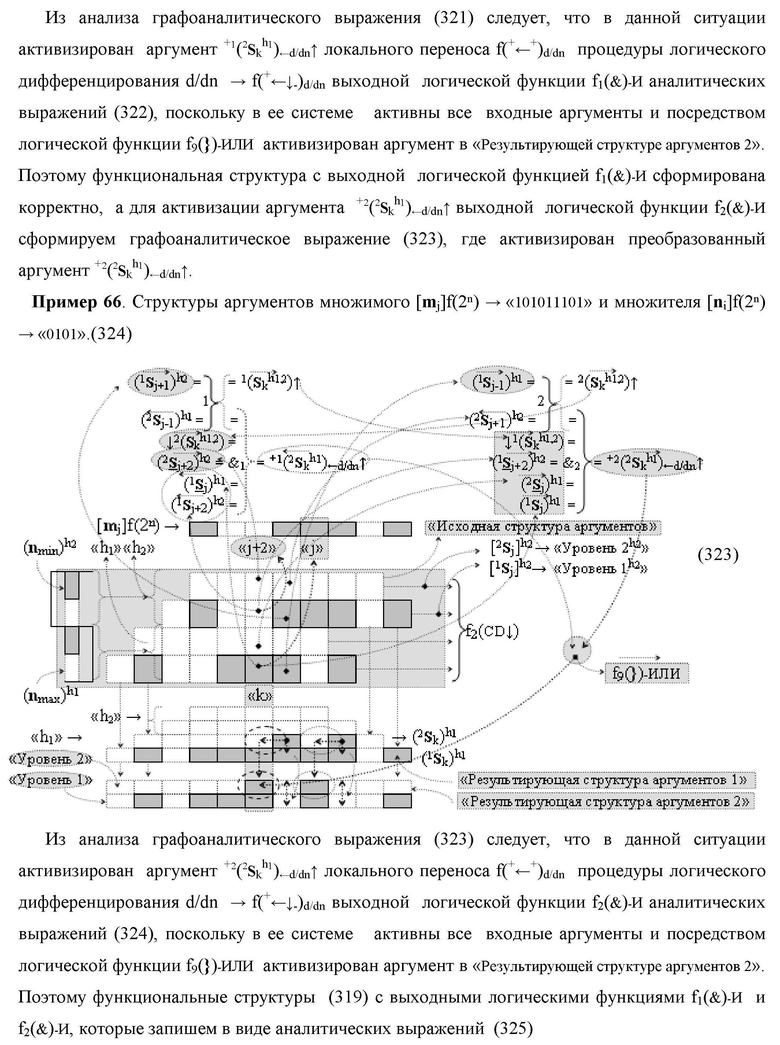
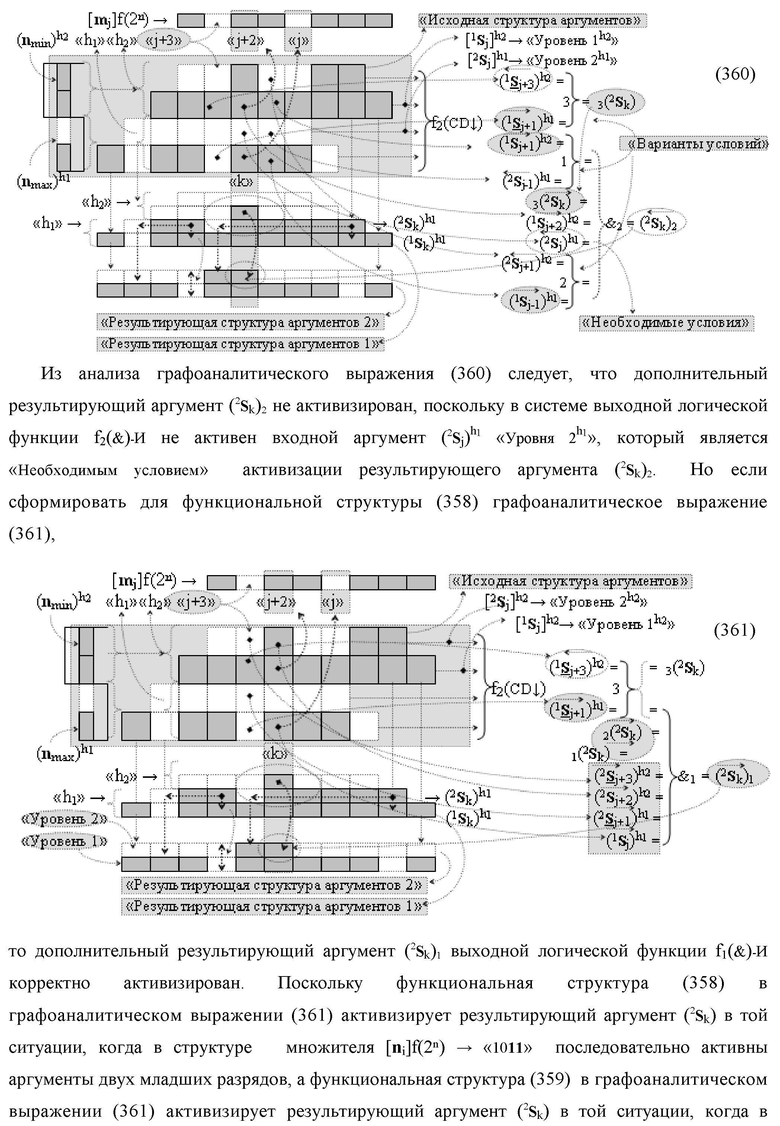
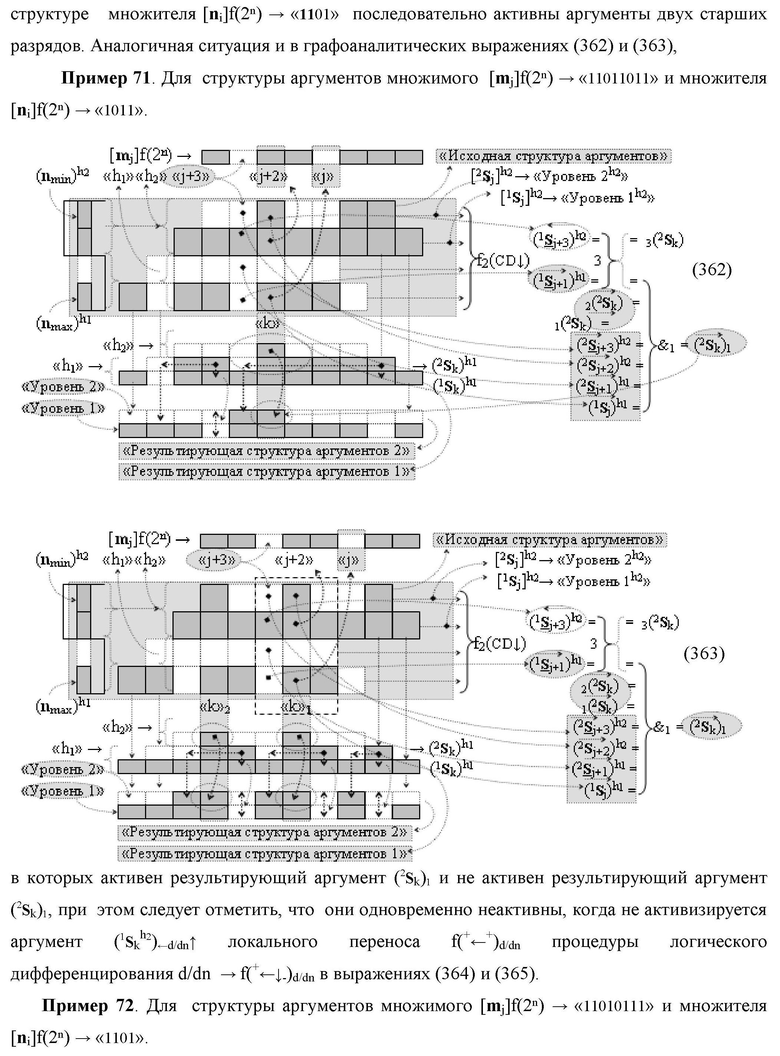
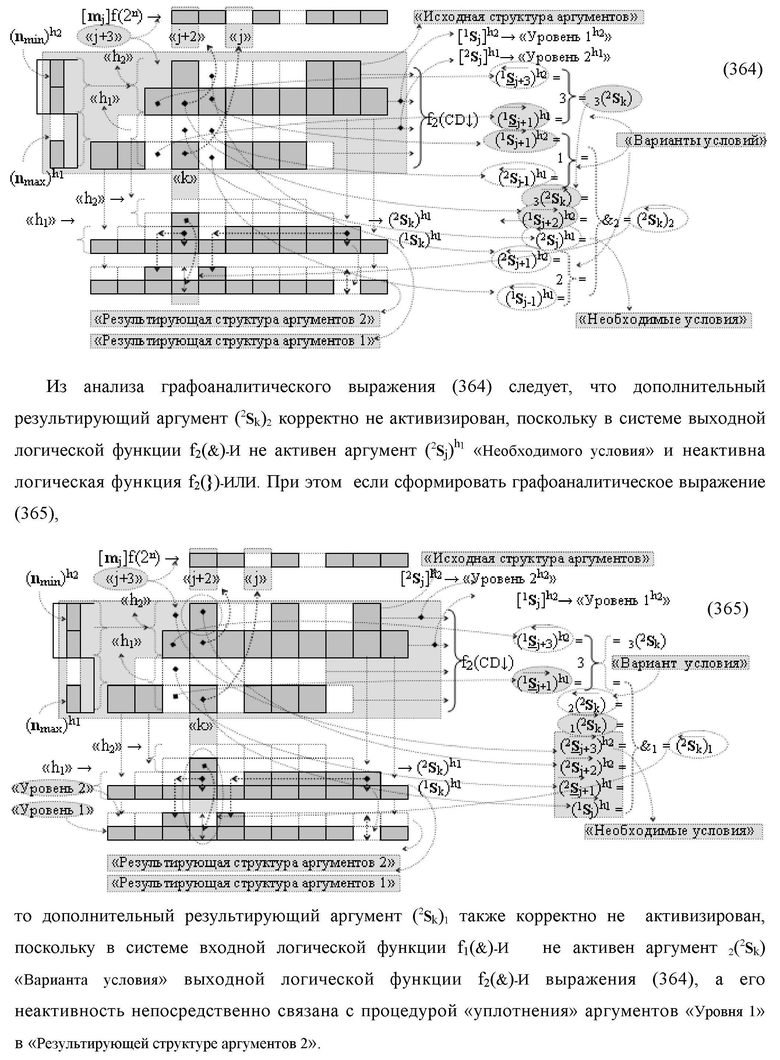
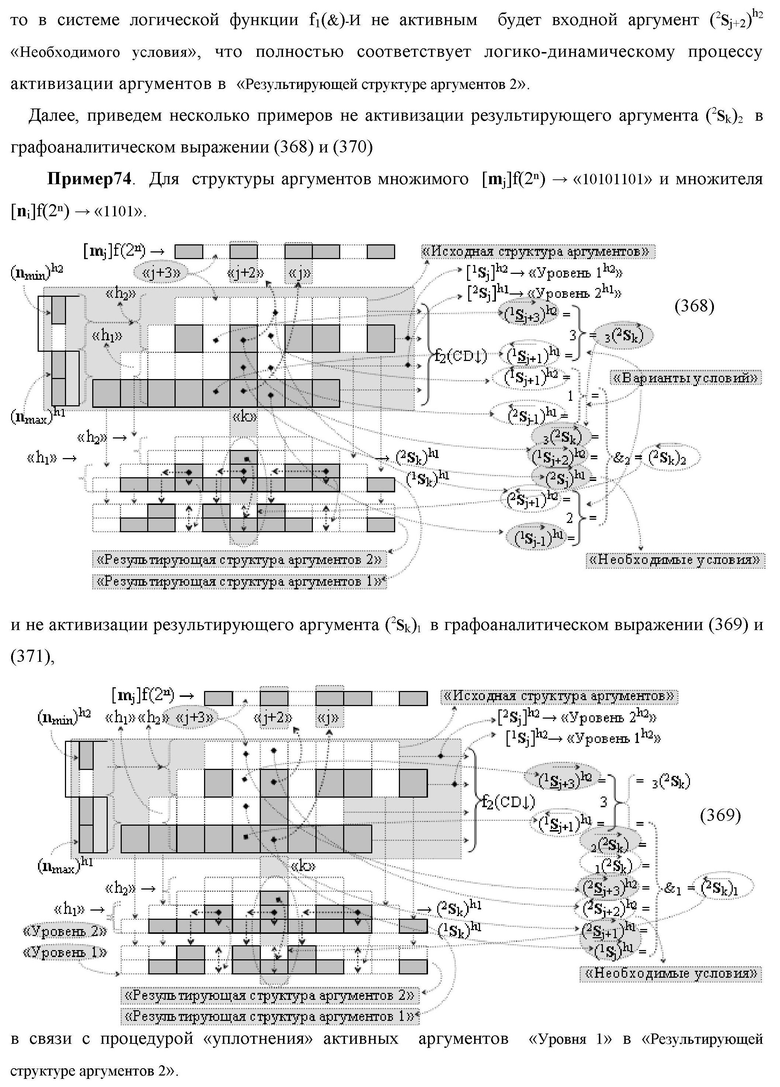
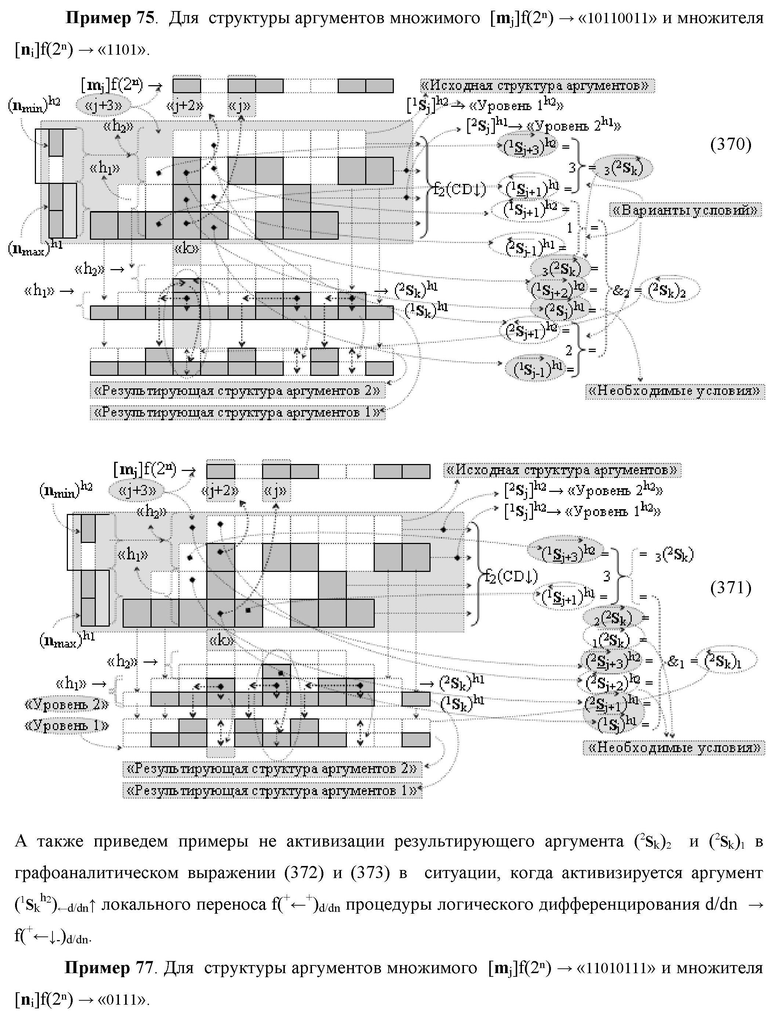
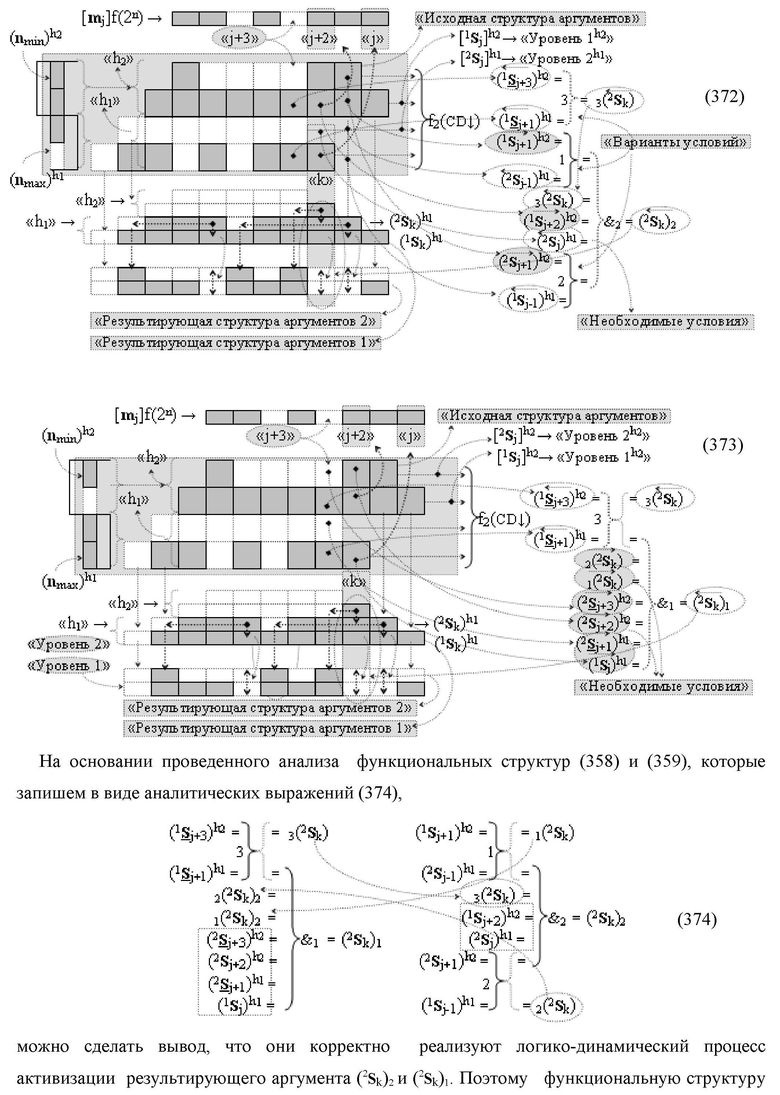
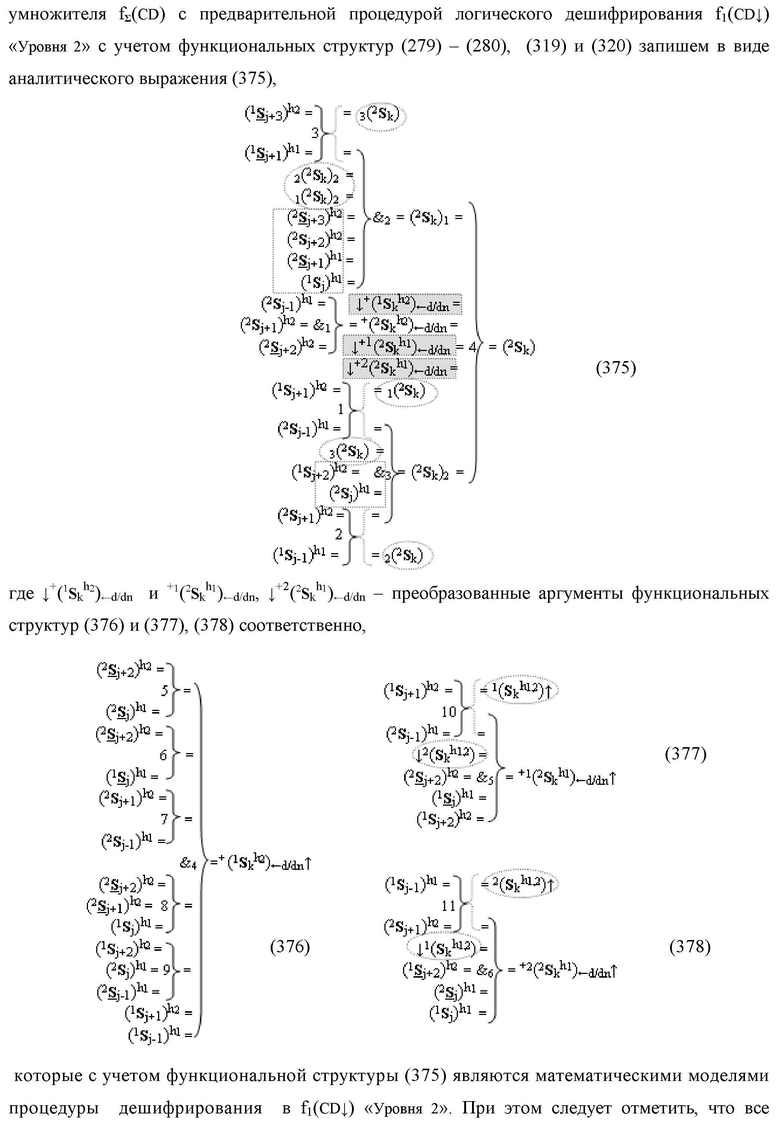
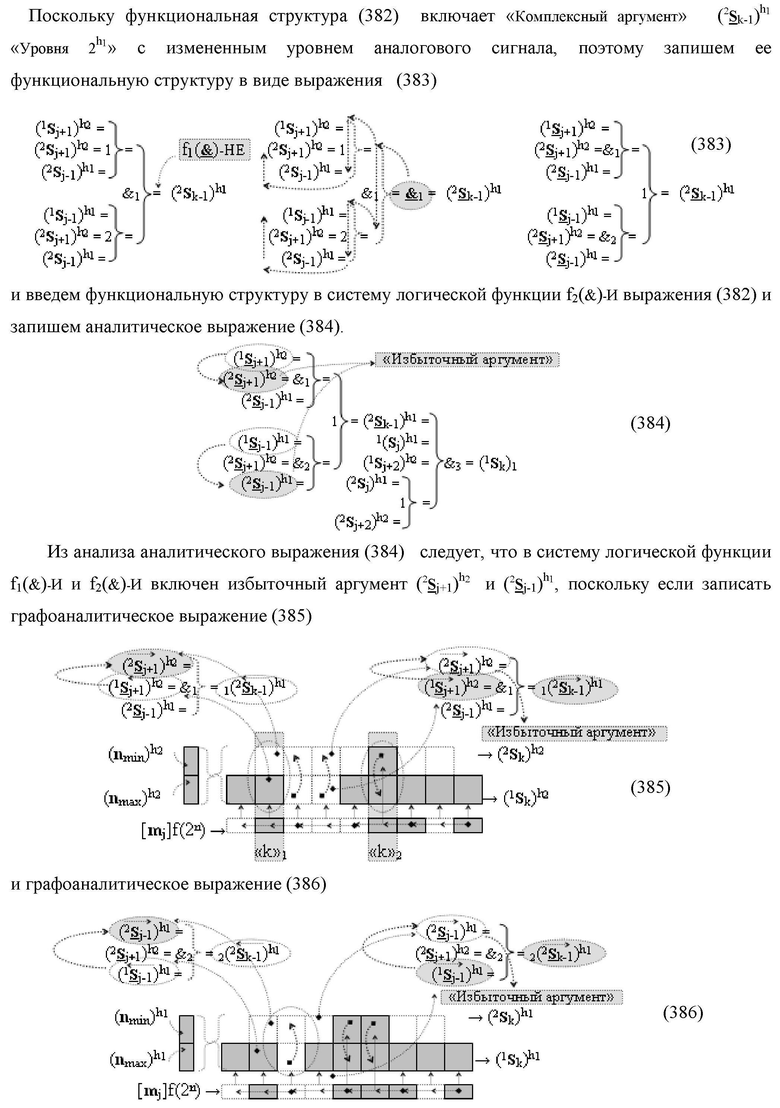
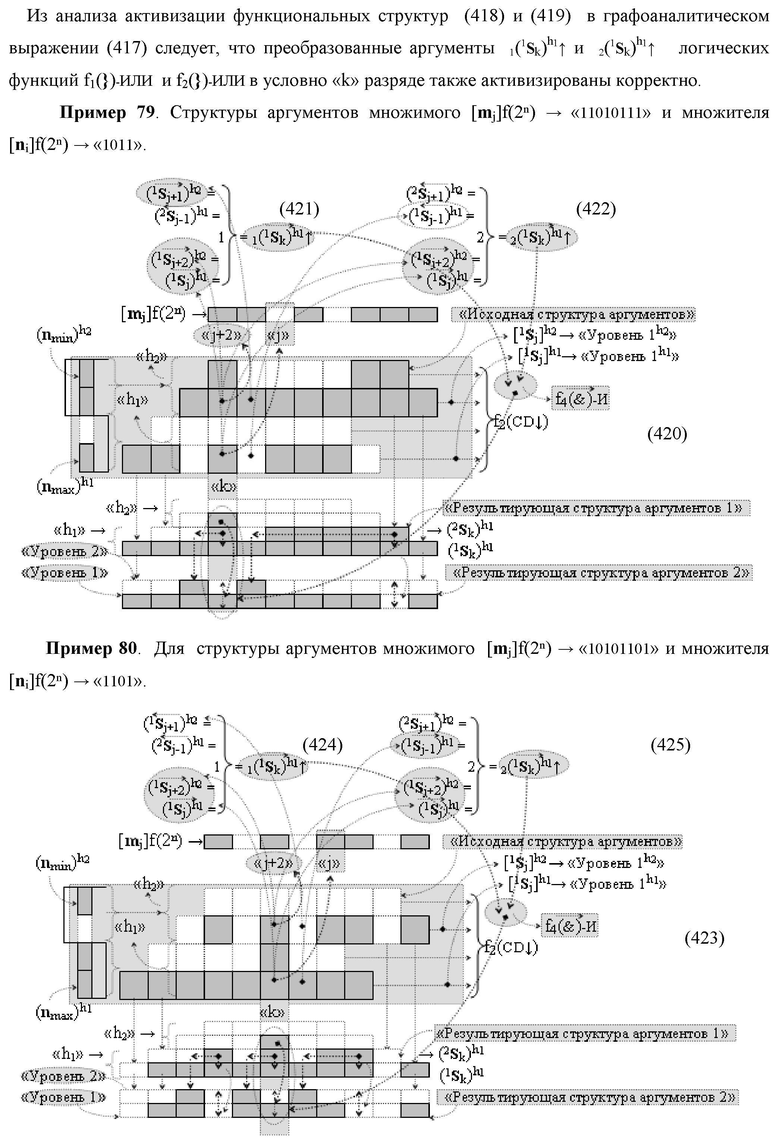
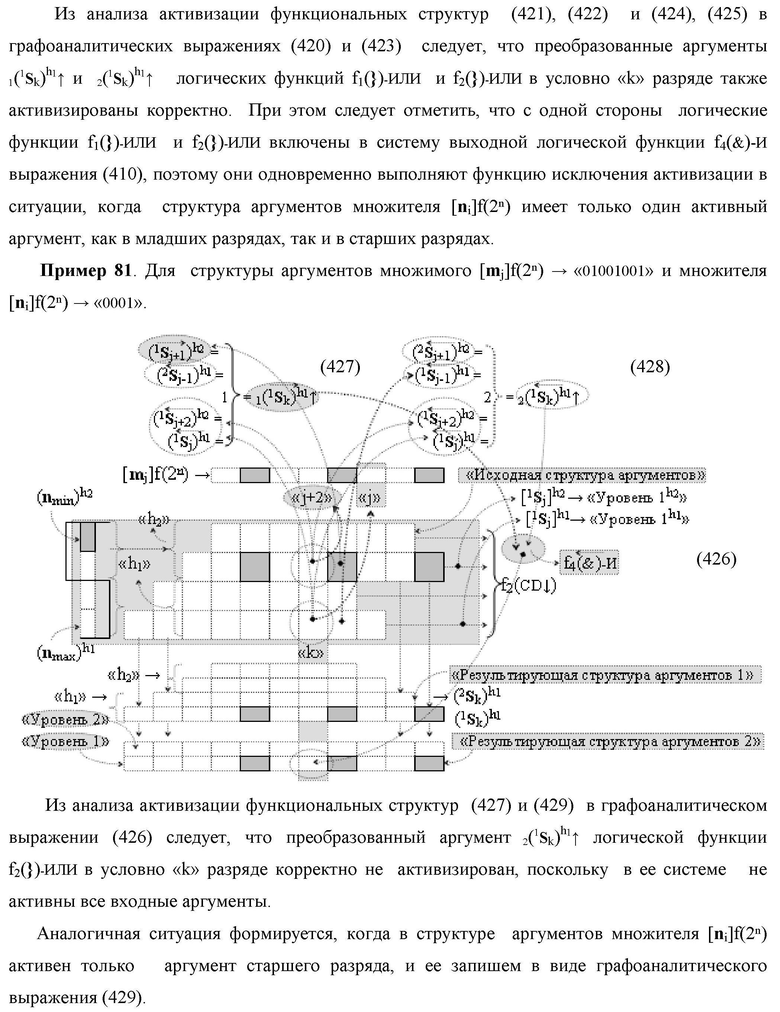
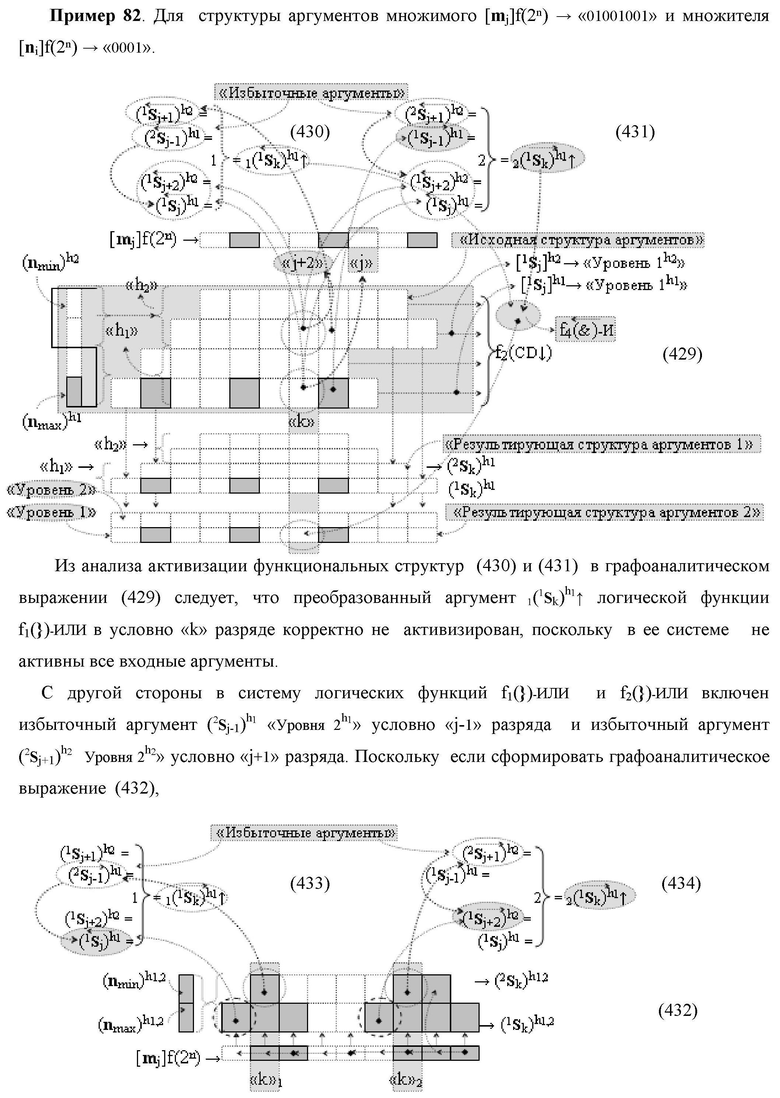
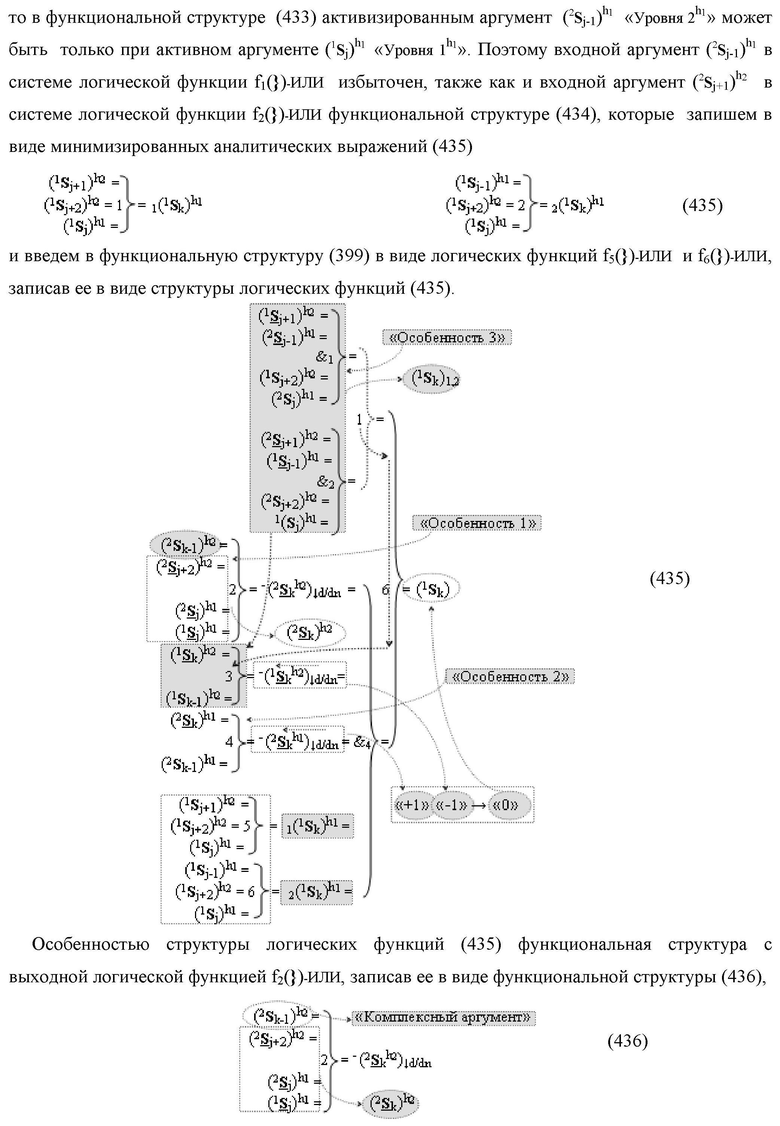
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнении арифметических процедур суммирования позиционных аргументов аналоговых сигналов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1). Техническим результатом является повышение быстродействия. Функциональная структура реализована с использованием логических элементов И, ИЛИ.
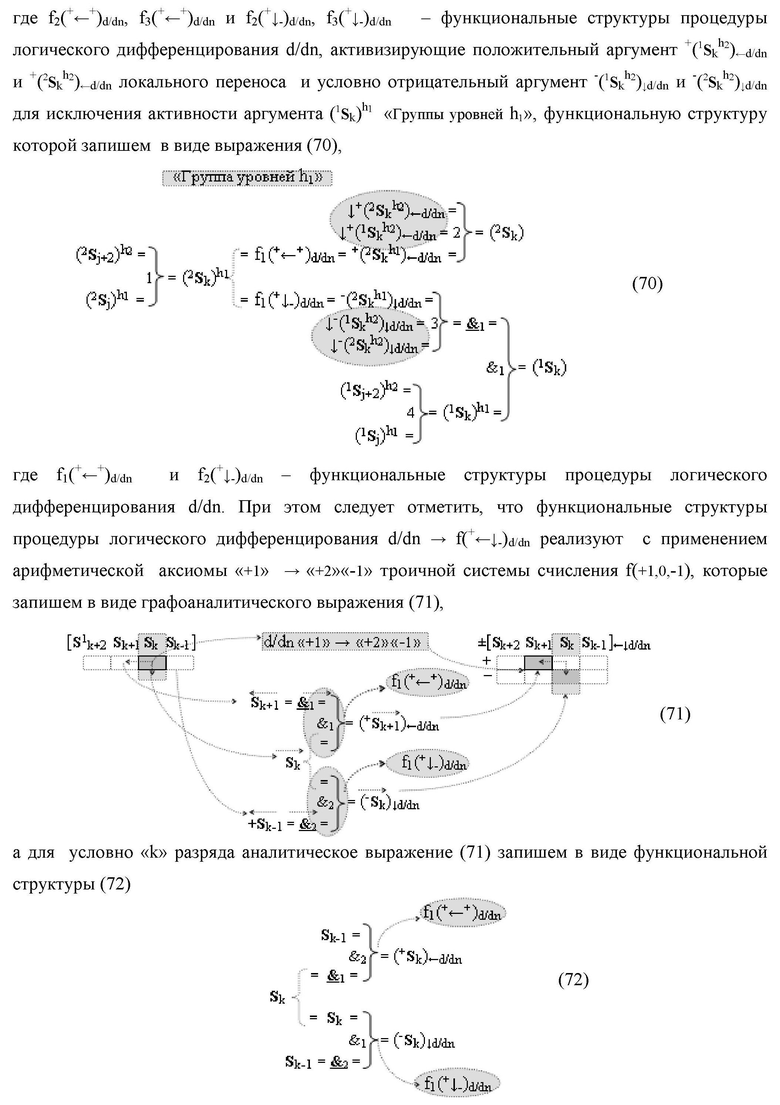
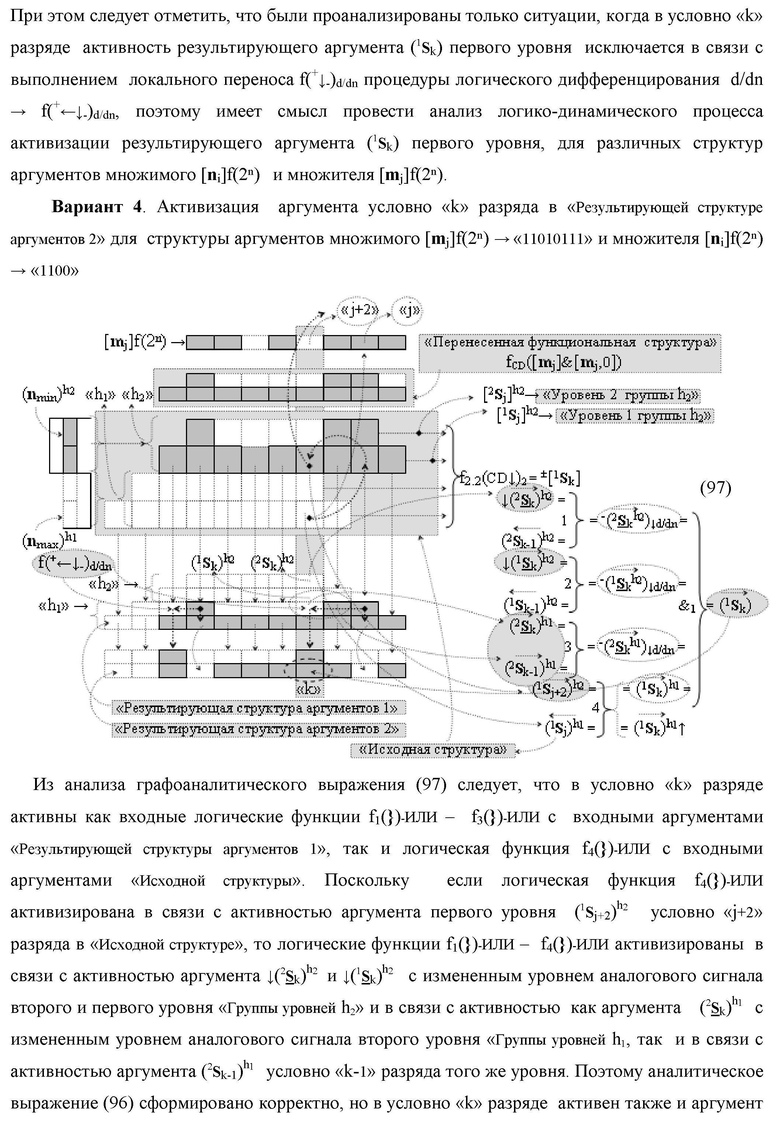
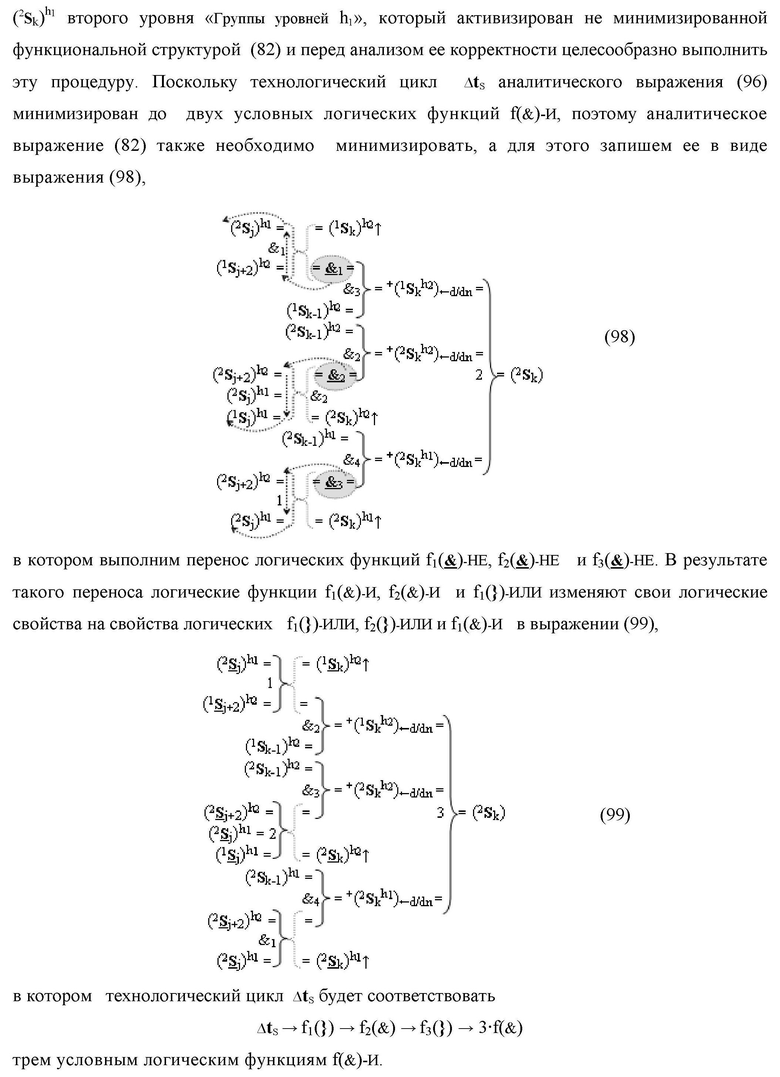
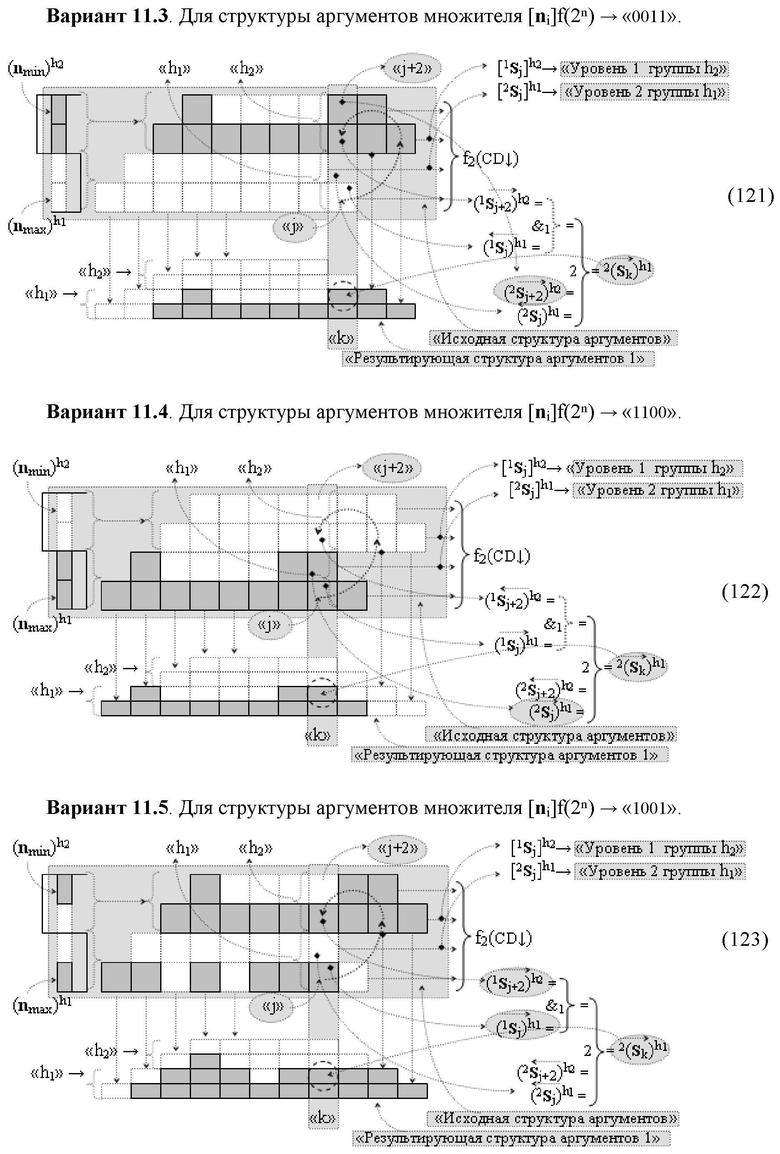
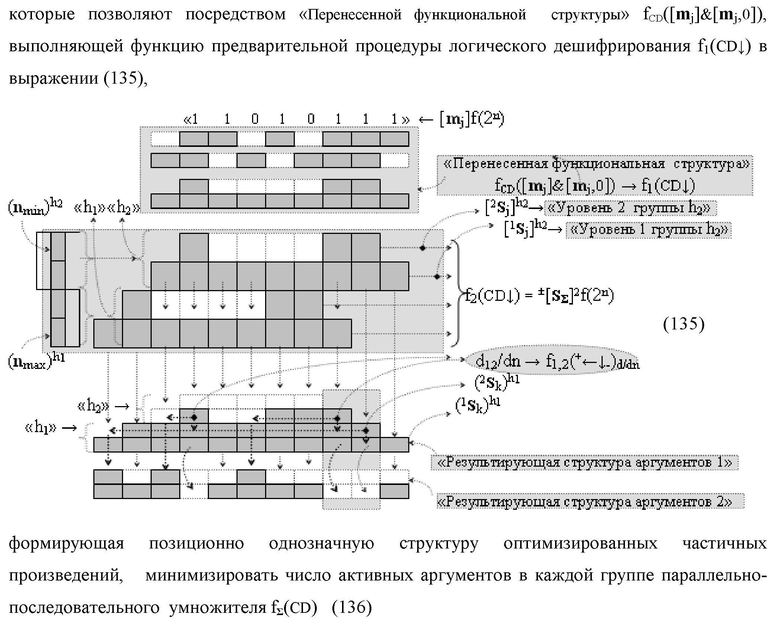
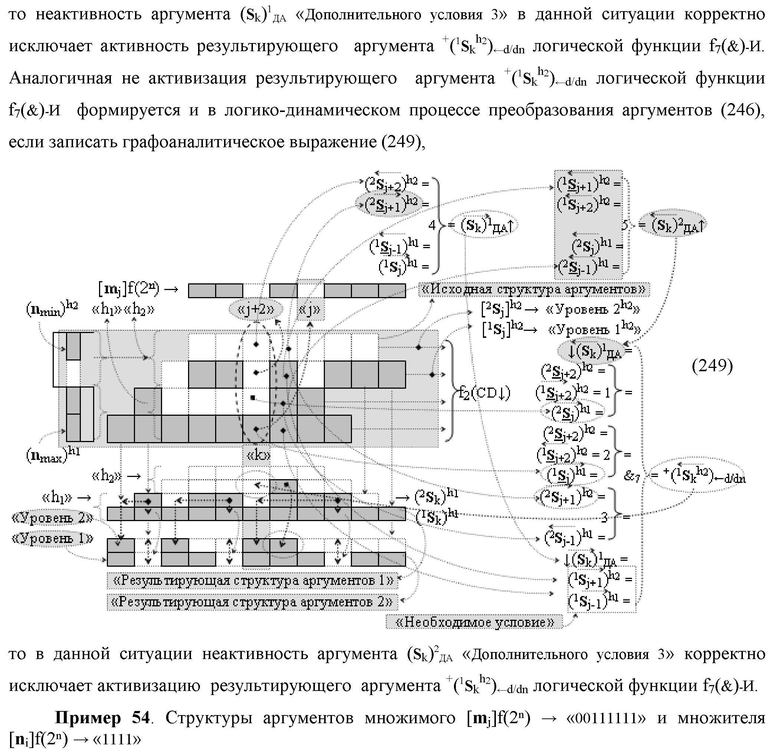
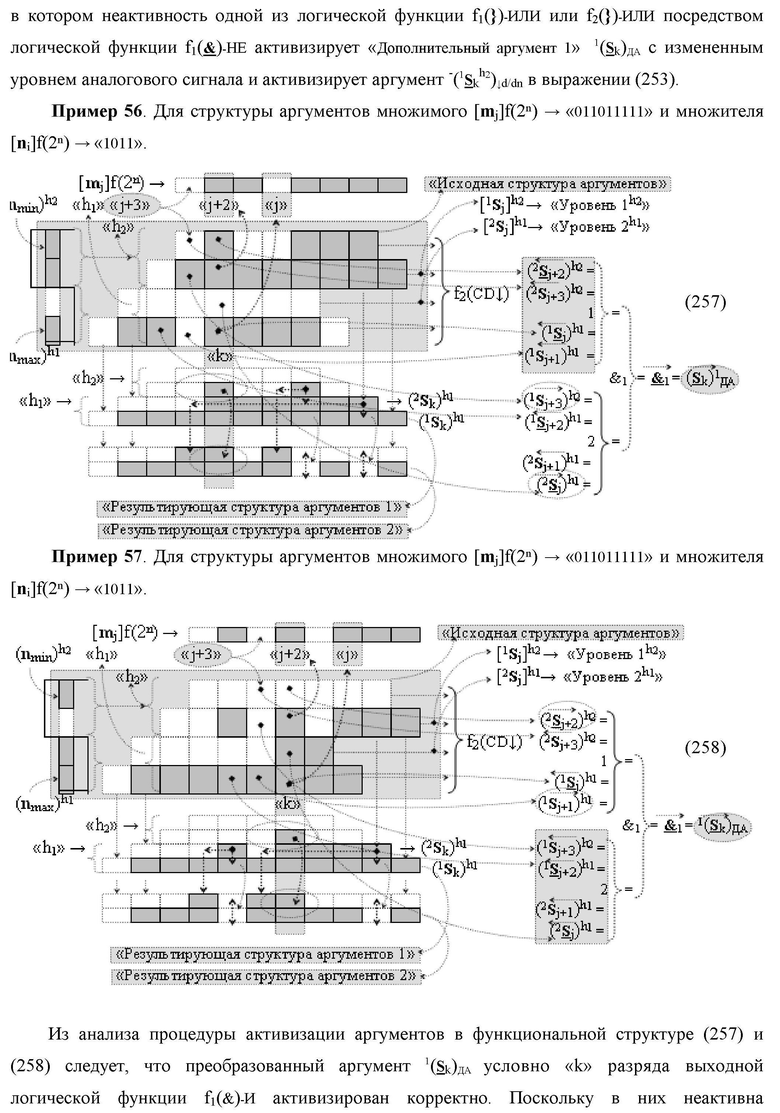
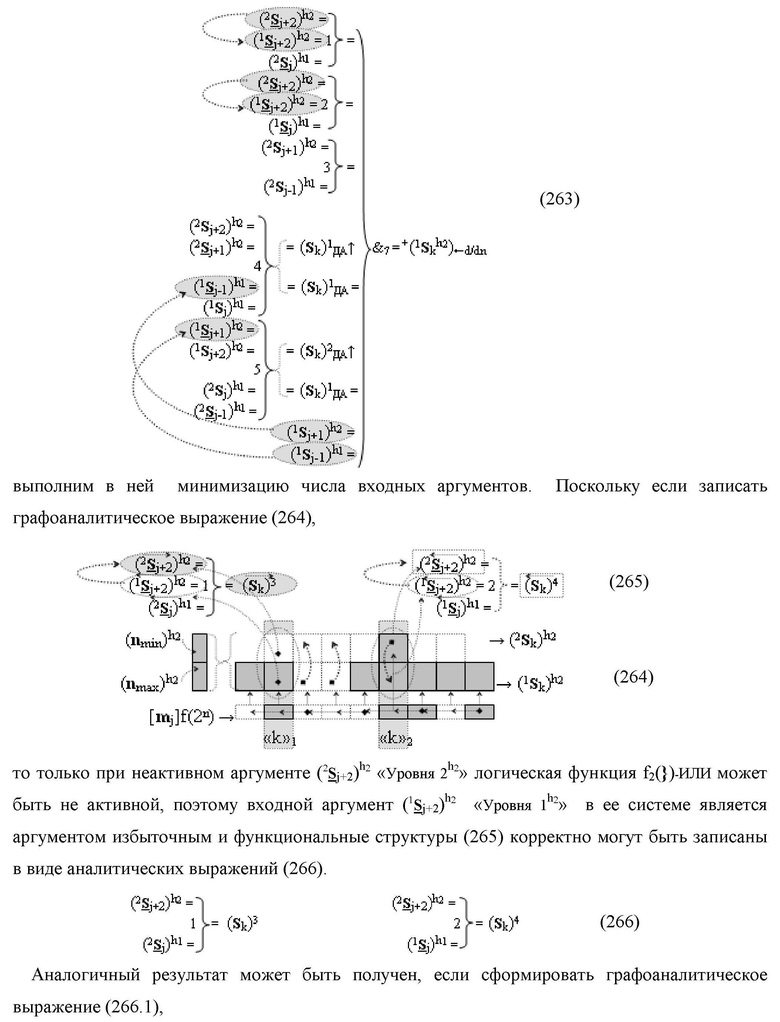
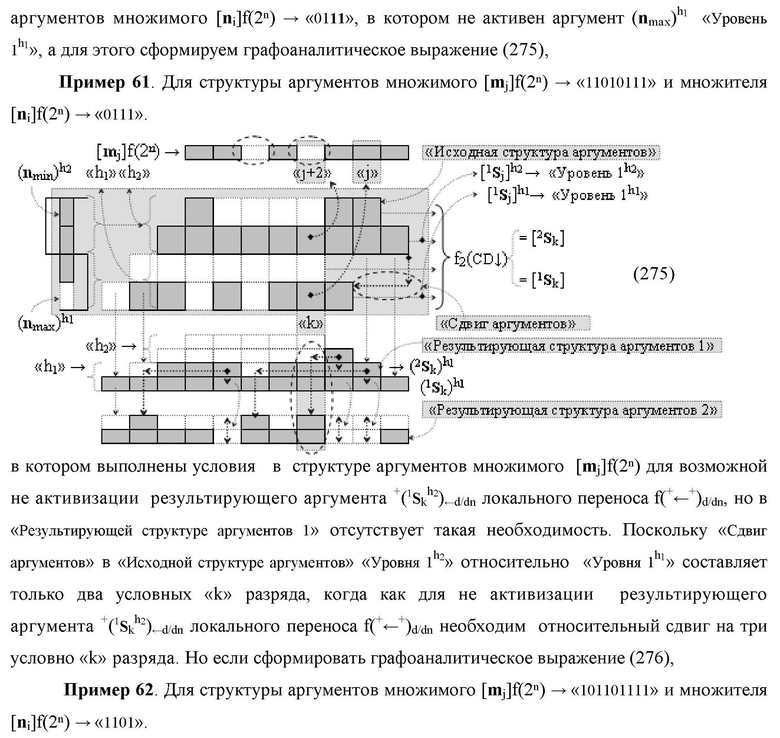
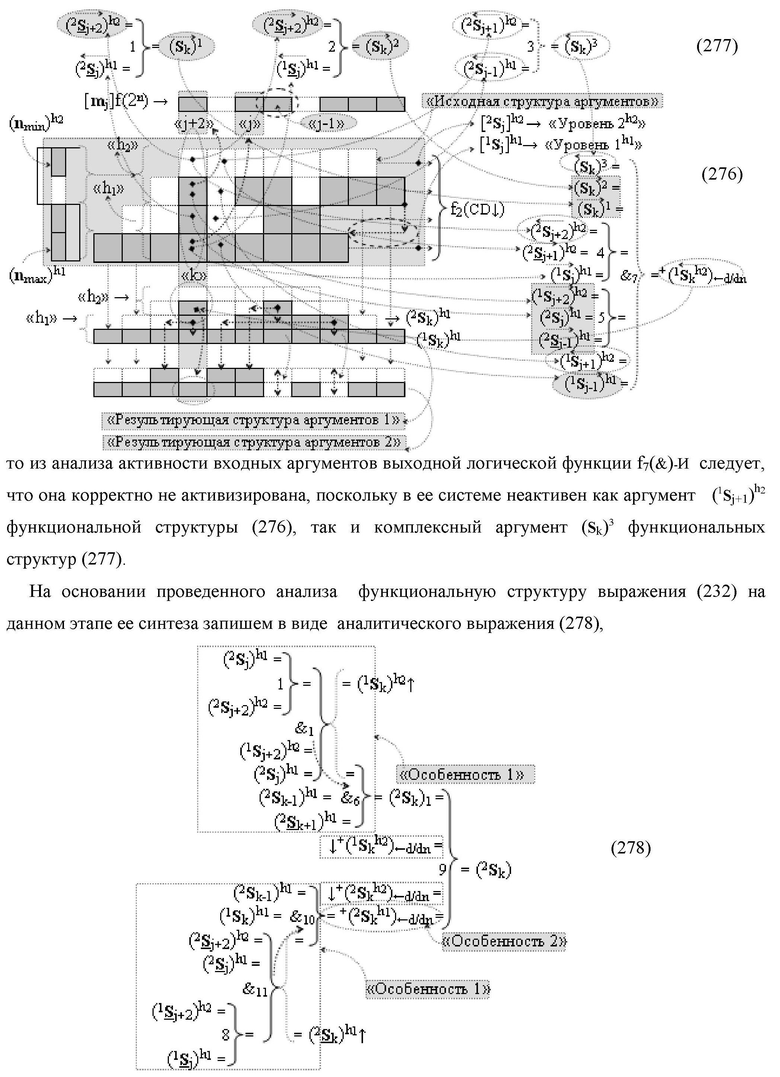
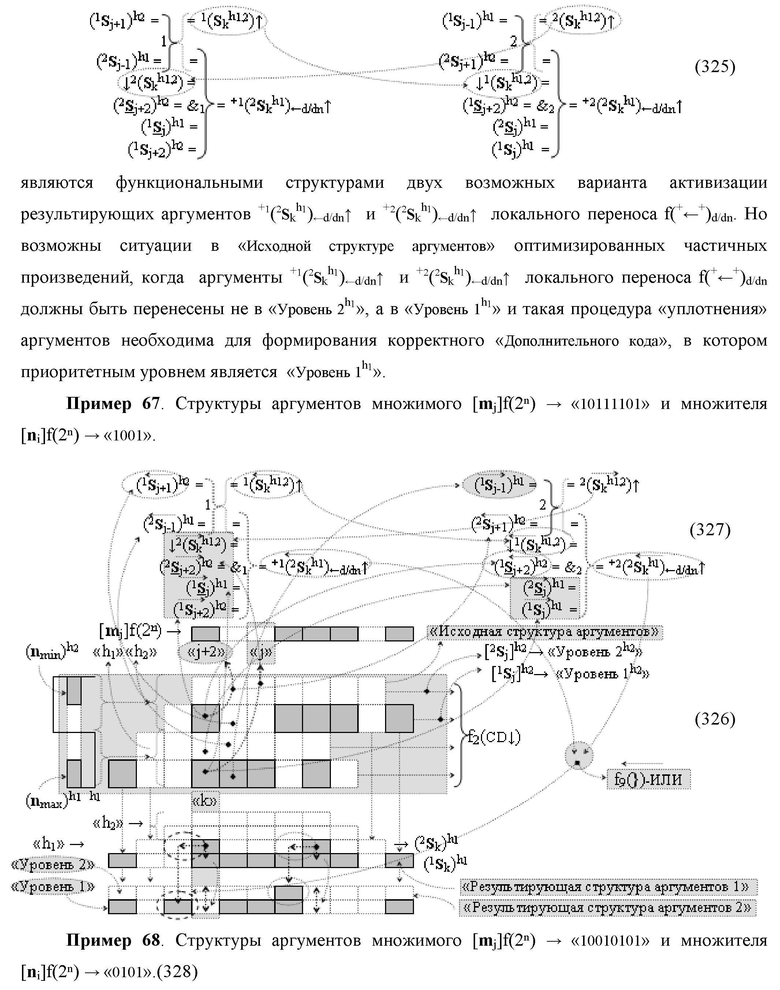
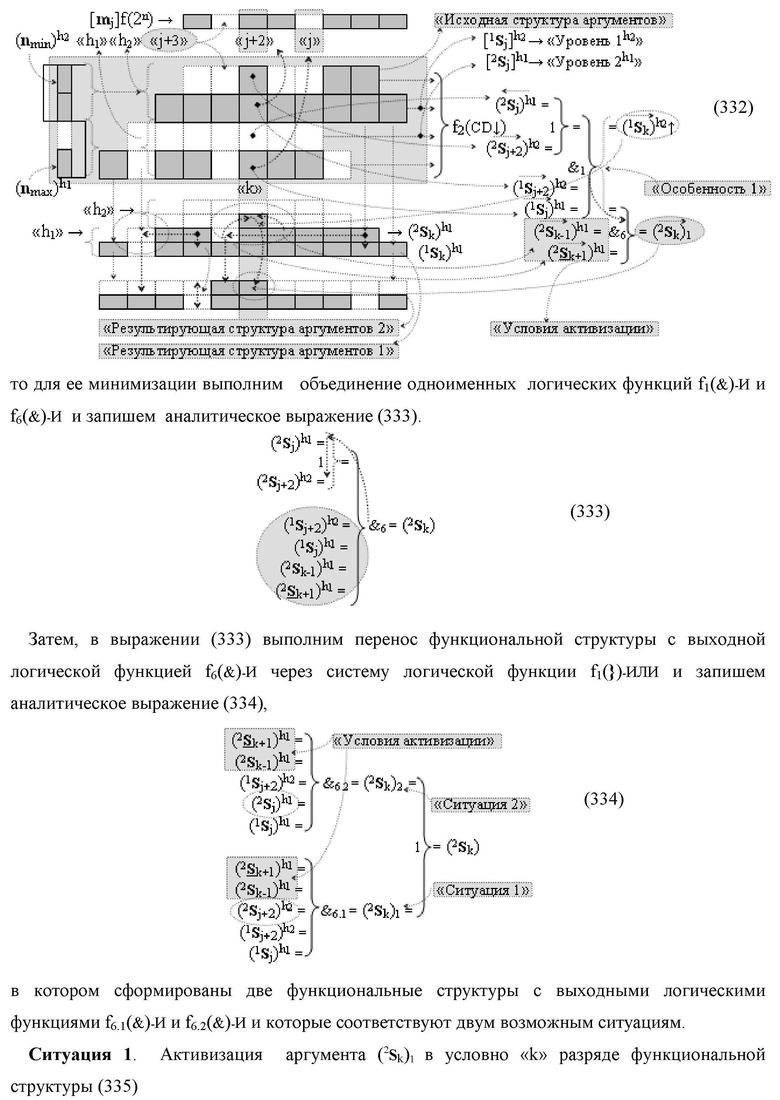
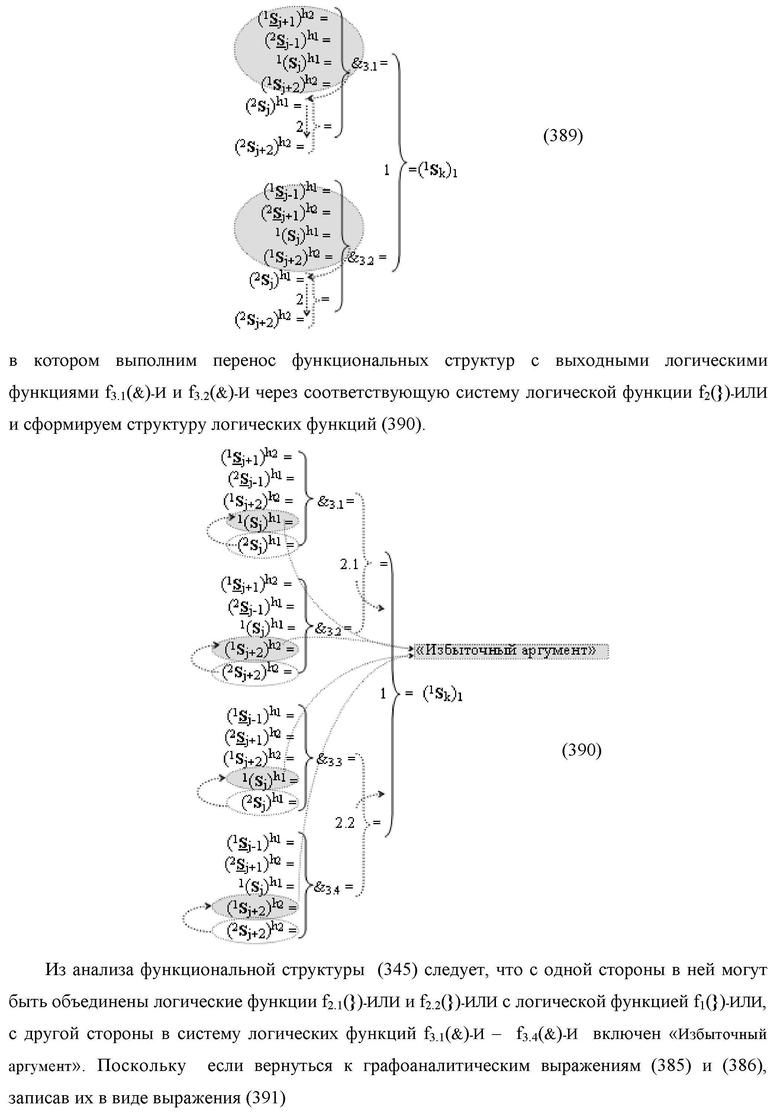
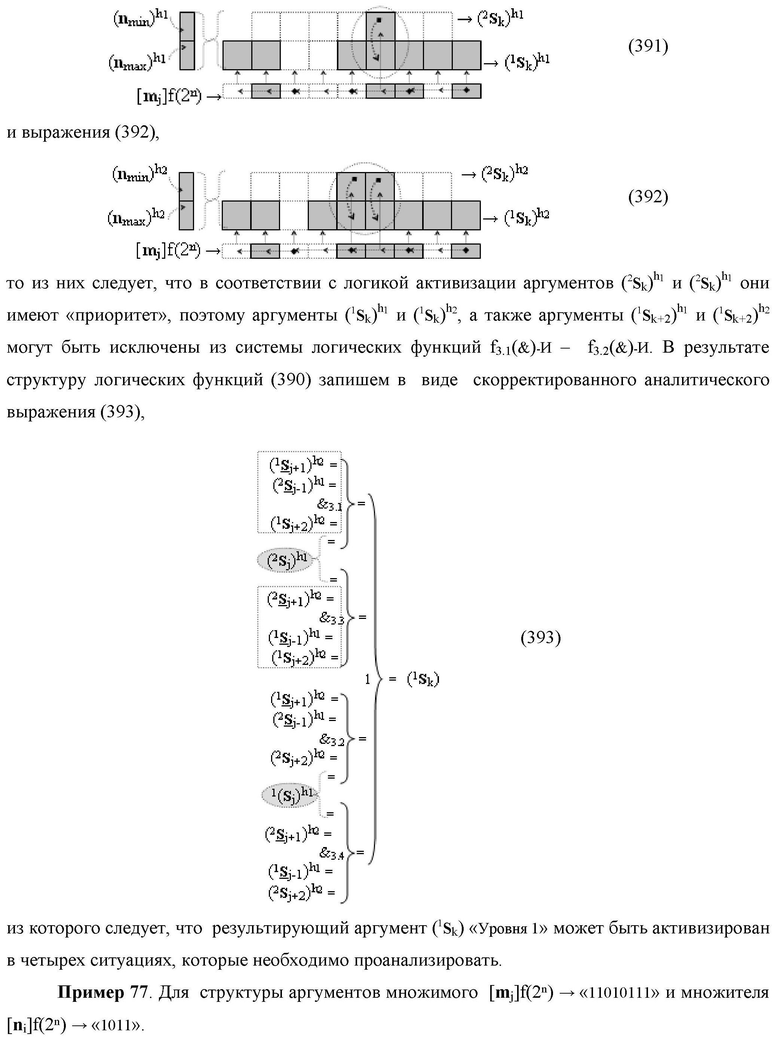
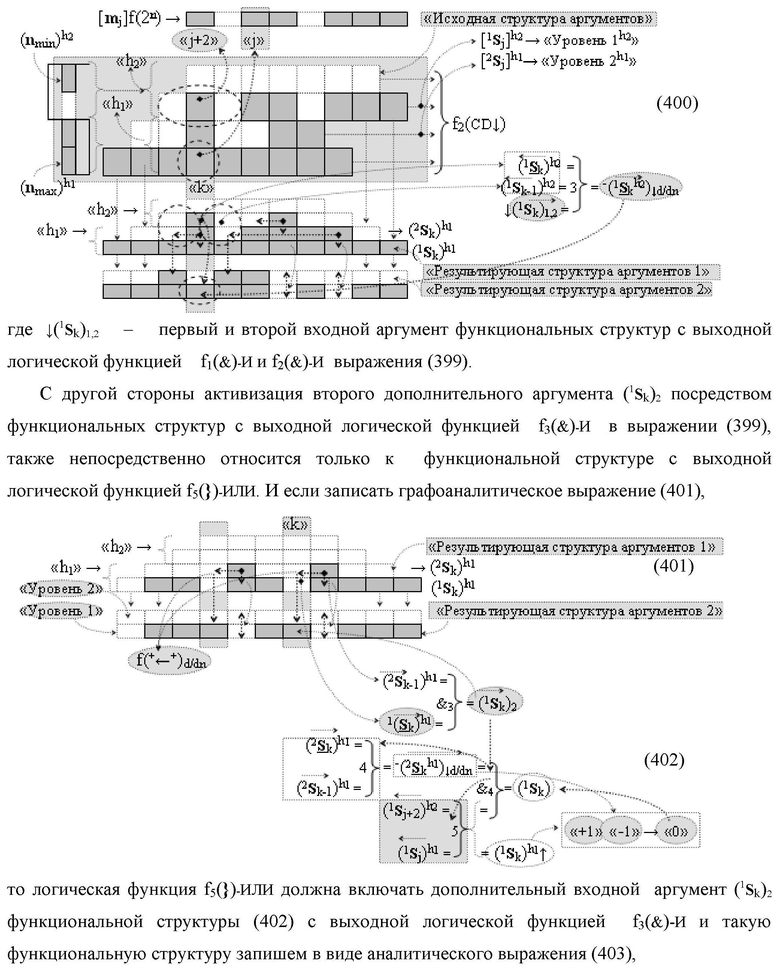
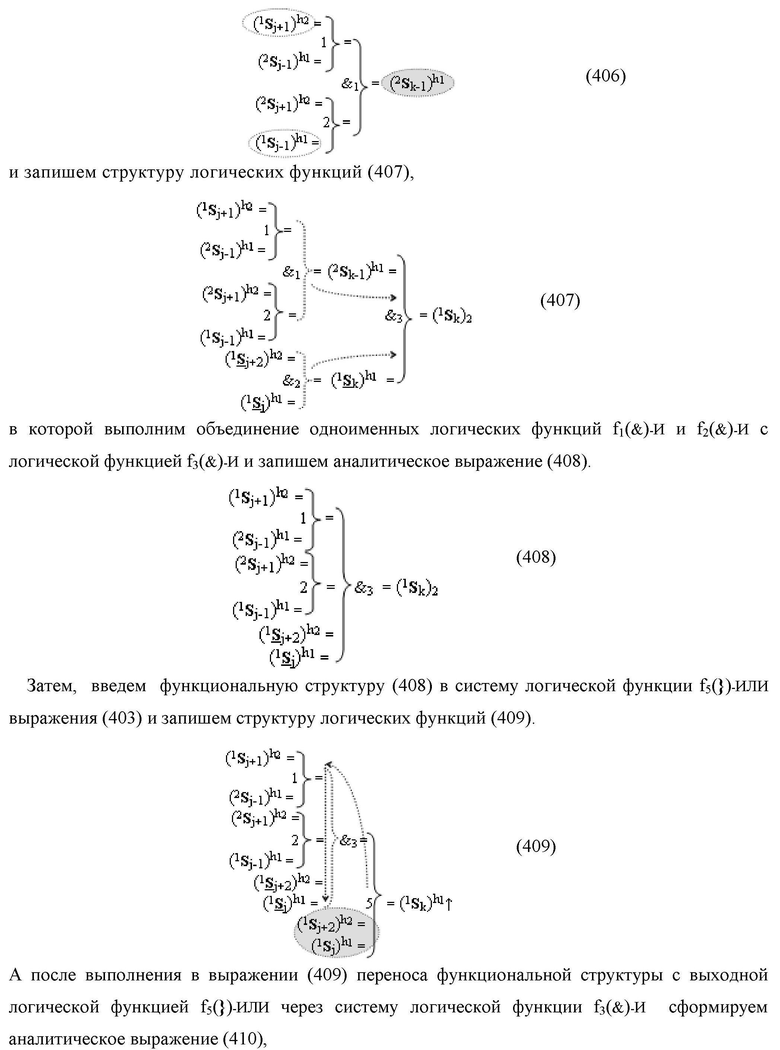
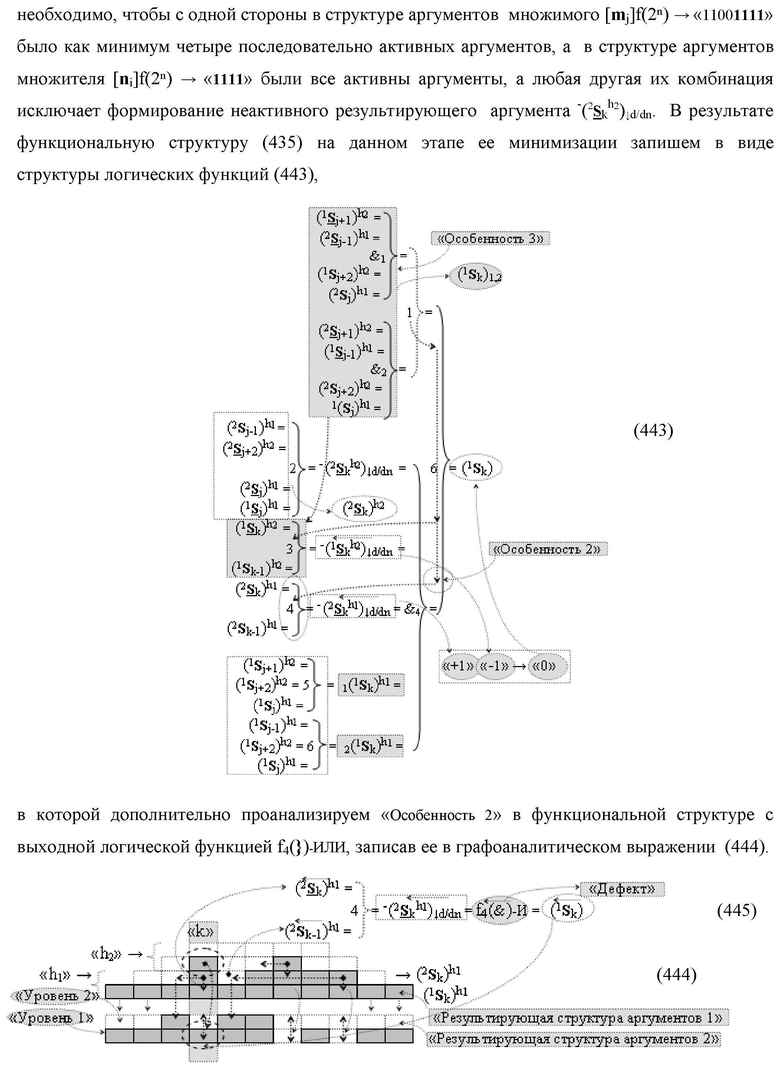
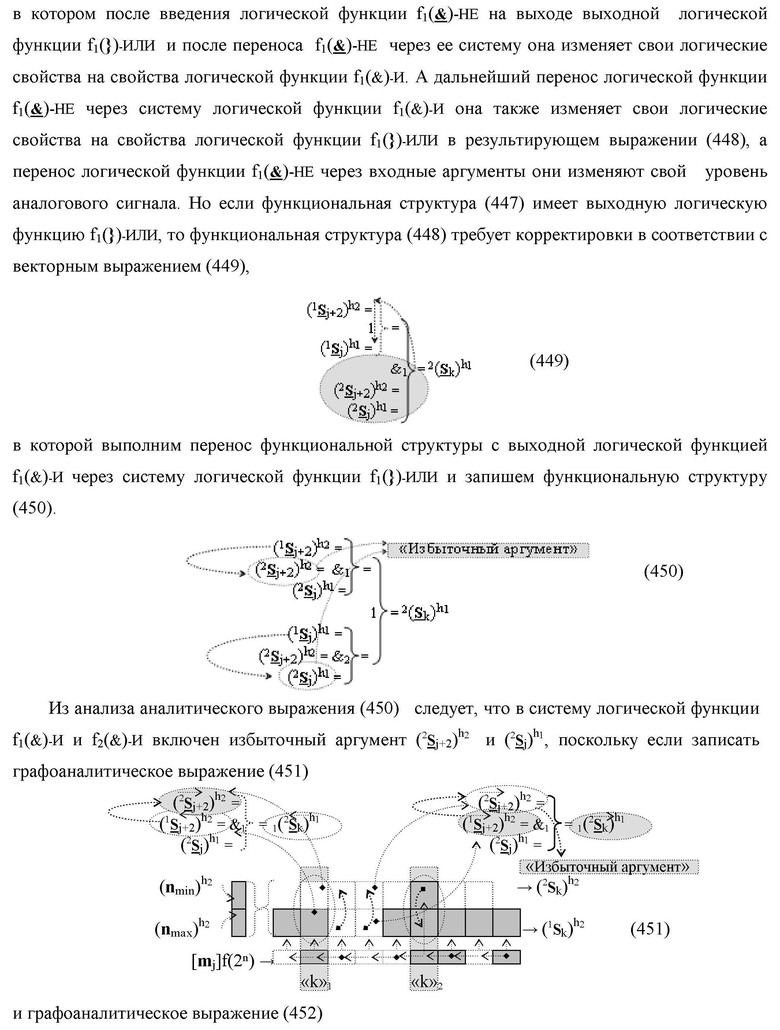
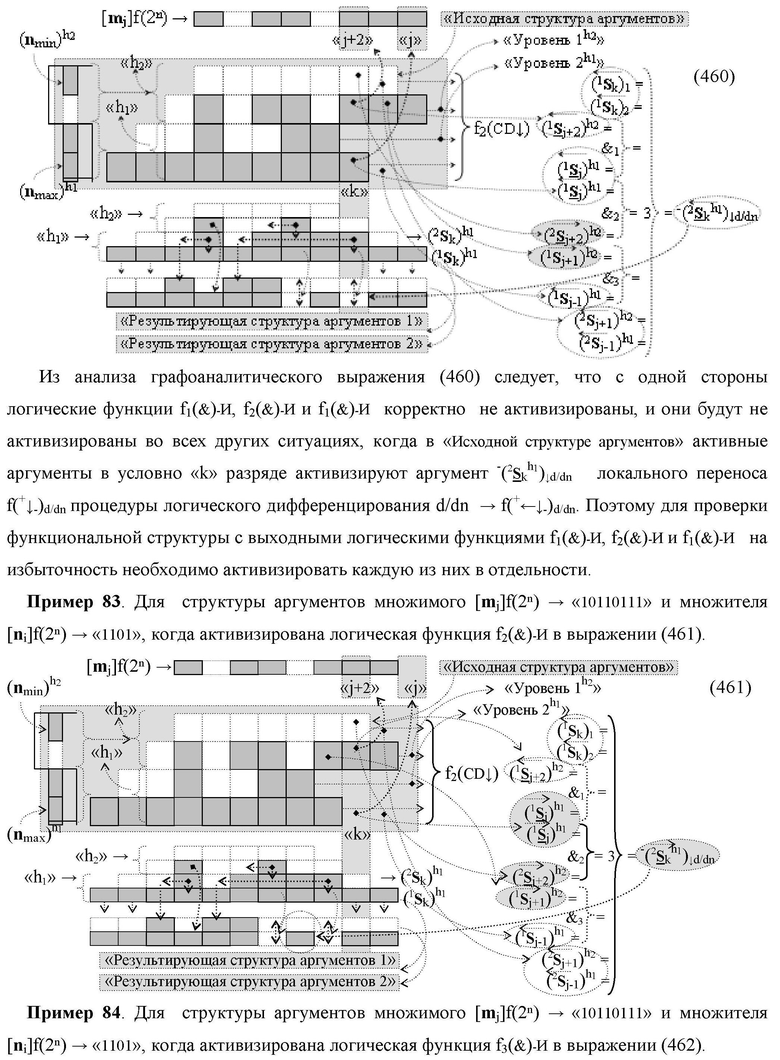
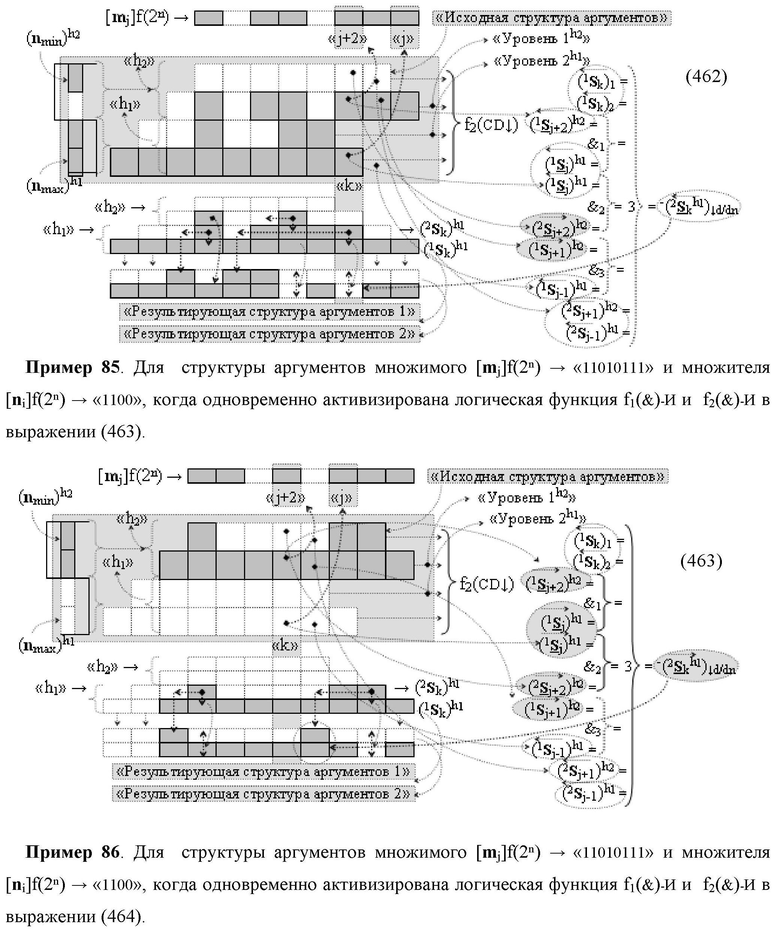
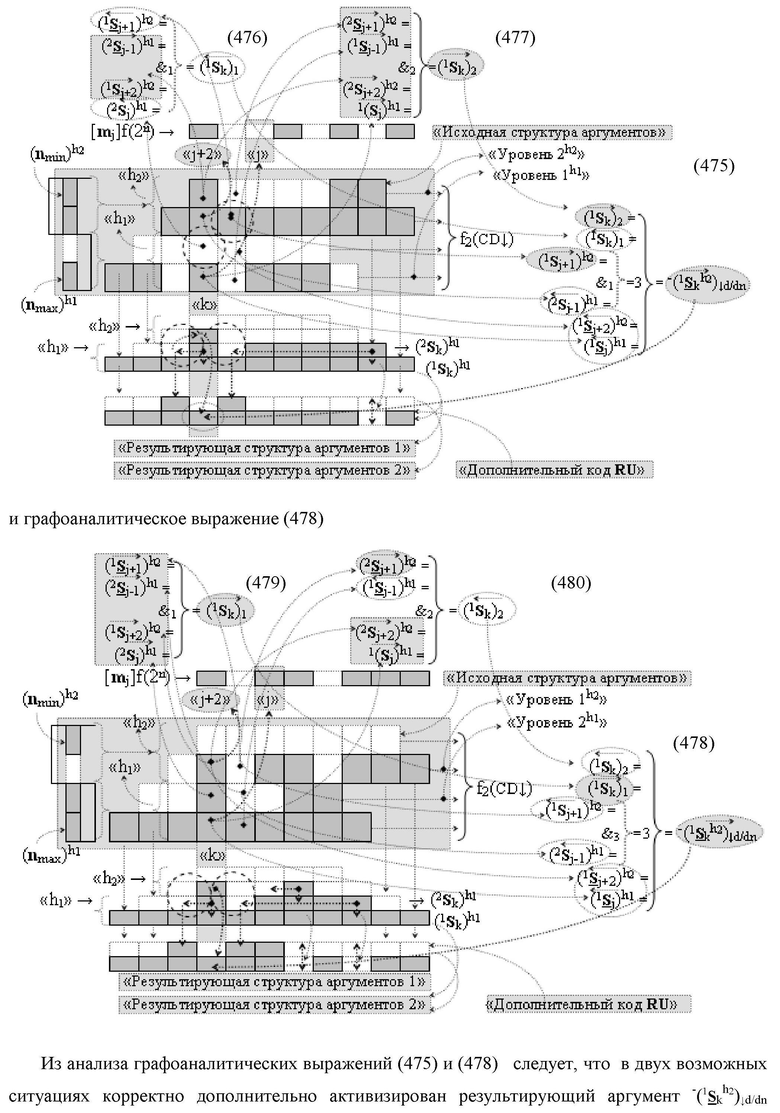
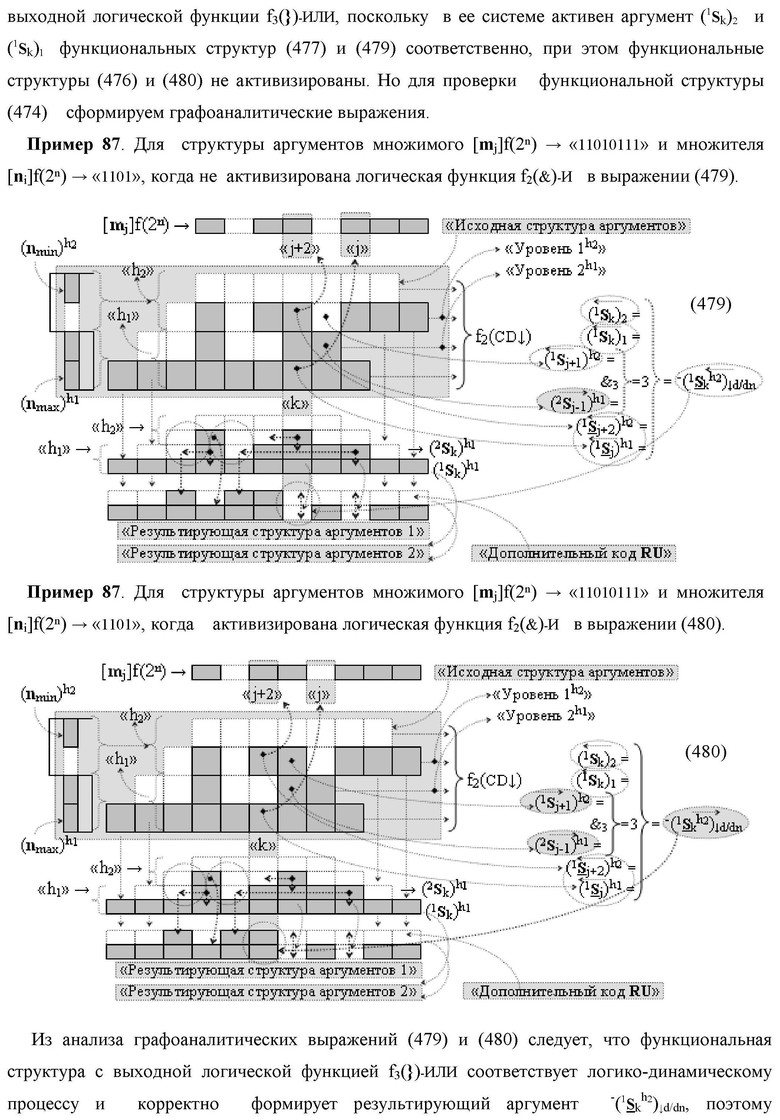
Функциональная структура сумматора f2(ΣCD)
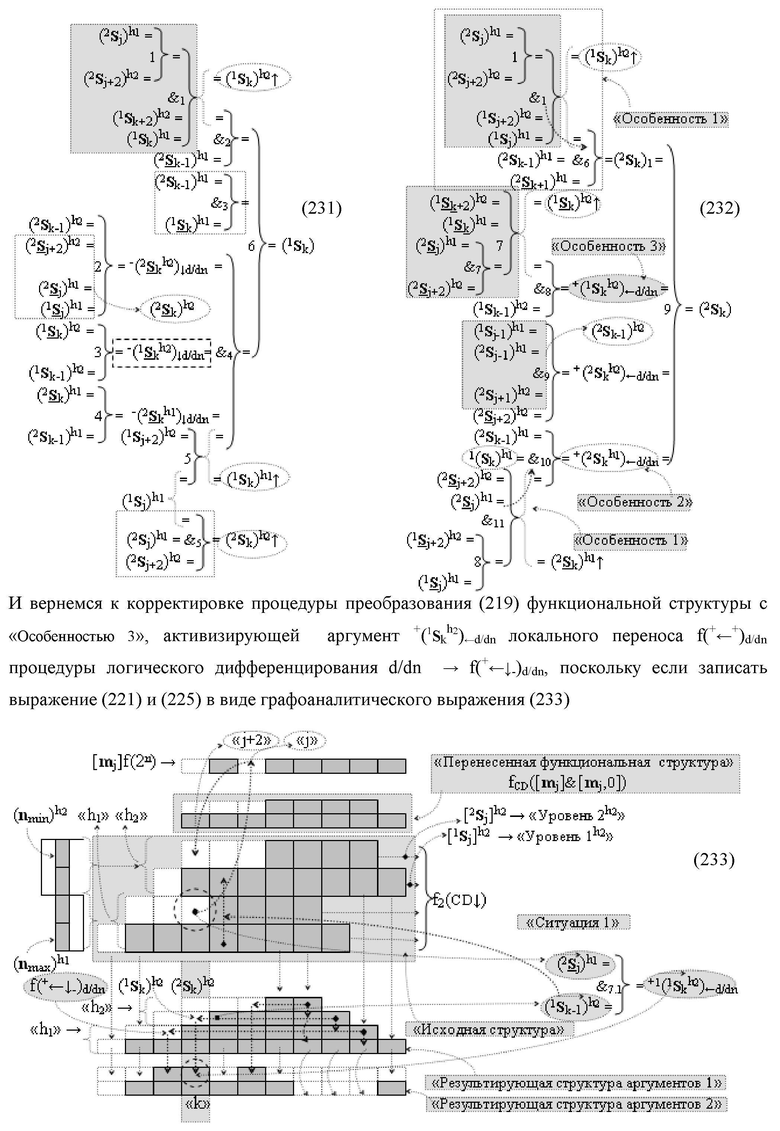
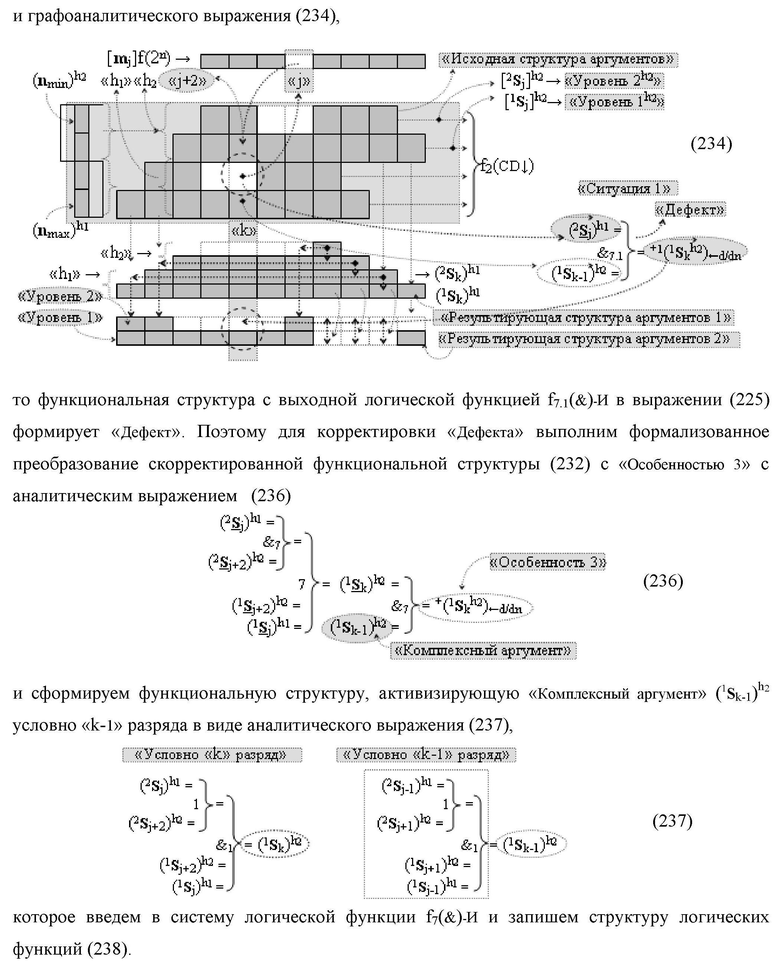
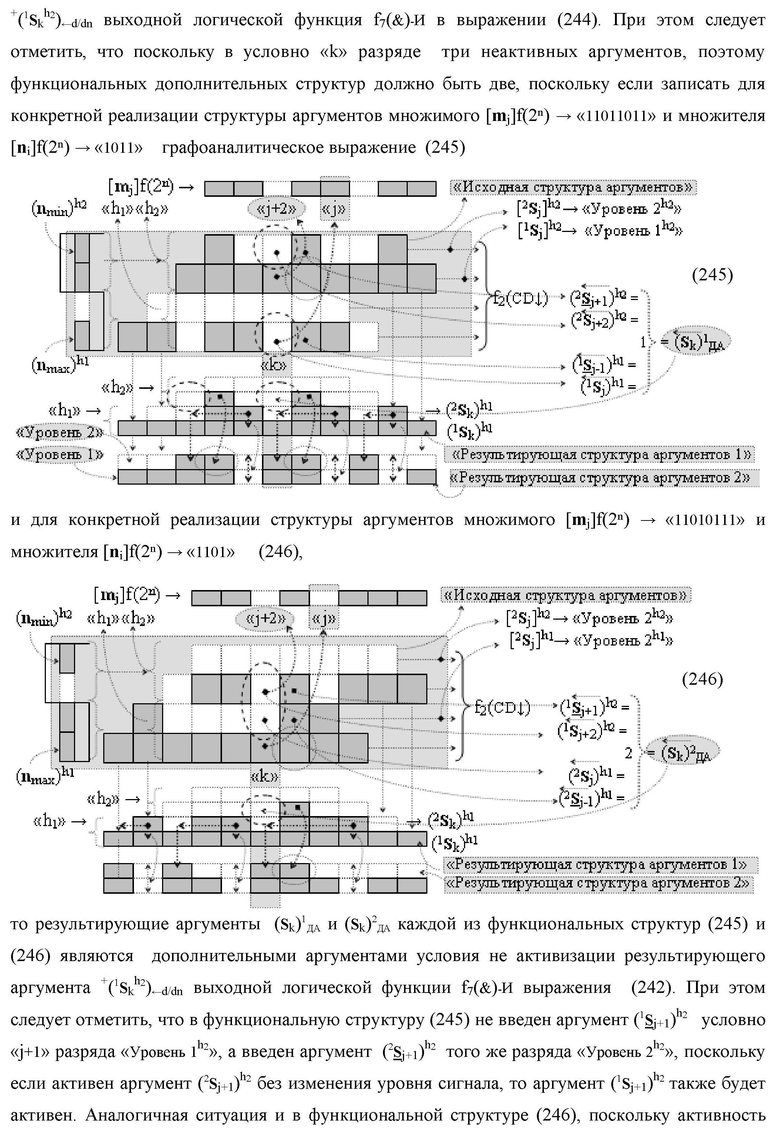
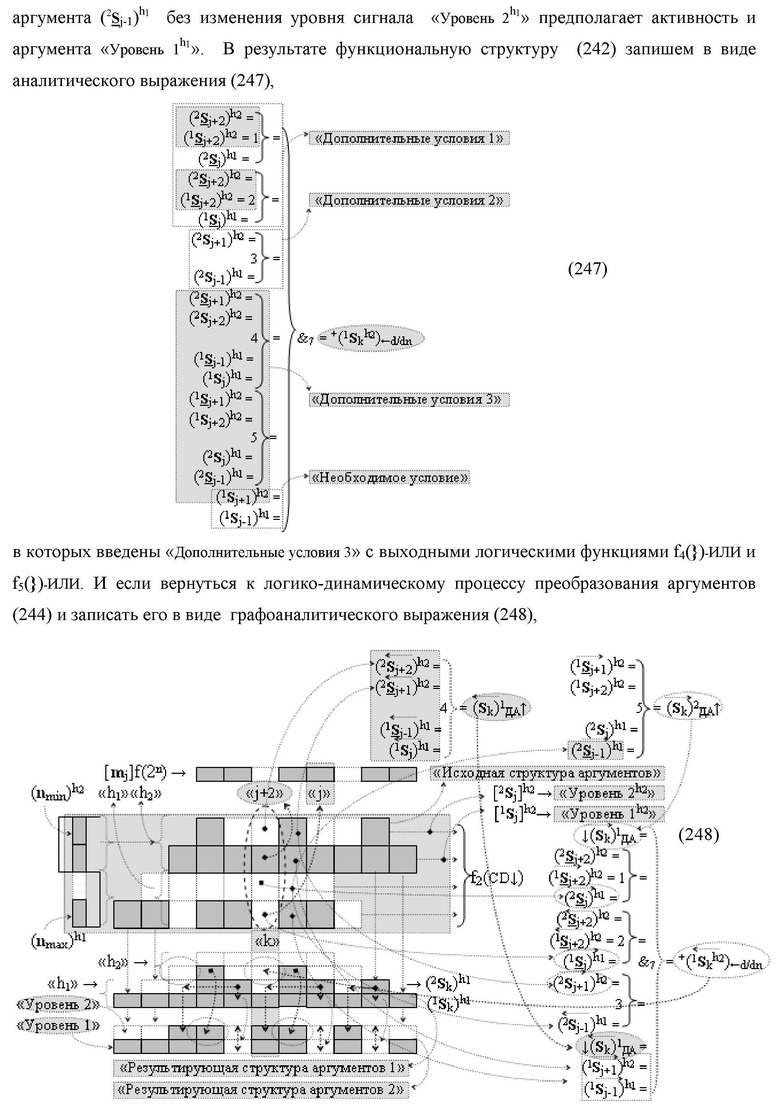
условно «k» разряда параллельно-последовательного умножителя fΣ(ΣCD), реализующая процедуру «дешифрирования» входных структур аргументов слагаемых [1,2Sj h1]f(2n) и [1,2Sj h2]f(2n) позиционного формата «Дополнительный код RU» посредством применения арифметических аксиом троичной системы счисления f(+1,0,-1) и логического дифференцирования d1/dn → f1(+←↓-)d/dn аргументов в объединенной их структуре, включающая логическую функцию f1(})-ИЛИ, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f1(&)-И, а также включает логическую функцию f2(&)-И, в которой функциональные входные связи являются функциональными входными связями структуры, отличающаяся тем, что в структуру условно «k» разряда для активизации результирующего аргумента (1
S
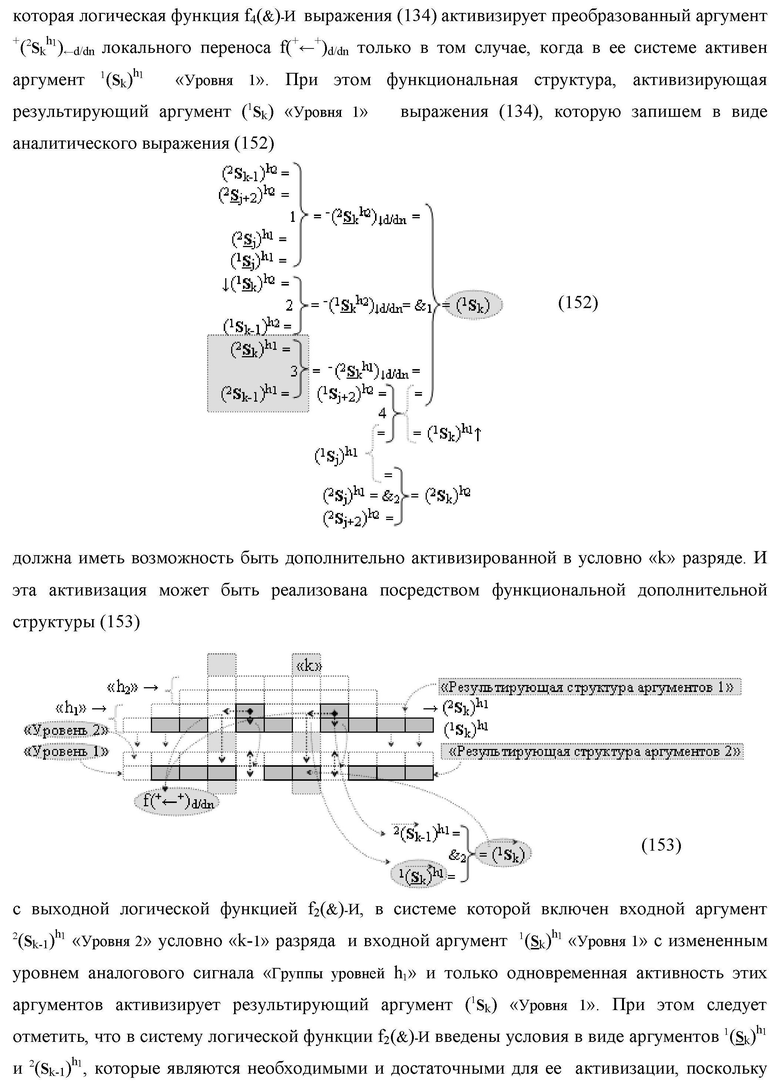
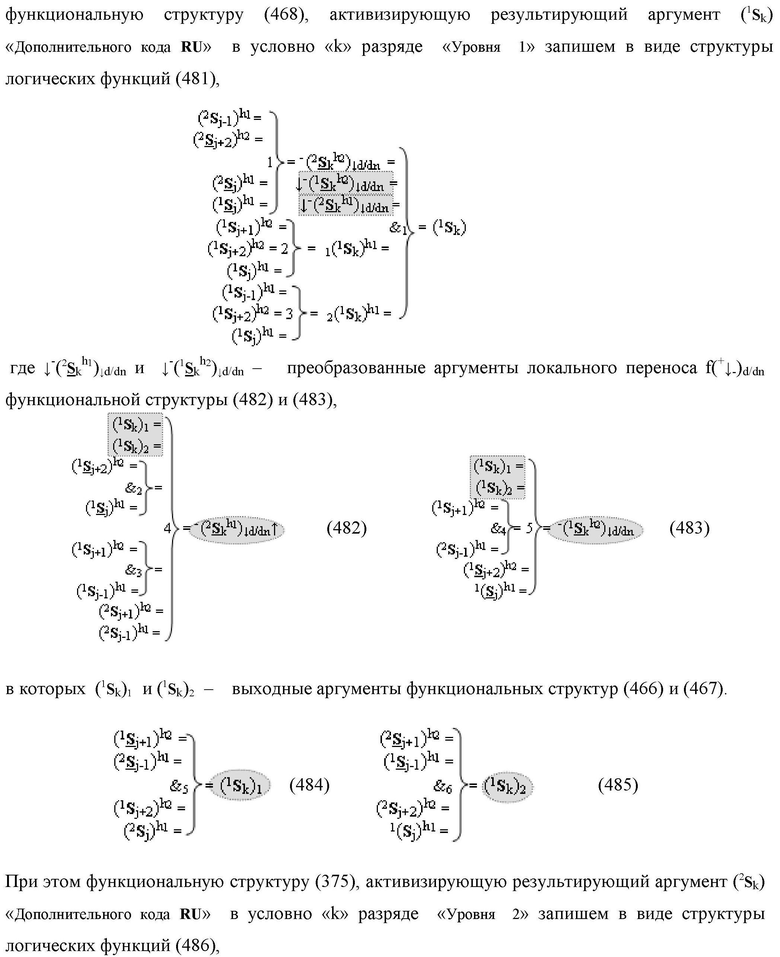
k) «Уровня 1» введены логические функции f2(})-ИЛИ, f3(})-ИЛИ, f4(})-ИЛИ и f5(})-ИЛИ, а также логические функции f3(&)-И и f4(&)-И, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
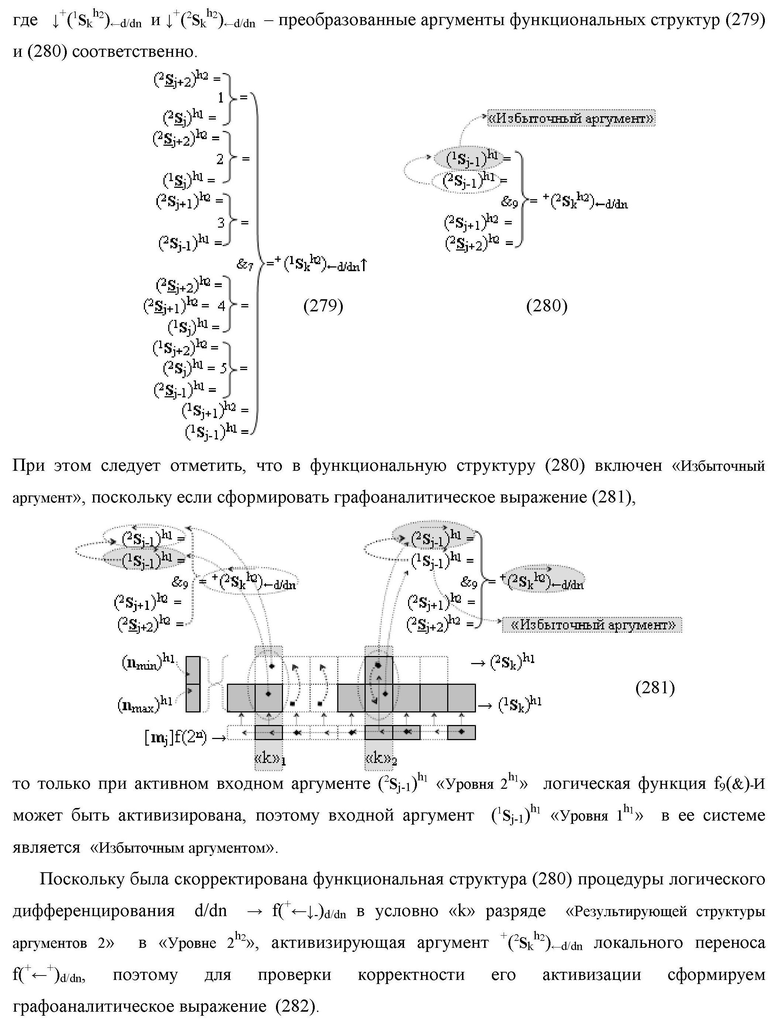
где ↓-(2
S
k h1)↓d/dn и ↓-(1
S
k h2)↓d/dn - преобразованные аргументы локального переноса f(+↓-)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn
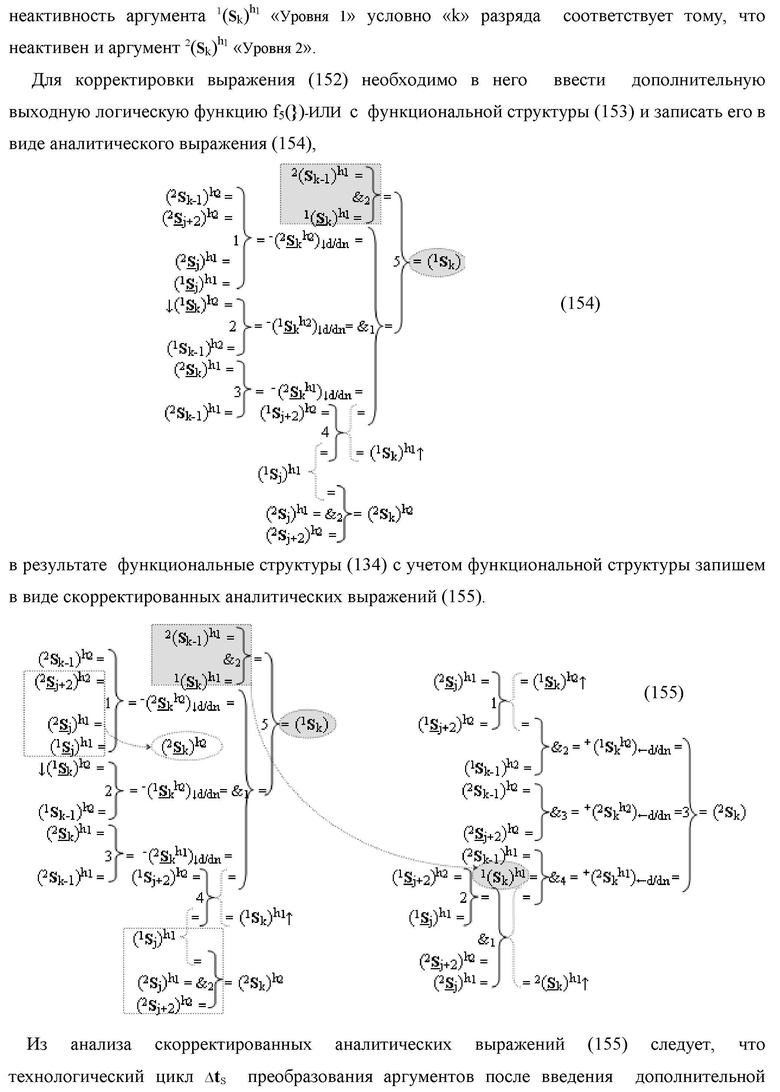
являются результирующими аргументами функциональных дополнительных структур, в которых функциональные связи выполнены в соответствии с математической моделью
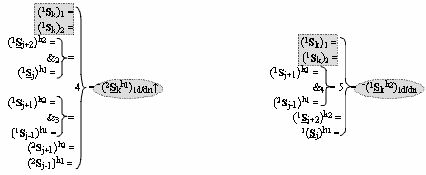
в которых (1
S
k)1 и (1
S
k)2 - выходные аргументы являются результирующими аргументами функциональных дополнительных структур, в которых функциональные связи выполнены в соответствии с математической моделью
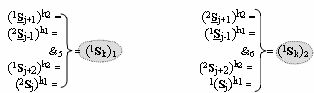
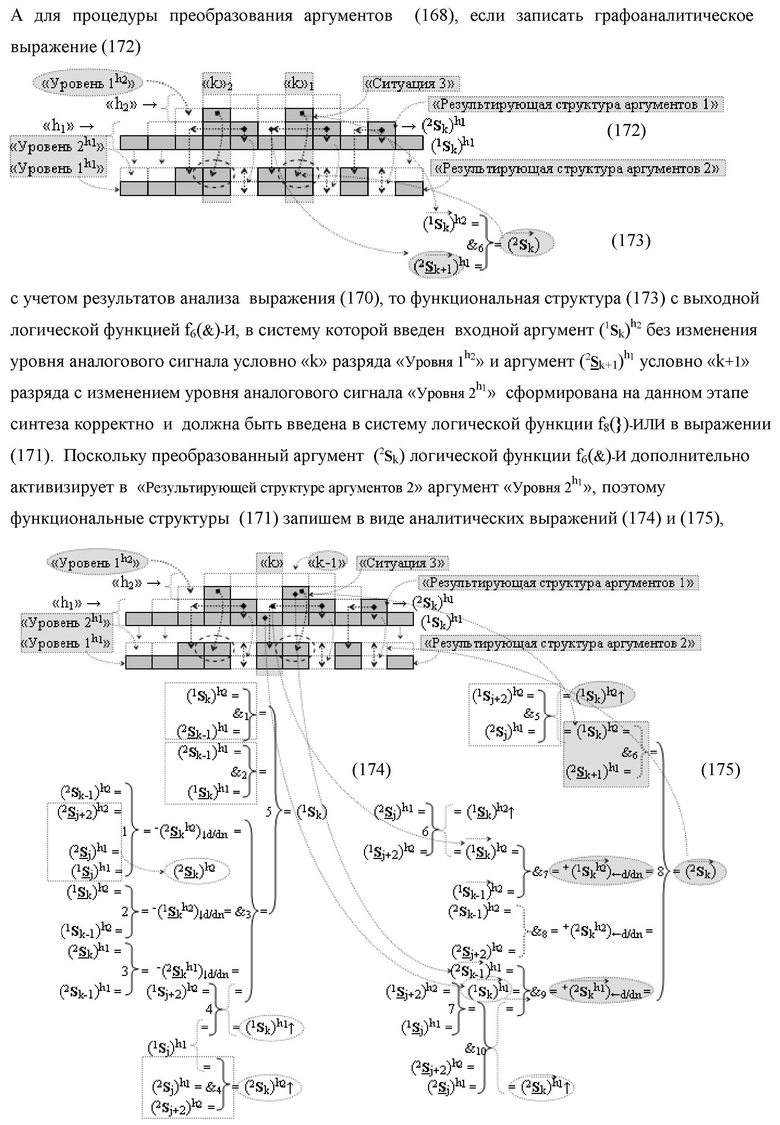
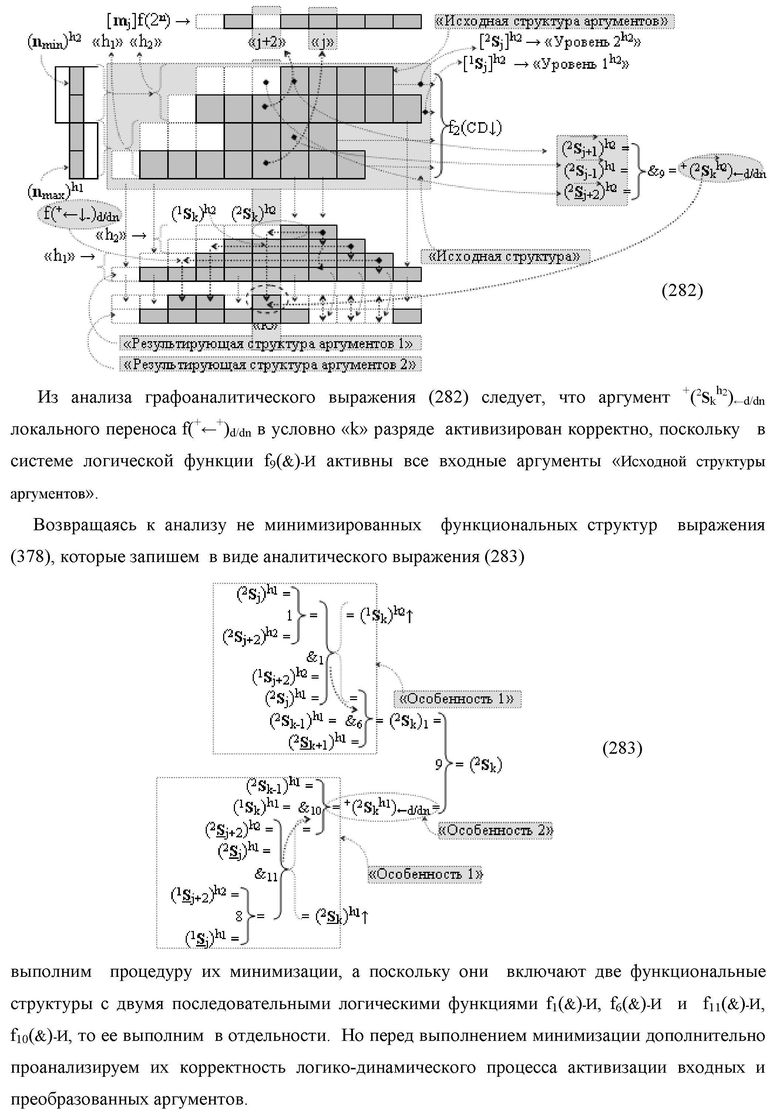
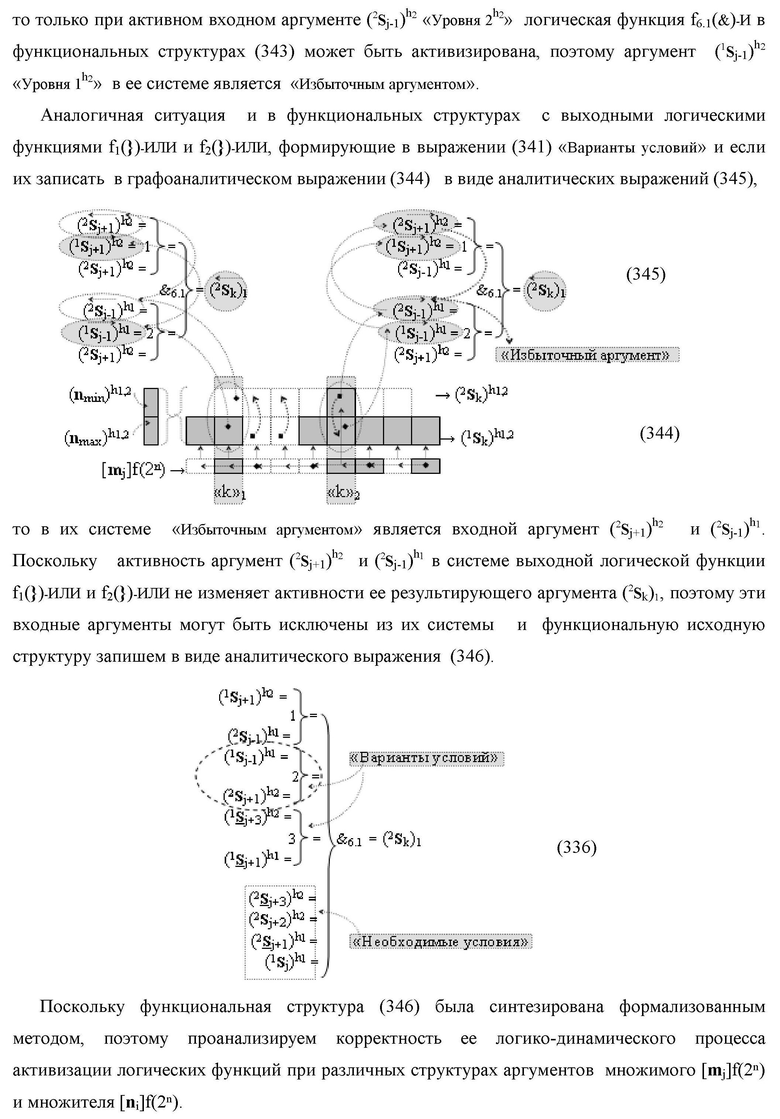
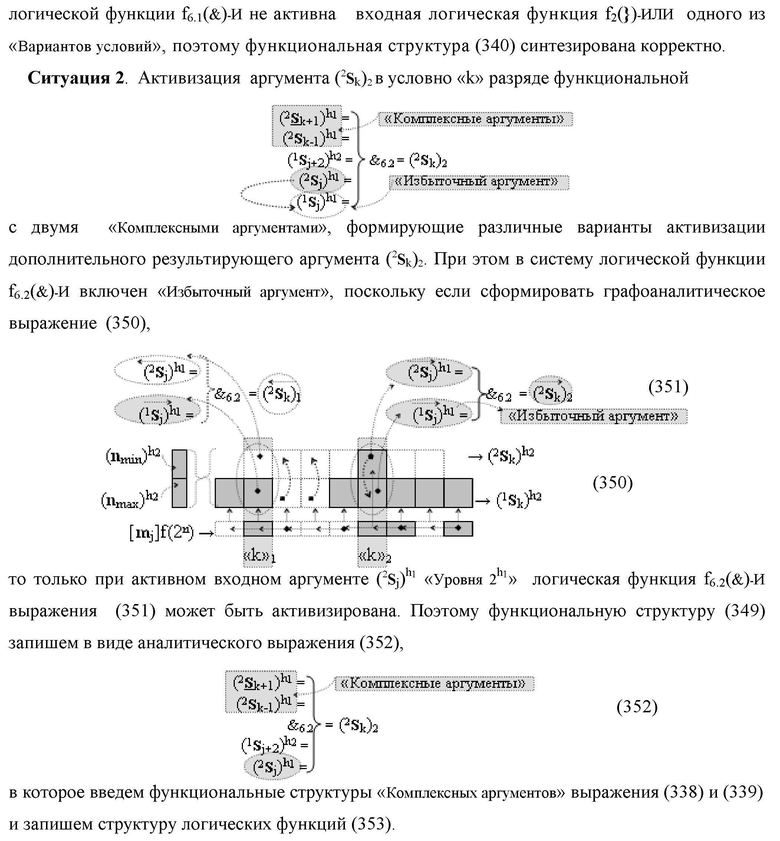
а для активизации результирующего аргумента (2
S
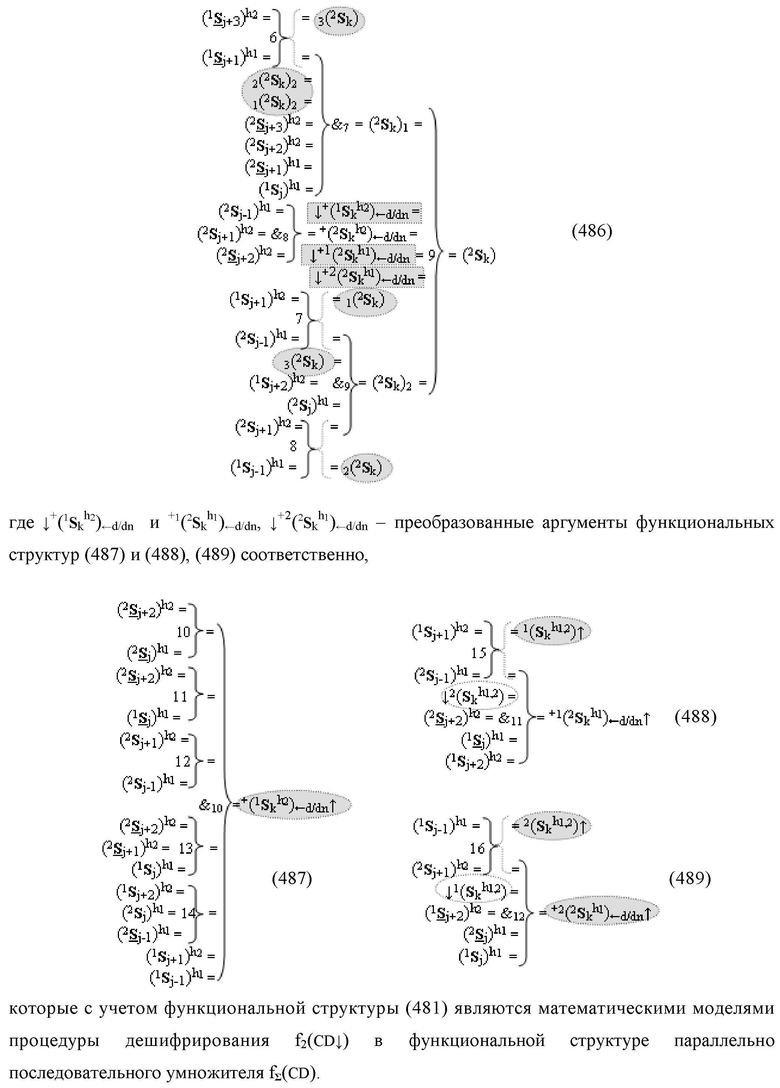
k) «Уровня 2» «Дополнительного кода RU» в условно «k» разряд введены логические функции f6(})-ИЛИ, f7(})-ИЛИ, f8(})-ИЛИ, f9(})-ИЛИ, f10(})-ИЛИ, f11(})-ИЛИ, f12(})-ИЛИ, f13(})-ИЛИ, f14(})-ИЛИ, f15(})-ИЛИ и f16(})-ИЛИ, а также логические функции f7(&)-И, f8(&)-И, f9(&)-И, f10(&)-И, f11(&)-И и f12(&)-И, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
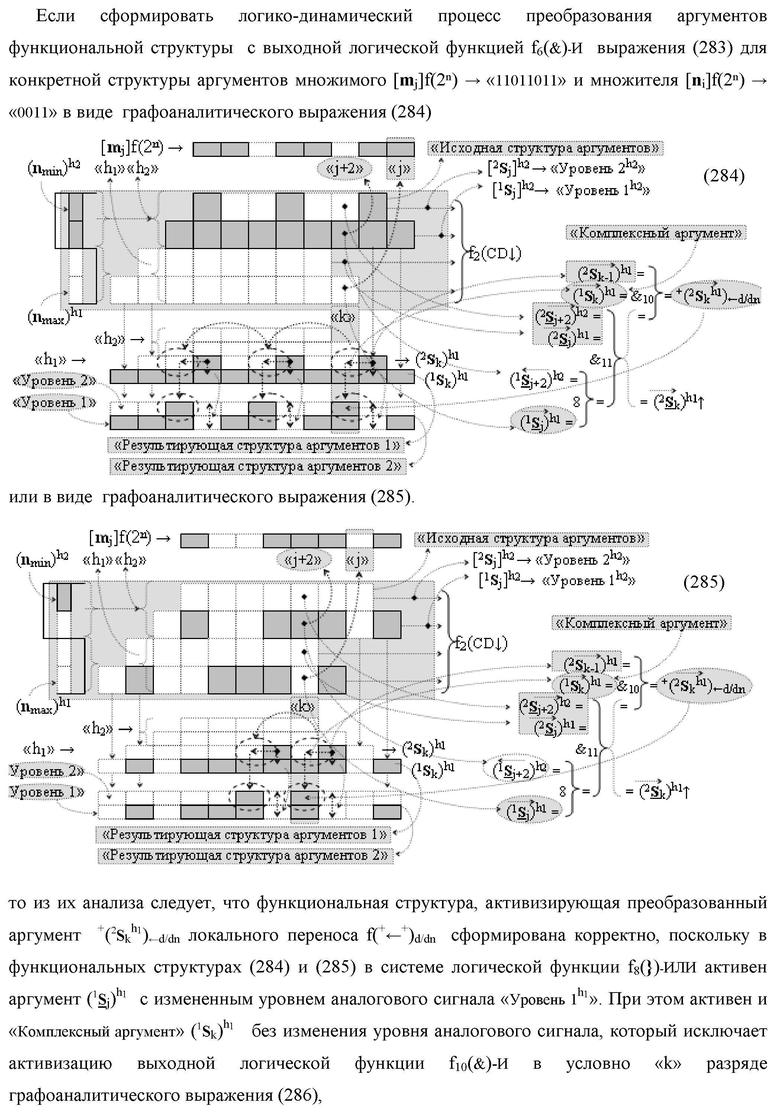
где ↓+(1
S
k h2)←d/dn и +1(2
S
k h1)←d/dn, ↓+2(2
S
k h1)←d/dn - преобразованные аргументы локального переноса f1(+←+)d/dn процедуры логического дифференцирования d1/dn → f1(+←↓-)d/dn
являются результирующими аргументами функциональных дополнительных структур, в которых функциональные связи выполнены в соответствии с математической моделью
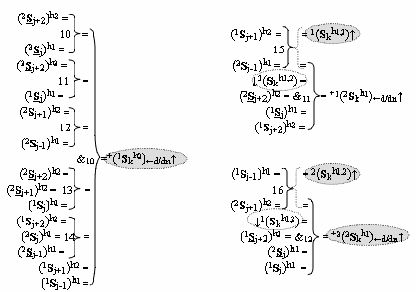
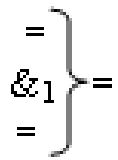- логическая функция f1(&)-И; 
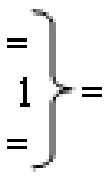- логическая функция f1(})-ИЛИ.
| Дж.Уэйкерли | |||
| Проектирование цифровых устройств | |||
| - М.: ПОСТМАРКЕТ, 2002, с.508 | |||
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА ДЛЯ УМНОЖИТЕЛЯ, В КОТОРОМ АРГУМЕНТЫ СЛАГАЕМЫХ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ ЯВЛЯЮТСЯ АРГУМЕНТАМИ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1, 0, -1) В ПОЗИЦИОННО-ЗНАКОВОМ ЕЕ ФОРМАТЕ f(+/-) (ВАРИАНТЫ) | 2008 |
|
RU2386162C2 |
| JP 20053269 A, 24.11.2005 | |||
| JP 2002014804 A, 18.01.2002 | |||
| US 7274211 B1, 25.09.2007. | |||
