Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнении арифметических операций, в частности процессов суммирования и вычитания, в позиционно-знаковых кодах. Схемная реализация устройств позволяет минимизировать сквозные переносы путем логического дифференцирования последовательности аргументов слагаемых и организовать параллельные функциональные структуры сумматоров с локальными переносами (в соседний разряд) независимо от разрядности самого сумматора, что, в конечном счете, приведет к существенному повышению быстродействия процесса суммирования. При этом характерной чертой параллельных сумматоров является наличие схемной реализации операции логического дифференцирования, которая, в конечном счете, позволяет исключить сквозные переносы, при этом чем выше разрядность сумматора, тем больший выигрыш в быстродействии.
Известен преобразователь двоичного кода в позиционно-знаковый код (см. А.С. №1438005 от 29.01.87 г.), содержащий группу из (n-1) элементов НЕ-(логическая функция f(&)-HE), где n - разрядность входного кода, и группу из (n-1) элементов И - (логическая функция f(&)-И), выходы которых являются выходами младших разрядов положительной группы преобразователя, выход старшего разряда которой является входом старшего разряда преобразователя, i-й (i=2,…, n) вход которого соединен с входом (i-1)-го элемента НЕ группы, выход которого соединен с первым входом (i-1)-го элемента И группы, второй вход которого соединен с входом (i-1)-го разряда преобразователя, при этом в него введена r группа из (n-1) элементов ИЛИ-НЕ, первые входы которых соединены с входами соответствующих разрядов преобразователя, вторые входы элементов ИЛИ-НЕ - (логическая функция f1(}&)-ИЛИ-НЕ) группы соединены с выходами соответствующих элементов НЕ группы, вход младшего разряда преобразователя совместно с выходами элементов ИЛИ-НЕ группы образует n младших разрядов выходов отрицательной группы преобразователя, выход (n+1)-го разряда которого соединен с выходом (п-1)-го элемента НЕ группы (прототип).
Прототип имеет технологические возможности, которые заключаются в том, что для решения задачи повышения быстродействия арифметических операций умножения исключает сквозные переносы в функциональных структурах процесса суммирования частичных произведений, но не позволяет минимизировать сквозные переносы условно отрицательных аргументов результирующей суммы процесса умножения.
Недостатком прототипа является ограниченность функциональных возможностей, поскольку не минимизирует время на преобразование результирующей структуры умножения аргументов из формата позиционно-знаковой системы счисления f(+/-) в формате двоичной системы счисления f(2n).
Техническим результатом предложенного изобретения является расширение функциональных возможностей при использовании его в структурах умножителя повышенного быстродействия.
Указанный технический результат достигается следующей функциональной структурой избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
Функциональная структура избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
Функциональная структура избирательного логического дифференцирования аргументов формата двоичной системы f(2n), в которой условно «j» разряд выполнен в виде положительного и условно отрицательного каналов для формирования результирующих преобразованных аргументов соответственно положительного +(±)mj и условно отрицательного преобразованного аргумента -mj и содержит логическую функцию f1(&)-НЕ, логическую функции f2(&)-И и логическую функцию f3(&)-И, в которой функциональная выходная связь формирования условно отрицательного аргумента -mj является функциональной выходной связью условно отрицательного канала, в котором функциональная входная связь приема аргумента +mj является функциональной входной связью логической функции f1(&)-НЕ, в которой функциональная выходная связь является функциональной выходной связью функциональной структуры условно «j» разряда и первой функциональной входной связью логической функции f2(&)-И, в которой третья функциональная входная связь приема аргумента +mj-1 является функциональной входной связью функциональной структуры и первой функциональной входной связью логической функции f3(&)-И, третья функциональная входная связь приема аргумента +mj является функциональной входной связью функциональной структуры, при этом в условно «j» разряда введены дополнительные логическая функция f1(&)-И и логическая функция f1(})-ИЛИ, в которой функциональная выходная связь преобразованного аргумента +(±)mj является функциональной выходной связью положительного канала, а вторая функциональная входная связь является функциональной выходной связью логической функции f2(&)-И, при этом первая функциональная связь является функциональной выходной связью логической функции f1(&)-И, в которой первая и вторая функциональные входные связи приема аргумента +mj условно «j» разряда и приема аргумента +m j-1 условно «j-1» разряда являются соответствующей функциональной входной связью функциональной структуры, в котором две функциональные входные связи приема соответственно аргумента +mj-2 и приема аргумента с измененным уровнем аналогового сигнала +mj-2 являются соответственно второй функциональной входной связью логической функции f2(&)-И и второй функциональной входной связью логической функции f3(&)-И, при этом логические функции и их функциональные связи с соответствующими аргументами имеют математическую модель, которая в аналитической форме положительного и условно отрицательного каналов имеет вид
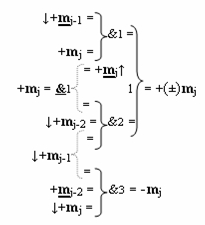
где 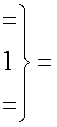 - логическая функция f1(})-ИЛИ;
- логическая функция f1(})-ИЛИ;
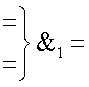 - логическая функция f1(&)-И;
- логическая функция f1(&)-И;
«=&=» - логическая функция отрицания f1(&)-НЕ.
Функциональная структура избирательного логического дифференцирования аргументов формата двоичной системы f(2n), в которой условно «j» разряд выполнен в виде положительного и условно отрицательного каналов для формирования результирующих преобразованных аргументов соответственно положительного +(±)mj и условно отрицательного преобразованного аргумента -mj и содержит логическую функцию f1(&)-НЕ, при этом в условно «j» разряд введены дополнительные логические функции f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ и логическая функция f1(}&)-ИЛИ-НЕ, при этом логические функции и их функциональные связи с соответствующими аргументами имеют математическую модель, которая в аналитической форме положительного и условно отрицательного каналов имеет вид
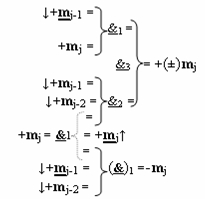
где  - логическая функция f1(&)-И-НЕ;
- логическая функция f1(&)-И-НЕ;
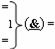 - логическая функция f1(}&)-ИЛИ-НЕ.
- логическая функция f1(}&)-ИЛИ-НЕ.
На фиг.1 изображена математическая модель первого варианта функциональной структуры избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
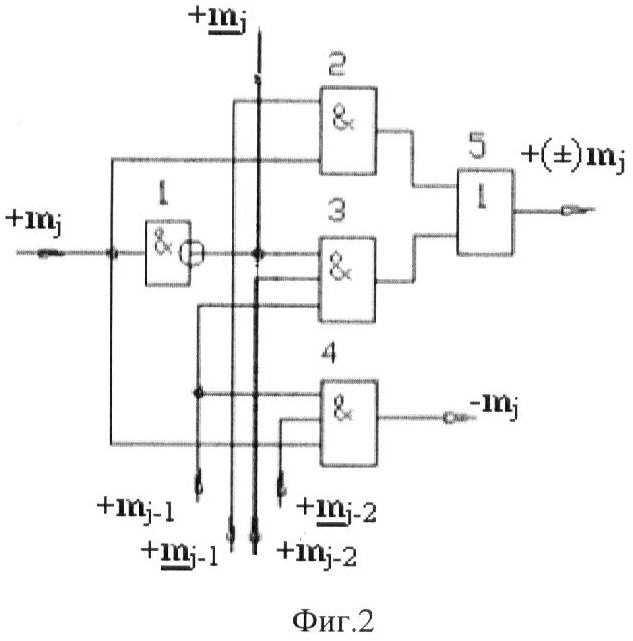
На фиг.2 изображена схемная реализация функциональной структуры первого варианта избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
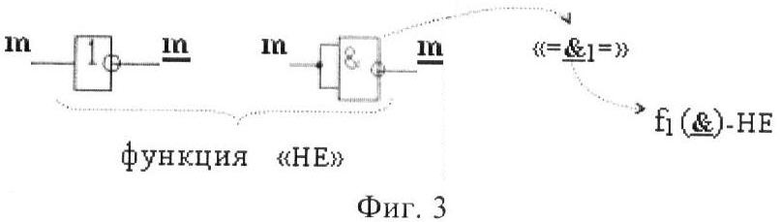
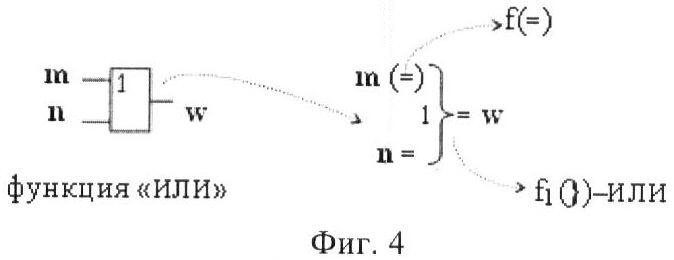
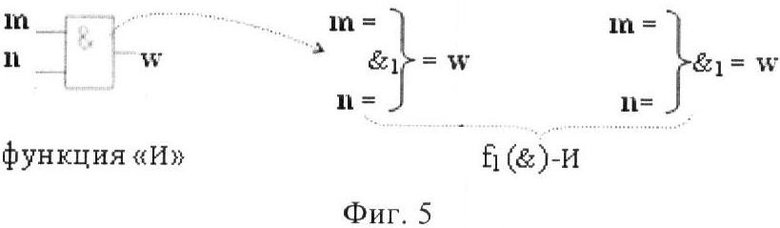
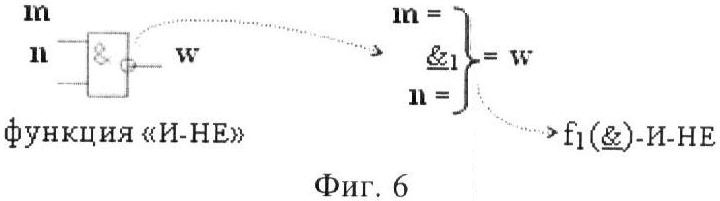
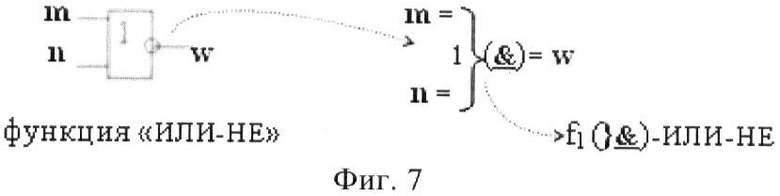
На фиг.3-7 изображена схемная и аналитическая запись логических функций f2(&)-НЕ (фиг.3) f(})-ИЛИ (фиг.4), f(&)-И (фиг.5), f(&)-И-НЕ (фиг.6) и f1(}&)-ИЛИ-НЕ (фиг.7).
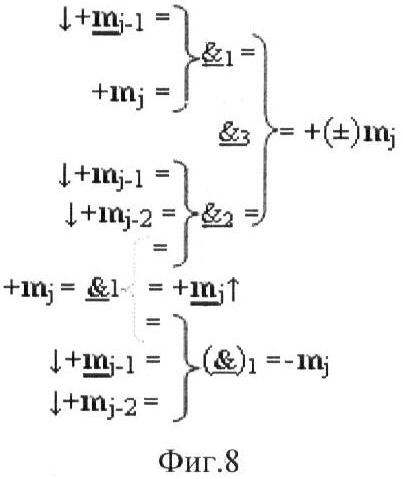
На фиг.8 изображена математическая модель второго варианта функциональной структуры избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
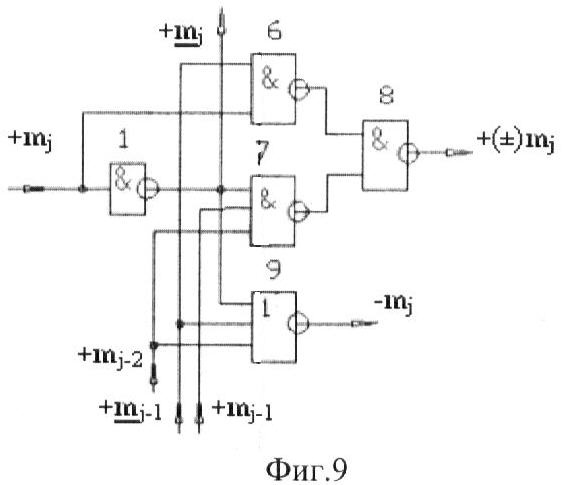
На фиг.9 изображена схемная реализация функциональной структуры второго варианта избирательного логического дифференцирования аргументов формата двоичной системы f(2n).
Схемная реализация функциональной структуры избирательного логического дифференцирования аргументов формата двоичной системы f(2n) в первом варианте содержит логическую функцию f(&)-НЕ 1, логические функции f1(&)-И 2, f2(&)-И 3 и f3(&)-И 4, логическую функцию функции f1(})-ИЛИ 5, а второй вариант схемной реализации (фиг.9) содержит логическую функцию f(&)-НЕ 1, логические функции f1(&)-И-НЕ 6, f2(&)-И-НЕ 7 и f3(&)-И-НЕ 8.
Работа функциональной структуры избирательного логического дифференцирования аргументов формата двоичной системы f(2n) будет пояснена в процессе ее анализа и синтеза математической модели.
Причинно-следственные связи синтеза математической модели процесса избирательного логического дифференцирования d*/dn структуры аргументов множимого ±[mj].
Для повышения быстродействия сумматоров и умножителей была разработана процедура логического дифференцирования d/dn, такая процедура позволяет структуры аргументов множимого [mj] формата двоичной системы счисления f(2n) с потенциально возможными сквозными переносами f(←←) преобразовывать в структуры аргументов множимого ±[mj] формата позиционно-знаковой системы счисления f(+/-). Суть процедуры логического дифференцирования d/dn заключается в том, что если выполнить операцию логического дифференцирования d/dn структуры аргументов [mj] → «11111110»,
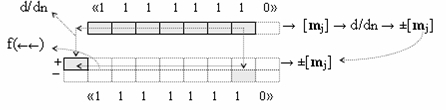
то вся последовательность активных аргументов «1» независимо от их количества преобразуется в положительный аргумент очередного разряда и условно отрицательный аргумент в младшем активном разряде. В результате логического дифференцирования d/dn предварительно вводят в структуру аргументов [mj] сквозной перенос f(←←) и процесс умножения аргументов [mj] → «11010111» и [nj] → «11100011» можно записать в виде графоаналитической структуры (1),
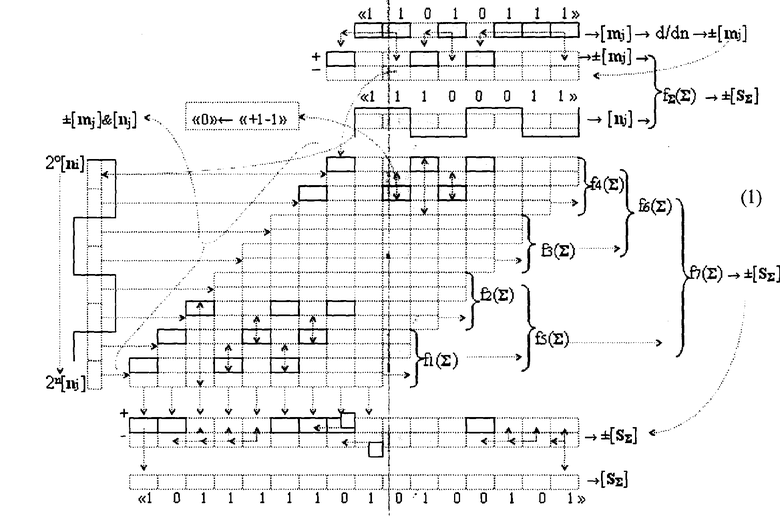
в которой процесс fΣ(Σ) суммирования частичных произведений ±[mj]&[nj] может быть реализован параллельно-последовательным методом. При этом процесс формирования частичных произведений ±[mj]&[nj] в графоаналитической структуре (1) и последующее их суммирование может быть записано в виде обобщенного аналитического выражения
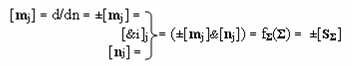
где [mj] - структура аргументов множимого; d/dn - логическое дифференцирование структуры аргумента множимого [mj]; [&i]j - структура логических функций f(&)-И, посредством которых формируются частичные произведения ±[mj]&[nj]; fΣ(Σ) - параллельно-последовательная структура сумматора. А первый этап суммирования f1(Σ) - f4(Σ) частичных произведений ±[mj]&n1 - ±[mj]&nj реализуется посредством процедуры удаления активного логического нуля «+1-1» → «0», что позволяет существенно повысить быстродействие умножителя. При этом особенностью суммирования частичных произведений первого этапа суммирования f1(Σ) - f4(Σ), который запишем в виде графоаналитической структуры (2)
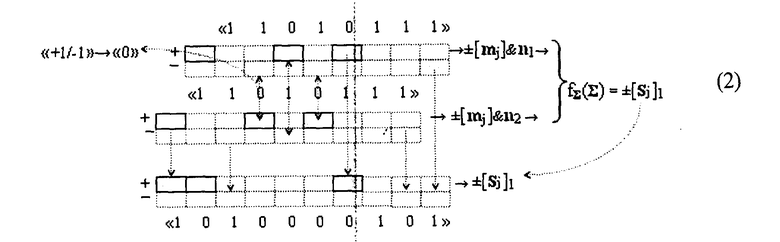
является то, что, с одной стороны, полностью отсутствуют сквозные переносы f(←←), при этом первая промежуточная сумма ±[Sj]1 реализована в формате позиционно-знаковой системы счисления f(+/-) и дальнейшей реализации процесса суммирования первых промежуточных сумм ±[Sj]1 - ±[Sj]4 не препятствует. С другой стороны, для формирования конечной суммы выражения (1) в формате двоичной системы счисления f(2n), необходимо выполнить процедуру переноса условно отрицательных активных аргументов в соответствии с арифметической аксиомой «-1» → «-2+1», например, для промежуточной суммы ±[Sj]1 этот процесс запишем в виде графоаналитической структуры (3).
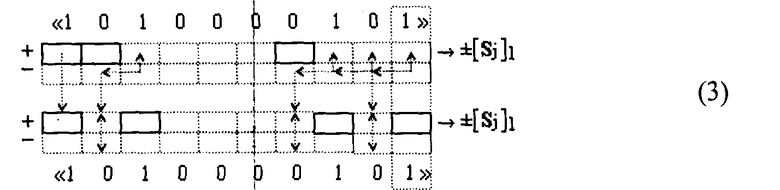
Из анализа процесса преобразования аргументов (3) следует, что аргумент младшего разряда структуры аргументов множимого [mj] целесообразно не подвергать процедуре логического дифференцирования d/dn, что сократит процесс перевода структуры конечной суммы ±[SΣ] формата позиционно-знаковой системы счисления f(+/-) в структуру конечной суммы [SΣ] формата двоичной системы счисления f(2n) в выражении (1). Поэтому такое преобразование структуры аргументов множимого [mj] назовем процедурой избирательного логического дифференцирования d/dn, в котором арифметическая аксиома «+1» → «+2» «-1» применяется ко всем активным аргументам, кроме аргумента младшего разряда, и процесс избирательного логического дифференцирования d/dn, например, для структуры аргументов [mj] → «11111110» можно записать в виде
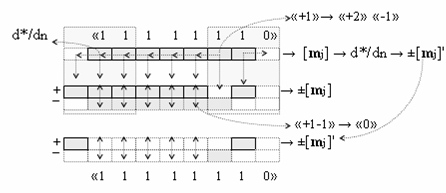
Из сравнительного анализа результирующих структур логического дифференцирования d/dn

и избирательного логического дифференцирования d*/dn той же структуры частичных произведений [mj] → «11111110»
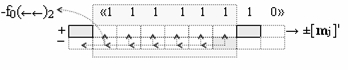
следует, что при выполнении условно отрицательных переносов -f0(←←)1 и -f0(←←)2 при избирательном логическом дифференцировании эта процедура, с одной стороны, короче на один разряд. С другой стороны, условно отрицательный аргумент, который соответствует потенциально возможному переносу положительного аргумента в процессе суммирования, может сформировать активный логический ноль «+1-1» → «0», т.е. быть реализован.
Если выполнить процесс суммирования частичных произведений (3) с учетом избирательного логического дифференцирования d*/dn, то его можно записать в виде графоаналитической структуры (4).
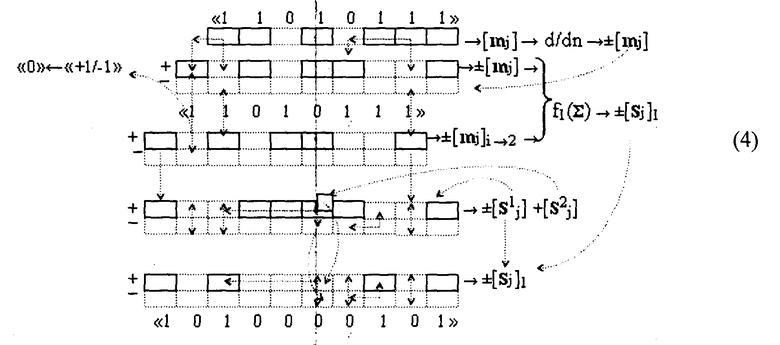
где ±[S1 j] и +[S2 j] - структуры аргументов первой и второй промежуточных сумм частичных произведений, которые сформированы в сумматоре f1(Σ) посредством логических функций f(})-ИЛИ и f(&)-И.
Из анализа процесса преобразования аргументов (4) следует, что при реализации функциональной структуры сумматора первого уровня f1(Σ) с процедурой избирательного логического дифференцирования d*/dn положительных аргументов первой промежуточной суммы ±[S1 j] и с процедурой логического дифференцирования d/dn условно отрицательных аргументов второй промежуточной суммы +[S2 j] может быть сформирована первая промежуточная сумма ±[Sj]1 в формате двоичной системы счисления f(2n). Поэтому целесообразно сформировать математическую модель процесса избирательного логического дифференцирования d*/dn структуры аргументов множимого [mj].
В связи с полученными результатами сформируем аналитическое выражение условно «j» разряда процесса избирательного логического дифференцирования d*/dn структуры аргументов множимого [mj], которое включает:
- Формирование аналитического выражения для структуры аргументов f1(«10»), которое запишем в виде графоаналитической структуры (5).
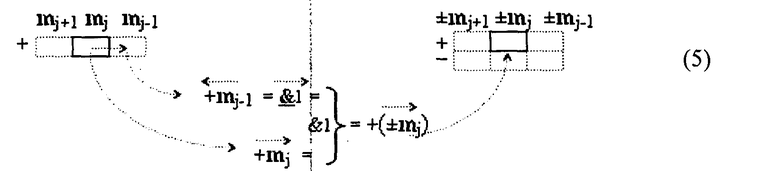
Из анализа аналитического выражения (5) следует, что посредством логической функции f1(&)-И может быть сформирован положительный активный аргумент +mj, который не подвергается логическому дифференцированию d/dn, при условии не активного аргумента +mj-1 «j-1» разряда, который активизируется посредством логической функции f1(&)-НЕ и активного аргумента +mj «j» разряда.
- Формирование аналитического выражения для структуры аргументов f2(«0←↓110»), которое запишем в виде графоаналитической структуры (6).
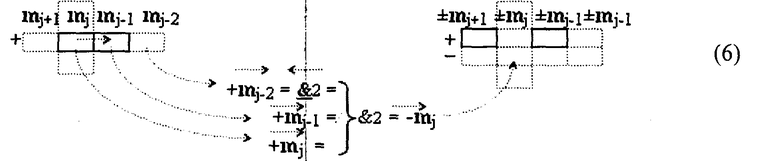
Из анализа аналитического выражения (6) следует, что посредством логической функции f2(&)-И может быть сформирован условно отрицательный активный аргумент -mj, который должен быть сформирован в соответствии с логикой процесса избирательного логического дифференцирования d*/dn, при условии не активного аргумента +mj-2 «j-2» разряда, который активизируется посредством логической функции f2(&)-НЕ и активных аргументов +mj-1 «j-1» разряда и +mj «j» разряда.
- Формирование аналитического выражения для структуры аргументов f2(«0←↓110»), которое запишем в виде графоаналитической структуры (7).
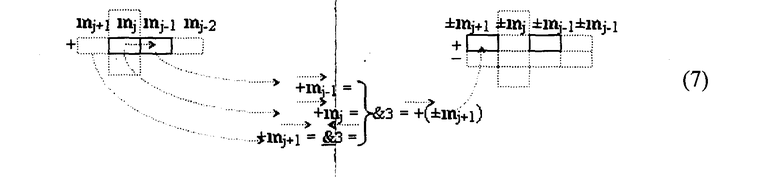
Из анализа аналитического выражения (7) следует, что посредством логической функции f3(&)-И может быть сформирован положительный активный аргумент +mj+1 «j+1» разряда, который подвергается логическому дифференцированию d/dn, при условии не активного аргумента +mj+1 «j+1» разряда, который активизируется посредством логической функции f3(&)-НЕ и активных аргументов +mj-1 «j-1» разряда и +mj «j» разряда.
Для формирования функционально законченной математической модели условно «j» разряда процесса избирательного логического дифференцирования d*/dn сформируем аналитическое выражение условно «j» разряда, в котором выполняется процедура формирования положительного аргумента переноса в очередной положительный разряд. При этом аналитическое выражение для этой ситуации будет аналогично аналитическому выражению (7) за исключением индексов входных и преобразованных аргументов, которое запишем в виде графоаналитического выражения (8)

Затем выполним объединение положительных аргументов +mj аналитических выражений (5) и (8) посредством логической функции f1(})-ИЛИ и сформируем общее для них выражение (9).
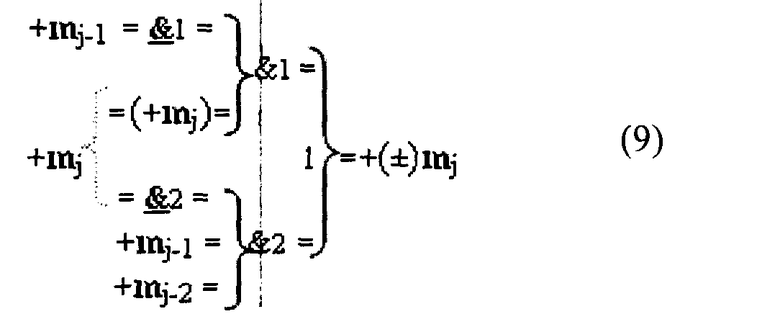
После чего введем в аналитическое выражение (9) функциональную структуру условно отрицательного аргумента (6) и сформируем функционально законченное аналитическое выражение (10).
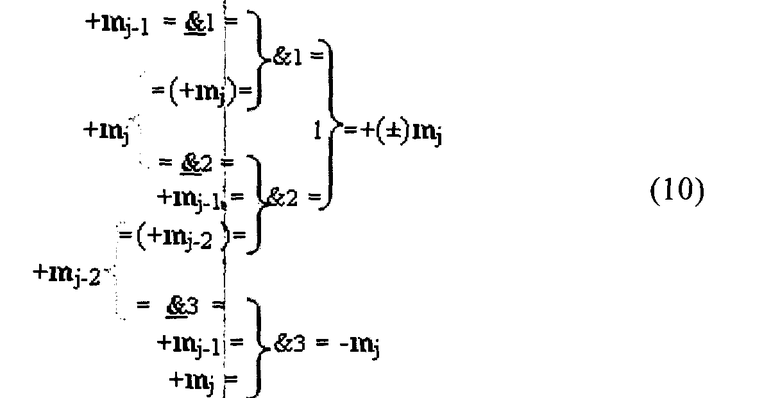
Сформированное аналитическое выражение (10) является математической моделью процесса избирательного логического дифференцирования d*/dn структуры аргументов множимого [mj] формата двоичной системы счисления f(2n). При этом из анализа структуры функций выражения (10) следует, что она может быть минимизирована, поскольку включает логические функции f(&)-НЕ трех разрядов, следовательно, если ввести измененный по уровню аналогового сигнала преобразованный аргумент m j, то могут быть исключены из аналитического выражения (10) логические функции f1(&)-НЕ и f3(&)-НЕ. В результате формируем минимизированное выражение математической модели процесса избирательного логического дифференцирования d*/dn первого варианта
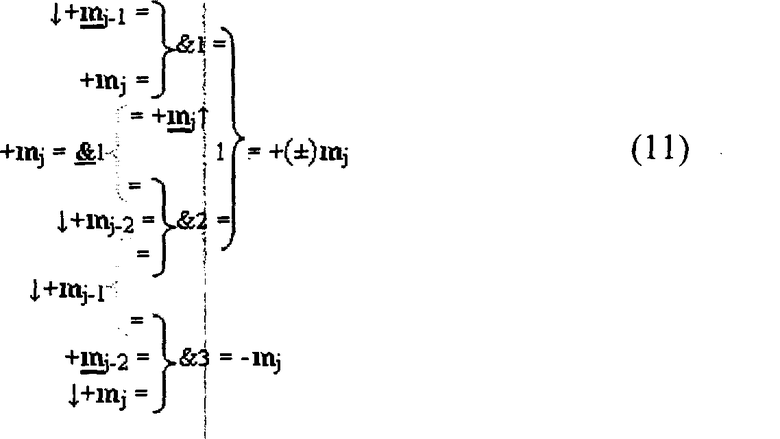
которое в схемной реализации изображено на фиг.2. При этом максимальное время преобразования ∆t процесса избирательного логического дифференцирования d*/dn соответствует трем условным логическим функциям f(&)-И.
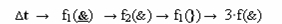
Для синтеза математической модели процесса избирательного логического дифференцирования d*/dn второго варианта выполним замену функциональных входных связей логической функции f1(})-ИЛИ и функциональную выходную связь логической функции f3(&)-И на соответствующие им функции двойного изменения уровня аналогового сигнала f(&=&) в соответствии с графоаналитической структурой (12).
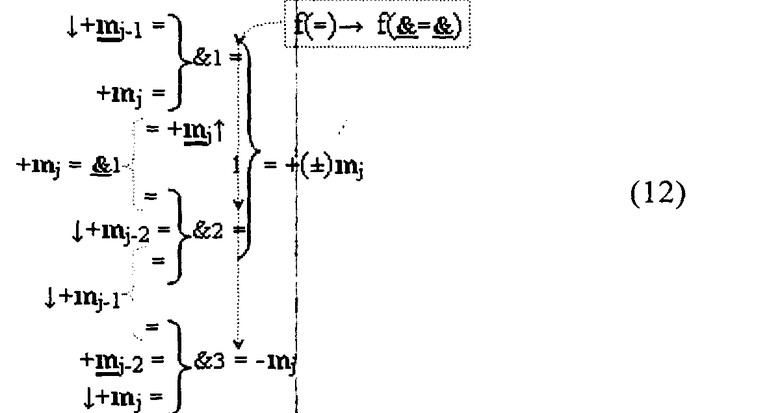
Затем в соответствии с векторной структурой (13)
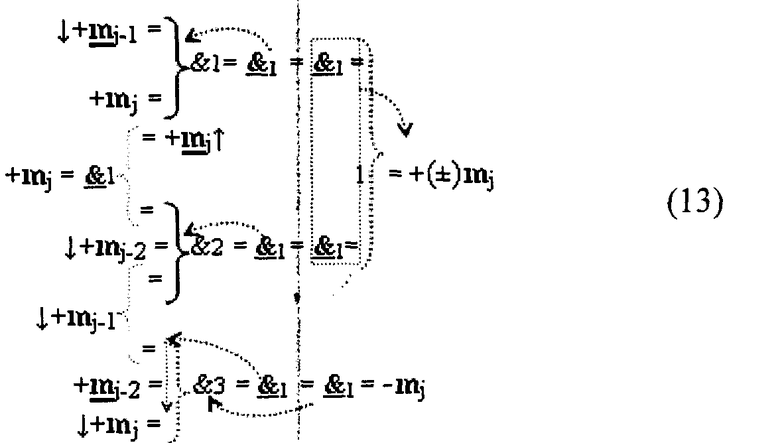
выполним перенос логических функций f(&)-НЕ, сформируем математическую модель (14)
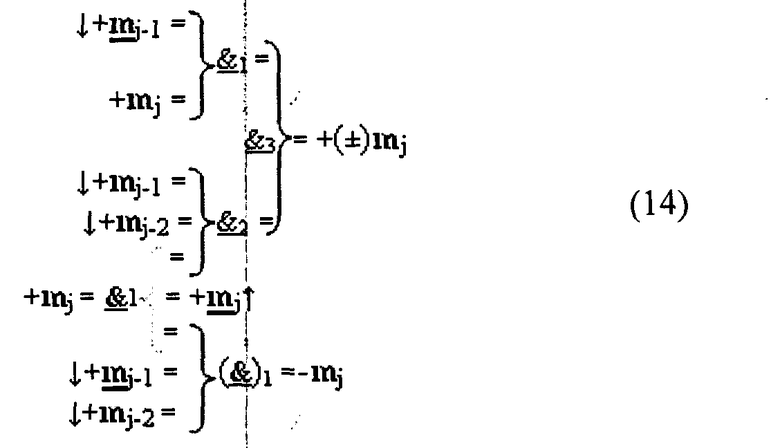
схемная реализация которой изображена на фиг.9.
Использование изобретения позволяет расширить область применения операции логического дифференцирования как в сумматорах, так и в быстродействующих умножителях.
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических операций суммирования и вычитания в позиционно-знаковых кодах. Техническим результатом является расширение функциональных возможностей устройства. Каждый разряд устройства в первом варианте реализации содержит логический элемент НЕ, три логических элемента И, логический элемент ИЛИ. 2 н.п. ф-лы, 9 ил.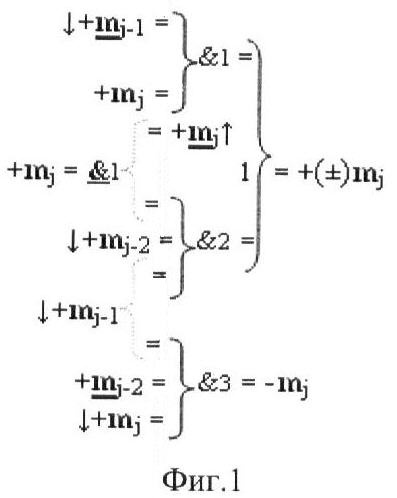
1. Функциональная структура избирательного логического дифференцирования аргументов формата двоичной системы f(2n), в которой условно «j» разряд выполнен в виде положительного и условно отрицательного каналов для формирования результирующих преобразованных аргументов соответственно положительного +(±)mj и условно отрицательного преобразованного аргумента -mj и содержит логическую функцию f1(&)-HE, логическую функцию f2(&)-И и логическую функцию f3(&)-И, в которой функциональная выходная связь формирования условно отрицательного аргумента -mj является функциональной выходной связью условно отрицательного канала, в котором функциональная входная связь приема аргумента +mj является функциональной входной связью логической функции f1(&)-HE, в которой функциональная выходная связь является функциональной выходной связью функциональной структуры условно «j» разряда и первой функциональной входной связью логической функции f2(&)-И, в которой третья функциональная входная связь приема аргумента +mj-1 является функциональной входной связью функциональной структуры и первой функциональной входной связью логической функции f3(&)-И, третья функциональная входная связь приема аргумента +mj является функциональной входной связью функциональной структуры, отличающаяся тем, что в условно «j» разряд введены дополнительные логическая функция f1(&)-И и логическая функция f1(})-ИЛИ, в которой функциональная выходная связь преобразованного аргумента +(±)mj является функциональной выходной связью положительного канала, а вторая функциональная входная связь является функциональной выходной связью логической функции f2(&)-И, при этом первая функциональная связь является функциональной выходной связью логической функции f1(&)-И, в которой первая и вторая функциональные входные связи приема аргумента +mj условно «j» разряда и приема аргумента +m
j-1 условно «j-1» разряда являются соответствующей функциональной входной связью функциональной структуры, в котором две функциональные входные связи приема соответственно аргумента +mj-2 и приема аргумента с измененным уровнем аналогового сигнала +mj-2 являются соответственно второй функциональной входной связью логической функции f2(&)-И и второй функциональной входной связью логической функции f3(&)-И, при этом логические функции и их функциональные связи с соответствующими аргументами имеют математическую модель, которая в аналитической форме положительного и условно отрицательного каналов имеет вид
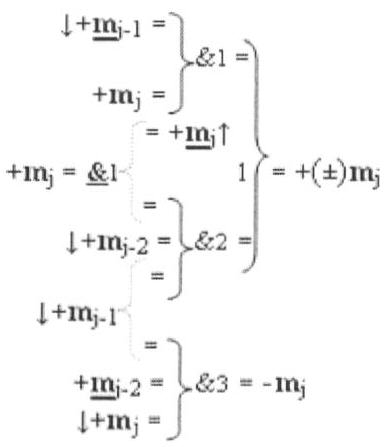
где 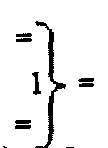 - логическая функция
- логическая функция
f1(})-ИЛИ;  - логическая функция
- логическая функция
f1(&)-И;
«=&=» - логическая функция отрицания f1(&)-HE.
2. Функциональная структура избирательного логического дифференцирования аргументов формата двоичной системы f(2n), в которой условно «j» разряд выполнен в виде положительного и условно отрицательного каналов для формирования результирующих преобразованных аргументов соответственно положительного +(±)mj, и условно отрицательного преобразованного аргумента -mj и содержит логическую функцию f1(&)-HE, отличающаяся тем, что в условно «j» разряд введены дополнительные логические функции f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ, и логическая функция f1(}&)-ИЛИ-НЕ, при этом логические функции и их функциональные связи с соответствующими аргументами имеют математическую модель, которая в аналитической форме положительного и условно отрицательного каналов имеет вид
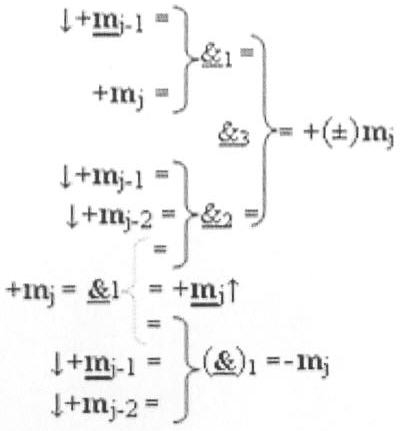
где 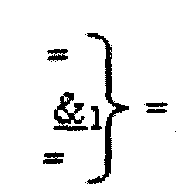 - логическая функция f1(&)-И-HE;
- логическая функция f1(&)-И-HE;
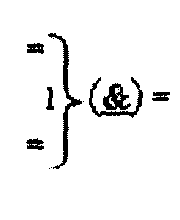 - логическая функция f1(}&)-ИЛИ-НЕ.
- логическая функция f1(}&)-ИЛИ-НЕ.
| Преобразователь двоичного кода в позиционно-знаковый код | 1987 |
|
SU1438005A1 |
| ПРЕОБРАЗОВАТЕЛЬ ПАРАЛЛЕЛЬНОГО ЗНАКОРАЗРЯДНОГО КОДА В ДОПОЛНИТЕЛЬНЫЙ ДВОИЧНЫЙ КОД | 1990 |
|
RU2022337C1 |
| СПОСОБ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2163391C1 |
| Устройство для преобразования дополнительного двоичного кода в знакоразрядный | 1987 |
|
SU1496004A1 |
| JP 9081369 A, 28.03.1997 | |||
| JP 57157350 A, 28.09.1982. | |||
Авторы
Даты
2009-11-20—Публикация
2008-04-29—Подача