Текст описания приведен в факсимильном виде. 






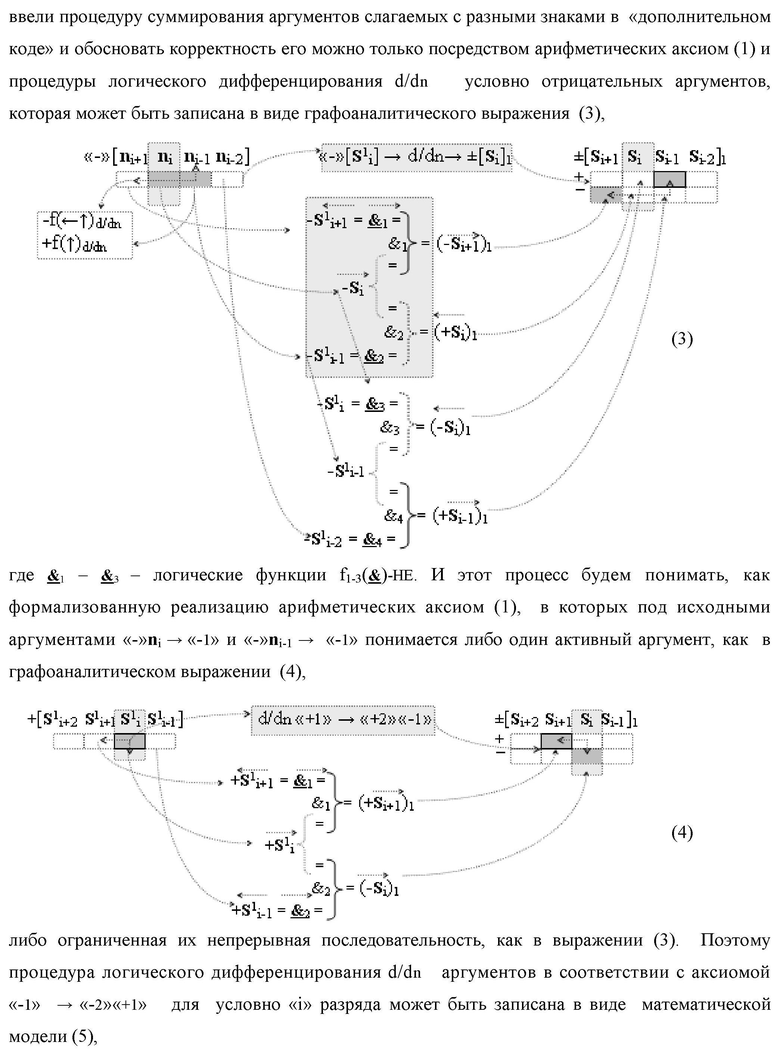



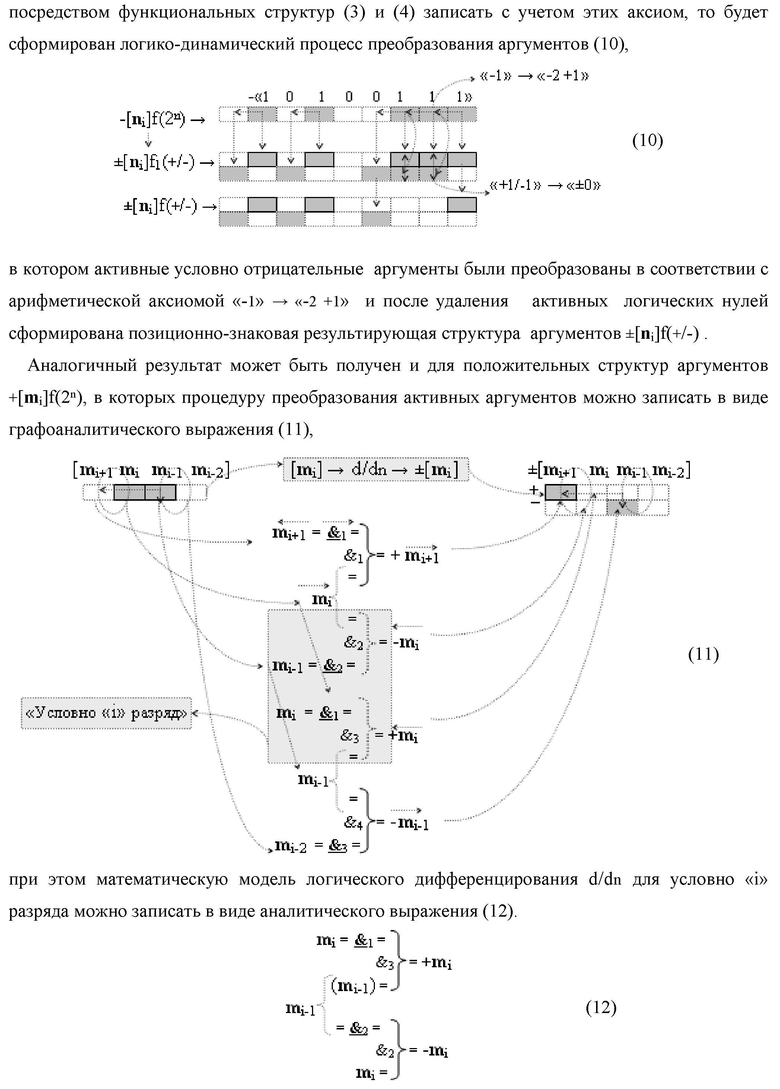





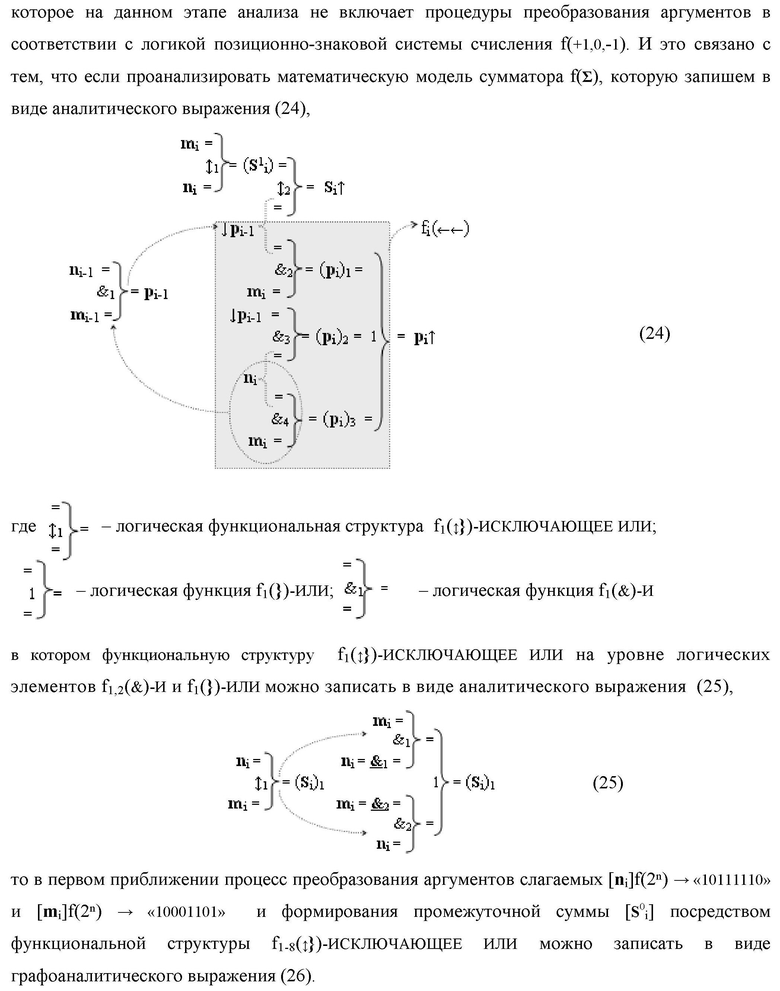
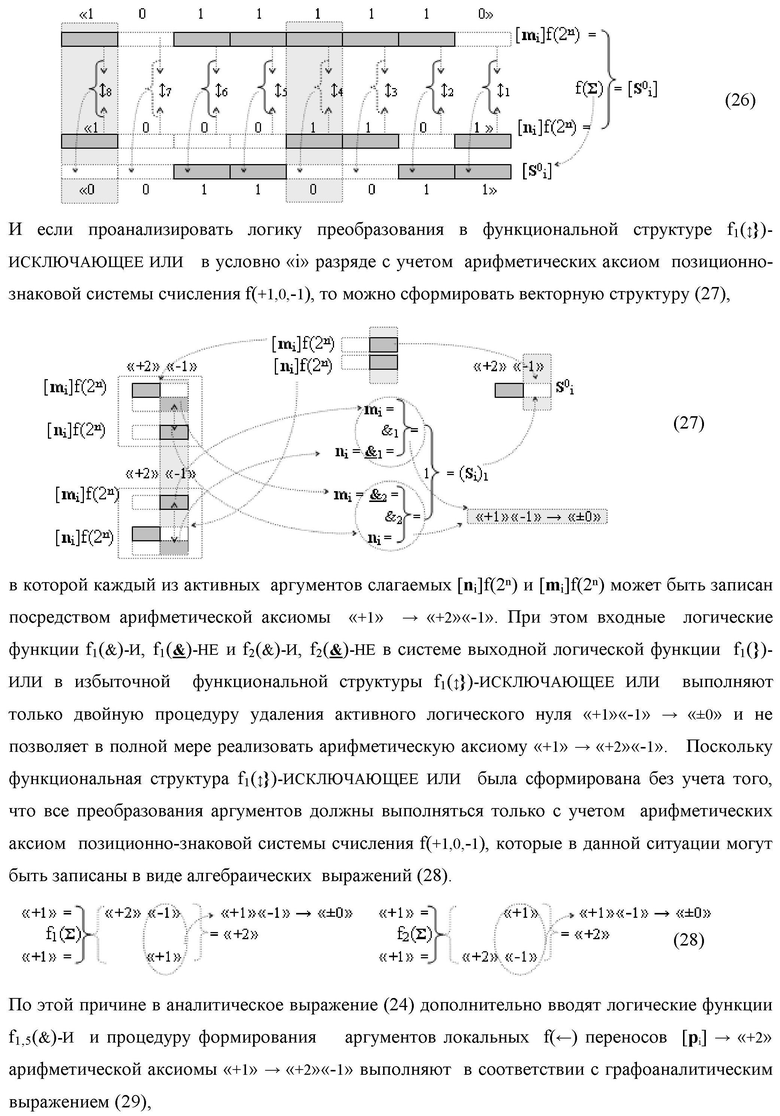





























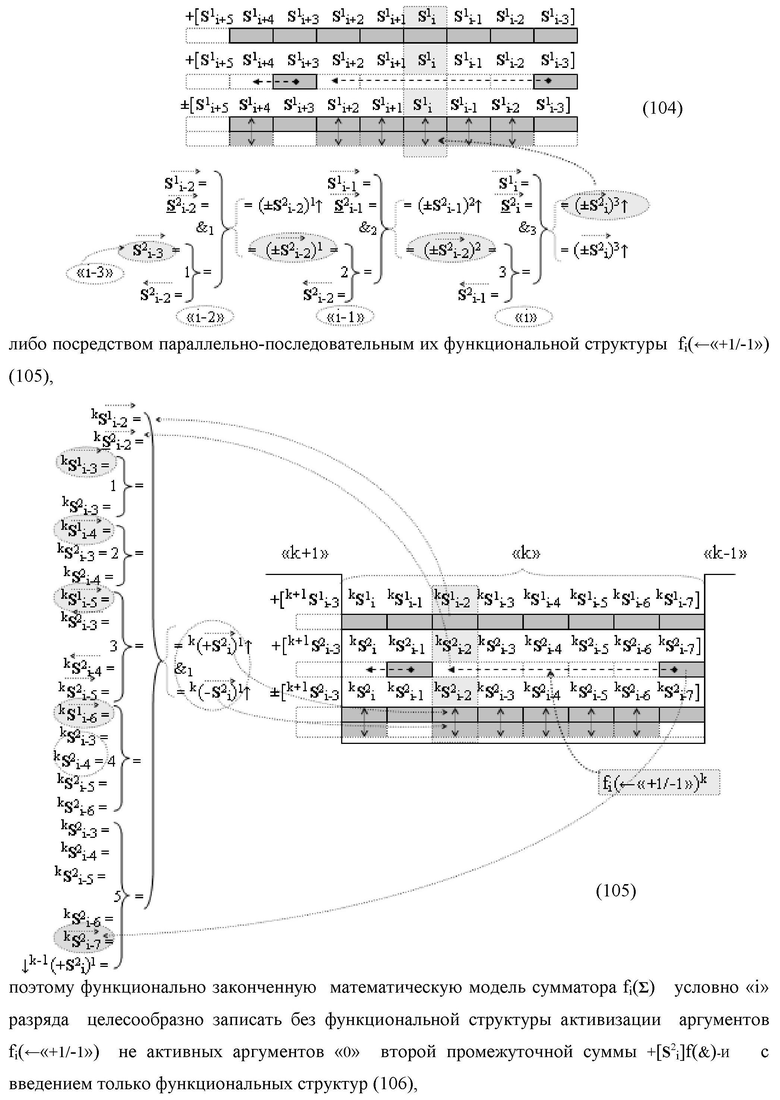

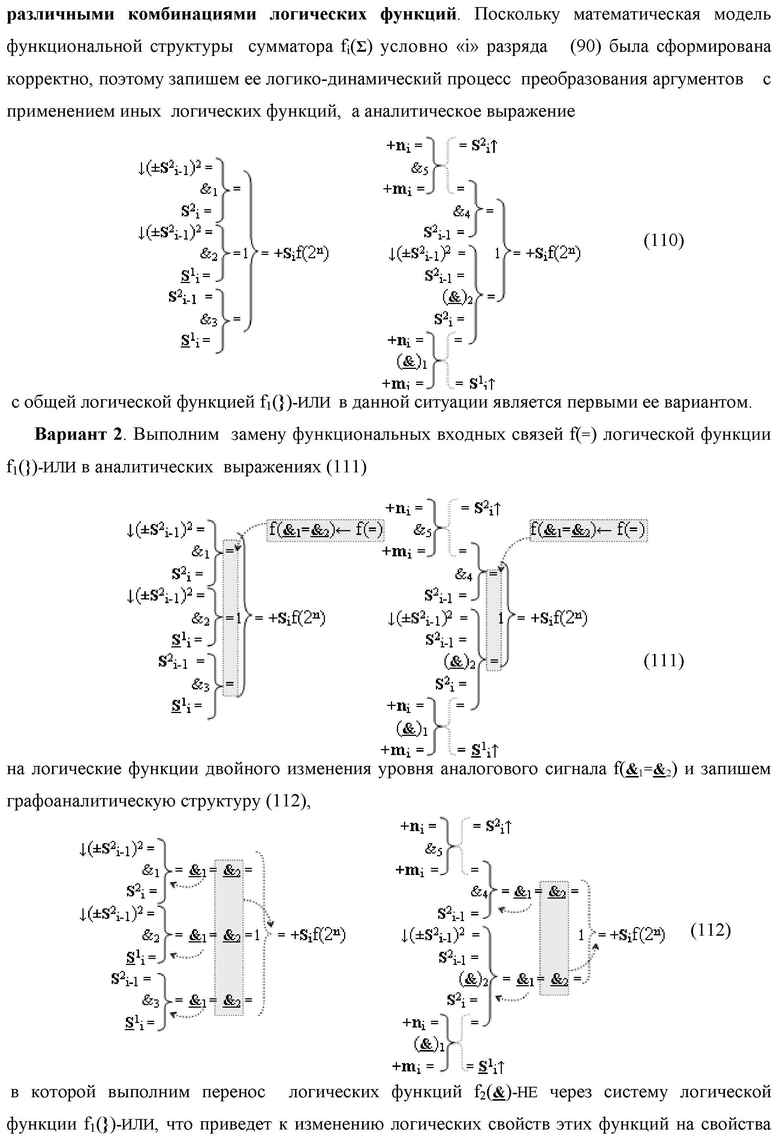








Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнения арифметических процедур суммирования позиционных аргументов аналоговых сигналов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1). Техническим результатом предложенного изобретения является сокращение технологического цикла преобразования аргументов слагаемых [ni]f(2n) и [mi]f(2n) в функциональной структуре сумматора fi(Σ) условно «i» разряда. Предложенные различные варианты функциональной структуры сумматора за счет введенных дополнительных логических функций и предложенных выполнений функциональных связей позволяют существенно повысить его быстродействие. 5 н.п. ф-лы.
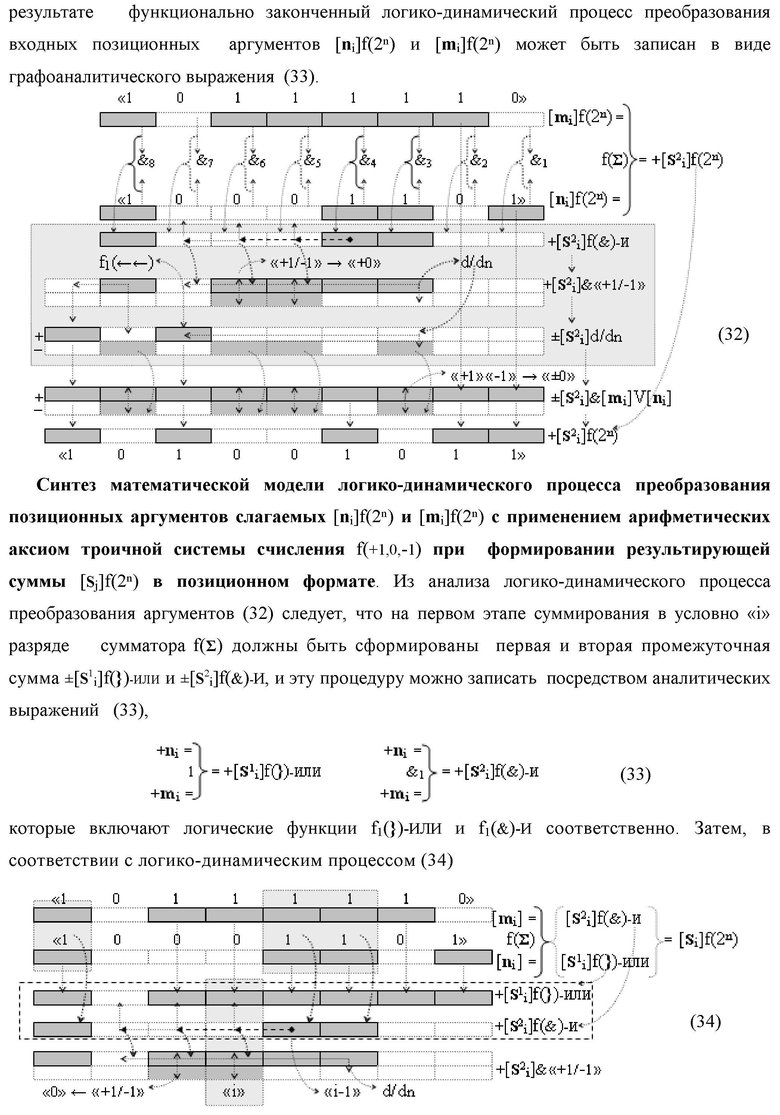
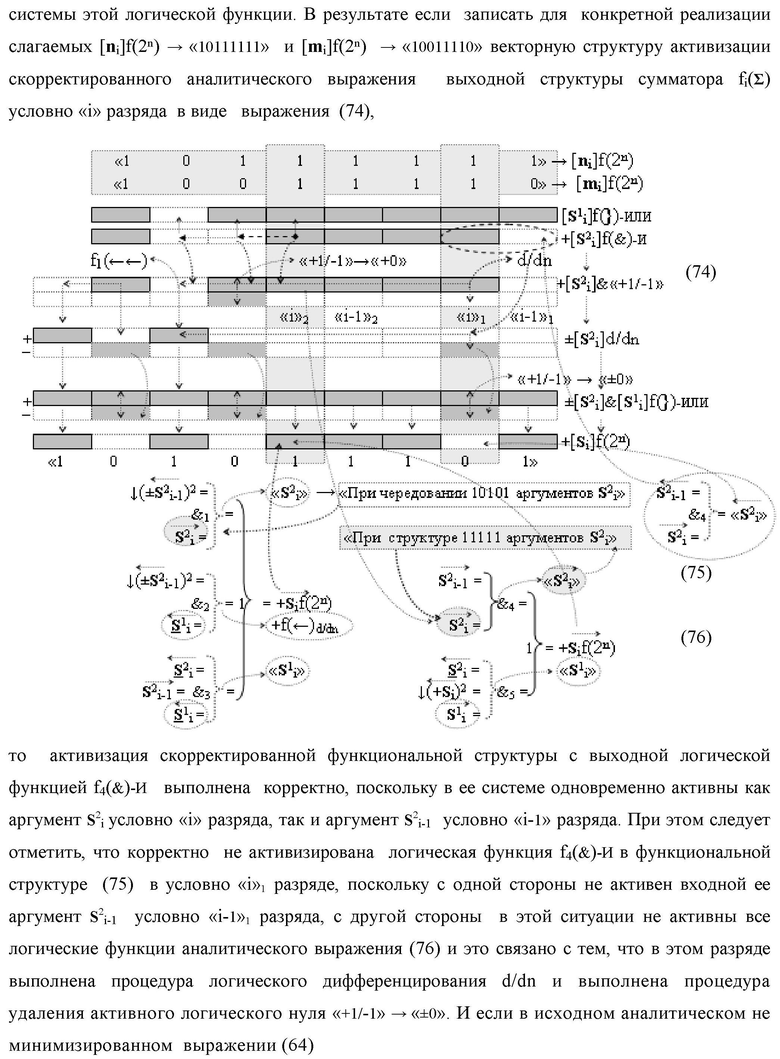
1. Функциональная структура сумматора fi(Σ) условно «i» разряда логико-динамического процесса суммирования позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f5(&)-И, f1(}&)-ИЛИ-НЕ и логические функции f1(&)-И и f2(&)-И, в которых функциональные выходные связи являются функциональными входными связями выходной логической функции f1(})-ИЛИ, а ее функциональная выходная связь является функциональной выходной связью сумматора для формирования результирующего позиционного аргумента +Sif(2n), при этом функциональные входные связи логической функции f1(}&)-ИЛИ-НЕ являются функциональными входными связями сумматора для приема входных аргументов +ni и +mi условно «i» разряда и формирования аргумента S
1 i первой промежуточной суммы с измененным уровнем аналогового сигнала, отличающаяся тем, что в функциональную структуру сумматора fi(Σ) условно «i» разряда введены дополнительные логические функции f3(&)-И, f4(&)-И и f2(}&)-ИЛИ-НЕ, а функциональные связи в функциональной структуре сумматора выполнены в соответствии с математической моделью вида
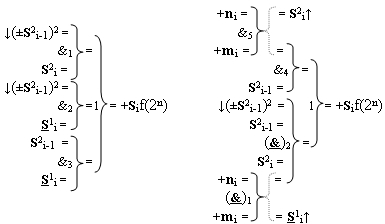
где 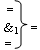 - логическая функция f1(&)-И;
- логическая функция f1(&)-И;
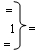 - логическая функция f1(})-ИЛИ;
- логическая функция f1(})-ИЛИ;
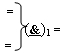 - логическая функция f1(}&)-ИЛИ-НЕ.
- логическая функция f1(}&)-ИЛИ-НЕ.
2. Функциональная структура сумматора fi(Σ) условно «i» разряда логико-динамического процесса суммирования позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f1(&)-И-НЕ, f1(}&)-ИЛИ-НЕ, f1(&)-И и логическую функцию f1(})-ИЛИ, в которой функциональная входная связь приема преобразованного аргумента S2 i второй промежуточной суммы является функциональной выходной связью логической функции f1(&)-И, а функциональные входные связи логической функции f1(}&)-ИЛИ-НЕ являются функциональными входными связями сумматора для приема входных аргументов +ni и +mi условно «i» разряда и формирования аргумента S
1 i первой промежуточной суммы с измененным уровнем аналогового сигнала, отличающаяся тем, что в функциональную структуру сумматора fi(Σ) условно «i» разряда введены дополнительные логические функции f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ и f1(&)-И-НЕ, а функциональные связи в функциональной структуре сумматора выполнены в соответствии с математической моделью вида
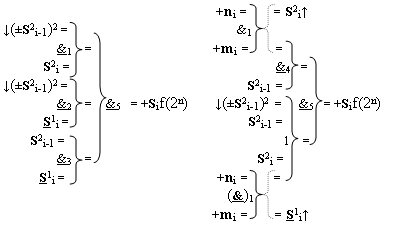
где 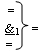 - логическая функция f1(&)-И-НЕ.
- логическая функция f1(&)-И-НЕ.
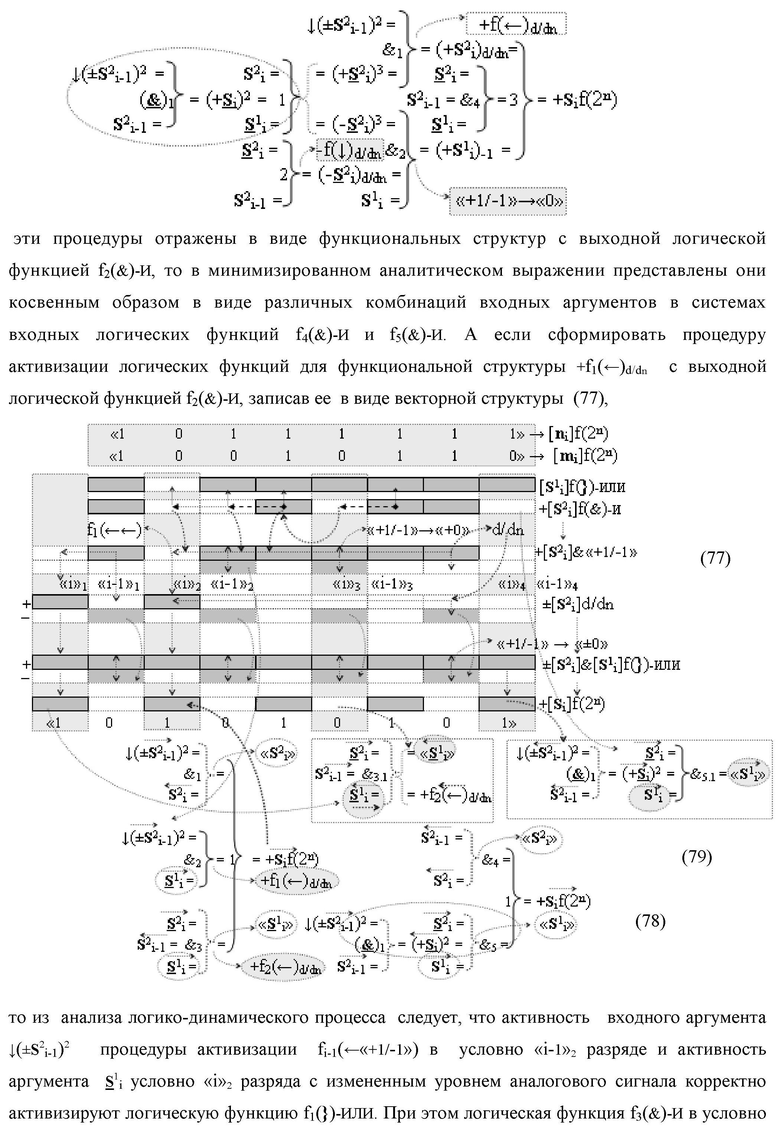
3. Функциональная структура сумматора fi(Σ) условно «i» разряда логико-динамического процесса суммирования позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логические функции f1(&)-И, f4(})-ИЛИ и логические функции f3(&)-И-НЕ и f1(}&)-ИЛИ-НЕ, в которых функциональные входные связи являются функциональными входными связями сумматора для приема входных аргументов +ni и +mi условно «i» разряда и формирования аргумента S
1 i и S
2 i первой и второй промежуточной суммы с измененным уровнем аналогового сигнала, а функциональная входная связь логической функции f4(})-ИЛИ является функциональной выходной связью логической функции f1(&)-И для приема преобразованного аргумента S2 i второй промежуточной суммы, отличающаяся тем, что в функциональную структуру сумматора fi(Σ) условно «i» разряда введены дополнительные логические функции f1(})-ИЛИ, f2(})-ИЛИ, f3(})-ИЛИ, f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ и f4(&)-И-НЕ, а функциональные связи в функциональной структуре сумматора выполнены в соответствии с математической моделью вида
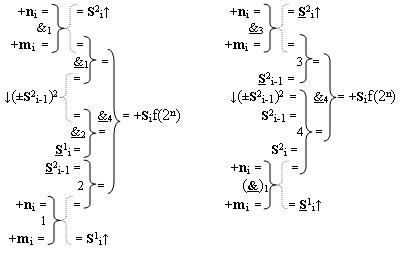
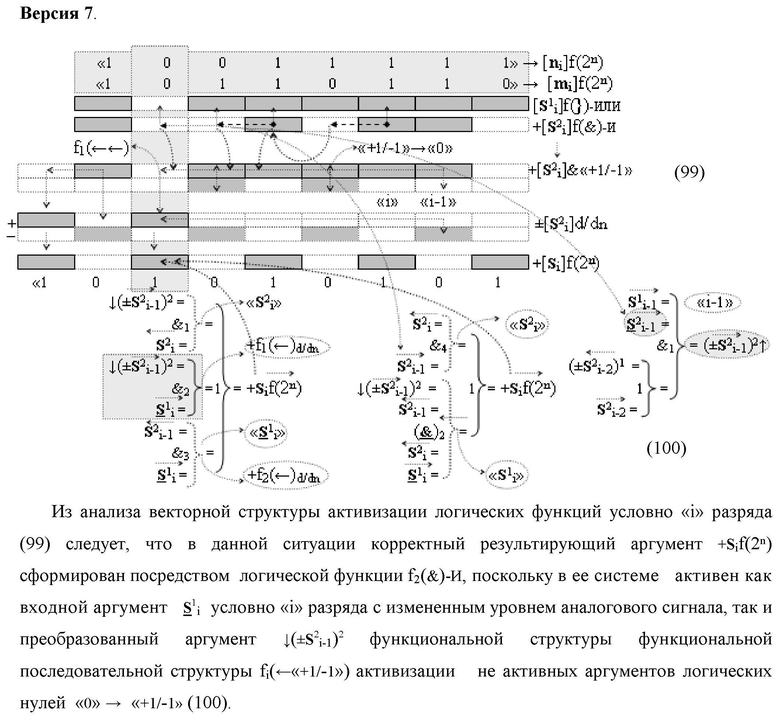
4. Функциональная структура сумматора fi(Σ) условно «i» разряда логико-динамического процесса суммирования позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логическую функцию f5(})-ИЛИ и логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются функциональными входными связями сумматора для приема входных аргументов +ni и +mi условно «i» разряда и формирования аргумента S
2 i второй промежуточной суммы с измененным уровнем аналогового сигнала, отличающаяся тем, что в функциональную структуру сумматора fi(Σ) условно «i» разряда введены дополнительные логические функции f1(})-ИЛИ, f2(})-ИЛИ, f3(})-ИЛИ, f4(})-ИЛИ, f2(&)-И-НЕ и f3(&)-И-НЕ, а функциональные связи в функциональной структуре сумматора выполнены в соответствии с математической моделью вида
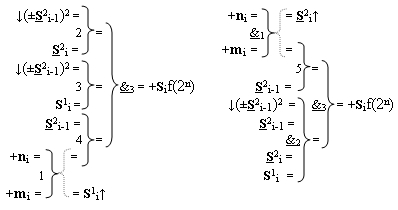
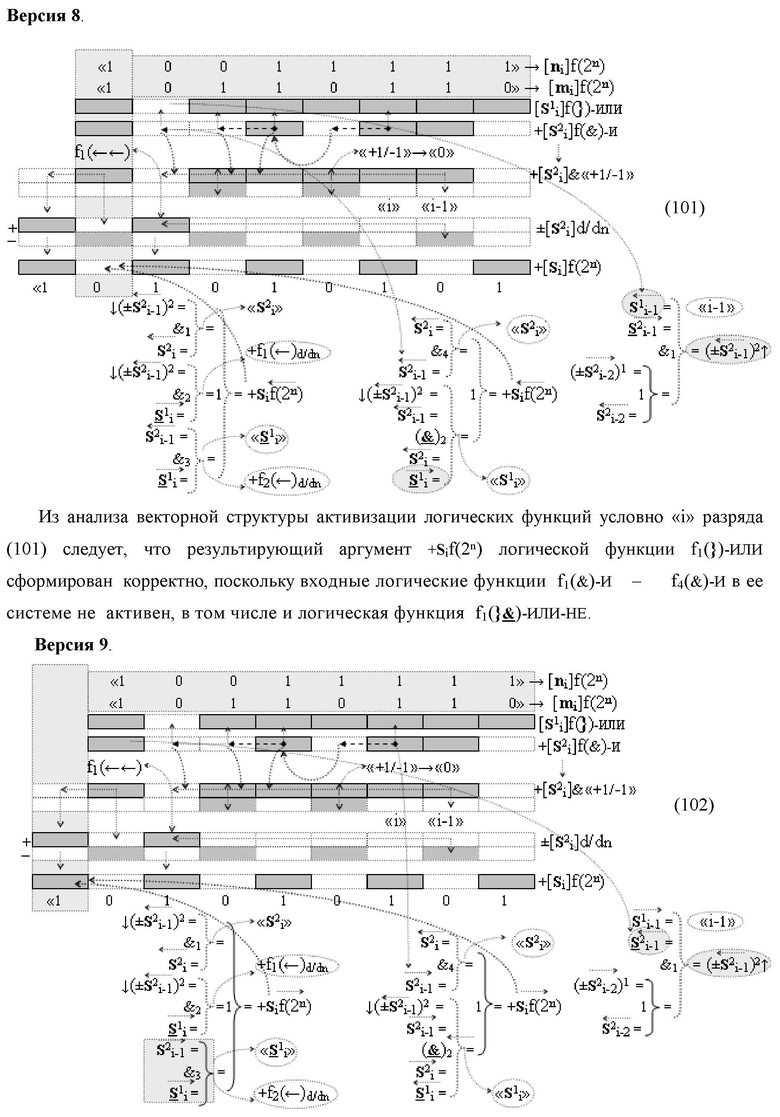
5. Функциональная структура сумматора fi(Σ) условно «i» разряда логико-динамического процесса суммирования позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1), которая включает логическую функцию f1(}&)-ИЛИ-НЕ и логическую функцию f1(&)-И-НЕ, в которой функциональные входные связи являются функциональными входными связями сумматора для приема входных аргументов +ni и +mi условно «i» разряда и формирования аргумента S
2 i второй промежуточной суммы с измененным уровнем аналогового сигнала, а также включает выходную логическую функцию f2(})-ИЛИ, в которой функциональная выходная связь является функциональной выходной связью для формирования результирующего аргумента суммы +Sif(2n), а функциональная входная связь является функциональной выходной связью логической функции f1(&)-И, в которой функциональная входная связь является функциональной входной связью сумматора для приема аргумента ↓(±S
2 i-1)2 условно «i-1» разряда функциональной структуры активизации неактивных аргументов второй промежуточной суммы, отличающаяся тем, что в функциональную структуру сумматора fi(Σ) условно «i» разряда введены дополнительные логические функции f2(}&)-ИЛИ-НЕ, f3(}&)-ИЛИ-НЕ, f4(}&)-ИЛИ-НЕ, f1(})-ИЛИ, а функциональные связи в функциональной структуре сумматора выполнены в соответствии с математической моделью вида
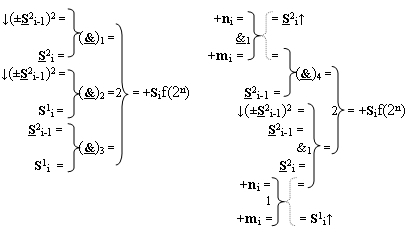
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО ПОЗИЦИОННО-ЗНАКОВОГО СУММАТОРА f(+/-) ДЛЯ КОМБИНАЦИОННОГО УМНОЖИТЕЛЯ, В КОТОРОМ ВЫХОДНЫЕ АРГУМЕНТЫ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ ПРЕДСТАВЛЕНЫ В ФОРМАТЕ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(2) (ВАРИАНТЫ) | 2008 |
|
RU2380740C2 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА УСЛОВНО "i" РАЗРЯДА ПАРАЛЛЕЛЬНОГО СУММАТОРА ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1,0,-1) В ЕЕ ПОЗИЦИОННО-ЗНАКОВОМ ФОРМАТЕ f(+/-) | 2008 |
|
RU2380741C1 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА ДЛЯ УМНОЖИТЕЛЯ, В КОТОРОМ АРГУМЕНТЫ СЛАГАЕМЫХ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ ЯВЛЯЮТСЯ АРГУМЕНТАМИ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1, 0, -1) В ПОЗИЦИОННО-ЗНАКОВОМ ЕЕ ФОРМАТЕ f(+/-) (ВАРИАНТЫ) | 2008 |
|
RU2386162C2 |
| JP 62204332 A, 09.09.1987 | |||
| JP 63197227 A, 16.08.1988. | |||
Авторы
Даты
2011-09-20—Публикация
2010-05-25—Подача