Изобретение относится к вычислительной технике и может быть использовано в системах контроля и управления в совокупности с арифметическими устройствами, которые реализуют различные арифметические процедуры над минимизированными позиционно-знаковыми структурами аргументов ±[mj]f(+/-)min троичной системой счисления f(+1,0,-1) с последующим преобразованием ее в аргумент аналогового сигнала напряжения ±UЦАПf([mj]) посредством функциональной структуры цифроаналогового преобразования f1(ЦАП).
Известен способ преобразования позиционно-знаковой структуры аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код» в аналоговый сигнал напряжения ±UЦАПf([mj]) (см. У.Титце, К.Шенк. Полупроводниковая схемотехника. М., «Мир», 1982 г.,с.451, рис.24.14), в котором преобразование позиционно-знаковой структуры аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код» в аналоговый сигнал напряжения ±UЦАПf([mj]) выполняют посредством функциональной структуры цифроаналогового преобразователя f1(ЦАП) и двух функциональных структур операционных усилителей f1(ОУ) и f2(ОУ). И для того чтобы сформировать логико-динамический процесс и на аналитическом уровне записать математическую модель преобразователя «-/+»[mj]f(+/-)→±Ukf([±mj]), предварительно определимся с логико-динамическими процессами, которые реализуют функциональные структуры f1(ЦАП), f1(ОУ) и f2(ОУ). При этом следует отметить, что логико-динамический процесс функциональных структур f1(ЦАП), f1(ОУ) и f2(ОУ) записан с применением такого понятия, как «электрический ток» с символом «I», который не может быть измерен никакими существующими приборами (в дальнейшем будут представлены с применением аналитических информационных технологий), поскольку является субстанцией системы функциональных химических структур. Поэтому в аналитических выражениях функциональных структур под символом «I» «ионизированного тока электрической энергии» будем понимать информационную величину аргумента тока «±I» с соответствующим положительным знаком или условно отрицательным знаком. При этом следует особо отметить, что положительный аргумент напряжения +U формирует положительную величину аргумента тока «+I», поскольку он имеет увеличенную величину «электрической энергии» и ее «расходует». А условно отрицательный аргумент напряжения -U имеет условно отрицательный информационный аргумент тока «-I», поскольку он имеет уменьшенную величину «электрической энергии» и он ее «принимает». И если проанализировать входные аргументы преобразователя «-/+»[mj]f(+/-)→±UЦАПf([mj]), то в данной ситуации положительными аргументами является аргумент опорного напряжения +Uоп и позиционно-знаковая структура аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код», которые, например, для аргумента с информационным содержанием «-1» и «+7» запишем в виде графоаналитических выражений (01) и (02)
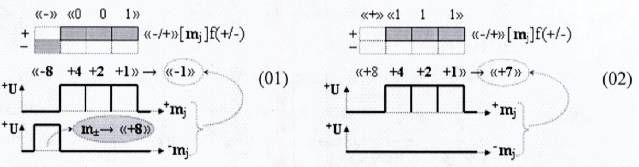
При этом особенностью структуры положительных аргументов в выражении (01) является аргумент знакового разряда m±±→«+8» как аргумент положительного напряжения +U, а как информационный аргумент в позиционно-знаковой структуре «-/+»[mj]f(+/-) «дополнительный код» является условно отрицательным m±→«-8», когда как и информационная структура аргументов +[mj] в выражении (01) и (02) является положительной. Поэтому положительную информационную величину аргумента знакового разряда m±→«+8» в структуре аргументов «-/+»[mj]f(+/-) «дополнительный код» на момент выполнения «арифметической» процедуры преобразований «-8»&«+4+2+1»→«-1» необходимо изменить на противоположную информационную величину. И эту процедуру реализуют посредством функциональной структуры операционного усилителя f1(ОУ) в соответствии с аналитическим выражением (03)
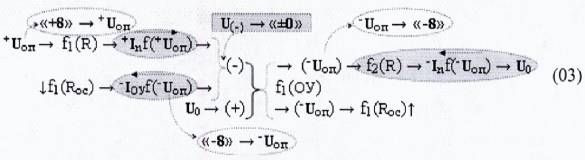
в котором функциональная система операционного усилителя f1(ОУ) выполняет функцию следящей системы и реализована она посредством функциональной структуры резистора обратной связи ↓f1(Roc)↑. Поскольку на инвертирующей функциональной связи (-) формируют аргумент ионизированного тока -Inf(-Uоп)→«-8», который равен аргументу ионизированного тока +Inf(+Uоп)→«-8» функциональной структуры резистора f1(R) с положительным входным аргументом напряжения +Uоп. В результате на функциональной выходной связи операционного усилителя f1(ОУ) формируется преобразованный условно отрицательный аргумент напряжения -Uоп→«-8», который позволяет реализовать «арифметическую» процедуру «-8»&«+4+2+1»→«-1» в выражении (01). Но для реализации «арифметической» процедуры «-8»&«+4+2+1»→«-1» необходимо в выражении (03) посредством функциональной структуры резистора f2(R) сформировать аргумент ионизированного тока -Inf(Uоп) условно отрицательного аргумента напряжения -Uоп с введением в систему инвертирующей функциональной связи (-) функциональной структурой операционного усилителя f2(ОУ) с резистором обратной связи f2(Roc). В результате следящую систему функциональной структуры цифроаналогового преобразователя f1(ЦАП) запишем в виде графоаналитического выражения (04)
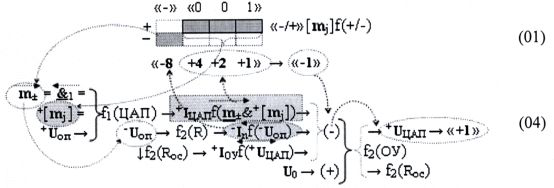
Из анализа графоаналитического выражения (04) следует, что логико-динамический процесс «арифметической» процедуры «-8»&«+4+2+1»→«-1» корректен только в системе инвертирующей функциональной связи (-) функциональной структурой операционного усилителя f2(ОУ), поскольку функциональная выходная структура операционного усилителя f2(ОУ) реализована в виде инвертирующего сумматора, в котором результирующий аргумент напряжения +UЦАП может быть записан в виде выражения (05)
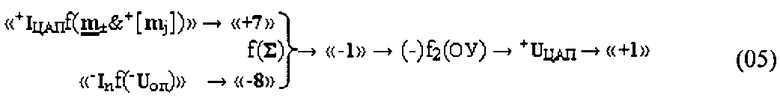
Аналогичный результат может быть получен и для структуры аргументов (02), если неактивный аргумент знакового разряда m± в положительной структуре аргументов +[mj] записать в соответствии с арифметической аксиомой «±0»→«+1/-1» троичной системы счисления f(+1,0,-1) в виде структуры аргументов (06)
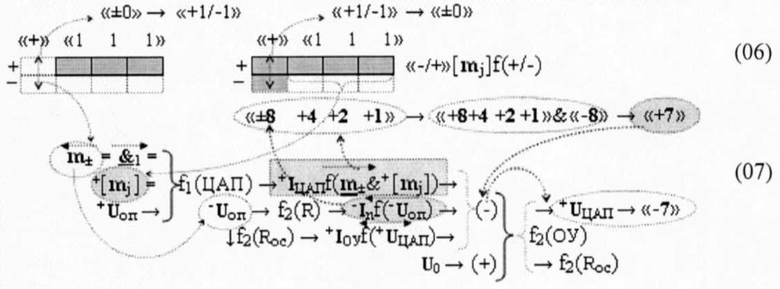
Действительно, если для структуры аргументов «-/+»[mj]f1(+/-)→«-»«01» и «-/+»[mj]f1(+/-)→«+»«11» сформировать векторную структуру аргументов слагаемых в «арифметическом пространстве» (в дальнейшем будут изложена логика его формирования), то можно записать графоаналитическое выражение (08)
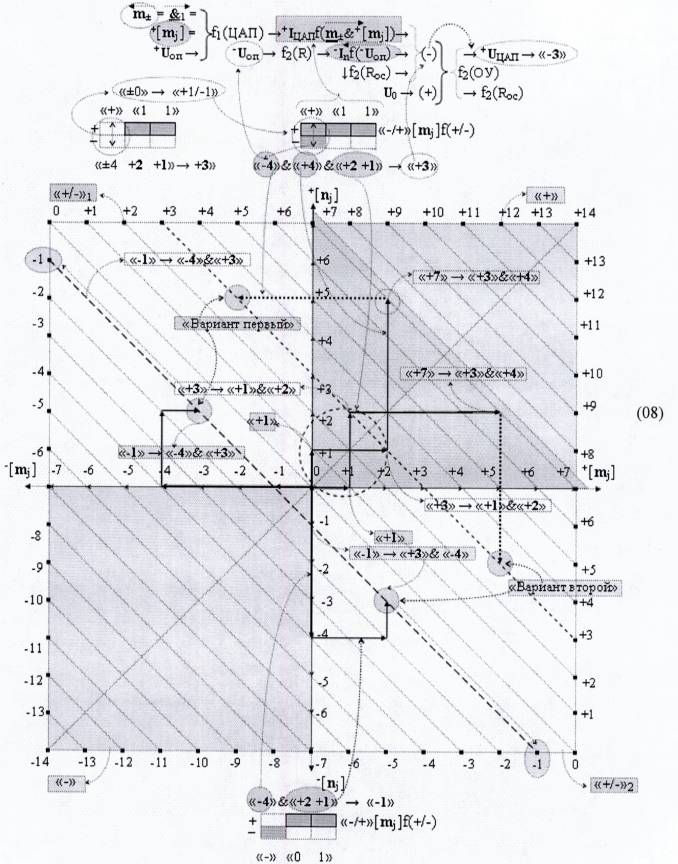
из которого следует, что корректный результирующий аргумент «+3» и «-1» векторной суммы сформирован на инвертирующей функциональной связи (-) функциональной структуры операционного усилителя f2(ОУ).
Аналогичный результат может быть получен и для многоразрядной структуры позиционно-знаковых аргументов «-/+»[mj]f(+/-)→«-»«111000011100100», который может быть записан в виде графоаналитического выражения (09),

где f1.1(ЦАП) и f1.2(ЦАП) - функциональная структура аргумента знакового разряда m± и функциональная структура положительной структуры аргументов +[mj] «дополнительный код» цифроаналогового преобразования f1(ЦАП); & 1 - логическая функция f1(&)-HE, реализующая процедуру изменения активности аргумента знакового разряда m± на функциональной связи f1.1(ЦАП); f1(ОУ) - функциональная структура операционного усилителя, реализующая процедуру изменения знака информационного содержания аргумента опорного напряжения +Uоп цифроаналогового преобразователя f1(ЦАП) на его инвертирующей функциональной связи (-); f(Σ) - функциональная структура сумматора операционного усилителя f2(ОУ), который реализует процедуру суммирования трех информационных аргументов функциональных структур f1.1(ЦАП), f1(ОУ) и f1.2(ЦАП) на инвертирующей функциональной связи (-).
Особенностью логико-динамического процесса преобразования информационных аргументов аналоговых сигналов «-/+»[mj]f(+/-)→«-»«111000011100100» в графоаналитическом выражении (08), если функциональную структуру операционного усилителя выполнить f2(ОУ) как сумматор, является то, что функциональная структура f1.1(ЦАП) цифроаналогового преобразователя f1(ЦАП) использована не по своему прямому назначению, а выполняет дискретный сдвиг положительного результирующего аргумента напряжения +UЦАПf([mj]) структуры f1.2(ЦАП) из положительной области в условно отрицательную область напряжения и наоборот, в зависимости от знакового аргумента m±. И положительная структура аргументов +UЦАПf([mj])→«+111000011100100» при активном знаковом разряде в структуры аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код» несет условно отрицательное информационное содержание. Поскольку если сформировать процедуру преобразования структуры аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код» в информационную структуру условно отрицательных аргументов в виде графоаналитического выражения (010)
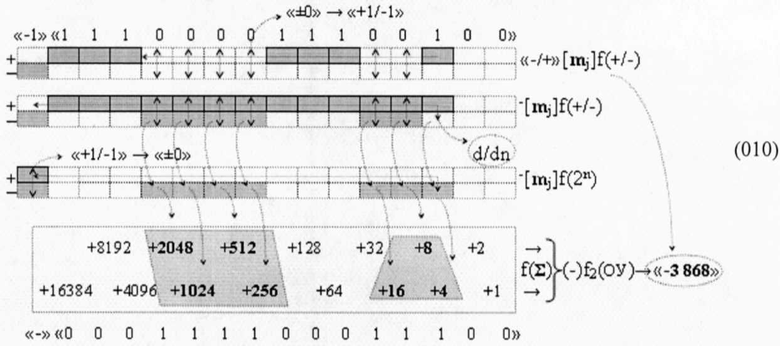
в котором выполнена активизация неактивных аргументов после первого активного положительного аргумента в соответствии с арифметической аксиомой «±0»→«+1/-1» с последующим выполнением процедуры логического дифференцировании d/dn, то будет сформирована структура -UЦАПf([mj])→«-»«000111100011100» с условно отрицательными аргументами информационным содержанием «-3868» посредством неинвертирующей функциональной структуры операционного усилителя (+)f2(ОУ). При этом позиционное положение структуры активных условно отрицательных аргументов в выражении (09) позиционно расположено на более низком информационном уровне, чем структура активных положительных аргументов в выражении (09), а из этого следует, что динамический диапазон структуры аргументов аналоговых сигналов «-/+»[mj]f(+/-) «дополнительный код» существенно ограничен.
Объединяя аналитические выражения (03) и (04), запишем математическую модель преобразователя «-/+»[mj]f(+/-)→± U ЦАПf([mj]) с измененным уровнем результирующего аргумента аналогового сигнала в виде аналитического выражения (011)
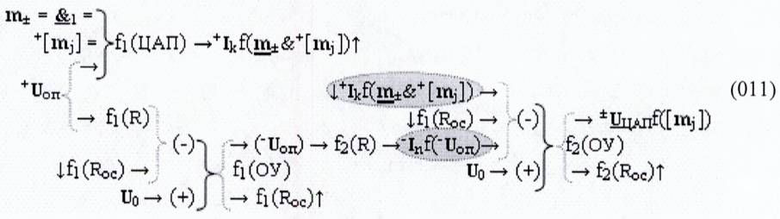
в котором на первой функциональной входной связи (-) операционного усилителя f2(ОУ) с функциональной структурой резистора f2(Roc) обратной связи формируют аргумент информационного тока +Ikf(m ±&+[mj]) из аналогового сигнала аргумента знака m± и положительной структуры аргументов аналоговых сигналов +[mj] посредством функциональной структуры цифроаналогового преобразователя f1(ЦАП). При этом на второй функциональной входной связи (-) операционного усилителя f2(ОУ) формируют аргумент ионизированного тока условно отрицательного аргумента опорного напряжения -Uоп, который формируют посредством функциональной структуры операционного усилителя f1(ОУ) с резистором обратной связи f1(Roc) и входным резистором f1(R) с положительным аргументом опорного напряжения Uоп (прототип).
Известный прототип имеет технологические и технические возможности, которые заключаются в том, что реализует процедуру преобразования позиционно-знаковой структуры аргументов «-/+»[mj]f(+/-) «дополнительный код» в аргумент аналогового сигнала напряжения ±UЦАПf([mj]).
Недостатком известного технологического решения является существенное ограничение динамического диапазона изменения аргумента результирующего «аналогового» сигнала ±UЦАПf([mj]), поскольку для этой цели не используется старший разряд функциональной структуры f1(ЦАП).
Технологическим и техническим результатом предложенного изобретения является увеличение динамического диапазона аргумента аналогового сигнала ±UЦАПf([mj]), при преобразовании минимизированной позиционно-знаковой структуры аргументов напряжений ±[mj]f(+/-)min.
Указанный технологический результат достигается следующим способом и посредством функциональной структуры.
Способ преобразования ±[mj]f(+/-)min→±Ukf([±mi]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+1,0,-1) в аргумент аналогового напряжения ±UЦАПf(±[mj]min), в котором выполняют посредством функциональной структуры цифроаналогового преобразователя f1(ЦАП) преобразование положительной позиционной минимизированной структуры аргументов аналоговых сигналов напряжения -[mj]f(+/-)min с условно отрицательным информационным содержанием в положительный аргумент ионизированного тока +IЦАПf(+[mj]), который подают на инвертирующую функциональную связь (-) функциональной структуры операционного усилителя f1(ОУ), выполняющей функцию сумматора f(Σ), и формируют аргумент аналогового напряжения ±UЦАПf(±[mj]min), при этом одновременно выполняют посредством функциональной структуры цифроаналогового преобразователя f2(ЦАП) преобразование положительной позиционной минимизированной структуры аргументов аналоговых сигналов напряжения +[mj]f(+/-)min с положительным информационным содержанием в положительный аргумент ионизированного тока +IЦАПf(-[mj]) и подают его на не инвертирующую функциональную связь (+) функциональной структуры операционного усилителя f1(ОУ), в котором формируют аргумент аналогового напряжения ±UЦАПf(±[mj]min) равный арифметической разности положительного аргумента ионизированного тока +IЦАПf(+[mj]) с положительным информационным содержанием и положительного аргумента ионизированного тока +IЦАПf(-[mj]) с условно отрицательным информационным содержанием в соответствии с графоаналитическим выражением логико-динамического процесса преобразования аргументов аналоговых сигналов вида
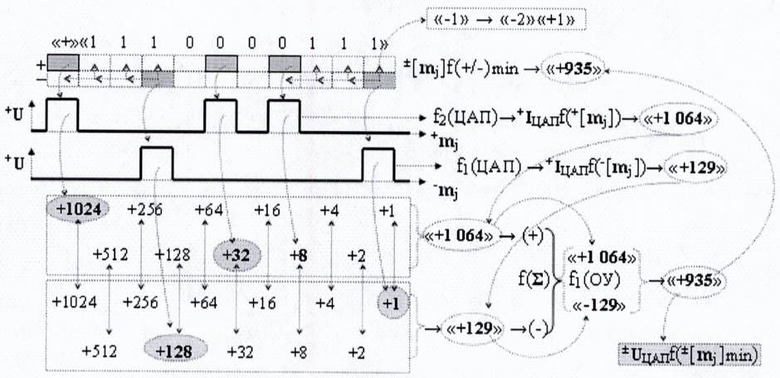
Функциональная структура преобразователя ±[mj]f(+/-)min→±Ukf([±mi]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+1,0,-1) в аргумент аналогового напряжения ±UЦАПf(±[mj]min), включающая функциональную структуру операционного усилителя f1(ОУ), выполняющей функцию сумматора f(Σ), в котором функциональная выходная связь, формирующая аналоговый аргумент напряжения ±UЦАПf(±[mj]min), является выходной функциональной связью преобразователя и функциональной входной связью функциональной резисторной структуры f1(Roc) обратной связи, функциональная выходная связь которой является инвертирующей функциональной связью (-) операционного усилителя f1(ОУ) и функциональной выходной связью функциональной структуры цифроаналогового преобразователя f1(ЦАП), в котором функциональная аналоговая связь (→) и функциональная логическая связь (=) являются функциональными связями структуры для приема входных аргументов опорного напряжения +Uоп и минимизированной структуры аргументов напряжения -[mj]f(+/-)min с условно отрицательным информационным содержанием соответственно, и включает также функциональную резисторную структуру f1(R), при этом введена функциональная дополнительная структура цифроаналогового преобразователя f2(ЦАП) для преобразования минимизированной структуры аргументов напряжения ±[mj]f(+/-)min с положительным информационным содержанием, при этом функциональные связи выполнены в соответствии с математической моделью вида
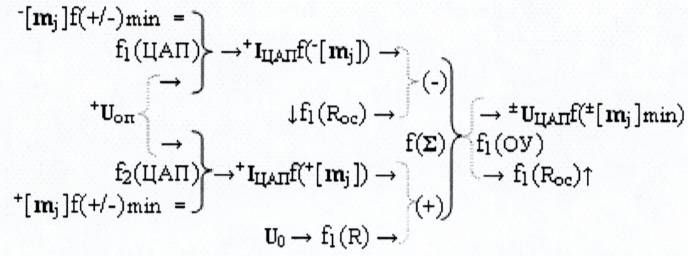
где 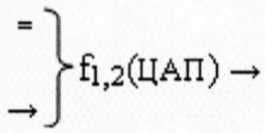 - функциональная структура цифроаналогового
- функциональная структура цифроаналогового
преобразователя f1(ЦАП) и f2(ЦАП);
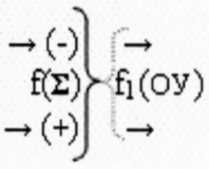
- функциональная структура операционного усилителя
f1(ОУ).
Сущность логико-динамического процесса преобразования ±[mj]f(+/-)min→±Ukf([±mi]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+l,0,-l) в аргумент аналогового напряжения ±UЦАПf(±[mj]min) будет пояснена в процессе его синтеза.
Синтез математической модели логико-динамического процесса цифроаналогового преобразования структуры аналоговых минимизированных позиционно-знаковых аргументов ±[mj]f(+/-)min в дискретный аналоговый сигнал ±UЦАПf(±[mj]min). Если проанализировать на формализованном уровне позиционную структуру положительных активных аргументов слагаемых «+»[mj]f(2n) в виде выражения (1)
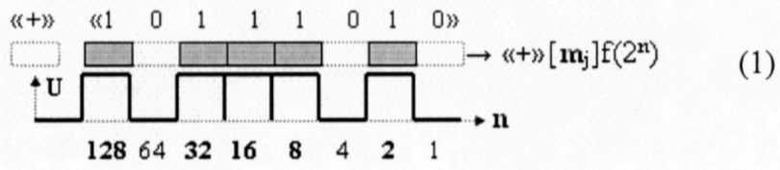
и позиционную структуру условно отрицательных аргументов слагаемых «-»[mj]f(2n) в виде формализованного выражения (2)
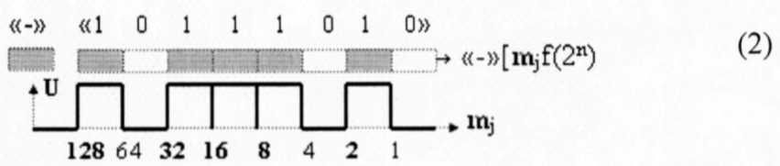
то по уровню аналогового сигнала, за исключением аргумента знака «+» и «-», они эквивалентны. Поэтому выполнение каких-либо арифметических действий над аргументами слагаемых «+»[ni]f(2n) и «-»[mj]f(2n) на формализованном уровне вызывает определенную проблему, которая связана с необходимостью учета знакового разряда «+» и «-», и он в данной ситуации представляет собой какой-то символ или «метку» о принадлежности структуры одной или другой категории информационного содержания. И только позиционное положение может исключить неоднозначность, поэтому положительная структура аргументов слагаемого (1) может быть записана в виде выражения (3)

а условно отрицательная структура аргументов слагаемого (2) может быть записана в виде выражения (4)
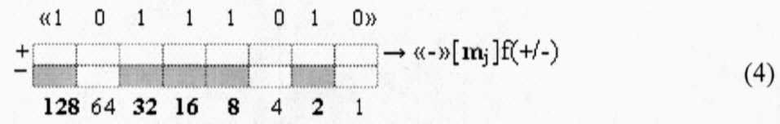
и только в такой интерпретации не только исключается необходимость введения в выражениях (1) и (2) дополнительных символов «+» и «-», но и возникает возможность выполнения арифметических действий над аргументами без перевода структуры аргументов «-»[mj]f(+/-) в так называемый «Дополнительный код». При этом следует особо отметить, что если структуру аргументов (4) перевести в «Дополнительный код», а эту процедуру арифметически корректно можно реализовать только с применением арифметических аксиом троичной системы счисления f(+1,0,-1) (5)

к которым относится и процедура логического дифференцирования ±d/dn как условно отрицательной последовательности активных аргументов, так и положительной последовательности аргументов, которую запишем в виде графоаналитического выражения (6)
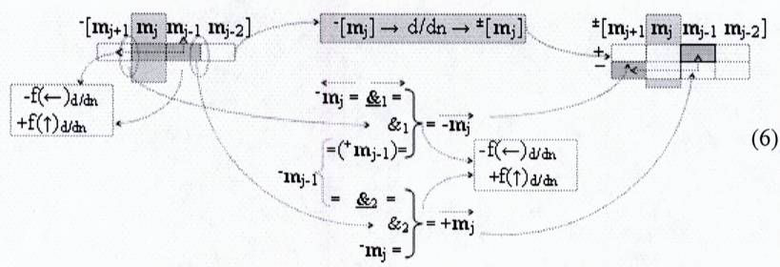
И она, по существу, представляет собой процедуру предварительного введения сквозного переноса, но выполняется на локальном уровне, в котором логическая функция f1(&)-И формирует положительный аргумент +mj локального переноса +f(+←+)d/dn активного аргумента из предыдущего старшего разряда непрерывной последовательности в последующий неактивный старший разряд. А логическая функция f2(&)-И формирует условно отрицательный аргумент -mj локального переноса -f(↓)d/dn, и этот перенос выполняется в условно «i» разряде, который соответствует младшему аргументу непрерывной последовательности и при его переносе положительный аргумент преобразуется в условно отрицательный аргумент. При этом следует отметить, что применение арифметических аксиом троичной системы счисления f(+1,0,-1) (5) позволяет на научно обоснованном уровне выполнять любые процедуры преобразования аргументов, например, процедуру формирования «Дополнительного кода» можно записать в виде графоаналитического выражения (7)

в котором неактивные аргументы после первого активного условно отрицательного аргумента в исходной структуре «-»[mj]f(+/-) преобразуют в соответствии с арифметической аксиомой «±0»→«+1/-1» и выполняют процедуру логического дифференцирования -d/dn условно отрицательных аргументов. В результате формируется позиционно-знаковая структура «-/+»[mj]f(+/-) с тем же информационным содержанием «-»«186», но с максимальным числом положительных аргументов в младших разрядах, число которых может быть минимизировано, и, в данной ситуации, с применением процедуры логического дифференцирования -d/dn условно отрицательных аргументов в структуре, которая выполняется в соответствии с графоаналитическим выражением (8)
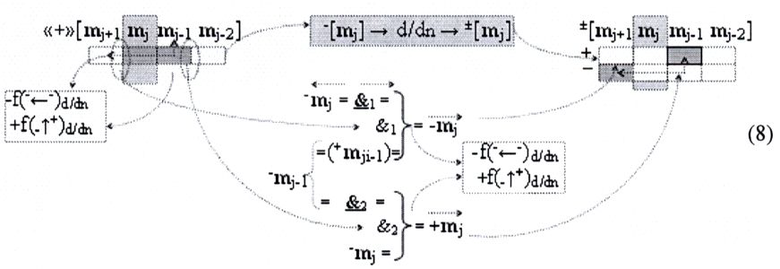
И она, по существу, представляет собой процедуру предварительного введения сквозного переноса, но выполняется на локальном уровне, в которой логическая функция f1(&)-И формирует условно отрицательный аргумент -mj локального переноса -f(-←-)d/dn активного аргумента из предыдущего старшего разряда непрерывной последовательности в последующий неактивный старший разряд. А логическая функция f2(&)-И формирует положительный аргумент +mj локального переноса +f(-↑+)d/dn, и этот перенос выполняется в условно «i» разряде, который соответствует младшему аргументу непрерывной последовательности, и при его переносе положительный аргумент преобразуется в условно отрицательный аргумент. И если применить процедуру логического дифференцирования d/dn, но только к последовательности как минимум двух активных аргументов в результирующей структуре «-/+»[mi]f(+/-) выражения (7), то может быть записано графоаналитическое выражение (9),
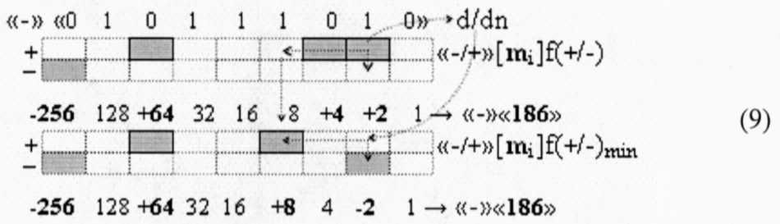
в котором активные как положительные аргументы, так и условно отрицательные аргументы чередуются, как минимум, через один не активный аргумент. При этом следует отметить, что «Дополнительный код» может быть сформирован не только для структуры условно отрицательных аргументов, но и для структуры положительных аргументов. Например, если выполнить активизацию логических нулей в соответствии с арифметической аксиомой «±0»→«+1/-1» в выражении (3) и записать логико-динамический процесс преобразования аргументов в виде графоаналитического выражения (10)
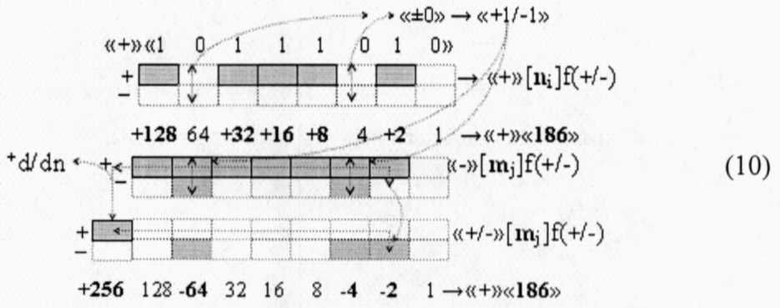
будет сформирована позиционно-знаковая структура «+/-»[mj]f(+/-). И эта структура аргументов «+/-»[mj]f(+/-) может быть минимизирована по числу активных аргументов, а для этого в выражении (11)
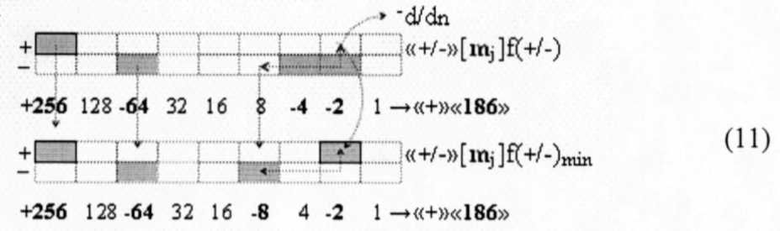
выполним процедуру логического дифференцирования -d/dn условно отрицательных аргументов, но только последовательность активных аргументов.
Из анализа полученных результатов следует, что любая структура позиционно-знаковых аргументов, в том числе и не лучший ее вариант так называемый «Дополнительный код» может быть минимизирован по числу активных аргументов в структуре, что позволит сформировать функциональные структуры сумматоров f(Σ)min и умножителей fΣ(Σ)min с максимально уменьшенным технологическим циклом ΔtΣ формирования результирующей минимизированной суммы позиционно-знаковых аргументов ±[Si]f(+/-)min. Например, если для позиционно-знаковой структуры аргументов «Дополнительный код» (12)
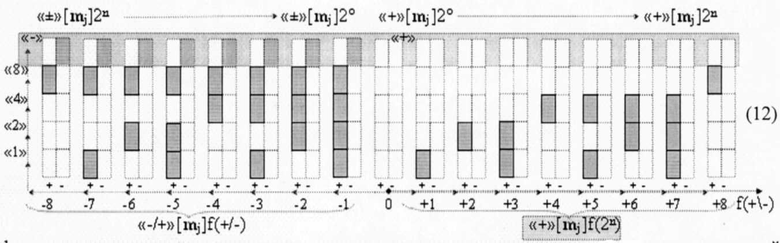
сформировать процедуру параллельно-последовательного умножения fΣ(Σ) для конкретной позиционной структуры аргументов сомножителей +[mj]f(2n) и +[nj]f(2n)→«+»«11111111»f(2n) в виде графоаналитического выражения (13)
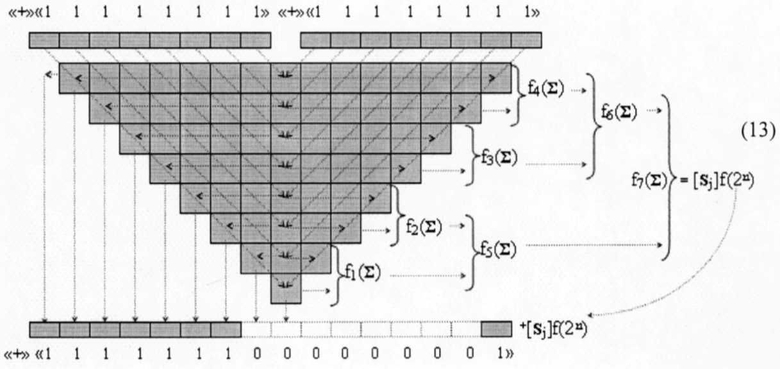
и для позиционно-знаковой структуры аргументов (14)
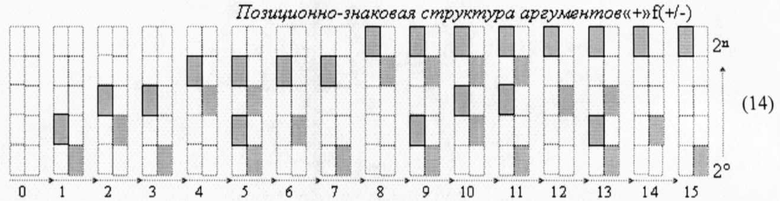
сформировать процедуру параллельно-последовательного умножения fΣ(Σ) для конкретной позиционной структуры аргументов сомножителей ±[mj]f(+/-) и ±[nj]f(+/-)→«+»«l01010l0»f(2n) в виде выражения (15)
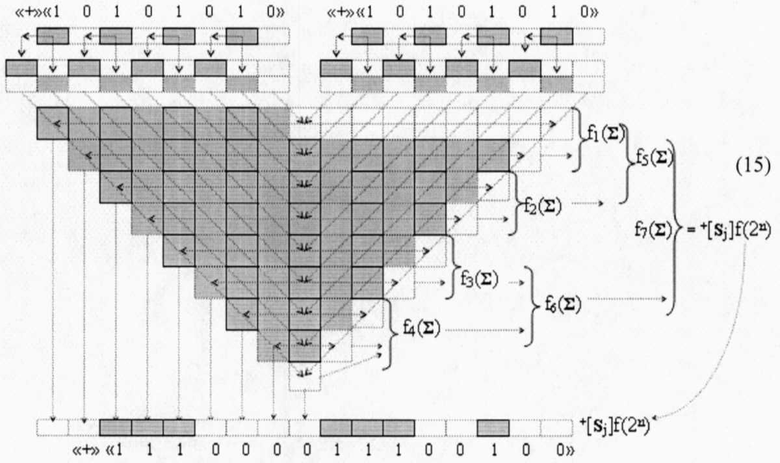
и для минимизированной позиционно-знаковой структуры аргументов (16)
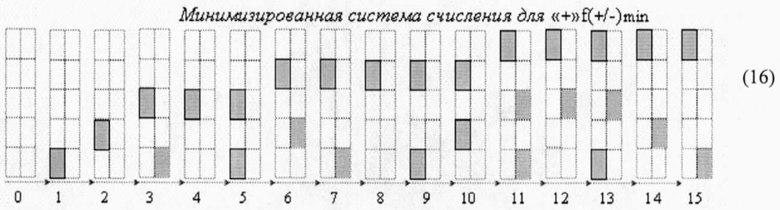
сформировать процедуру параллельно-последовательного умножения fΣ(Σ) в виде графоаналитического выражения (17),
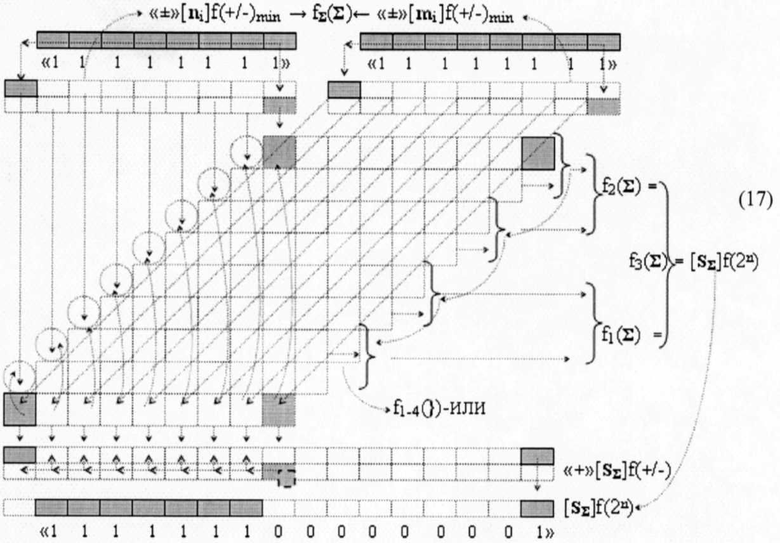
где f(CD) - функциональная структура шифратора частичных произведений,
и сравнить с позиционной структурой умножителя (13), то позиционно-знаковые структуры аргументов сомножителей ±[mj]f(+/-)min и ±[nj]f(+/-)min позволяют существенно повысить быстродействие логико-динамического процесса преобразования аргументов в умножителе. А для этого необходимо минимизировать позиционно-знаковые структуры аргументов сомножителей ±[mj]f(+/-) и ±[nj]f(+/-), которые в своей структуре включают последовательные положительные и условно отрицательные аргументы. И если применить к таким структурам, например, к позиционно-знаковым сомножителям ±[mj]f(+/-) и ±[nj]f(+/-)→«10101010»f(2n) обратную арифметическую аксиому «+2»«-1»→«+1» и записать такой процесс в виде логико-динамического выражения (18)
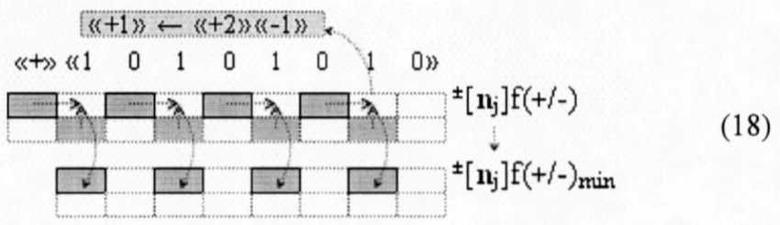
то процедуру формирования пирамидально расположенных частичных произведений (18) можно сформировать в виде графоаналитического выражения (19)
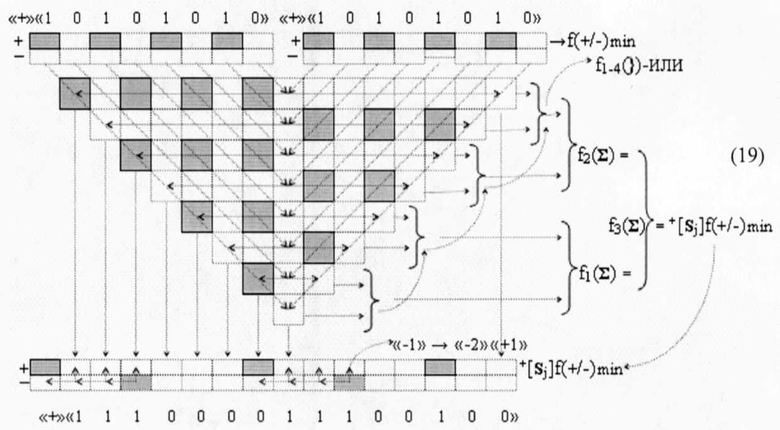
в котором особенностью является первый уровень суммирования частичных произведений. И он может быть выполнен путем объединения каждых двух их уровней посредством логических функций f1-4(})-ИЛИ, что приведет, с одной стороны, к замене сумматоров в первом уровне суммирования частичных произведений на линейные логические функции f1-4(})-ИЛИ. С другой стороны, приводит к существенному уменьшению технологического цикла ΔtΣ логико-динамического процесса умножения минимизированных структур аргументов сомножителей ±[mj]f(+/-)min и ±[nj]f(+/-)min. При этом следует отметить, что так называемый ((Дополнительный код» «-/+»[mi]f(+/-) или один из возможных вариантов позиционно-знаковой структуры аргументов ±[mj]f(+/-), с одной стороны, не позволяет минимизировать функциональную структуру умножителя fΣ(Σ) и существенно уменьшить технологический цикл ΔtΣ его по сравнению с минимизированными структурами аргументов сомножителей ±[mj]f(+/-)min и ±[nj]f(+/-)min. С другой стороны, при выполнении процедуры умножения аргументов сомножителей в «Дополнительных кодах» с разными знаками «-/+»[mj]f(+/-) и «+/-»[mi]f(+/-) помимо функциональной структуры самого умножителя fΣ(Σ) необходима функциональная дополнительная структура анализа и активизации знака «+» или «-» результирующей структуры аргументов, когда как при умножении минимизированных структур аргументов сомножителей ±[mj]f(+/-)min и ±[nj]f(+/-)min такая дополнительная процедура исключена. Например, если сформировать процедуру умножения минимизированных структур аргументов сомножителей ±[mj]f(+/-)min→«-»«10101010»f(2n) и ±[nj]f(+/-)min→«+»«10101010»f(2n) с разными знаками в виде графоаналитического выражения (20)
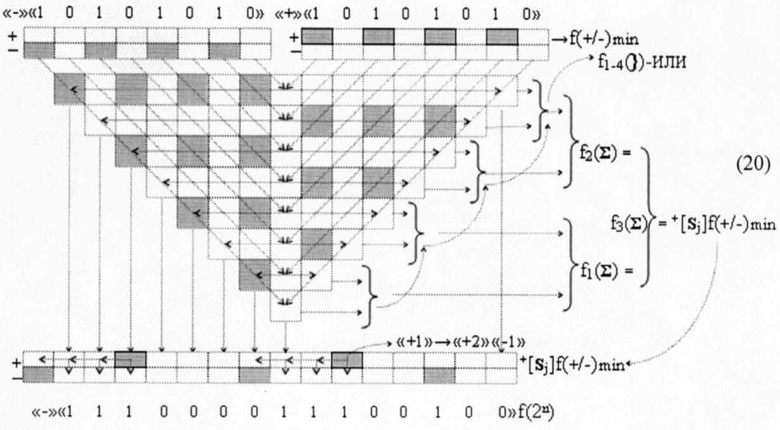
то минимизированная структура результирующей суммы +[Sj]f(+/-)min→«-»«111000011100100»f(2n) является позиционно знаковой, поскольку ее структура несет информацию о знаке. В этой связи возникает вопрос, как существенно отличаются процедуры преобразования положительных и условно отрицательных промежуточных сумм частичных произведений в графоаналитическом выражении (19), имеющие положительную структуру аргументов частичных произведений и в графоаналитическом выражении (20), имеющие условно отрицательную структуру аргументов частичных произведений. А для этого имеет смысл сформировать два логико-динамических процесса преобразования аргументов в функциональных структурах сумматоров f1(Σ)-f3(Σ), в которых процедура минимизации выполняется только с учетом арифметических аксиом троичной системы счисления f(+1,0,-1) (5). При этом следует учесть, что и процедура логического дифференцирования +d/dn положительных аргументов и условно отрицательных аргументов -d/dn является многократным применением арифметических аксиом (5). Действительно, если сформировать процедуру преобразования частичных произведений в сумматоре f2(Σ) графоаналитического выражения (19), записав ее в виде логико-динамического процесса (21)
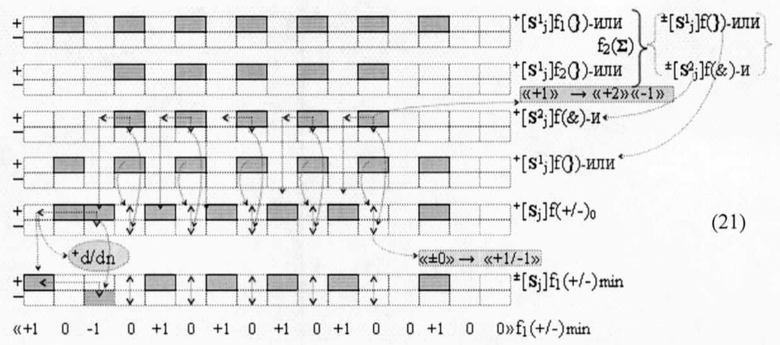
то после преобразования аргументов второй промежуточной суммы +[S2 j]f(&)- и в соответствии с арифметической аксиомой «+1»→«+2»«-1» в структуре промежуточной суммЫ +[Sj]f(+/-)0 сформирована последовательность активных положительных аргументов, а и после ее логического дифференцирования +d/dn результирующая позиционно-знаковая сумма +[Sj]f(+/-)min имеет минимизированную структуру активных аргументов.
Аналогичные преобразования и в сумматоре f1(Σ), которые запишем в виде логико-динамического выражения (22)
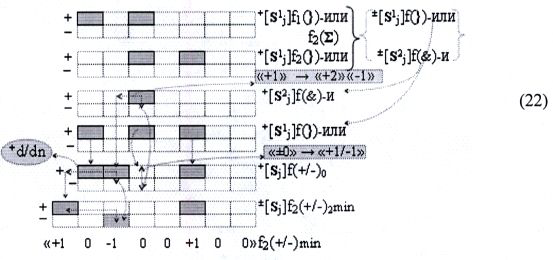
в котором также после логического дифференцирования +d/dn промежуточной суммы +[Sj]f(+/-)0 результирующая позиционно-знаковая сумма ±[Sj]f2(+/-)min имеет минимизированную структуру активных аргументов. И если после объединения в выходном сумматоре f3(Σ) предварительных сумм ±[Sj]f(+/-)1 и ±[Sj]f1(+/-)2 (23)

и выполнения преобразований аргументов в соответствии с обратными арифметическими аксиомами «+1/-1»→«±0» и «-2»«+1»→«-1» и логического дифференцирования -d1/dn непрерывной последовательности положительных аргументов будет сформирована результирующая позиционно-знаковая сумма ±[Sj]f1(+/-)min, которая имеет минимизированную структуру активных аргументов. При этом следует особо отметить, что сформированная результирующая минимизированная позиционно-знаковая сумма ±[Sj]f1(+/-)min может быть использована как корректная структура слагаемого или сомножителя. Но если возникает необходимость преобразования условно отрицательных аргументов +[Sj]f(+/-)min в структуру положительных аргументов +[Sj]f(2n), то эта процедура выполняется с применением арифметической аксиомы «-1»→«-2»«+1» в выражении (24)
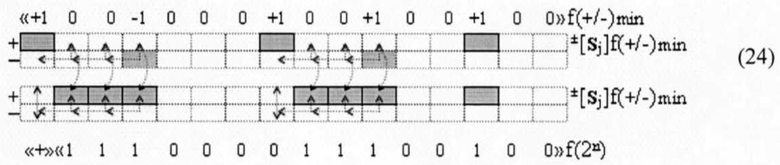
но она эквивалентна, по существу, сквозному переносу f(←←), который увеличивает технологический цикл ΔtΣ формирования результирующей суммы.
Далее, если сформировать процедуру преобразования частичных произведений в сумматоре f2(Σ) графоаналитического выражения (20), записав ее в виде логико-динамического процесса (25)
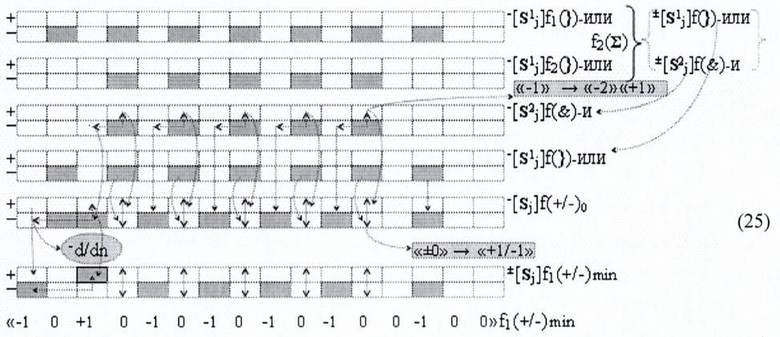
то после преобразования аргументов второй промежуточной суммы -[S2 j]f(&)- и в соответствии с арифметической аксиомой «-1»→«-2»«+1» в структуре промежуточной сумме -[Sj]f(+/-)0 сформирована последовательность активных условно отрицательных аргументов, а и после ее логического дифференцирования -d/dn результирующая позиционно-знаковая сумма ±[Sj]f1(+/-)min имеет минимизированную структуру активных аргументов.
Аналогичные преобразования и в сумматоре f1(Σ), которые запишем в виде логико-динамического выражения (26)
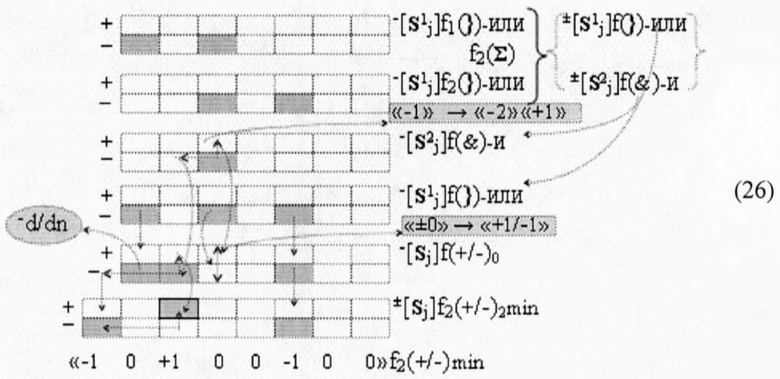
в котором также после логического дифференцирования -d/dn условно отрицательных аргументов в структуре -[Sj]f(+/-)0 результирующая позиционно-знаковая сумма ±[Sj]f2(+/-)min имеет также минимизированную структуру активных аргументов. И если после объединения в выходном сумматоре f3(Σ) результирующих сумм ±[Sj]f(+/-)1 и ±[Sj]f1(+/-)2 (27)
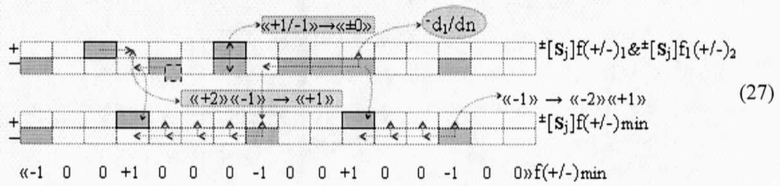
и также выполнения преобразований аргументов в соответствии с обратными арифметическими аксиомами «+1/-1»→«±0» и «+2»«-1»→«+1» и логического дифференцирования -d1/dn непрерывной последовательности условно отрицательных аргументов будет сформирована результирующая позиционно-знаковая сумма ±[Sj]f1(+/-)min, которая имеет также минимизированную структуру активных аргументов. При этом следует особо отметить, что сформированная результирующая минимизированная позиционно-знаковая сумма ±[Sj]f1(+/-)min может быть использована, как корректная структура слагаемого или сомножителя. Но если возникает необходимость преобразования условно отрицательных аргументов +[Sj]f(+/-)min в структуру положительных аргументов +[Sj]f(2n), то эта процедура выполняется с применением той же арифметической аксиомы «-1»→«-2»«+1» в выражении (28)
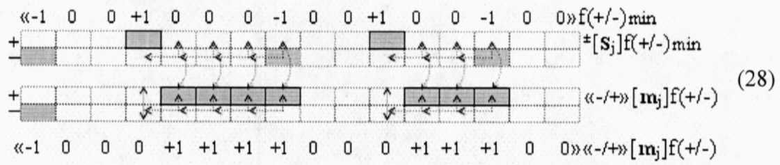
но она, по существу, также эквивалентна сквозному переносу f(←←), который увеличивает технологический цикл ΔtΣ формирования результирующей суммы «-/+»[mj]f(+/-).
Из сопоставительного анализа в выражении (28) минимизированной структуры аргументов ±[Sj]f(+/-)min и неминимизированной структуры «-/+»[mj]f(+/-) «Дополнительный код» следует, что минимизированная структура аргументов ±[Sj]f(+/-)min имеет существенное качество, которое заключается в том, что, с одной стороны, непрерывная последовательность положительных аргументов «111…1» в ней представлена с предварительно введенными сквозными переносами в виде условно отрицательных аргументов в структуре «+100…-1». С другой стороны, активные аргументы в структуре ±[Sj]f(+/-)min чередуются, как минимум, через один неактивный разряд, что полностью исключает процедуру сквозного переноса f(←←) в функциональных структурах сумматоров f(Σ)min и умножителей fΣ(Σ)min. При этом следует особо отметить, что при непрерывном выполнении каких-то арифметических действий (вычислений) нет необходимости в преобразовании минимизированной структуры промежуточных аргументов ±[Sj]f(+/-)min в структуру аргументов «-/+»[mj]f(+/-) «Дополнительный код». Поскольку технологический цикл +ΔtΣ функциональных структур позиционно-знаковых сумматоров f(Σ)min в четыре раза меньше технологического цикла +ΔtΣ позиционных сумматоров f(Σ)+, в которых только структура условно отрицательных аргументов слагаемых в выражении (12) имеет так называемый «Дополнительный код». Поэтому имеет смысл провести дополнительный анализ целесообразности дальнейшего применения в функциональных структурах сумматоров и умножителей неминимизированной структуры «-/+»[mj]f(+/-) «Дополнительный код», а для этого сформируем графоаналитическое выражение (29)
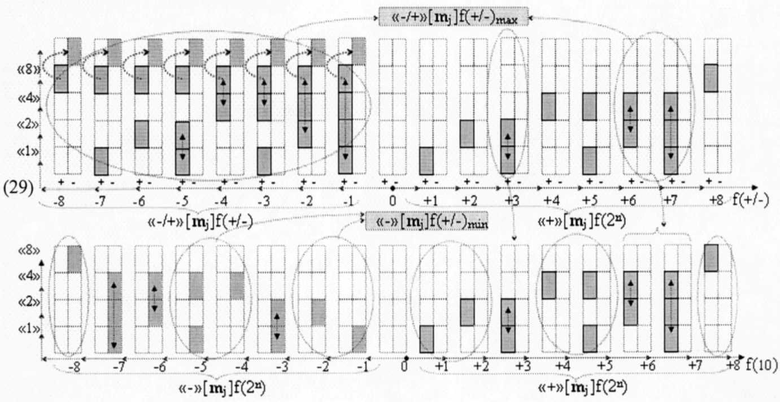
Из анализа графоаналитического выражения (29) следует, что если в позиционной структуре условно отрицательных аргументов «-»[mj]f(2n) есть структуры «-»[mj]f(+/-)min, в которых активные аргументы чередуются с неактивными аргументами и при суммировании таких аргументов не формируется сквозной перенос f(←←), а в позиционно-знаковой структуре «-/+»[mj]f(+/-) «Дополнительный код» условно отрицательных аргументов они полностью отсутствуют. При этом следует отметить, что и в структуре положительных аргументов «-/+»[mj]f(+/-) также есть отдельные структуры, и они могут в сумматоре f(Σ)+ и умножителе fΣ(Σ) сформировать сквозной перенос f(←←), поэтому необходимо сформировать иную систему счисления, которая минимизировала сквозной перенос f(←←) до локального переноса f(←), которые ограничены очередным разрядом. И такая возможность есть, если, например, к неминимизированным структурам в графоаналитическом выражении (29) применить арифметические аксиомы троичной системы счисления f(+1,0,-1) (5), к которым относятся и обратные арифметические аксиомы (30)
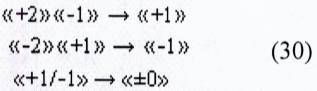
Но прежде чем выполнить минимизацию структуры «-/+»[mj]f(+/-) «Дополнительный код» (29), следует отметить, что условно отрицательный ее блок, как позиционно-знаковая категория записан с некорректно расположенным знаковым аргументом, которые должны быть скорректированы с применением обратной арифметической аксиомой «-2»«+1»→«-1» и в соответствии с графоаналитическим выражением (31)
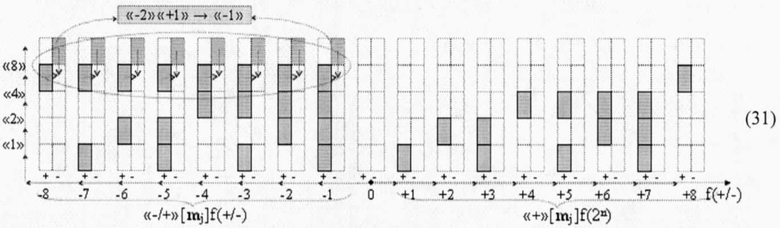
и записаны как информационные аргументы в неминимизированных позиционно-знаковых структурах условно отрицательного блока «-/+»[mj]f(+/-) в выражении (32)
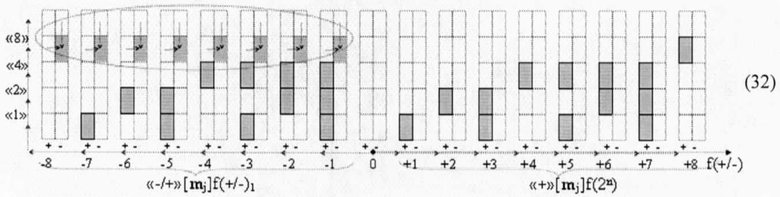
В результате выполненных преобразований в условно отрицательном блоке «-/+»[mj]f(+/-) условно отрицательный информационный знаковый аргумент включен в информационную структуру аргументов слагаемых и сомножителей, которые только частично минимизированы. Поскольку если процедуру минимизации скорректированных структур «-/+»[mj]f(+/-)1 «Дополнительный код» (32) записать в виде графоаналитического выражения (33)
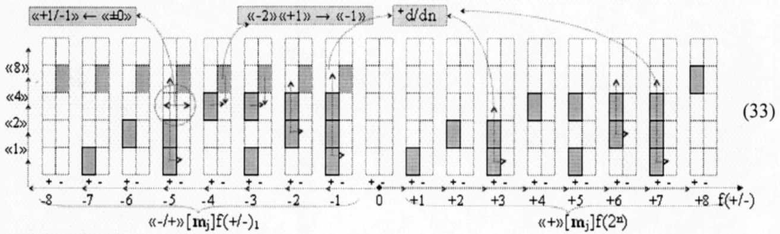
то может быть записано минимизированное ее выражение (34)
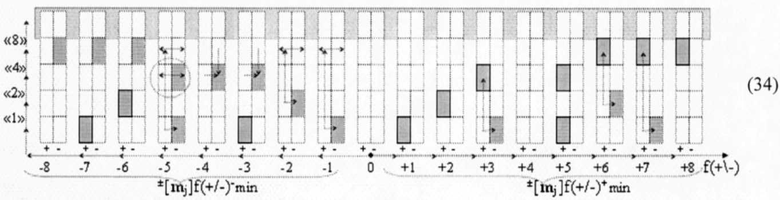
в котором все активные положительные и условно отрицательные аргументы в позиционно-знаковых выражениях ±[mj]f(+/-)+ min и ±[mj]f(+/-)- min позиционно расположены, как минимум, через неактивный разряд. При этом следует отметить, что, с одной стороны, логика преобразования положительных аргументов как в позиционно-знаковом блоке «-/+»[mj]f(+/-)1, так и в позиционном блоке «+»[mj]f(2n), по существу, сводится к процедуре логического дифференцирования +d/dn положительной последовательности аргументов и применения обратной арифметической аксиомы «-2»«+1»→«-1». В результате в минимизированном выражении (34) как в условно отрицательный ее блок ±[mj]f(+/-)- min, так и в положительный блок ±[mj]f+(+/-)+min активные аргументы в своей последовательности чередуются, как минимум, через один неактивный разряд, то и приводит при их суммировании к формированию только локальных переносов f(←). При этом следует отметить, что сформировать минимизированные структуры ±[mj]f(+/-)+ min и ±[mj]f(+/-)- min выражения (34) можно и непосредственно из предварительно не преобразованных структур «-/+»[mj]f(+/-1)&«+»[mj]f(2n) «Дополнительный код» с применением тех же процедур.
Действительно, если процедуру минимизации структур «-/+»[mj]f(+/-) «Дополнительный код» записать в виде графоаналитического выражения (35)
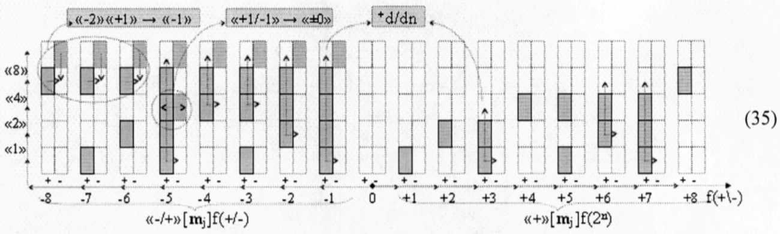
то может быть записано минимизированное ее выражение (36)

в котором все активные положительные и условно отрицательные аргументы в позиционно-знаковых выражениях ±[mj]f(+/-)+ min и ±[mj]f(+/-)- min позиционно расположены, как минимум, через неактивный разряд. При этом следует отметить, что при формировании минимизированного блока условно отрицательных аргументов ±[mj]f(+/-)- min в структуре аргумента с информационным содержанием «-5» как в выражении (33), так и в выражении (35) выполнена процедура активизации неактивных аргументов логического нуля «±0»→«+1/-1», и только после этой активизации была реализована процедура логического дифференцирования +d/dn положительной последовательности аргументов.
Из сопоставительного анализа «Системы счисления «-/+»[mj]f(+/-) «Дополнительный код» (35) и «Минимизированной системы счисления ±[mj]f(+/-)min» (36) следует, что в минимизированных структурах аргументов ±[mj]f(+/-)- min и [mj]f(+/-)+ min отсутствует дополнительный знаковый разряд, и это обстоятельство позволяет существенно увеличить динамический диапазон в технологических процессах систем управления, в которых «цифровую» форму информации в виде позиционно-знаковых аргументов необходимо преобразовать в аналоговую форму информации в виде непрерывного аналогового сигнала напряжения ±U(+[mj]). И это увеличение динамического диапазона аналогового сигнала напряжения ±U(+[mj]) может быть реализовано с использованием существующих функциональных структур f1(ЦАП) цифроаналогового преобразования позиционных аргументов. При этом расширение динамического диапазона изменения аналоговых сигналов включает как его увеличение положительного уровня аналогового напряжения +UЦАП(+[mj]), так и увеличение отрицательного уровня аналогового напряжения -UЦАП(+[mj]). Поскольку если записать функциональную структуру цифроаналогового преобразователя f1(ЦАП) с входными информационными аргументами m±&+[mj] и преобразованным аргументом ±UЦАП(t), в виде аналитического выражения (37)
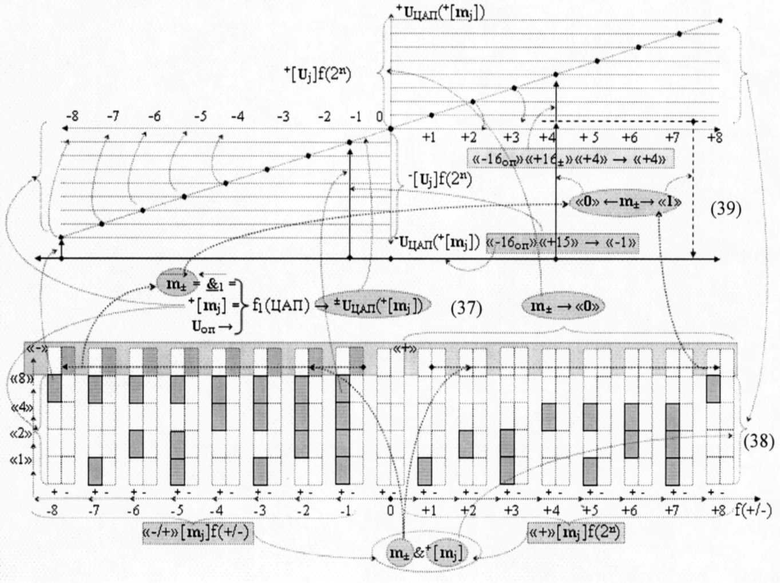
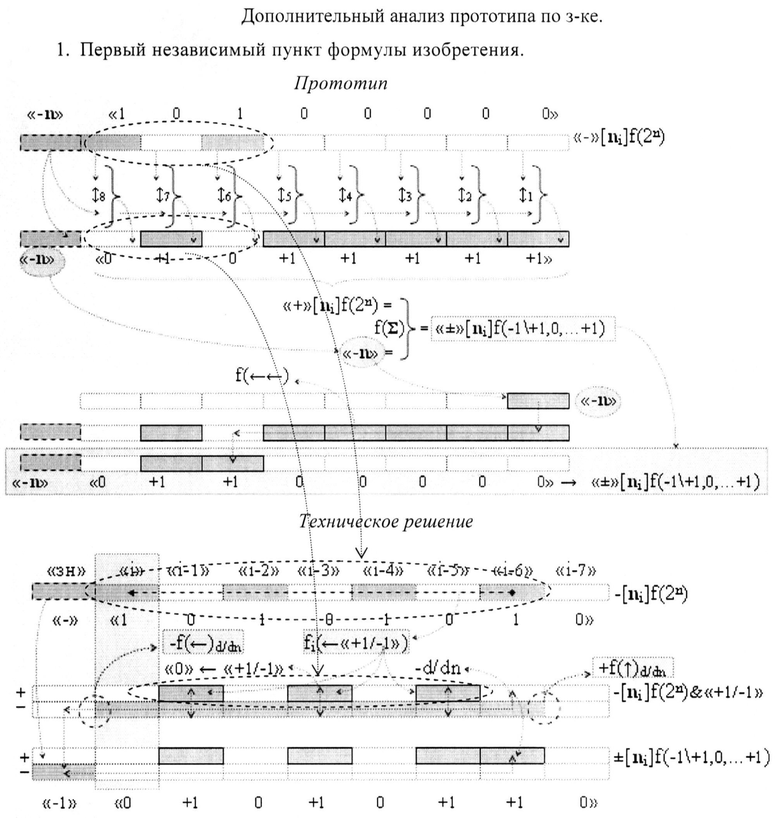
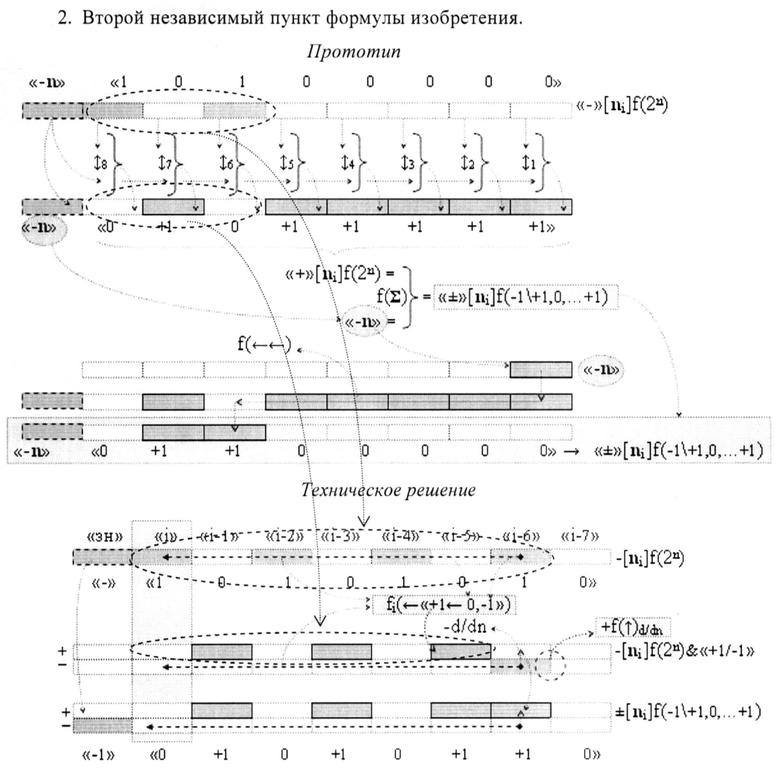
то аргумент старшего разряда m± структуры аргументов (38) «Системы счисления «-/+»[mj]f(+/-) «Дополнительный код» выполняет функцию дискретного сдвига «0»←m±→«1» в графоаналитическом выражении (39) результирующего аналогового аргумента ±UЦАП(t) функциональной структуры цифроаналогового преобразователя f1(ЦАП) (37) либо в интервале аргументов «+»[mj]f(2n) положительных уровней аналогового сигнала +UЦАП(t) при m±→«0», либо в интервале условно отрицательных аргументов «-/+»[mj]f(+/-) отрицательных уровней аналогового сигнала -UЦАП(+[mj]) при m±→«1». И эту процедуру в формализованном арифметическом пространстве, например, для аргумента с информационным содержанием «-1» (40) и «+7» (41)
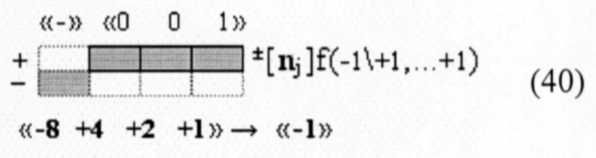
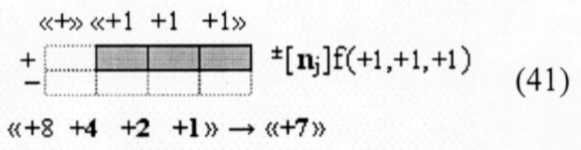
можно записать в виде графоаналитического выражения (42)
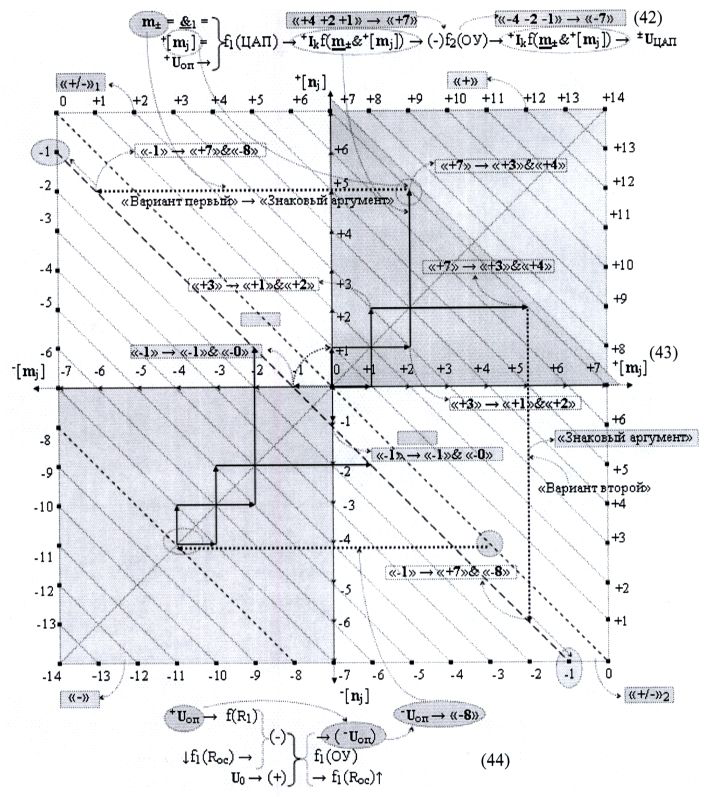
При этом следует отметить, что формализованное арифметическое пространство представляет собой не абстрактную, а вполне конкретную последовательность информационных аргументов и основой ее, как и в системе координат Рене Декарта (1596-1650), являются два ортогональных множества ±[nj] и ±[mj], которые формируют четыре функциональные области комбинационных аргументов. И это формализованное арифметическое пространство запишем в виде графоаналитического выражения (45)
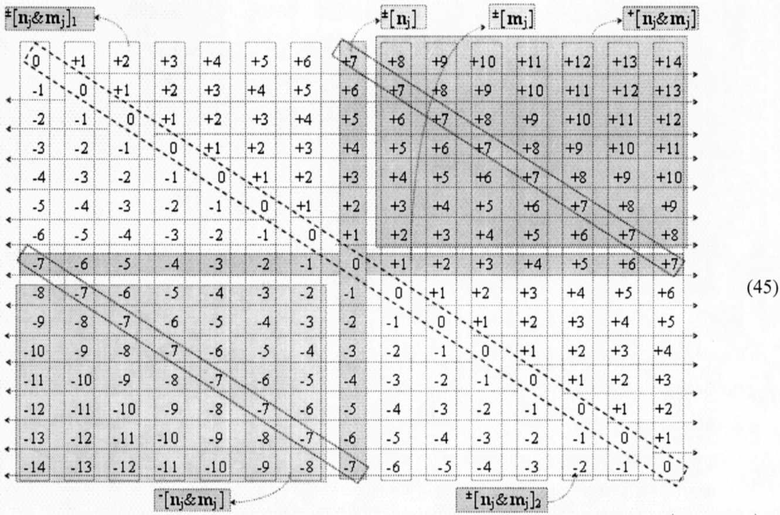
в котором информационные аргументы двух ортогональных множеств ±[nj] и ±[mj] разграничивают все арифметическое пространство на область положительных комбинационных аргументов +[nj&mj] и область условно отрицательных комбинационных аргументов -[nj&mj]. При этом следует отметить, что комбинационные аргументы +[nj&mj] и -[nj&mj] представляют собой информационную результирующую величину векторной суммы поочередно принадлежащих двум ортогональным множествам ±[nj] и ±[mj], и их эквивалентные аргументы позиционно расположены таким образом, что совпадают с эквивалентными информационными аргументами, в том числе и двух ортогональных множеств, и формируют общие эквипотенциальные уровни. Аналогичная ситуация и в двух других позиционно-знаковых областях ±[nj&mj]1 и ±[nj&mj]2, но в них есть общий для всего арифметического пространства эквипотенциальный уровень «0», который разграничивает все арифметическое пространство (45) на положительную область «+» и условно отрицательную область «-», что можно записать в виде формализованного графоаналитического выражения (43).
Возвращаясь к анализу логико-динамического процесса в функциональной структуре цифроаналогового преобразования выражения f1(ЦАП) (42), то в нем есть особенность в виде положительного входного аргумента +Uоп с информационным уровнем, например, для конкретных примеров (40) и (41), равным «+8», и аргумент знакового разряда m± с логической функции f1(&)-HE, эквивалентный также информационному уровню «+8». При этом следует отметить, что структура входных аргументов +[mj] эквивалентна максимальному информационному содержанию «+4+2+1»→«+7», и это информационное содержание в арифметическом пространстве (43) имеет векторную структуру в виде последовательно ортогональных весовых векторов в его положительной области «+», которые имеют два варианта. Поскольку каждое из последующих слагаемых векторов в информационном содержании «+4+2+1»→«+7» функционально принадлежат равновероятно ортогональным множествам +[nj], -[nj]→±[nj] и +[mj], -[nj]→±[mj] или ±[mj] и ±[nj], при этом процедура векторного суммирования в арифметическом пространстве выполняется путем совмещения конца предыдущего информационного вектора с началом очередного информационного вектора в эквипотенциальном уровне, который позиционно совмещен с эквивалентными уровнями ортогональных множеств ±[nj] и ±[mj]. В результате только такой процедуры суммирования векторных аргументов «+4+2+1» конец последнего из них позиционно располагается на эквипотенциальном уровне «+7», который соответствует их результирующей информационной сумме при условии, но при условии, что очередной вектор, который соответствует эквипотенциальному уровню «±0» пример выражения (41).
Аналогичную векторную структуру в арифметическом пространстве (43) имеет и пример выражения (40) за исключением условно отрицательного аргумента с информационным содержанием «-8», начало которого также совмещено с концом векторной структуры «+4+2+1» и его конец также совмещен с эквивалентным уровнем «-1» ортогональных множеств ±[nj] и ±[mj], но в позиционно-знаковых областях «+/-», поскольку выполнена так называемая процедура «вычитания». При этом следует особо отметить, что направление векторов в арифметическом пространстве должно соответствовать направлению положительных векторных множеств +[nj], +[mj] и направлению условно отрицательных векторных множеств -[nj], -[mj] ортогональных множеств ±[mj] и ±[nj], а они в отличие от общепринятого представления в формализованном арифметическом пространстве имеют взаимно противоположное направление. Поскольку в данной ситуации важен не условный знак, а величина информационного содержания, а то, что аргумент имеет либо положительные свойства, либо условно отрицательные свойства на направление увеличения его информационного содержания, эта условность не влияет, поэтому направление вектора указывает направление увеличения его информационной величины. И если записать логико-динамический процесс формирования структуры аргументов «-1» выражения (40) в «Дополнительном коде» в виде графоаналитического выражения (45),
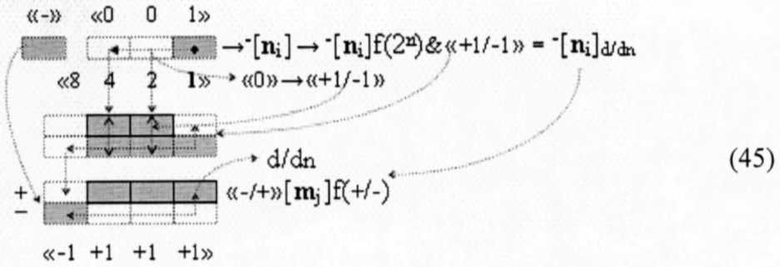
в котором перед логическим дифференцированием -d/dn условно отрицательных аргументов позиционной структуры -[nj]f(2n) активизируют все неактивные аргументы «0»→«+1/-1» после первого активного аргумента в младшем разряде, то после выполнения процедуры логического дифференцирования -d/dn в младшем разряде активизируется положительный дополнительный аргумент, а в старшем разряде активизируется условно отрицательный аргумент и в отличие от знакового разряда «-» в структуре -[nj]f(2n) он является уже информационным аргументом «-8». И с одной стороны, в арифметическом пространстве (43) вектор информационного аргумента «-8» расположен компланарно одному из ортогональных множеств ±[mj] или ±[nj] и его ориентация соответствует ориентации векторных условно отрицательным множествам -[nj], -[mj]. С другой стороны, в арифметическом пространстве (43) конец информационного аргумента «-8» выражения (45) совмещен с эквипотенциальным уровнем «-1», а его начало позиционно расположено в положительной области «+» формализованного пространства и является логическим продолжением векторной структуры как положительного аргумента «+1»d/dn процедуры логического дифференцирования -d/dn, так и положительных аргументов «+4»±1 и «+2»±1 процедуры активизации неактивных аргументов «0»→«+1/-1» выражения (45). При этом следует отметить, что существенное усложнение минимизированной структуры аргументов, которое соответствует аргументу с минимизированным информационным содержанием «-1», в данной ситуации, непосредственно связано с «желанием» выполнять все арифметические действия суммирования и умножения, включая и переход аргументов из одной формы информации (позиционной или аналоговой) в другую форму информации (аналоговую или позиционную) только в положительной области «+» арифметического пространства (43). Но это «желание» не корректно, поскольку арифметическое пространство (43) не ограничено только положительной областью «+», а включает условно отрицательную область «-» и две позиционно-знаковые области «+/-»1 и «+/-»2 и только их совокупность представляет собой формализованное арифметическое пространство. И в этом формализованном арифметическом пространстве (43) посредством знакового аргумента m± и логической функции f1(&)-HE в старшем разряде функциональной структуры f1(ЦАП) (42) дискретно изменяют выходной аргумент ионизированного тока +Ikf(m ±&+[mj]), величина которого, а точнее позиционное положение векторной структуры аргументов +[mj]→«+4+2+1» в арифметическом пространстве (43) существенно зависит от аргумента знакового разряда m ± с измененным уровнем аналогового сигнала. Если аргумент знакового разряда является активным m ±→«1», то начало векторной структуры аргументов +[mj]→«+4+2+1» расположено на эквипотенциальном уровне «0», а ее конец - на эквипотенциальном уровне «+7», но если аргумент знакового разряда является не активным m ±→«0», то начало векторной структуры аргументов +[mj]→«+4+2+1» смещают на эквипотенциальный условно отрицательный уровень «-8», в результате такого смещения ее конец расположен на эквипотенциальном уровне «-1», что полностью соответствует информационному содержанию позиционно-знаковой структуры условно отрицательного аргумента ±[mj]→«-8+4+2+1»→«-1». А такое смещение выполняет функциональная структура операционного усилителя f1(ОУ) (44), в которой логико-динамический процесс преобразования входного аргумента опорного напряжения +Uоп заключается в том, что он преобразуется в аргумент ионизированного поля тока -Inf(Uоп), который, с одной стороны, соответствует информационному аргументу «-8». С другой стороны, аргумент ионизированного поля тока -Inf(Uоп) операционного усилителя f1(ОУ) (44) соответствует информационному содержанию аргумента знакового разряда m ±, а он как вектор включен в векторную структуру аргумента ионизированного тока +Ikf(m ±&+[mj]) функциональной структуры f1(ЦАП). И если записать математическую модель цифроаналогового преобразования (46),

то на инвертирующем входе выходного операционного усилителя f2(ОУ) активный аргумент ионизированного поля тока -Inf(Uоп) операционного усилителя f1(ОУ) компенсирует активный аргумент знака m ±→«1» векторной структуры ↓+Ikf(m ±&+[mj]). В результате начало векторной структуры аргументов +[mj]→«+4+2+1» совмещается с эквипотенциальным уровнем «0», а ее конец совмещается с эквипотенциальным уровнем «+7» в арифметическом пространстве (43) и преобразованный аргумент ±UЦАПf([mj]) операционного усилителя f2(ОУ) также будет иметь информационное содержание «+7». А если в векторной структуре ↓+Ikf(m ±&+[mj]) аргумент знака m ±→«0» не активен, то входной аргумент -Inf(+Uоп) функциональной структуры операционного усилителя f2(ОУ) (46) в арифметическом пространстве (43) выполняет смещение начала векторной структуры аргументов +[mj]→«+4+2+1» и совмещает ее с эквипотенциальным уровнем «-8», в результате ее конец совмещается с эквипотенциальным уровнем «-1» и преобразованный аргумент ±UЦАПf([mj]) операционного усилителя f2(ОУ) также будет иметь информационное содержание «-1». При этом из анализа функциональной структуры цифроаналогового преобразователя fi(ЦАП) следует, что его разрядность уменьшена на один старший разряд, поскольку он выполняет функцию дискретного смещения результирующей векторной структуры аргументов ионизированного тока ↓+Ikf(m ±&+[mj]). И если записать условно отрицательную область от «Системы счисления «-/+»[mj]f(+/-) - Дополнительный код» (38) и аналогичную область «Минимизированной системы счисления ±[mj]f(+/-)min» в виде графоаналитического выражения (47),
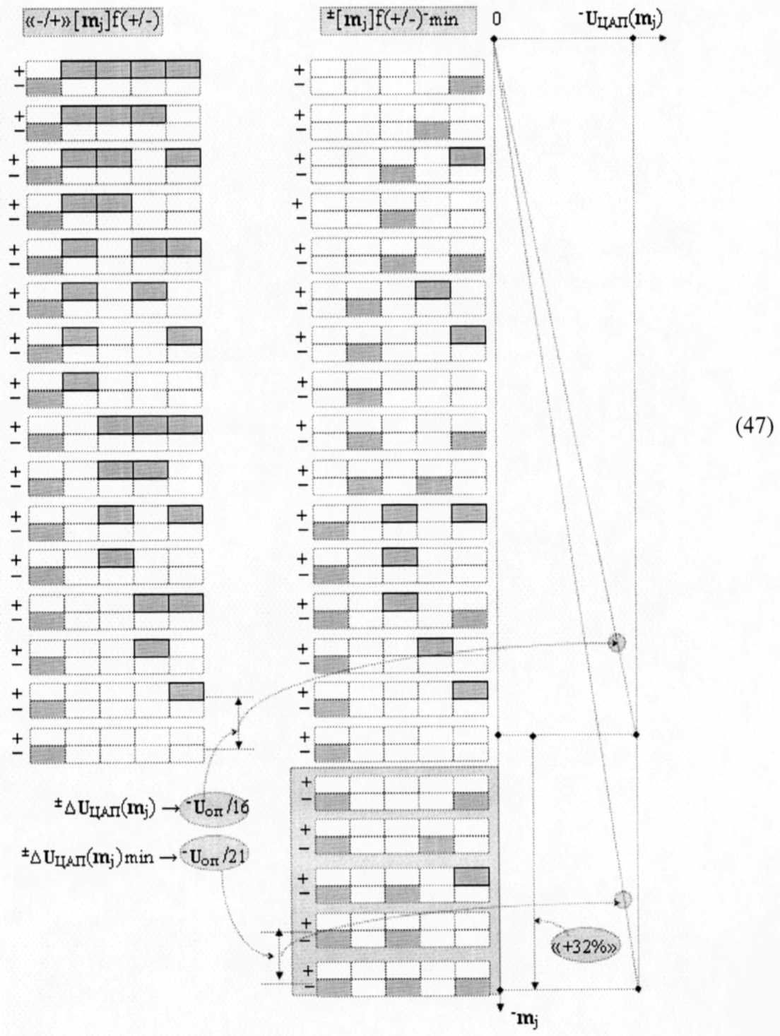
то из его анализа следует, что при переходе от ((Системы счисления «-/+»[mj]f(+/-) -Дополнительный код» (38), в которой аргумент старшего разряда m± выполняет функцию знака преобразованного аналогового сигнала ±UЦАП(mj) функциональной структуры цифроаналогового преобразователя ^(ЦАП) к «Минимизированной системы счисления ±[mj]f(+/-)min», с одной стороны, приведет к увеличению динамического диапазона результирующего аргумента напряжения ±UЦАПf([mj]) в функциональной структуре f1(ЦАП) на «32%». С другой стороны, если функциональную структуру цифроаналогового преобразования (46) записать в виде аналитического выражения (48),
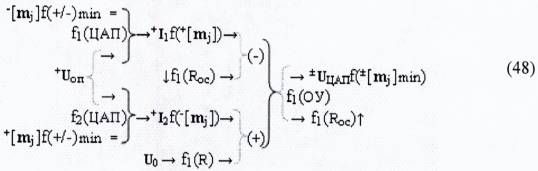
в котором функциональная неинвертирующая связь (+) выходного операционного усилителя f1(ОУ) включает функциональную дополнительную резисторную структуру f(R1) и функциональную дополнительную структуру цифроаналогового преобразователя f2(ЦАП), то аргумент напряжения ±Uj шага дискретизации в аргументе выходного напряжения ±UЦАПf(±[mj]min) операционного усилителя f1(ОУ) уменьшится в два раза. Поскольку если записать графоаналитическое выражение (49),
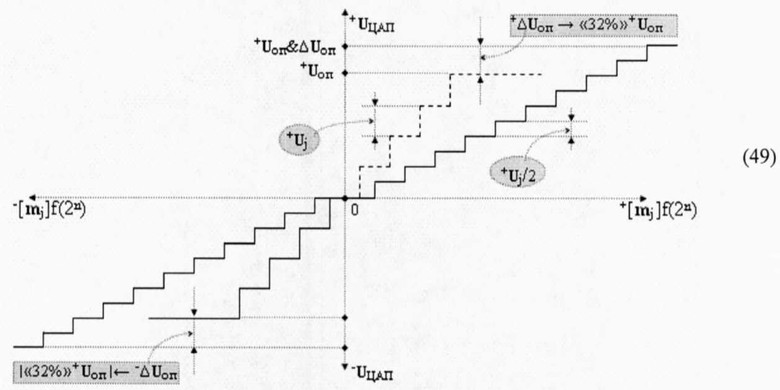
то для максимального использования информационного интервала «Минимизированной системы счисления ±[mj]f(+/-)min» выражения (47) исходное опорное напряжение +Uоп должно быть увеличено на +ΔUоп→«32%»+Uoп. При этом если вернуться к анализу аналитического выражения (46) и, в частности, к анализу функциональной структуры цифроаналогового преобразователя f1(ЦАП) (50)

и логико-динамическому процессу (39) формирования преобразованного аргумента ±UЦАП(+[mj]), то его старший разряд не используется по назначению как старший дополнительный разряд информационной структуры аргументов +[mj]. В результате шаг дискретизации +Uj в цифроаналоговом преобразователе f1(ЦАП) (50) определяется уменьшенной на старший разряд разрядностью, а сам старший разряд выполняет функцию дискретного смещения векторной структуры аргументов ↓+Ikf(m ±&+[mj]). А в аналитическом выражении (48), как в функциональной структуре f1(ЦАП), так и в функциональной структуре f2(ЦАП), шаг дискретизации +Uj формируется с учетом их полной разрядности, включая и старший разряд, что приводит к уменьшению шага дискретизации +Uj/2 в графоаналитическом выражении (49) в два раза. А если учесть дополнительный динамический диапазон минимизированных структур аргументов выражения (47), то для них шаг дискретизации +Uj/2 дополнительно уменьшается на «32%». При этом если записать для конкретной реализации минимизированной структуры аргументов +[mj]f(+/-)min→«+»«111000011100100»f(2n) логико-динамический процесс одновременного преобразования условно отрицательной ее последовательности аргументов в функциональной структуре f1(ЦАП) и положительной последовательности аргументов в функциональной структуре f2(ЦАП) в виде графоаналитического выражения (51),
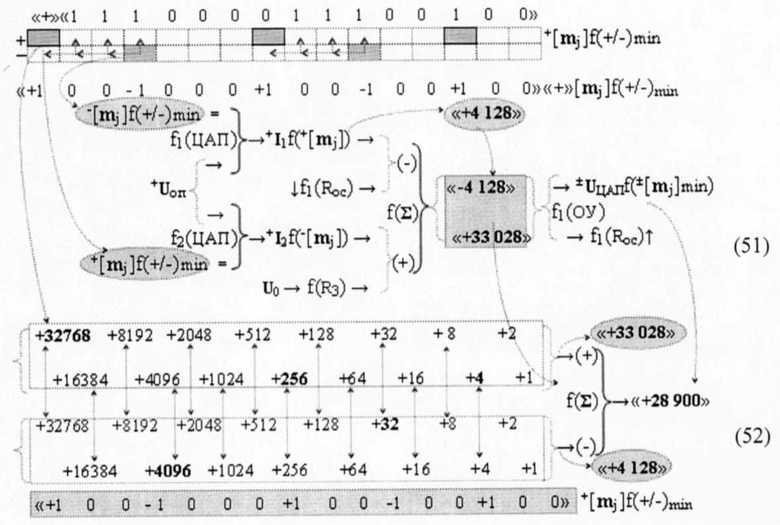
то особенностью в нем является процедура преобразования структуры условно отрицательных ее аргументов -[mj]f(+/-)min. И эта особенность заключается в том, что на первом этапе преобразования как положительной структуры аргументов +[mj]f(+/-)min в f1(ЦАП), так и условно отрицательных аргументов -[mj]f(+/-)min в f2(ЦАП) формируется преобразованная векторная информационная сумма «+33028» и «+4128» положительного знака. И если на не инвертирующей функциональной связи (+) сумматора f(Σ) операционного усилителя f1(ОУ) векторная информационная сумма «+33028» аргумента ионизированного поля тока +I1f(+[mj]) f2(ЦАП) не изменяет результирующий знак, то на инвертирующей (-) функциональной связи сумматора f(Σ) операционного усилителя f1(ОУ) информационная сумма «+4128» свой +I1f(+[mj]) f2(ЦАП) изменяет результирующий знак и становится условно отрицательной «-4128». В результате результирующий преобразованный аргумент напряжения ±UЦАПf(±[mj]min) операционного усилителя f1(ОУ) будет соответствовать информационной сумме «+33028»&«-4128»→«+28900» выражения (52), а аналитическое выражение (52) является математической моделью логико-динамического процесса преобразования минимизированных структур аргументов ±[mj]f(+/-)min как с положительным информационным содержанием, так и с условно отрицательным информационным содержанием. Поскольку если минимизированную систему счисления ±[mj]f(+/-)min записать в виде выражения (52),
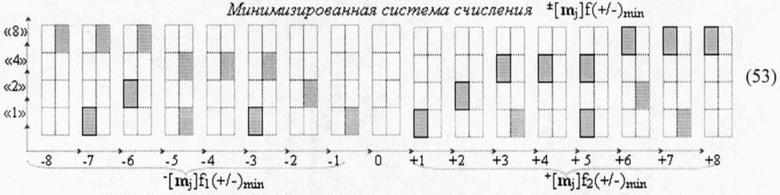
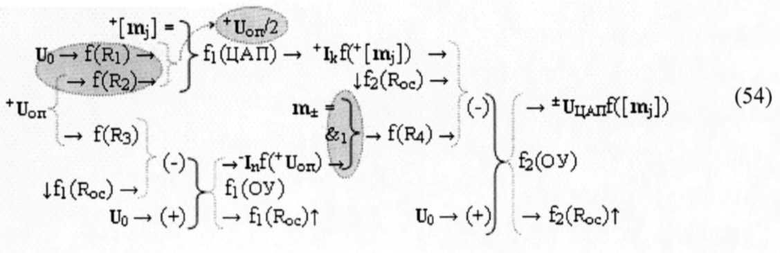
то как ее положительная область структур аргументов +[mj]f2(+/-)min, так и условно отрицательная область структур аргументов -[mj]f1(+/-)min включает различные комбинации, как положительных аргументов, так и условно отрицательных аргументов, в отличие от «Системы счисления «-/+»[mj]f(+/-) - Дополнительный код» (38), в которой только вся условно отрицательная область структур аргументов «-/+»[mj]f(+/-) включает условно отрицательный аргумент знакового разряда m±. И для уменьшения шага дискретизации +Uj функциональную структуру цифроаналогового преобразования (46) можно записать либо в виде аналитического выражения (54),
где 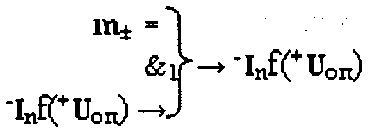 - функциональная структура с аналого-
- функциональная структура с аналого-
цифровой логической функцией f(&)-И, реализующей процедуру активизации входного аргумента ионизированного тока -Inf(+Uоп);
в котором, с одной стороны, введена функциональная структура с резисторными функциями f(R1) и f(R2) деления входного аналогового аргумента напряжения +Uоп на два для подачи на функциональную аналоговую связь (→) f1(ЦАП) аргумента аналогового напряжения +Uоп/2. С другой стороны, введена функциональная структура с аналоговой логической функцией f(&)-И, при активном аргументе знака m± позволяет выполнить процедуру дискретного смещения векторной структуры +Ikf(+[mj]) f1(ЦАП) с минимизированным шагом дискретизации из условно отрицательной области арифметического пространства (43) в его положительную область. Либо в виде аналитического выражения (55),
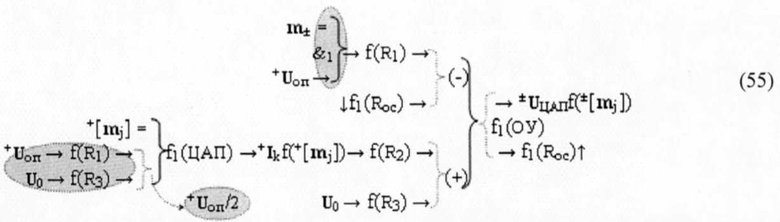
особенностью которого является аргумент знака m± и логика активизации результирующего аргумента ±UЦАПf(±[mj]) операционного усилителя f1(ОУ) и эта особенность заключается в том, что вектор информационного содержания положительной векторной структуры преобразованного аргумента +Ikf(+[mj]) f1(ЦАП), когда он является аргументом в положительной области арифметического пространства (43), то в этой ситуации в системе аналоговой логической функции f(&)-И не активен знака m±. В результате информационное содержание преобразованного аргумента ±UЦАПf(±[mj]) операционного усилителя f1(ОУ) полностью повторяет информационное содержание ионизированного поля аргумента тока +Ikf(+[mj]) f1(ЦАП), но как только аргумент знака m± активизирован, то на выходной связи аналоговой логической функции f(&)-И активизируется аргумент опорного напряжения +Uоп и поступает на инвертирующую функциональную связь (-) операционного усилителя f1(ОУ), что в арифметическом пространстве (43) приводит к дискретному смещению векторной структуры +Ikf(+[mj]) в область условно отрицательных аргументов, но не приводит к дополнительному «32%» уменьшению шага дискретизации преобразованного аргумента напряжения ±UЦАПf(±[mj]), который формируется в функциональной структуре цифроаналогового преобразования (54) и (55) в отличие от функциональной структуры (51).
На основании полученных результатов можно сделать вывод, что ((Система счисления «-/+»[mj]f(+/-) - Дополнительный код» (38) как не минимизированная позиционно-знаковая система счисления не может реализовать потенциальных возможностей «Минимизированной системы счисления ±[mj]f(+/-)min» (53), как при цифроаналоговом преобразовании, так и при выполнении арифметических операций суммирования и умножения. При этом следует особо отметить, что в логико-динамическом процессе преобразования минимизированных аргументов слагаемых +[nj]f(+/-)min и +[mj]f(+/-)min в сумматоре ±f(Σ)min, так же как и в логико-динамическом процессе преобразования позиционно-знаковых аргументов слагаемых «-/+»[mj]f(+/-) - «Дополнительный код» не зависит от их знакового информационного содержания. Например, если записать логико-динамический процесс преобразования аргументов в сумматоре ±f(Σ)min для конкретных минимизированных структур положительного слагаемого +[nj]f(+/-)min→ «0100110010110011»f(2n) и условно отрицательного слагаемого -[mj]f(+/-)min→«0111000101110100»f(2n) в позиционной системе f(2n) в виде логического выражения с экономическим понятием «Заем» (56)

и с применение арифметических аксиом (5) в виде графоаналитического выражения (57),
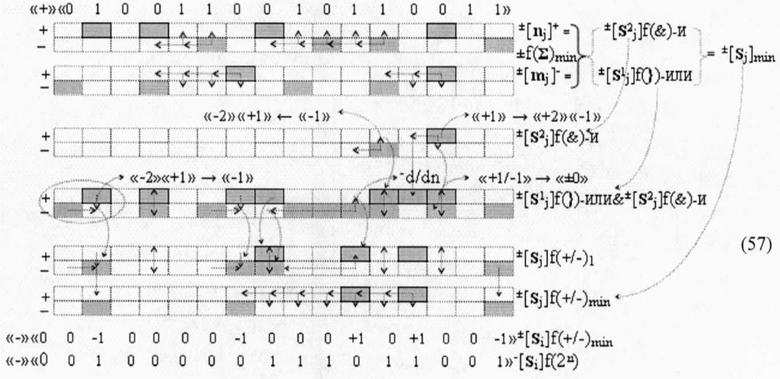
то после преобразования второй промежуточной суммы ±[S2 j]f(&)-и в соответствии с арифметическими аксиомами «+1»→«+2»«-1» и «-1»→«-2»«+1» формируется объединенная структура первой и второй промежуточных сумм ±[S1 j]f({)-или &±[S1 j]f({)-и, в которой необходимо выполнить только локальные преобразования аргументов. И эти локальные преобразования не минимизированных аргументов также выполняют с применением процедуры логического дифференцирования -d/dn и обратных арифметических аксиом «-2»«+1»→«-1» и «+1/-1»→«±0». При этом следует отметить, что, учитывая многовариантность структур аргументов слагаемых ±[nj]f(+/-)min и ±[mj]f(+/-)min, возможна ситуация в сумматоре ±f(Σ)min, когда объединенная структура первой и второй промежуточных сумм ±[S1 j]f({)-или &±[S2 j]f({)-и будет сформирована полностью эквивалентной структуре аргументов «-/+»[mj]f(+/-) - «Дополнительный код». И такая ситуация формируется всегда, когда структура минимизированных аргументов слагаемых ±[nj]f(+/-)min и ±[mj]f(+/-)min имеет либо все положительные активные аргументы, либо когда только аргумента старшего разряда является условно отрицательным. Например, если записать логико-динамический процесс преобразования аргументов в сумматоре ±f(Σ)min Для конкретных минимизированных структур положительного слагаемого +[nj]f(+/-)min→ «+»«0100010100010010»f(2n) и условно отрицательного слагаемого -[mj]f(+/-)min→«-» «111010110110110»f(2n) в виде графоаналитического выражения (58),

то объединенная структура первой и второй промежуточных сумм ±[S1 j]f({)-или &±±[S1 j]f({)-и за исключением активного логического нуля «+1/-1»→«±0» сформирована полностью эквивалентной структуре аргументов «-/+»[mj]f(+/-) - «Дополнительный код». Поэтому имеет смысл сформировать функциональную структуру логико-динамического процесса преобразования аргументов структуры «-/+»[mj]f(+/-) - «Дополнительный код» в минимизированную позиционно-знаковую структуру ±[mj]f(+/-)min, например, для последующего применения ее в параллельно-последовательных умножителях ±fΣ(Σ) для существенного сокращения технологического его цикла ΔtΣ и увеличения динамического диапазона информационного содержания аргументов в «Минимизированной системе счисления ±[mj]f(+/-)min». А для этого запишем структуру аргументов «-/+»[mj]f2(+/-) - «Дополнительный код» и эквивалентную ей минимизированную структуру ±[mj]f1(+/-)min в виде графоаналитического выражения (59)
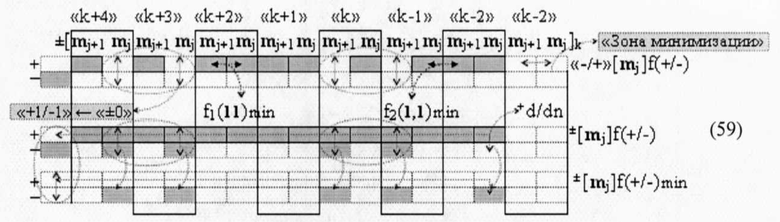
где f1(11)min и f2(1,1)min - функциональные структуры, активизирующие не активный аргумент логического нуля «±0»→«+1/-1», которые активизируются при наличии в положительной структуре двух последовательно активных аргумента позиционно расположенные в «Зоне минимизации» и между «Зонами минимизации» соответственно;
и структуру «-/+»[mj]f2(+/-) - «Дополнительный код» и эквивалентную ей минимизированную структуру ±[mj]f2(+/-)min в виде графоаналитического выражения (60),
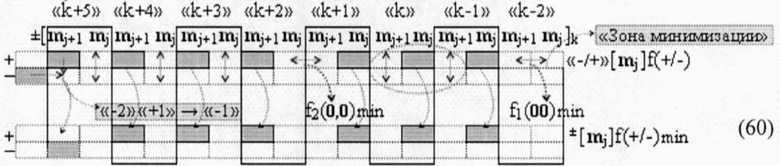
где f1(00)min и f2(0,0)min - функциональные структуры, активизирующие минимизированные структуры аргументов «01» и «10» в условно «k» «Зоне минимизации», которые активизируются при наличии в положительной структуре «-/+»[mj]f2(+/-) - «Дополнительный код» двух последовательно не активных аргумента, позиционно расположенных в «Зоне минимизации» и между «Зонами минимизации» соответственно;
в которых логико-динамический процесс преобразования активного положительного минимизированного аргумента f1(01,0)min условно «j» разряда и активного положительного минимизированного аргумента f1(01,0)min условно «j+1» разряда существенно отличается. И это отличие для каждого из минимизированных аргументов f1(01,0)min и непосредственно связано с активностью или не активностью преобразованного аргумента либо функциональной структуры f1(11)min или f1(00)min, активизирующиеся в «Зоне минимизации», либо функциональных структур f2(1,1)min и f2(0,0)min, активизирующиеся между «Зонами минимизации». При этом из анализа графоаналитических выражений (59) и (60) следует, что, с одной стороны, преобразованные аргументы функциональных структур f1(11)min, f2(1,1)min и f1(00)min, f2(0,0)min реализуют разные процедуры. И если преобразованные аргументы функциональных структур f1(11)min и f2(1,1)min в выражении (59) выполняют функцию сквозной активизации не активных аргументов в структуре f1(0,1,0,1) в соответствии с арифметической аксиомой «±0»→«+1/-1», то преобразованные аргументы функциональных структур f1(00)min и f2(0,0)min в выражении (60) выполняют функцию активизации минимизированных аргументов f1(01,0)min и f2(l0,0)min в результирующей структуре минимизированных аргументов ±[mj]f(+/-)min, но имеют общую особенность. И эта особенность заключается, по существу, в активизации минимизированного аргумента в результирующей структуре аргументов ±[mj]f(+/-)min. Например, если ввести векторы активизации функциональных структур f1(11)min и f1(00)min в конкретную реализацию структуры аргументов «-/+»[mj]f(+/-) - «Дополнительный код» и записать ее в виде графоаналитического выражения (61),
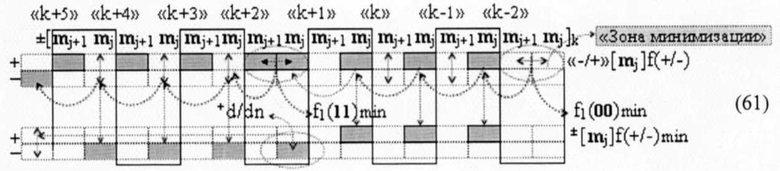
то из его анализа следует, что введенные векторы указывают на аргумент mj условно «j» разряда в каждой «Зоне минимизации», который должен быть активизирован. И если вектор активизации функциональной структуры f1(00)min активизирует активный положительный аргумент в «Зоне минимизации», то вектор активизации функциональной структуры f1(00)min также и косвенно активизирует в результирующей структуре аргументов ±[mj]f(+/-)min не активный условно отрицательный аргумент того же условно «j» разряда «Зоны минимизации».
Аналогичная ситуация формируется и при введении векторов активизации функциональных структур f2(1,1)min и f2(0,0)min в конкретную реализацию структуры аргументов «-/+»[mj]f(+/-) - «Дополнительный код» в графоаналитическом выражении (62),
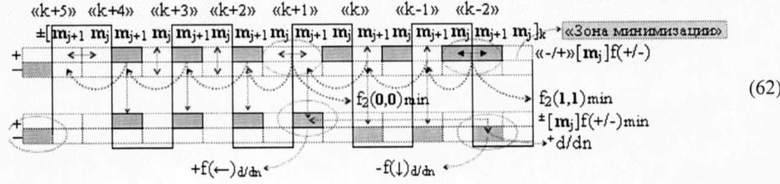
в котором также введенные векторы активизации указывают на аргумент mj+1 условно «j+1» разряда в каждой «Зоне минимизации», который должен быть активизирован. И в данной структуре аргументов «-/+»[mj]f(+/-) активизирован результирующий аргумент функциональных структур f2(1,1)min и f2(0,0)min, который сформирован между «Зонами минимизации» и функционально относится только к аргументу mj+1 условно «j+1» разряда в каждой «Зоне минимизации», как при активизации положительных минимизированных аргументов, так и при активизации условно отрицательных минимизированных аргументов в результирующей структуре ±[mj]f(+/-)min. При этом следует отметить особенность реализации процедуры логического дифференцирования +d/dn в выражении (62), которая непосредственно относится к формированию аргумента локального переноса +f(+←+)d/dn. Поскольку процедуру логического дифференцирования +d/dn положительных аргументов с условно отрицательным информационным содержанием и с положительным информационным содержанием можно записать в виде графоаналитических выражений (63) и (64),
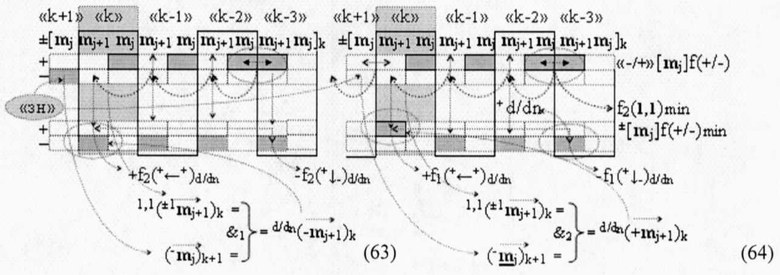
где 1,1(±1mj+1)k - результирующий аргумент условно «j+1» разряда функциональной структуры f2(1,1)min «k» «Зоны минимизации», сформированный в результате активизации не активного логического нуля «±0»→«+1/-1» в «Зоне минимизации»; (-mj)k+1 - аргумент знакового разряда в структуре положительных аргументов «-/+»[mj]f(+/-) - «Дополнительный код».
Особенностью активизации аргумента 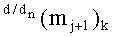
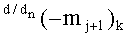
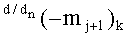
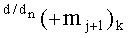
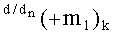
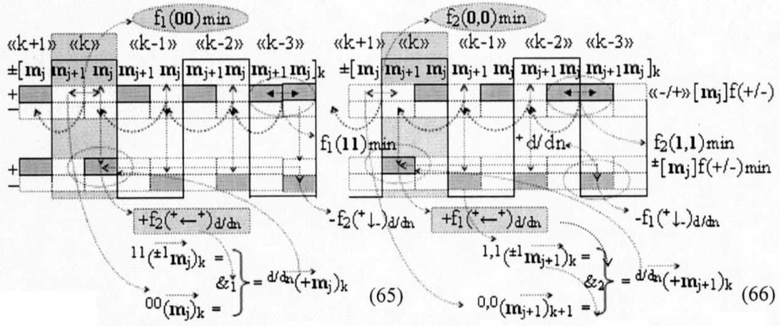
где 11(±1mj)k - результирующий аргумент условно «j» разряда функциональной структуры f1(11)min «k» «Зоны минимизации», сформированный в результате активизации не активного логического нуля «±0»→«+1/-1» в «Зоне минимизации»; 00(mj)k - результирующий аргумент «j» разряда функциональной структуры f1(00)min «k» «Зоны минимизации»; 0,0(mj+1)k+1 - результирующий аргумент условно «j+1» разряда функциональной структуры f1(1,1)min «k+1» «Зоны минимизации».
Из анализа графоаналитических выражений (65) и (66) следует, что логические функции f1(&)-И и f2(&)-И корректно активизируют как положительный аргумент 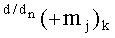
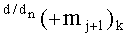
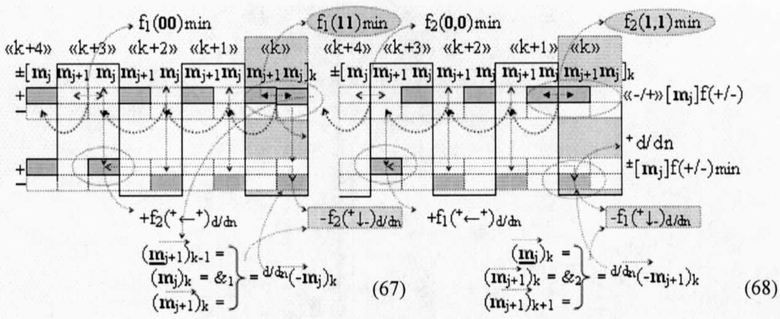
то они с выходной логической функцией f1(&)-И и f2(&)-И корректно активизируют как условно отрицательный аргумент 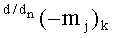
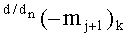

то дополнительно введенные в систему логической функции f1(})-ИЛИ и f2(})-ИЛИ функциональные структуры с выходной логической функцией f2(&)-И условно «j» разряда и с выходной логической функцией f4(&)-И и условно «j+1» разряда корректно активизируют, как условно отрицательный аргумент ±1(-mj)k и минимизированный условно отрицательный аргумент min(-mj)k условно «j» разряда в выражении (69), так и условно отрицательный аргумент ±1(-mj+1)k-1 «k-1» «Зоны минимизации» и минимизированный условно отрицательный аргумент min(-mj+1)k условно «j+1» разряда в выражении (70) «k» «Зоны минимизации». Поскольку в системе логической функции f2(&)-И одновременно активны аргумент (mj+1)k условно «j+1» разряда и аргумент (m j)k условно «j» разряда с измененным уровнем аналогового сигнала, которые являются условием активизации результирующего аргумента 11(±1mj)k-1 «k-1» «Зоны минимизации» функциональной структуры f1(11)min активизации не активных аргументов логического нуля «±0»→«+1/-1». А в системе логической функции f4(&)-И одновременно активны аргумент с измененным уровнем аналогового сигнала (m j+1)k условно «j+1» разряда «k» «Зоны минимизации» и аргумент (mj)k+1 условно «j» разряда «k+1» «Зоны минимизации», которые также являются условием активизации результирующего аргумента 1,1(±1mj+1)k функциональной структуры f2(1,1)min активизации не активных аргументов логического нуля «±0»→«+1/-1». При этом следует отметить, что функциональные структуры с выходными логическими функциями f2(&)-И и f4(&)-И в аналитических выражениях (69) и (70), по существу, являются аналитическими выражениями функциональной структуры активизации f1(11)min условно «j» разряда и функциональной структурой f2(1,1)min условно «j+1» разряда, которые могут быть записаны в виде графоаналитических выражений (71) и (72),
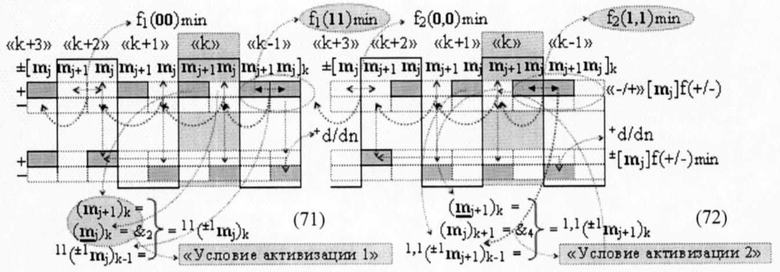
которые являются функциональными структурами последовательной активизации не активных аргументов логического нуля «±0»→«+1/-1» при минимизации структуры аргументов «-/+»[mj]f(+/-) - дополнительный код». Поскольку в систему логических функций f2(&)-И и f4(&)-И как аналитических выражений (69) и (70) включены два аргумента «Условия активизации», так и в систему аналитических выражений (71) и (72) также включены те же два аргумента «Условия активизации». А если учесть, что основным качеством любой функциональной структуры преобразования аргументов является ее минимизированный технологический цикл ΔtΣ, а он минимизирован в функциональной параллельной структуре активизации f2(1,1)min условно «j» разряда и функциональной структурой f2(1,1)min условно «j+1» разряда. Поэтому аналитические выражения (71) и (72) для условно «j» разряда и «j+1» разряда запишем в виде аналитических выражений (73) и (74),
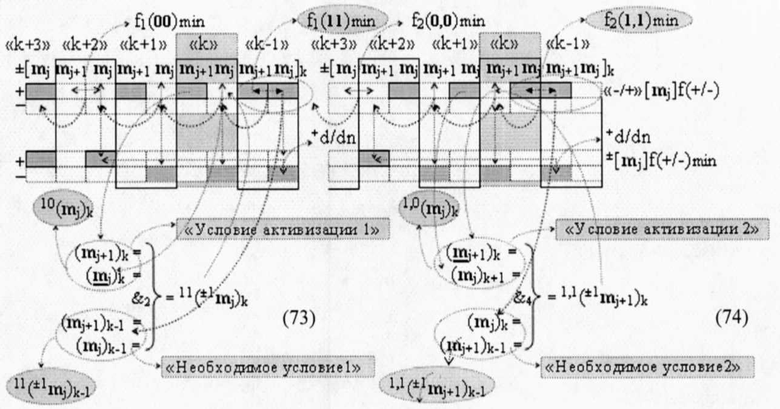
в которых системы логических функций f2(&)-И и f3(&)-И, по существу, включают преобразованные аргументы 11(±1mj)k-1 и 1,1(±1mj+1)k-1 «k-1» «Зоны минимизации», являющиеся «Необходимым условием» активизации и преобразованные аргументы 10(mj)k и 1,0(mj)k «Условие активизации» активизации неактивных аргументов логического нуля «±0»→«+1/-1» в «k» «Зоне минимизации». При этом следует отметить, что преобразованные аргументы 11(mj)k-1 и 1,1(mj+1)k «k-1» «Зоны минимизации» и преобразованные аргументы 10(mj)k и 1,0(mj)k «k» «Зоны минимизации» формируются посредством логических функций f(&)-И, поэтому аналитические выражений (73) и (74) запишем в виде функциональных структур (75)и(76).
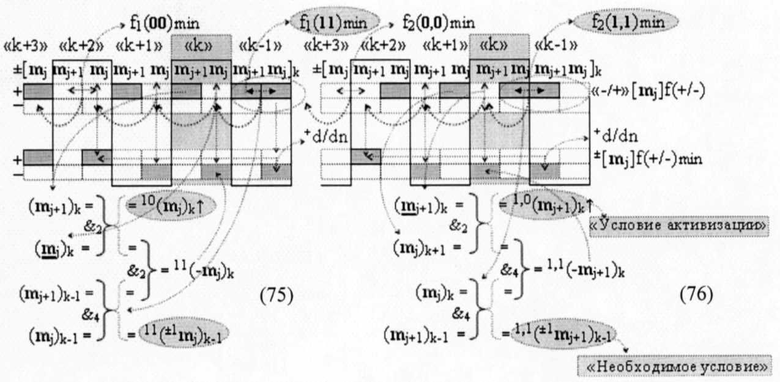
И если записать функциональную параллельную структуру активизации f1(11)min условно «j» разряда и f2(1,1)min условно «j+1» разряда для очередной «k», «Зоны минимизации» запишем в виде аналитических выражений (77) и (78),
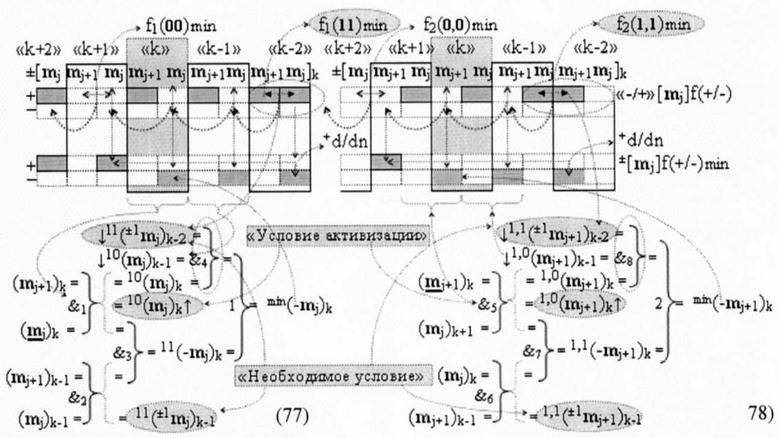
то для активизации результирующего минимизированного условно отрицательного аргумента min(-mj+1)k и min(-mj+1)k в этой «k» «Зоны минимизации» достаточно ввести функциональную дополнительную структуру с выходной логической функцией f4(&)-И и f8(&)-И в систему выходной логической функции f1(})-ИЛИ и f2(})-ИЛИ с соответствующим аргументом ↓11(±1mj)k-2 и ↓1,1(±1mj+1)k-2 «Необходимого условия» активизации «k-2» «Зоны минимизации» и только по одному преобразованному аргументу ↓10(mj)k-1 и ↓1,0(mj+1)k-1 «k-1» «Зоны минимизации» и по одному преобразованному аргументу ↓10(mj)k и ↓1,0(mj+1)k «k» «Зоны минимизации», которые соответствуют «Условию активизации». При этом следует отметить, что логические функции f3(&)-И и f7(&)-И в аналитических выражениях (77) и (79) активизируют преобразованным аргументом 11(-mj)k и 1,1(-mj+1)k выходную логическую функцию f1-(})-ИЛИ и f2(})-ИЛИ только в том случае, когда активен аргумент 11(±1mj)k-1 и 1,1(±1mj+1)k-1 «Необходимого условия» в «k-1» «Зоне минимизации», а преобразованный аргумент логических функций функцией f4(&)-И и f8(&)-И активизирует их, только когда одновременно активны как преобразованный аргумент ↓10(mj)k-1 и ↓1,0(mj+1)k-1 «k-1» «Зоне минимизации», так и преобразованный аргумент ↓10(mj)k и ↓1,0(mj+1)k «k» «Зоне минимизации». Поскольку в структуре аргументов «-/+»[mj]f(+/-) - «Дополнительный код» как «Условие активизации», так и «Необходимое условие» равновероятно в любой из предыдущих «Зон минимизации». И если для очередной «k» «Зоны минимизации» функциональную параллельную структуру активизации f1(11)min условно «j» разряда и f2(1,1)min условно «j+1» разряда записать в виде аналитических выражений (79) и (80),
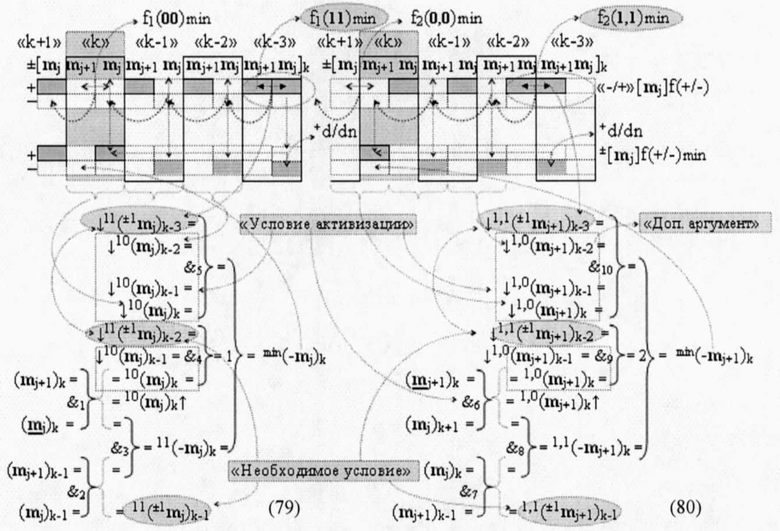
то для активизации результирующего минимизированного условно отрицательного аргумента min(-mj+1)k и min(-mj+1)k в этой «k» «Зоны минимизации» также достаточно ввести функциональную дополнительную структуру с выходной логической функцией f5(&)-И и f10(&)-И в систему выходной логической функции f1(})-или и f2(})-или только с одним «Дополнительным аргументом» ↓10(mj)k-2 и ↓1,0(mj+1)k-2 «k-2» «Зоны минимизации». При этом в системе логической функцией f5(&)-И и f10(&)-И «Необходимым условием» является аргумент ↓11(mj)k-3 и ↓1,1(mj+1)k-3 «k-3» «Зоны минимизации», а из этого следует, что для 8- разрядной структуры аргументов «-/+»[mj]f(+/-) - ((Дополнительный код» в функциональную параллельную структуру активизации как f1(11)min условно «j» разряда, так и f2(1,1)min условно «j+1» разряда введены только три логические функции f(&)-И, посредством которых будет сформирован корректный минимизированный аргумент min(-mj+1)k и min(-mj+1)k. А с очередной дополнительной «Зоной минимизации» должна быть введена функциональная дополнительная структура с выходной логической функцией f(&)-И с одним дополнительным аргументом. И если минимизируется 16-ти разрядная структура аргументов «-/+»[mj]f(+/-) - «Дополнительный код», то функциональная параллельная структура активизации как f1(11)min условно «j» разряда, так и f2(1,1)min условно «j+1» разряда в своей системе выходной логической функции f1(})-ИЛИ и f2(})-ИЛИ дополнительно необходимо включить четыре логических функций f(&)-И и их общее количество с учетом процедуры логического дифференцирования +d/dn будет соответствовать 6-логическим функциям f(&)-И. При этом технологический цикл ΔtΣ активизации результирующих минимизированных условно отрицательных аргументов min(-mj+1)k и min(-mj+1)k в аналитических выражениях (79) и (80) будет соответствовать
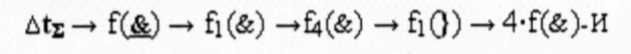
четырем условным логическим функциям f(&)-И. А если учесть, что функциональные структуры активизации f1(11)min условно «j» разряда и f2(1,1)min условно «j+1» разряда, по существу, эквивалентны сквозному переносу f(←←) в позиционном сумматоре f(Σ), например, в 16- разрядном сумматоре f(Σ)16, число последовательных логических элементов составляет
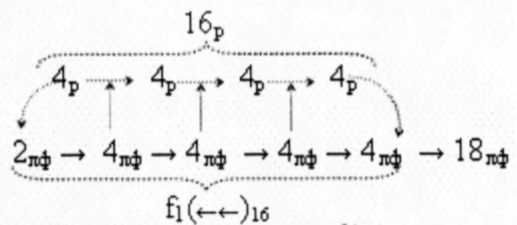
восемнадцать условных логических функций f(&)-И, а сквозной перенос f(←←)32 32-х разрядного сумматора f(Σ)32 число последовательных логических элементов составляет
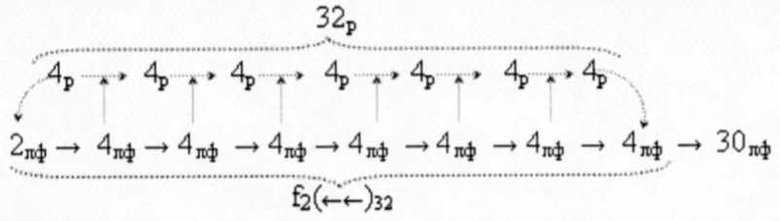
тридцать условных логических функций f(&)-И. А если учесть, что функциональные структуры активизации f1(11)min условно «j» разряда и f2(1,1)min условно «j+1» разряда также входят в функциональную структуру сумматора ±f(Σ)min, который реализует процедуру суммирования минимизированных аргументов слагаемых «+»[n1]f(+/-)min и «+»[mi]f(+/-)min, то минимизированный технологический цикл ΔtΣ этих функциональных структур обосновывают необходимостью перехода от позиционно-знаковой структуры аргументов «-/+»[mj]f(+/-) - «Дополнительный код» к минимизированной ее структуре ±[mj]f(+/-)min. При этом следует особо отметить, что необходимость перехода от системы счисления «-/+»[mj]f(+/-) -«Дополнительный код» к минимизированной ее системе ±[mj]f(+/-)min не только связана с существенным снижением технологического цикла функциональных структур сумматоров ±f(Σ)min и умножителей ±fΣ(Σ)min, но и с возможностью сформировать иное качество. И это качество структуры аргументов системы счисления ±[mj]f(+/-)min при цифроаналоговом преобразовании в функциональной структуре f1(ЦАП) позволяет формировать результирующий его аргумент выходного напряжения ±UЦАПf(±[mj]min) с шагом дискретизации ±Ujf(+/-)min в два раза меньшим, чем аналогичный аргумент напряжения ±Ujf(+/-), который формирует структура аргументов системы счисления «-/+»[mj]f(+/-) - «Дополнительный код». А такое уменьшение шагом дискретизации ±Ujf(+/-)min позволит существенно уменьшить погрешность в управлении технологическими процессами, но его реальное уменьшение меньше еще на «+32%», поскольку «Минимизированная система счисления ±[mj]f(+/-)min» имеет увеличенное информационное содержание на «+32%» при той же разрядности структуры аргументов. И это увеличенное информационное содержание на «+32%» связано непосредственно с тем, что если в «Системе счисления «-/+»[mj]f(+/-) - Дополнительный код» аргумент старшего разряда m±выполняет, по существу, только функцию условно отрицательного знака (-), то в «Минимизированной системе счисления ±[mj]f(+/-)min» аргумент ±maxjmax старшего разряда не только выполняет функцию знака и является либо положительным аргументом, либо условно отрицательным аргументом, но и позволяет увеличить число дополнительных информационных комбинаций в структурах аргументов, как в условно отрицательной ее области (81),
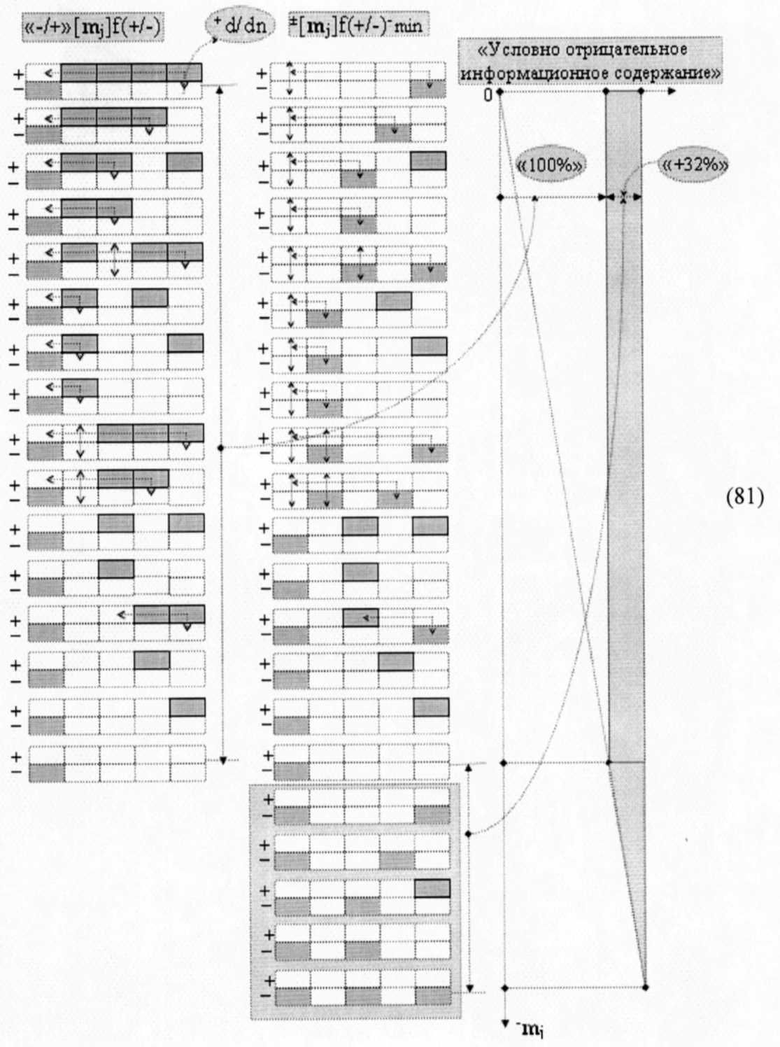
так и в положительной ее области (82).
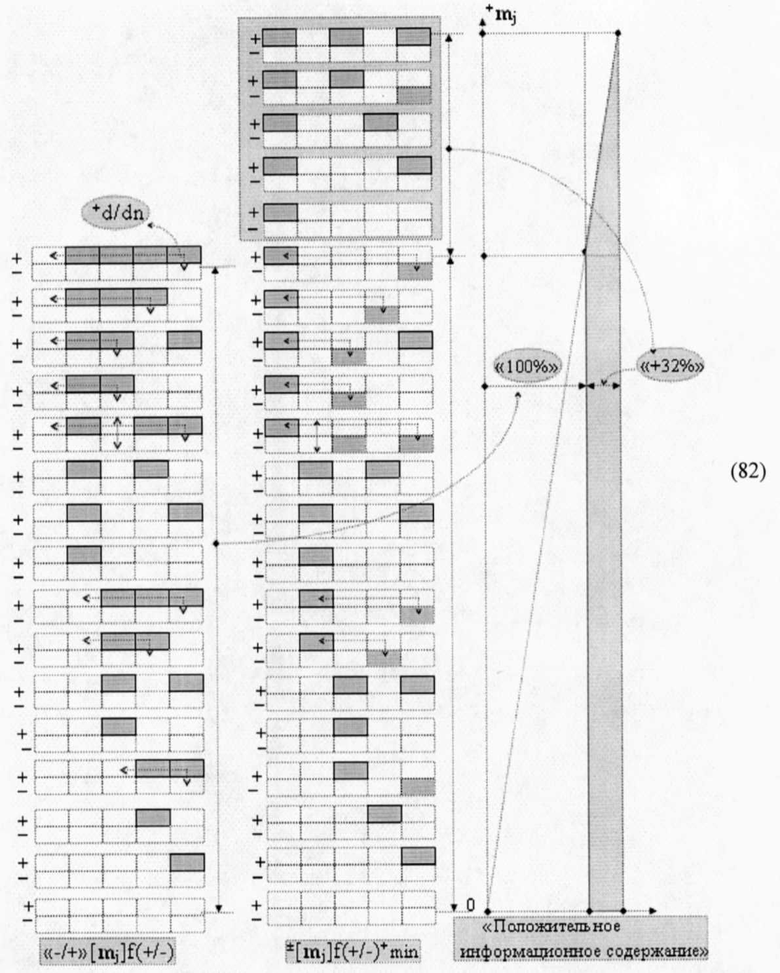
И это увеличение информационного содержания на «+32%» «Минимизированной системе счисления ±[mj]f(+/-)min» позволяет существенно расширить арифметические возможности функциональных структур сумматоров ±f(Σ)min и умножителей ±fΣ(Σ)min с этой системой счисления.
выражения (91),
Использование предложенного способа и функциональной структуры преобразователя ±[mj]f(+/-)min→±UЦАПf([mj]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+1,0,-1) в аргумент аналогового напряжения ±UЦАПf([mj]) позволяет существенно расширить диапазон преобразования минимизированной позиционно-знаковой структуры аргументов аналоговых сигналов ±[mj]f(+/-)min «дополнительного кода» в аналоговый сигнал напряжения «±UЦАПf([mj]).
Дополнительный анализ прототипа по заявке приведен в графической части.
Изобретение относится к вычислительной технике и может быть использовано в системах контроля и управления в совокупности с арифметическими устройствами, которые реализуют различные арифметические процедуры над минимизированными позиционно-знаковыми структурами аргументов ±[mj]f(+/-)min троичной системой счисления f(+1,0,-1) с последующим преобразованием ее в аргумент аналогового сигнала напряжения ±UЦАПf([mj]) посредством функциональной структуры цифро-аналогового преобразования f1(ЦАП). Предложенный способ позволяет существенно расширить диапазон преобразования минимизированной позиционно-знаковой структуры аргументов аналоговых сигналов ±[mj]f(+/-)min «дополнительного кода» в аналоговый сигнал напряжения «±UЦАПf([mj]). 2 н.п. ф-лы, 2 ил.
1. Способ преобразования ±[mj]f(+/-)min→±Ukf([±mi]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+1,0,-1) в аргумент аналогового напряжения ±UЦАПf(±[mj]min), в котором выполняют посредством функциональной структуры цифроаналогового преобразователя f1(ЦАП) преобразование положительной позиционной минимизированной структуры аргументов аналоговых сигналов напряжения -[mj]f(+/-)min с условно отрицательным информационным содержанием в положительный аргумент ионизированного тока +IЦАПf(+[mj]), который подают на инвертирующую функциональную связь (-) функциональной структуры операционного усилителя f1(ОУ), выполняющей функцию сумматора f(Σ), и формируют аргумент аналогового напряжения ±UЦАПf(±[mj]min), отличающийся тем, что одновременно выполняют посредством функциональной структуры цифроаналогового преобразователя f2(ЦАП) преобразование положительной позиционной минимизированной структуры аргументов аналоговых сигналов напряжения +[mj]f(+/-)min с положительным информационным содержанием в положительный аргумент ионизированного тока +IЦАПf(+[mj]) и подают его на не инвертирующую функциональную связь (+) функциональной структуры операционного усилителя f1(ОУ), в котором формируют аргумент аналогового напряжения ±UЦАПf(±[mj]min), равный арифметической разности положительного аргумента ионизированного тока +IЦАПf(+[mj]) с положительным информационным содержанием и положительного аргумента ионизированного тока +IЦАПf(-[mj]) с условно отрицательным информационным содержанием в соответствии с графоаналитическим выражением логико-динамического процесса преобразования аргументов аналоговых сигналов вида
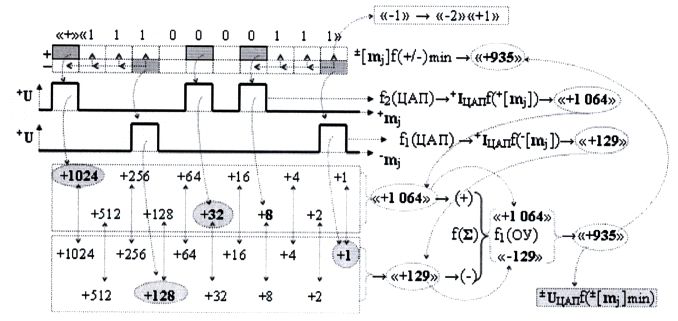
2. Функциональная структура преобразователя ±[mj]f(+/-)min→±Ukf([±mi]) минимизированной структуры позиционно-знаковых аргументов ±[mj]f(+/-)min троичной системы счисления f(+1,0,-1) в аргумент аналогового напряжения ±UЦАПf(±[mj]min), включающая функциональную структуру операционного усилителя f1(ОУ), выполняющую функцию сумматора f(Σ), в котором функциональная выходная связь, формирующая аналоговый аргумент напряжения ±UЦАПf(±[mj]min), является выходной функциональной связью преобразователя и функциональной входной связью функциональной резисторной структуры f1(Roc) обратной связи, функциональная выходная связь которой является инвертирующей функциональной связью (-) операционного усилителя f1(ОУ) и функциональной выходной связью функциональной структуры цифроаналогового преобразователя f1(ЦАП), в котором функциональная аналоговая связь (→) и функциональная логическая связь (=) являются функциональными связями структуры для приема входных аргументов опорного напряжения +Uоп и минимизированной структуры аргументов напряжения -[mj]f(+/-)min с условно отрицательным информационным содержанием соответственно, и включает также функциональную резисторную структуру f1(R), отличающаяся тем, что введена функциональная дополнительная структура цифроаналогового преобразователя f2(ЦАП) для преобразования минимизированной структуры аргументов напряжения +[mj]f(+/-)min с положительным информационным содержанием, при этом функциональные связи выполнены в соответствии с математической моделью вида
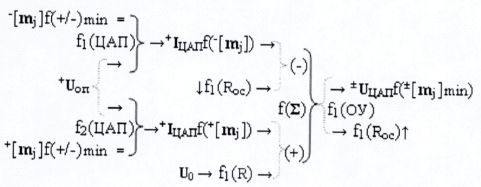
где 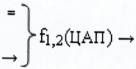 - функциональная структура цифроаналогового
- функциональная структура цифроаналогового
преобразователя f1(ЦАП) и f2(ЦАП);
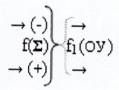
- функциональная структура операционного усилителя
f1(ОУ).
| ТИТЦЕ У., ШЕНК К | |||
| ПОЛУПРОВОДНИКОВАЯ СХЕМОТЕХНИКА | |||
| - Москва: Мир, 1982, с.451, рис.24.14 | |||
| ЦИФРОАНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ | 1991 |
|
RU2029430C1 |
| Устройство для цифроаналогового преобразования | 1985 |
|
SU1327294A1 |
| JP 57116419 A, 20.07.1982 | |||
| JP 4081129 A, 13.03.1992. | |||
Авторы
Даты
2013-12-10—Публикация
2012-05-21—Подача