Текст описания приведен в факсимильном виде.






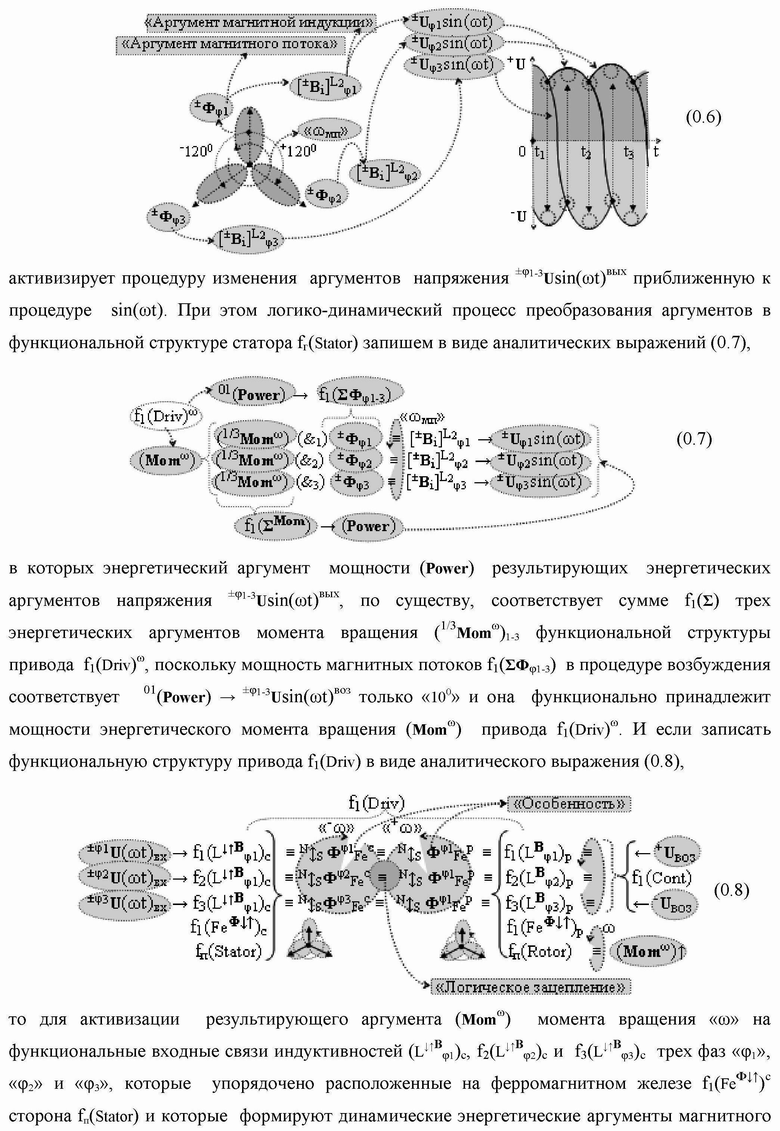

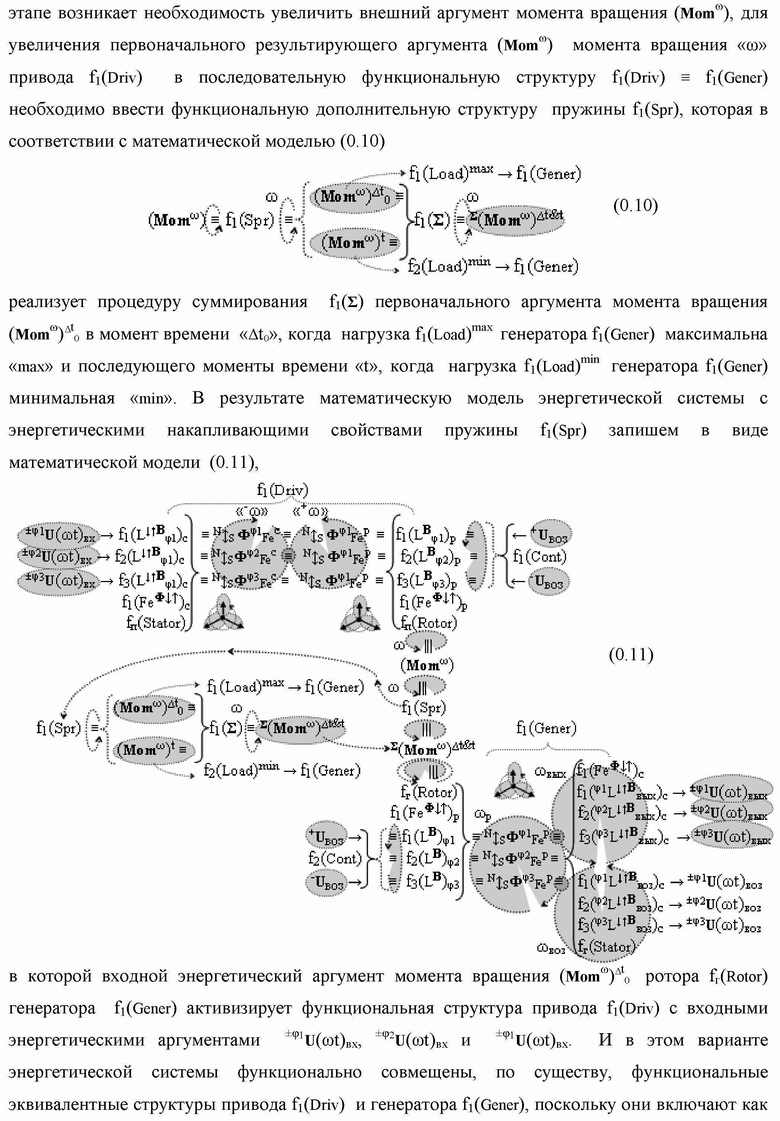


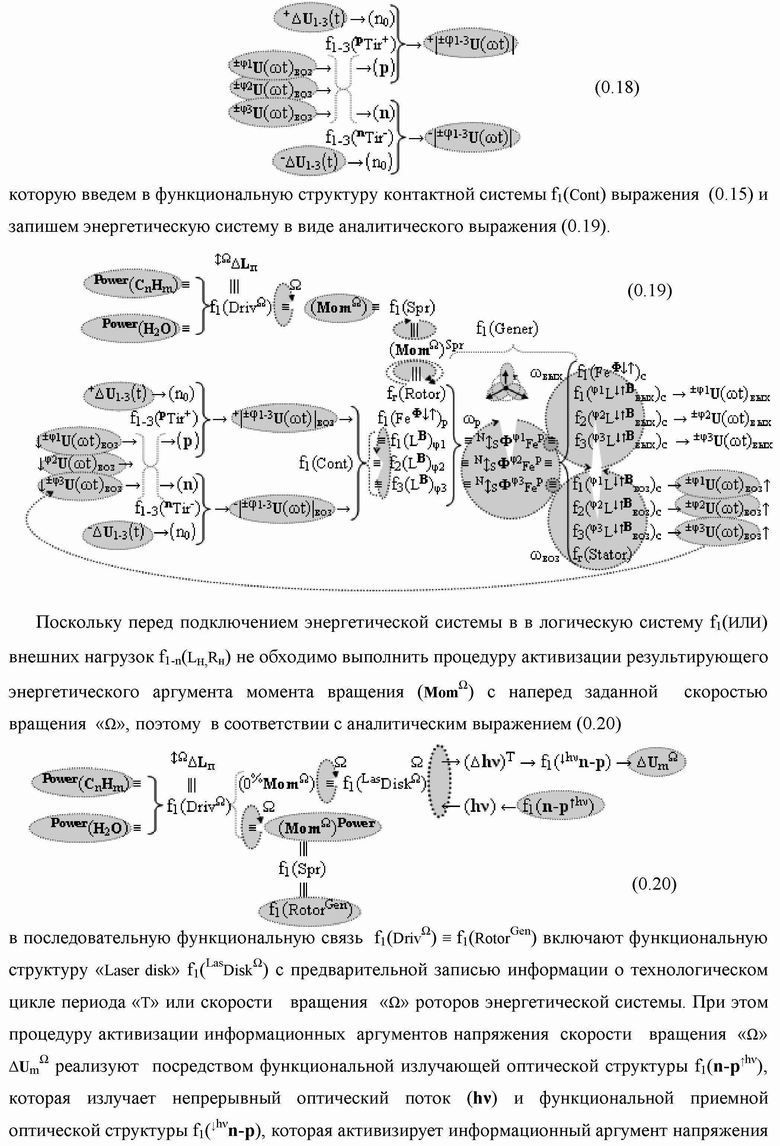

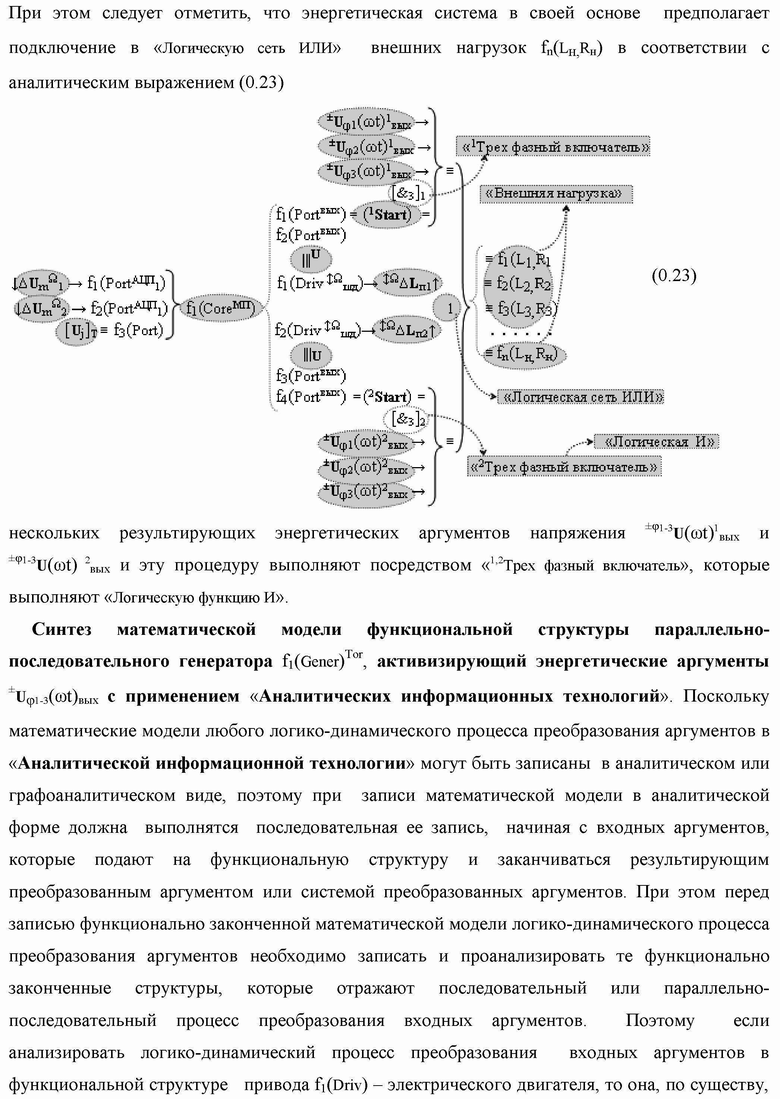

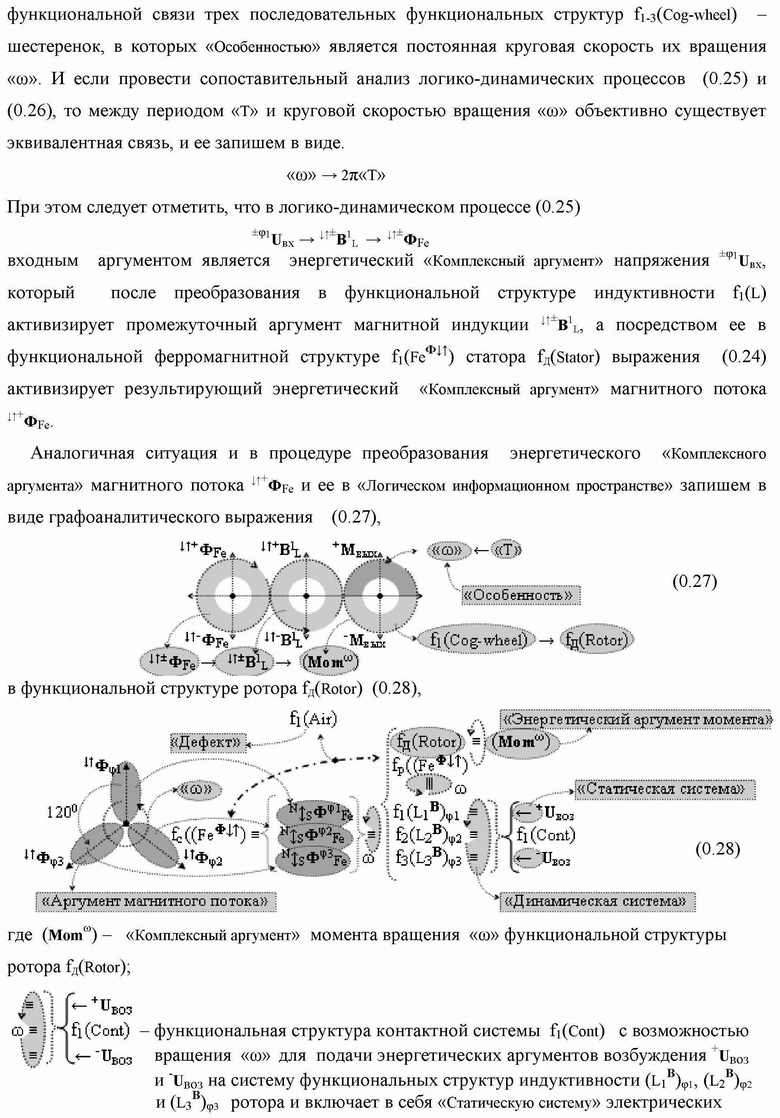


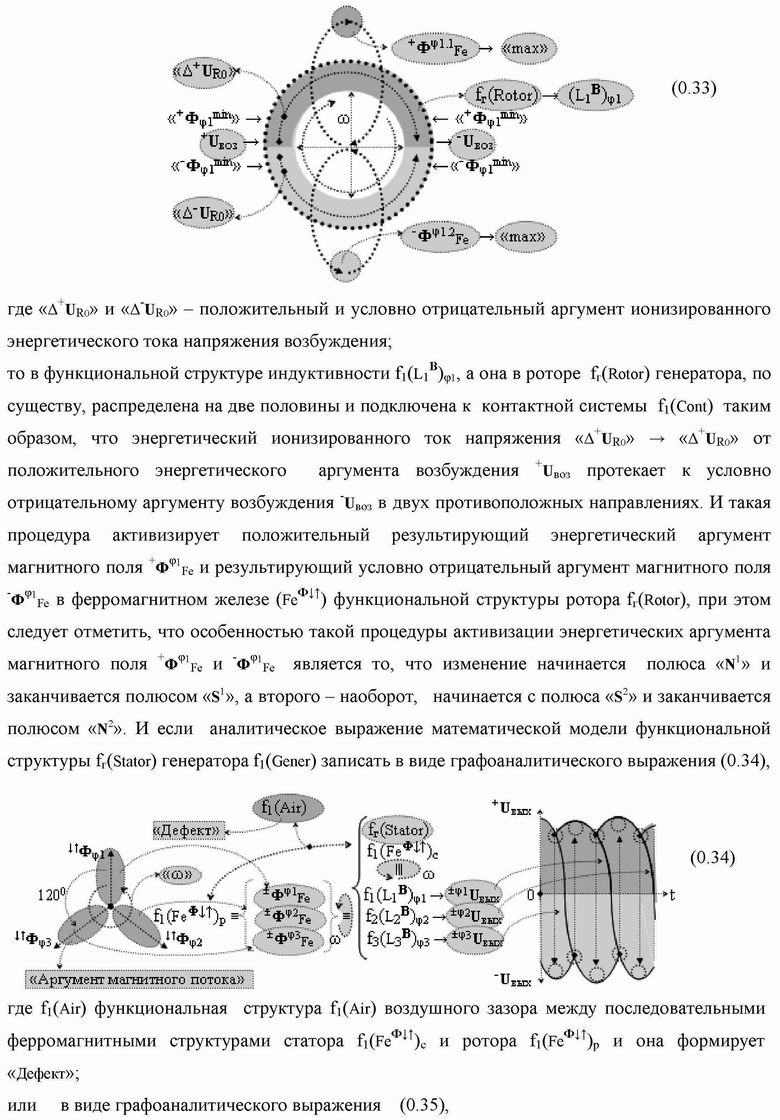

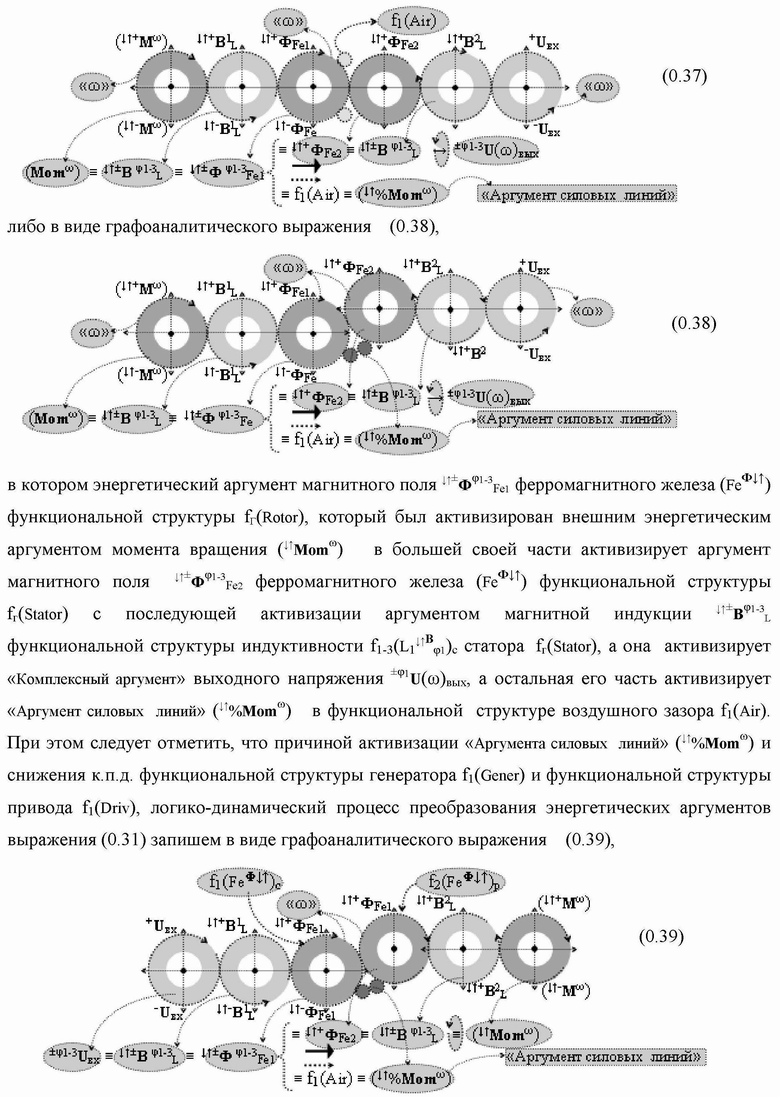

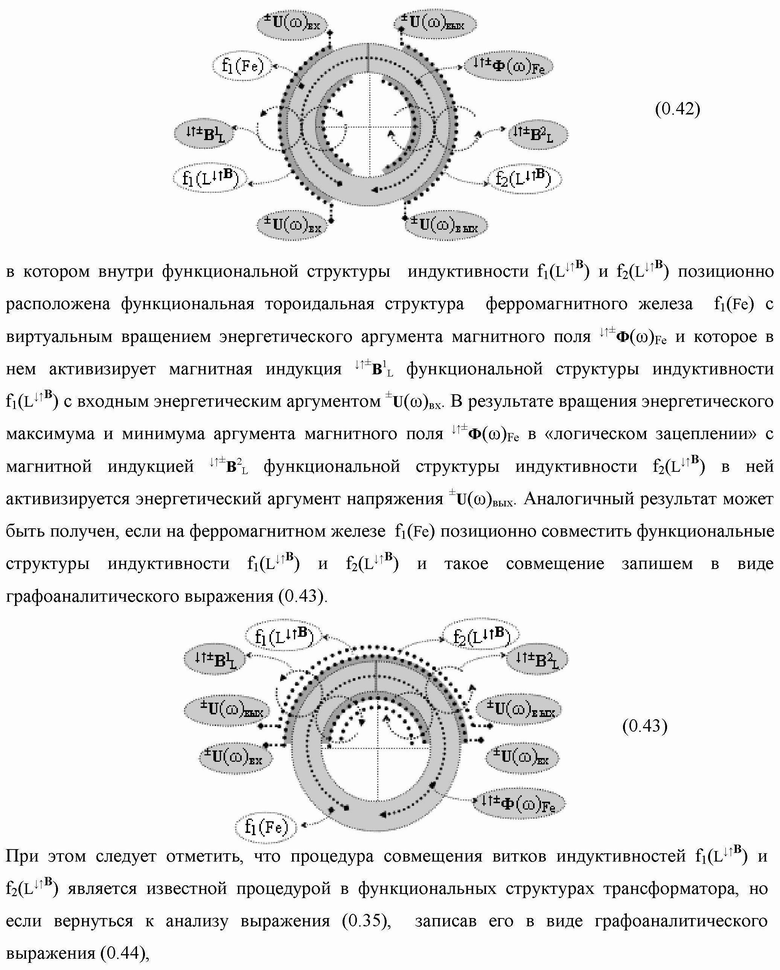


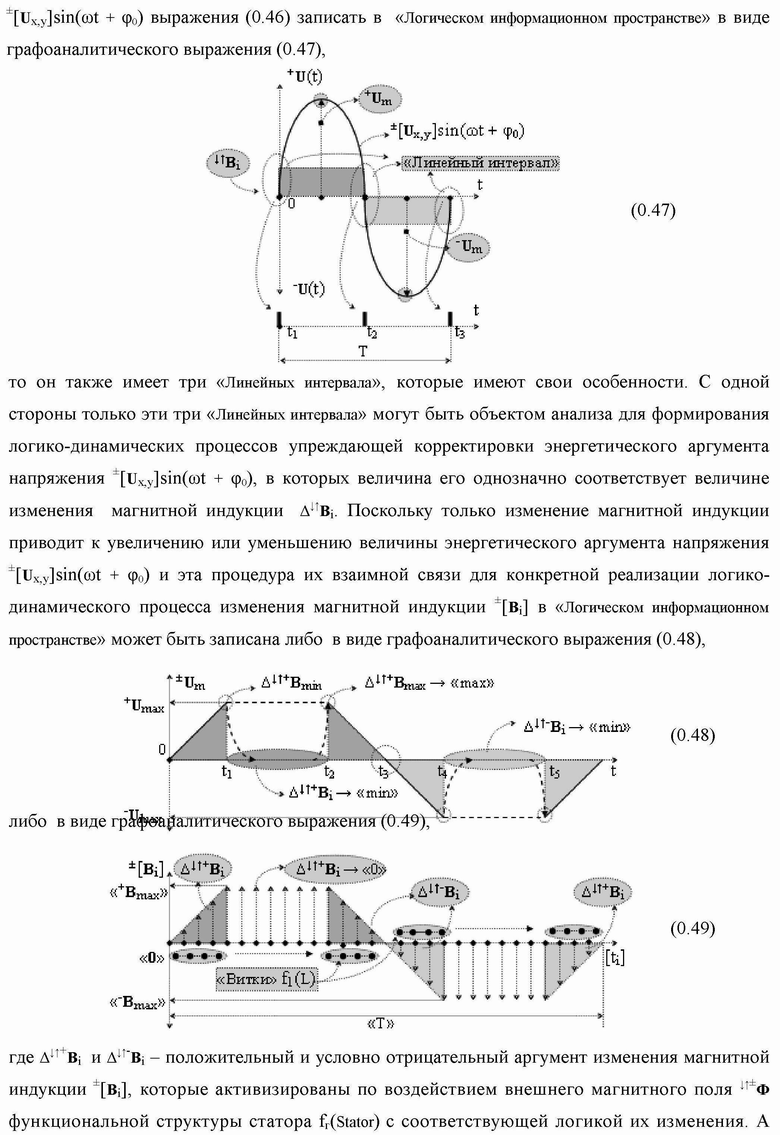
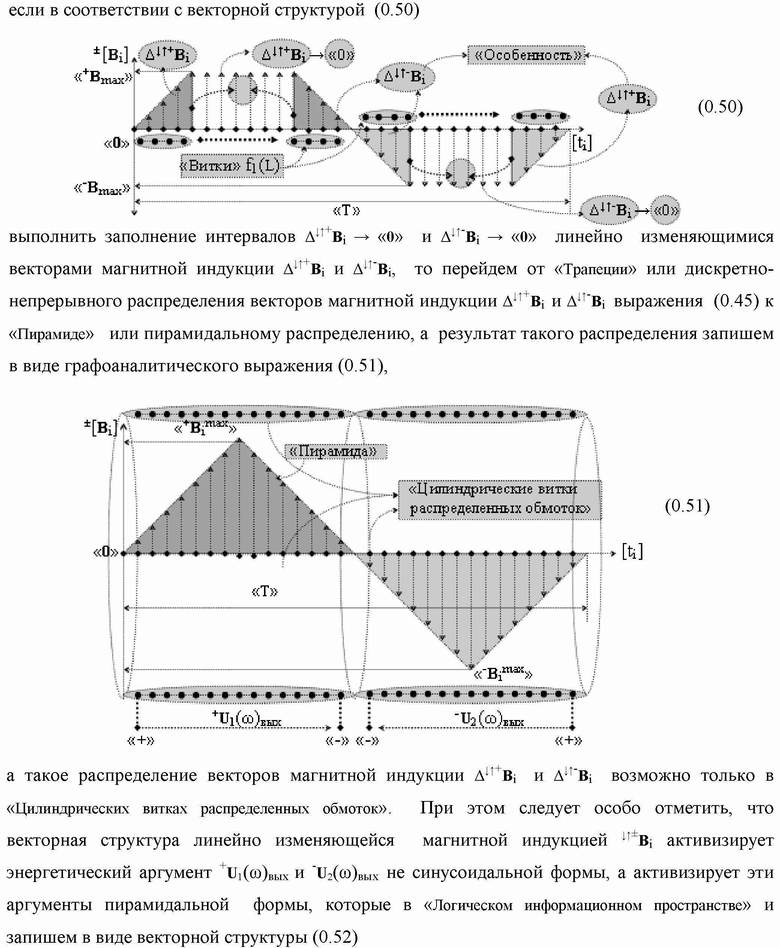
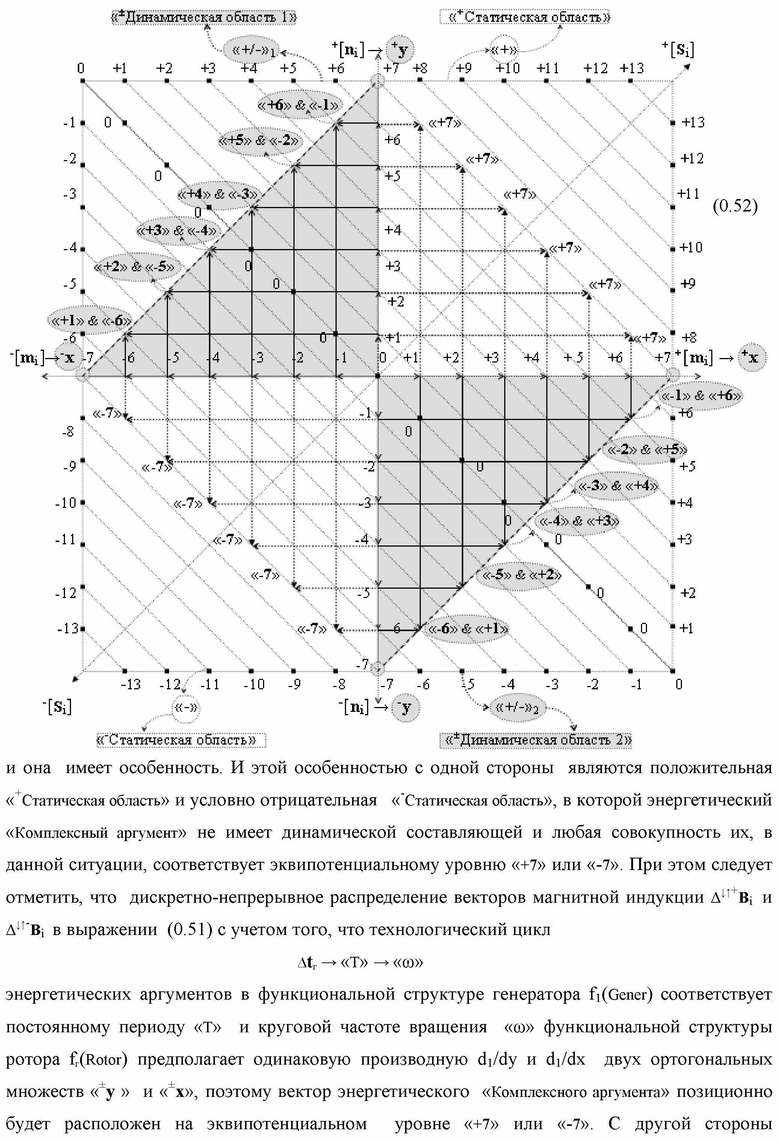

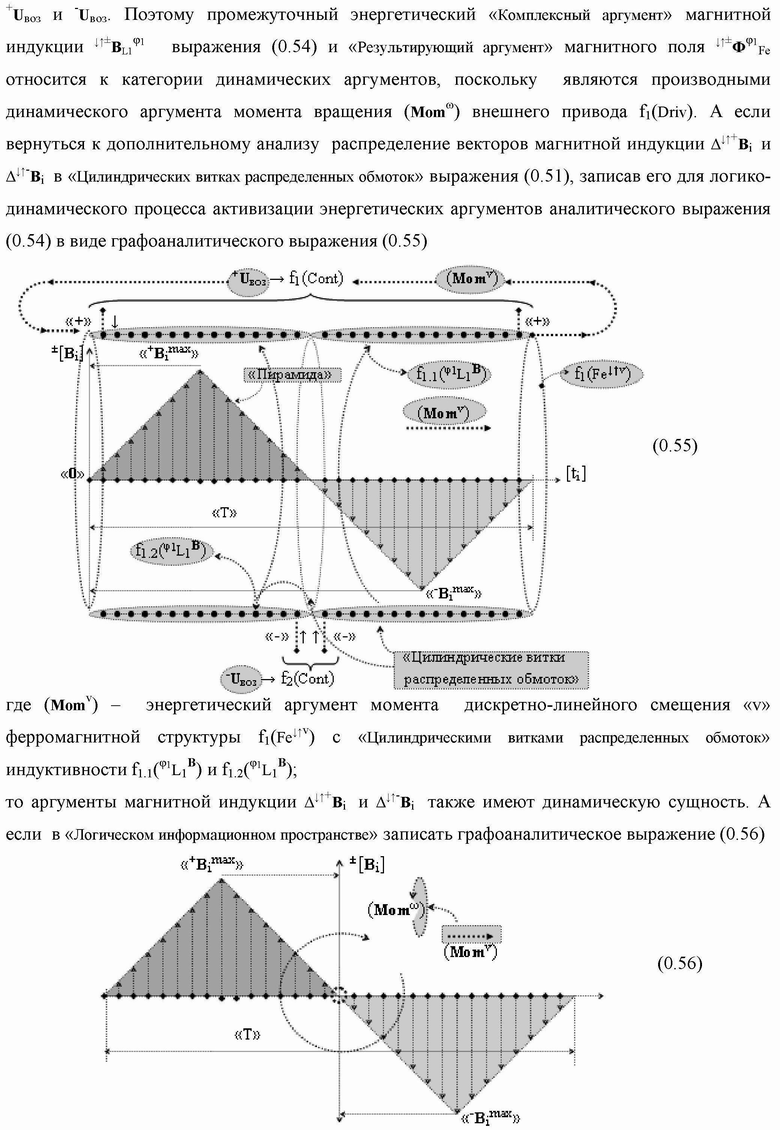
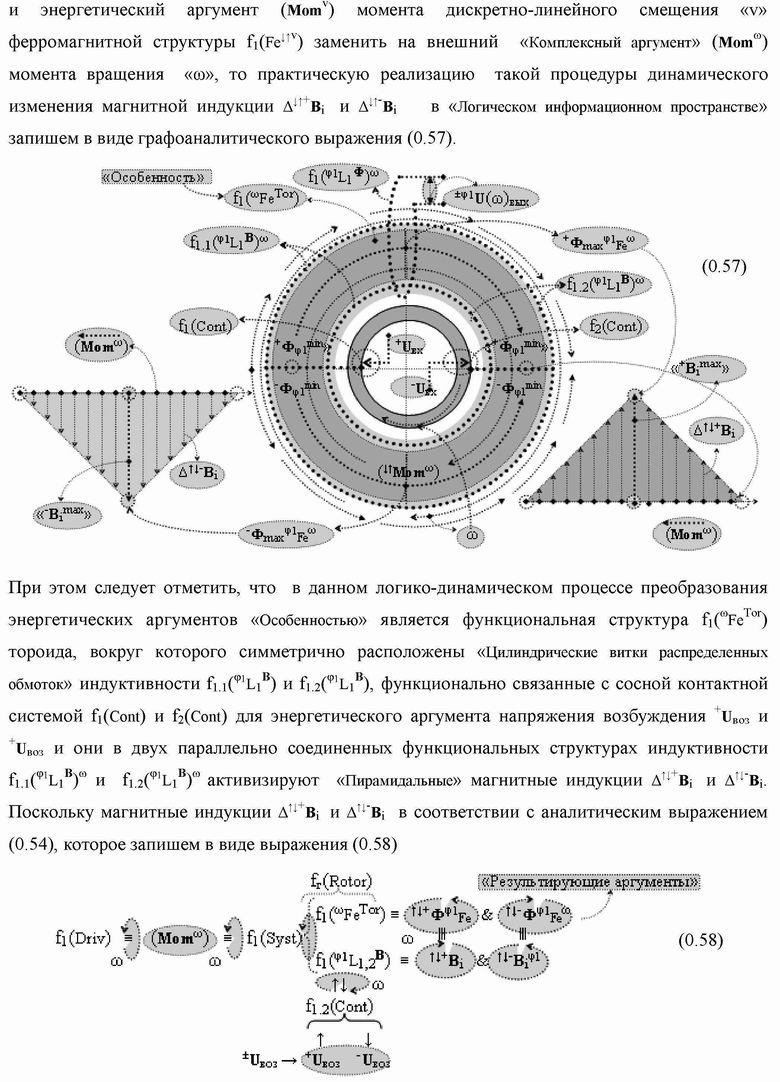
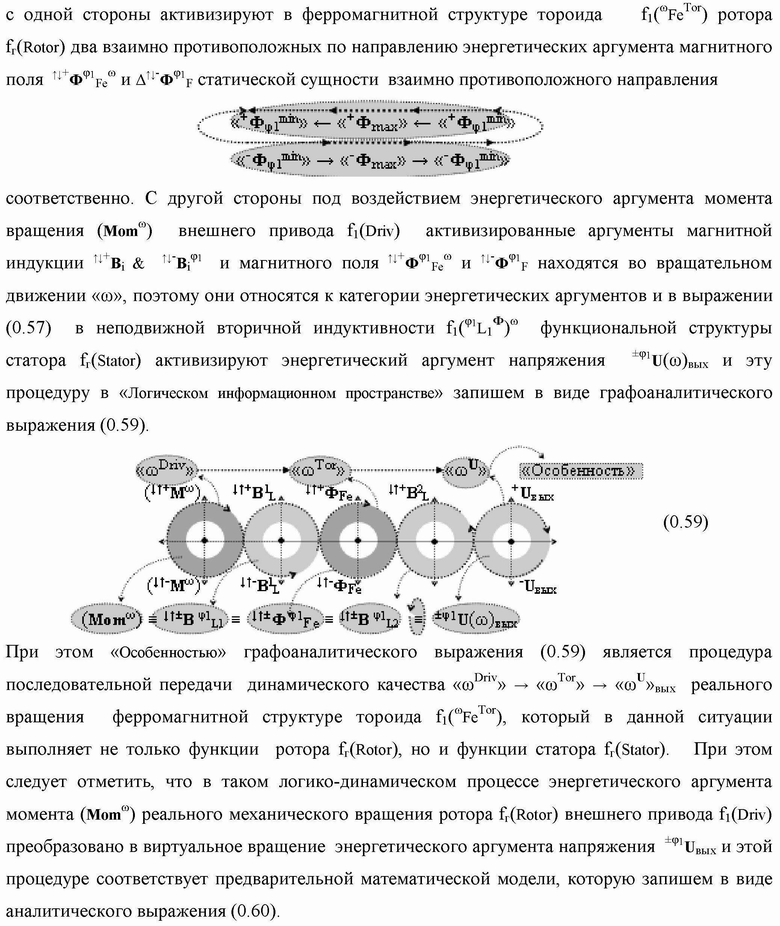

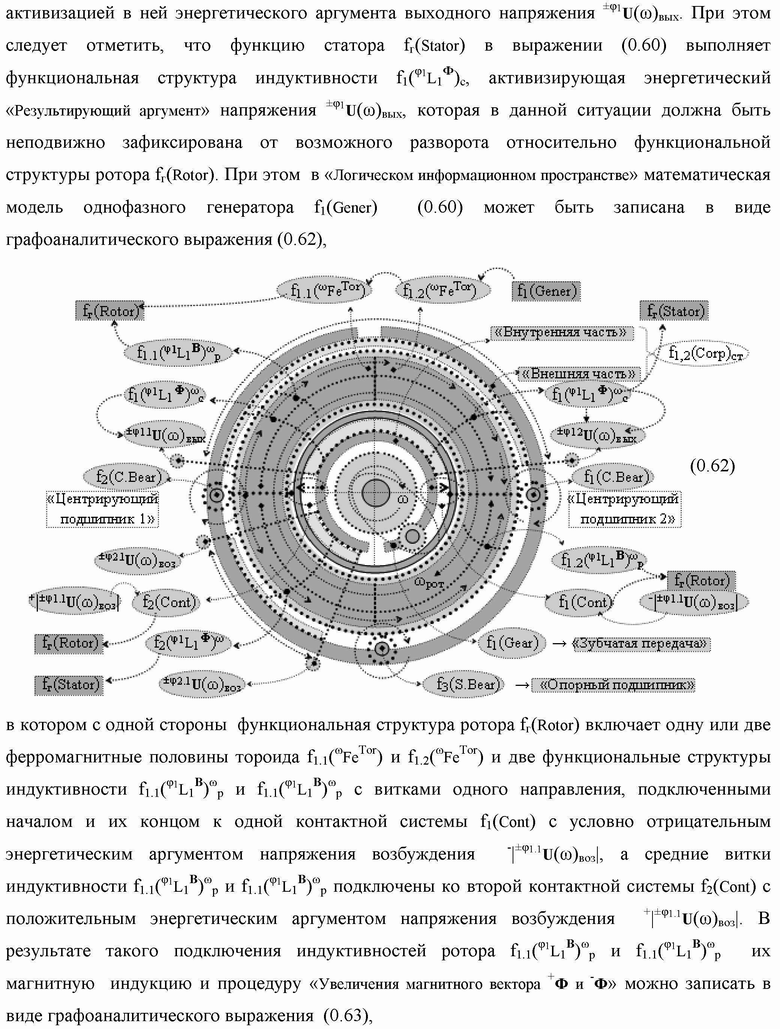




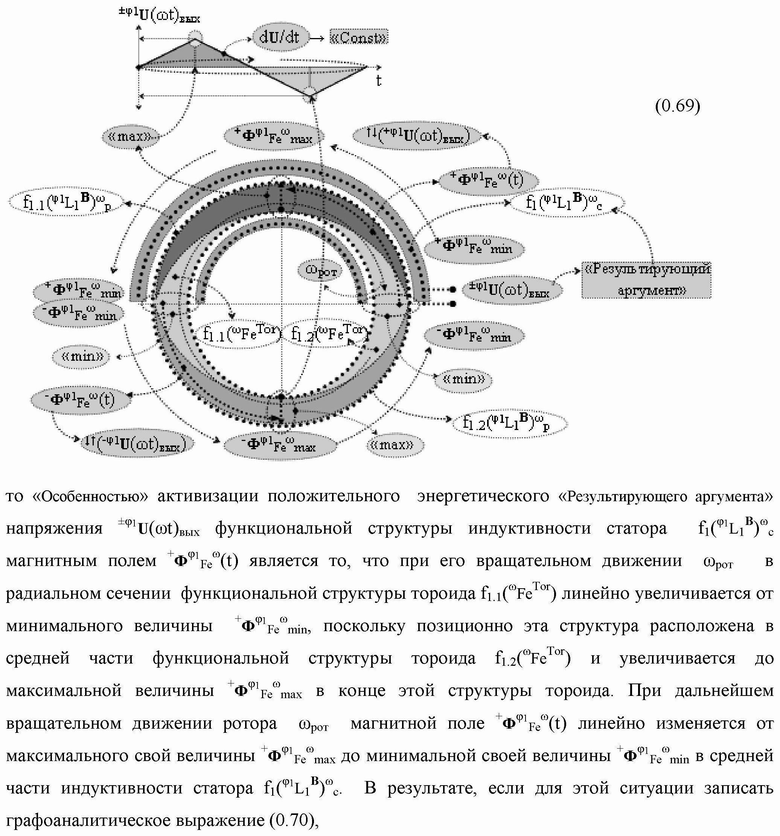
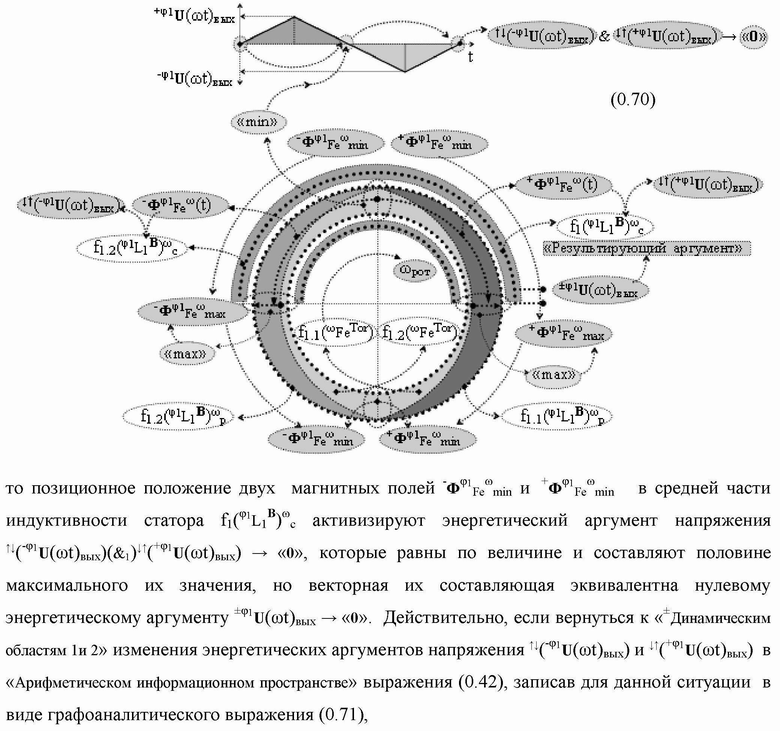
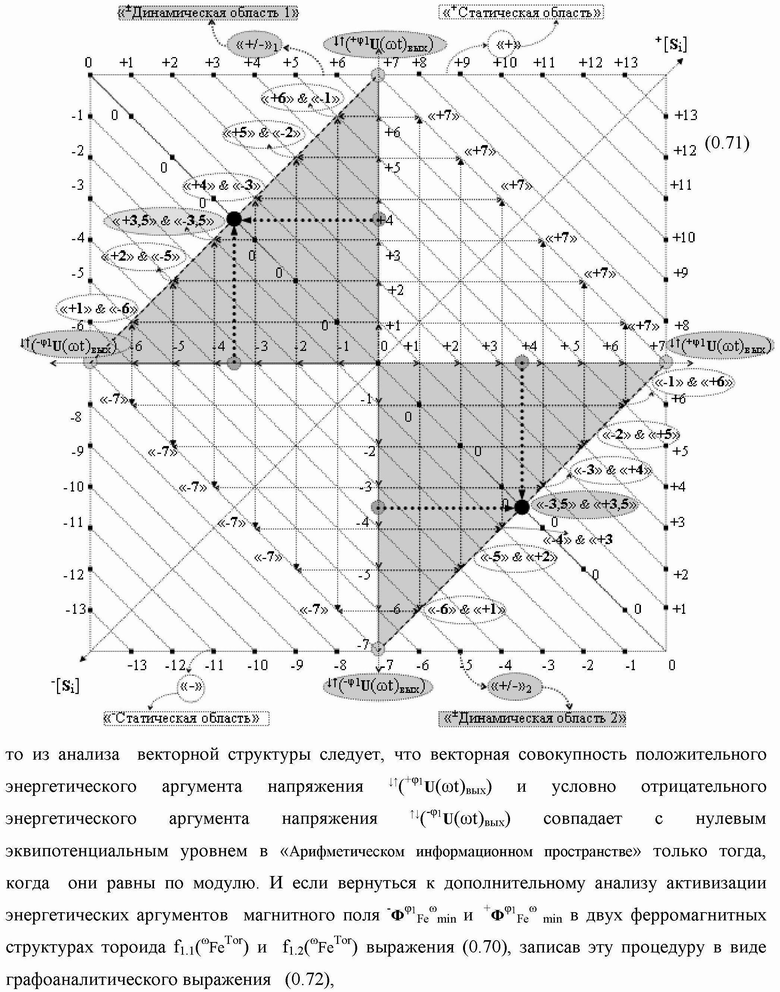

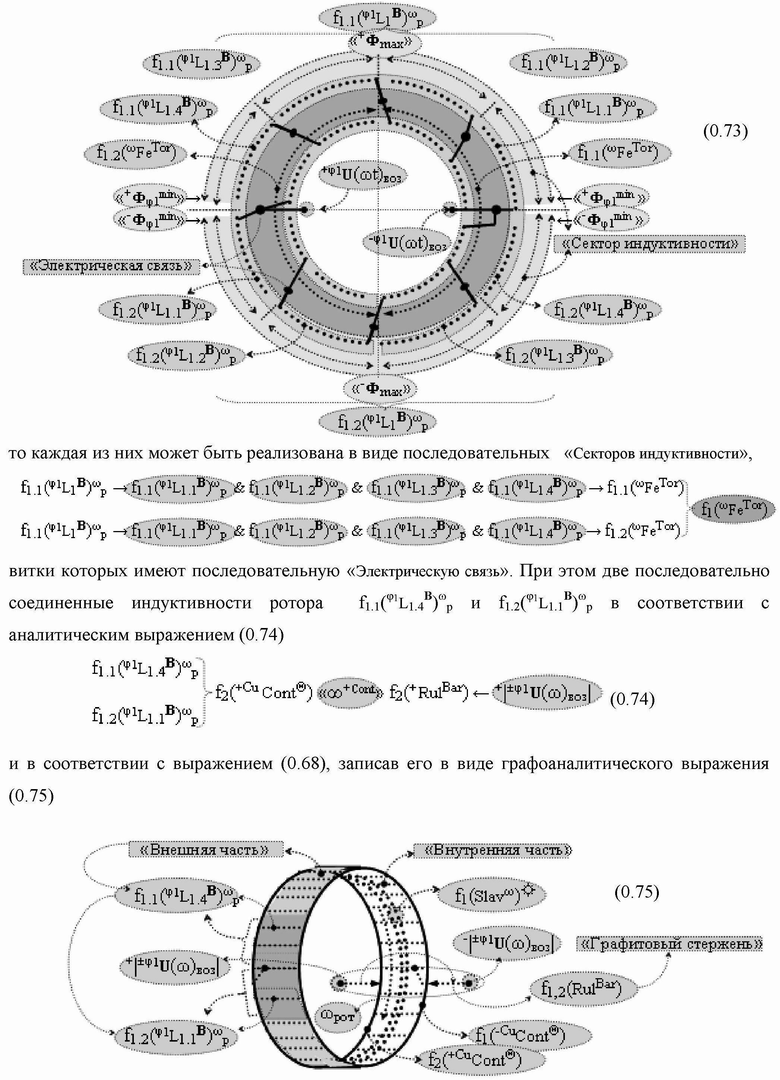

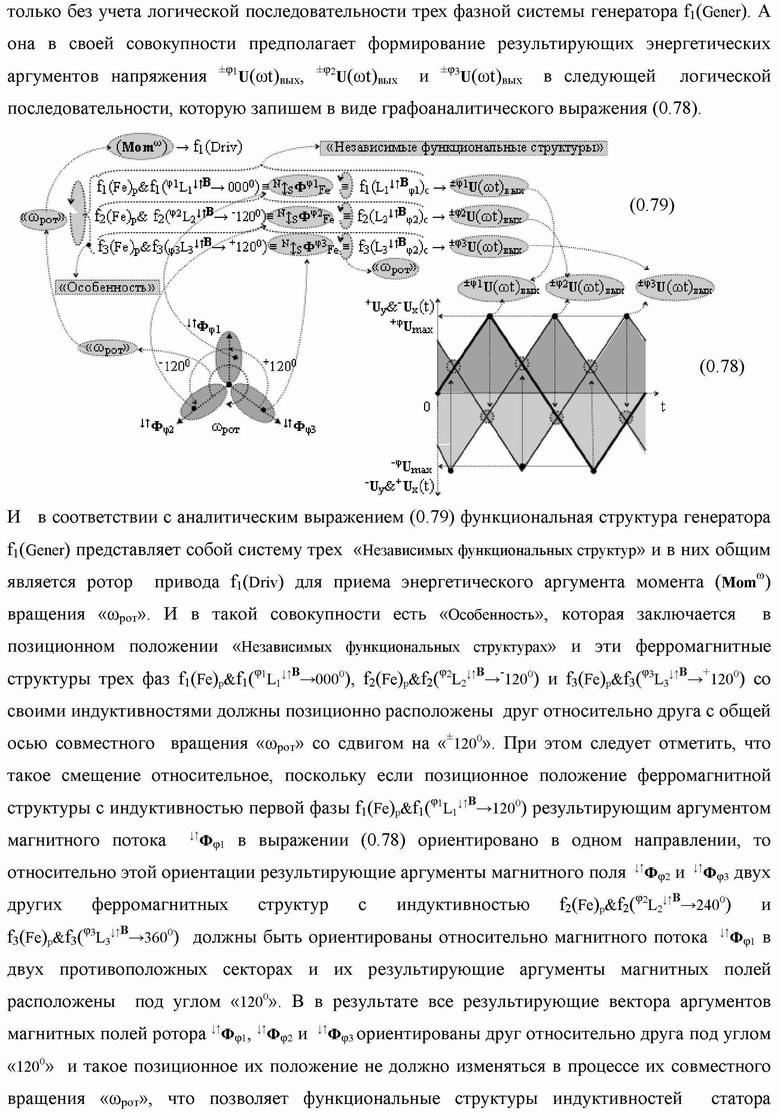
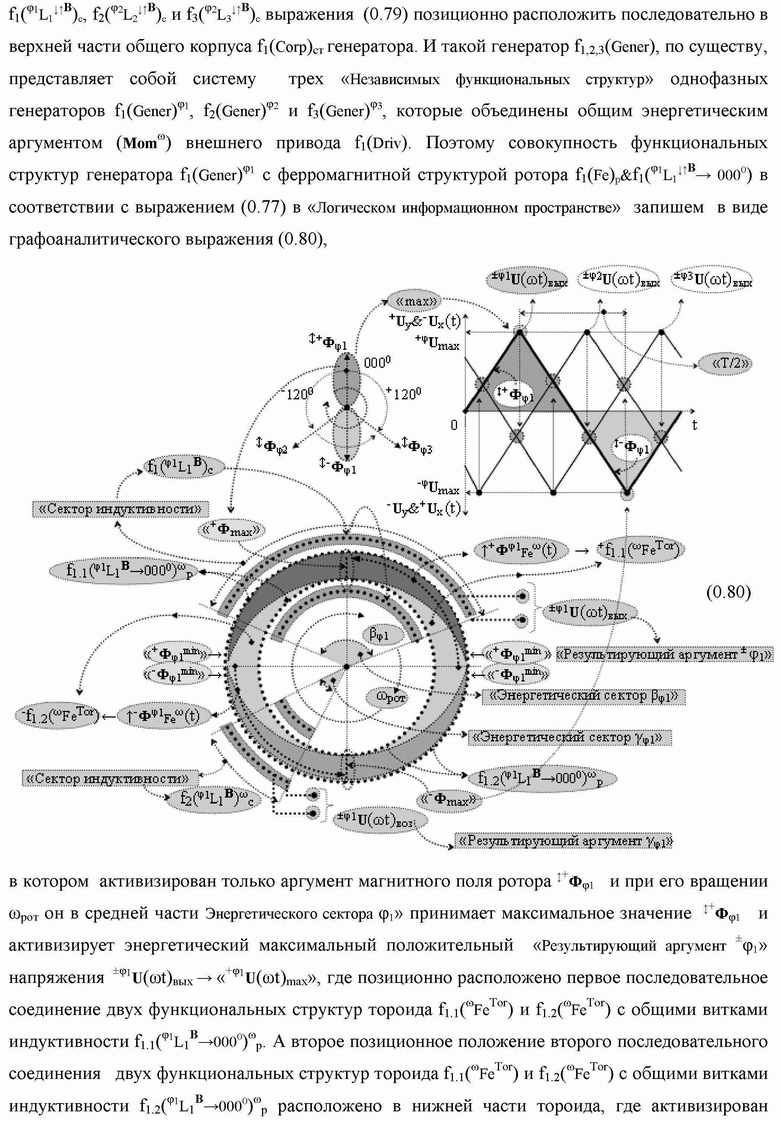
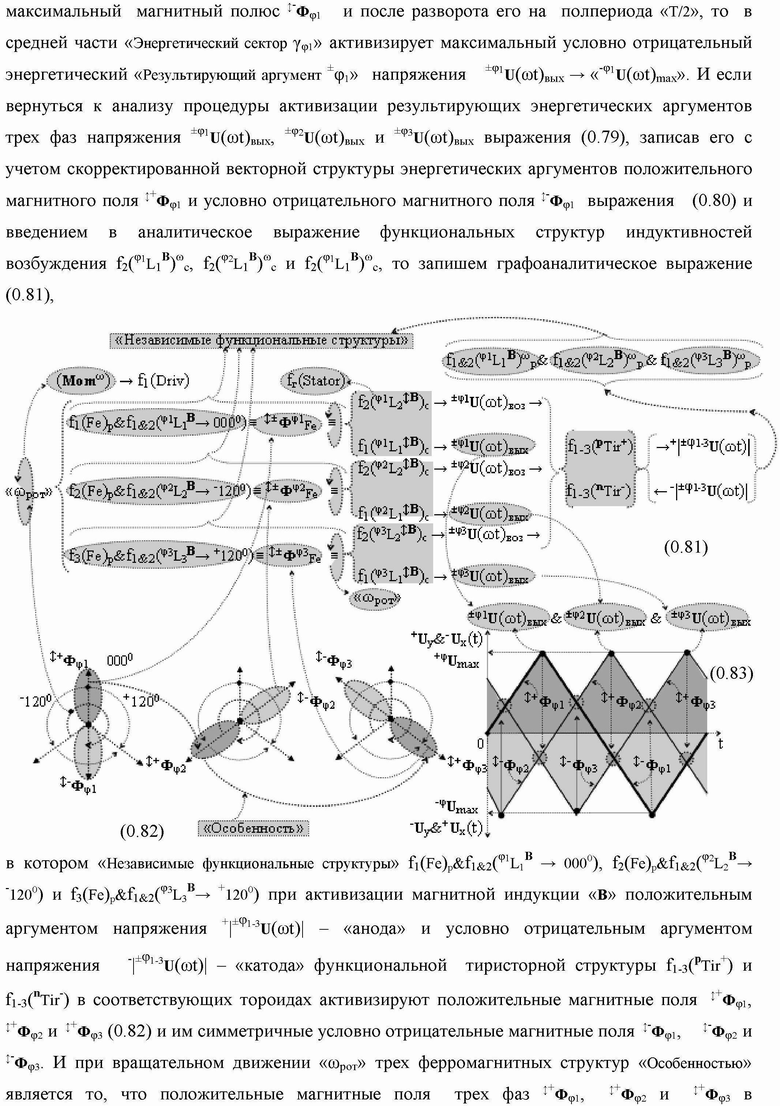

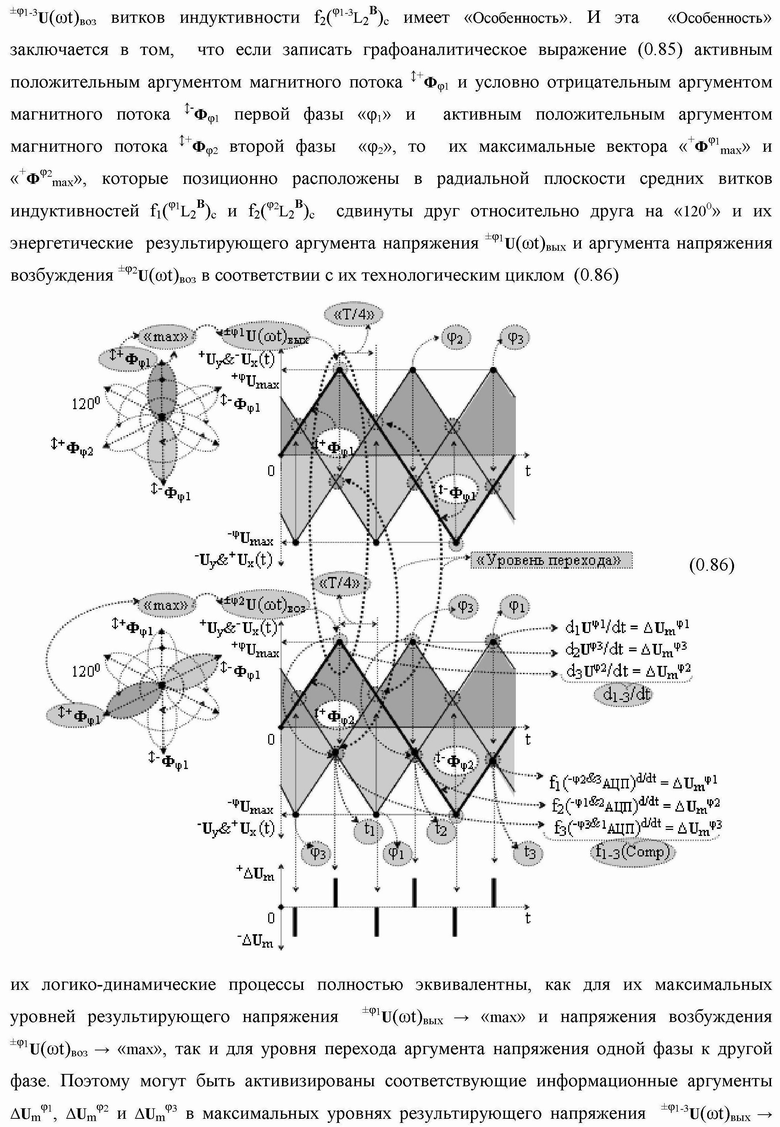
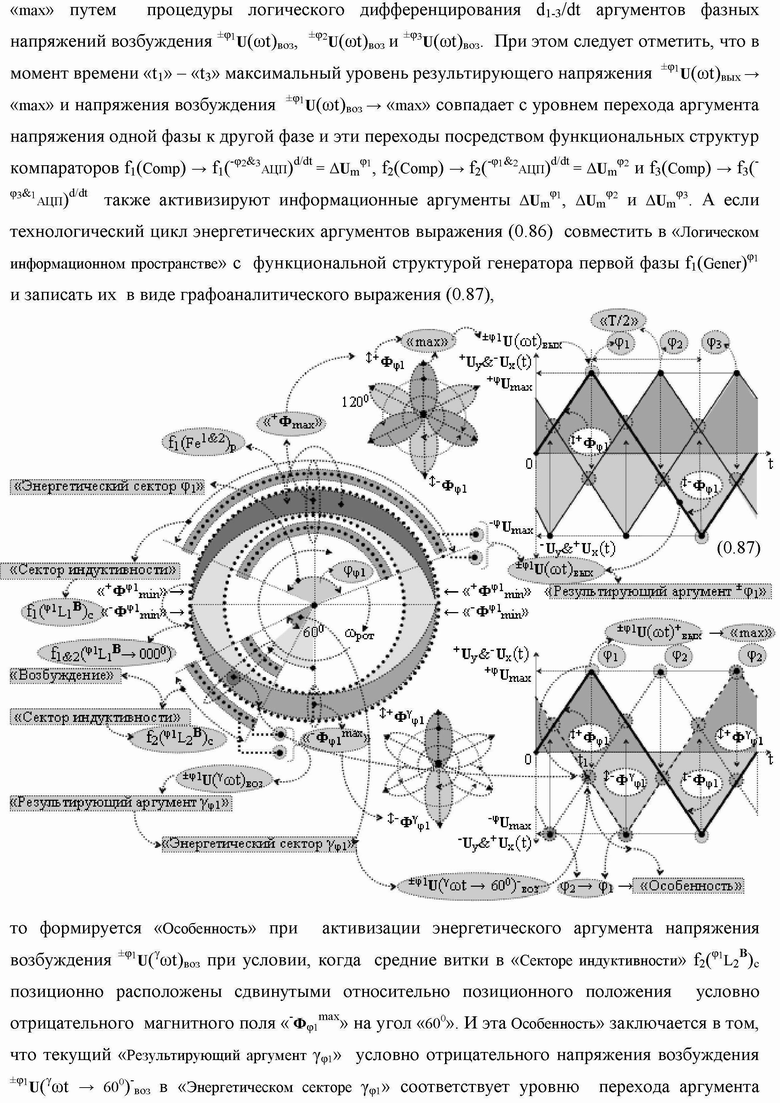

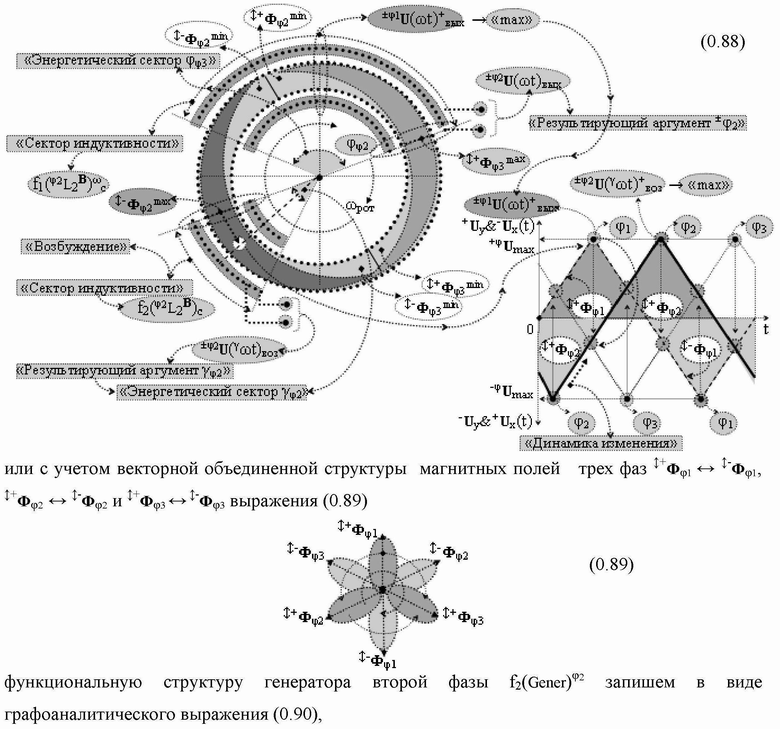
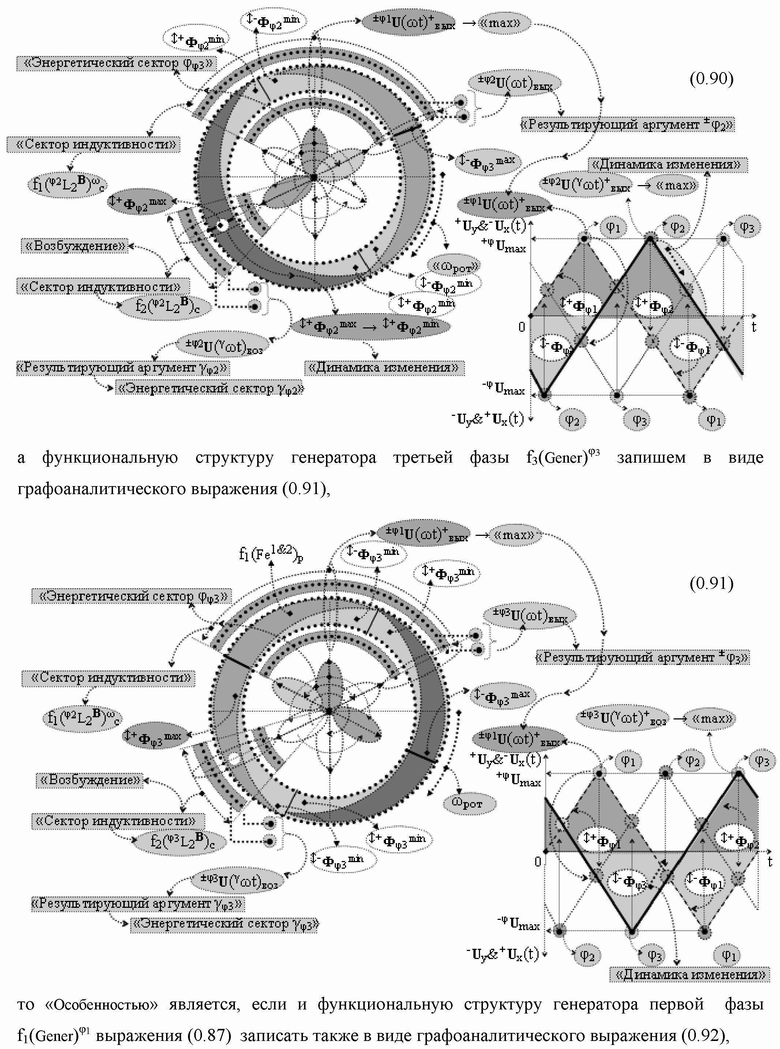



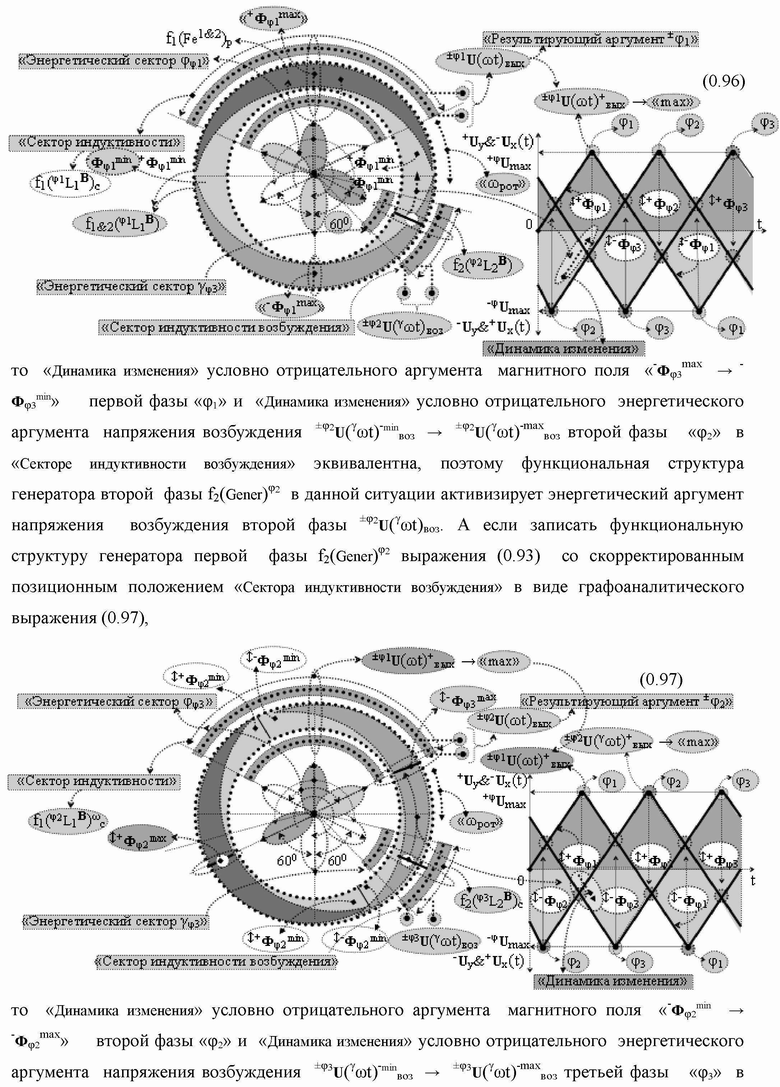
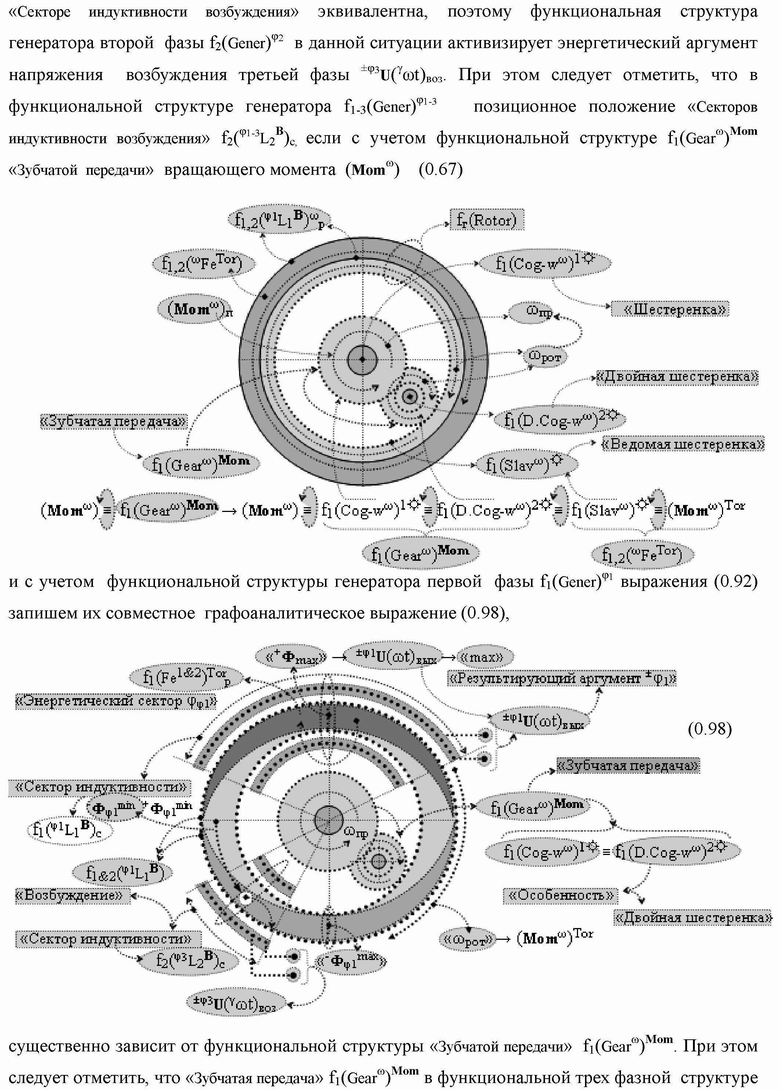
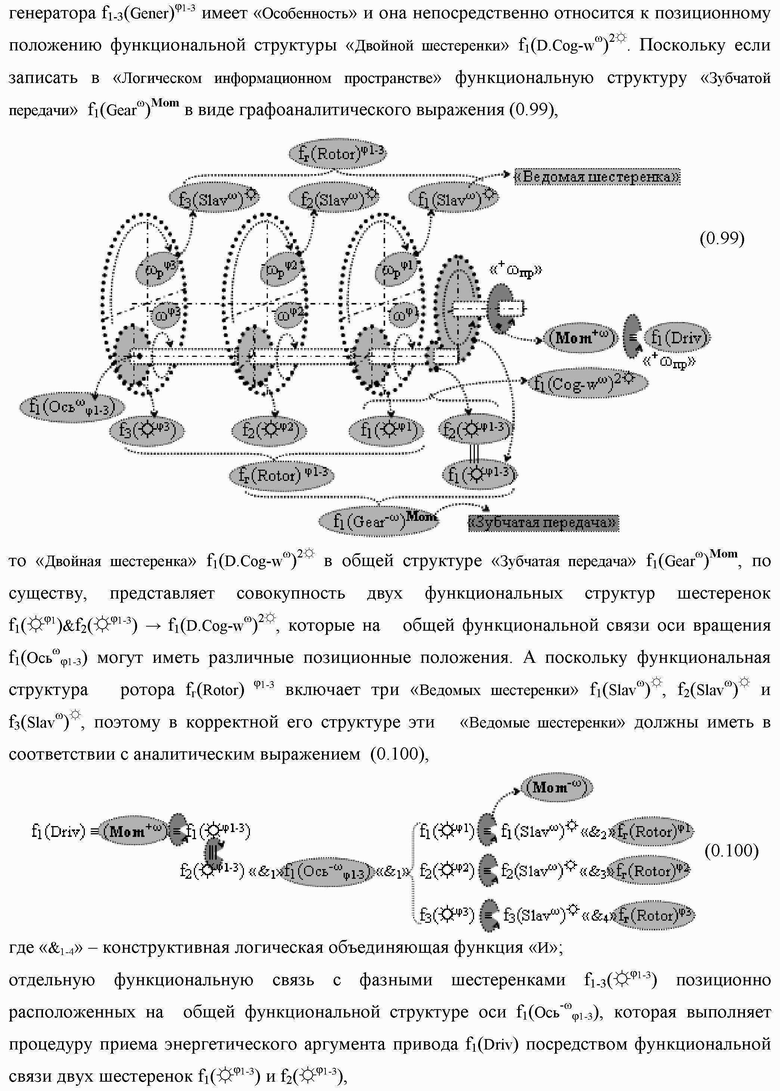
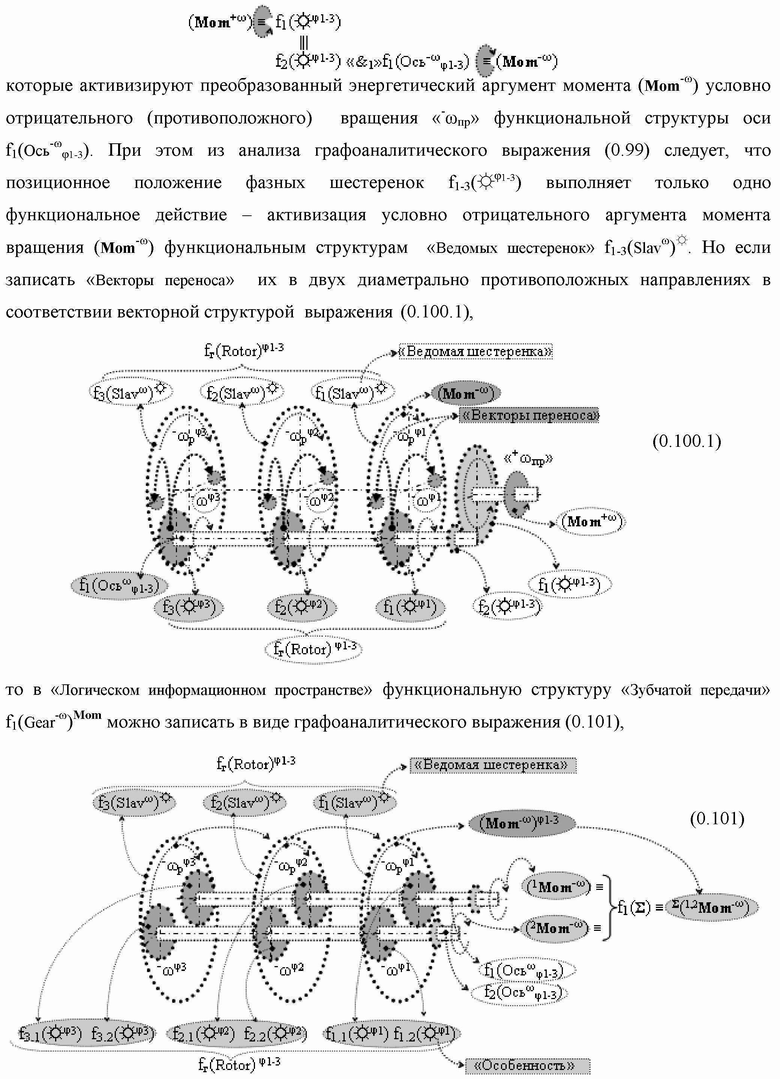
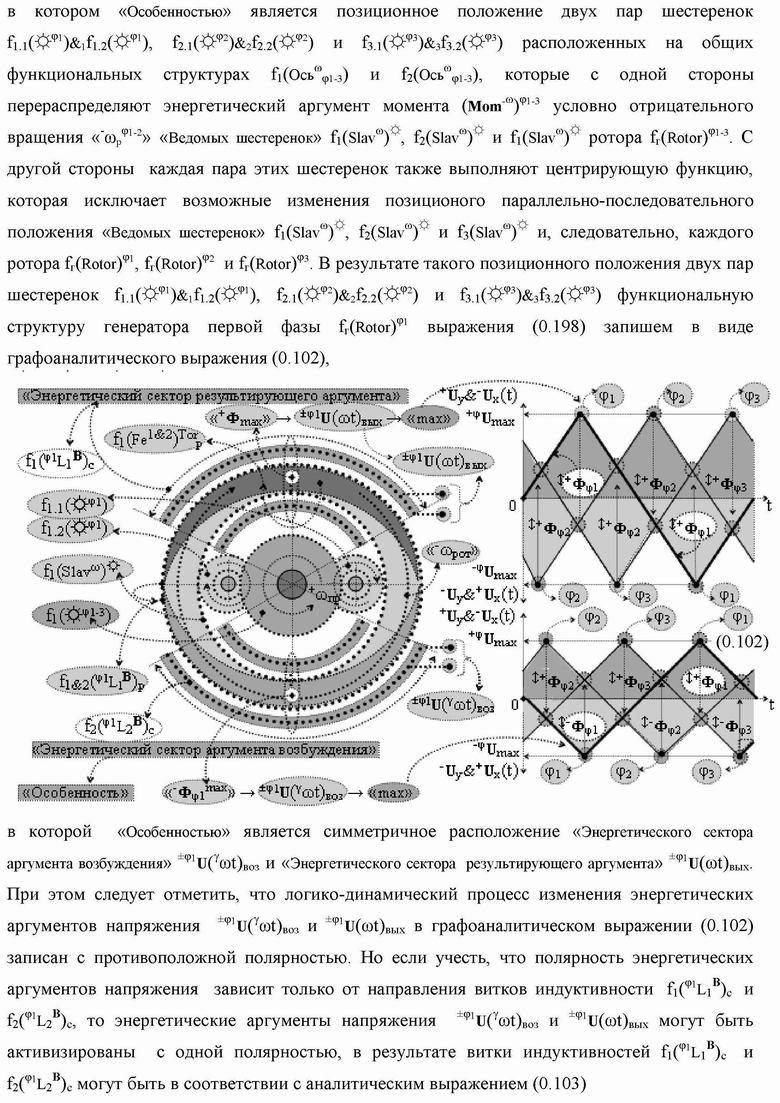
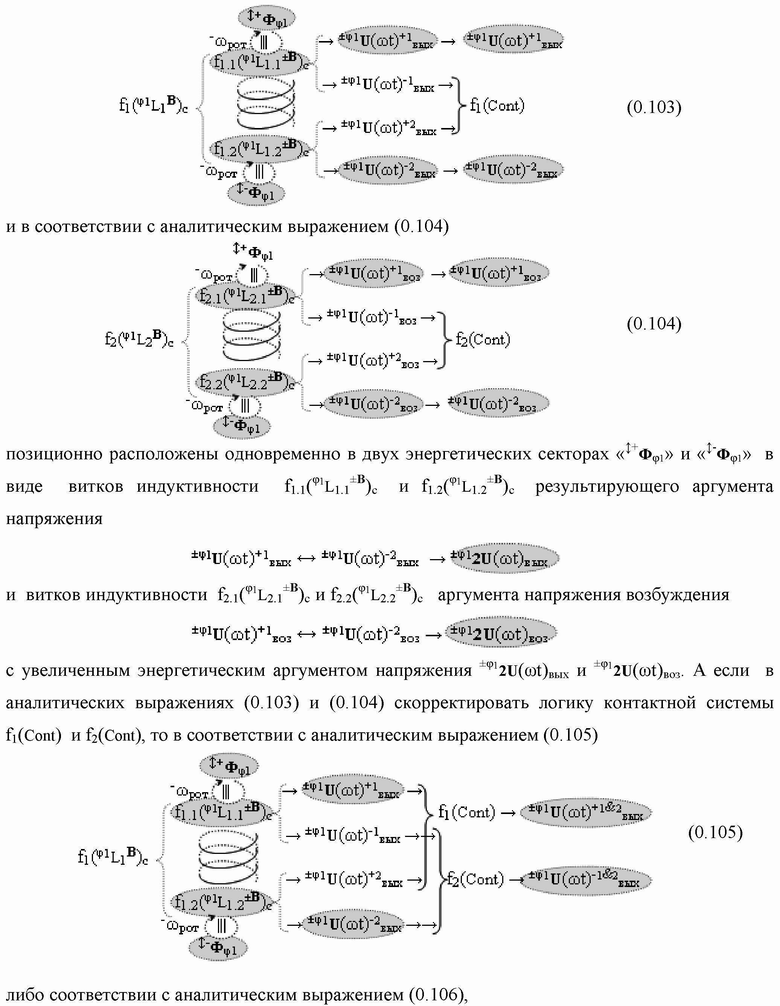
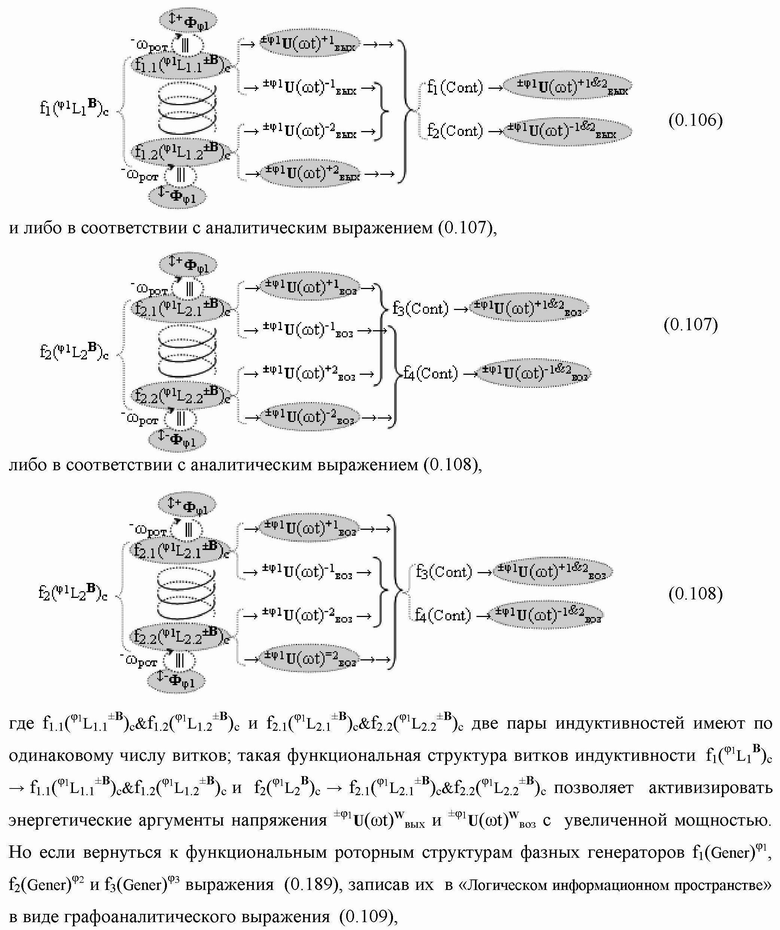
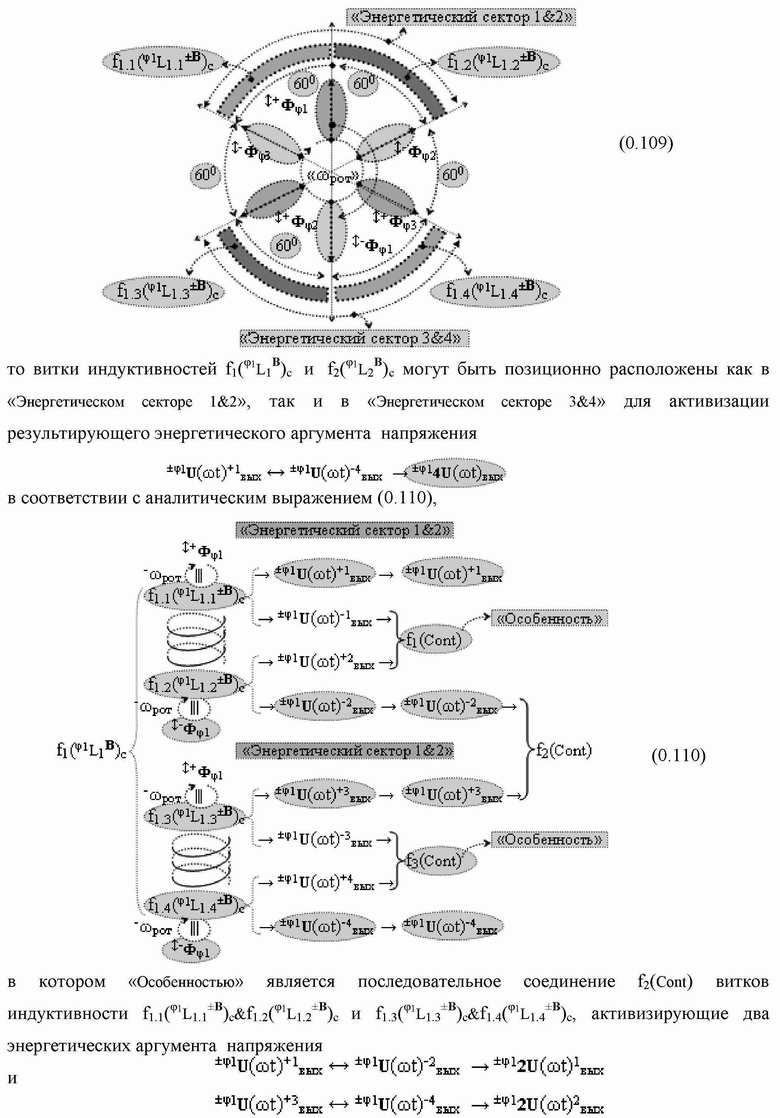
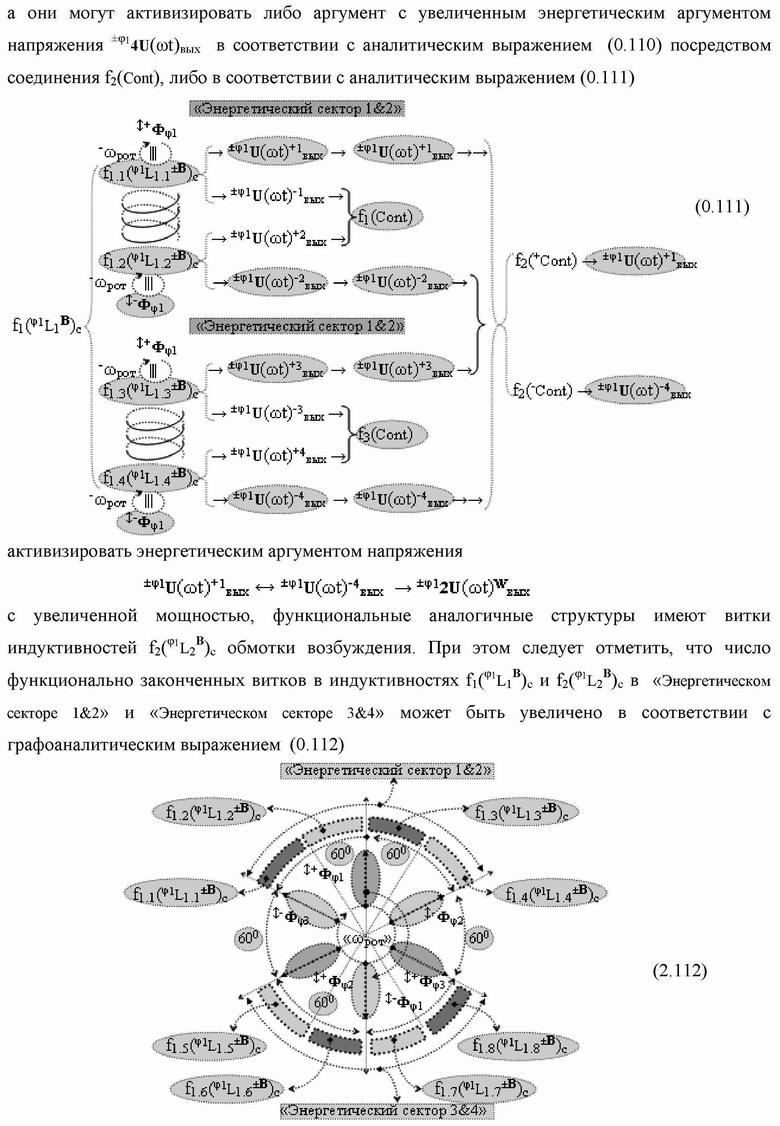
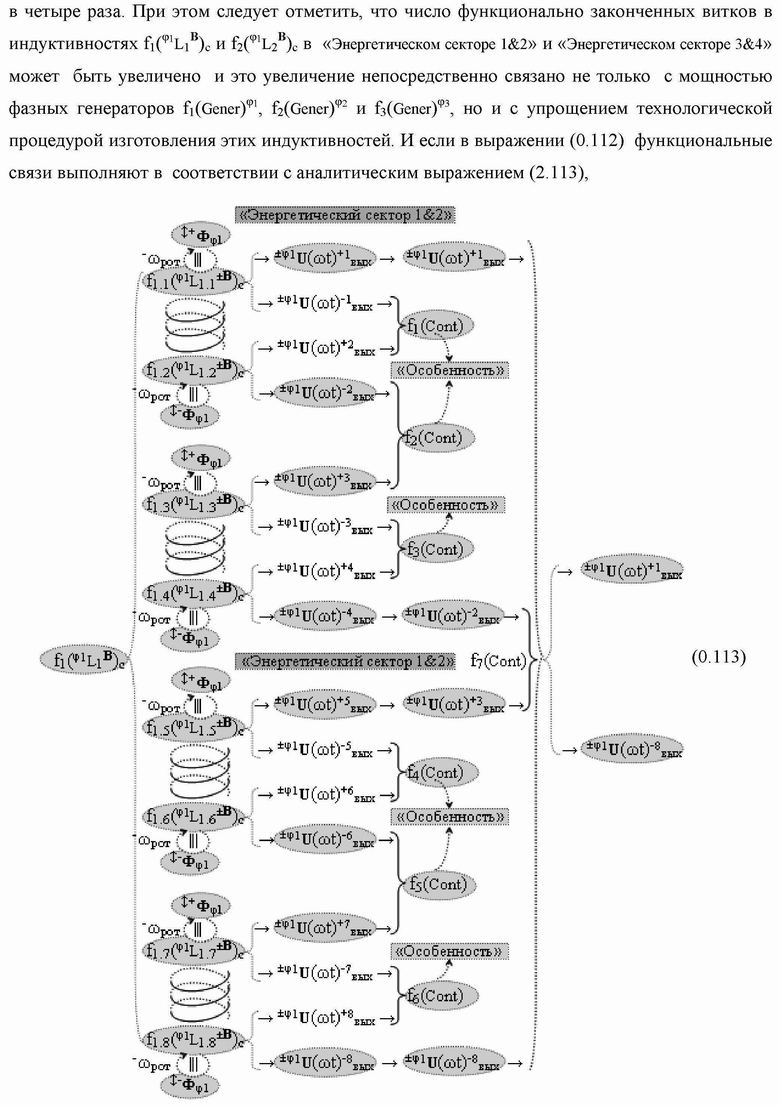

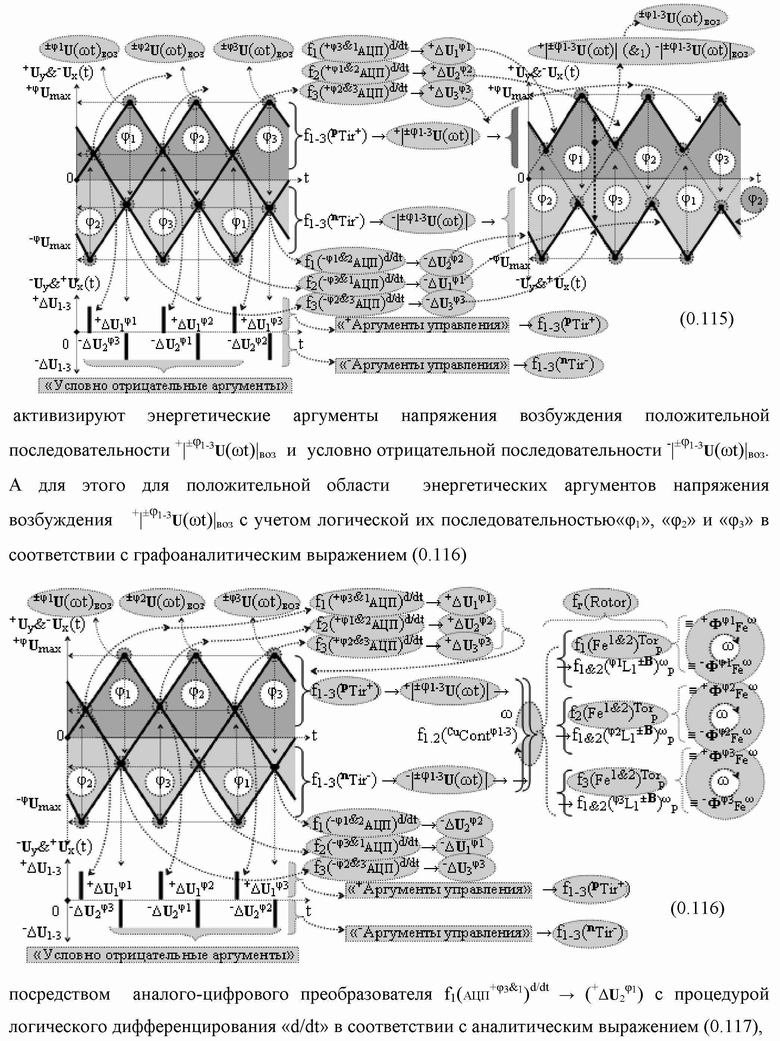

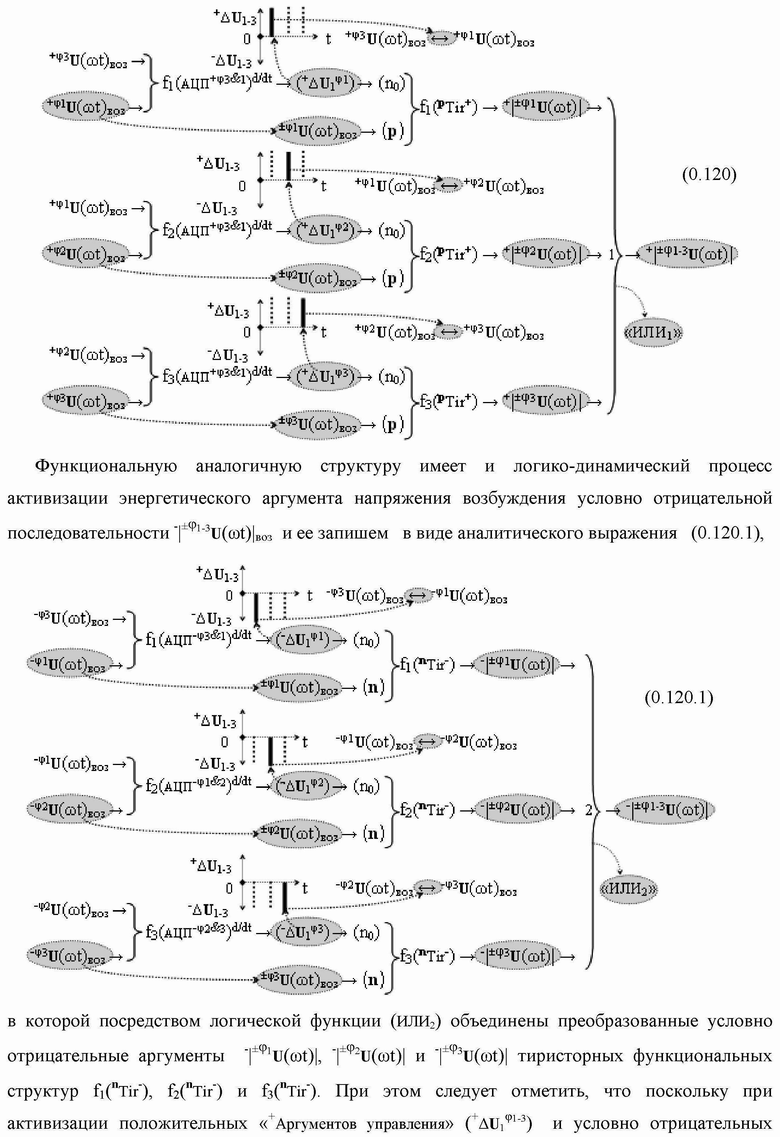
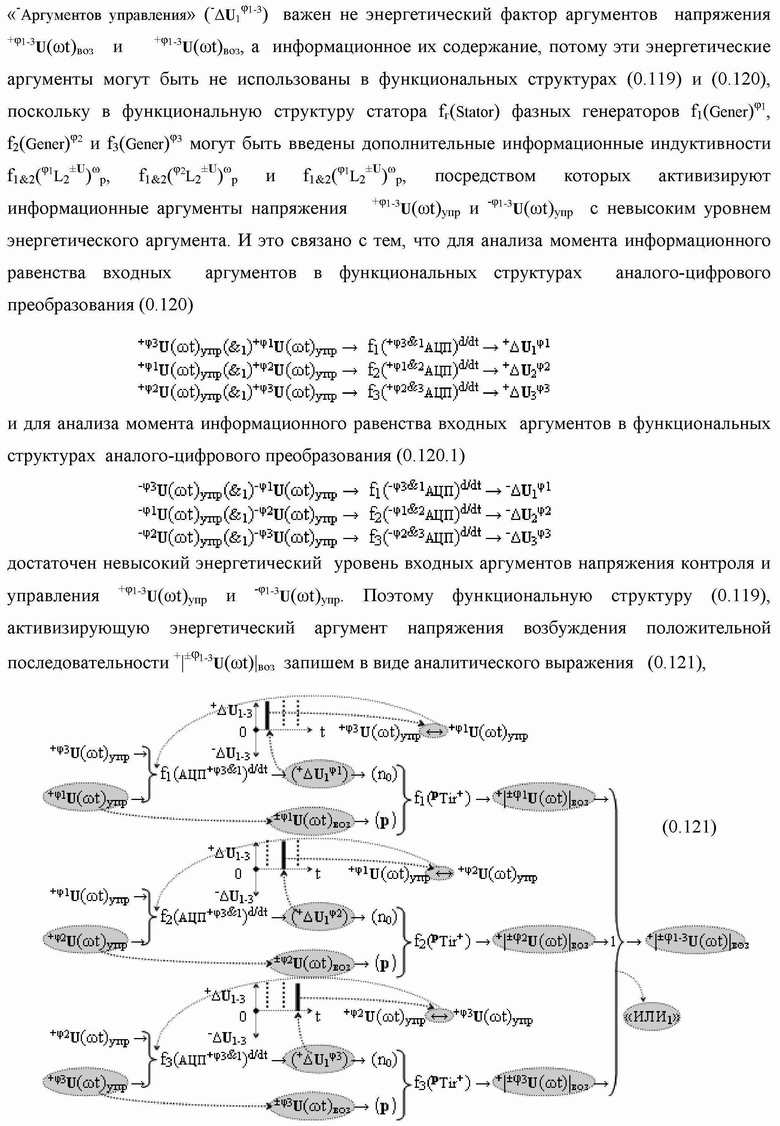
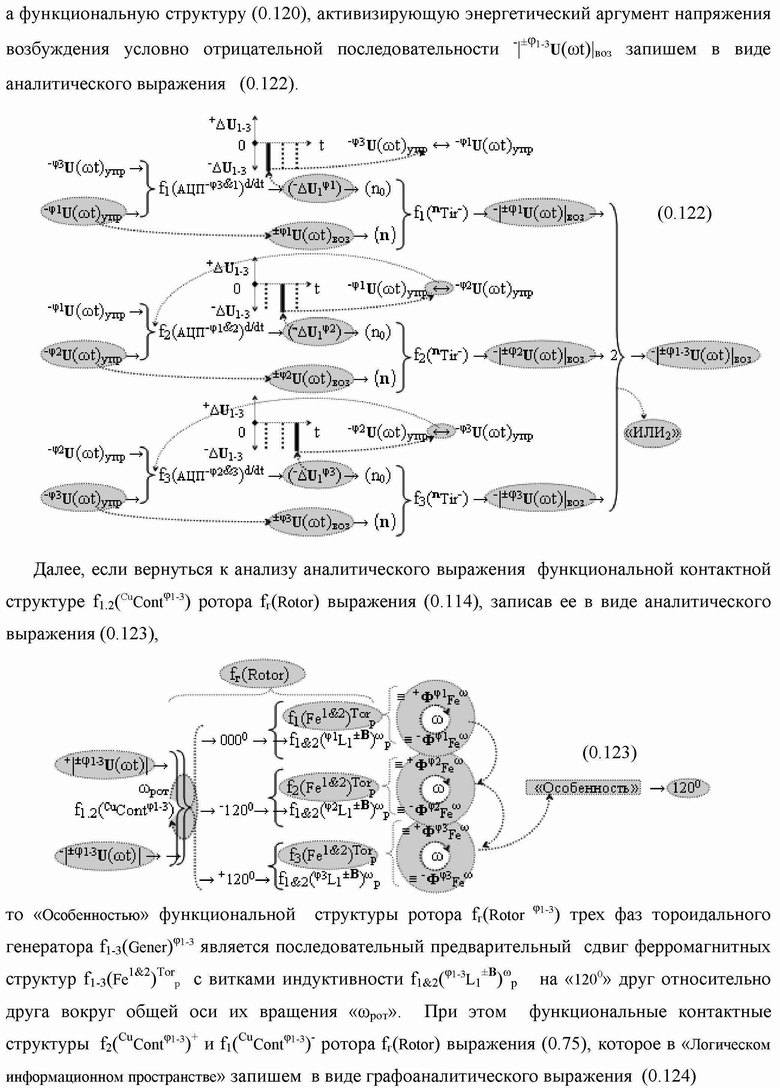
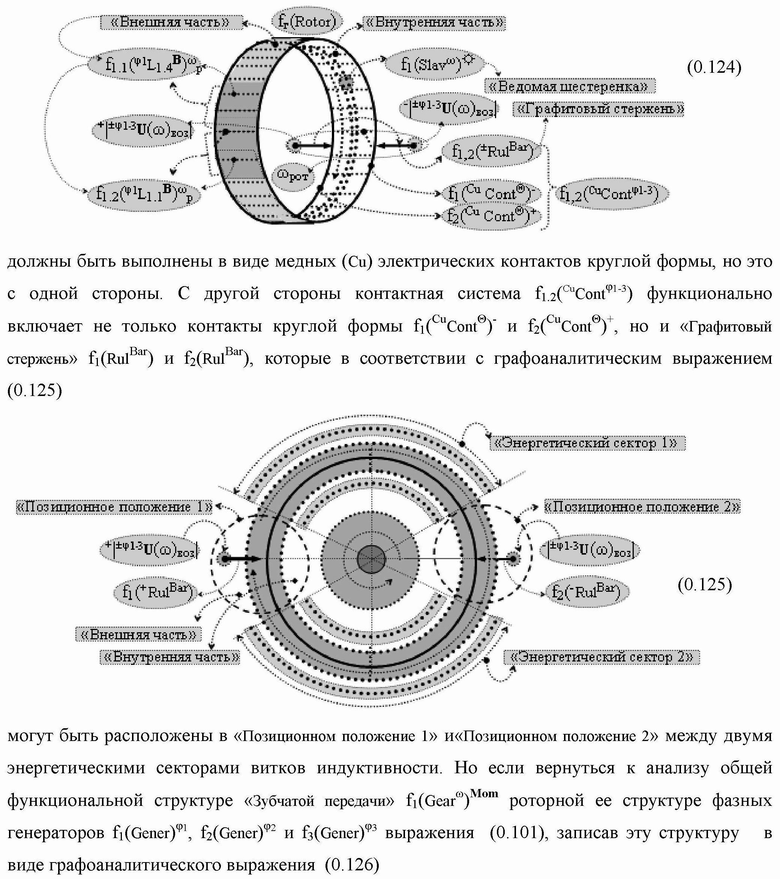
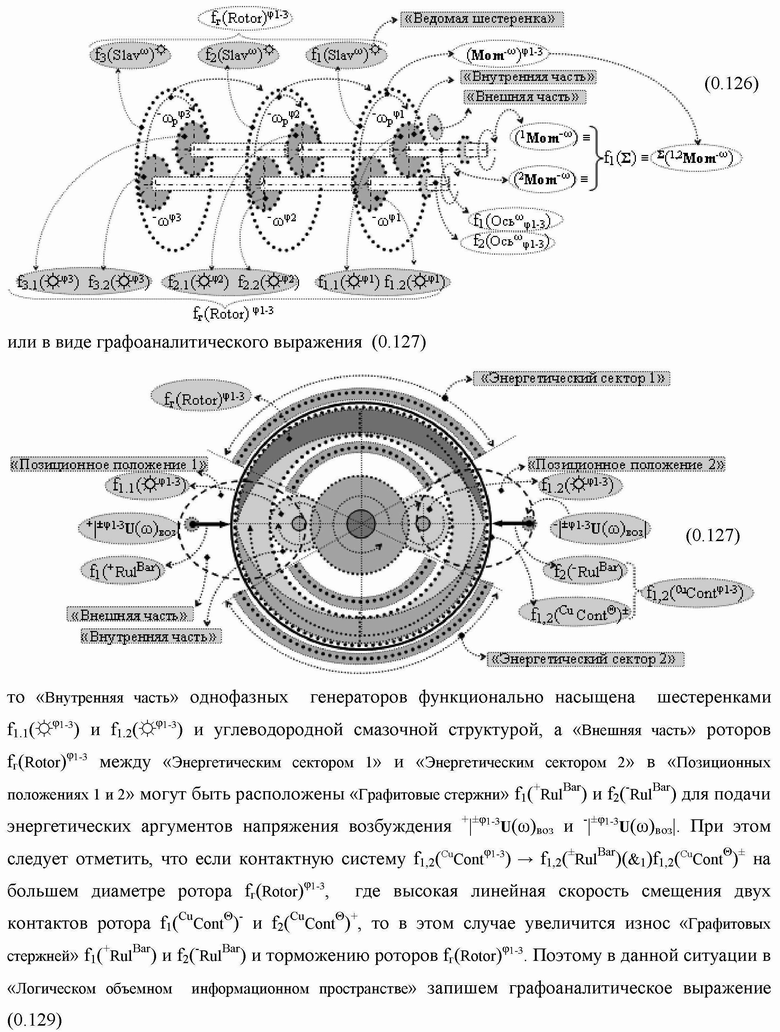
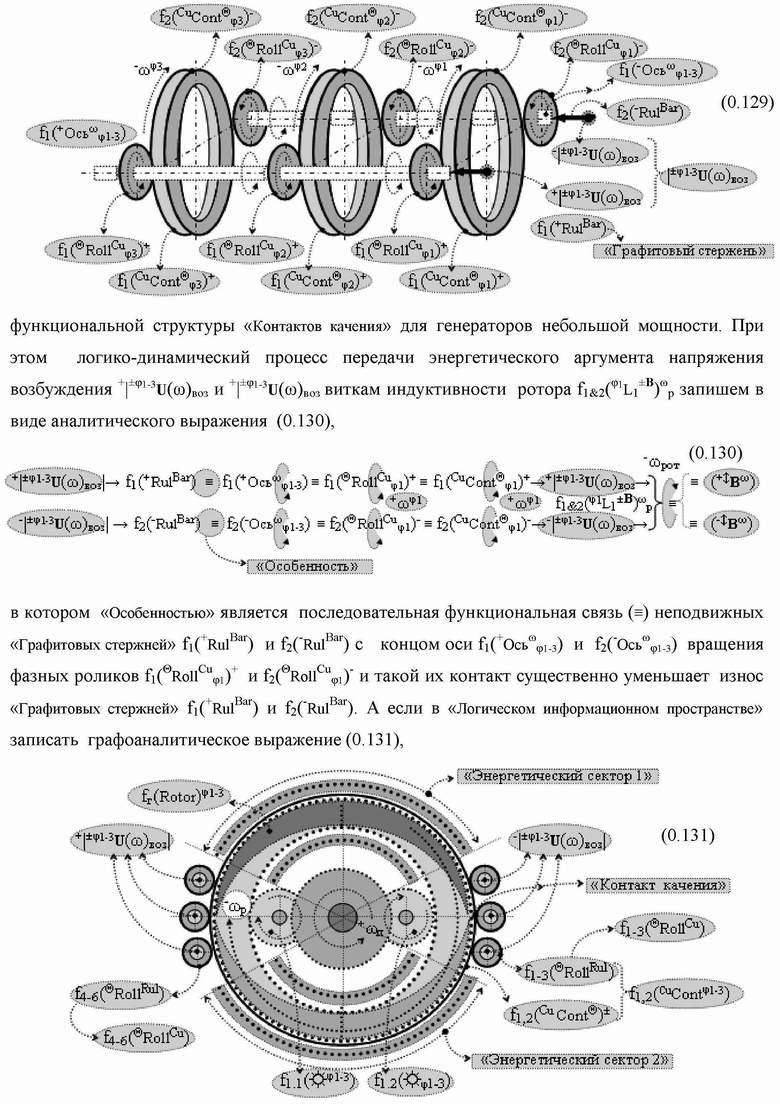

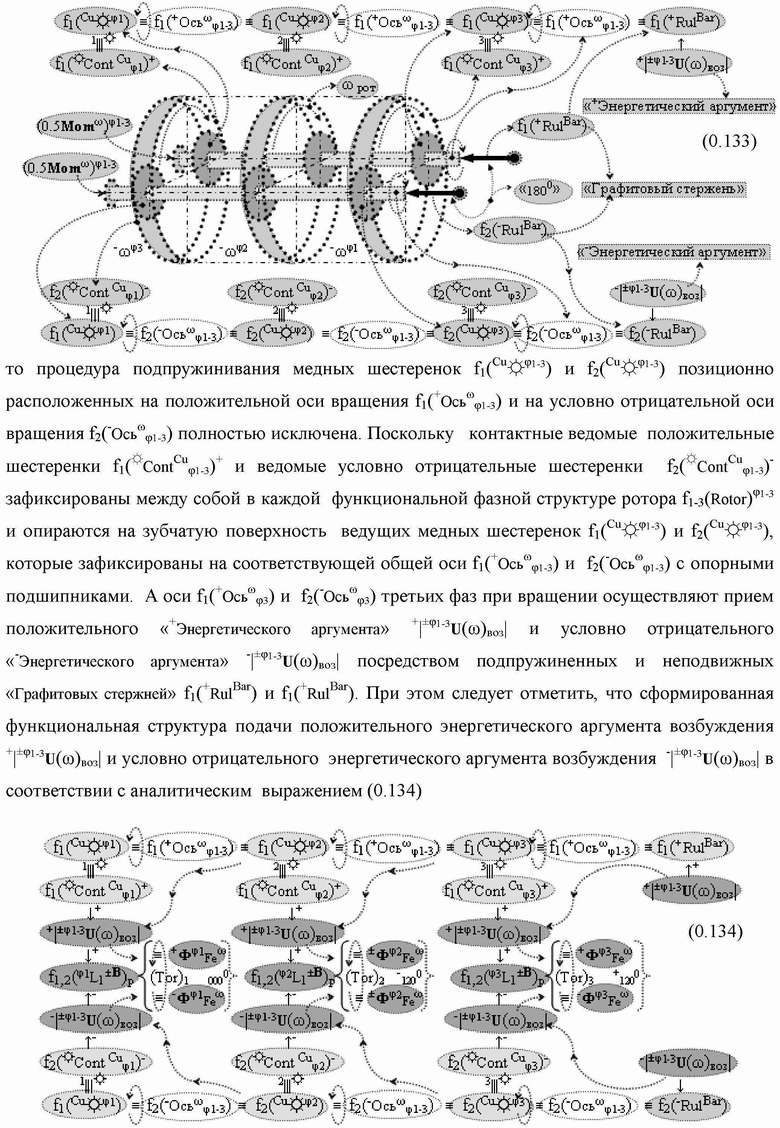


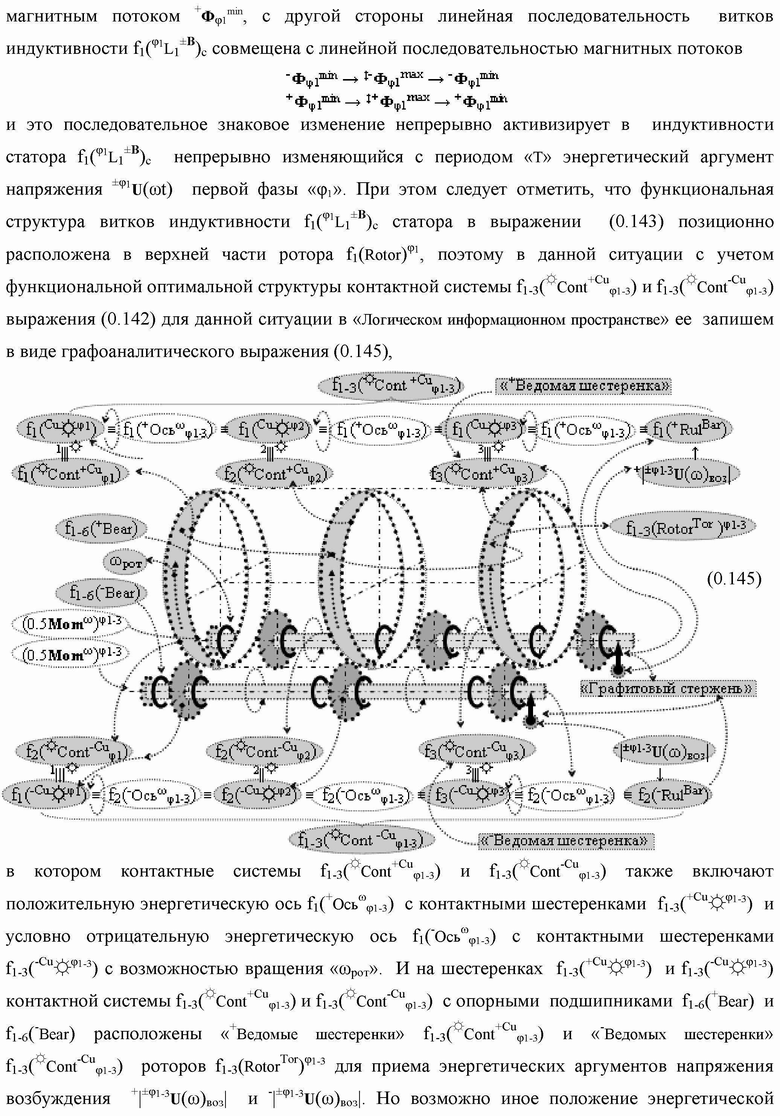
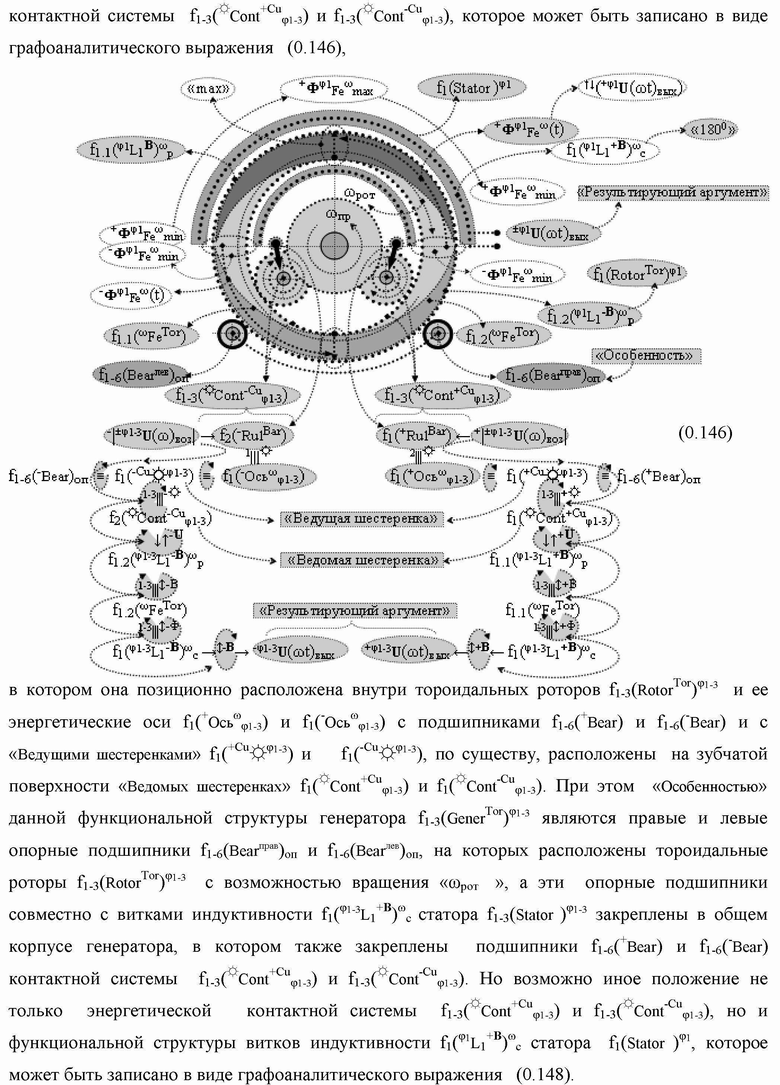
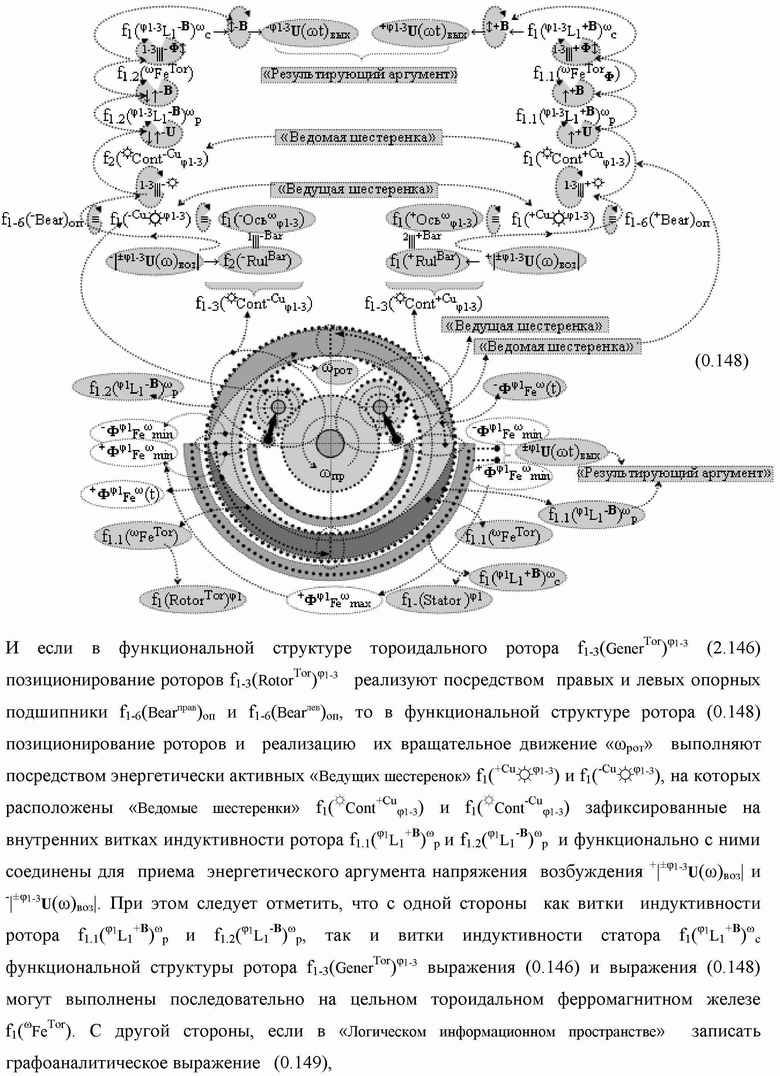

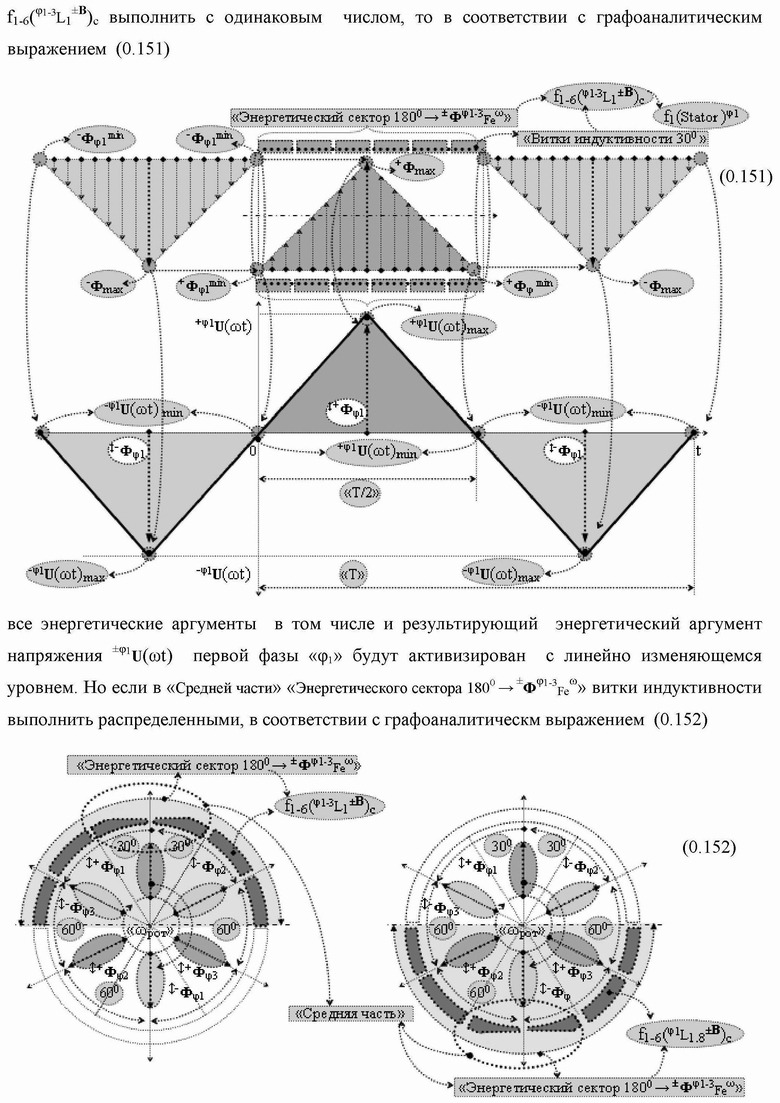

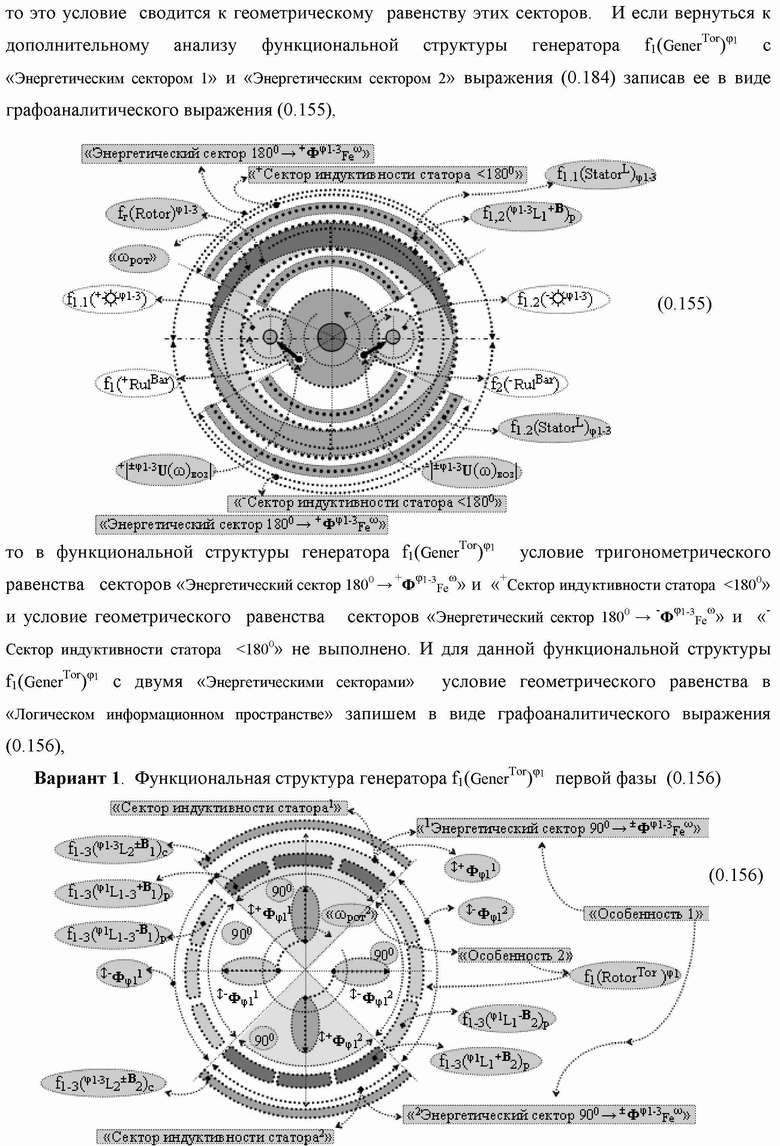


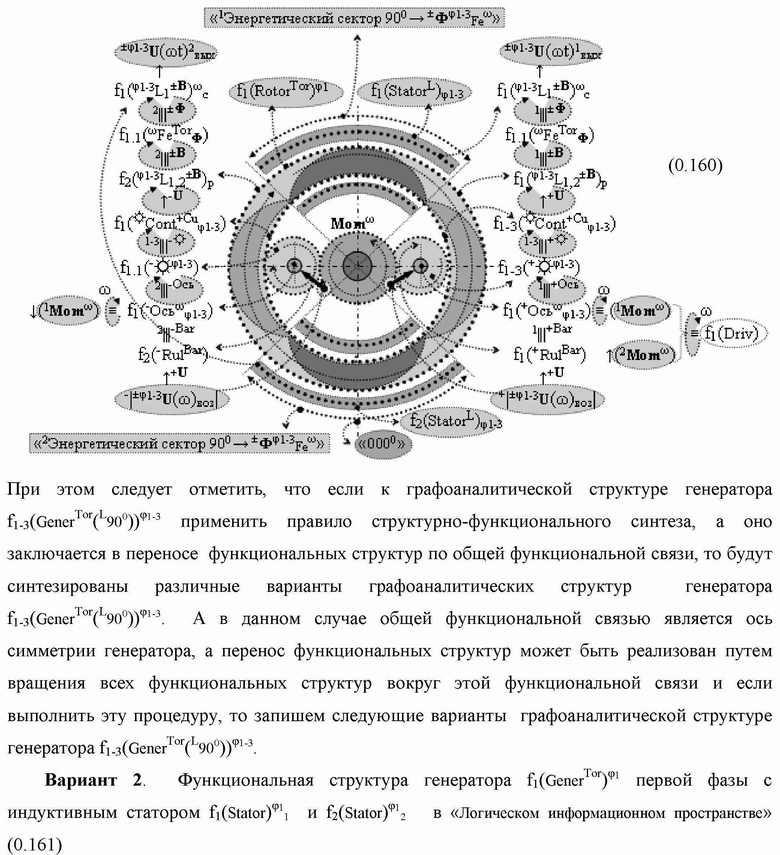
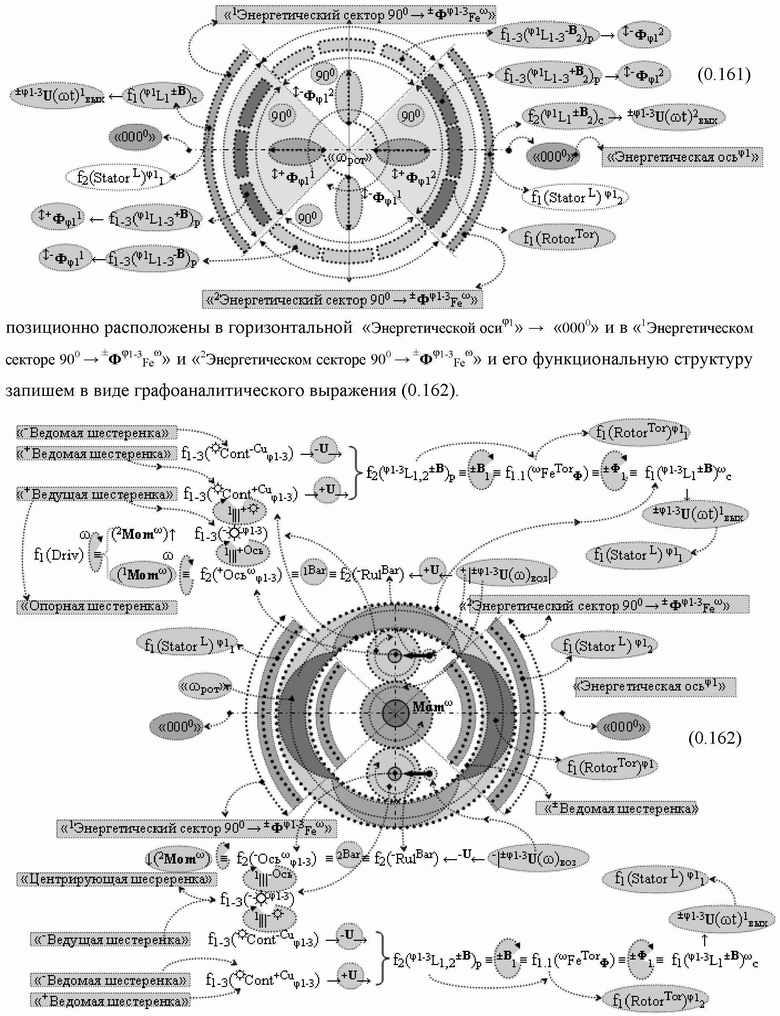

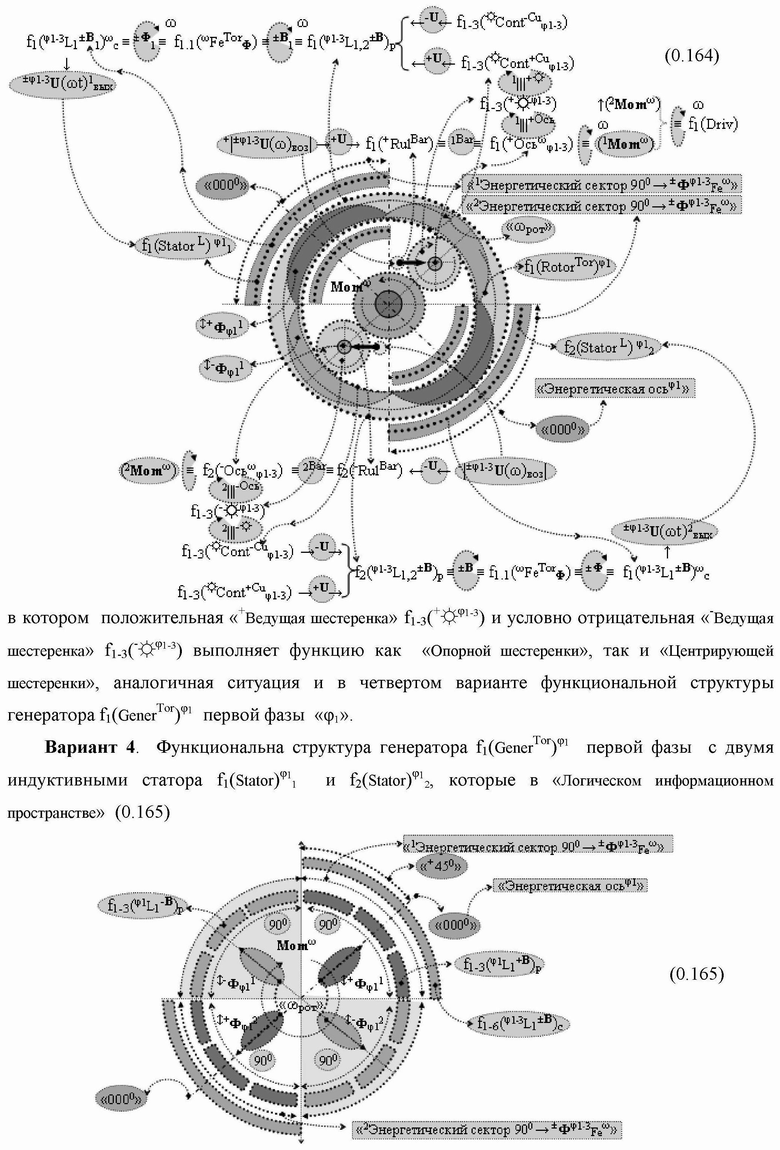
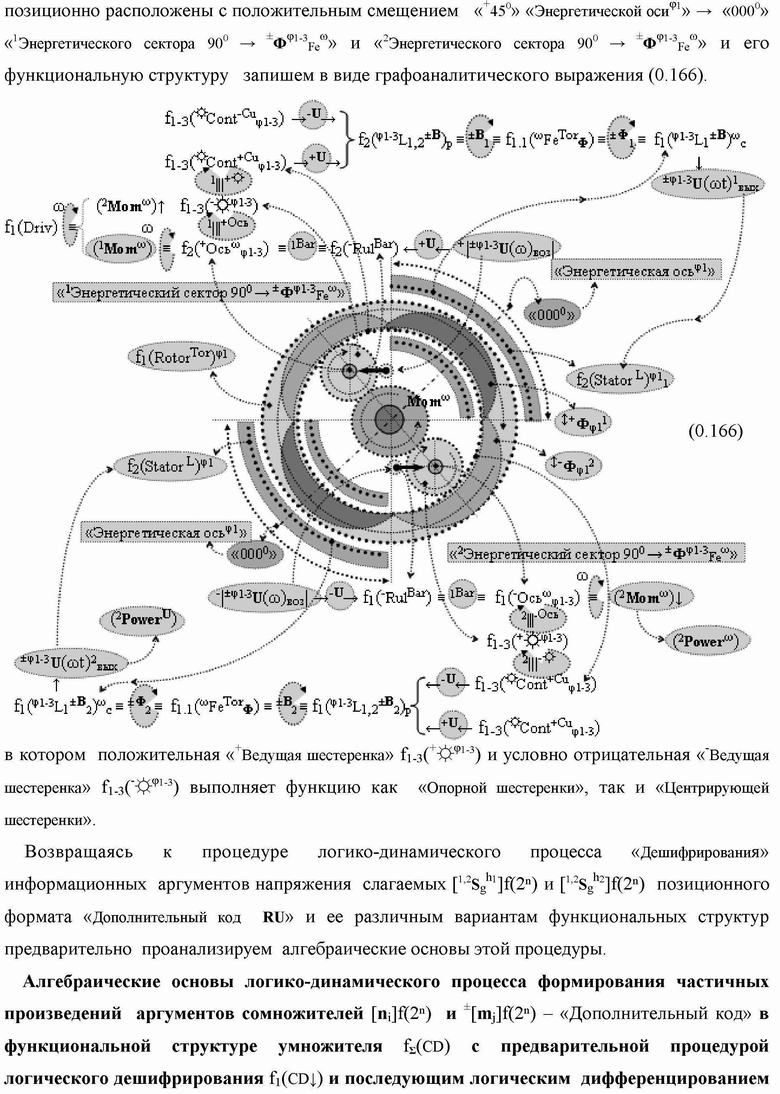






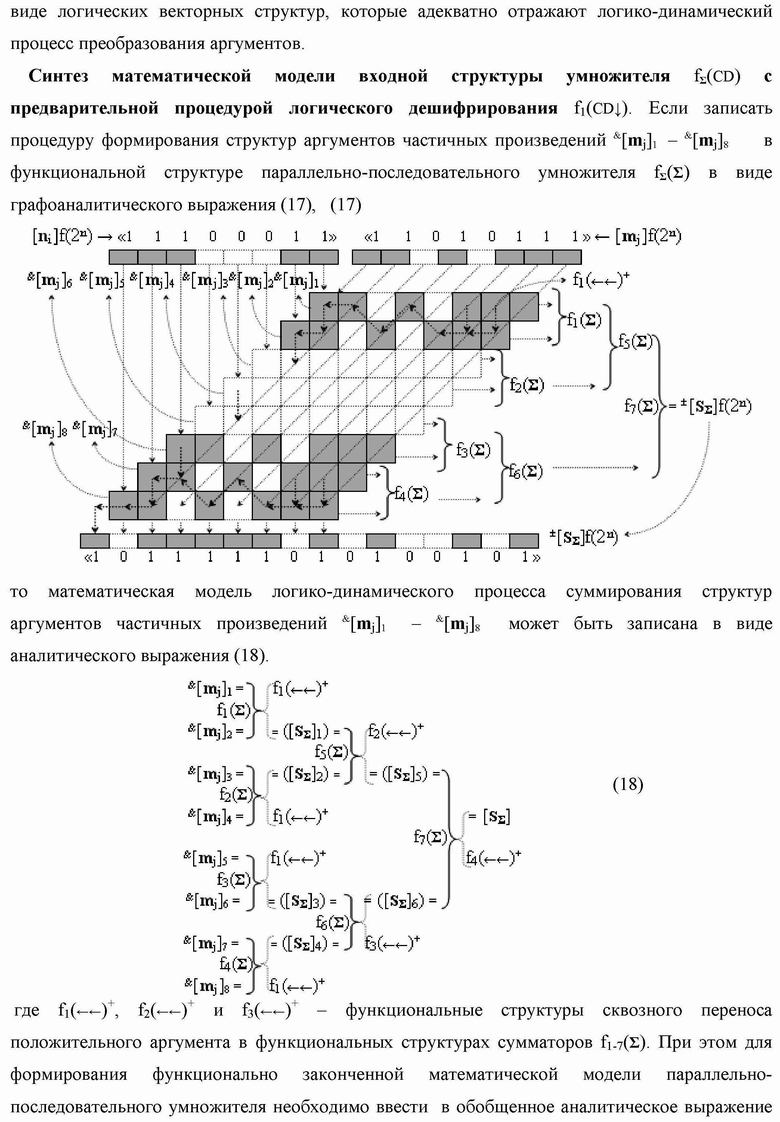



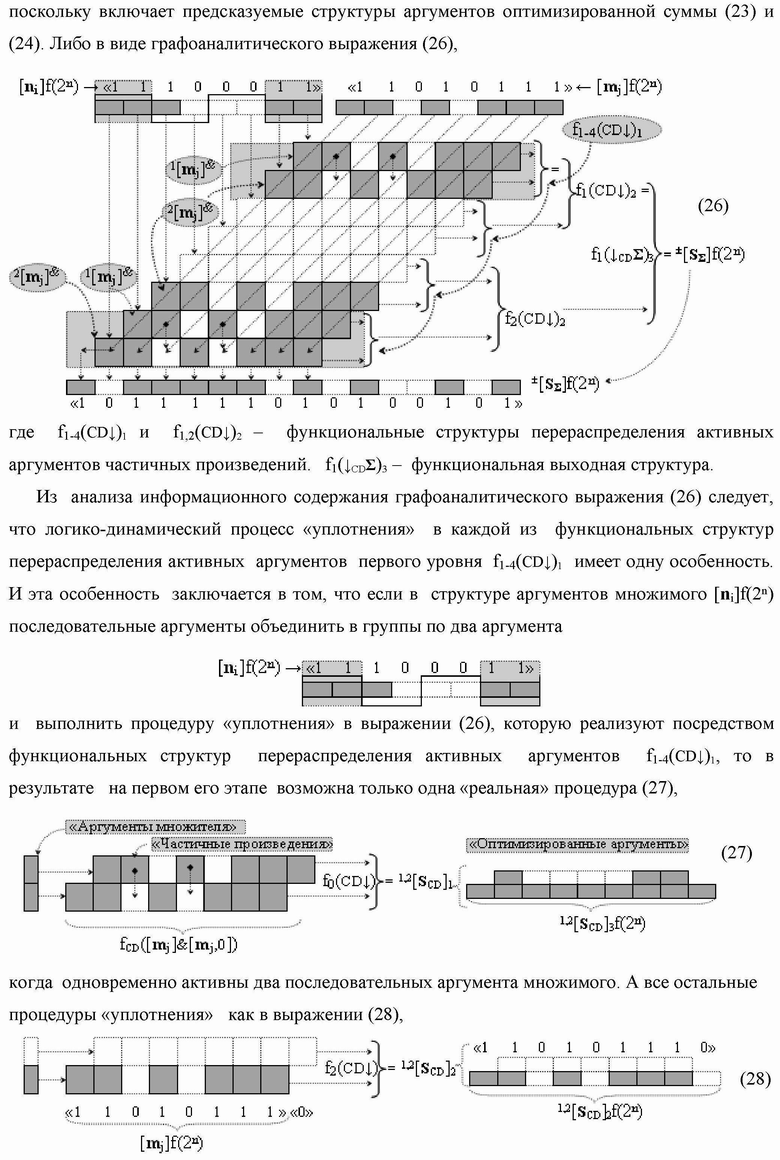




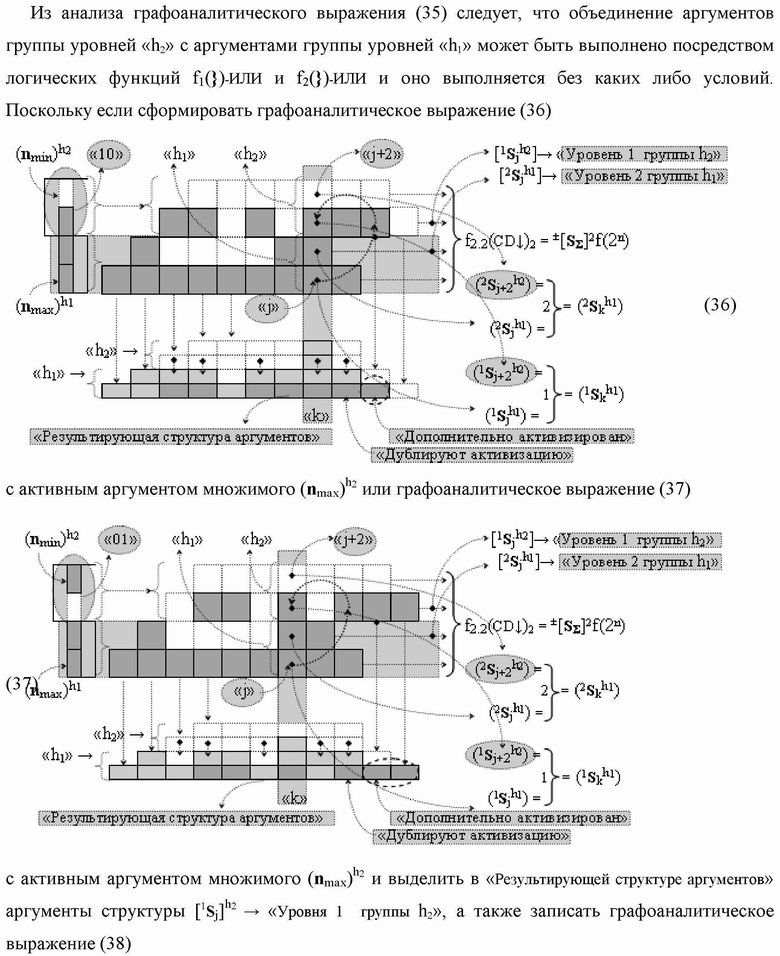




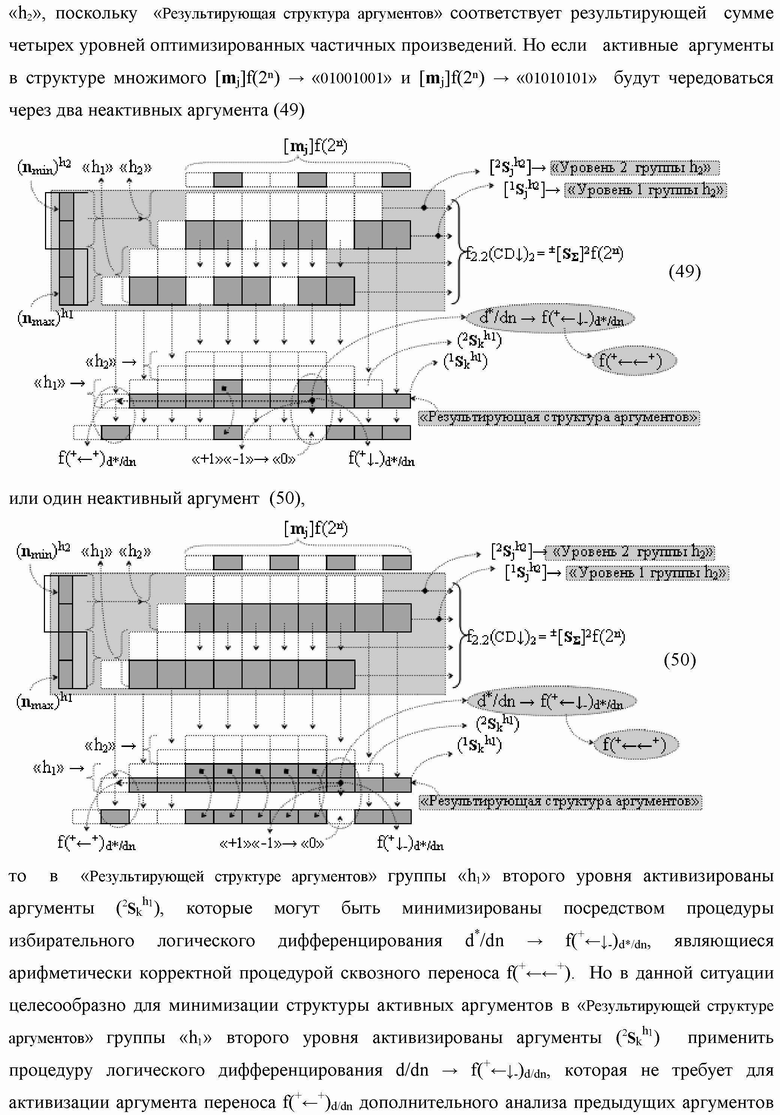


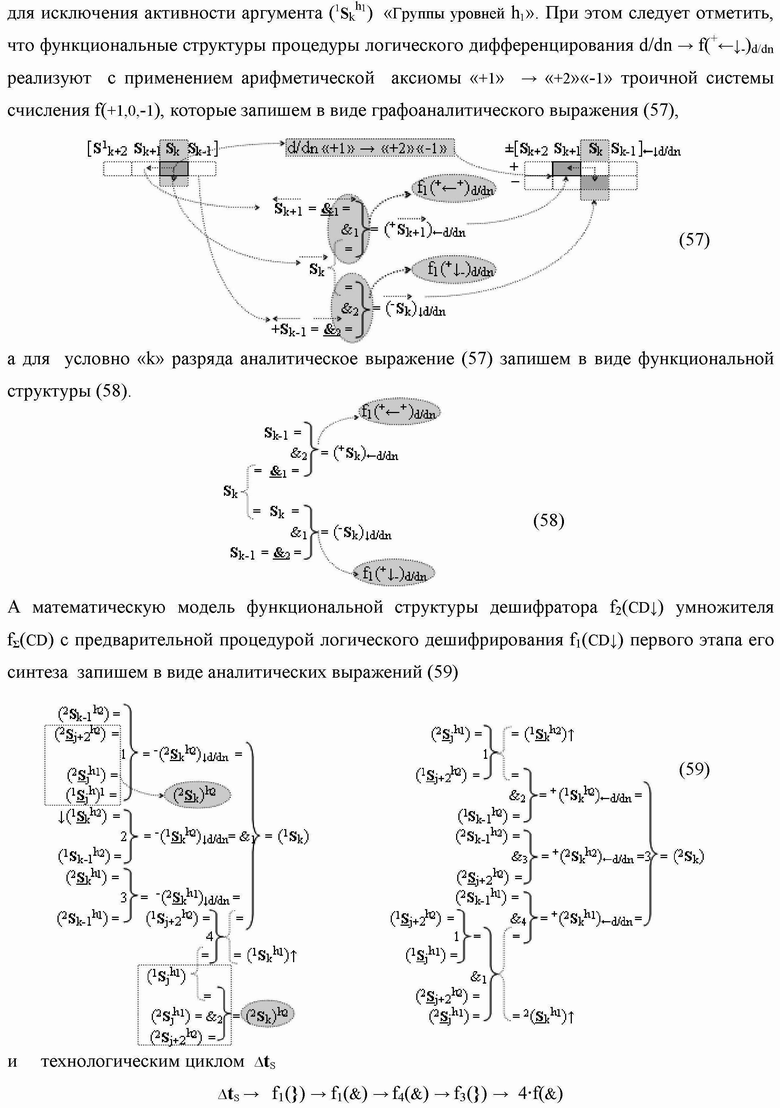
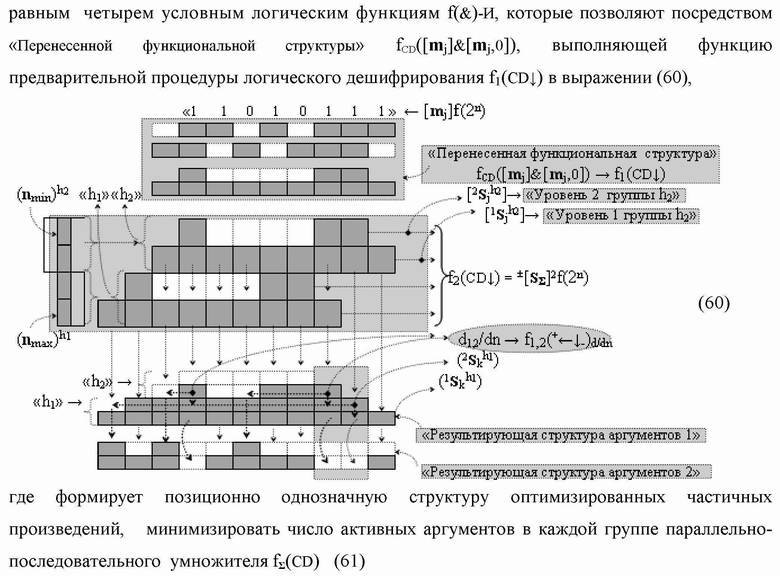
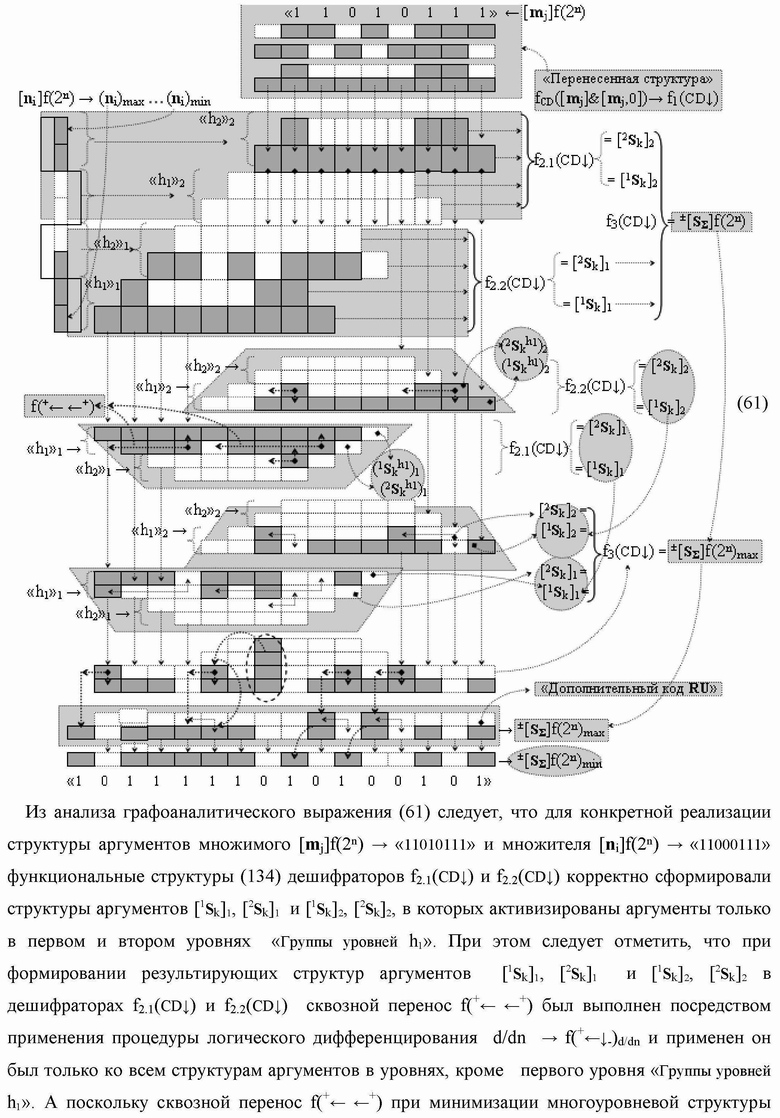





































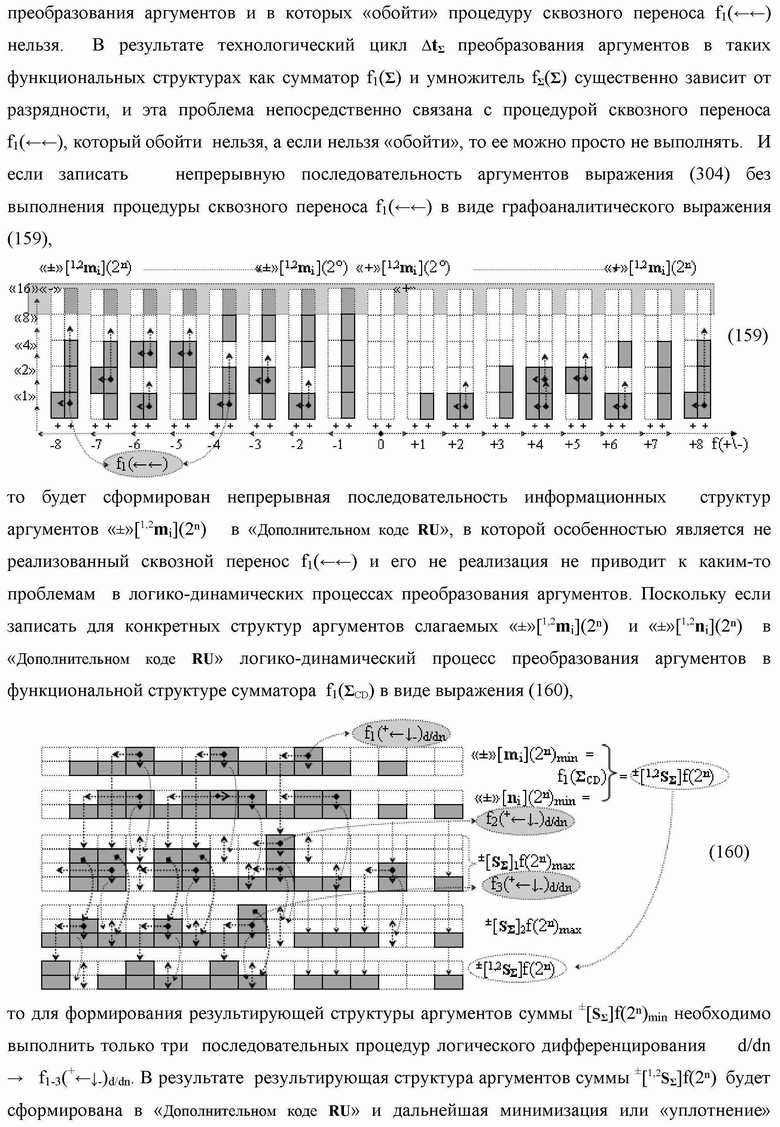

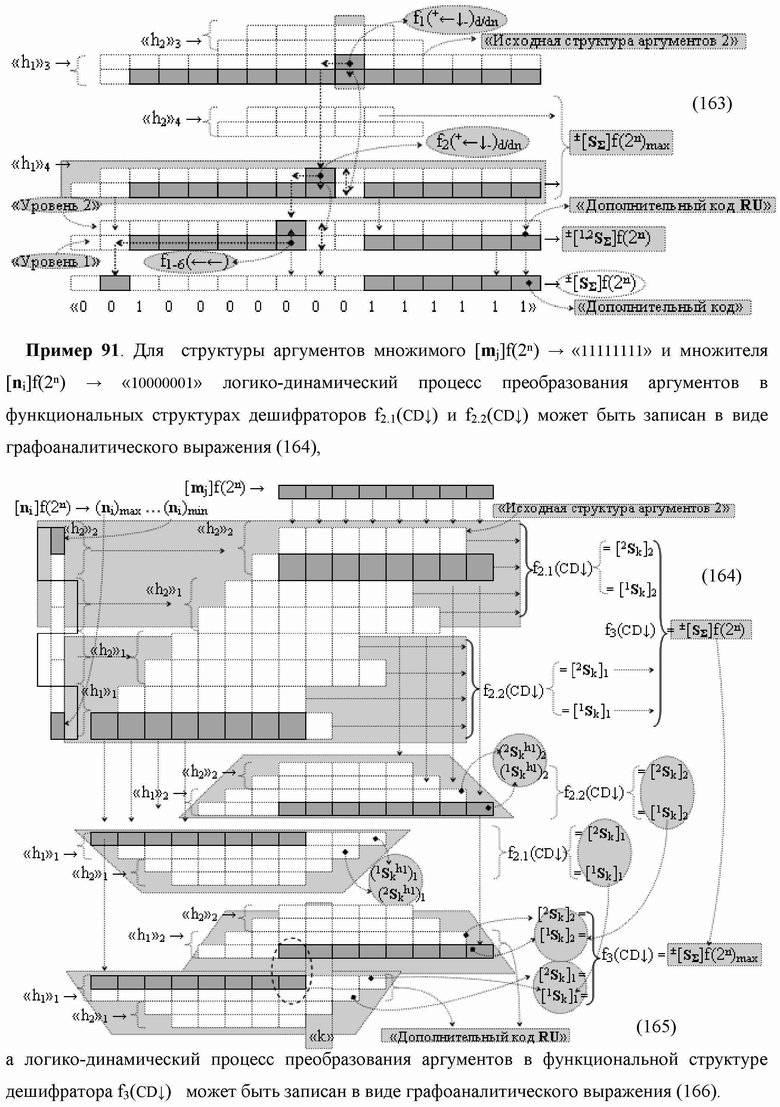



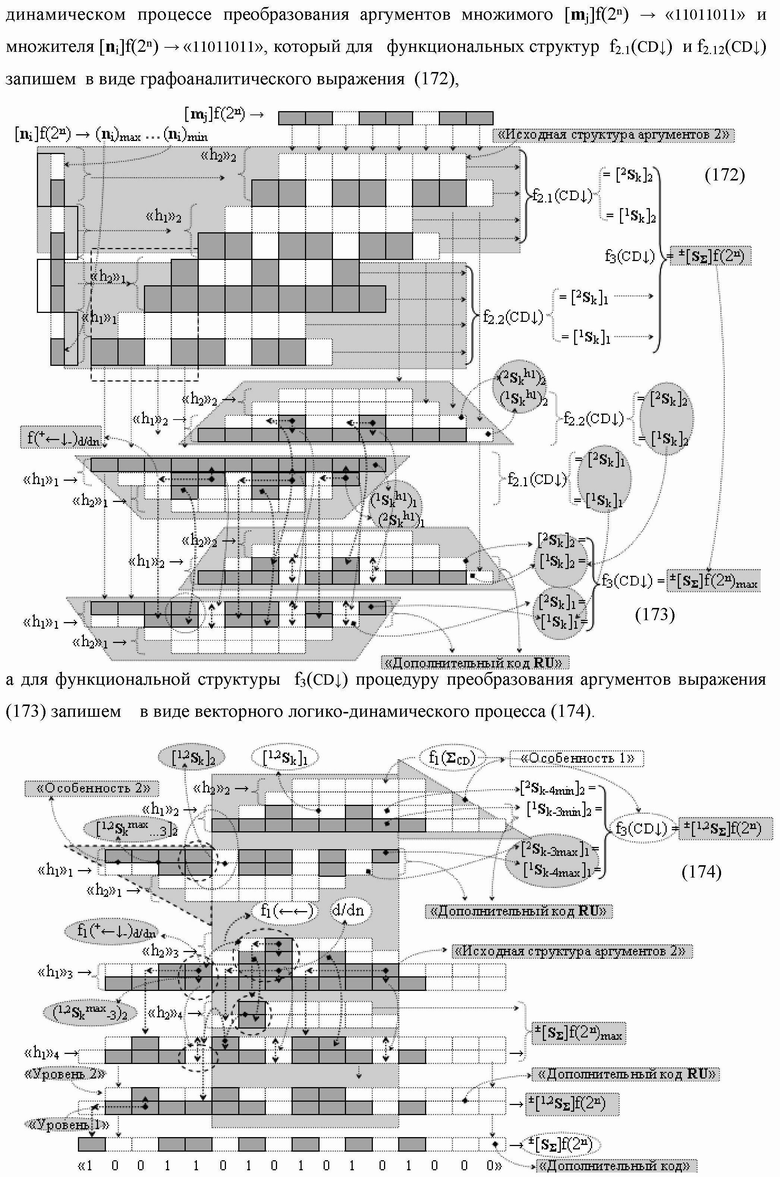

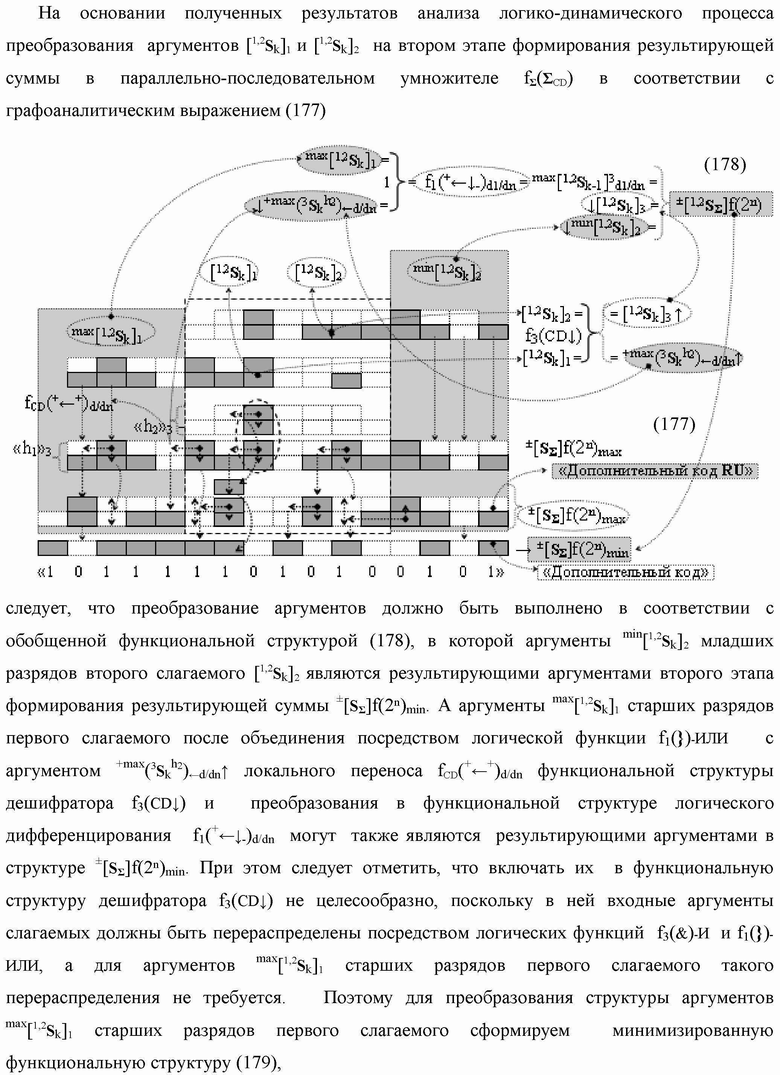


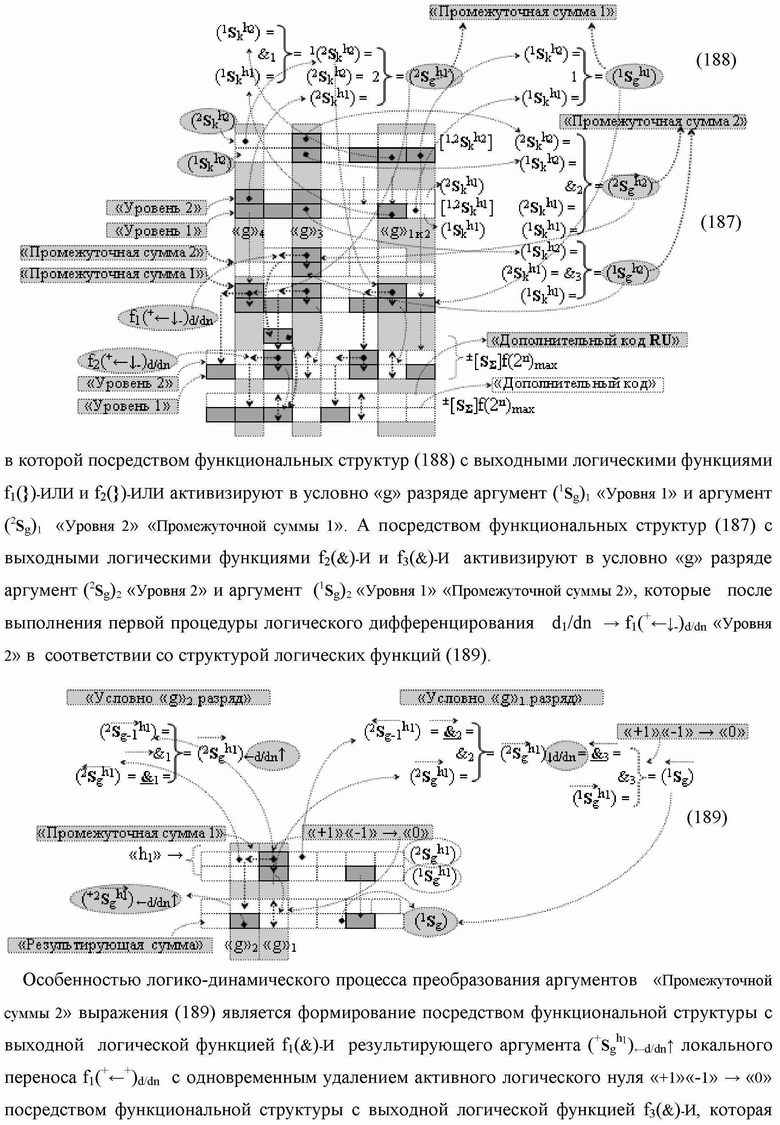
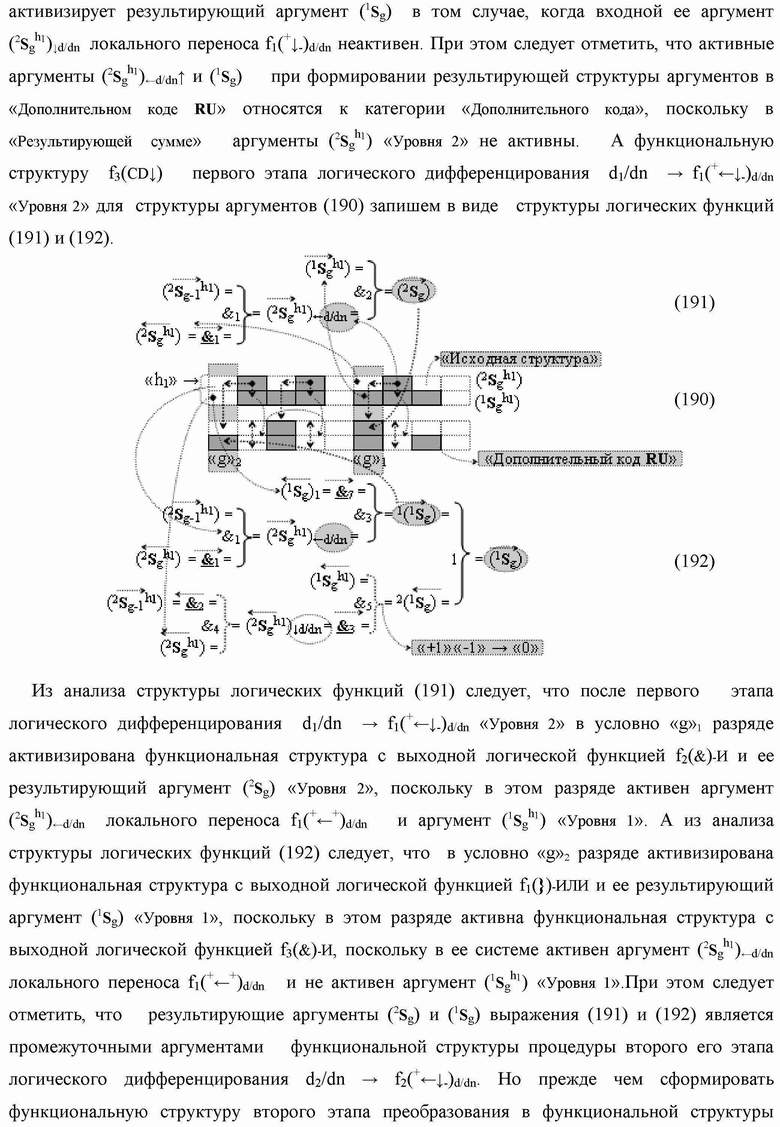



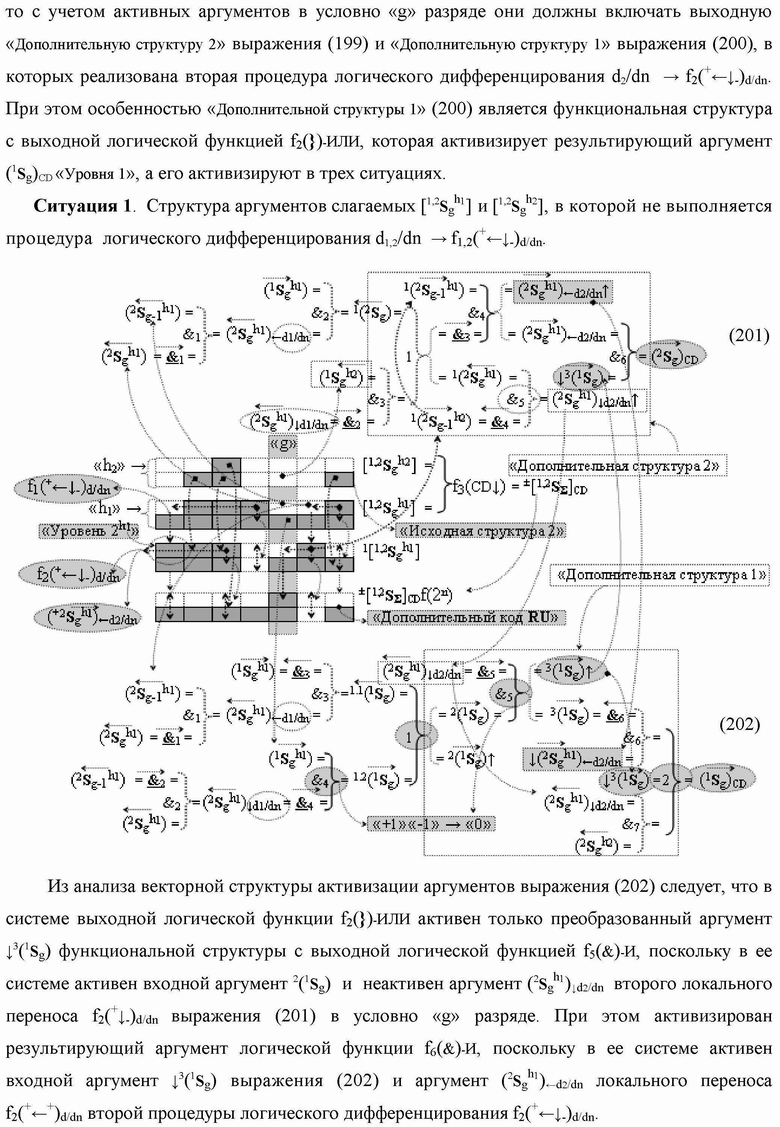
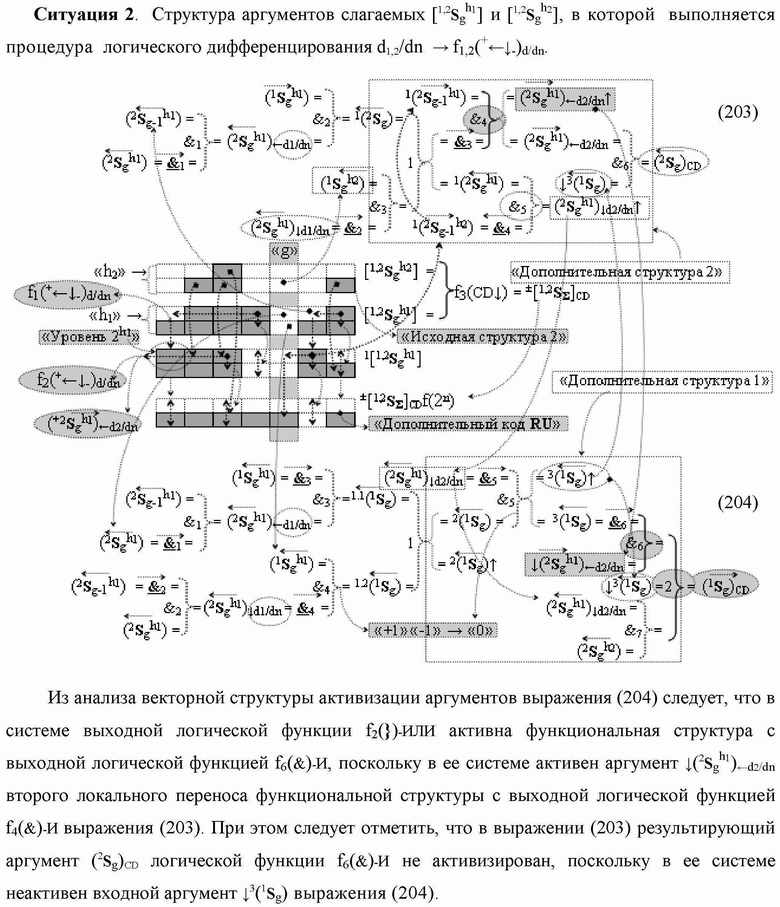
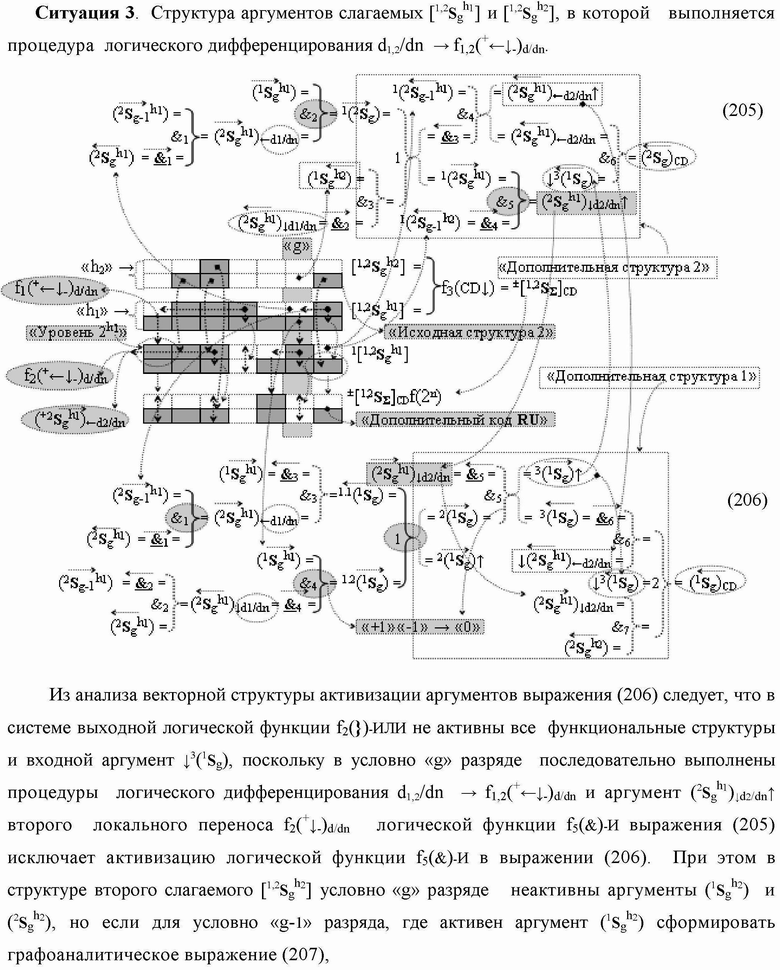
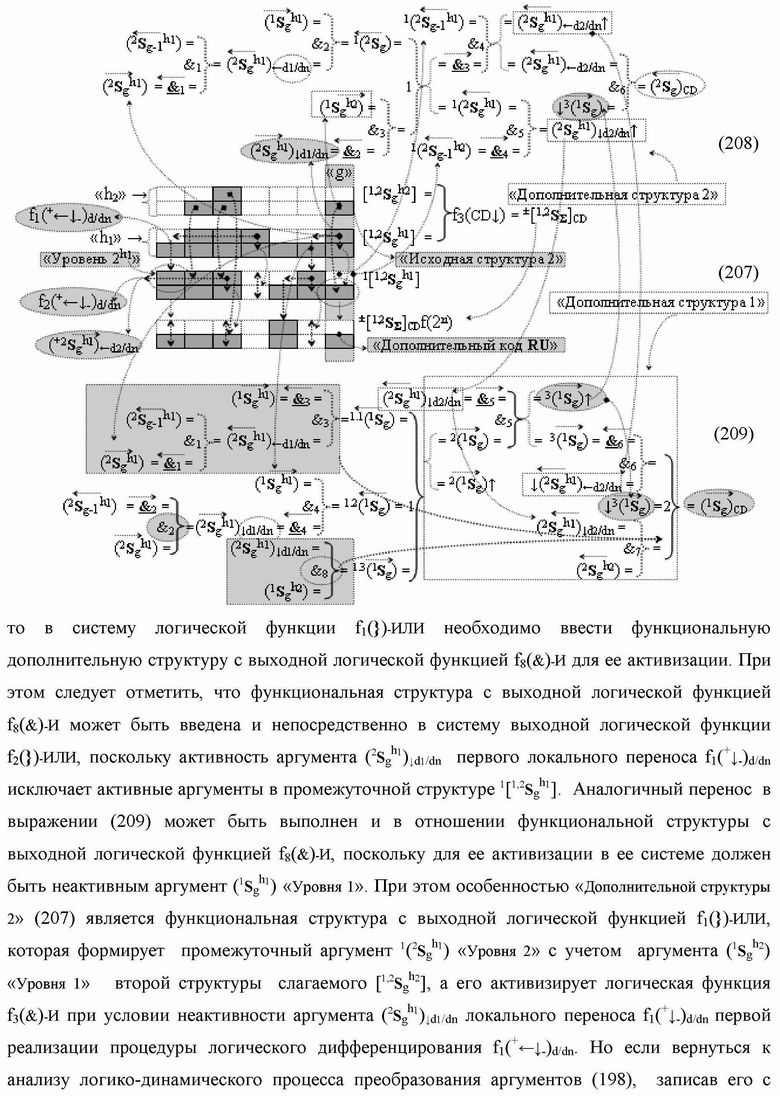
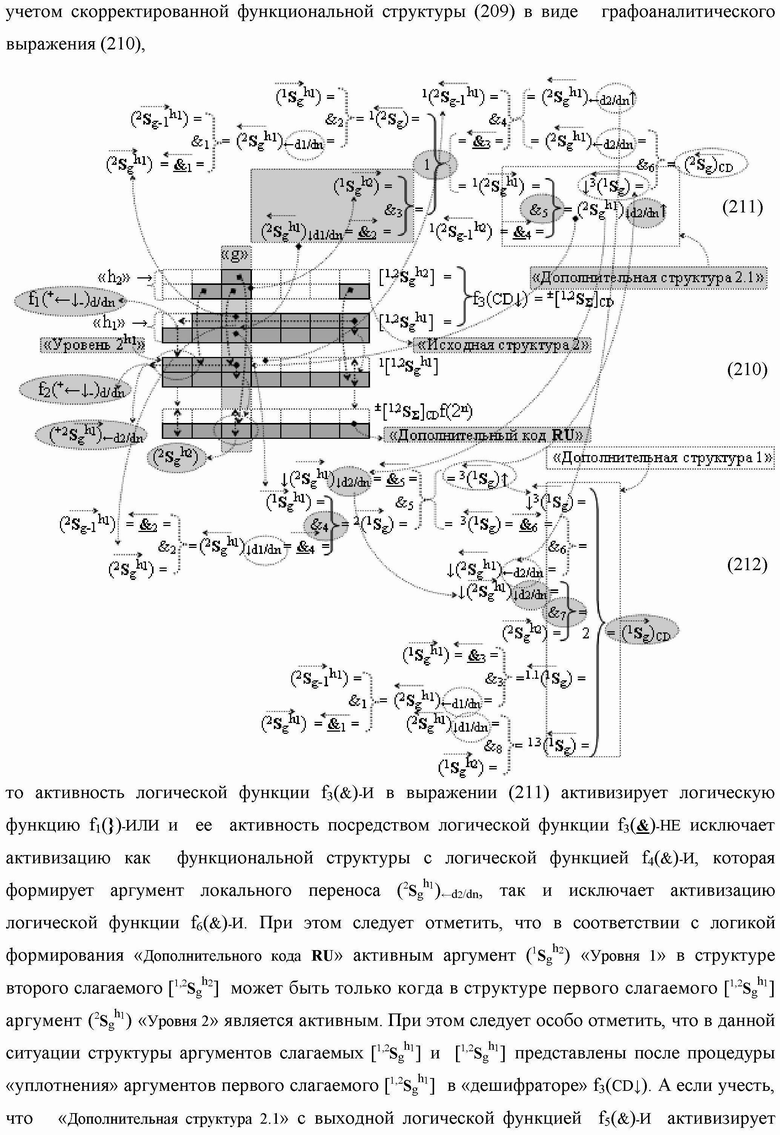
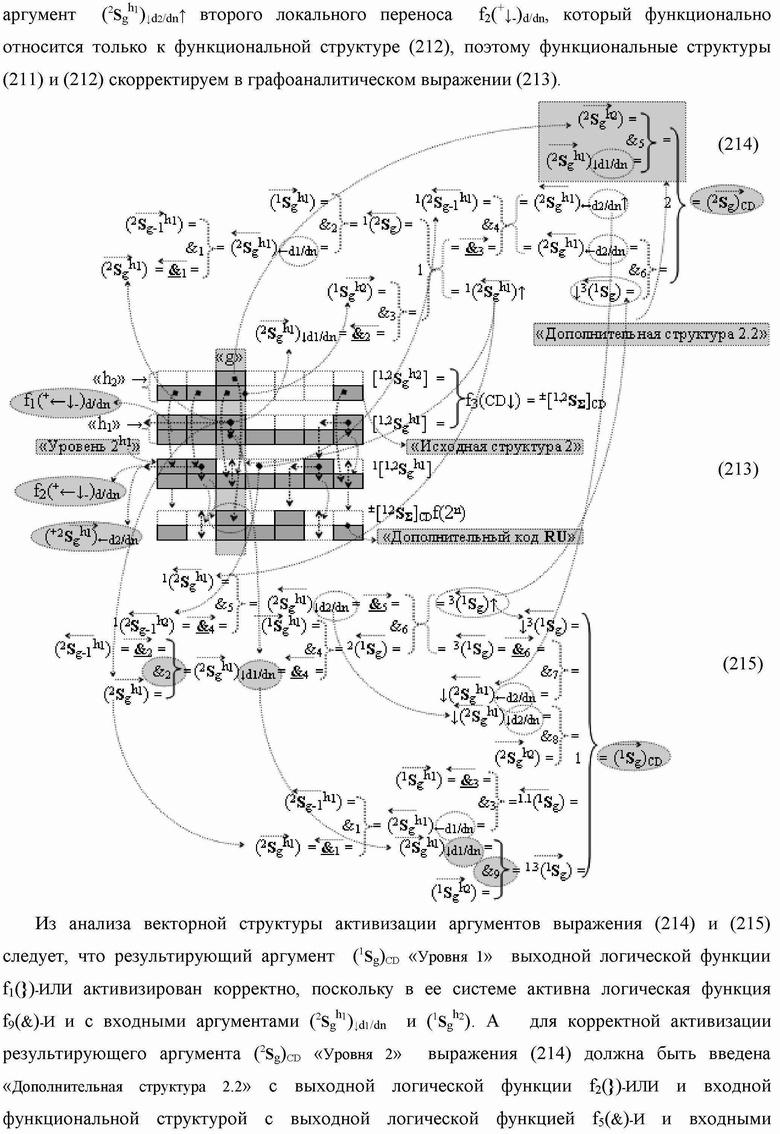





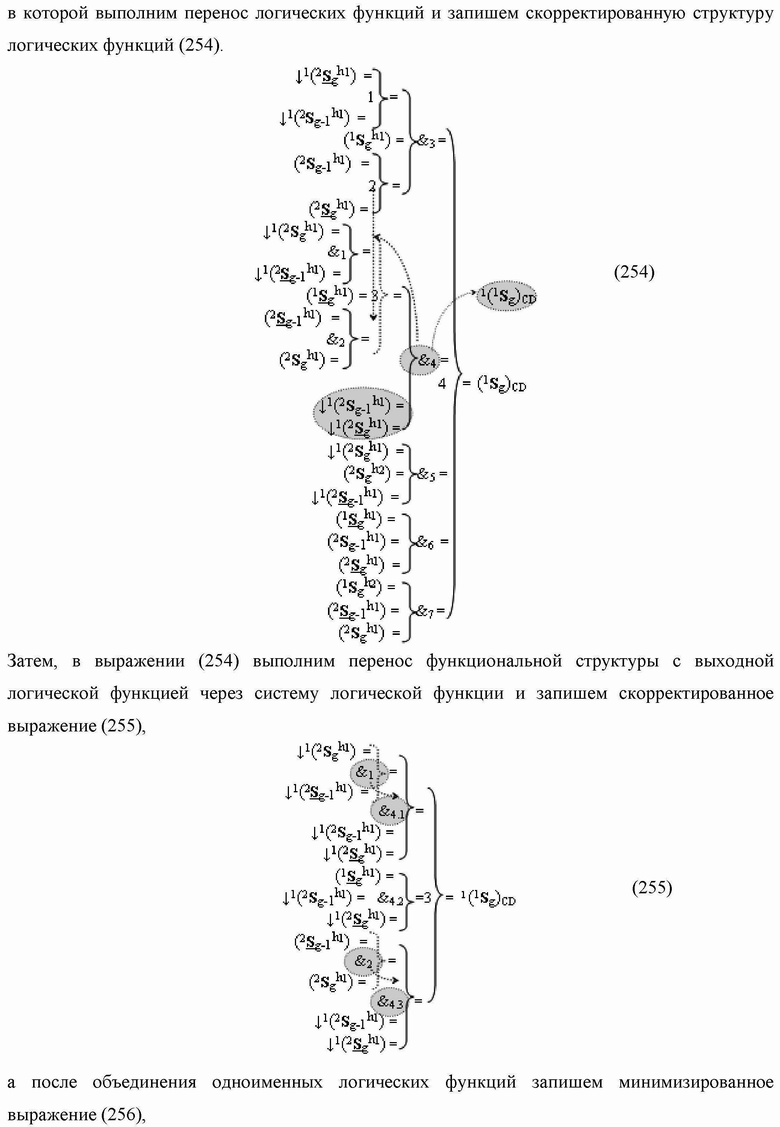
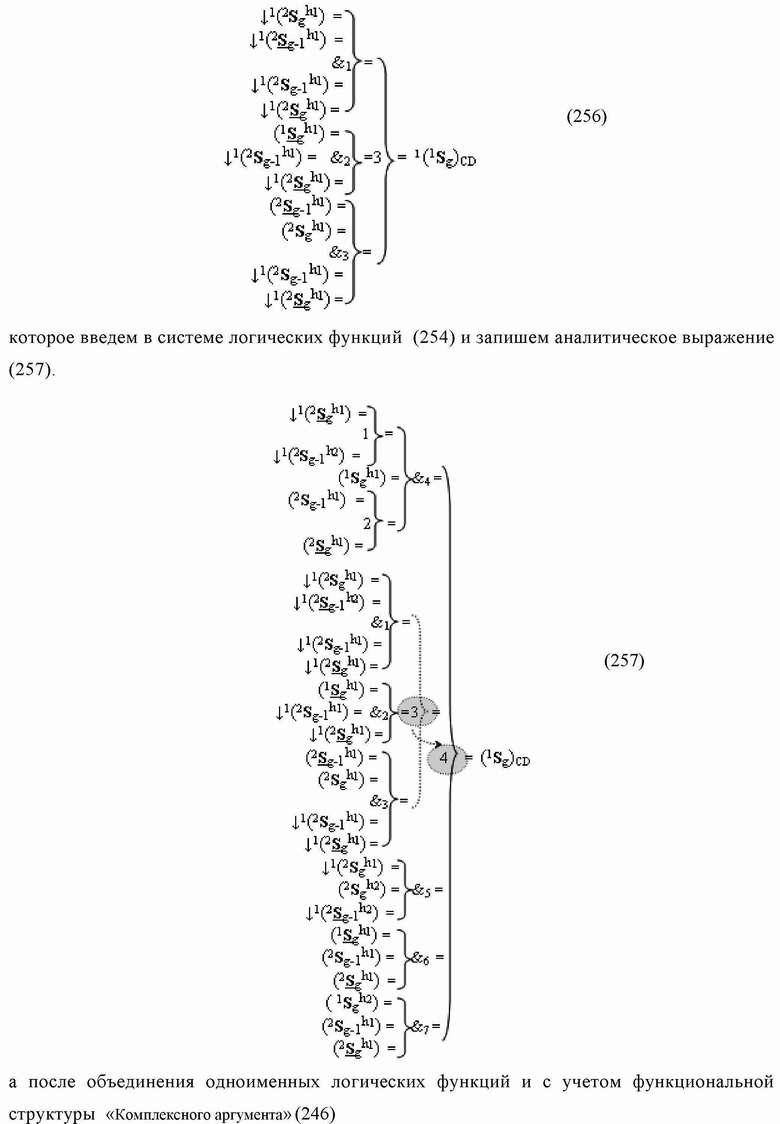
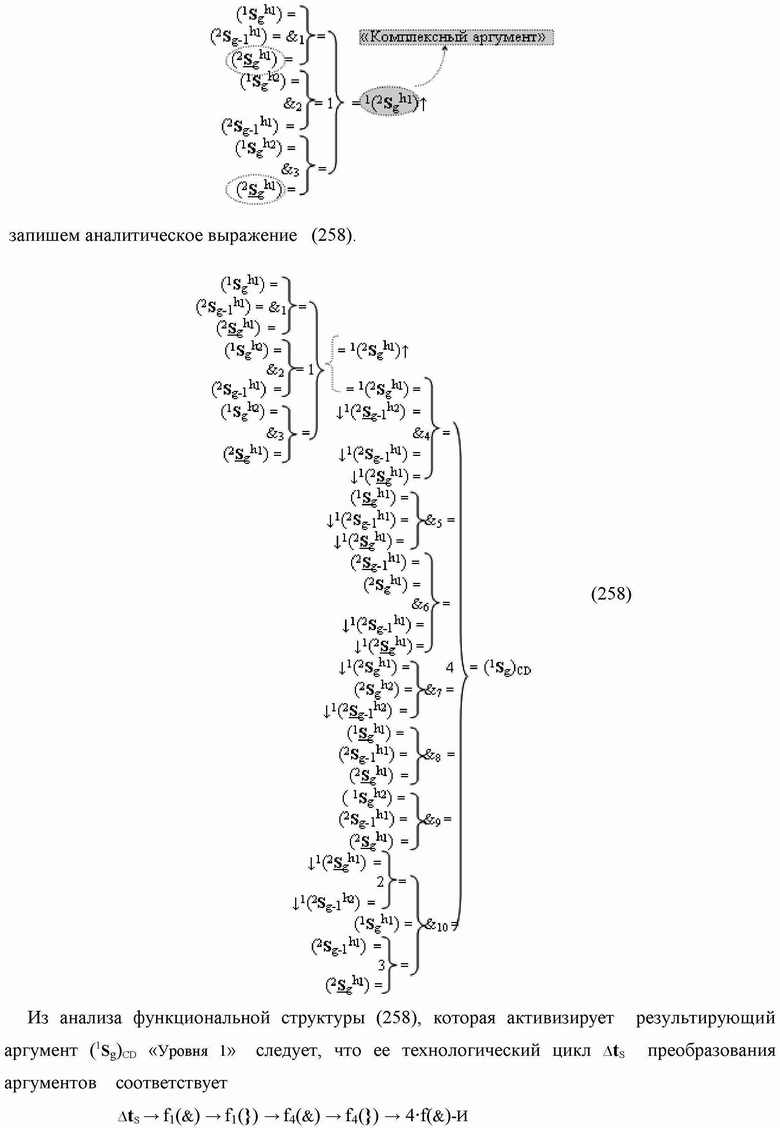
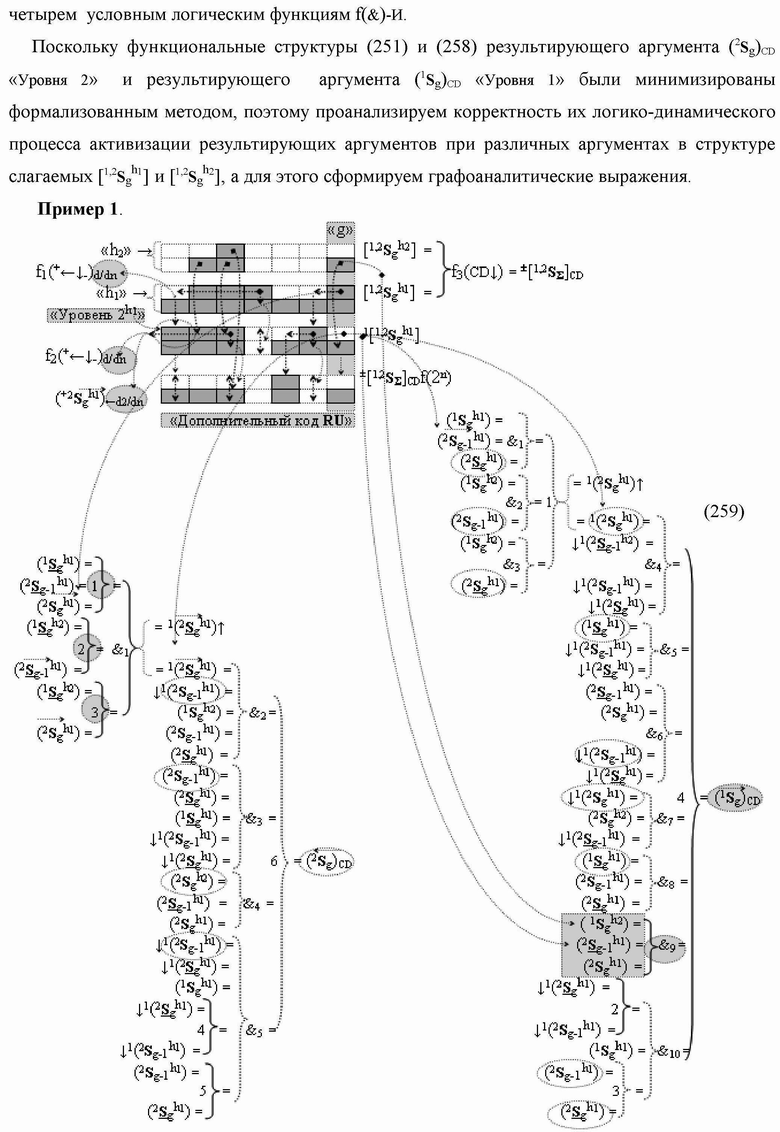
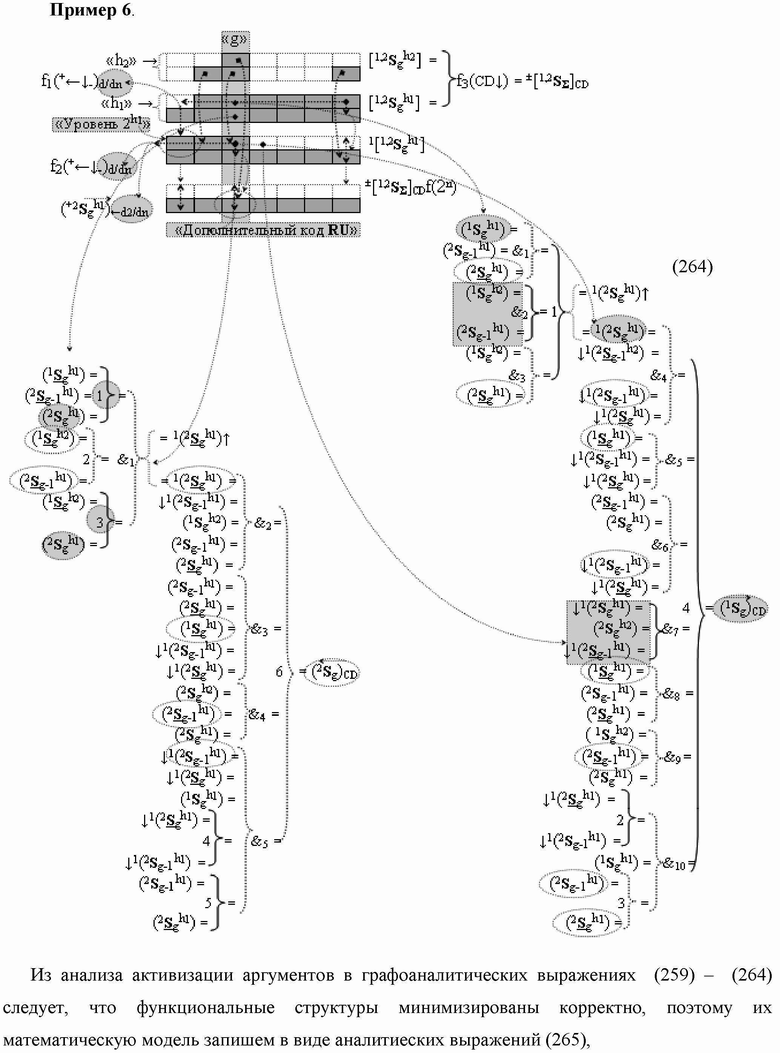
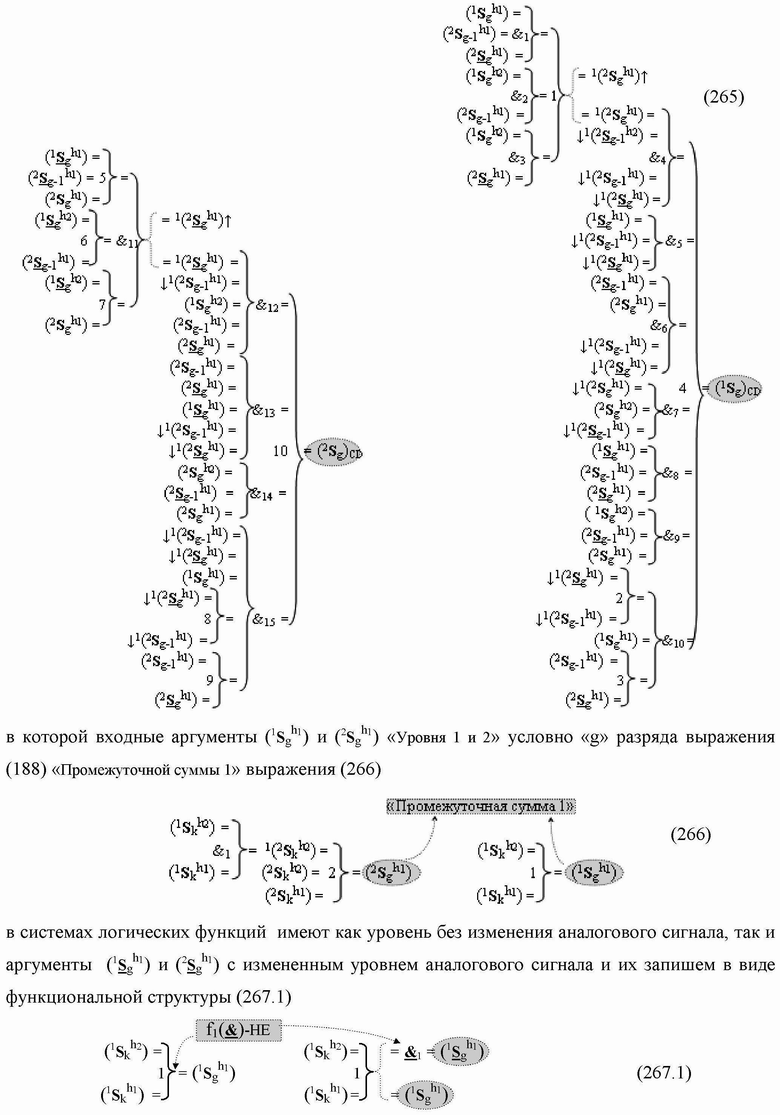
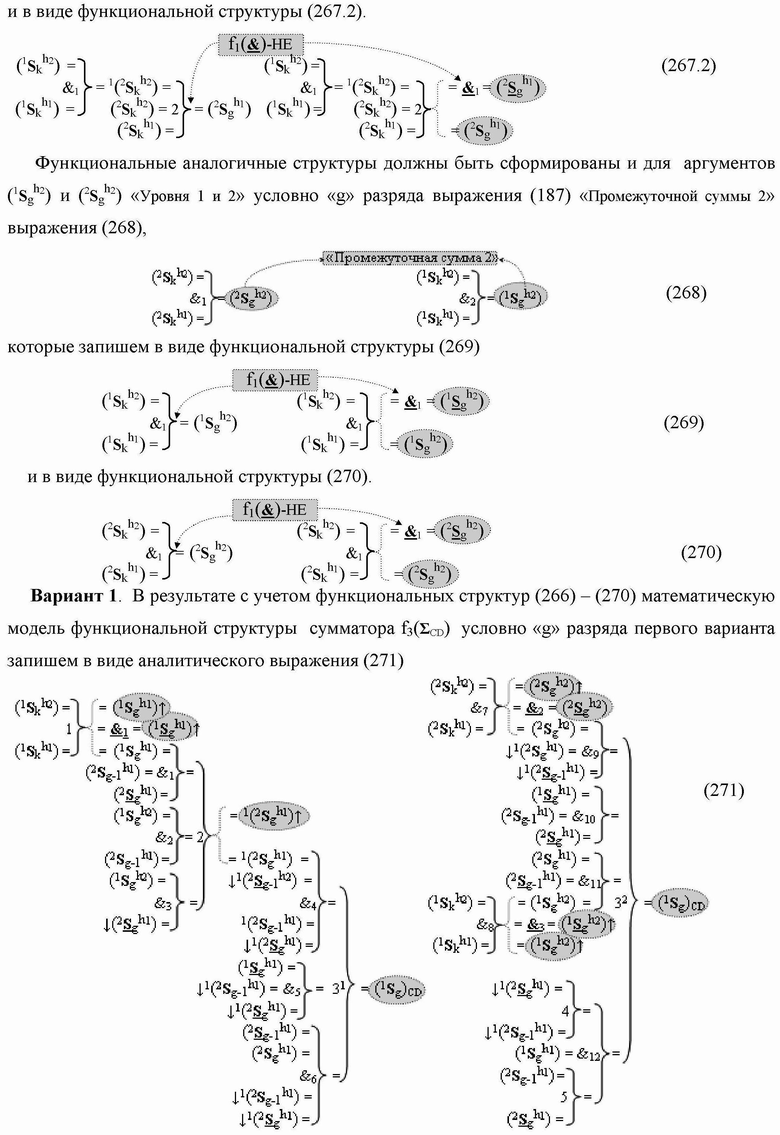
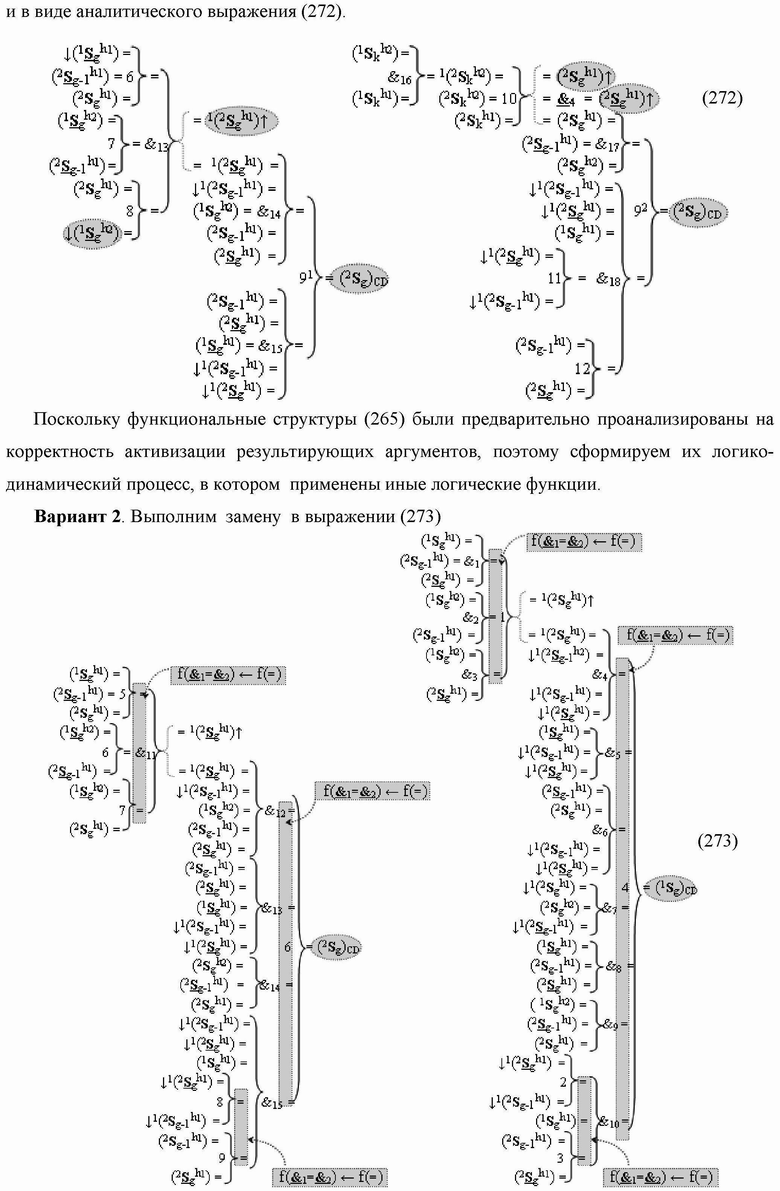

Группа изобретений относится к вычислительной технике и может быть использована при построении арифметических устройств и выполнения арифметических процедур суммирования позиционных аргументов аналоговых сигналов слагаемых с применением арифметических аксиом троичной системы счисления f(+1,0,-1). Техническим результатом является повышение быстродействия. В одном из вариантов функциональная структура выполнена с использованием логических элементов И, ИЛИ, НЕ. 4 н.п. ф-лы.
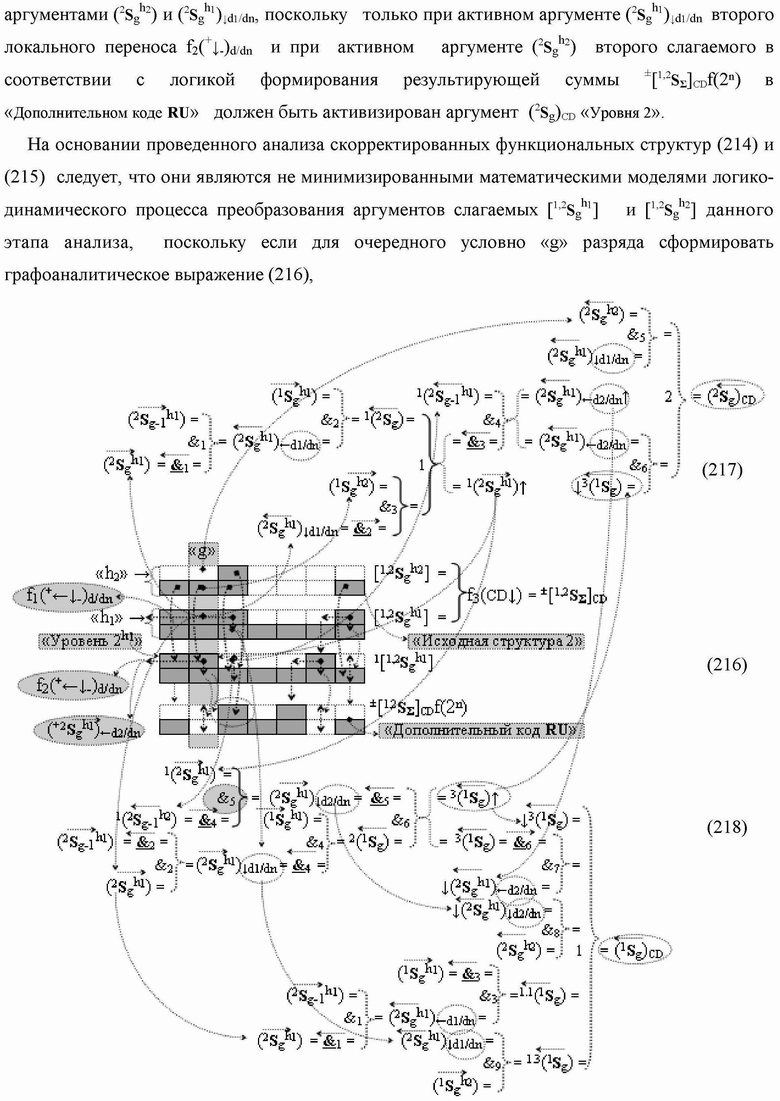
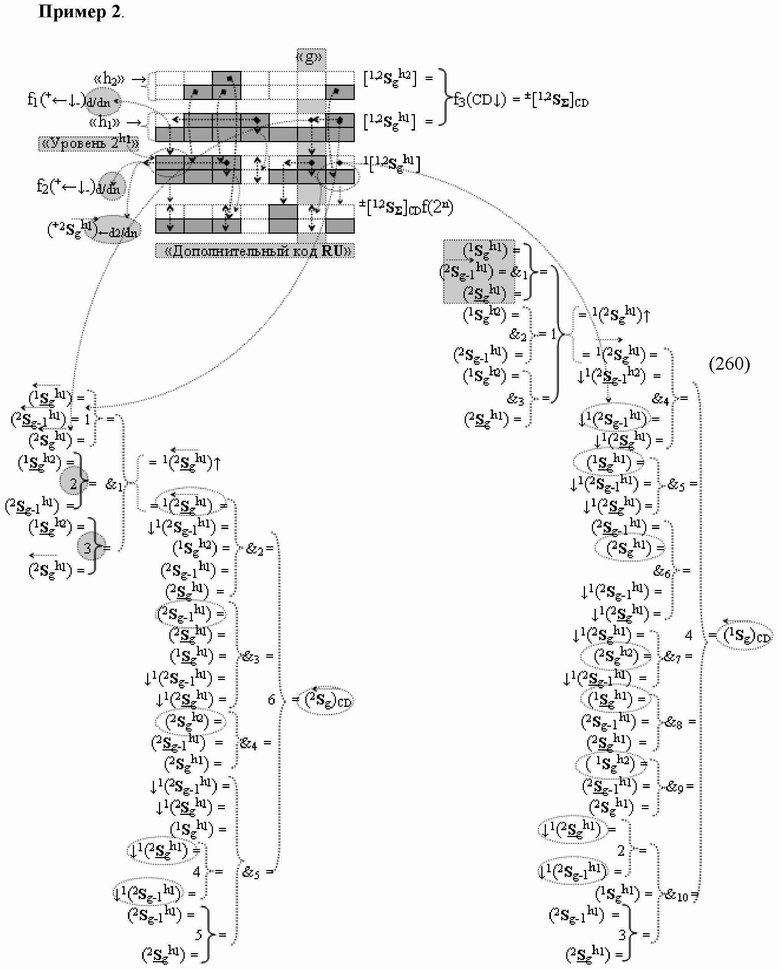
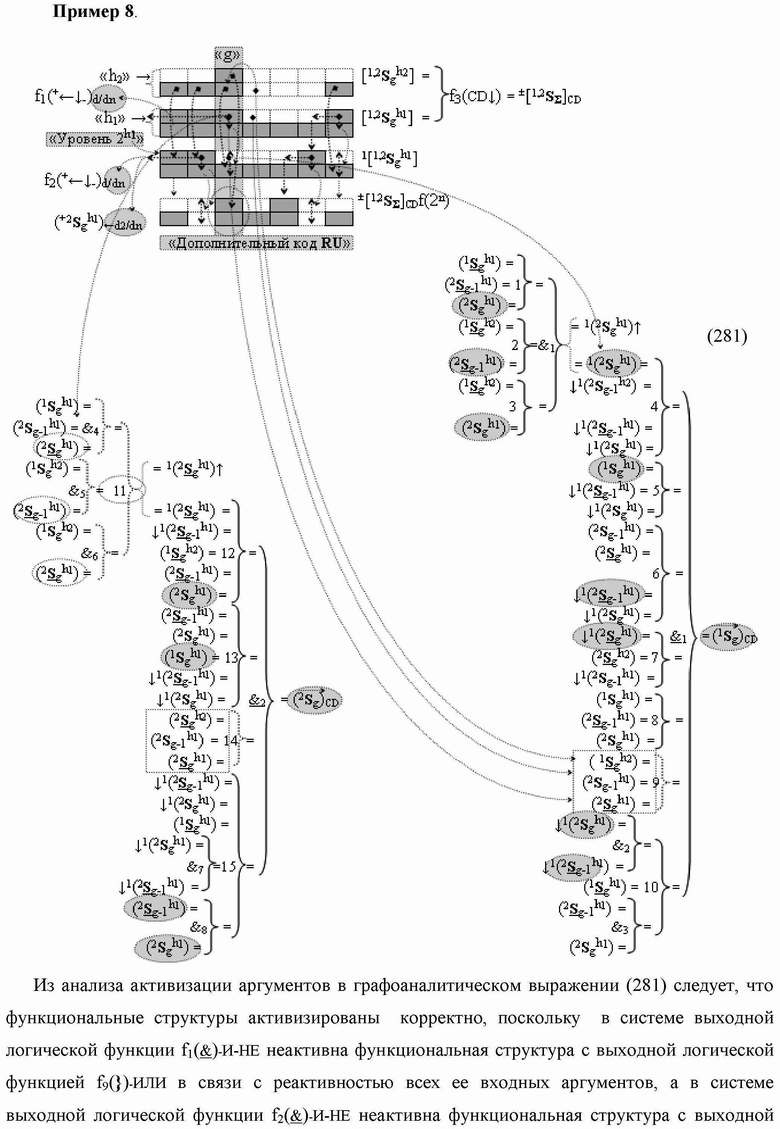
1. Функциональная структура сумматора
f3(Σ
CD) условно
«g» разряда, реализующая процедуру «дешифрирования» аргументов слагаемых [1,2
S
g h1]f(2n) и [1,2
S
g h2]f(2n) позиционного формата «Дополнительный код RU»
посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и двойного логического дифференцирования
d1,2/dn → f1,2(+←↓-)d/dn активных аргументов
«Уровня 2» и удаления активных логических нулей
«+1»«-1» → «0» в «Уровне 1», включающая логическую функцию f1(})-ИЛИ, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f1(&)-И, а также включает логическую функцию f7(&)-И, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f2(
&
)-НЕ, отличающаяся тем, что в структуру условно «g» разряда для активизации результирующего аргумента (1
S
g)CD «Уровня 1» введены логические функции f1(
&
)-НЕ, f3(
&
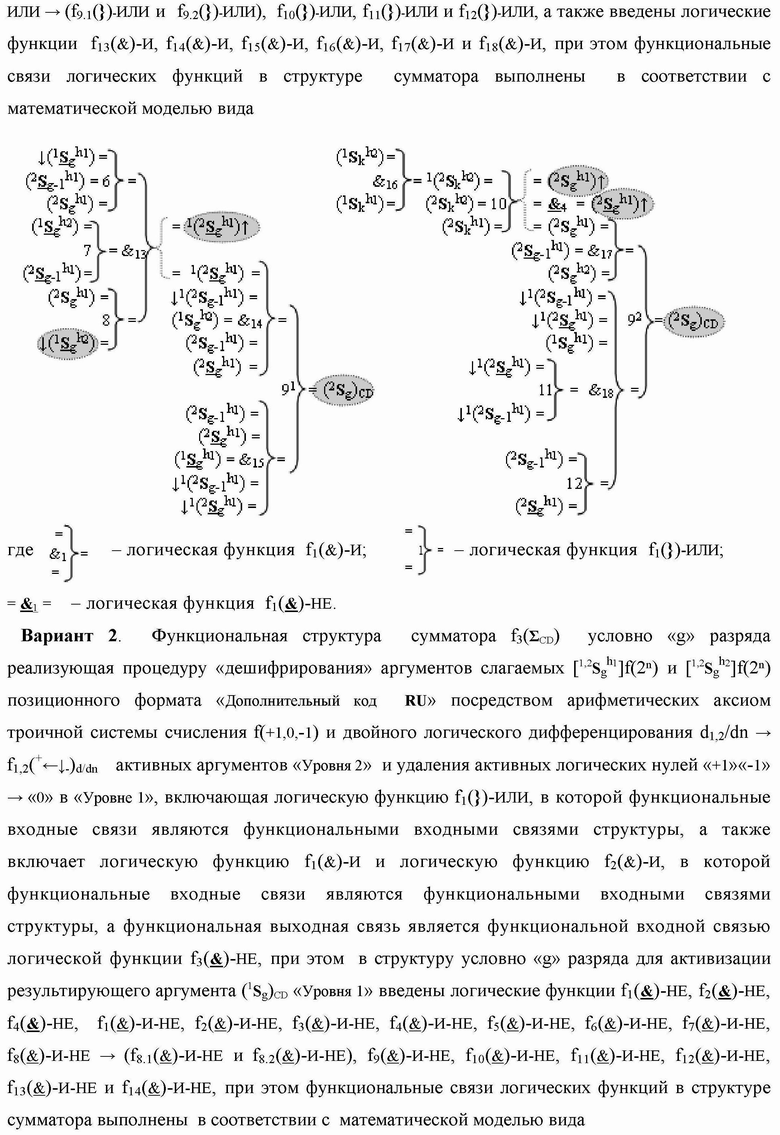
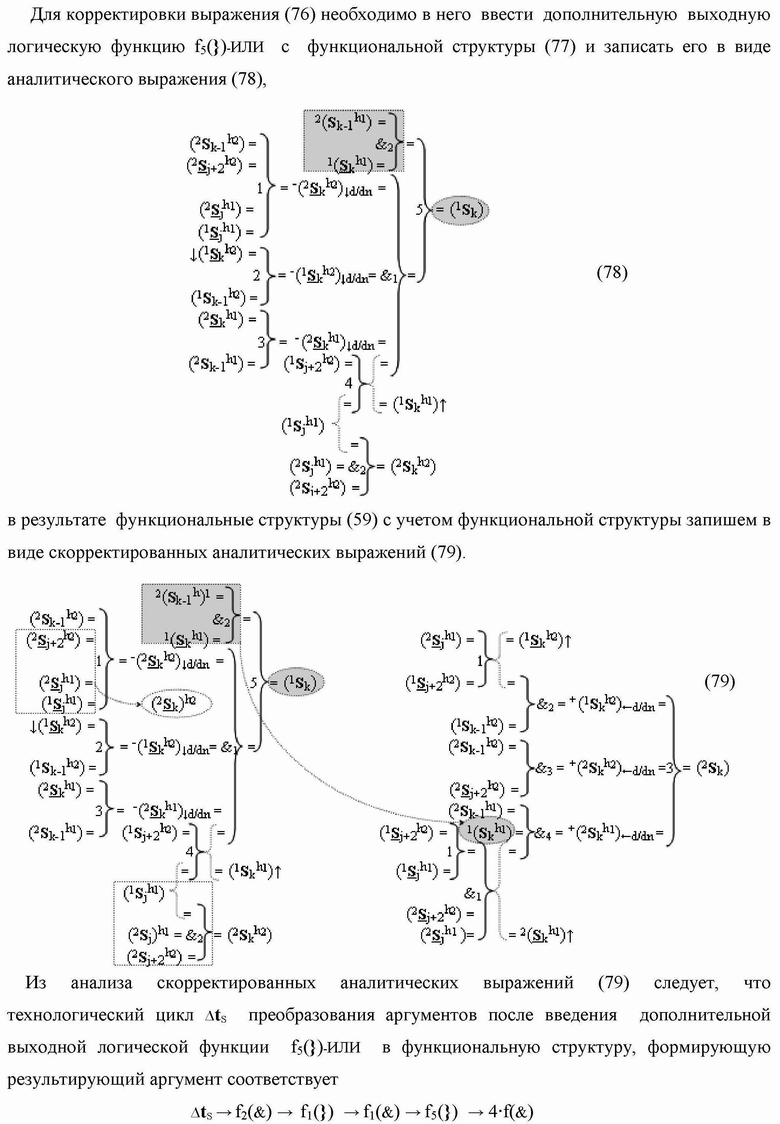
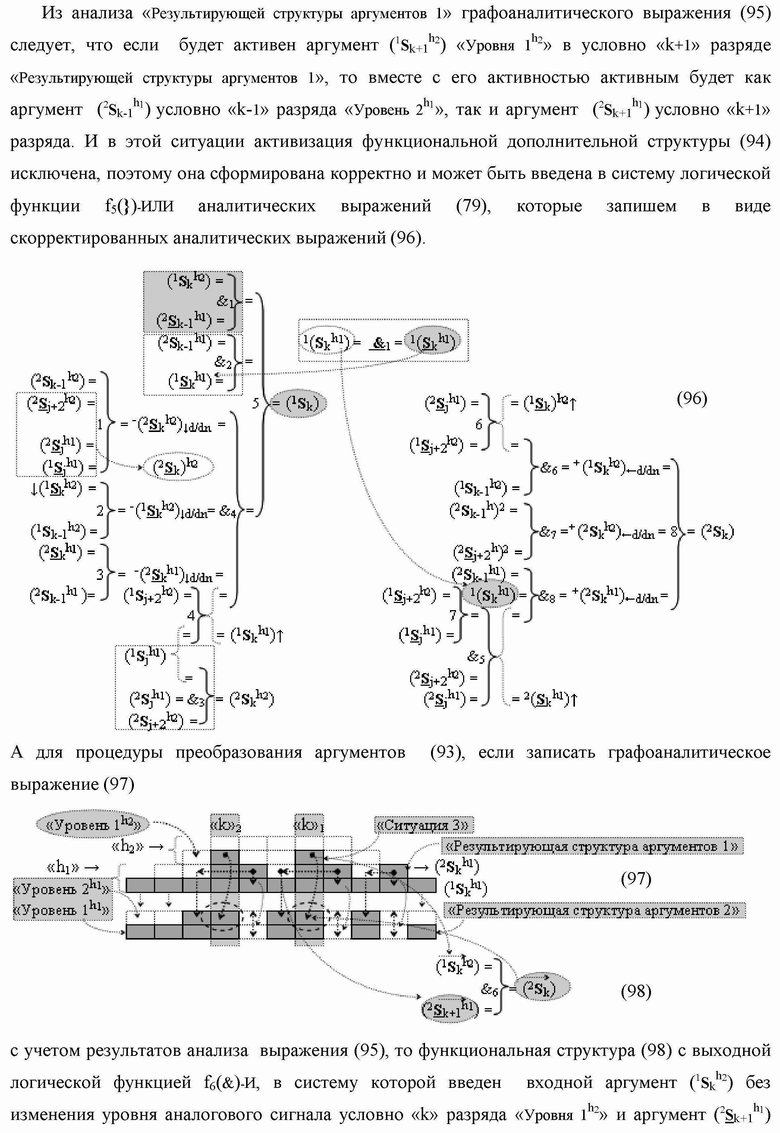
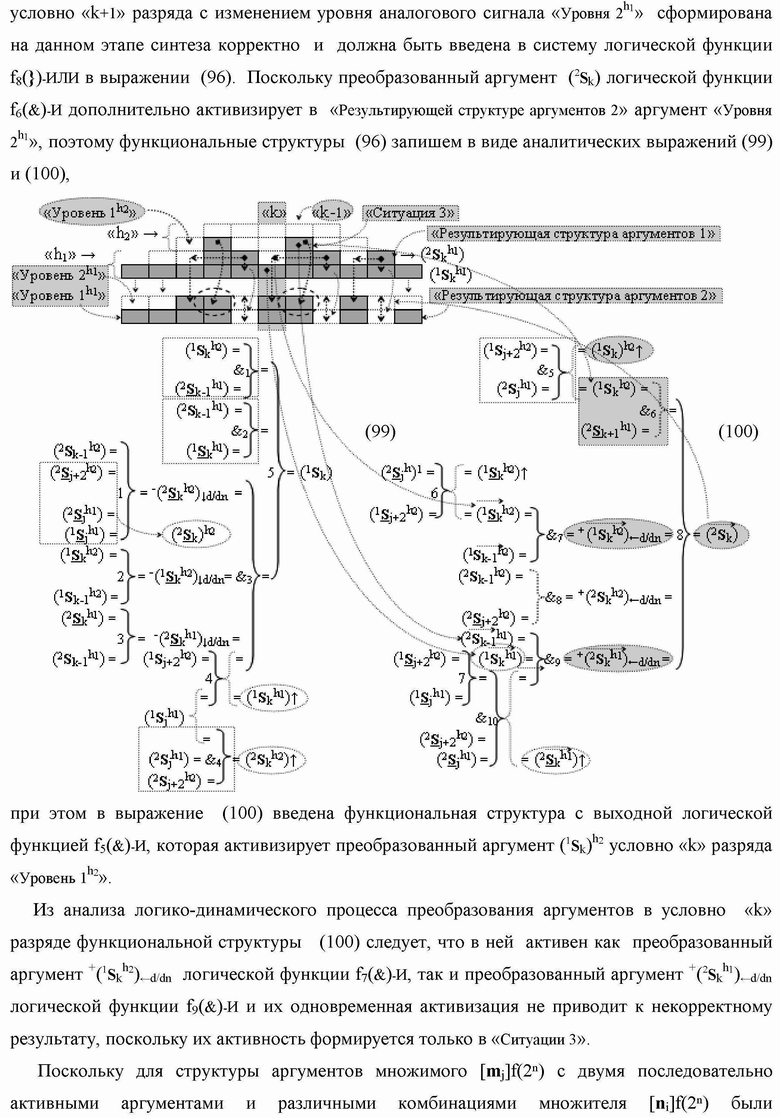
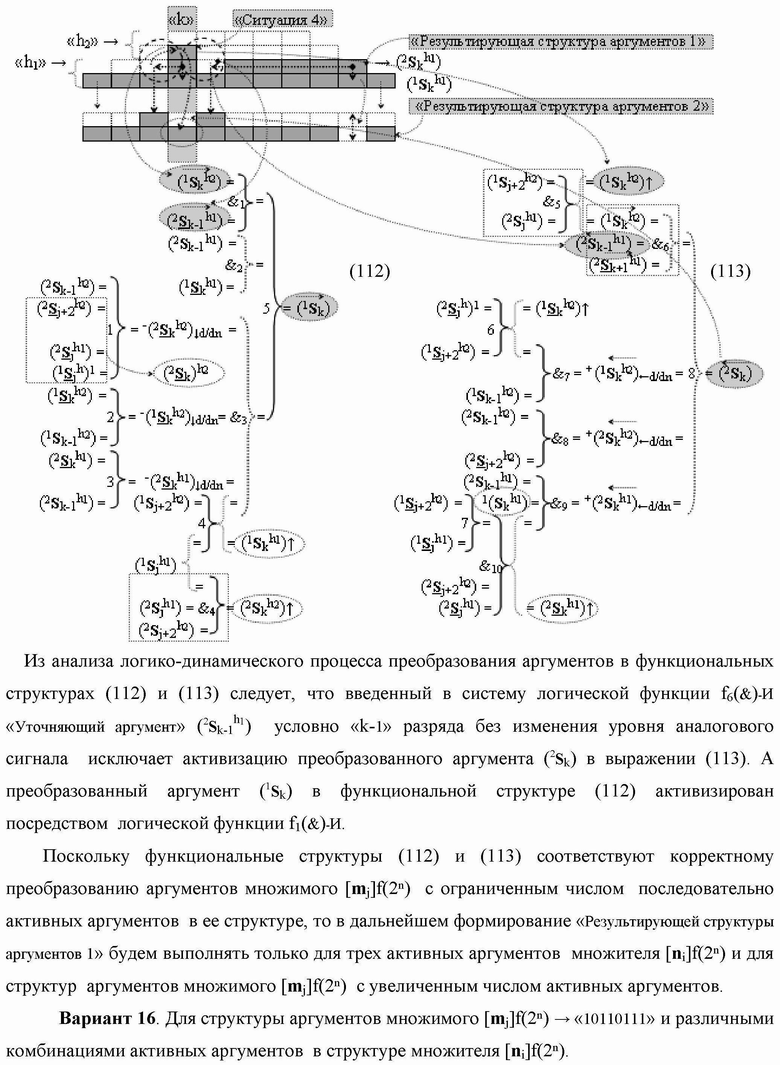
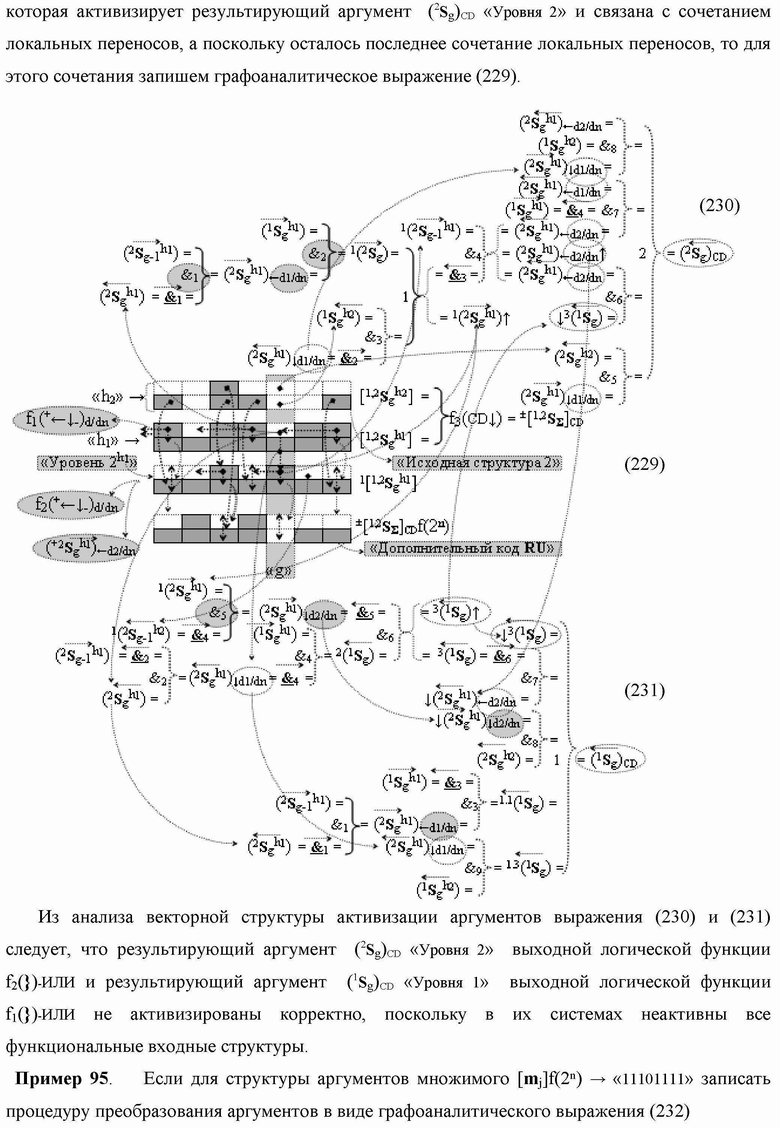
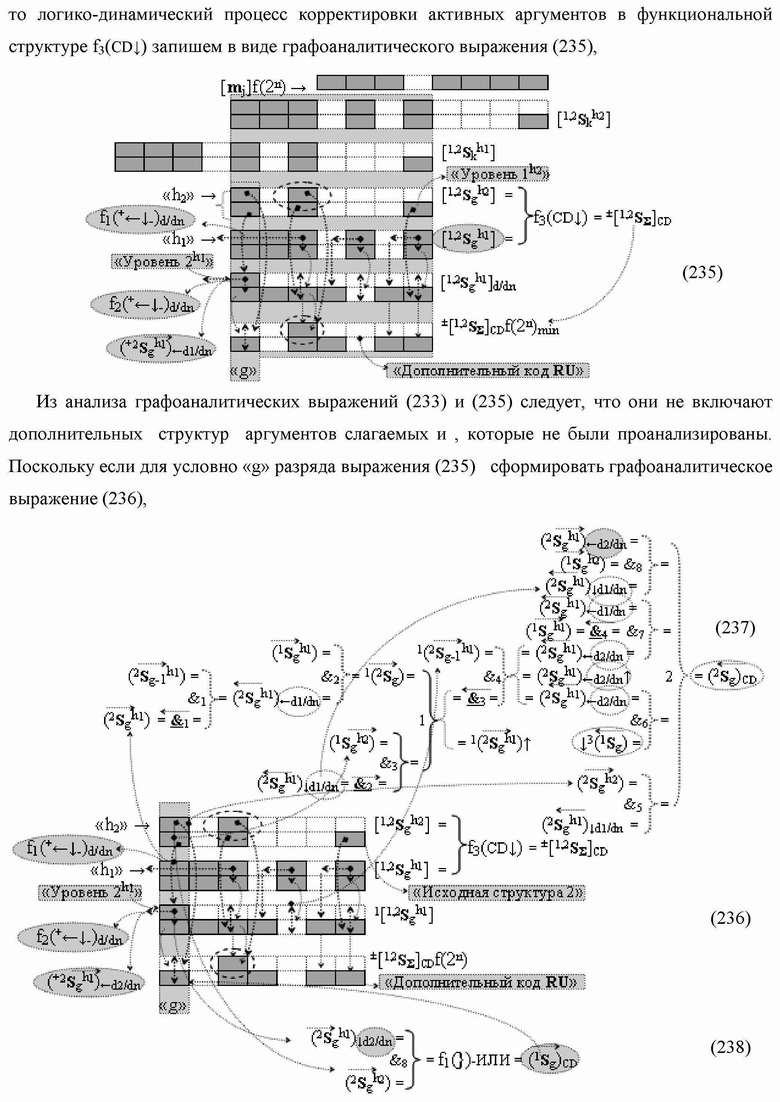
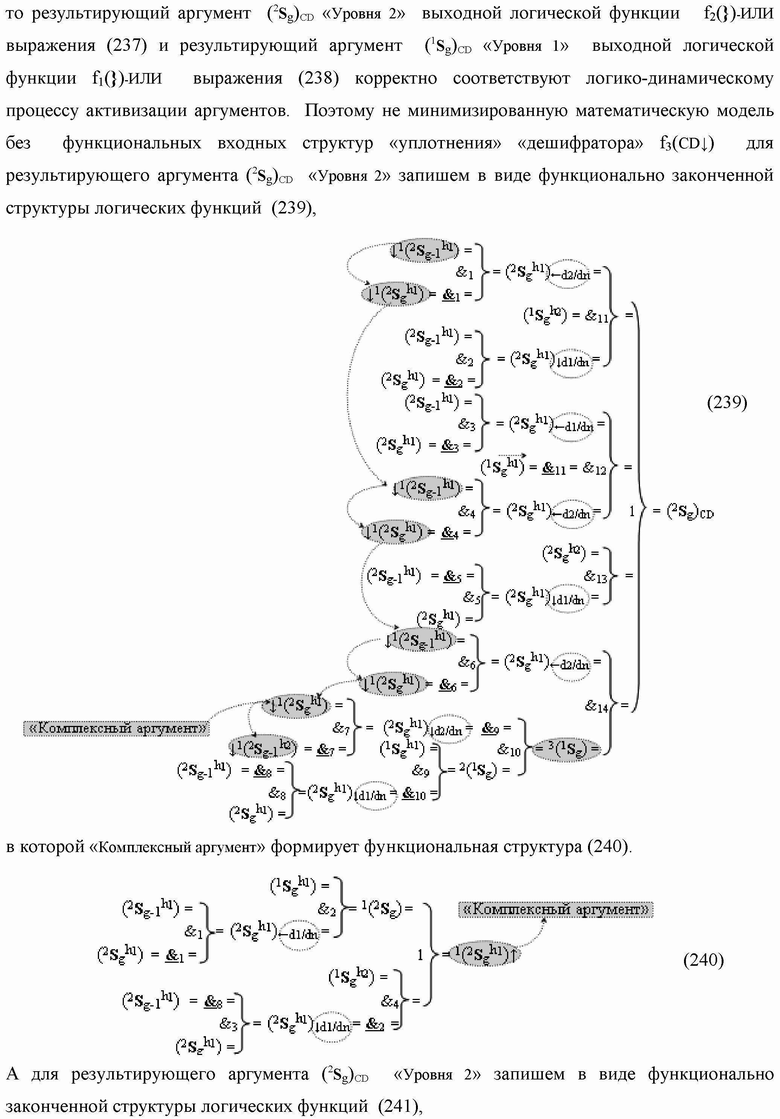
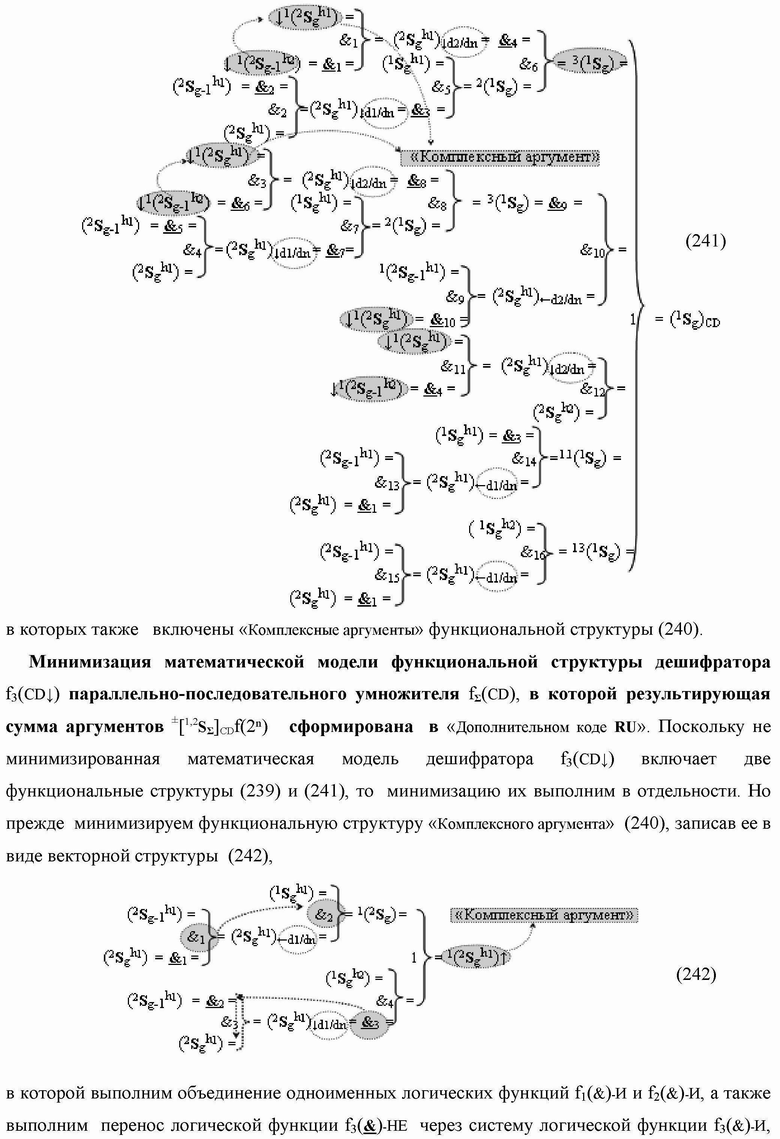
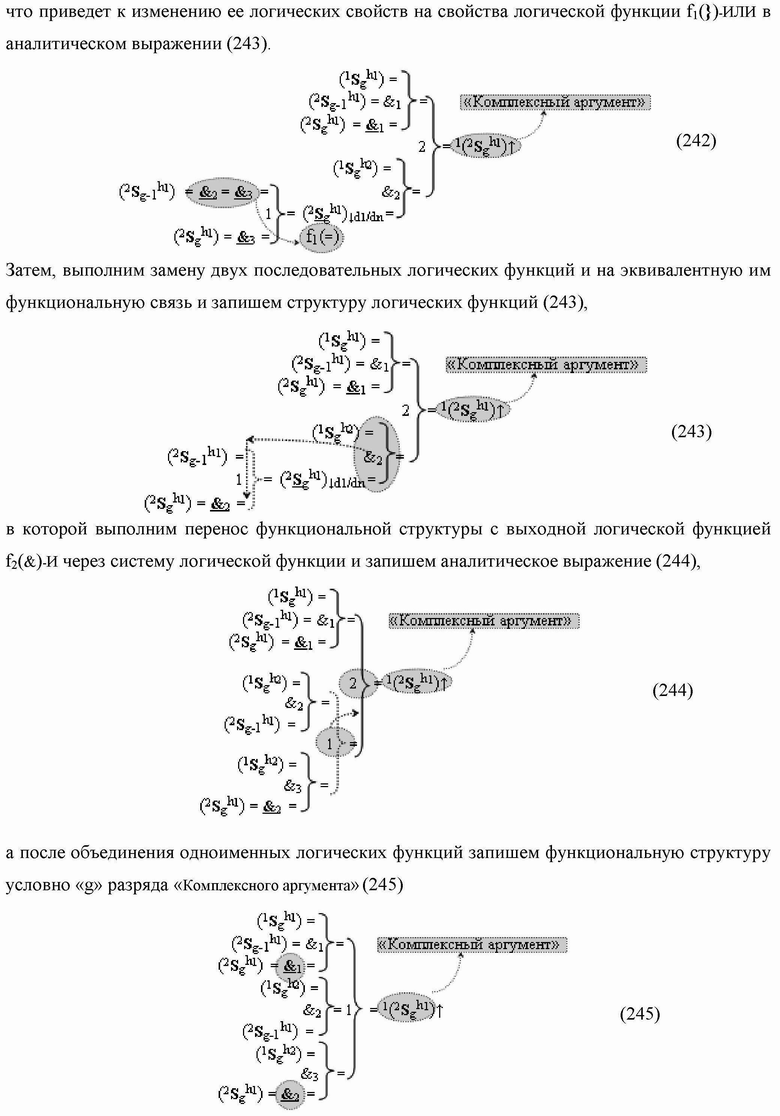
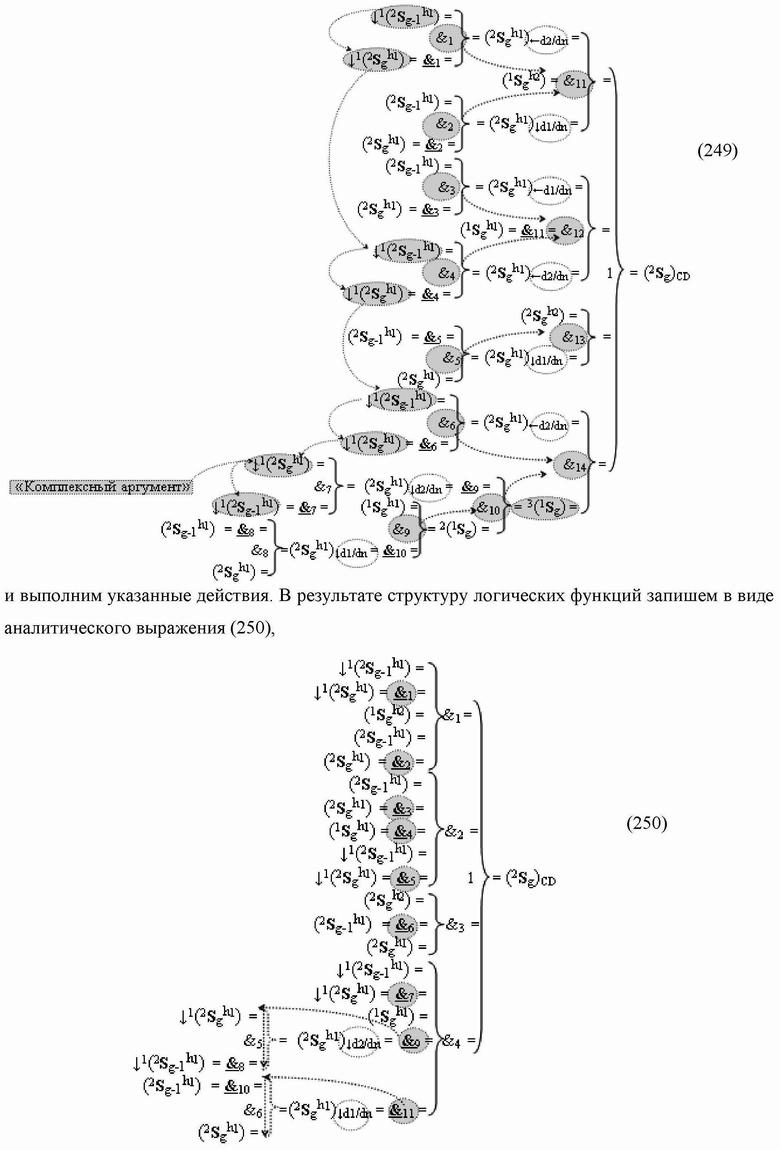
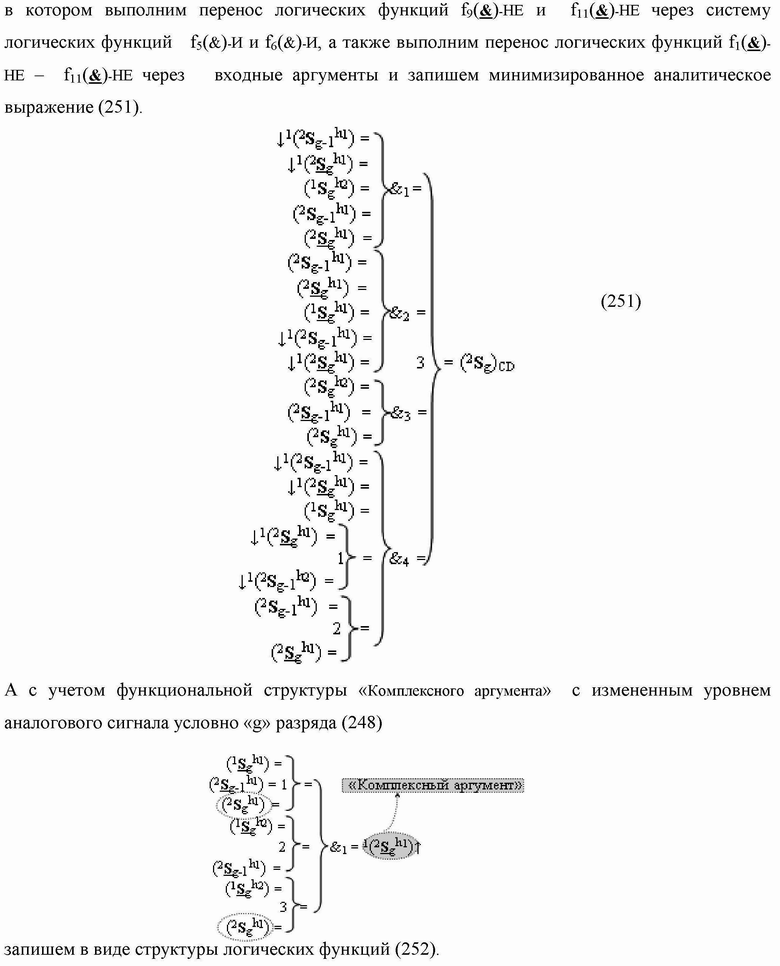
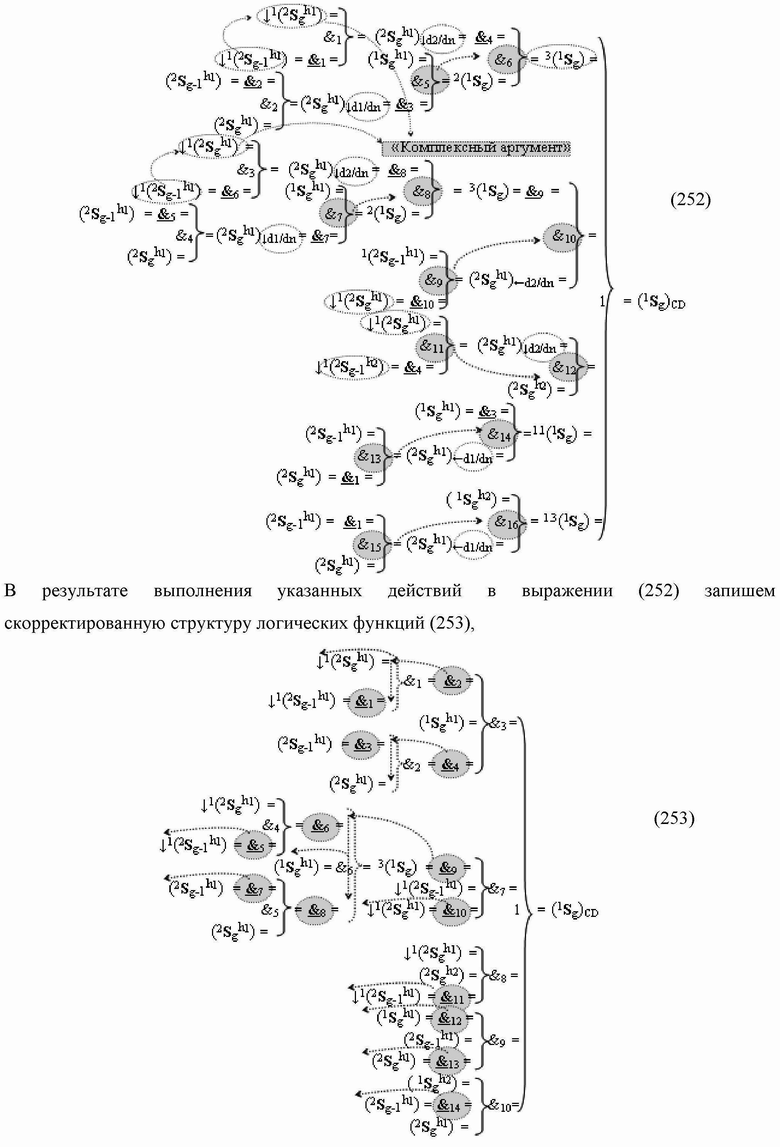
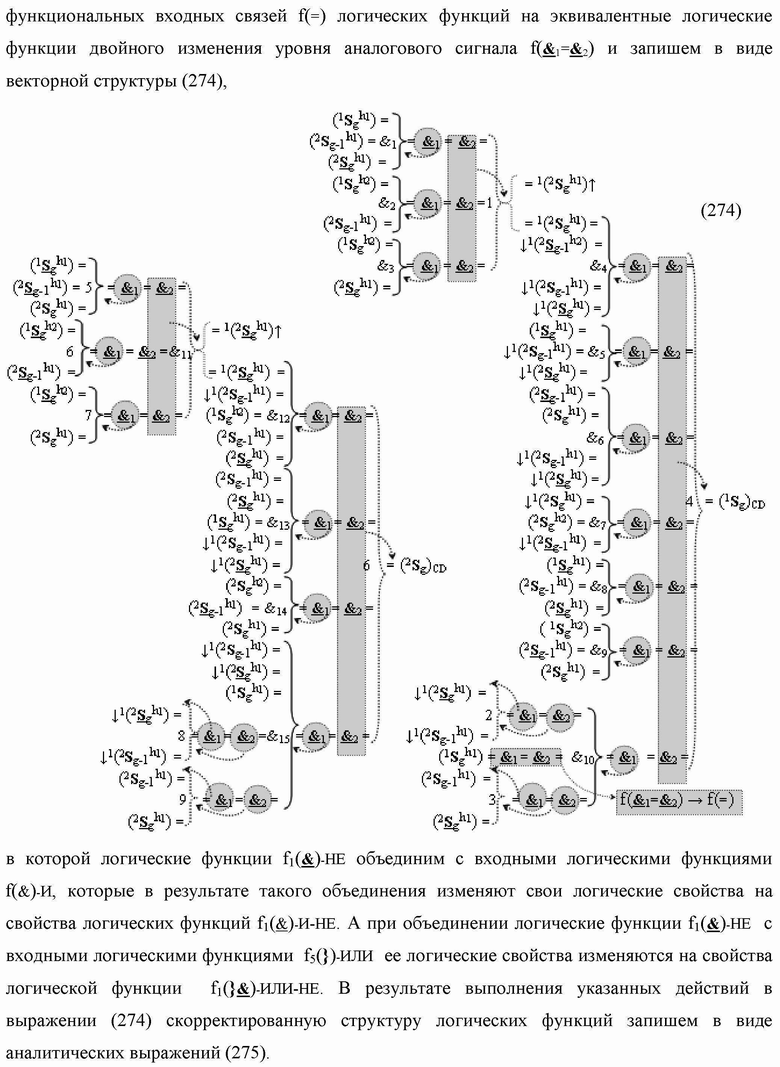
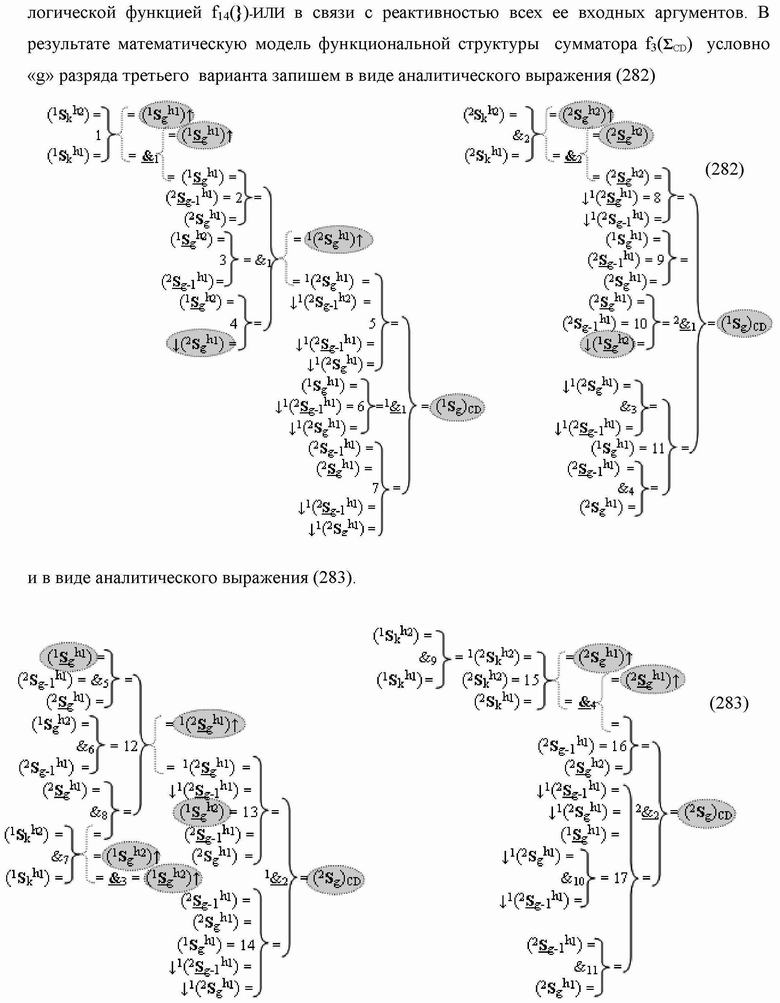
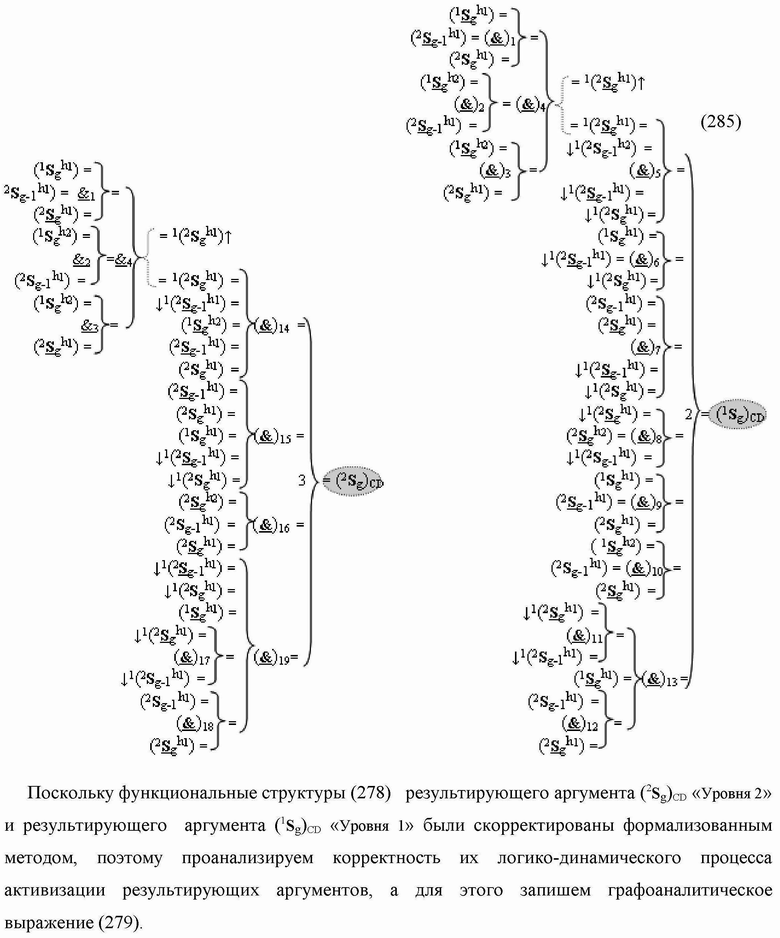
)-НЕ, f2(})-ИЛИ, f3(})-ИЛИ → (f3.1(})-ИЛИ и f3.2(})-ИЛИ), f4(})-ИЛИ и f5(})-ИЛИ, а также логические функции f2(&)-И, f3(&)-И, f4(&)-И, f5(&)-И, f6(&)-И, f8(&)-И, f9(&)-И, f10(&)-И, f11(&)-И и f12(&)-И, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида

а для активизации результирующего аргумента (2
S
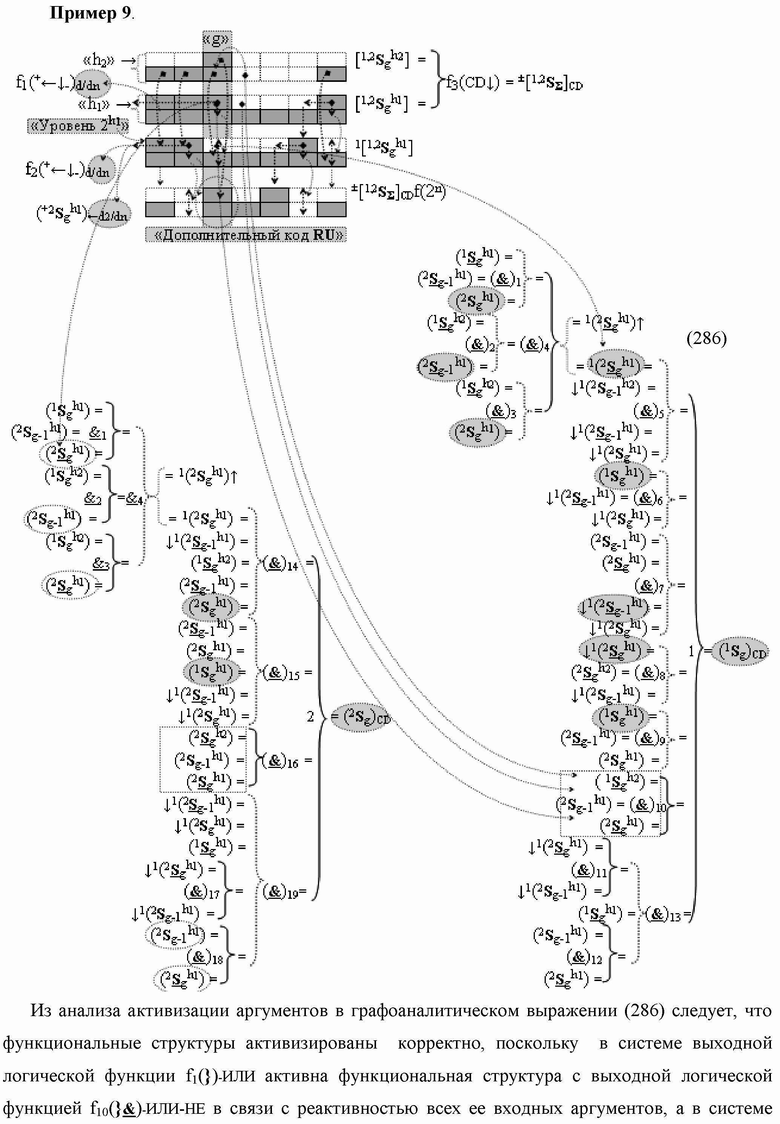
g)CD «Уровня 2» «Дополнительного кода RU» в условно «g» разряд введены логические функции f4(
&
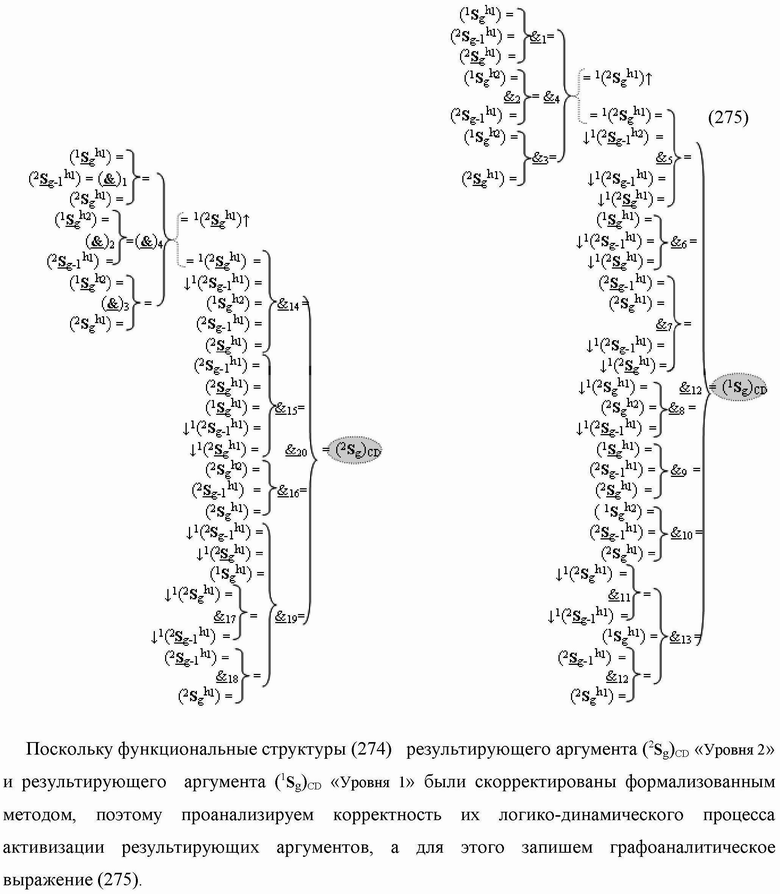
)-НЕ, f6(})-ИЛИ, f7(})-ИЛИ, f8(})-ИЛИ, f9(})-ИЛИ → (f9.1(})-ИЛИ и f9.2(})-ИЛИ), f10(})-ИЛИ, f11(})-ИЛИ и f12(})-ИЛИ, а также введены логические функции f13(&)-И, f14(&)-И, f15(&)-И, f16(&)-И, f17(&)-И и f18(&)-И, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
где 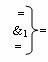 - логическая функция f1(&)-И;
- логическая функция f1(&)-И; 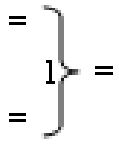 - логическая функция f1(})-ИЛИ;
- логическая функция f1(})-ИЛИ;
=
&
1 = - логическая функция f1(
&
)-НЕ.
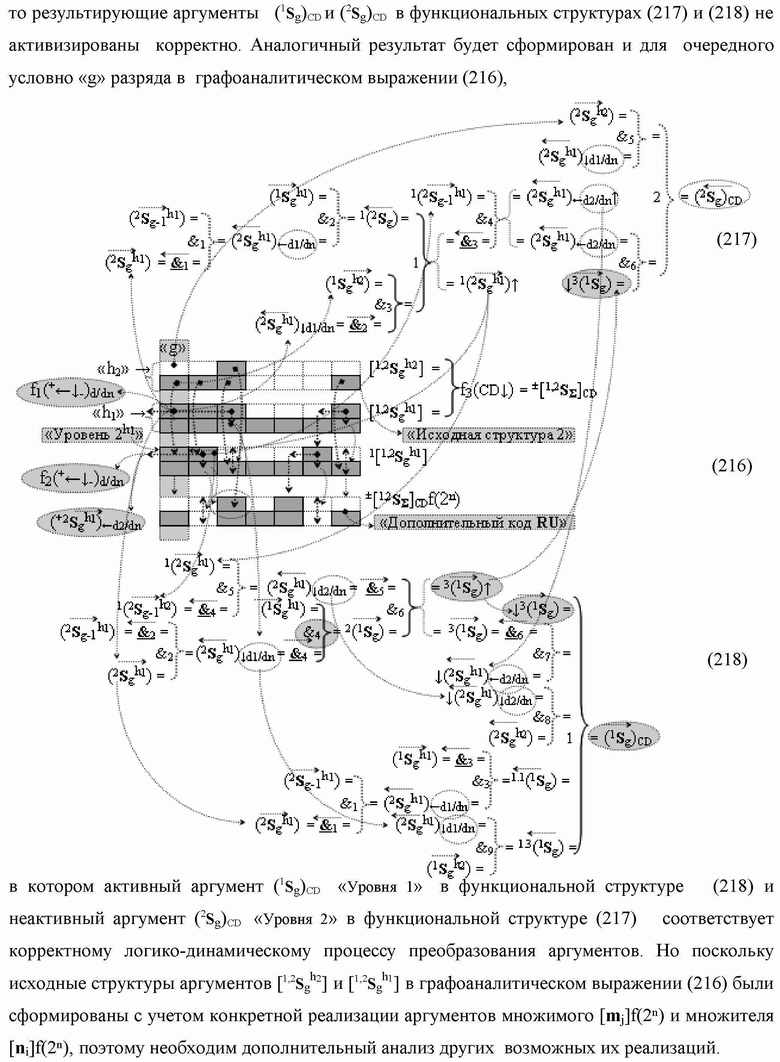
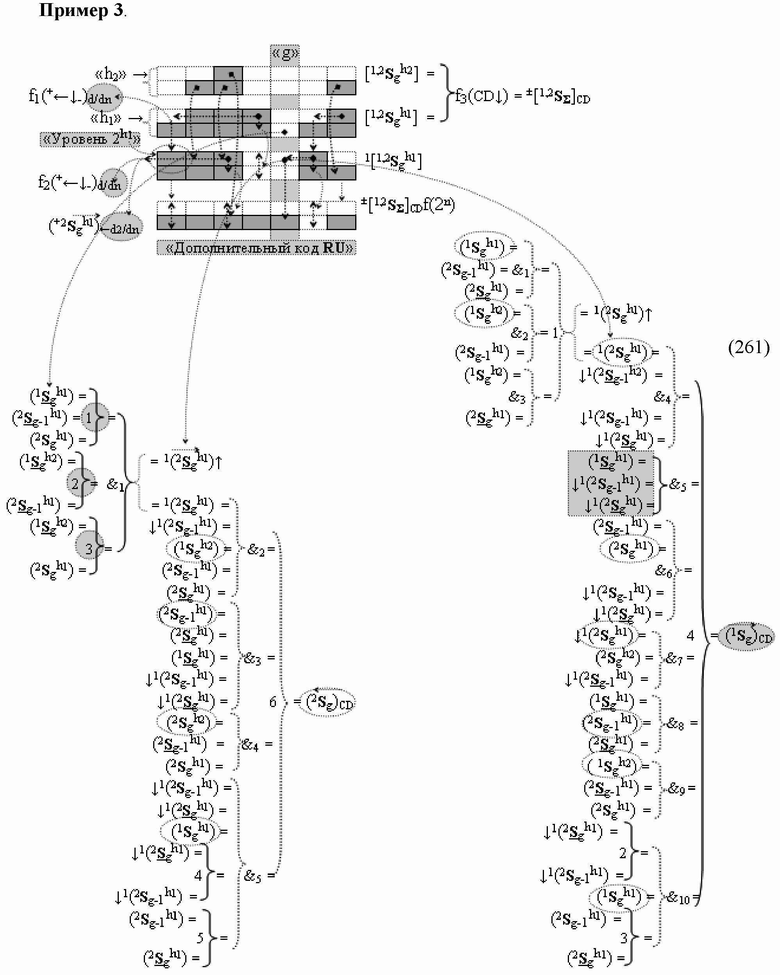
2. Функциональная структура сумматора
f3(Σ
CD) условно «g» разряда, реализующая процедуру «дешифрирования» аргументов слагаемых [1,2
S
g h1]f(2n) и [1,2
S
g h2]f(2n) позиционного формата «Дополнительный код RU»
посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и двойного логического дифференцирования
d1,2/dn → f1,2(+←↓-)d/dn активных аргументов
«Уровня 2» и удаления активных логических нулей «+1»«-1» → «0» в «Уровне 1», включающая логическую функцию f1(})-ИЛИ, в которой функциональные входные связи являются функциональными входными связями структуры, а также включает логическую функцию f1(&)-И и логическую функцию f2(&)-И, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f3(
&
)-НЕ, отличающаяся тем, что в структуру условно «g» разряда для активизации результирующего аргумента (1
S
g)CD «Уровня 1» введены логические функции f1(
&
)-НЕ, f2(
&
)-НЕ, f4(
&
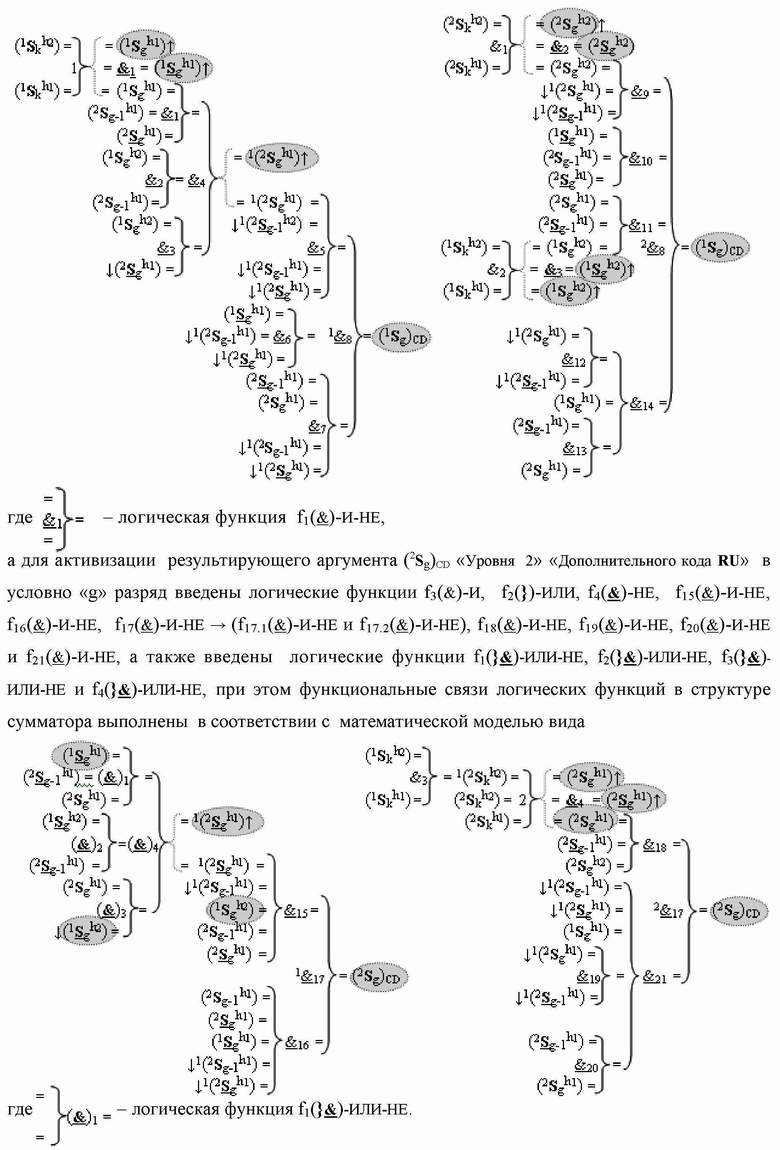
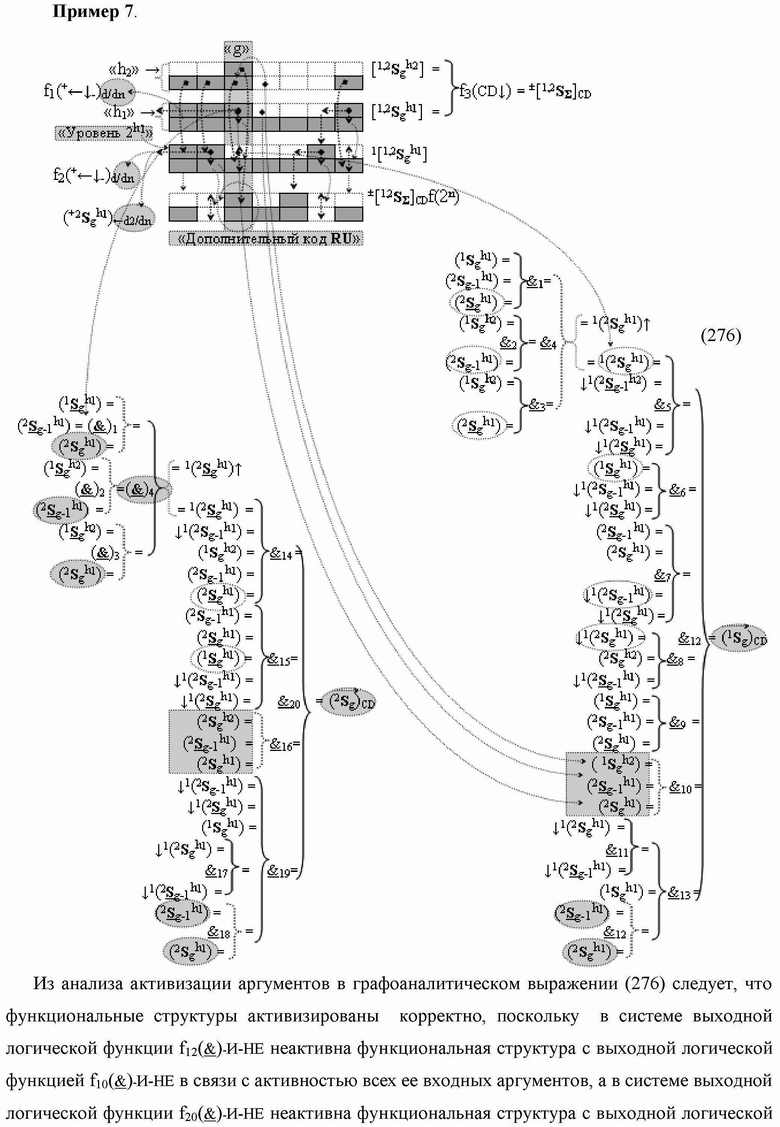
)-НЕ, f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ, f6(&)-И-НЕ, f7(&)-И-НЕ, f8(&)-И-НЕ → (f8.1(&)-И-НЕ и f8.2(&)-И-НЕ), f9(&)-И-НЕ, f10(&)-И-НЕ, f11(&)-И-НЕ, f12(&)-И-НЕ, f13(&)-И-НЕ и f14(&)-И-НЕ, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
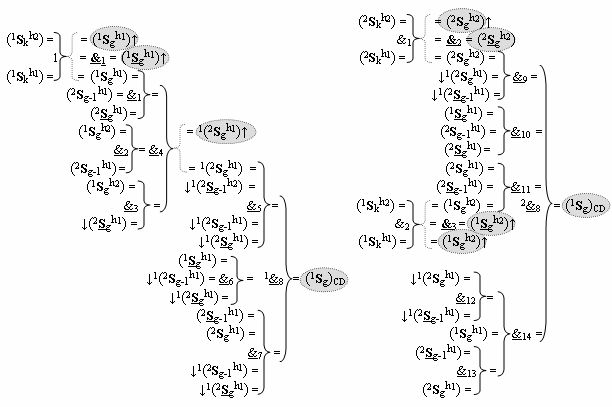
где 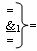 - логическая функция f1(&)-И-НЕ,
- логическая функция f1(&)-И-НЕ,
а для активизации результирующего аргумента (2
S
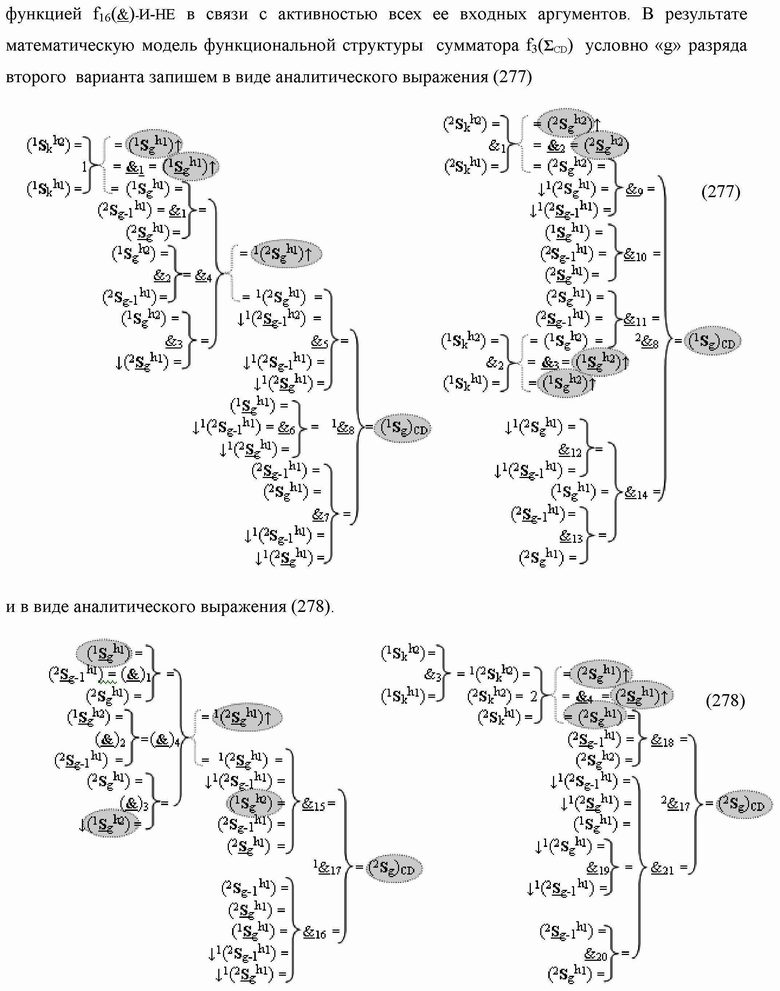
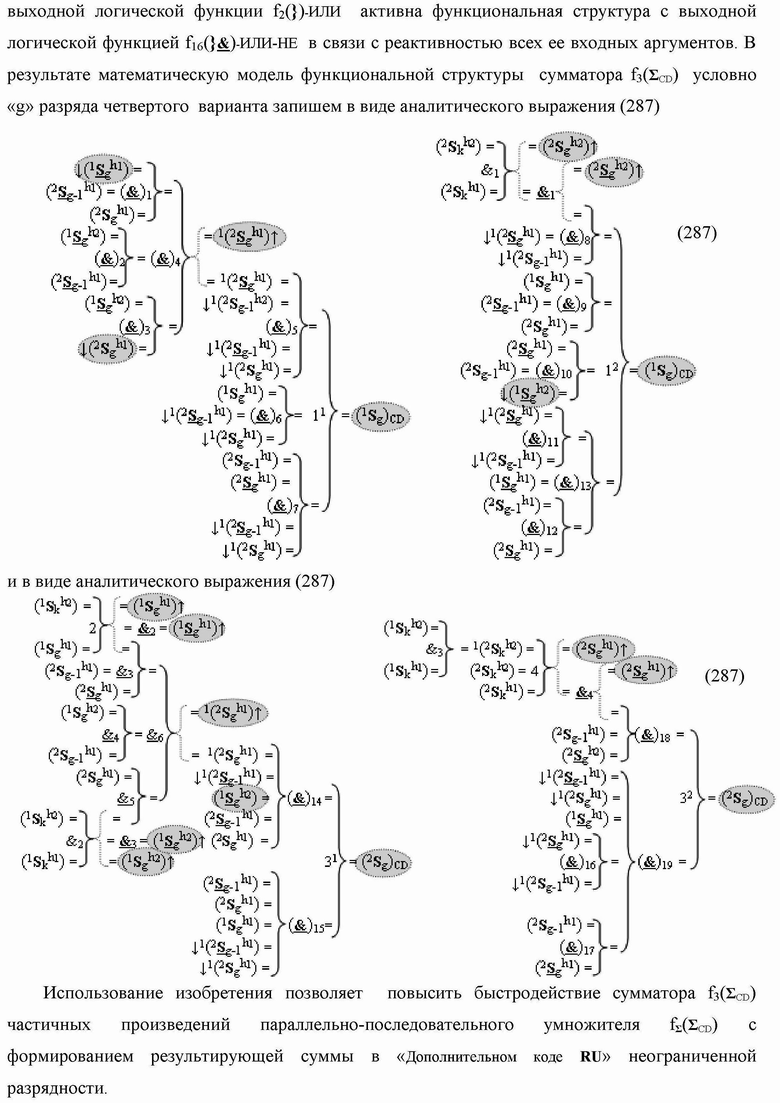
g)CD «Уровня 2» «Дополнительного кода RU» в условно «g» разряд введены логические функции f3(&)-И, f2(})-ИЛИ, f4(
&
)-НЕ, f15(&)-И-НЕ, f16(&)-И-НЕ, f17(&)-И-НЕ → (f17.1(&)-И-НЕ и f17.2(&)-И-НЕ), f18(&)-И-НЕ, f19(&)-И-НЕ, f20(&)-И-НЕ и f21(&)-И-НЕ, а также введены логические функции f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ и f4(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
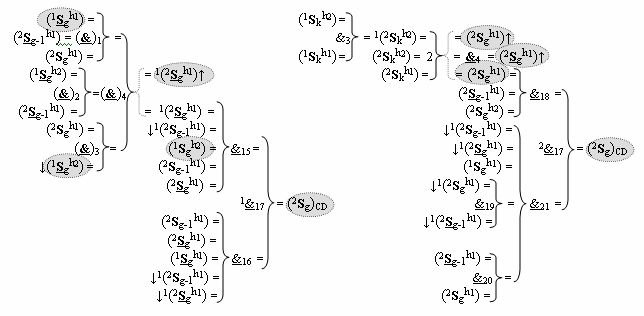
где 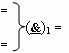 - логическая функция f1(}&
)-ИЛИ-НЕ.
- логическая функция f1(}&
)-ИЛИ-НЕ.
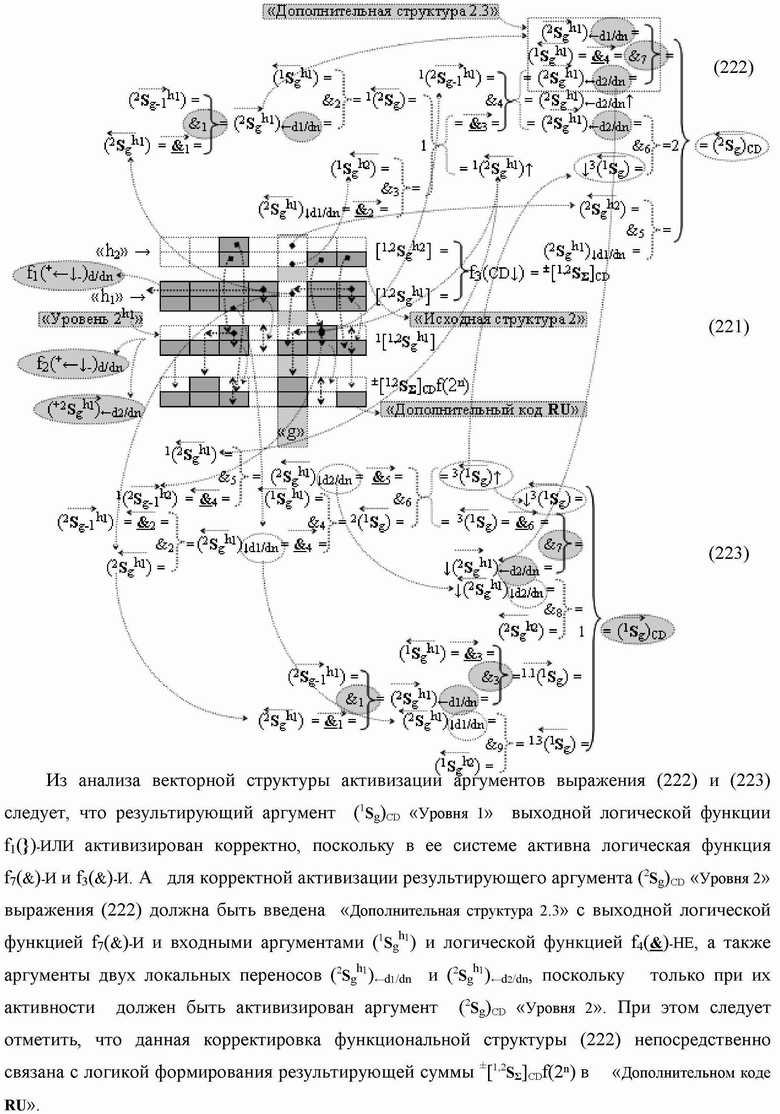
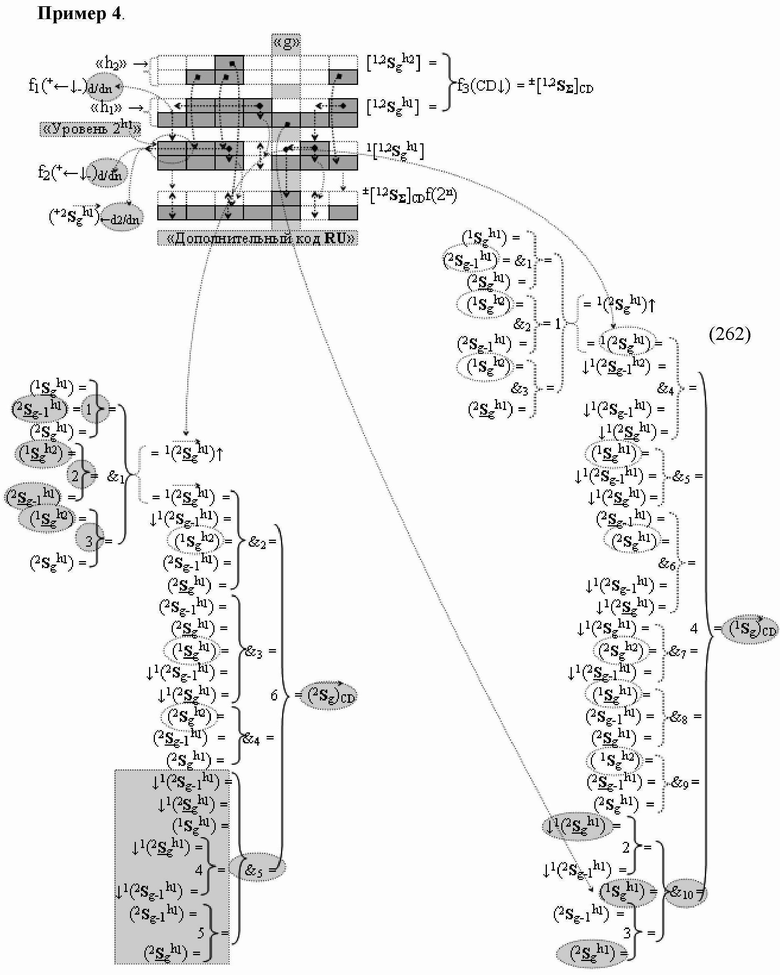
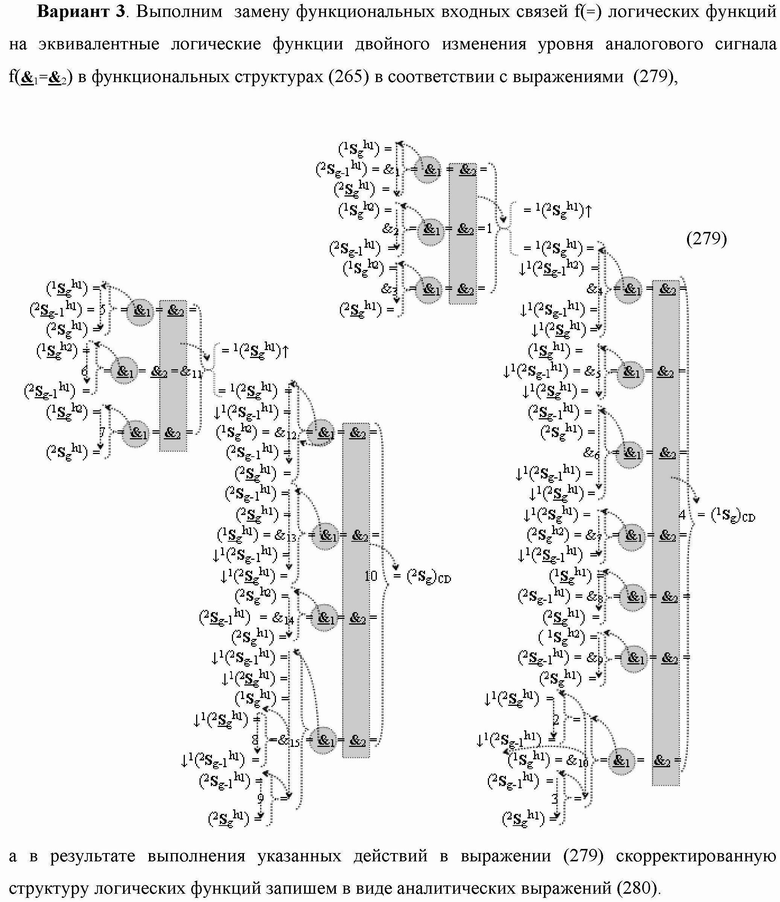
3. Функциональная структура сумматора
f3(Σ
CD) условно
«g» разряда, реализующая процедуру «дешифрирования» аргументов слагаемых [1,2
S
g h1]f(2n) и [1,2
S
g h2]f(2n) позиционного формата «Дополнительный код RU»
посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и двойного логического дифференцирования
d1,2/dn → f1,2(+←↓-)d/dn активных аргументов
«Уровня 2» и удаления активных логических нулей
«+1»«-1» → «0» в «Уровне 1», включающая логическую функцию f1(})-ИЛИ, в которой функциональные входные связи являются функциональными входными связями структуры, а также включает логическую функцию f1(&)-И и логическую функцию f2(&)-И, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f2(
&
)-НЕ, отличающаяся тем, что в структуру условно «g» разряда для активизации результирующего аргумента (1
S
g)CD «Уровня 1» введены логические функции f1(
&
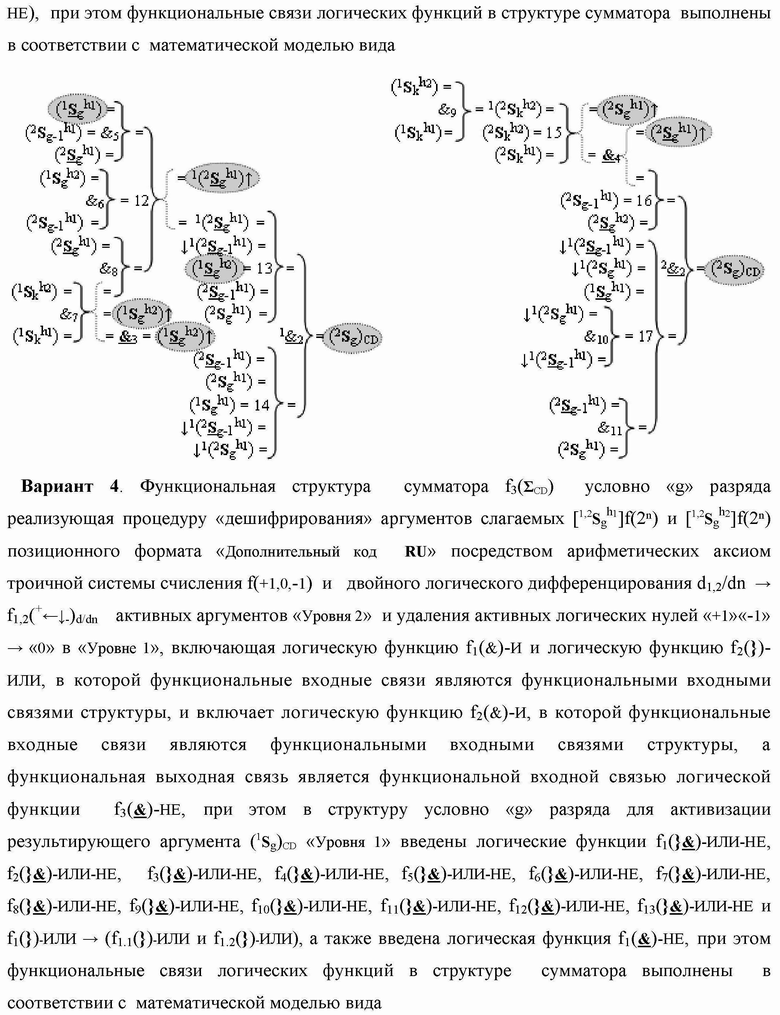
)-НЕ, f1(&)-И-НЕ → (f1.1(&)-И-НЕ и f1.2(&)-И-НЕ), f3(&)-И, f4(&)-И, f2(})-ИЛИ, f3(})-ИЛИ, f4(})-ИЛИ, f5(})-ИЛИ, f6(})-ИЛИ, f7(})-ИЛИ, f8(})-ИЛИ, f9(})-ИЛИ, f10(})-ИЛИ и f11(})-ИЛИ, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
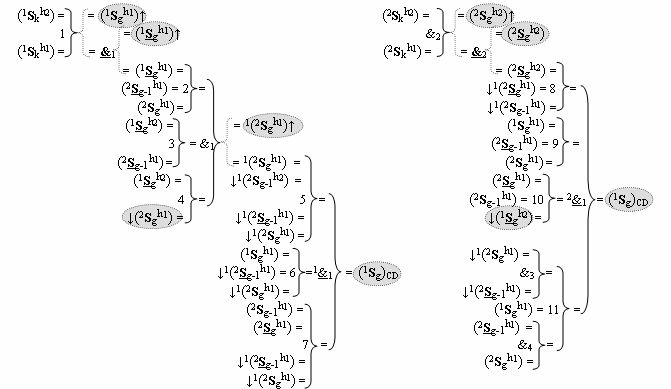
а для активизации результирующего аргумента (2
S
g)CD «Уровня 2» «Дополнительного кода RU» в условно «g» разряд введены логические функции f3(
&
)-НЕ, f4(
&
)-НЕ, f12(})-ИЛИ, f13(})-ИЛИ, f14(})-ИЛИ, f15(})-ИЛИ, f16(})-ИЛИ и f17(})-ИЛИ, а также введены логические функции f5(&)-И, f6(&)-И, f7(&)-И, f8(&)-И, f9(&)-И, f10(&)-И, f11(&)-И и f2(&)-И-НЕ → (f2.1(&)-И-НЕ и f2.2(&)-И-НЕ), при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
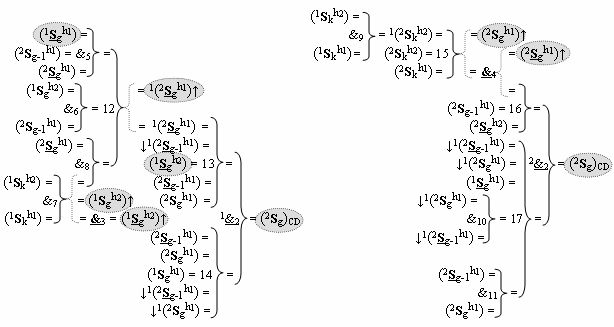
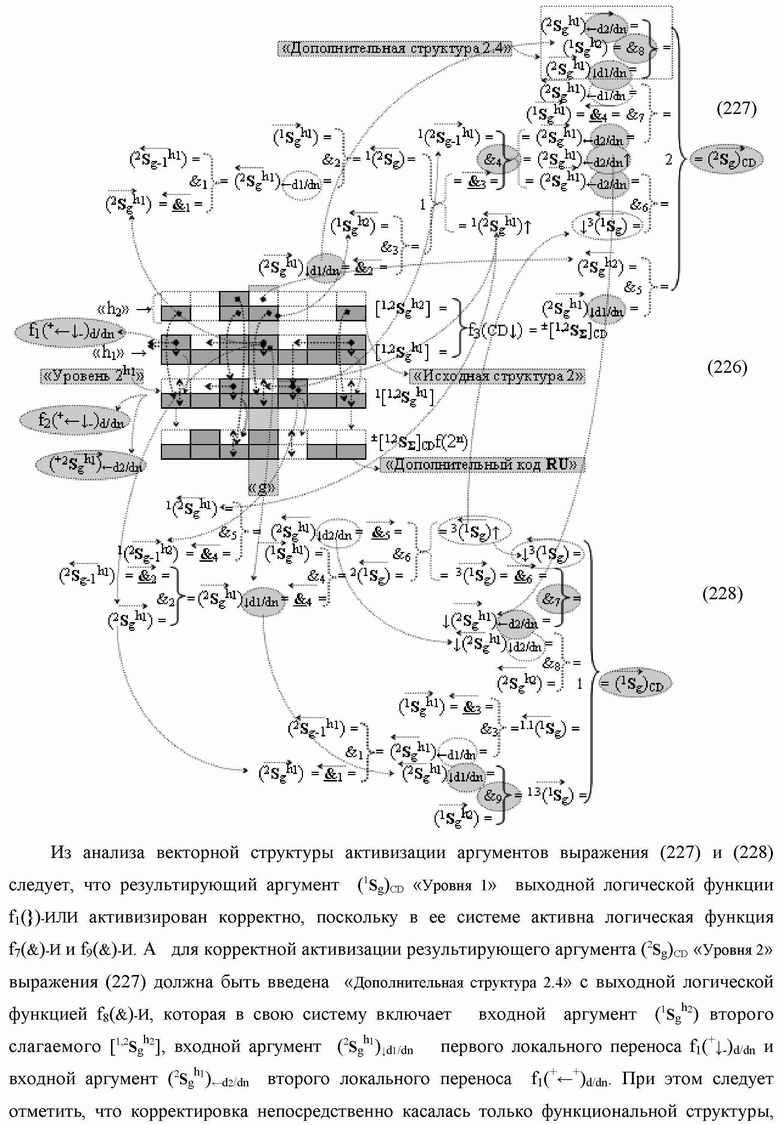
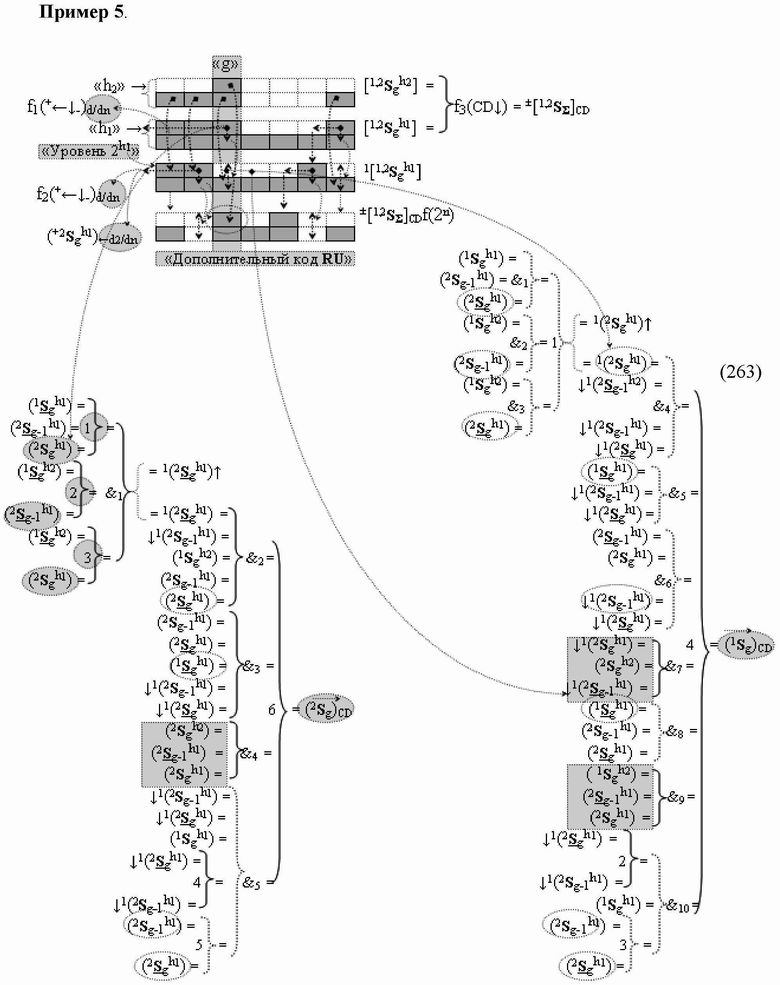
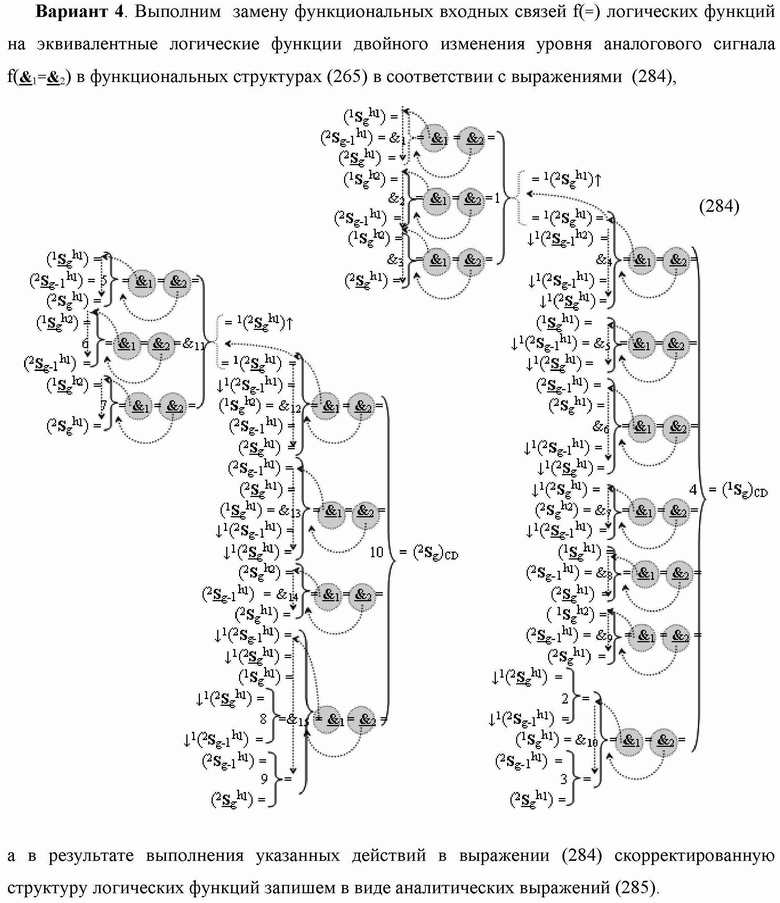
4. Функциональная структура сумматора
f3(Σ
CD) условно
«g» разряда, реализующая процедуру «дешифрирования» аргументов слагаемых [1,2
S
g h1]f(2n) и [1,2
S
g h2]f(2n) позиционного формата «Дополнительный код RU»
посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и двойного логического дифференцирования
d1,2/dn → f1,2(+←↓-)d/dn активных аргументов
«Уровня 2» и удаления активных логических нулей
«+1»«-1» → «0» в «Уровне 1», включающая логическую функцию f1(&)-И и логическую функцию f2(})-ИЛИ, в которой функциональные входные связи являются функциональными входными связями структуры, и включает логическую функцию f2(&)-И, в которой функциональные входные связи являются функциональными входными связями структуры, а функциональная выходная связь является функциональной входной связью логической функции f3(
&
)-НЕ, отличающаяся тем, что в структуру условно «g» разряда для активизации результирующего аргумента (1
S
g)CD «Уровня 1» введены логические функции f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ, f5(}&
)-ИЛИ-НЕ, f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ, f8(}&
)-ИЛИ-НЕ, f9(}&
)-ИЛИ-НЕ, f10(}&
)-ИЛИ-НЕ, f11(}&
)-ИЛИ-НЕ, f12(}&
)-ИЛИ-НЕ, f13(}&
)-ИЛИ-НЕ и f1(})-ИЛИ → (f1.1(})-ИЛИ и f1.2(})-ИЛИ), а также введена логическая функция f1(
&
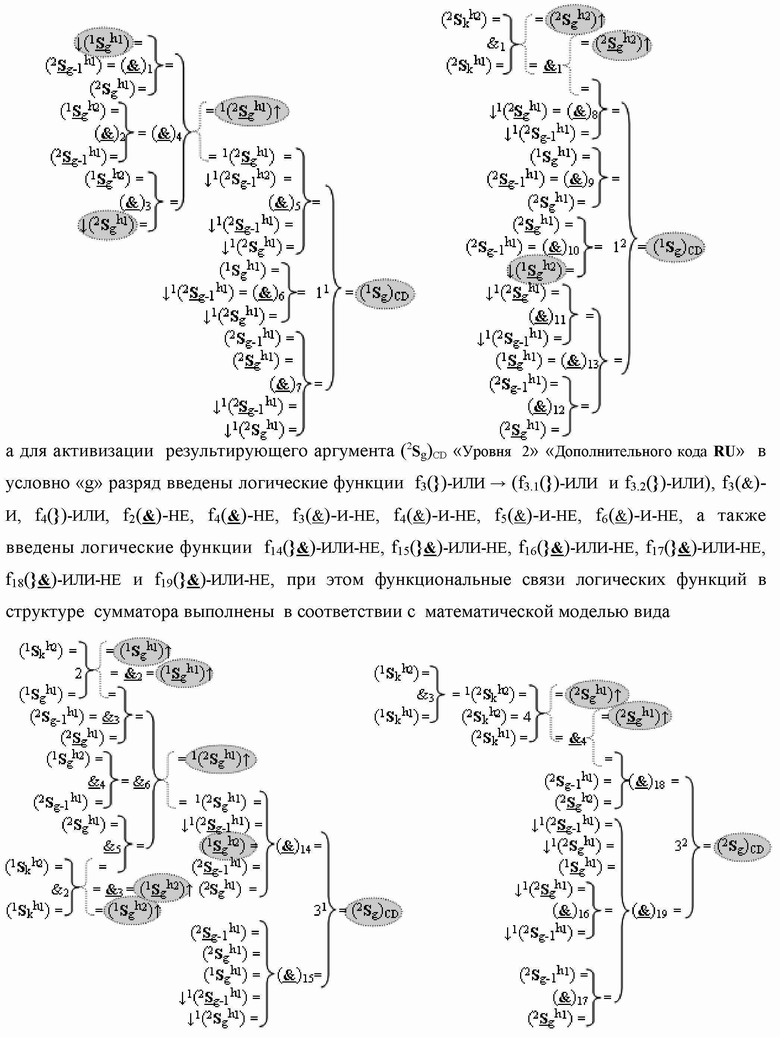
)-НЕ, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
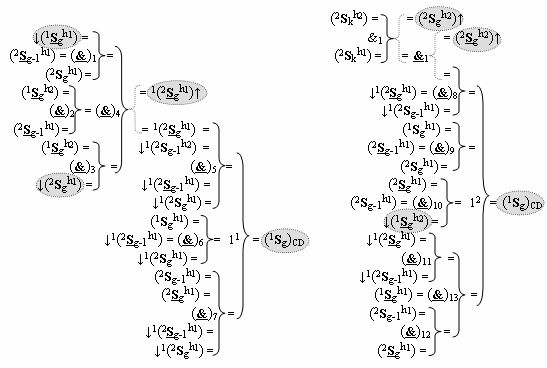
а для активизации результирующего аргумента (2
S
g)CD «Уровня 2» «Дополнительного кода RU» в условно «g» разряд введены логические функции f3(})-ИЛИ → (f3.1(})-ИЛИ и f3.2(})-ИЛИ), f3(&)-И, f4(})-ИЛИ, f2(
&
)-НЕ, f4(
&
)-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ, f6(&)-И-НЕ, а также введены логические функции f14(}&
)-ИЛИ-НЕ, f15(}&
)-ИЛИ-НЕ, f16(}&
)-ИЛИ-НЕ, f17(}&
)-ИЛИ-НЕ, f18(}&
)-ИЛИ-НЕ и f19(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре сумматора выполнены в соответствии с математической моделью вида
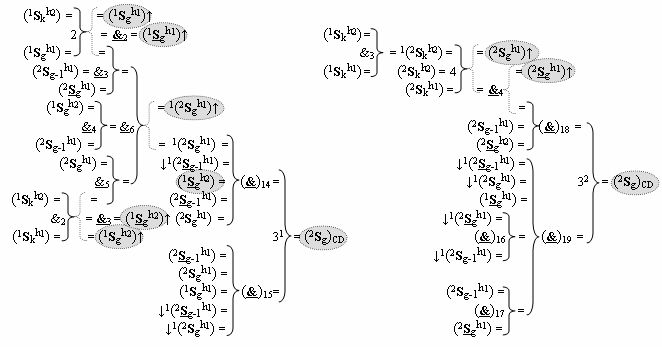
| ДЖ | |||
| УЭЙКЕРЛИ, ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ УСТРОЙСТВ, Москва, ПОСТМАРКЕТ, 2002, с | |||
| Способ выделения сульфокислот из нефтяных масел | 1913 |
|
SU508A1 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА ДЛЯ УМНОЖИТЕЛЯ, В КОТОРОМ АРГУМЕНТЫ СЛАГАЕМЫХ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ ЯВЛЯЮТСЯ АРГУМЕНТАМИ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1, 0, -1) В ПОЗИЦИОННО-ЗНАКОВОМ ЕЕ ФОРМАТЕ f(+/-) (ВАРИАНТЫ) | 2008 |
|
RU2386162C2 |
| JP 2005326914 A, 24.11.2005 | |||
| JP 2002014804 A, 18.01.2002 | |||
| US 7274211 B1, 25.09.2007 | |||
Авторы
Даты
2014-05-27—Публикация
2011-12-20—Подача